Матричные игры: примеры решения задач
- Платёжная матрица, чистые стратегии, цена игры
- Седловая точка в матричных играх
- Матричные игры с оптимальной смешанной стратегией
- Сведение матричной игры к задаче линейного программирования
- Игры с матрицей 2 Х 2
- Составление матричной игры
Матричной игрой в математической теории игр называется игра двух лиц с нулевой суммой, в которой в распоряжении каждого из них имеется конечное множество стратегий. Правила матричной игры определяет платёжная матрица, элементы которой — выигрыши первого игрока, которые являются также проигрышами второго игрока.
Матричная игра является антагонистической игрой.
Первый игрок получает максимальный гарантированный (не зависящий от поведения второго игрока) выигрыш,
равный цене игры, аналогично, второй игрок добивается минимального гарантированного проигрыша.
Под стратегией понимается совокупность правил (принципов), определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от сложившейся ситуации.
Теперь обо всём по порядку и подробно.
В матричной игре её правила определяет платёжная матрица.
Рассмотрим игру, в которой имеются два участника: первый игрок и второй игрок. Пусть в распоряжении первого игрока имеется m чистых стратегий, а в распоряжении второго игрока — n чистых стратегий. Поскольку рассматривается игра, естественно, что в этой игре есть выигрыши и есть проигрыши.
В платёжной матрице элементами являются числа, выражающие выигрыши и проигрыши игроков. Выигрыши и проигрыши могут выражаться в пунктах, количестве денег или в других единицах.
Составим платёжную матрицу:.
Если первый игрок выбирает i-ю чистую стратегию, а второй игрок — j-ю чистую стратегию, то выигрыш первого игрока составит aij единиц, а проигрыш второго игрока — также aij единиц.
Так как aij + (- aij) = 0, то описанная игра является матричной игрой с нулевой суммой.
Простейшим примером матричной игры может служить бросание монеты. Правила игры следующие. Первый и второй игроки бросают монету и в результате выпадает «орёл» или «решка». Если одновременно выпали «орёл» и «орёл» или «решка» или «решка», то первый игрок выиграет одну единицу, а в других случаях он же проиграет одну единицу (второй игрок выиграет одну единицу). Такие же две стратегии и в распоряжении второго игрока. Соответствующая платёжная матрица будет следующей:
.
Задача теории игр — определить выбор стратегии первого игрока, которая гарантировала
бы ему максимальный средний выигрыш, а также выбор стратегии второго игрока, которая гарантировала бы ему
максимальный средний проигрыш.
Как происходит выбор стратегии в матричной игре?
Вновь посмотрим на платёжную матрицу:
.
Сначала определим величину выигрыша первого игрока, если он использует i-ю чистую стратегию. Если первый игрок использует i-ю чистую стратегию, то логично предположить, что второй игрок будет использовать такую чистую стратегию, благодаря которой выигрыш первого игрока был бы минимальным. В свою очередь первый игрок будет использовать такую чистую стратегию, которая бы обеспечила ему максимальный выигрыш. Исходя из этих условий выигрыш первого игрока, который обозначим как v1, называется максиминным выигрышем или нижней ценой игры.
При решении задач на цену игры и определение стратегии для этих величин у первого
игрока следует поступать следующим образом. Из каждой строки выписать значение минимального элемента и
уже из них выбрать максимальный.
Таким образом, выигрыш первого игрока будет максимальным из минимальных.
Отсюда и название — максиминный выигрыш. Номер строки этого элемента и будет номером чистой стратегии,
которую выбирает первый игрок.
Теперь определим величину проигрыша второго игрока, если он использует j-ю
стратегию. В этом случае первый игрок использует такую свою чистую стратегию, при которой проигрыш
второго игрока был бы максимальным. Второй игрок должен выбрать такую чистую стратегию, при которой его
проигрыш был бы минимальным. Проигрыш второго игрока, который обозначим
как
При решении задач на цену игры и определение стратегии для определения этих величин у второго игрока следует поступать следующим образом. Из каждого столбца
выписать значение максимального элемента и уже из них выбрать минимальный.
Таким образом, проигрыш второго
игрока будет минимальным из максимальных. Отсюда и название — минимаксный выигрыш. Номер столбца этого
элемента и будет номером чистой стратегии, которую выбирает второй игрок. Если второй игрок использует
«минимакс», то независимо от выбора стратегии первым игроком, он проиграет не более v2 единиц.
Пример 1. Дана матричная игра с платёжной матрицей
.
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них:
Наибольший из наименьших элементов строк — 2, это нижняя цена игры, ей соответствует первая строка,
следовательно, максиминная стратегия первого игрока первая.
Наименьший из наибольших элементов столбцов —
5, это верхняя цена игры, ей соответствует второй столбец, следовательно, минимаксная стратегия второго
игрока — вторая.
Теперь, когда мы научились находить нижнюю и верхнюю цену игры, максиминную и минимаксную стратегии, пришло время научиться обозначать эти понятия формально.
Итак, гарантированный выигрыш первого игрока:
.
Первый игрок должен выбрать чистую стратегию, которая обеспечивала бы ему максимальный из минимальных выигрышей. Этот выигрыш (максимин) обозначается так:
.
Первый игрок использует такую свою чистую стратегию, чтобы проигрыш второго игрока был максимальным. Этот проигрыш обозначается так:
.
Второй игрок должен выбрать свою чистую стратегию так, чтобы его проигрыш был минимальным. Этот проигрыш (минимакс) обозначается так:
.
Ещё пример из этой же серии.
Пример 2. Дана матричная игра с платёжной матрицей
.
Определить максиминную стратегию первого игрока, минимаксную стратегию второго игрока, нижнюю и верхнюю цену игры.
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них:
Наибольший из наименьших элементов строк — 3, это нижняя цена игры, ей соответствует вторая строка, следовательно, максиминная стратегия первого игрока вторая. Наименьший из наибольших элементов столбцов — 5, это верхняя цена игры, ей соответствует первый столбец, следовательно, минимаксная стратегия второго игрока — первая.
Если верхняя и нижняя цена игры одинаковая, то считается, что матричная игра имеет
седловую точку.
Таким образом, если , то — оптимальная чистая стратегия первого игрока, а — оптимальная чистая стратегия второго игрока. То есть равные между собой нижняя и верхняя цены игры достигаются на одной и той же паре стратегий.
В этом случае матричная игра имеет решение в чистых стратегиях.
Пример 3. Дана матричная игра с платёжной матрицей
.
Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?
Решение. Справа от платёжной матрицы выпишем наименьшие элементы в её строках и отметим максимальный из них, а снизу от матрицы — наибольшие элементы в столбцах и выберем минимальный из них:
Нижняя цена игры совпадает с верхней ценой игры.
Таким образом, цена игры равна 5.
То есть . Цена игры равна
значению седловой точки .
Максиминная стратегия первого игрока — вторая чистая стратегия, а минимаксная стратегия второго игрока —
третья чистая стратегия. Данная матричная игра имеет решение в чистых стратегиях.
Решить задачу на матричную игру самостоятельно, а затем посмотреть решение
Пример 4. Дана матричная игра с платёжной матрицей
.
Найти нижнюю и верхнюю цену игры. Имеет ли данная матричная игра седловую точку?
Правильное решение и ответ.
В большинстве случаев матричная игра не имеет седловой точки, поэтому соответствующая матричная игра не имеет решений в чистых стратегиях.
Но она имеет решение в оптимальных смешанных стратегиях. Для их нахождения нужно
принять, что игра повторяется достаточное число раз, чтобы на основании опыта можно было предположить,
какая стратегия является более предпочтительной.
Поэтому решение связывается с понятием вероятности
и среднего (математического ожидания). В окончательном же решении есть и аналог седловой точки (то есть
равенства нижней и верхней цены игры), и аналог соответствующих им стратегий.
Итак, чтобы чтобы первый игрок получил максимальный средний выигрыш и чтобы средний проигрыш второго игрока был минимальным, чистые стратегии следует использовать с определённой вероятностью.
Если первый игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией первого игрока. Иначе говоря, это «смесь» чистых стратегий. При этом сумма этих вероятностей равна единице:
.
Если второй игрок использует чистые стратегии с вероятностями , то вектор называется смешанной стратегией второго игрока. При этом сумма этих вероятностей равна единице:
.
Нет времени вникать в решение? Можно заказать работу!
Если первый игрок использует смешанную стратегию p, а второй игрок —
смешанную стратегию q, то имеет смысл математическое ожидание выигрыша первого игрока (проигрыша второго игрока).
Чтобы его найти, нужно перемножить вектор
смешанной стратении первого игрока (который будет матрицей из одной строки), платёжную матрицу и вектор
смешанной стратегии второго игрока (который будет матрицей из одного столбца):
.
Если уже подзабыто произведение матриц, то следует повторить материал.
Пример 5. Дана матричная игра с платёжной матрицей
.
Определить математическое ожидание выигрыша первого игрока (проигрыша второго игрока), если смешанная стратегия первого игрока , а смешанная стратегия второго игрока .
Решение. Согласно формуле математического ожидания выигрыша первого игрока (проигрыша второго игрока) оно равно произведению вектора смешанной стратегии первого игрока, платёжной матрицы и вектора смешанной стратегии второго игрока:
Оптимальной смешанной стратегией первого игрока
называется такая смешанная стратегия ,
которая обеспечивала бы ему максимальный средний выигрыш
, если игра повторяется
достаточное число раз.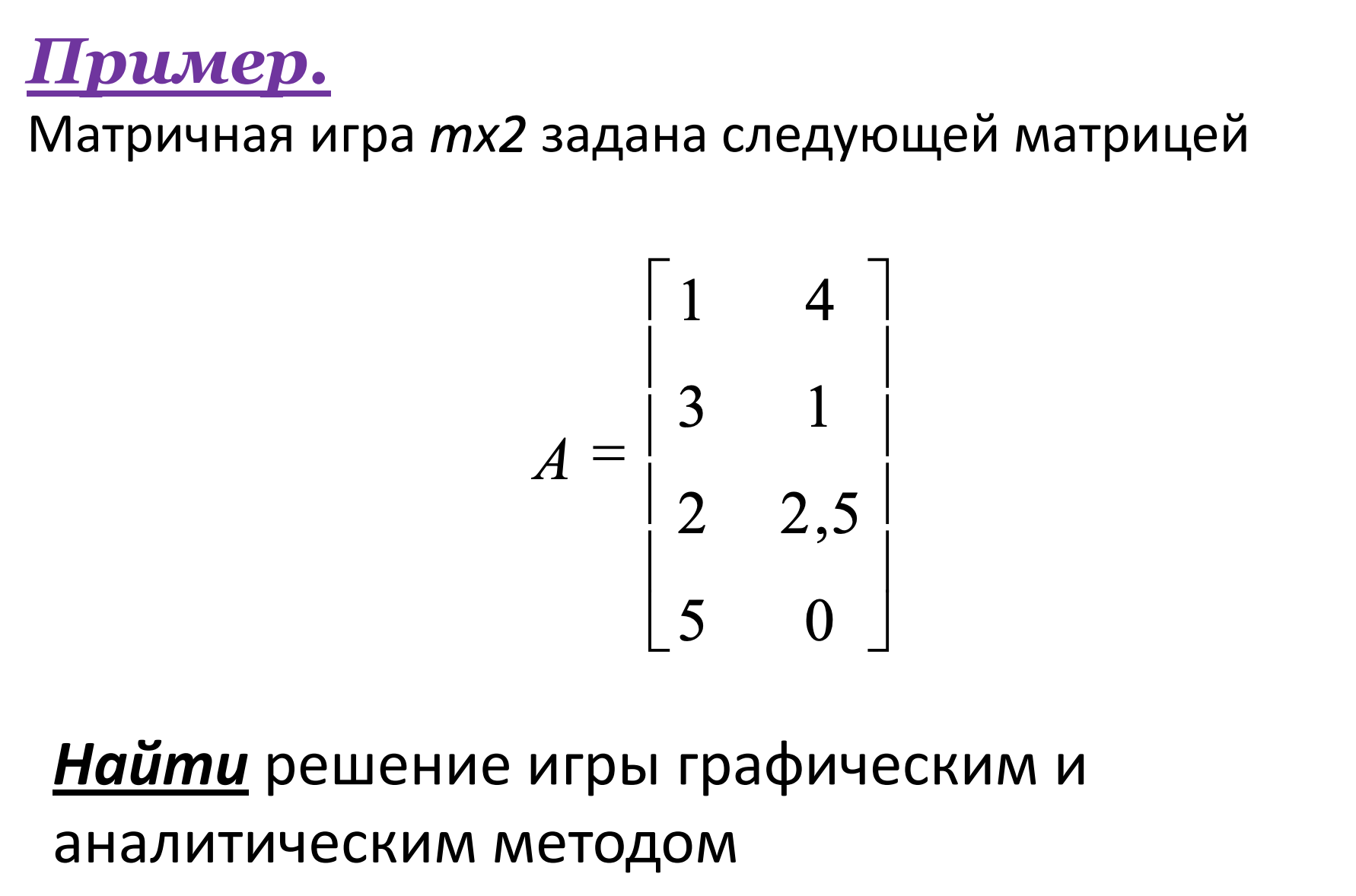
Оптимальной смешанной стратегией второго игрока называется такая смешанная стратегия , которая обеспечивала бы ему минимальный средний проигрыш , если игра повторяется достаточное число раз.
По аналогии с обозначениями максимина и минимакса в случах чистых стратегий оптимальные смешанные стратегии обозначаются так (и увязываются с математическим ожиданием, то есть средним, выигрыша первого игрока и проигрыша второго игрока):
,
.
В таком случае для функции E существует седловая точка, что означает равенство .
Для того, чтобы найти оптимальные смешанные стратегии и седловую точку, то есть решить матричную игру в смешанных стратегиях, нужно свести матричную игру к задаче линейного программирования,
то есть к оптимизационной задаче, и решить соответствующую задачу линейного программирования.
Для того, чтобы решить матричную игру в смешанных стратегиях, нужно составить прямую задачу линейного программирования и двойственную ей задачу. В двойственной задаче расширенная матрица, в которой хранятся коэффициенты при переменных в системе ограничений, свободные члены и коэффициенты при переменных в функции цели, транспонируется. При этом минимуму функции цели исходной задачи ставится в соответствие максимум в двойственной задаче.
Функция цели в прямой задаче линейного программирования:
.
Система ограничений в прямой задаче линейного программирования:
Функция цели в двойственной задаче:
.
Система ограничений в двойственной задаче:
Оптимальный план прямой задачи линейного программирования обозначим
,
а оптимальный план двойственной задачи обозначим
Линейные формы для соответствующих оптимальных планов обозначим и ,
а находить их нужно как суммы соответствующих координат оптимальных планов.
В соответствии определениям предыдущего параграфа и координатами оптимальных планов, в силе следующие смешанные стратегии первого и второго игроков:
,
.
Математики-теоретики доказали, что цена игры следующим образом выражается через линейные формы оптимальных планов:
,
то есть является величиной, обратной суммам координат оптимальных планов.
Нам, практикам, остаётся лишь использовать эту формулу для решения матричных игр в смешанных стратегиях. Как и формулы для нахождения оптимальных смешанных стратегий соответственно первого и второго игроков:
,
,
в которых вторые сомножители — векторы. Оптимальные смешанные стратегии также, как
мы уже определили в предыдущем параграфе, являются векторами. Поэтому, умножив число (цену игры) на вектор
(с координатами оптимальных планов) получим также вектор.
Пример 6. Дана матричная игра с платёжной матрицей
.
Найти цену игры V и оптимальные смешанные стратегии и .
Решение. Составляем соответствующую данной матричной игре задачу линейного программирования:
Приводим задачу к канонической форме и решаем задачу и двойственную ей задачу симплекс-методом.
Получаем решение прямой задачи:
.
Находим линейную форму оптимальных планов как сумму найденных координат:
.
Получаем решение двойственной задачи:
.
Находим линейную форму оптимальных планов как сумму найденных координат:
.
Находим цену игры:
.
Находим оптимальную смешанную стратегию первого игрока:
.
Находим оптимальную смешанную стратегию второго игрока:
.
Пусть дана игра с платёжной матрицей
Если эта матричная игра имеет седловую точку, то она имеет решение в чистых стратегиях, как показано в параграфах 1 и 2.
Если же игра не имеет седловой точки, то она имеет решение в оптимальных смешанных стратегиях. Для этого простейшего случая матричной игры при её решениях путём сведения к задаче линейного программирования были найдены формулы стратегий игроков и цены игры, благодаря которым такая игра решается менее трудоёмким способом.
Формула для нахождения оптимальной смешанной стратегии первого игрока:
.
Формула для нахождения оптимальной смешанной стратегии второго игрока:
.
Формула для нахождения цены игры:
.
Пример 7.
Дана матричная игра с платёжной матрицей
.
Найти оптимальные смешанные стратегии игроков и цену игры.
Решение. Оптимальные смешанные стратегии первого игрока получаем по соответствующей из приведённых формул:
.
Оптимальные смешанные стратегии второго игрока получаем также по соответствующей формуле:
.
Цена игры:
.
Матричная игра, седловая точка, чистые стратегии, смешанные стратегии… А для чего всё это? Рассмотрим на примере, как с помощью матричных игр решаются экономические задачи.
Пример 8. Составить матричную игру для следующей задачи.
Предприятие может выпускать три вида продукции (A1, A2, A3),
получая при этом прибыль, зависящую от спроса, который может быть в одном из четырёх состояний
(B1, B2, B3, B4).
Дана матрица, элементы которой aij
характеризуют прибыль, которую получит предприятие при выпуске i-й продукции с j-м
состоянием спроса.
| B1 | B2 | B3 | B1 | |
| A1 | 3 | 3 | 6 | 8 |
| A2 | 9 | 10 | 4 | 2 |
| A3 | 7 | 7 | 5 | 4 |
Решение. Задача сводится к матричной игре предприятия A против спроса B.
Прежде чем решать задачу, можно упростить игру, проведя анализ платёжной матрицы и
отбросив стратегии, заведомо невыгодные или дублирующие.
Вторая стратегия (второй столбец матрицы)
является явно невыгодной для игрока B по сравнению с первой
(элементы второго столбца больше элементов первого столбца), так как цель игрока B —
уменьшить выигрыш игрока A. Поэтому второй столбец можно отбросить.
Получим следующую матрицу:
.
Далее составляется и решается задача линейного программирования. Это мы уже умеем.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Поделиться с друзьями
Теория игр: основы. Примеры записи и решения игр из жизни
Материалы по векторам и матрицам
Векторы: определения и действия над векторами
Произведение двух матриц
Линейное программирование
Задача и теоремы линейного программирования, примеры формулировки задач
Симплекс-метод решения задач линейного программирования: типичный пример и алгоритм
Пример решения задачи — игра, графическим методом
Ниже приведено условие и решение задачи.
Закачка решения в формате doc начнется автоматически через 10 секунд.
Оптимизация мощности ателье.
Ателье по пошиву одежды рассчитано на выполнение не более 8 тыс. заявок в год. Будем считать, что поток заявок выражается цифрами 6, 8 тыс. в год. Накопленный опыт аналогичных предприятий показывает, что прибыль от выполнения одной заявки составляет 8 ден. ед., а потери, вызванные отказом из-за недостатка мощностей, оцениваются в 5 ден. ед., а убытки от простоя специалистов и оборудования при отсутствии заявок обходятся в 6 ден. ед. в расчете на каждую заявку.
1. Придать описанной ситуации игровую схему, установить характер игры и выявить ее
участников, указать возможные чистые стратегии сторон;
2. Составить платежную матрицу (матрицу затрат).
3. Решить задачу сведением ее к задаче линейного программирования и решить её графическим способом (т.е. найти оптимальные стратегии игроков и цену игры). Дать рекомендации о мощности ателье.
Решение.
1. Одним из участников рассматриваемой в задаче ситуации является руководство предприятия, озабоченное необходимостью выполнения определенного количества заявок. Если описанной ситуации придать игровую схему, то руководство ателье выступает в ней в качестве сознательного игрока А, заинтересованного в максимизации прибыли от выполнения заказов . Вторым участником является природа — совокупность объективных факторов (П), которая реализует свои состояния по присущим ей законам. Такого рода ситуация представляется типичной для стратегической игры.
Рассчитывая количество заявок, руководство предприятия может ориентироваться на величины: 6 тыс. ед. (первая чистая стратегия А1), либо 8 тыс. ед. (вторая чистая стратегия А2).
Природа (совокупность объективных неопределенных факторов) может реализовать состояния П1, П2, необходимое количество заявок 6, 8 тыс. ед. соответственно.
Таким образом, платежная матрица статистической игры будет иметь размерность 2х2.
2.
Платежная матрица игры представлена в табл. 2.1.
Таблица 2.1
|
|
П1=6 |
П2=8 |
тin aj |
|
A1=6 |
48 |
48-2·5=38 |
18 |
|
А2=8 |
48-2·6=36 |
64 |
36 |
При расчете элементов матрицы учтена прибыль за вычетом дополнительных затрат, связанных с недостатком мощностей, а также с убытком от простоя . Заметим, что в теории игр элементы aij обычно называются выигрышами игрока A, а наилучшей для А считается стратегия, при которой выигрыш максимизируется .
Рассмотрим ситуацию (а1;П2), т.е. случай, когда не хватает мощности на 2 тыс.
ед. при этом прибыль составит 64-2·5=54 . Так что «выигрыш» в этом случае равен 54 и т. д.
В ситуации (А2;П1) мощность превысит потребности на 8-6=2 (вес. ед.). Поэтому затраты связанные с простоем составят 2·6=12 (ед.). Следовательно, a21 = 48-2·6=36.
Рассуждая аналогично, находим и остальные элементы платежной матрицы.
Определим седловой элемент:
Матрица не имеет седлового элемента т.к. А ≠ В 36 ≤ v ≤ 48
3. Для определения оптимальных стратегий игроков по платежной матрице составляем пару двойственных задач.
Для игрока А:
f = Х1 + Х2 (min)
48Х1 +36Х2 ≥1
38Х1 +64Х2 ≥1 (1)
Хj ≥0 (j=1,2)
Для игрока В:
φ = Y1 + Y2 (max)
48Y1 + 38Y2 ≤ 1
36Y1 + 64Y2 ≤ 1 (2)
Yi ≥0 (i=1,2)
Решим задачу для игрока А графическим способом.
Строим прямые:
48Х1 +36Х2 =1 (I) по точкам (1/48, 0) и (0, 1/36)
38Х1 +64Х2 =1 (II) по точкам (1/38, 0) и (0, 1/64)
Долее определяем область допустимых решений. На рисунке 2.1 выделена граница области допустимых решений. Разрешающая прямая fmin, перпендикулярная вектору целевой функции 0,03С, засекает область в точке А, найдем координаты точки А, решив систему уравнений:
48Х1 +36Х2 =1 (16)
38Х1 +64Х2 =1 (-9)
Умножаем первое уравнение на 16, а второе на (-9), складывая, получаем:
426Х1=7, откуда Х1*=7/426
Х2* = (1 — 48∙(7/426) )/36= 5/852
fmin = 7/426 + 5/852 = 19/852
Цена игры: v = 1/fmin = 852/19.
Тогда оптимальные стратегии для игрока А:
Р1* = v∙X1* = (852/19)∙(7/426) = 14/19;
Р1* = v∙X2* = (852/19)∙(5/852) = 5/19.
Рис. 2.1
Следовательно, руководству надо ориентироваться на (6000∙14+8000∙5)/19 = 6526 заявок в год.
Решим задачу для игрока В. Так как неравенства в задаче для игрока А при оптимальном решении превращаются в строгие равенства, то оптимальное решение, найдем, решив систему:
48Y1 + 38Y2 =1 (-3)
36Y1 + 64Y2 =1 (4)
Умножаем первое уравнение на (-3), а второе на 4, складывая, получаем:
142Y2=1, откуда Y2*= 1/142 = 6/852
Y1* = (1 — 38∙(1/142))/48 = 104/(142∙48) = 13/852
fmin = 13/852 + 6/852 = 19/852
Цена игры: v = 1/ φ max = 852/19.
Тогда оптимальные стратегии для игрока B:
Q1* = v∙Y1* = (852/19)∙(13/852) = 13/19;
Q1* = v∙Y2* = (852/19)∙(6/852) = 6/19.
Теория игр | Coursera
Об этом курсе
149 500 недавних просмотров
Теория игр, ставшая популярной благодаря таким фильмам, как «Игры разума», представляет собой математическое моделирование стратегического взаимодействия между рациональными (и иррациональными) агентами. Помимо того, что мы называем «играми» на обычном языке, например, шахматы, покер, футбол и т. д., сюда входит моделирование конфликтов между нациями, политических кампаний, конкуренции между фирмами и торгового поведения на таких рынках, как Нью-Йоркская фондовая биржа. Как можно было начать моделировать аукционы ключевых слов и одноранговые сети обмена файлами, не принимая во внимание стимулы людей, их использующих? Курс предоставит основы: представление игр и стратегий, расширенную форму (которую ученые-компьютерщики называют игровыми деревьями), байесовские игры (моделирование таких вещей, как аукционы), повторяющиеся и стохастические игры и многое другое.
Мы будем включать множество примеров, включая классические игры и несколько приложений.
Гибкие сроки
Сбрасывайте сроки в соответствии с вашим расписанием.
Общий сертификатСовместно используемый сертификат
Получите сертификат по завершении
100 % онлайн100 % онлайн
Начните сразу и учитесь по собственному графику.
Начальный уровеньНачальный уровень
Часов для прохожденияПрибл. 17 часов
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), китайский (упрощенный), итальянский, вьетнамский, корейский, немецкий, русский, английский, испанский
Навыки, которые вы приобретете
- Теория игр
- Обратная индукция
- Байесовская игра
- Решение проблем
Гибкие сроки
Сброс сроков в соответствии с вашим графиком.
Общий сертификат
Получите сертификат по завершении
100% онлайн100% онлайн
Начните сразу и учитесь по собственному графику.
Начальный уровеньНачальный уровень
Часов для прохожденияПрибл. 17 часов, чтобы закончить
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), китайский (упрощенный), итальянский, вьетнамский, корейский, немецкий, русский, английский, испанский
Экономика
519 882 Учащиеся 3 КурсыКевин Лейтон-Браун
ПрофессорКомпьютер Естествознание
470 894 Учащиеся 2 КурсыЙоав Шохам
ПрофессорИнформатика
470 894 Учащиеся 2 КурсыПредлагает
Стэнфордский университет
Стэнфордский младший университет Леланда, обычно называемый как Стэнфордский университет или Стэнфорд, является американским частным исследовательским университетом, расположенным в Стэнфорде, Калифорния, на территории кампуса площадью 8 180 акров (3310 га) недалеко от Пало-Альто, Калифорния, США.
Университет Британской Колумбии
Университет Британской Колумбии является глобальным центром исследований и обучения.
Отзывы
4.6
Заполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаНаполовину заполненная звезда 899 отзывов5 звезд
71,55%
90 0344 звезды
22,24%
3 звезды
3,92%
2 звезды
1,09%
1 звезда
1,18%
ЛУЧШИЕ ОТЗЫВЫ ИЗ ТЕОРИИ ИГРОВ очень интересный курс я когда-либо присоединяюсь. это очень практично и тренирует наш мозг использовать логику, когда мы что-то принимаем. Я очень рад продолжить свой курс по Теории игр II.
Filled StarFilled StarFilled StarFilled StarStarby PRD 12 декабря 2018 г.
Удивительный курс! Дает глубокое погружение в тему! Просто нравится, как Кевин объясняет! Мэтт действительно мог работать над своим заиканием; или, возможно, немного замедлить.
Контент был на высоте! 😉
by AG 5 июля 2017 г.
Курс действительно хорош. Охватывает много контента. Одно из лучших мест в Интернете для изучения теории игр. Активный дискуссионный форум. Еще несколько примеров можно добавить в виде отдельных видео.
Заполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаот WY17 мая 2017 г.
Отлично! Интересно и много одновременно. Надеюсь, что профессора разъяснят функцию стратегической полезности более четко, потому что это сложно для студентов с плохим знанием математики (забудьте о большинстве><) прямо сейчас!
Просмотреть все отзывыЧасто задаваемые вопросы
Еще вопросы? Посетите Справочный центр для учащихся.
Как это работает в теории игр, примеры, плюс дилемма заключенного
Что такое равновесие Нэша?
Равновесие по Нэшу — это концепция теории игр, согласно которой оптимальный результат достигается тогда, когда у игроков нет стимула отклоняться от своей первоначальной стратегии.
Игроки знают стратегию своего противника и все равно не будут отклоняться от первоначально выбранной стратегии, потому что она остается оптимальной стратегией для каждого игрока.
В целом, человек не может получить дополнительную выгоду от изменения действий, если предположить, что другие игроки остаются неизменными в своих стратегиях. В игре может быть несколько равновесий Нэша или вообще не быть ни одного.
Ключевые выводы
- Равновесие Нэша — это теорема принятия решений в рамках теории игр, которая утверждает, что игрок может достичь желаемого результата, не отклоняясь от своей первоначальной стратегии.
- В равновесии Нэша стратегия каждого игрока оптимальна при рассмотрении решений других игроков. Каждый игрок выигрывает, потому что каждый получает желаемый результат.
- Дилемма заключенного — распространенный пример из теории игр, который адекватно демонстрирует эффект равновесия Нэша.
- Равновесие Нэша часто обсуждается в связи с доминирующей стратегией, которая утверждает, что выбранная действующим лицом стратегия приведет к лучшим результатам из всех возможных стратегий, которые можно использовать, независимо от стратегии, используемой противником.
- Равновесие Нэша не всегда означает выбор наиболее оптимальной стратегии.
Равновесие Нэша
Понимание равновесия Нэша
Равновесие Нэша названо в честь его изобретателя Джона Нэша, американского математика. Это считается одним из наиболее важных понятий теории игр, которая пытается математически и логически определить действия, которые должны предпринять участники игры, чтобы обеспечить себе наилучшие результаты.
Причина, по которой равновесие Нэша считается таким важным понятием теории игр, связана с его применимостью. Равновесие Нэша может быть включено в широкий спектр дисциплин, от экономики до социальных наук.
Чтобы быстро найти равновесие Нэша или проверить, существует ли оно вообще, раскройте стратегию каждого игрока другим игрокам. Если никто не меняет свою стратегию, то равновесие Нэша доказано.
Равновесие Нэша против доминирующей стратегии
Равновесие Нэша часто сравнивают с доминирующей стратегией, поскольку обе стратегии являются стратегиями теории игр.
Равновесие по Нэшу утверждает, что оптимальная стратегия для действующего лица состоит в том, чтобы придерживаться своей первоначальной стратегии, зная стратегию противника, и что все игроки придерживаются одной и той же стратегии.
Доминирующая стратегия утверждает, что выбранная субъектом стратегия приведет к лучшим результатам из всех возможных стратегий, которые можно использовать, независимо от стратегии, используемой противником.
Все модели теории игр работают только в том случае, если вовлеченные игроки являются «рациональными агентами», что означает, что они желают конкретных результатов, действуют, пытаясь выбрать наиболее оптимальный результат, включают неопределенность в свои решения и реалистичны в своих вариантах.
Оба термина похожи, но немного отличаются. Равновесие Нэша утверждает, что ничего не выиграно, если один из игроков изменит свою стратегию, в то время как все остальные игроки сохранят свою стратегию. Доминирующая стратегия утверждает, что игрок выберет стратегию, которая приведет к наилучшему результату, независимо от стратегий, выбранных другими игроками.
Доминирующая стратегия может быть включена в равновесие Нэша, тогда как равновесие Нэша может не быть лучшей стратегией в игре.
Пример равновесия Нэша
Представьте себе игру между Томом и Сэмом. В этой простой игре оба игрока могут выбрать стратегию А, чтобы получить 1 доллар, или стратегию Б, чтобы проиграть 1 доллар. Логически оба игрока выбирают стратегию А и получают выигрыш в размере 1 доллара.
Если вы раскрыли стратегию Сэма Тому и наоборот, вы увидите, что ни один игрок не отклоняется от первоначального выбора. Знание хода другого игрока мало что значит и не меняет поведения ни одного из игроков. Результат A представляет собой равновесие Нэша.
Джули Бэнг / Инвестопедия
Дилемма заключенного
Дилемма заключенного — обычная ситуация, анализируемая в теории игр, в которой можно использовать равновесие Нэша. В этой игре двое преступников арестованы, и каждый содержится в одиночной камере, не имея возможности общаться друг с другом.
У прокуратуры нет улик, чтобы осудить эту пару, поэтому они предлагают каждому заключенному возможность либо предать другого, дав показания о том, что другой совершил преступление, либо сотрудничать, храня молчание.
Если оба заключенных предадут друг друга, каждый отбывает по пять лет тюрьмы. Если A предает B, но B хранит молчание, заключенный A освобождается, а заключенный B отбывает 10 лет тюрьмы, или наоборот. Если каждый промолчит, то каждый отбывает всего по году тюрьмы.
В этом примере равновесие Нэша заключается в том, что оба игрока предают друг друга. Хотя взаимное сотрудничество приводит к лучшему результату, если один заключенный выбирает взаимное сотрудничество, а другой нет, результат одного заключенного хуже.
Что такое равновесие Нэша в теории игр?
Равновесие по Нэшу в теории игр — это ситуация, в которой игрок будет продолжать придерживаться выбранной стратегии, не имея стимула отклоняться от нее, приняв во внимание стратегию противника.
Как найти равновесие Нэша?
Чтобы найти равновесие Нэша в игре, нужно смоделировать каждый из возможных сценариев, чтобы определить результаты, а затем выбрать оптимальную стратегию. В игре с двумя людьми это будет учитывать возможные стратегии, которые могут выбрать оба игрока. Если ни один из игроков не меняет свою стратегию, зная всю информацию, наступило равновесие Нэша.
Почему равновесие Нэша важно?
Равновесие Нэша важно, потому что оно помогает игроку определить наилучший выигрыш в ситуации, основываясь не только на своих решениях, но и на решениях других вовлеченных сторон. Равновесие Нэша можно использовать во многих сферах жизни, от бизнес-стратегий до продажи дома, от войны до социальных наук и так далее.
Как рассчитать равновесие Нэша?
Специальной формулы для расчета равновесия Нэша не существует. Его можно определить путем моделирования различных сценариев в данной игре, чтобы определить выигрыш каждой стратегии и выбрать оптимальную стратегию.
Каковы ограничения равновесия Нэша?
Основным ограничением равновесия Нэша является то, что оно требует от человека знания стратегии своего противника. Равновесие Нэша может возникнуть только в том случае, если игрок решит остаться со своей текущей стратегией, если он знает стратегию своего противника.
В большинстве случаев, например, на войне — будь то военная война или война торгов — человек редко знает стратегию противника или то, что он хочет, чтобы был результат. В отличие от доминирующей стратегии, равновесие Нэша не всегда приводит к наиболее оптимальному результату. Это просто означает, что человек выбирает наилучшую стратегию на основе имеющейся у него информации.
Кроме того, в нескольких играх с одними и теми же противниками равновесие Нэша не принимает во внимание прошлое поведение, которое часто предсказывает будущее поведение.
Практический результат
Равновесие Нэша — это компонент теории игр, который утверждает, что игрок будет продолжать придерживаться выбранной стратегии, зная стратегию своего противника, поскольку у него нет стимула менять курс.