Сложение и вычитание дробей с одинаковыми знаменателями 8 класс | Тест по алгебре (8 класс):
Опубликовано 20.10.2019 — 11:14 — Валиева Наталья Евгеньевна
Сложение и вычитание дробей с одинаковыми знаменателями 8 класс
Скачать:
Предварительный просмотр:
По теме «Сложение и вычитание алгебраических дробей»
№ | Задание |
1 | |
2 | |
3 | |
4 | |
5 | |
№ | Задание |
1 | |
2 | |
3 | |
4 | |
5 | |
По теме: методические разработки, презентации и конспекты
Открытый урок «Сложение и вычитание дробей с одинаковыми знаменателями» для 5 классов
Цели урока:обучающие:закрепить знания и умения учащихся применять правила сложения и вычитания дробей с одинаковыми знаменателями при решении примеров, уравнений и задач;воспитывающие:форм. ..
..
Учебный проект по теме «Обыкновенные дроби (сложение и вычитание дробей с одинаковыми знаменателями)»
Реализация учебного проекта «Обыкновенные дроби» способствует повышению интереса учащихся к математике и расширению их знаний об истории возникновения дробей. Большое внимание уделяется работе учащихс…
Сложение и вычитание дробей с одинаковыми знаменателями 5 класс
Разработка урока по теме : » Сложение и вычитание дробей с одинаковыми знаменателями «…
Конспект урока математики «Сложение и вычитание дробей с одинаковыми знаменателями», 7 класс
Конспект урока математики в 7 классе коррекционной школы VIII вида по теме «Сложение и вычитание дробей с одинаковыми знаменателями»….
Конспект открытого урока в 5 классе по теме: Сложение и вычитание дробей с одинаковыми знаменателями
Урок обобщения и систематизации с дидактической игрой «Путешествие в страну Дроби»…
Технологическая карта урока математики в 5 классе по теме «Сложение и вычитание дробей с одинаковым знаменателем»
Технологическая карта урока математики в 5 классе. ..
..
урок-игра «Дроби.Сложение и вычитание дробей с одинаковыми знаменателями.»
конспект урока в 5 классе по учебнику Виленкина Н.Я. «Математика 5"…
Поделиться:
Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень 8 класс онлайн-подготовка на
113. Сумма и разность дробей. Произведение и частное дробей. Возведение дроби в степень.
При сложении обыкновенных дробей с одинаковыми знаменателями складывают их числители, а знаменатель оставляют прежним. Например:
27+37=2+37=57.
Таким же образом складывают любые рациональные дроби с одинаковыми знаменателями:
ac+bc=a+bc,
где а, b и с — многочлены, причем с — ненулевой многочлен.
Это равенство выражает правило сложения рациональных дробей с одинаковыми знаменателями:
Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.
Вычитание рациональных дробей выполняется аналогично сложению:
ac-bc=a-bc.
Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.
Пример 1. Сложим дроби:
3a-7b15ab+2a+2b15ab=3a-7b+2a+2b15ab=5a-5b15ab=5(a-b)15ab=a-b3ab.
Пример 2. Вычтем дроби:
a2+95a-15-6a5a-15=a2+9-6a5a-15=a-325a-3=a-35.
Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание рациональных дробей с разными знаменателями сводится к сложению и вычитанию рациональных дробей с одинаковыми знаменателями. Для этого данные дроби приводят к общему знаменателю.
Пример 3. Сложим дроби x4a3b+56ab4.
Знаменатели дробей представляют собой одночлены. Наиболее простым общим знаменателем является одночлен 12а3b4. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей. Дополнительные множители к числителям и знаменателям этих дробей соответственно равны 3b3и 2a2.
Наиболее простым общим знаменателем является одночлен 12а3b4. Коэффициент этого одночлена равен наименьшему общему кратному коэффициентов знаменателей дробей, а каждая переменная взята с наибольшим показателем, с которым она входит в знаменатели дробей. Дополнительные множители к числителям и знаменателям этих дробей соответственно равны 3b3и 2a2.
Имеем
x4a3b+56ab4=x∙3b3+5∙2a212a3b4=3b3x+10a212a3b4.
Пример 4. Преобразуем разность a+3a2+ab-b-3ab+b2.
Чтобы найти общий знаменатель, разложим знаменатель каждой дроби на множители:
a+3a2+ab-b-3ab+b2=a+3a(a+b)-b-3b(a+b).
Простейшим общим знаменателем служит выражение ab(a+b). Дополнительные множители к числителям и знаменателям этих дробей соответственно равны b и а.
Имеем:
a+3a(a+b)-b-3ba+b=a+3b-b-3aaba+b=ab+3b-ab+3aaba+b=3a+baba+b=3ab.
Преобразование рационального выражения, которое является суммой или разностью целого выражения и дроби, сводится к преобразованию суммы или разности дробей.
Пример 5. Упростим выражение a-1-a2-3a+1
Представим выражение a-1 в виде дроби со знаменателем 1 и выполним вычитание дробей:
a-1-a2-3a+1=a-11-a2-3a+1=a-1a+1-a2-3a+1=a2-1-a2+3a+1=2a+1.
Умножение и деление дробей. Возведение дроби в степень.
При умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели и первое произведение записывают в числителе, а второе — в знаменателе дроби. Например: 23∙45=2∙43∙5=815.
Таким же образом перемножают любые рациональные дроби:
ab∙cd=acbd,
где а, b, с и d — некоторые многочлены, причем b и d — ненулевые многочлены. Это равенство выражает правило умножения рациональных дробей:
чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе — знаменателем дроби.
Пример 6. Умножим дроби a34b2∙6ba2.
Воспользуемся правилом умножения дробей:
a34b2∙6ba2=a3∙6b4b2∙a2=6a3b4a2b2=3a2b.
Правило умножения дробей распространяется на произведение трех и более рациональных дробей. Например:
ab∙cd∙mn=acbd∙mn=acmbdn.
Выясним теперь, как выполняется возведение рациональной дроби в степень.
Рассмотрим выражение abn, являющейся n-й степенью рациональной дроби ab и докажем, что
abn=anbn.
По определению степени имеем
abn=ab·ab∙…∙ab (n раз).
Применяя правило умножения рациональных дробей и определение степени, получим
ab·ab∙…∙ab=a∙a∙…∙ab∙b∙…∙b=anbn.
Следовательно, abn=anbn.
Из доказанного тождества следует правило возведения рациональной дроби в степень:
чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй — в знаменателе дроби.
Пример 7. Возведем дробь 2a2b4 в третью степень.
Воспользуемся правилом возведения в степень:
2a2b43=(2a2)3(b4)3=8a6b12.
Деление дробей
При делении обыкновенных дробей первую дробь умножают на дробь, обратную второй. Например: 38:25=38∙52=1516.
Так же поступают при делении любых рациональных дробей:
ab:cd=ab∙dc=adbc,
где а, b, с и d — некоторые многочлены, причем b, c и d — ненулевые многочлены.
Это равенство выражает правило деления рациональных дробей:
чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
Пример 8. Разделим дроби 7a2b3:14ab.
Воспользуемся правилом деления дробей:
7a2b3:14ab=7a2b3·b14a=7a2b14ab3=a2b2.
Как легко складывать и вычитать дроби
Страх перед дробями!Дробь — это новое понятие с совершенно другим обозначением, которое затрудняет понимание учащимися. Одной из причин, по которой студенты находят это утомительным, также является то, что они когда-либо работали только с целыми числами. Поэтому, естественно, дроби кажутся им незнакомыми.
Борьба и вызовы с фракциями реальны.
В Национальной оценке образовательного прогресса, 2005 г. говорится, что «Литература по математическому образованию громогласна в своих выводах о том, что понимание дробей является сложной областью математики для североамериканских учащихся». Именно этот первоначальный страх перед дробями продвигает дальше и делает понимание сложения и вычитания дробей обременительным.
Эта статья поможет учащимся понять, как складывать и вычитать дроби с помощью простых шагов и визуальных моделей. Мы также рассмотрим некоторые приемы, позволяющие упростить сложение и вычитание дробей.
Читайте дальше, чтобы убедиться, что дроби — друзья ваших детей, а не враги!
Что такое дроби?Большинство учебных программ фокусируются на дробях в виде заштрихованных областей или областей, но они выходят за рамки этого. Учащиеся часто рассматривают дроби как процесс деления и закрашивания частей фигур, поэтому они упускают из виду тот факт, что дроби — это числа между целыми числами.
Внимательно посмотрите на изображение линейки ниже. Маркировка между 0 и 1 представляет числа, которые отличаются от целых чисел. Они называются дробями.
SplashLearn пробуждает любознательность на протяжении всей жизни своей игровой программой обучения PreK-5, которую полюбили более 40 миллионов детей. С более чем 4000 веселых игр и занятий, это идеальный баланс между обучением и игрой для вашего малыша.
Попробуйте бесплатно
Дроби чисел между целыми числамиПохожие чтения: Блестящие математические цитаты, которыми можно поделиться со студентами, чтобы вдохновить их
Важно подчеркнуть, что дроби — это числа, которые помогают нам быть точными и аккуратными в числах.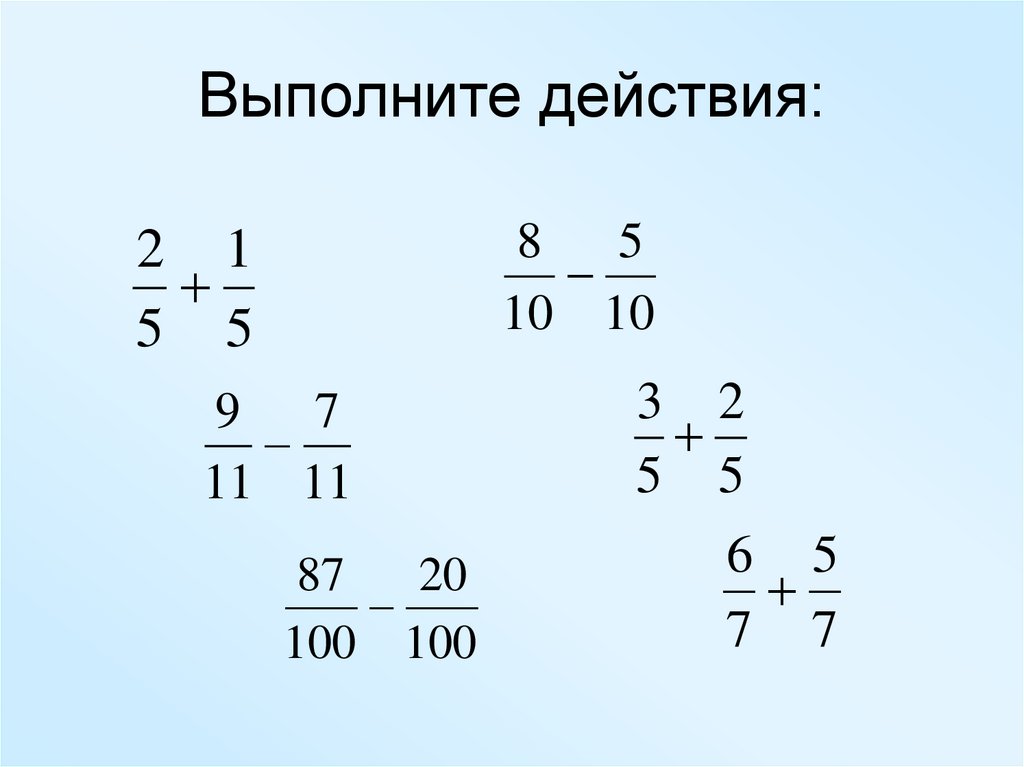 У нас не всегда есть один полный килограмм или один полный дюйм при измерении. Поэтому становится критически важным найти способ представления этих «частей», и именно здесь дроби берут на себя ответственность.
У нас не всегда есть один полный килограмм или один полный дюйм при измерении. Поэтому становится критически важным найти способ представления этих «частей», и именно здесь дроби берут на себя ответственность.
Дроби записываются как a/b, где «a» — это число сверху, которое называется числителем. В то время как «b» является числом внизу и называется знаменателем.
Например: Для дроби 1/2; 1 — числитель, 2 — знаменатель.
Студенты часто путают числитель со знаменателем и наоборот. Чтобы запомнить эти запутанные термины, проще всего запомнить их так: D — вниз и D – знаменатель. Так что знаменатель всегда идет вниз!
ВИДЫ ДРОБЕЙ: Наиболее распространенные типы дробей:
Наиболее часто используемые дроби при сложении и вычитании дробей:
Подобные и отличные дроби .
Дроби с одинаковыми знаменателями называются Подобными дробями.
Пример:
Подобные дроби Дроби с различными знаменателями называются в отличие от дробей .
Пример:
В отличие от дробейЕще один тип дроби, который учащиеся должны знать перед тем, как научиться складывать и вычитать дроби: Эквивалент дроби
Дроби, имеющие разные числители и знаменатели, но равные одному и тому же значению, называются эквивалентными дробями.
Пример:
Все дроби 1/2, 2/4, 3/6 и 4/8 представляют одно и то же значение, равное «ПОЛОВИНА»
Поскольку дроби похожи на любые другие числа, их можно представить с помощью различных моделей .
Модели для представления дробей:Наиболее распространенные модели для представления дробей:
a) Модель района:В модели района дроби представлены как части района или региона.
Наборы круглых и прямоугольных дробей используются для понимания того, что дроби являются частями целого.
Примеры модели площади:
Модель площади b) Линейная модель: В линейной модели дроби рассматриваются как длины, а не площади. Числовая линия является важной линейной моделью, позволяющей учащимся воспринимать дроби как числа.
Числовая линия является важной линейной моделью, позволяющей учащимся воспринимать дроби как числа.
Линейная модель для дроби ¾ будет:
Линейная модель c) Дискретная модель:В дискретной модели под целым понимается набор дискретных объектов. Подмножества этого целого составляют дробные части.
Например, половина класса, 1/3 лотка с яйцами. Счетчики, шарики, кубики или любой другой набор объектов, которые можно посчитать, можно использовать в качестве манипулятора для моделирования дробей.
Как упростить сложение и вычитание дробей ? Работа с дробями > Изучение дробейПервое и главное, что учащиеся должны сделать, изучая сложение и вычитание дробей, — это лучше понимать дроби. Им нужно практиковать дроби, чтобы установить связь с реальным миром, т. е. им нужно складывать листы бумаги, вырезать детали, раскрашивать фигуры и т. д.
Одна из основных проблем с дробями заключается в том, что они не всегда конкретны. Мы начинаем учить дроби с помощью наглядных материалов, но когда дело доходит до операций с дробями, мы переключаемся на правила и процедуры для того же. Механическое заучивание шагов приводит к еще большей путанице.
Мы начинаем учить дроби с помощью наглядных материалов, но когда дело доходит до операций с дробями, мы переключаемся на правила и процедуры для того же. Механическое заучивание шагов приводит к еще большей путанице.
При сложении дробей мы складываем числители, но не знаменатели. Но при умножении дробей мы умножаем не только числители, но и знаменатели. Это еще больше озадачивает студентов.
Лучше всего использовать визуальные модели, чтобы показать добавление дробей, которые помогут учащимся понять шаги, а не грабить шаги без концептуальной ясности.
Связанное Чтение: Наиболее важные математические символы, необходимые учащимся для решения задач
Упражнение:
Чтобы добавить 1/8 и 3/8, возьмите пиццу, разрезанную на 8 ломтиков. из 8 ломтиков,
Теперь, если мы сложим или сложим вместе обе дроби/кусочки пиццы, мы получим 3 ломтика из 8 ломтиков пиццы, что подразумевает 3/8.
Конкретный -> Контекстный -> Вычислительный Чтобы представить новое сложное понятие, такое как дроби, очень важно предоставить учащимся широкие возможности для его конкретного усвоения. Это означает погружение учащихся в такие занятия, как вырезание из бумаги, складывание бумаги, рисование, приготовление бумажной пиццы, яблок, шоколадных батончиков и т. д. Только используя такой опыт, они смогут увидеть, потрогать и почувствовать концепцию дробей и сделать свои собственные открытия. .
Это означает погружение учащихся в такие занятия, как вырезание из бумаги, складывание бумаги, рисование, приготовление бумажной пиццы, яблок, шоколадных батончиков и т. д. Только используя такой опыт, они смогут увидеть, потрогать и почувствовать концепцию дробей и сделать свои собственные открытия. .
Как только учащиеся получат достаточное количество этого конкретного воздействия, они начнут устанавливать связи между этими объектами и реальным миром.
Много времени нужно потратить на создание, исследование, сложение и визуализацию дробей, прежде чем переходить к задачам с дробями, включающим голые числа.
Например: Прежде чем спрашивать ¼ от 20 =? , мы можем представить реальный сценарий следующим образом:
«У Рона было 20 долларов. Он потратил ¼ из них. Сколько денег у него осталось?»
Это поможет даже учащемуся, плохо разбирающемуся в дробях, начать строить связи.
Покажите им, «ПОЧЕМУ» правила работают Если представление о дробях как о числах развито хорошо, то легче понять и операции над дробями. Точно так же, как мы складываем и вычитаем числа, можно складывать и вычитать дроби. Важно подчеркнуть концептуальное понимание наряду с процедурным знанием шагов.
Точно так же, как мы складываем и вычитаем числа, можно складывать и вычитать дроби. Важно подчеркнуть концептуальное понимание наряду с процедурным знанием шагов.
Например:
Мы знаем, что 1 яблоко + 1 яблоко = 2 яблока
Точно так же мы можем складывать дроби.
Мы также знаем, что 2 яблока + 3 яблока = 5 яблок
Точно так же мы можем складывать дроби:
Чтобы узнать сумму 2/6 и 3/6; считайте это двумя шестыми и тремя шестыми, которые в сумме дадут пять шестых точно так же, как мы складываем числа.
Теперь давайте рассмотрим пример с вычитанием:
Мы знаем, что 5 яблок – 2 яблока = 3 яблока
Аналогично мы можем вычитать дроби:
В случае «похожих дробей» мы можем просто сложить/вычесть числители и оставить знаменатель прежним. Но мы не можем складывать разные дроби, как складываем одинаковые дроби.
Причина этого очень проста.
Точно так же, как мы не можем сложить 2 яблока и 3 апельсина и сказать, что сумма равна 5 апплонгов , мы не можем складывать дроби с разными знаменателями. Таким образом, важно сначала определить сложение как комбинацию двух или более одинаковых величин. Точно так же вычитание отнимает подобные единицы количества.
Таким образом, важно сначала определить сложение как комбинацию двух или более одинаковых величин. Точно так же вычитание отнимает подобные единицы количества.
Итак, как складывать/вычитать разные дроби? Давайте посмотрим на это дальше!
Теперь давайте посмотрим на шаги, которые мы можем выполнить, чтобы сложить или вычесть дроби:
Шаг 1 : Сделать знаменатели одинаковыми
9
7 Шаг 2 : Добавить или Вычтите числители (сохраняя знаменатель)
Шаг 3 : Упростите дробь
Чтобы складывать или вычитать разные дроби, первым делом нужно сделать знаменатели одинаковыми, чтобы числители можно было складывать так же, как мы для подобных дробей.
ШАГ 1: ОДИНАКОВЫЕ ЗНАМЕНАТЕЛИ
Как сделать знаменатели одинаковыми?
В случае одинаковых дробей знаменатели уже будут одинаковыми, поэтому вы можете пропустить шаг 1 и перейти к шагу 2. кратное другому знаменателю
кратное другому знаменателю
Пример: ½ + ¾
В этом случае – 4 кратно 2. Мы можем умножить 2 на 2, чтобы получить 4, и в результате знаменатели станут одинаковыми. Таким образом, большее число становится общим знаменателем.
Применение :
Итак, теперь задача принимает следующий вид:
Если один знаменатель кратен другому, мы можем умножить меньший знаменатель на число (скажем, k) , что даст больший знаменатель. Тогда больший знаменатель становится общим знаменателем.
ii) Если оба знаменателя не имеют общего множителя
Пример: ¼ + ⅗
Связанное чтение: Простые способы сделать математику увлекательной для детей
В этом случае числа 4 и 5 не имеют общих делителей. Мы можем просто перемножить знаменатели, чтобы получить общий знаменатель.
4 X 5 = 20, поэтому 20 является общим знаменателем для обеих дробей.
Если у обоих знаменателей нет общего множителя, то вы умножаете оба знаменателя, чтобы получить общий знаменатель.
Давайте посмотрим, как мы получим 20 в качестве общего знаменателя для обеих дробей:
Если мы умножим знаменатель, мы должны умножить и числитель, чтобы получить эквивалентную дробь.
Таким образом, задача теперь выглядит так:
ШАГ 2: СОБЛЮДЕНИЕ/ВЫЧИТАНИЕ ЧИСЛИТЕЛЕЙ
Этот шаг довольно прост и прямолинеен. Мы должны сложить/вычесть числители, и результатом их суммы/разности будет новый числитель. Общий знаменатель (как обсуждалось на шаге 1) остается прежним.
Возьмем наши предыдущие примеры и продолжим оттуда:
- ½ + ¾
После того, как знаменатели одинаковы, эта задача выглядит так:
Теперь нам нужно сложить два числителя вместе (2+3=5), чтобы получить новый числитель, в то время как знаменатель (4) остается прежним.
Таким образом, ответ будет 5/4.
- ¼ + ⅗.
После того, как знаменатели одинаковы, эта задача выглядит так:
Теперь нам нужно сложить числители вместе (5 + 12 = 17), чтобы получить новый числитель, в то время как знаменатель (20) остается прежним.
Таким образом, ответ будет 17/20.
ШАГ 3: УПРОЩЕНИЕ Дроби
Ответы, которые мы получили выше, верны, но мы можем упростить дробь до тех пор, пока в числителе и знаменателе не будет общих множителей, кроме 1.
Дробь можно привести к упрощенной форме, удалив общие факторы.
Продолжим наши предыдущие примеры:
И,
В приведенных выше случаях – 5/4 и 17/20 уже упрощенные дроби, так как числитель и знаменатель не имеют общих множителей.
Приведем несколько примеров дробей, которые можно упростить:
4/12 не упрощается.
4 является общим множителем как в числителе, так и в знаменателе, поэтому его можно привести к упрощенной форме следующим образом:
Обратите внимание: также дроби, записанные в разной (смешанной) форме.
Подытожим эти шаги, взяв по одному примеру сложения и вычитания.
Время попрактиковаться во всех трех шагах вместе!
Задача на сложение: 3/4 + 1/12
Шаг 1: Приведите знаменатели к одному
Знаменатели равны 4 и 12. 12 кратно 4, поэтому общий знаменатель будет 12.
12 кратно 4, поэтому общий знаменатель будет 12.
6 Шаг 2: Сложите/вычтите числители (сохранив знаменатель)
Шаг 3: Упростите дробь
Чтобы упростить 10/12, общий делитель равен 2
Итак, 10/12= 5/6 (в упрощенной форме)
Следовательно, 3/4 + 1/12= 5/6
Теперь давайте рассмотрим задачу на вычитание:
Пример: 2/5 – 1/3
Шаг 1: Совместите знаменатели
Общий знаменатель будет равен 3 x 5 = 15
Шаг 2: Сложите/вычтите 4 знаменателя 007 Шаг 3: Упростите дробь
1/15 уже в упрощенной форме, так как 1 и 15 не имеют общих множителей.
Связанные материалы: Способы умножения чисел за считанные секунды
Метод бабочки Очень интересный и полезный метод быстрого сложения/вычитания дробей.
Источник В этом методе мы рисуем крылья бабочки, чтобы понять, какие два числа нужно перемножить. Затем мы продолжаем записывать результат в соответствующую антенну. Знаменатели умножаются, а результат записывается внизу живота.
В конце мы просто добавляем/вычитаем антенну и пишем ее над брюшком, чтобы получить результат.
Сложение/вычитание дробей – распространенные ошибки Учителя должны следить за тем, чтобы учащиеся постепенно переходили от конкретного к контекстуальному и вычислительному уровням.
Учащимся нужно дать много примеров, чтобы помочь им преодолеть некоторые распространенные ошибки и неправильные представления:
1. Сложение/вычитание числителей и знаменателей
При сложении/вычитании дробей важно обращать особое внимание на то, как ученики представляют их:
Наиболее распространенная ошибка при сложении дробей — сложение числителей и знаменателей по отдельности, как мы складываем целые числа.
Например: при сложении 2/3 и 1/4 распространенной ошибкой является представление каждой дроби, как показано выше, а затем сложение их вместе, чтобы получить 3/7 в качестве ответа.
Когда учащиеся складывают, комбинируют или находят сумму, складывая вместе целые числа и обе дробные части, кажется разумным, что они рассматривают каждую дробь независимо друг от друга.
Итак, важно подчеркнуть, что дробными частями нельзя манипулировать независимо от их целого.
Вот почему важно иметь общий знаменатель. В случае общего знаменателя дроби можно интерпретировать на одной диаграмме и объединять. Давайте посмотрим на этот же пример, но в целом.
В этом случае общий знаменатель для 2/3 и 1/4 будет равен 12.
Теперь рассмотрим целое, состоящее из 12 частей.
Теперь найдем ⅔ и ¼.
Чтобы найти 2/3 сначала разделите целое на 3 равные части:
2/3 будет 2 из этих 3 равных частей:
/12
Аналогично, чтобы найти 1/4, мы нужно разделить целое на 4 равные части:
1/4 будет:
1/4 = 3/12
8/ части 4 и 1 можно сложить 2/2. сумма равна 11 частей.
сумма равна 11 частей.
2/3 + 1/4 = 8/12+ 3/12 = 11/12
Точно такая же ошибка наблюдается и при вычитании дробей. И числители, и знаменатели вычитаются по отдельности, как вычитаются целые числа.
Например: 5/6 – 1/3 = (5-1)(6-3) = 4/3
Найдем правильный способ решения 5/6 – 1/3 =?
В этом случае общий знаменатель для 5/6 и 1/3 будет равен 6 (общее кратное).
Теперь рассмотрим целое, состоящее из 6 частей:
5/6 будет:
для 1/3. Мы разделяем целое на 3 равных частях:
1/3 будет одной из трех равных частей:
1/3 = 2/6
Сейчас от 5/6 отнимем 1/3, от 5 частей одного и того же целого отнимем 2 части.
5/6 – 1/3 = 5/6 – 2/6 = 3/6
2. Сложение/вычитание числителей без учета знаменателей часто рассматривают их как целые числа.
12/13 + 7/8 = 19, потому что 12 + 7 = 19
12/13 – 7/8 = 5, потому что 12 – 7 = 5
Главное здесь – сделать их понимание дробей конкретным , с самого начала.
3. Сложение/вычитание знаменателей без учета числителей
Некоторые учащиеся складывают только знаменатели и игнорируют числители. Они смотрят на знаменатели как на два целых числа и складывают/вычитают их.
12/13 + 7/8 = 21, потому что 13 + 8 = 21
13/12 – 7/8 = 5, потому что 13 – 8 = 5
Интересные занятия по сложению и вычитанию дробей
Включите простые действия, такие как разрезание предметов реального мира, чтобы развить интерес и лучше понять дроби. Такие действия, как крестики-нолики, БИНГО или сопоставление, могут быть выполнены, чтобы сделать дроби более увлекательными.
Дроби в повседневной жизни
Родители должны поощрять разговоры о дробях с детьми в повседневной жизни. Поощряйте детей применять дроби в повседневных задачах, таких как деление продуктов на равные доли, в измерениях или при приготовлении их любимых новых рецептов. Мы также можем использовать дроби, когда говорим о времени или оценках, которые дети набрали в школе!
Мы также можем использовать дроби, когда говорим о времени или оценках, которые дети набрали в школе!
Рассказывая о дробях, вы избавляетесь от страха перед ними, и детям больше нравится практиковать их.
Игры с дробями Игры побуждают учащихся практиковаться в ответах на множество вопросов, которые им обычно не нравятся в других случаях. Ознакомьтесь с этими играми с забавными дробями на SplashLearn
Модели дробей/манипуляторы
Использование манипулятивных элементов, таких как полоски дробей, модели площадей, кубики лего и числовые линии, делает дроби интересными и увлекательными для детей. Эти манипуляции помогают детям визуализировать дроби и, следовательно, лучше их понимать.
Проблемы со словами на дроби
Решение контекстных задач помогает учащимся связать изучение дробей с реальными жизненными ситуациями. Они понимают значение, необходимость и важность дробей и то, как их применять для решения задач. Вы можете проверить эти игры с дробными словами на SplashLearn и сделать дроби намного проще!
Вы можете проверить эти игры с дробными словами на SplashLearn и сделать дроби намного проще!
Подводя итог: - Учащимся важно понимать, что дроби нельзя закрасить и раскрасить.
- Дроби — это числа, которые используются для представления чисел между любыми двумя последовательными целыми числами.
- Помогите учащимся практиковать дроби, вырезая, вставляя и раскрашивая их, чтобы лучше понимать дроби и получать от них удовольствие.
- Используйте модели дробей, чтобы помочь им визуализировать и понять сложение и вычитание дробей.
- Убедитесь, что они знают, почему шаги сложения/вычитания дробей работают, а не просто слепо применяют шаги.
- Как родитель, используйте дроби в повседневных разговорах, связывайте дроби с контекстом реальной жизни и предоставляйте им примеры из повседневной деятельности, такой как приготовление пищи, выпечка, время и измерения.
Обучение дробям с помощью SplashLearn
Любимое более чем 40 миллионами родителей приложение SplashLearn — это универсальное решение для обучения ваших детей математике и чтению. Вы можете заставить своих маленьких учеников играть в игры на сложение и вычитание дробей или учиться с помощью рабочих листов. Благодаря обучению, согласованному с учебной программой, SplashLearn обеспечивает персонализированный опыт, который адаптируется к потребностям каждого ребенка.
Вы можете заставить своих маленьких учеников играть в игры на сложение и вычитание дробей или учиться с помощью рабочих листов. Благодаря обучению, согласованному с учебной программой, SplashLearn обеспечивает персонализированный опыт, который адаптируется к потребностям каждого ребенка.
Родители, зарегистрируйтесь бесплатно!
Часто задаваемые вопросы (FAQ)
1. Что такое дроби?
Дроби — это числа между целыми числами (0,1,2,3,4). Они представляют собой часть/часть целого. Дробь состоит из двух частей – числителя и знаменателя.
2. Как складывать и вычитать дроби?
Шаг 1 : Уравнять знаменатели
Шаг 2 : Сложить/вычесть числители (сохранив знаменатель)
Шаг 3 : Упростить дробь
3. Как складывать и вычитать дроби с разными знаменателями?
Дроби с разными знаменателями можно складывать путем преобразования их в дроби с одинаковыми знаменателями с помощью эквивалентных дробей.
4. Как складывать и вычитать смешанные числа?
Сначала запишите смешанные числа в виде дробей. Теперь сложите/вычтите так же, как вы делаете это с дробями. В конце не забудьте преобразовать ответ (дробь) в смешанное число!
5. Как складывать и вычитать отрицательные дроби?
Отрицательные дроби можно рассматривать как дроби с отрицательными числителями. Шаги для сложения и вычитания отрицательных дробей остаются такими же, как и для дробей, за исключением того, что теперь детям нужно будет добавлять отрицательные или положительные числители.
Сложение и вычитание в отличие от дробей План урока: проверьте знаменатель!
Представлено: Анджелой Уотсон
Уровни классов: 3–5, 6–8
В этом плане урока, адаптированном для классов 3–8, учащиеся используют BrainPOP, чтобы научиться находить наименьший общий знаменатель в уравнениях, а также складывать и вычитание в отличие от дробей. Они также объяснят словами и картинками, как складывать и вычитать дроби.
План урока Согласование общих основных стандартов штата
Студенты:
- Определите наименьший общий знаменатель в уравнениях 90 314.
- Сложение и вычитание дробей с разными знаменателями
- Объясните словами и картинками, как складывать и вычитать дроби
Материалов:
- Два небольших контейнера, сумки или корзины для карточек во время занятия
- Один большой лист нелинованной бумаги на каждую пару учащихся
- Компьютер и проектор для показа ресурсов BrainPOP
- Одна каталожная карточка на каждого учащегося
- Ножницы для студентов, чтобы разрезать каталожные карточки (или вы можете их предварительно разрезать)
Словарь:
дробь, половина, числитель, знаменатель, общий знаменатель, LCD (наименьший общий знаменатель)
Подготовка:
На первом уроке проведите повторение сложения дробей с одинаковыми знаменателями и познакомьте учащихся с концепцией наименьшего общего знаменателя (LCD). Убедитесь, что учащиеся понимают, как находить общие кратные, и вместе потренируйтесь решать несколько задач на сложение и вычитание дробей с разными знаменателями.
Убедитесь, что учащиеся понимают, как находить общие кратные, и вместе потренируйтесь решать несколько задач на сложение и вычитание дробей с разными знаменателями. Процедура урока:
- После вводного урока по сложению и вычитанию дробей с разными знаменателями активизируйте знания учащихся, начав этот урок с вопроса на странице «Полезная литература»: Какой самый простой способ найти общий знаменатель двух дробей? Дайте учащимся время вспомнить и обсудить эту информацию с партнером, а затем поделитесь страницей «Полезное чтение» с классом.
- Углубите понимание темы учащимися, показав фильм «Сложение и вычитание дробей».
- Раздайте каталожные карточки каждому учащемуся и попросите их сложить карточки пополам. Каждый учащийся должен написать числовое предложение, которое включает сложение или вычитание дробей с разными знаменателями, поместив часть ответа уравнения на вторую половину каталожной карточки. Попросите учащихся показать свое уравнение партнеру, чтобы проверить его точность.

- Попросите учеников разрезать свои каталожные карточки пополам, чтобы задача и ответ на их уравнение теперь были на двух отдельных частях.
- Соберите все части учетных карточек от учеников, поместив задачи в один контейнер, а ответы в другой.
- Разделите класс пополам и случайным образом раздайте задачи одной половине класса, а ответы другой половине.
- По вашему сигналу учащиеся встают и толкают свои стулья, а затем подходят к учащимся в группе напротив них, чтобы найти совпадающую половину их уравнения. Затем учащиеся должны сесть рядом друг с другом, чтобы указать, что они нашли свою пару.
- Организуйте обсуждение всем классом оставшихся учеников, которые не могут найти совпадение, чтобы убедиться, что у всех есть правильное уравнение. Возможно ли, что несколько задач могут иметь один и тот же ответ?
- Предложите учащимся вернуть свои каталожные карточки в контейнеры и вернуться на свои места, а затем повторите игру еще один или два раунда.

- После финального раунда игры пусть ученики сохранят свои каталожные карточки и партнеров. Попросите пары учащихся найти наименьший общий знаменатель дробей на карточке и написать его на обратной стороне.
- Раздайте большой лист нелинованной бумаги каждой паре учащихся и попросите их скопировать уравнение с карточек и наименьший общий знаменатель уравнения на большой лист.
- Затем учащиеся должны использовать большой лист бумаги, чтобы проиллюстрировать дроби таким образом, чтобы показать взаимосвязь между исходным уравнением и уравнением, в котором используется наименьший общий знаменатель, чтобы сделать возможным сложение/вычитание. Студенты могут пожелать добавить инструкции, которые показывают, как преобразовывать числа и решать.
- Соедините каждую пару учеников с другой парой, чтобы они образовали группу из 4 человек, и пусть они представят свои плакаты двум другим ученикам в своей группе.
Расширение деятельности:
Предложите учащимся выполнить викторину в качестве оценки.
Шаг 3 : Упростите дробь
Как сделать знаменатели одинаковыми?
В случае одинаковых дробей знаменатели уже будут одинаковыми, поэтому вы можете пропустить шаг 1 и перейти к шагу 2.
 кратное другому знаменателю
кратное другому знаменателюЕсли у обоих знаменателей нет общего множителя, то вы умножаете оба знаменателя, чтобы получить общий знаменатель.

Давайте посмотрим, как мы получим 20 в качестве общего знаменателя для обеих дробей:
Возьмем наши предыдущие примеры и продолжим оттуда:

Продолжим наши предыдущие примеры:
Знаменатели равны 4 и 12.
 12 кратно 4, поэтому общий знаменатель будет 12.
12 кратно 4, поэтому общий знаменатель будет 12.Чтобы упростить 10/12, общий делитель равен 2
Пример: 2/5 – 1/3
Шаг 1: Совместите знаменатели
Общий знаменатель будет равен 3 x 5 = 15
Шаг 3: Упростите дробь
1/15 уже в упрощенной форме, так как 1 и 15 не имеют общих множителей.
Связанные материалы: Способы умножения чисел за считанные секундыМетод бабочки
Очень интересный и полезный метод быстрого сложения/вычитания дробей.
В этом методе мы рисуем крылья бабочки, чтобы понять, какие два числа нужно перемножить. Затем мы продолжаем записывать результат в соответствующую антенну. Знаменатели умножаются, а результат записывается внизу живота.
В конце мы просто добавляем/вычитаем антенну и пишем ее над брюшком, чтобы получить результат.
Сложение/вычитание дробей – распространенные ошибкиУчителя должны следить за тем, чтобы учащиеся постепенно переходили от конкретного к контекстуальному и вычислительному уровням.
Учащимся нужно дать много примеров, чтобы помочь им преодолеть некоторые распространенные ошибки и неправильные представления:
1. Сложение/вычитание числителей и знаменателей
При сложении/вычитании дробей важно обращать особое внимание на то, как ученики представляют их:
Наиболее распространенная ошибка при сложении дробей — сложение числителей и знаменателей по отдельности, как мы складываем целые числа.
Например: при сложении 2/3 и 1/4 распространенной ошибкой является представление каждой дроби, как показано выше, а затем сложение их вместе, чтобы получить 3/7 в качестве ответа.
Когда учащиеся складывают, комбинируют или находят сумму, складывая вместе целые числа и обе дробные части, кажется разумным, что они рассматривают каждую дробь независимо друг от друга.
Итак, важно подчеркнуть, что дробными частями нельзя манипулировать независимо от их целого.
Вот почему важно иметь общий знаменатель. В случае общего знаменателя дроби можно интерпретировать на одной диаграмме и объединять. Давайте посмотрим на этот же пример, но в целом.
В этом случае общий знаменатель для 2/3 и 1/4 будет равен 12.
Теперь рассмотрим целое, состоящее из 12 частей.
Теперь найдем ⅔ и ¼.
Чтобы найти 2/3 сначала разделите целое на 3 равные части:
2/3 будет 2 из этих 3 равных частей:
/12
Аналогично, чтобы найти 1/4, мы нужно разделить целое на 4 равные части:
1/4 будет:
1/4 = 3/12
8/ части 4 и 1 можно сложить 2/2. сумма равна 11 частей.
сумма равна 11 частей.
2/3 + 1/4 = 8/12+ 3/12 = 11/12
Точно такая же ошибка наблюдается и при вычитании дробей. И числители, и знаменатели вычитаются по отдельности, как вычитаются целые числа.
Например: 5/6 – 1/3 = (5-1)(6-3) = 4/3
Найдем правильный способ решения 5/6 – 1/3 =?
В этом случае общий знаменатель для 5/6 и 1/3 будет равен 6 (общее кратное).
Теперь рассмотрим целое, состоящее из 6 частей:
5/6 будет:
для 1/3. Мы разделяем целое на 3 равных частях:
1/3 будет одной из трех равных частей:
1/3 = 2/6
Сейчас от 5/6 отнимем 1/3, от 5 частей одного и того же целого отнимем 2 части.
5/6 – 1/3 = 5/6 – 2/6 = 3/6
2. Сложение/вычитание числителей без учета знаменателей часто рассматривают их как целые числа.
Включите простые действия, такие как разрезание предметов реального мира, чтобы развить интерес и лучше понять дроби. Такие действия, как крестики-нолики, БИНГО или сопоставление, могут быть выполнены, чтобы сделать дроби более увлекательными.
Родители должны поощрять разговоры о дробях с детьми в повседневной жизни. Поощряйте детей применять дроби в повседневных задачах, таких как деление продуктов на равные доли, в измерениях или при приготовлении их любимых новых рецептов.
 Мы также можем использовать дроби, когда говорим о времени или оценках, которые дети набрали в школе!
Мы также можем использовать дроби, когда говорим о времени или оценках, которые дети набрали в школе!Использование манипулятивных элементов, таких как полоски дробей, модели площадей, кубики лего и числовые линии, делает дроби интересными и увлекательными для детей. Эти манипуляции помогают детям визуализировать дроби и, следовательно, лучше их понимать.
Решение контекстных задач помогает учащимся связать изучение дробей с реальными жизненными ситуациями. Они понимают значение, необходимость и важность дробей и то, как их применять для решения задач.
 Вы можете проверить эти игры с дробными словами на SplashLearn и сделать дроби намного проще!
Вы можете проверить эти игры с дробными словами на SplashLearn и сделать дроби намного проще!  Вы можете заставить своих маленьких учеников играть в игры на сложение и вычитание дробей или учиться с помощью рабочих листов. Благодаря обучению, согласованному с учебной программой, SplashLearn обеспечивает персонализированный опыт, который адаптируется к потребностям каждого ребенка.
Вы можете заставить своих маленьких учеников играть в игры на сложение и вычитание дробей или учиться с помощью рабочих листов. Благодаря обучению, согласованному с учебной программой, SplashLearn обеспечивает персонализированный опыт, который адаптируется к потребностям каждого ребенка.Шаг 2 : Сложить/вычесть числители (сохранив знаменатель)
Шаг 3 : Упростить дробь





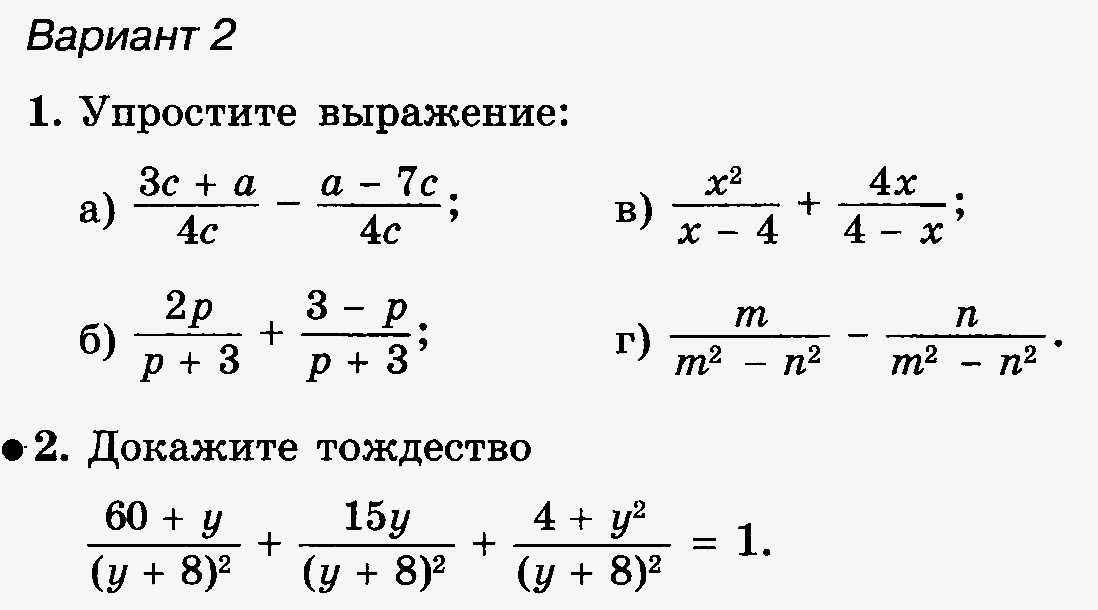 Убедитесь, что учащиеся понимают, как находить общие кратные, и вместе потренируйтесь решать несколько задач на сложение и вычитание дробей с разными знаменателями.
Убедитесь, что учащиеся понимают, как находить общие кратные, и вместе потренируйтесь решать несколько задач на сложение и вычитание дробей с разными знаменателями. 