4.3. Статистическое оценивание. Оценка параметров генеральной совокупности. Точечная оценка и ее свойства
Числовые характеристики генеральной совокупности называются Параметрами генеральной совокупности.
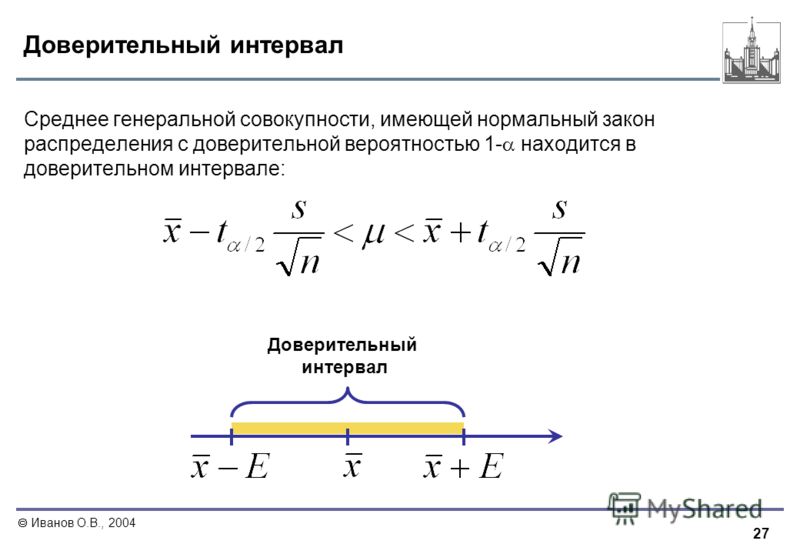
Например, для нормального распределения это математическое ожидание и среднее квадратическое отклонение (СКО), для равномерного распределения – это границы интервала, в котором наблюдаются значения этой случайной величины
Оценка параметра – соответствующая числовая характеристика, рассчитанная по выборке. Если оценка определяется одним числом, она называется Точечной оценкой.
Например, среднее арифметическое выборочных значений служит оценкой математического ожидания. Выборочные значения случайны, поэтому оценки можно рассматривать как случайные величины. Построим точечную оценку параметра по выборке как значение некоторой функции и перечислим «желаемые» свойства оценки .
Определение 4.1. Оценка называется Несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра: .
Данное свойство характеризует отсутствие Систематической ошибки, т. е. при многократном использовании вместо параметра его оценки среднее значение ошибки приближения равно нулю.
Так, выборочное среднее арифметическое является Несмещенной оценкой математического ожидания, а выборочная дисперсия – Смещенная оценка генеральной дисперсии D. Несмещенной оценкой генеральной дисперсии является оценка («исправленная дисперсия»)
Определение 4.2. Оценка называется Состоятельной, если она сходится по вероятности к оцениваемому параметру при
Данное свойство характеризует улучшение оценки с увеличением объема выборки.
Сходимость по вероятности означает, что при большом объеме выборки вероятность больших отклонений оценки от истинного значения мала.
Определение 4.3.. Несмещенная оценка является Эффективной, если она имеет наименьшую среди всех несмещенных оценок дисперсию.
Пример 4.4. :
:1. Вычислить среднее значение массы тела детей 6 лет.
2. Если выборочное среднее вычисляется по вариационному ряду, то находят сумму произведений вариант на соответствующие частоты, и делят на количество элементов в выборке: .
3. В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего значениями вариант считают середины интервалов. Так, для вычисления среднего значения массы тела женщин 30 лет из примера 4.3. используют формулу:
.
Другими характеристиками являются Мода И Медиана.
В теории вероятностей Модой Мо дискретной случайной величины называется ее значение, которое имеет максимальную вероятность. Модой непрерывной случайной величины называется такое ее значение, при котором достигается максимум плотности распределения Закон распределения называется унимодальным, если мода единственна. В математической статистике мода
Медианой называется варианта, расположенная в центре Ранжированного ряда. Если ряд состоит из четного числа вариант, то медианой считают среднее арифметическое двух вариант, расположенных в центре ранжированного ряда.
Пример 4.5. Найти моду и медиану выборочной совокупности по массе тела детей 6 лет.
Ответ: Мо = 24; Ме = 24.
Основные числовые характеристики выборочной совокупности:
1) Размах вариационного ряда R=Xmax – Xmin. Этот показатель является наиболее простой характеристикой рассеяния и показывает диапазон варьирования величины. Этой характеристикой пользуются при работе с малыми выборками;
2) Выборочное среднее
находится как взвешенное среднее арифметическое , которое характеризует среднее значение признака X в пределах рассматриваемой выборки;3) Выборочная дисперсия Определяется по формуле: , которая является мерой рассеяния возможных значений показателя X вокруг своего среднего значения, и ее размерность совпадает с квадратом размерности варианты;
4) Выборочное среднее квадратическое отклонение описывает абсолютный разброс значений показателя X. Его размерность совпадает с размерностью варианты;
Его размерность совпадает с размерностью варианты;
5) «Исправленная» Дисперсия (вычисляют при малых N, n<30) и «Исправленное» стандартное отклонение ;
6) Коэффициент вариации характеризует относительную изменчивость показателя X, то есть относительный разброс вокруг его среднего значения . Коэффициент вариации является безразмерной величиной, поэтому он пригоден для сравнения рассеяния вариационных рядов, варианты которых имеют различную размерность.
Пример 4.6.: Измерена длина (Х) и масса тела (Y) девочек 10-ти лет. Получены следующие показатели: Х=130 см, SХ = 5 см, Y = 32 кг, SY = 4 кг. Какая величина имеет большую вариативность?
Так как длина и масса тела измеряются в разных единицах, то вариативность нельзя сравнить при помощи СКО. Необходимо вычислить относительный показатель вариации.
Таким образом, масса тела имеет большую вариативность, чем длина тела.
| < Предыдущая | Следующая > |
|---|
Точечная оценка параметров генеральной совокупности — Студопедия
Поделись
Точечная оценка – это оценка, которая определяется одним числом. И это число определяется по выборке. Это функция результатов выборки, и она является точечной оценкой генерального параметра, т. е. принимает только одно значение.
Качество оценки устанавливается по трем свойствам: быть состоятельной, эффективной и несмещенной.
Точечная оценка называется состоятельной, если при увеличении объема выборки выборочная характеристика стремится к соответствующей характеристике генеральной совокупности.
Точечная оценка называется эффективной, если она имеет наименьшую дисперсию выборочного распределения по сравнению с другими аналогичными оценками.
Точечную оценку называют несмещенной, если ее математическое ожидание равно оценивающему параметру при любом объеме выборки.
Несмещенной оценкой генеральной средней (математического ожидания) служит выборочная средняя :
где — варианты выборки; — частота встречаемости вариант ; n — объем выборки.
Выборочная средняя является несмещенной оценкой генеральной средней, так как ,т.е. она эквивалентна истинной средней в генеральной совокупности (популяции).
Выборочная дисперсия не обладает свойством несмещенности. Это смещенная оценка генеральной дисперсии .
— это и означает, что выборочная дисперсия является смещенной оценкой
На практике используют исправленную выборочную дисперсию , которая является несмещенной оценкой дисперсии генеральной совокупности:
Кроме того, в расчетах используют S — исправленное среднее квадратическое отклонение, называемое стандартным отклонением в выборке и ошибку выборочной средней
(стандартную ошибку средней) :
которая отражает точность оценки.
Стандартная ошибка уменьшится, т. е. оценка станет более точной, если объем выборки n увеличится и данные имеют небольшое рассеяние S.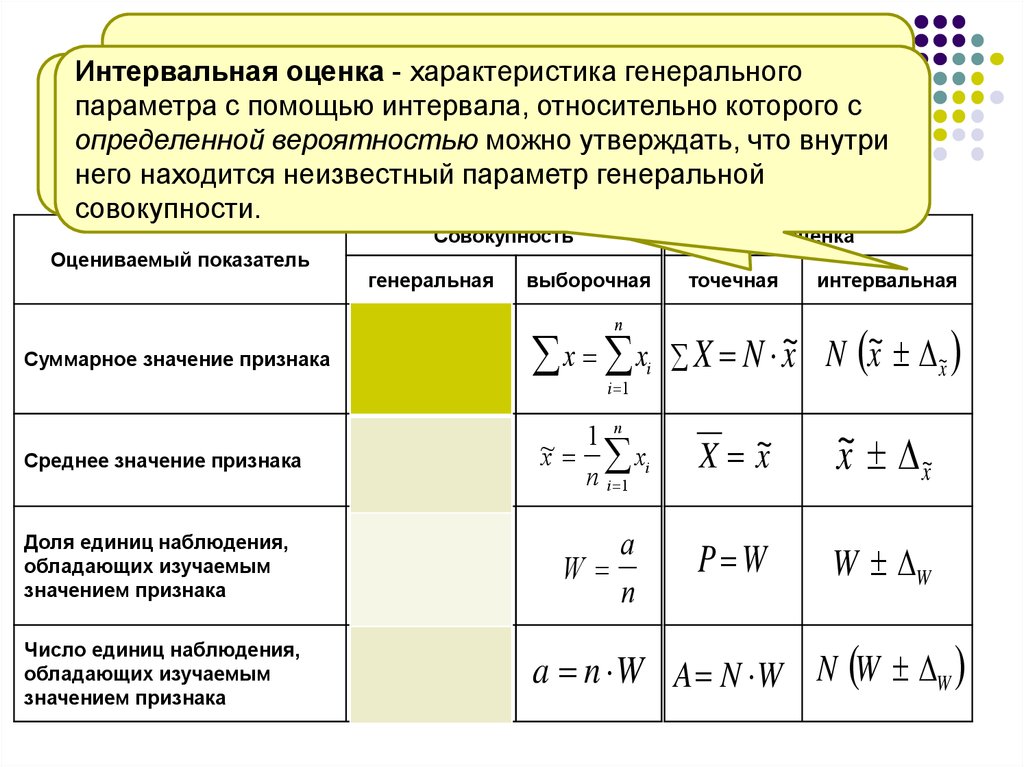
Рассмотрим разницу между S — стандартным отклонением в выборке и — стандартной ошибкой среднего.
На первый взгляд, они очень схожи, но их используют в разных целях. Среднее квадратическое отклонение S отражает вариабельность в значениях данных, и его указывают, если надо пояснить изменчивость в наборе данных, разброс данных.
Ошибка выборочной средней характеризует точность выборочного среднего и должна быть указана, если интерес представляет среднее значение выборки.
Из генеральной совокупности извлечена выборка объема n=50.
Найти несмещенную оценку генеральной средней.
Решение:
По выборке объема 30 найдена смещенная оценка = 3 генеральной дисперсии. Найти несмещенную оценку дисперсии генеральной совокупности.
Решение:
Эта несмещенная оценка равна исправленной дисперсии:
Найти несмещенную оценку генеральной средней, дисперсии генеральной совокупности и стандартное отклонение по выборке объема 12, описывающую продолжительность в секундах физической нагрузки до развития приступа стенокардии:
289,203,359,243,232,210,251,251,246,224,239,220,211.
Решение:
Варианты заданий
№ 13.1. При исследовании клинической оценки тяжести серповидноклеточной анемии была получена выборка объема 33.
0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 3; 3; 3; 3; 4; 4; 5;
5;5;5;6;7;9;10;11.
Найдите среднюю, среднее квадртическое отклонение и
медиану. Можно ли считать, что выборка извлечена из
совокупности с нормальным распределением?
№ 13.2. Исследуя продолжительность (в секундах) физической нагрузки до развития приступа стенокардии у 12 человек с ишемической болезнью сердца, получили следующие данные:
289;203; 359; 243; 232; 210; 215; 246; 224; 239; 220; 211. Найдите среднюю, среднее квадратическое отклонение, медиану. Можно ли считать, что данная выборка извлечена из совокупности с нормальным распределением?
№ 13.3. Найдите среднее число очков, выпадающих при бросании игральной кости. Опишите это распределение. Может ли оно быть нормальным?
Может ли оно быть нормальным?
Оценка в баллах: определение, примеры — статистика Как сделать
Примером точечной оценки является выборочная дисперсия. Изображение: Бостонский университет
Что такое балльная оценка?
Посмотрите видео с обзором и примером или прочитайте ниже:
Оценка в баллах Определение и пример
Посмотрите это видео на YouTube.
Видео не видно? Кликните сюда.
Проще говоря, любая статистика может быть точечной оценкой. Статистика — это оценка некоторого параметра в совокупности. Например:
- Стандартное отклонение выборки (s) представляет собой точечную оценку стандартного отклонения генеральной совокупности (σ).
- Среднее значение выборки (̄x) представляет собой точечную оценку среднего значения генеральной совокупности, μ.
- Выборочная дисперсия (s 2 ) является точечной оценкой дисперсии генеральной совокупности (σ 2 ).

Говоря более формально, оценка получается в результате точечной оценки, примененной к набору выборочных данных. Точки — это отдельные значения по сравнению с интервальными оценками, которые представляют собой диапазон значений. Например, доверительный интервал является одним из примеров интервальной оценки.
Нахождение оценок
Четыре наиболее распространенных способа нахождения оценок:
- Метод моментов : основан на законе больших чисел и использует относительно простые уравнения для нахождения точечных оценок. Часто не слишком точен и склонен к предвзятости. Подробнее .
- Максимальное правдоподобие: использует модель (например, нормальное распределение) и использует значения в модели для максимизации функции правдоподобия. Это приводит к наиболее вероятному параметру для выбранных входных данных.
- Байесовские оценщики: минимизируют средний риск (ожидание случайных величин).
 Подробнее .
Подробнее . - Наилучшие несмещенные оценщики: для аппроксимации параметра можно использовать несколько несмещенных оценщиков. Какой из них «лучший», зависит от того, какой параметр вы пытаетесь найти. Например, с дисперсией оценщик с наименьшей дисперсией является «лучшим». Подробнее .
Ссылки
Beyer, WH CRC Standard Mathematical Tables, 31st ed. Бока-Ратон, Флорида: CRC Press, стр. 536 и 571, 2002 г.
Агрести А. (1990) Категориальный анализ данных. Джон Уайли и сыновья, Нью-Йорк.
Додж, Ю. (2008). Краткая энциклопедия статистики. Спрингер.
«Кляйн, Г. (2013). Мультфильм Введение в статистику. Хилл и Вамг».
УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Оценка в баллах: определение, примеры» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/probability-and-statistics/statistics-definitions/point-estimate/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
Средняя оценка
Марко Табога, доктор философии
Средняя оценка статистический задача вывода, в которой выборка используется для получения точечная оценка среднего неизвестного распределение.
Проблема обычно решается с использованием выборочного среднего в качестве оценка среднего значения населения.
В этой лекции мы приводим два примера, касающихся:
нормальные образцы IID;
Образцы IID, которые не обязательно являются нормальными.
Для каждого из этих двух случаев мы получаем ожидаемое значение, дисперсию и асимптотические свойства средней оценки.
Содержание
Нормальные образцы IID
Оценщик
Ожидаемое значение оценщика
Variance of the estimator
Distribution of the estimator
Risk of the estimator
Consistency of the estimator
IID samples
The estimator
Ожидаемое значение оценщика
Дисперсия оценщика
Распределение оценщика
Риск оценщика
Consistency of the estimator
Asymptotic normality
Solved exercises
Exercise 1
Exercise 2
Normal IID samples
В этом примере оценки среднего, который, вероятно, является наиболее важным в
История статистики, выборка взята из
нормальное распределение.
В частности, мы наблюдаем реализацию независимые случайные величины , …, , все имеют нормальное распределение с неизвестным средним и дисперсия .
Оценщик
В качестве оценки среднего , мы используем образец среднее
Ожидаемое значение оценщика
Ожидаемое значение оценщика равно истинному среднему .
Это можно доказать, используя линейность ожидаемого значение:
Следовательно, оценщик является беспристрастным.
Дисперсия оценщика
Дисперсия оценщика равно .
Это можно доказать, используя формулу дисперсии независимого сумма:
Таким образом, дисперсия оценки стремится к нулю по мере увеличения размера выборки. стремится к бесконечности.
Рассылка оценщика
Оценщик имеет нормальный распределения:
Доказательство
Обратите внимание, что выборочное среднее
представляет собой линейную комбинацию нормальных и независимых случайных величин
(все коэффициенты линейной комбинации равны
). Следовательно,
это нормально, потому что
линейная комбинация
независимые нормальные случайные величины нормальны. Среднее значение и дисперсия
дистрибутива уже получено
выше.
Следовательно,
это нормально, потому что
линейная комбинация
независимые нормальные случайные величины нормальны. Среднее значение и дисперсия
дистрибутива уже получено
выше.
Риск оценщика
Среднеквадратическая ошибка оценщик
Непротиворечивость оценщика
Последовательность является последовательностью IID с конечным средним значением.
Следовательно, он удовлетворяет условиям Усиленный закон больших Колмогорова Числа.
Следовательно, выборочное среднее почти наверное сходится к истинному среднему :что есть, оценщик сильно последователен.
Оценщик тоже слабо непротиворечивым, потому что сходимость почти наверняка подразумевает сходимость в вероятность:
образцы IID
В этом примере оценки среднего мы ослабляем сделанное ранее предположение о нормальность.
Выборка состоит из реализаций
независимые случайные величины
,
. ..,
,
все имеют одинаковое распределение со средним значением
и дисперсия
.
..,
,
все имеют одинаковое распределение со средним значением
и дисперсия
.
Оценщик
Опять же, оценка среднего образец среднее значение:
Ожидаемое значение оценщика
Ожидаемое значение оценщика равно истинному среднее значение:
Следовательно, оценщик является несмещенным.
Доказательство такое же, как и в предыдущем примере.
Дисперсия оценщика
Дисперсия оценщика
И в этом случае доказательство такое же, как и в предыдущем примере.
Распределение оценщика
В отличие от предыдущего примера, оценщик не обязательно имеет нормальное распределение: его распределение зависит от те из членов последовательности .
Однако ниже мы увидим, что
асимптотически имеет нормальное распределение, то есть сходится к нормальному
случайная величина, когда
становится большим.
Риск оценщика
Среднеквадратическая ошибка оценки это
Доказательство такое же, как и в предыдущем примере.
Непротиворечивость оценщика
Поскольку последовательность является последовательностью IID, члены которой имеют конечное среднее значение, она удовлетворяет условиям Усиленный закон больших чисел Колмогорова.
Следовательно, оценщик является как строго непротиворечивым, так и слабо непротиворечивым (см. пример выше).
Асимптотическая нормальность
Последовательность представляет собой последовательность IID с конечным средним значением и дисперсией.
Следовательно, он удовлетворяет условиям Линдеберг-Леви Центральный Предельная теорема.
Следовательно, выборочное среднее
асимптотически нормально:
куда
является стандартной нормальной случайной величиной и
обозначает сходимость в распределении.
Другими словами, выборка означает сходится по распределению к нормальному случайному переменная со средним значением и дисперсия .
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Рассмотрим эксперимент, который может иметь только два исхода: либо успех, либо вероятность , или отказ, с вероятностью .
Вероятность успеха неизвестна, но мы знаем что
Предположим, что мы можем независимо повторить эксперимент столько раз, сколько желать и использовать отношения оценщик .
Какое минимальное количество опытов нужно провести, чтобы убедиться, что стандартное отклонение оценщика меньше 1/100?
Раствор
Обозначим
в
оценщик
.
Это может быть написано
как где
— количество повторений эксперимента и
находятся
независимые случайные величины, имеющие
Распределение Бернулли с
параметр
.


 Подробнее .
Подробнее .