Транспонированная матрица — Энциклопедия по экономике
Транспонировать матрицу размерностью 5 строк на 2 столбца или сокращенно — 5×2 (рис. 5.18). Элементы матрицы находятся в ячейках А1 В5. Первый элемент транспонированной матрицы начинается в ячейке D3. [c.366]Для оценки вектора неизвестных параметров р применим метод наименьших квадратов. Так как произведение транспонированной матрицы е» на саму матрицу е [c.83]
Знаком обозначается операция транспонирования матриц. [c.83]
Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. (ХЬУ=Ь Х после раскрытия скобок получим [c.84]
Найдем транспонированный вектор остатков е . Так как при транспонировании матрица (Х Х) не меняется, т. е. [c.95]
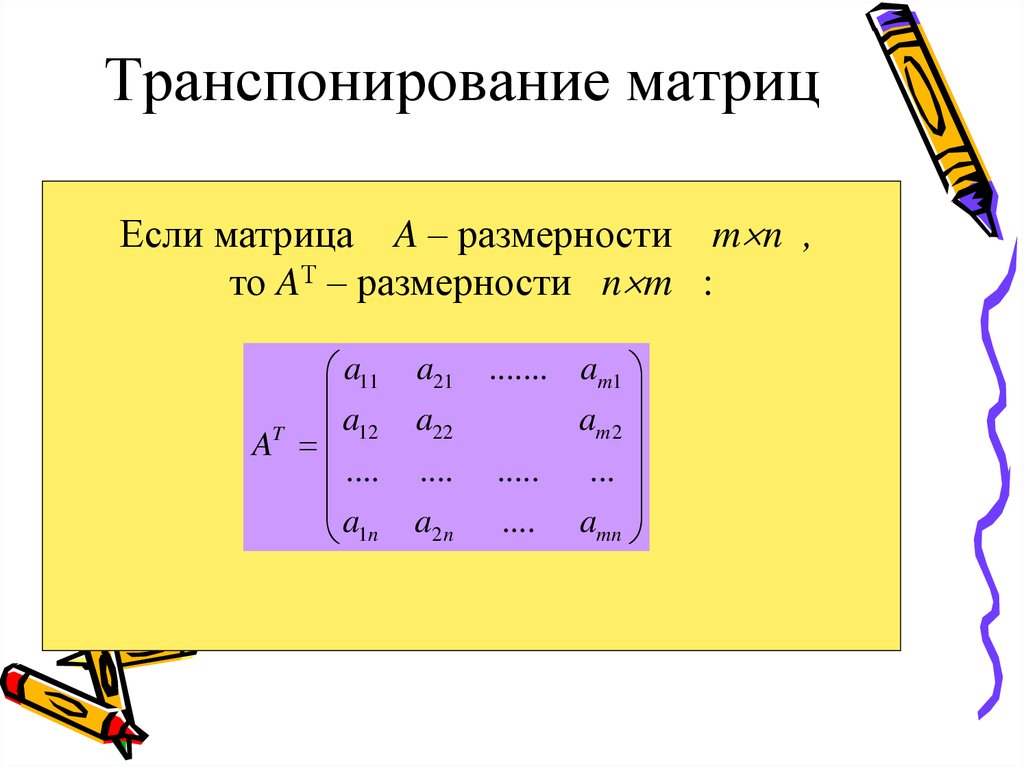
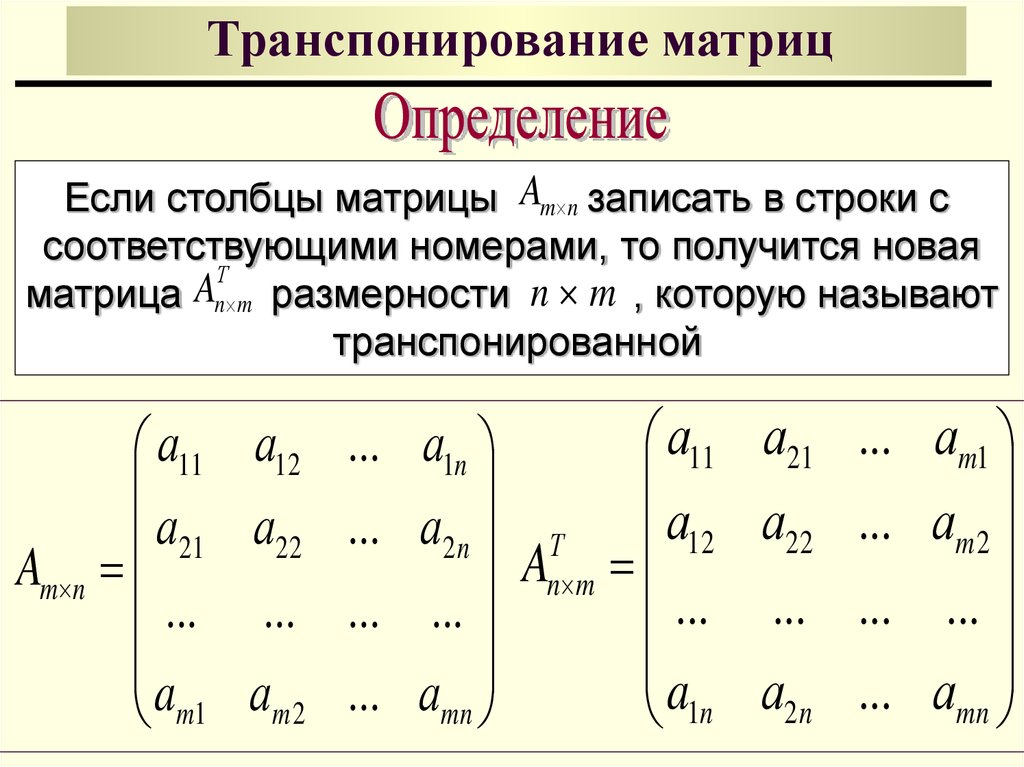
Транспонирование матрицы — переход от матрицы А к матрице А (или АТ), в которой строки и столбцы поменялись местами с сохранением их порядка. [c.260]
Чоу 122, 123, 124 Точечная оценка 44 Транспонирование матрицы 260, 261
[c.
А — матрица кредитов предприятий (транспонированная матрица ). [c.84]
Отсюда видно, что при перемножении транспонированной матрицы на исходную (при условии, что столбцы исходной матрицы ортогональны) получаемая результирующая матрица является диагональной. Это свойство используется при планировании экспериментов уровни факторов выбираются так, чтобы векторы-столбцы исходной матрицы были ортогональны. [c.163]
Составляем исходную и транспонированную матрицы [c.167]
Вычисляем информационную матрицу, для чего транспонированную матрицу умножаем на исходную [c.188]
Рассмотрим транспонированную матрицу дТ. Из свойств определителя следует, что характеристическое уравнение матрицы дТ совпадает с характеристическим уравнением мат- [c.263]
Здесь det А — детерминант (определитель) этой матрицы [А..] — транспонированная матрица алгебраических дополнений. [c.233]
Для 7п х п матрицы А = (а ) транспонированной матрицей будем называть п х 7п матрицу Д, ij-й элемент которой равен a,ji.
Транспонированной матрицей к Л, приведенной в (1), будет [c.32]
При вычислении якобиана функций, связанных с транспонированием матриц, часто приходится иметь дело с коммутационной матрицей К. Например, дифференциал функции [c.238]
Из (8) следует, что JJL = у. Прибавляя (7) к транспонированной матрице и используя (9), получим l l(Z — ггП) «1 = 0 и, как следствие, желаемый результат. П [c.396]
Если обозначить транспонированную матрицу X через А, то матрицы для записи нормальных уравнений могут быть представлены в виде [c.248]
Назовем эту таблицу для краткости таблицей выигрышей и обозначим ее буквой S, что понадобится нам при дальнейшем изложении. В математике таблицы чисел называются матрицами и над ними определены операции сложения, вычитания, умножения и транспонирования. Нам понадобятся только операции вычитания (сложения) и транспонирования матриц. [c.15]
Вектор-столбец кредитовых оборотов получаем умножением матрицы кредитовых оборотов, т. е. транспонированной матрицы, на оператор выделения итогового столбца [c.122]
е. транспонированной матрицы, на оператор выделения итогового столбца [c.122]
Для понимания главы 7 в целом достаточно того, что в ней сообщено об операции транспонирования матриц (таблиц), но, вместе с тем полезно иметь под рукой небольшой справочник, где бы содержались необходимые сведения о матрицах и основных операциях над ними. [c.363]
А а.. = а , т. е. он равен типичному элементу транспонированной матрицы A n m с переставленными (инвертированными индексами для всех i = 1, 2,. .., m и j = 1, 2,. .., п. В связи с этим, можно дать более строгое определение операции транспонирования матрицы. [c.376] Дважды транспонированная матрица всегда равна исходной матрице, т. е. всегда (А ) = А . [c.376]
Это свойство легко доказать, основываясь ла последнем определении транспонированной матрицы. [c.377]
Таким образом, четное число операций транспонирования матрицы не изменяет ее, нечетное число операций транспонирования исходной матрицы изменяет ее в общем случае. [c.377]
[c.377]
Задача теперь состоит только в том, чтобы найти такие проводки S(I, J), чтобы каждая их разность была бы равна соответствующему элементу транспонированной матрицы, т. е. нужно заполнить матрицу дебетовых оборотов S таким образом, чтобы AS = S — S и тогда будет получен нулевой баланс [c.384]
Из транспонированной матрицы сводных проводок S путем ее умножения на специальный вектор-столбец em +, выделяем вектор-столбец кредитовых оборотов [c.402]
Определение. Транспонированной матрицей называется матрица, у которой строки и столбцы поменялись местами, а именно для т х п матрицы А = (ojj) транспонированной является n x т матрица А = (а -), где о — = Ojj. Например, [c.490]
Предложение. Свойства операции транспонирования матриц (А + В) = А + В, (А) = А. [c.490]
См. также Блочная матрица, Блоч-но-диагональная матрица, Блочно-треу-голъная матрица, Вырожденная матрица, Диагональная матрица, Единичная матрица, Идемпотентная матрица, Квадратная матрица, Транспонированная матрица, Треугольная матрица, а также Алгебраическое дополнение, Главная диагональ матрицы, Обращение матрицы, Определитель матрицы, Плотность матрицы, Разлоокимость матрицы, Ранг матрицы. [c.188]
[c.188]
ТРАНСПОНИРОВАННАЯ МАТРИЦА [transposed matrix] — результат операции транспонирования, т.е. перемены местами столбцов и строк исходной матрицы. Если исходная матрица [а.], то транспонированная по отношению к ней записывается [а]. [c.366]
Определяется решение о з (t) системы г э = — Л г з, где А — транспонированная матрица. Таккака1=0, то система принимает вид (аз = 1) [c.87]
Последний пример -транепонирование симметричной матрицы в результате транспонирования ничего не изменилось и А = А. Во всех остальных случаях операция транспонирования матрицы изменяет ее и в общем случае А Ф А. Например, при транспонировании других, также особого вида матриц происходит их изменение [c.375]
Рассмотрим n-мерное векторное пространство Rn, снабженное стандартным евклидовым скалярным произведением (х, у) = х у = XtYt, где х — транспонированная матрица, т. е. в данном случае 1 х п вектор-строка. Пусть [c.36]
RESET-тест, 133 Точная идентификация, 236 Транспонирование матрицы, 490 Тренд, 285
[c.
Оператор транспонирования (клавиши trl + 1 ) Ат. Возвращает транспонированную матрицу размерности п х m (исходная матрица размерностью п х т). [c.178]
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Транспонирование матрицы.
 Онлайн калькулятор
Онлайн калькулятор
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
При помощи данного калькулятора вы можете легко транспонировать матрицу и получить подробное решение с объяснением
Как транспонировать матрицу
Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов.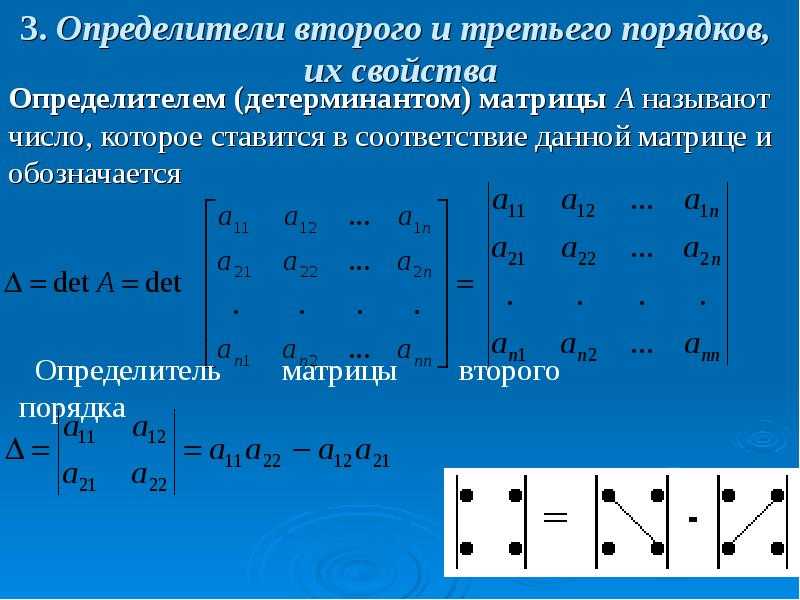 Элементы матрицы обозначаются как aij, где i – номер строки, j – номер столбца.
Элементы матрицы обозначаются как aij, где i – номер строки, j – номер столбца.
Транспонированная матрица для матрицы A обозначается AT
Для того чтобы транспонировать матрицу A необходимо каждую строку данной матрицы представить в виде столбца соблюдая порядок.
При транспонировании матрицы A размерности m × n получаем матрицу AT размерности n × m.
Приведем пример, транспонируем матрицу A.
| A = |
|
|||||||||
Решение
Как было сказано выше, для того, чтобы получить транспонированную матрицу AT из исходной матрицы A необходимо каждую строку исходной матрицы A записать в виде столбца в том же порядке.
При транспонировании матрицы A размерности m × n получаем матрицу AT размерности n × m
| 3 × 3 | |||||||||||||||||||||
| A = |
|
= |
|
| A = |
|
где, | a11 = 0 |
|||||||||
Так как ATij = Aji тогда
| 3 × 3 | |||||||||||||||||||||
| AT = |
|
= |
|
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Линейная алгебра на Python.[Урок 2].Транспонирование Матрицы
В этом уроке мы рассмотрим операцию “транспонирование матрицы” и как она выполняется на Python. Также разберем на примерах свойства этой операции.
Транспонирование матрицыТранспонирование матрицы – это процесс замены строк матрицы на ее столбцы, а столбцов соответственно на строки. Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T.
Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T.
➣ Численный пример
Для исходной матрицы:
Транспонированная будет выглядеть так:
➤ Пример на Python
Решим задачу транспонирования матрицы на Python. Создадим матрицу A:
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
[[1 2 3]
[4 5 6]]Транспонируем матрицу с помощью метода transpose():
>>> A_t = A.transpose() >>> print(A_t) [[1 4] [2 5] [3 6]]
Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:
>>> print(A.T) [[1 4] [2 5] [3 6]]
Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.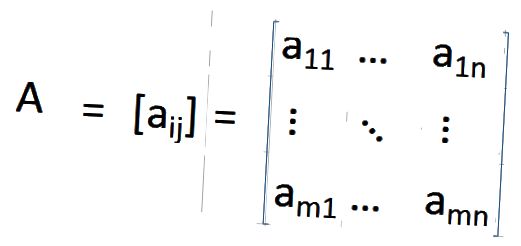
Свойство 1. Дважды транспонированная матрица равна исходной матрице:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
[[1 2 3]
[4 5 6]]
>>> R = (A.T).T
>>> print(R)
[[1 2 3]
[4 5 6]]Свойство 2. Транспонирование суммы матриц равно сумме транспонированных матриц:
➣ Численный пример
➤Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8 9; 0 7 5')
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
[[ 8 4]
[10 12]
[12 11]]
>>> print(R)
[[ 8 4]
[10 12]
[12 11]]Свойство 3. Транспонирование произведения матриц равно произведению транспонированных матриц расставленных в обратном порядке:
Транспонирование произведения матриц равно произведению транспонированных матриц расставленных в обратном порядке:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = (A.dot(B)).T
>>> R = (B.T).dot(A.T)
>>> print(L)
[[19 43]
[22 50]]
>>> print(R)
[[19 43]
[22 50]]В данном примере, для умножения матриц, использовалась функция dot() из библиотеки Numpy.
Свойство 4. Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6') >>> k = 3 >>> L = (k * A).T >>> R = k * (A.T) >>> print(L) [[ 3 12] [ 6 15] [ 9 18]] >>> print(R) [[ 3 12] [ 6 15] [ 9 18]]
Свойство 5. Определители исходной и транспонированной матрицы совпадают:
➣ Численный пример
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> A_det = np.linalg.det(A)
>>> A_T_det = np.linalg.det(A.T)
>>> print(format(A_det, '.9g'))
-2
>>> print(format(A_T_det, '.9g'))
-2Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.9g’).
P.S.Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Интересное: Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 4Следующая ⇒
· Дважды транспонированная матрица А равна исходной матрице А.
· Транспонированная сумма матриц равна сумме транспонированных матриц.
· Транспонированное произведение матриц равно произведению транспонированных матриц
· При транспонировании можно выносить скаляр.
· Определитель транспонированной матрицы равен определителю исходной матрицы
4. Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица. Определение Элементарными преобразованиями строк называют:
· перестановка местами любых двух строк матрицы; · умножение любой строки матрицы на константу , · прибавление к любой строке матрицы другой строки, умноженной на константу ,
Обозначение указывает на то, что матрица может быть получена из путём элементарных преобразований (или наоборот)
Свойства
· Инвариантность ранга при элементарных преобразованиях Теорема (об инвариантности ранга при элементарных преобразованиях) Если , то
· Эквивалентность СЛАУ при элементарных преобразованиях Назовём элементарными преобразованиями над системой линейных алгебраических уравнений: перестановку уравнений; умножение уравнения на ненулевую константу; сложение одного уравнения с другим, умноженным на некоторую константу. Т.е. элементарные преобразования над её расширенной матрицей. Тогда справедливо следующее утверждение:
Теорема (об эквивалентности систем уравнений при элементарных преобразованиях). Система линейных алгебраических уравнений, полученная путём элементарных преобразований над исходной системой, эквивалентна ей
· Нахождение обратных матриц Теорема (о нахождении обратной матрицы). Пусть определитель матрицы не равен нулю, пусть матрица определяется выражением . Тогда при элементарном преобразовании строк матрицы к единичной матрице в составе одновременно происходит преобразование к
· Приведение матриц к ступенчатому виду Введём понятие ступенчатых матриц:
Матрица имеет ступенчатый вид, если: Все нулевые строки матрицы стоят последними; Для любой ненулевой строки матрицы (пусть для определённости её номер равен ) справедливо следующее: если — первый ненулевой элемент строки , то .
Тогда справедливо следующее утверждение: Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду.
Эквивалентные матрицы
Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.
Надо отметить, что равные матрицы и эвивалентные матрицы — понятия совершенно различные.
Теорема. Наибольшее число линейно независимых столбцов в матрице равно числу линейно независимых строк.
Т.к. элементарные преобразования не изменяют ранг матрицы, то можно существенно упростить процесс нахождения ранга матрицы.
5. Блочная (клеточная) матрица — вид квадратной матрицы, каждый элемент которой является квадратной подматрицей меньшей, кратной размерности.
Пример записи Матрица размерностью 4×4 является блочной, состоящей из четырех подматриц-блоков размерностью 2×2
Если каждый блок будет определен как то, блочная матрица может быть записана в следующем виде
1234Следующая ⇒ Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… |
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
Стр 1 из 2Следующая ⇒ Транспонирование матриц. Обратная матрица. Теорема о существовании обратной матрицы (с доказательством) Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером. Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице. Вырожденной матрицей называется такая матрица, определитель которой равен нулю. Теорема: Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.
4) Ранг матрицы. Элементарные преобразования, не меняющие ранг матрицы (с доказательством). 1) Определитель k-го порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо её k строк и k столбцов, называется минором k-го порядка матрицы A. 2) Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Минор, имеющий порядок r, называется базисным. Строки и столбцы, на пересечении которых расположен базисный минор, называется соответственно базисными строками и столбцами. Т.е. ранг матрицы не изменится если в матрице следующие преобразования:
5) Системы линейных уравнений: основные понятия, теорема Кроннекера-Капелли. Система уравнений – множество уравнений с n<=2 неизвестными, для которых требуется найти значения, удовлетворяющие всем ур-м системы. Совокупность чисел a1, a2 …an называется решением системы, если она обращает все ур-я системы в тождества. Если система имеет решения, то её называют совместной, иначе – несовместная. Если совместная система имеет одно решение – определённая, если >1, то неопределённая. Теорема Кронекера-Капелли: Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу основной матрицы.
Решение систем линейных уравнений: матричный метод, формулы Крамера (с выводом). Матричный метод. Вывод: Матрица-столбец X неизвестных равна произведению обратной матрицы системы на столбец свободных членов. Формулы Крамера. Последовательно заменяются столбцы системы столбцом свободных членов. Определители = значения неизвестных, соответственно заменённым столбцам.
Решение систем линейных уравнений методом Гаусса. Метод – последовательное исключение неизвестных путём элементарных преобразований матрицы.
Однородные системы линейных уравнений, фундаментальная система решений. Однородная система – если свободные члены в системе равны нулю. ( => всегда совместна )
Чтобы система имела ненулевые решения, необходимо и достаточно, чтобы а) ранг её основной матрицы был меньше количества неизвестных, б) определитель = 0. Множество решений, полученных при решении методом Гаусса – фундаментальная система решений.
9) Векторы: Основные определения, линейные операции над векторами, проекция вектора на ось. Вектор – направленный отрезок. Модуль вектора – его длина (| расстояние между его началом и концом |). Нулевой вектор – начало и конец совпадают. Единичный вектор – длина равна единице.
Векторы коллинеарные, если они лежат на одной или на параллельных прямых. Три вектора, если на одной или на параллельных плоскостях. Операции: Сумма векторов – вектор, начало которого совпадает с началом первого, а конец с концом второго, при условии, что второй вектор отложен из конца первого. Разность двух векторов – такой вектор, который при сложении с меньшим равен большему. Произведение вектора на число
Проекция вектора на ось – число, равное произведению длины вектора и угла между осью и этим вектором.
Декартовы прямоугольные координаты вектора в пространстве. Действия над векторами, заданными своими координатами. Деление отрезка в данном отношении. Декартовы прямоугольные координаты вектора – его проекции на координатные оси. Действия над векторами: Сумма векторов – сумма соответствующих координат. Разность – разность соответствующих координат. Произведение вектора на число – произведение координат на число. Деление отрезка в данном отношении:
Прямая на плоскости: уравнение прямой, проходящей через данную точку перпендикулярно данному вектору; общее уравнение прямой; исследование общего уравнения прямой; взаимное расположение прямых, заданных общими уравнениями. Уравнение: Даны точка и вектор , Т.к вектор и прямая перпендикулярны, их скалярное произведение равно нулю, т.е, в координатной форме: Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение прямой — Исследование прямой: При B=0, прямая будет параллельна оси Oy; При C=0, прямая будет проходить через начало координат; При A=C=0, при B не= 0, прямая совпадает с осью Ox; при B=C=0, А не= 0, с осью Oy. Взаимное расположение двух прямых: Параллельны и совпадают, если A/A1 = B/B1 = C/C1, Параллельны и не совпадают, если A/A1 = B/B1 не= C/C1, Пересекаются, если A/A1 не= B/B1.
Прямая на плоскости: векторное уравнение прямой; параметрические уравнения прямой; каноническое уравнение прямой; уравнение прямой, проходящей через две точки; взаимное расположение двух прямых, заданных каноническими уравнениями. r = r0 + st — векторное уравнение прямой. S (m, n) – направляющий вектор, M0(r0)точка на прямой М0(x0, y0). Параметрическое уравнение: {х = х0 + mt {y= y0 + nt
x – x0 / m = t и y – y0 / n = t, т. x – x0 / m = y – y0 / n = t – каноническое ур-е прямой. Уравнение прямой, через две точки.
Условие параллельности — равное соотношение соответствующих величин. Перпендикулярности – скалярное произведение направляющих векторов = 0.
Прямая на плоскости: уравнение прямой, проходящей через данную точку в заданном направлении; уравнение прямой с угловым коэффициентом; взаимное расположение двух прямых, заданных уравнениями с угловым коэффициентом; расстояние от точки до прямой. По направлению: С угловым коэффициентом: Число называется угловым коэффициентом прямой. y = kx + b – уравнение прямой с угловым коэффициентом. b – отрезок, отсекаемы на оси Oy. Прямые: Расстояние от точки до прямой:
25) Кривые второго порядка. Эллипс: основные определения; вывод канонического уравнения. Эллипс – множество точек плоскости, сумма расстояний до которых до двух данных точек плоскости, называемых фокусами – постоянная величина. отношение фокального расстояния к длине большой оси (эксцентриситет). Директрисы: (две прямые, перпендикулярные оси Ox, на расстоянии от центра) 26) Кривые второго порядка. Гипербола: основные определения; вывод канонического уравнения. Гипербола – множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек этой плоскости, называемых фокусами – постоянная величина. отношение фокального расстояния к длине действительной(фокальной) оси (эксцентриситет). Директрисы: Ось, сопряженная с гиперболой: 27) Кривые второго порядка. Парабола: основные определения; вывод канонического уравнения. Парабола – множество всех точек плоскости, равноудалённых от точки-фокуса и данной прямой, называемой директрисой. Директриса:
Транспонирование матриц. Обратная матрица. Транспонированная матрица получается из исходной заменой каждой её строки столбцом с тем же номером. Квадратная матрица называется обратной к данной квадратной матрице, если их произведение равно единичной матрице. Вырожденной матрицей называется такая матрица, определитель которой равен нулю. Теорема: Для того, чтобы матрица A имела обратную матрицу, необходимо и достаточно, чтобы она была невырожденной.
4) Ранг матрицы. Элементарные преобразования, не меняющие ранг матрицы (с доказательством). 1) Определитель k-го порядка, составленный из элементов матрицы A, лежащих на пересечении каких-либо её k строк и k столбцов, называется минором k-го порядка матрицы A. 2) Рангом матрицы называется наибольший из порядков её миноров, отличных от нуля. Минор, имеющий порядок r, называется базисным. Строки и столбцы, на пересечении которых расположен базисный минор, называется соответственно базисными строками и столбцами. Т.е. ранг матрицы не изменится если в матрице следующие преобразования:
5) Системы линейных уравнений: основные понятия, теорема Кроннекера-Капелли. Система уравнений – множество уравнений с n<=2 неизвестными, для которых требуется найти значения, удовлетворяющие всем ур-м системы. Совокупность чисел a1, a2 …an называется решением системы, если она обращает все ур-я системы в тождества. Если система имеет решения, то её называют совместной, иначе – несовместная. Если совместная система имеет одно решение – определённая, если >1, то неопределённая. Теорема Кронекера-Капелли: Для того, чтобы система была совместной, необходимо и достаточно, чтобы ранг расширенной матрицы системы был равен рангу основной матрицы. При этом если они равны числу неизвестных, то система определённая. Если <числа неизвестных, то система неопределённая.
12Следующая ⇒ Читайте также: Как правильно слушать собеседника Типичные ошибки при выполнении бросков в баскетболе Принятие христианства на Руси и его значение Средства массовой информации США |
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1121; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
— MathCracker.com
Решатели Алгебра
Инструкции: Это калькулятор транспонирования матрицы с шагами. Все, что вам нужно сделать, это предоставить матрицу \(A\), введя ее значения ниже.
При необходимости измените размер матриц, указав количество строк и количество столбцов. Как только вы
имеют правильные размеры, которые вы хотите, вы вводите матрицы (набирая числа и перемещаясь по матрице с помощью «TAB»)
Как только вы
имеют правильные размеры, которые вы хотите, вы вводите матрицы (набирая числа и перемещаясь по матрице с помощью «TAB»)
Количество строк и столбцов должно быть целым числом больше 1. Максимальное количество строк – 8, максимальное количество столбцов – 8
\(A\) = \ начало{bmatrix} & \\ & \end{bmatrix}
Часто идея транспонирования матриц представлена в разных контекстах. Как мы часто видели, матрицы очень полезно при решении линейных систем, где коэффициенты уравнения представлены строками.
В некоторых случаях может быть полезно рассмотреть коэффициенты, представленные столбцами, для которых транспонированные
матрица пригодится.
Как найти транспонирование матрицы?
Как обычно в математике, будет способ определить транспонирование с помощью символов. Давайте сначала попробуем это. Рассмотрим \(A\) и заданная матрица размера \(m \times n\) (тогда она имеет \(m\) строк и \(n\) столбцов). 9T\) строятся с использованием столбцов \(A\). Легко и просто.
Итак, это очень просто, и вы должны выполнить следующие шаги:
- Установить матрицу А, которую вы хотите транспонировать
- Определите столбцы матрицы A
- Сформируйте матрицу транспонирования, используя в качестве строк то, что вы идентифицировали как столбцы A . 9Т\). Сделанный.
Нужно также транспонировать текст и форматирование ячеек? Попробуйте скопировать, вставить и использовать опцию Transpose. Но имейте в виду, что это создает дубликаты. Поэтому, если ваши исходные ячейки изменятся, копии не будут обновлены.
Есть еще что узнать о формулах массива. Создайте формулу массива или ознакомьтесь с подробными рекомендациями и примерами здесь.
массив Обязательный. Массив или диапазон ячеек на листе, которые вы хотите транспонировать. Транспонирование массива создается путем использования первой строки массива в качестве первого столбца нового массива, второй строки массива в качестве второго столбца нового массива и так далее. Если вы не знаете, как ввести формулу массива, см.
 раздел Создание формулы массива.
раздел Создание формулы массива.- Параметры
[in] transA magma_trans_t. При входе transA определяет форму op( A ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( A ) = A.
- = MagmaTrans: op( A ) = A**T.
- = MagmaConjTrans: op( A ) = A**H.
[дюйм] трансБ magma_trans_t. При вводе, transB указывает форму op( B ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( B ) = B.
- = MagmaTrans: op( B ) = B**T.
- = MagmaConjTrans: op( B ) = B**H.
[дюйм] m INTEGER Количество строк матрицы op( dA ). M >= 0. [in] n INTEGER Количество столбцов матрицы op( dA ).  N >= 0.
N >= 0.[in] альфа COMPLEX При входе ALPHA указывает скалярную альфа. [in] dA Массив COMPLEX, размерность (LDDA,k), где k равно N, когда transA = MagmaNoTrans, и равно M в противном случае. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N, когда трансА = MagmaNoTrans, и LDDA >= M в противном случае. [in] бета КОМПЛЕКС При вводе БЕТА указывает скалярную бета. [in] дБ Массив COMPLEX, размерность (LDDB,k), где k равно N, когда transB = MagmaNoTrans, и равно M в противном случае. [in] lddb INTEGER Начальное измерение массива, дБ. LDDB >= N, когда transB = MagmaNoTrans, и LDDB >= M в противном случае. [вход, выход] dC Массив COMPLEX, размерность (LDDC,N). Можно ввести dC, выполняя операцию на месте, если dC передается как один из указателей на dA или dB.  Матрица M-by-N dC.
Матрица M-by-N dC.[in] lddc INTEGER Начальное измерение массива dC. LDDC >= M. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] m INTEGER Количество строк матрицы dA. М >= 0, [дюйм] n INTEGER Количество столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX, размерность (LDDA,N) Матрица M-by-N dA. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= M. [in] dAT Массив COMPLEX, размерность (LDDAT,M) Матрица dAT размером N на M. [дюйм] лддат INTEGER Начальное измерение массива dAT. LDDAT >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] m INTEGER Количество строк матрицы dA. M >= 0. [in] n INTEGER Количество столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX, размерность (LDDA,N) Матрица M-by-N dA. [дюйм] ldda INTEGER Начальное измерение массива dA. LDDA >= M. [in] dAT Массив COMPLEX, размерность (LDDAT,M) Матрица dAT размером N на M. [in] lddat INTEGER Начальное измерение массива dAT. LDDAT >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[дюйм] нет INTEGER Количество строк и столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX, размерность (LDDA,N) Матрица N на N dA. На выходе dA(j,i) = dA_original(i,j), для 0 <= i,j < N. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] n INTEGER Количество строк и столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX, размерность (LDDA,N) Матрица N на N dA. На выходе dA(j,i) = dA_original(i,j), для 0 <= i,j < N. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] transA magma_trans_t. При входе transA определяет форму op( A ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( A ) = A.
- = MagmaTrans: op( A ) = A**T.
- = MagmaConjTrans: op( A ) = A**H.
[дюйм] трансБ magma_trans_t. При вводе, transB указывает форму op( B ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( B ) = B.
- = MagmaTrans: op( B ) = B**T.
- = MagmaConjTrans: op( B ) = B**H.
[дюйм] m INTEGER Количество строк матрицы op( dA ). M >= 0. [in] n INTEGER Количество столбцов матрицы op( dA ).  N >= 0.
N >= 0.[in] альфа DOUBLE PRECISION При вводе ALPHA указывает скалярную альфа. [in] dA Массив DOUBLE PRECISION, размерность (LDDA,k), где k равно N, когда transA = MagmaNoTrans, и равно M в противном случае. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N, когда трансА = MagmaNoTrans, и LDDA >= M в противном случае. [in] бета DOUBLE PRECISION При вводе БЕТА указывает скалярную бета. [in] дБ Массив DOUBLE PRECISION, размерность (LDDB,k), где k равно N, когда transB = MagmaNoTrans, и равно M в противном случае. [дюйм] lddb INTEGER Начальное измерение массива в дБ. LDDB >= N, когда transB = MagmaNoTrans, и LDDB >= M в противном случае. [вход, выход] dC Массив DOUBLE PRECISION, размерность (LDDC,N).  Можно ввести dC, выполняя операцию на месте, если dC передается как один из указателей на dA или dB. Матрица M-by-N dC.
Можно ввести dC, выполняя операцию на месте, если dC передается как один из указателей на dA или dB. Матрица M-by-N dC.[in] lddc INTEGER Начальное измерение массива dC. LDDC >= М. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] m INTEGER Количество строк матрицы dA. M >= 0. [in] n INTEGER Количество столбцов матрицы dA. N >= 0. [in] dA Массив DOUBLE PRECISION, размерность (LDDA,N) Матрица M-by-N dA. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= М. [дюйм] dAT Массив DOUBLE PRECISION, размерность (LDDAT,M) Матрица dAT размером N на M. [in] lddat INTEGER Начальное измерение массива dAT. LDDAT >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] n INTEGER Количество строк и столбцов матрицы dA. N >= 0. [in] dA Массив DOUBLE PRECISION, размерность (LDDA,N) Матрица N на N dA. На выходе dA(j,i) = dA_original(i,j), для 0 <= i,j < N. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] transA magma_trans_t. При вводе трансА указывает форму op( A ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( A ) = A.
- = MagmaTrans: op( A ) = A**T.
- = MagmaConjTrans: op( A ) = A**H.
[дюйм] трансБ magma_trans_t. При входе transB определяет форму op( B ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( B ) = B.
- = MagmaTrans: op( B ) = B**T.
- = MagmaConjTrans: op( B ) = B**H.
[in] m INTEGER Количество строк матрицы op( dA ). M >= 0. [in] n INTEGER Количество столбцов матрицы op( dA ).  N >= 0.
N >= 0.[in] альфа REAL При вводе ALPHA указывает скалярную альфа. [in] dA Массив REAL, размерность (LDDA,k), где k равно N, когда transA = MagmaNoTrans, и равно M в противном случае. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N, когда трансА = MagmaNoTrans, и LDDA >= M в противном случае. [in] бета REAL При вводе БЕТА указывает скалярную бета. [in] дБ Массив REAL, размерность (LDDB,k), где k равно N, когда transB = MagmaNoTrans, и равно M в противном случае. [in] lddb INTEGER Начальное измерение массива, дБ. LDDB >= N, когда transB = MagmaNoTrans, и LDDB >= M в противном случае. [вход,выход] dC Массив REAL, размерность (LDDC,N). Можно ввести dC, выполняя операцию на месте, если dC передается как один из указателей на dA или dB.  Матрица M-by-N dC.
Матрица M-by-N dC.[in] lddc INTEGER Начальное измерение массива dC. LDDC >= М. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] m INTEGER Количество строк матрицы dA. M >= 0. [in] n INTEGER Количество столбцов матрицы dA. N >= 0. [in] dA Массив REAL, размерность (LDDA,N) Матрица M-by-N dA. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= М. [дюйм] dAT Массив REAL, размерность (LDDAT,M) Матрица dAT размером N на M. [in] lddat INTEGER Начальное измерение массива dAT. LDDAT >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] n INTEGER Количество строк и столбцов матрицы dA. N >= 0. [in] dA Массив REAL, размерность (LDDA,N) Матрица N на N dA. На выходе dA(j,i) = dA_original(i,j), для 0 <= i,j < N. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] transA magma_trans_t. При вводе трансА указывает форму op( A ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( A ) = A.
- = MagmaTrans: op( A ) = A**T.
- = MagmaConjTrans: op( A ) = A**H.
[дюйм] трансБ magma_trans_t. При входе transB определяет форму op( B ), которая будет использоваться при матричном умножении, следующим образом: - = MagmaNoTrans: op( B ) = B.
- = MagmaTrans: op( B ) = B**T.
- = MagmaConjTrans: op( B ) = B**H.
[in] m INTEGER Количество строк матрицы op( dA ). M >= 0. [in] n INTEGER Количество столбцов матрицы op( dA ).  N >= 0.
N >= 0.[in] альфа COMPLEX_16 При входе ALPHA указывает скалярную альфа. [in] dA Массив COMPLEX_16, размерность (LDDA,k), где k равно N, когда transA = MagmaNoTrans, и равно M в противном случае. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N, когда трансА = MagmaNoTrans, и LDDA >= M в противном случае. [in] бета COMPLEX_16 При вводе БЕТА указывает скалярную бета. [дюймы] дБ Массив COMPLEX_16, размерность (LDDB,k), где k равно N, когда transB = MagmaNoTrans, и равно M в противном случае. [in] lddb INTEGER Начальное измерение массива, дБ. LDDB >= N, когда transB = MagmaNoTrans, и LDDB >= M в противном случае. [вход,выход] dC Массив COMPLEX_16, размерность (LDDC,N). Можно ввести dC, выполняя операцию на месте, если dC передается как один из указателей на dA или dB.  Матрица M-by-N dC.
Матрица M-by-N dC.[in] lddc INTEGER Начальное измерение массива dC. LDDC >= M. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] m INTEGER Количество строк матрицы dA. M >= 0. [in] n INTEGER Количество столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX_16, размерность (LDDA,N) Матрица M-by-N dA. [дюйм] ldda INTEGER Начальное измерение массива dA. LDDA >= M. [in] dAT Массив COMPLEX_16, размерность (LDDAT,M) Матрица N на M dAT. [in] lddat INTEGER Начальное измерение массива dAT. LDDAT >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] m INTEGER Количество строк матрицы dA. М >= 0, [in] n INTEGER Количество столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX_16, размерность (LDDA,N) Матрица M-by-N dA. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= M. [in] dAT Массив COMPLEX_16, размерность (LDDAT,M) Матрица N на M dAT. [дюйм] lddat INTEGER Начальное измерение массива dAT. LDDAT >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] n INTEGER Количество строк и столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX_16, размерность (LDDA,N) Матрица N на N dA. На выходе dA(j,i) = dA_original(i,j), для 0 <= i,j < N. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N. [in] очередь magma_queue_t Очередь для выполнения. - Параметры
[in] n INTEGER Количество строк и столбцов матрицы dA. N >= 0. [in] dA Массив COMPLEX_16, размерность (LDDA,N) Матрица N на N dA. На выходе dA(j,i) = dA_original(i,j), для 0 <= i,j < N. [in] ldda INTEGER Начальное измерение массива dA. LDDA >= N. [in] очередь magma_queue_t Очередь для выполнения.
Что такое транспонирование матрицы 2×4?
Переходя к мельчайшим деталям, транспонирование матрицы 2×4 представляет собой матрицу 4×2. T = A\).
T = A\).
Итак, симметричные матрицы — это те, которые остаются неизменными после их перестановки. Таким образом, один из способов оценить, является ли матрица симметричный, вычисляя его транспонирование и сравнивая его с исходной матрицей.
Транспонирование — единственная операция, которую можно выполнять с матрицами?
Абсолютно нет! Матрицы являются универсальными объектами, и, как и числа, вы можете складывать матрицы, вычесть и умножать матрицы, и даже в некоторых случаях можно делить матрицы (при условии, что они обратимы).
Пример транспонирования матрицы
Вопрос: Рассмотрим следующую матрицу
\[ А = \begin{bmatrix}
\displaystyle 2&\displaystyle \frac{1}{3}&\displaystyle 1\\[0.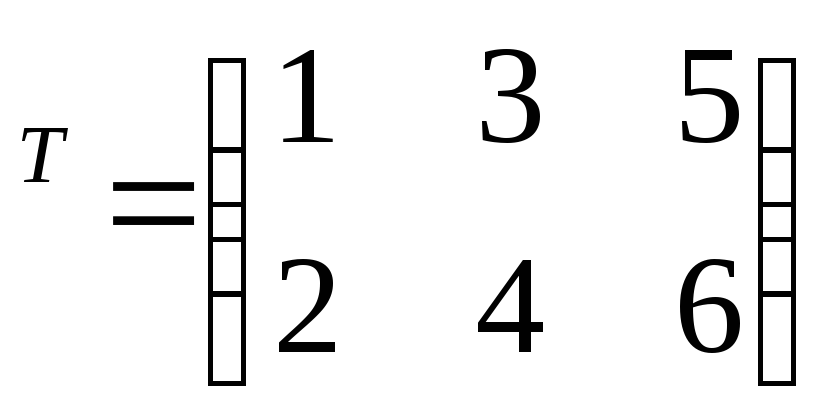 t\). 9{T}_{ij} = A_{ji}\]
t\). 9{T}_{ij} = A_{ji}\]
Другими словами, элемент, находящийся в i-й строке и j-м столбце транспонированной матрицы, совпадает с элементом, находящимся в j-й строке и i-м столбце исходной матрицы \( А\).
Следовательно, i-й столбец данной матрицы \(A\) соответствует i-й строке транспонированной матрицы. Итак, чтобы вычислить транспонирование матрицы \(A\), мы просто берем ее столбцы и делаем их строками транспонированной матрицы. Получаем:
9Т\).сбросить пароль
зарегистрироваться
Этот веб-сайт использует файлы cookie для улучшения вашего опыта. Мы предполагаем, что вы согласны с этим, но вы можете отказаться, если хотите. Принимать Читать далее
Транспонирование и трассировка матрицы
Определение 3.5.1. Транспонирование матрицы.
Транспонирование матрицы \(A\) представляет собой матрицу \(A^T\), полученную путем превращения первой строки \(A\) в первый столбец \(A^T\text{,}\) вторая строка \(A\) второй столбец \(A^T\text{,}\) и т. T=B=[b_{i,j}].\), то \(b_{i,j}=a_{j, я}\) 9п а_ {я, я}
\end{уравнение*}
T=B=[b_{i,j}].\), то \(b_{i,j}=a_{j, я}\) 9п а_ {я, я}
\end{уравнение*}
Теорема 3.5.6. Следы \(AB\) и \(BA\) равны.
Если \(AB\) и \(BA\) квадраты, то \(\tr (AB)=\tr (BA)\)
Доказательство.
Предположим, что \(A\) равно \(m\times n\), а \(B\) равно \(n\times m\) (помните, что тогда \(AB\) является определенным и квадратным). Чтобы оценить как \(\tr (AB)\), так и \(\tr (BA)\text{,}\), мы рассмотрим следующий прямоугольный массив чисел:
\begin{уравнение*} \begin{матрица} \amp\amp\amp\amp\amp\text{Суммы строк}\\ a_{1,1}b_{1,1}\amp a_{1,2}b_{2,1}\amp a_{1,3}b_{3,1}\amp\cdots\amp a_{1,n}b_{n,1} \amp\gets (AB)_{1,1}\\ a_{2,1}b_{1,2}\amp a_{2,2}b_{2,2}\amp a_{2,3}b_{3,2}\amp\cdots\amp a_{2,n}b_{n,2} \amp\gets(AB)_{2,2}\\ \vdots\amp\vdots\amp\vdots\amp\amp\vdots\amp\vdots\\ a_{m,1}b_{1,m}\amp a_{m,2}b_{2,m}\amp a_{m,3}b_{3,m}\amp\cdots\amp a_{m,n}b_{n,m} \amp\gets (AB)_{m,m}\\ \\ \uparrow\amp\uparrow\amp\uparrow\amp\amp\uparrow\\ \llap{\text{Суммы по столбцам:}\quad} (BA)_{1,1}\amp(BA)_{2,2}\amp(BA)_{3,3}\amp\amp(BA)_{n,n} \end{матрица} \end{уравнение*}
Мы собираемся вычислить сумму всех элементов этого массива двумя способами. Сделав это, два ответа будут равны.
Сделав это, два ответа будут равны.
Сначала мы находим сумму всех элементов массива путем сложения построчно. Обратите внимание, что сумма элементов в первой строке равна \((AB)_{1,1}\text{,}\), а сумма элементов во второй строке равна \((AB)_{2,2} \text{,}\) и так далее, пока сумма элементов в последней строке не станет \((AB)_{m,m}\text{.}\) Следовательно, сумма всех элементов в массиве равно \((AB)_{1,1}+(AB)_{2,2}+\cdots+(AB)_{m,m}=\tr (AB)\text{.}\)
Теперь добавляем по столбцам. Обратите внимание, что сумма первого столбца равна
.\начать{выровнять*} a_{1,1}b_{1,1}\amp +a_{2,1}b_{1,2}+\cdots+a_{m,1}b_{1,m}\\ \amp = b_{1,1}a_{1,1}+b_{2,1}a_{1,2}+\cdots+b_{m,1}a_{1,m}\\ \амп =(ВА)_{1,1}, \конец{выравнивание*}
сумма второго столбца равна \((BA)_{2,2}\) и так далее, пока сумма последнего столбца не будет равна \((BA)_{n,n}\text{.}\)Следовательно, сумма все элементы массива равны \((BA)_{1,1}+(BA)_{2,2}+\cdots+(BA)_{n,n}=\tr (BA)\text{ .}\) Приравнивание двух оценок дает \(\tr (AB)=\tr (BA)\text{.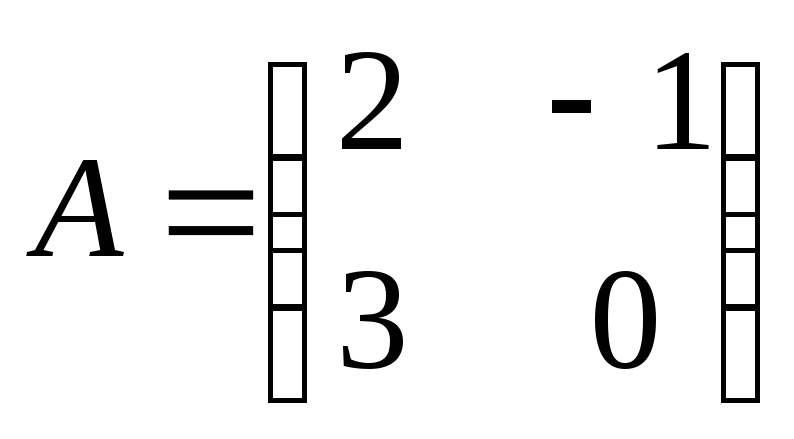 }\) 9п (ВА)_{j,j}\\
\амп = \тр (БА)
\end{align*}
}\) 9п (ВА)_{j,j}\\
\амп = \тр (БА)
\end{align*}
Найти транспонирование матрицы
Скоро Эти числовые инструменты уже в пути
Создание номеров Numberwang
Создание списка номеров Numberwang.
Переписать числа
Учитывая числа и грамматику, рекурсивно переписать их.
Создать число с плавающей запятой
Создать число из мантиссы, основания и экспоненты.
Визуализация числа с плавающей запятой 9б форма.
Преобразование научной записи в число
Преобразование числа в научной записи в обычное число.
Создать символьную нумерацию
Создать список буквенных чисел (a, b, c, …, z, aa, ab, …).
Создать римскую нумерацию
Создать список римских цифр (i, ii, iii, iv, v…).
Создать нумерацию Брайля
Создать список цифр Брайля (⠂, ⠆, ⠒, ⠲, ⠢, …).
Генерация случайных двоичных чисел
Создать список случайных двоичных чисел.
Создание случайных восьмеричных чисел
Создание списка случайных восьмеричных чисел.
Создание случайных десятичных чисел
Создание списка случайных десятичных чисел.
Создание случайных шестнадцатеричных чисел
Создание списка случайных шестнадцатеричных чисел.
Вычислить текущую сумму
Вычислить кумулятивную сумму списка чисел.
Вычисление текущего произведения
Вычисление кумулятивного произведения списка чисел.
Вычислить факториал
Найти факториал числа.
Создание числовых анаграмм
Создание одной или нескольких числовых анаграмм.
Создание числовых биграмм
Создание списка цифровых биграмм из числа.
Создание числовых триграмм
Создание списка цифровых триграмм из числа.
Генерация числовых N-грамм
Создание списка цифровых nграмм из числа.
Создание полиномиальной последовательности
Создать список чисел полиномиальной прогрессии.
Создание префиксов SI
Создание списка префиксов метрик.
Анализ числа
Сообщить, сколько цифр встречается сколько раз.
Преобразование числа в порядковое
Преобразование количественного числительного в порядковое.
Преобразование порядкового числа в число
Преобразование порядкового числа в количественное.
Преобразование числа в римское число
Преобразование арабских цифр в римские.
Преобразование римских чисел в обычные числа
Преобразование римских цифр в арабские.
Создание чисел Негафибоначчи
Вычисление серии расширенных чисел Фибоначчи.
Генерация простых чисел Фибоначчи
Поиск чисел, которые являются одновременно числами Фибоначчи и простыми числами.
Проверка числа Фибоначчи
Проверка, является ли число числом Фибоначчи.
Проверка простых чисел Фибоначчи
Проверяет, является ли число одновременно числом Фибоначчи и простым числом.
Построить слова Фибоначчи
Создать последовательность слов Фибоначчи.
Создать слова Трибоначчи
Создать последовательность слов Трибоначчи.
Генерировать числа Негалука
Вычислить серию расширенных чисел Лукаса.
Генерировать простые числа Лукаса
Вычислить серию расширенных чисел Лукаса.
Lucas Prime Test
Проверить, является ли число одновременно числом Лукаса и простым числом.
Вычисление следа матрицы
Найдите сумму элементов главной диагонали матрицы.
Вычислить собственные значения матрицы
Найти собственные значения матрицы.
Умножение матриц
Вычисление произведения двух матриц.
Добавить матрицы
Вычислить сумму двух матриц.
Вычитание матриц
Вычисление разности двух матриц.
Генерация чисел Мозера де Брюйна
Вычисление последовательности чисел Мозера-Брейна.
Сгенерировать числа Колакоски
Вычислить последовательность чисел Ольденбургера-Колакоски.
Сгенерировать числа Стэнли
Вычислить последовательность чисел Стэнли.
Генерировать числа Гийсвейта
Вычислить последовательность самоописывающих чисел Гийсвейта.
Сгенерировать числа Рудина-Шапиро
Вычислить последовательность чисел Русина-Шапиро.
Генерация чисел Баума-Свита
Вычисление последовательности чисел Баума-Свита.
Генерация последовательности Туэ-Морса
Вычисление членов ряда чисел Туэ-Морса.
Создание идеальных чисел
Создание списка совершенных чисел.
Создание почти идеальных чисел
Создание списка почти идеальных чисел.
Создать последовательность избыточных чисел
Вычислить последовательность избыточных чисел.
Создать последовательность неполных чисел
Вычислить последовательность неполных чисел.
Расчет чисел кривой дракона
Создать список порядковых номеров для складывания бумаги.
Создание составных чисел
Создание списка чисел, которые не являются простыми.
Нарисовать таблицу чисел
Создать таблицу чисел.
Проверить, является ли число совершенным
Проверить, является ли заданное число совершенным числом.
Проверить, является ли число обильным
Проверить, является ли данное число обильным числом.
Проверить, является ли число недостаточным
Проверить, является ли данное число недостаточным.
Вычислить модуль
Найти модуль числа.
Группировка цифр числа
Группировка цифр числа.
Разделить число на цифры
Создать список цифр из числа.
Printf Numbers
Применение функций sprintf или printf к числам.
Создайте номера Zalgo
Позвольте Zalgo уничтожить ваши номера.
Повторить номер
Повторить номер несколько раз.
Зеркальное число
Создать зеркальную копию номера.
Дополнение числа нулями
Добавление нулей к числу.
Обратный порядок цифр
Обратный порядок цифр в числе.
Поворот числа
Циклический поворот цифр числа влево или вправо.
Увеличить число
Добавить единицу к заданному числу.
Увеличить все цифры в числе
Добавить единицу к каждой цифре в числе.
Уменьшить число
Вычесть единицу из заданного числа.
Уменьшить все цифры в числе
Вычесть единицу из каждой цифры в числе.
Находить закономерности в числах
Находить закономерности в последовательностях чисел.
Подсчет числа вхождений
Узнайте, как часто появляются числовые значения.
Вычисление процентов
Найти x% числа.
Создание больших чисел
Создание списка больших чисел.
Генерация малых чисел
Создать список маленьких чисел.
Создание натуральных чисел
Создание списка натуральных чисел.
Создание рациональных чисел
Создание списка рациональных чисел.
Создать последовательность констант
Создать серию чисел, в которой все термины одинаковы.
Создание действительных чисел
Создание последовательности действительных чисел.
Создание комплексных чисел
Создание списка комплексных чисел.
Создать двоичные числа
Создать последовательность двоичных чисел.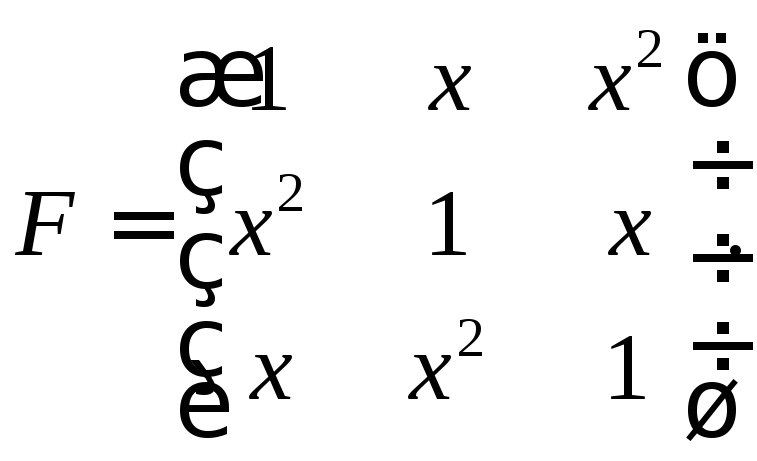
Создание пар чисел
Создание последовательности пар чисел.
Создание троек чисел
Создание последовательности троек чисел.
Создание кортежей чисел
Создание последовательности n-кортежей чисел.
Переплетение чисел
Переплетение двух или более чисел поразрядно.
Найти десятичное представление числа
Переписать число в десятичной форме.
Преобразование дроби в десятичную
Преобразование дроби в десятичное число.
Преобразование десятичного числа в дробь
Преобразование десятичного числа в дробь.
Преобразование двоичного числа в восьмеричное
Преобразование числа с основанием два в число с основанием восемь.
Преобразование двоичного числа в десятичное число
Преобразование числа с основанием два в число с основанием десять.
Преобразование двоичного числа в шестнадцатеричное
Преобразование числа с основанием два в число с основанием шестнадцать.
Преобразование восьмеричного числа в двоичное
Преобразование числа с основанием восемь в число с основанием два.
Преобразование восьмеричного числа в десятичное
Преобразование числа с основанием восемь в число с основанием десять.
Преобразование восьмеричного числа в шестнадцатеричное
Преобразование числа с основанием восемь в число с основанием шестнадцать.
Преобразование десятичного числа в двоичное
Преобразование числа с основанием десять в число с основанием два.
Преобразование десятичного числа в восьмеричное число
Преобразование десятичного числа в восьмеричное.
Преобразование десятичного числа в шестнадцатеричное
Преобразование числа с основанием десять в число с основанием шестнадцать.
Преобразование шестнадцатеричного числа в двоичное число
Преобразование числа с основанием шестнадцать в число с основанием два.
Преобразование шестнадцатеричного числа в восьмеричное
Преобразование числа с основанием шестнадцать в число с основанием восемь.
Преобразование шестнадцатеричного числа в десятичное число
Преобразование числа с основанием шестнадцать в число с основанием десять.
Преобразование любого числа в любое основание
Преобразование любого числа в любом основании в любое другое основание.
Изменение мантиссы числа
Изменение значения числа.
Изменить показатель степени числа
Изменить степень числа.
Замена цифр буквами
Замена цифр в числе буквами алфавита.
Создание спирали чисел
Создание спирали из цифр числа.
Удалить десятичную точку
Удалить десятичный разделитель из десятичного числа.
Проверка числа Numberwang
Проверка, является ли данный номер числом numberwang.
Функция ТРАНСП
Excel
Формулы и функции
Ссылка
Ссылка
Функция ТРАНСП
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Больше. ..Меньше
..Меньше
Иногда вам нужно переключать или вращать ячейки. Вы можете сделать это, скопировав, вставив и используя опцию Transpose. Но при этом создаются дублированные данные. Если вы этого не хотите, вы можете вместо этого ввести формулу, используя функцию ТРАНСП. Например, на следующем рисунке формула =ТРАНСП(A1:B4) берет ячейки с A1 по B4 и упорядочивает их по горизонтали.
Примечание. Если у вас установлена текущая версия Microsoft 365 , вы можете ввести формулу в верхнюю левую ячейку выходного диапазона, а затем нажать ENTER , чтобы подтвердить формулу как формулу динамического массива. В противном случае формулу необходимо ввести как устаревшую формулу массива, сначала выбрав выходной диапазон, введите формулу в верхнюю левую ячейку выходного диапазона, а затем нажмите Ctrl+Shift+Enter для подтверждения. Excel вставляет фигурные скобки в начале и в конце формулы. Дополнительные сведения о формулах массива см.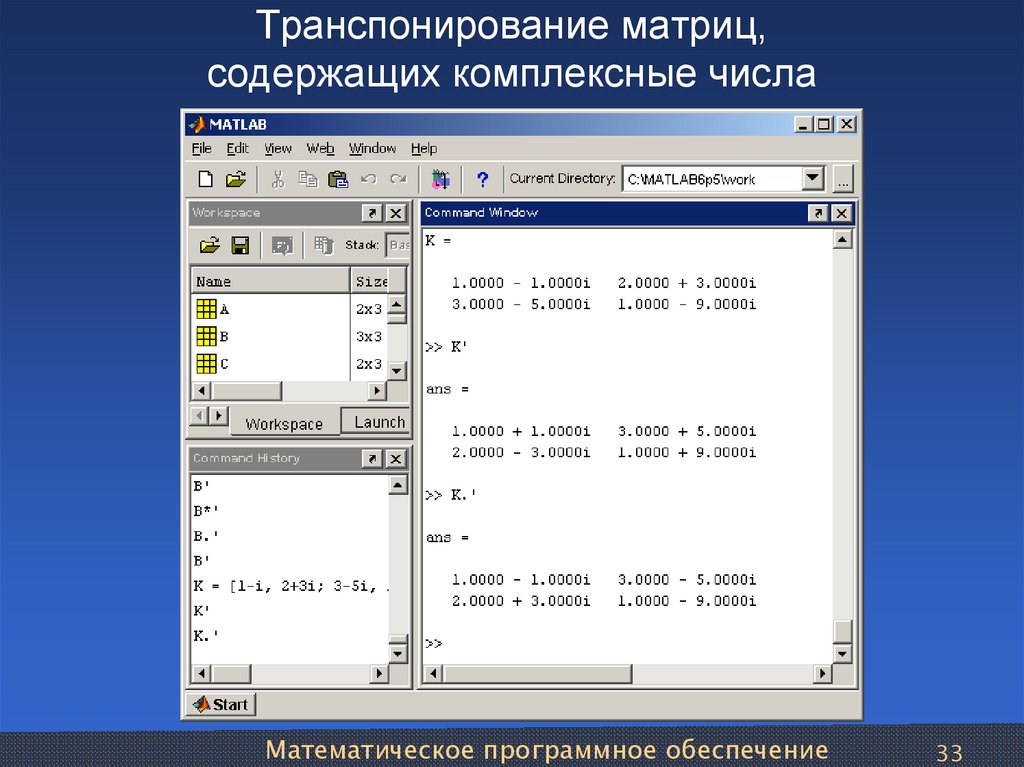 в разделе Рекомендации и примеры формул массива.
в разделе Рекомендации и примеры формул массива.
Шаг 1: выберите пустые ячейки
Сначала выберите несколько пустых ячеек. Но обязательно выберите то же количество ячеек, что и исходный набор ячеек, но в другом направлении. Например, здесь 8 ячеек, расположенных вертикально:
.Итак, нам нужно выделить восемь горизонтальных ячеек, вот так:
Здесь окажутся новые транспонированные ячейки.
Шаг 2: Введите =ТРАНСП(
С выделенными пустыми ячейками введите: =ТРАНСП(
Excel будет выглядеть примерно так:
Обратите внимание, что восемь ячеек по-прежнему выделены, несмотря на то, что мы начали вводить формулу.
Шаг 3: Введите диапазон исходных ячеек.
Теперь введите диапазон ячеек, которые вы хотите транспонировать. В этом примере мы хотим перенести ячейки из A1 в B4. Таким образом, формула для этого примера будет следующей: =ТРАНСП(A1:B4) — , но пока не нажимайте клавишу ВВОД! Просто прекратите печатать и перейдите к следующему шагу.
В этом примере мы хотим перенести ячейки из A1 в B4. Таким образом, формула для этого примера будет следующей: =ТРАНСП(A1:B4) — , но пока не нажимайте клавишу ВВОД! Просто прекратите печатать и перейдите к следующему шагу.
Excel будет выглядеть примерно так:
Шаг 4. Наконец, нажмите CTRL+SHIFT+ENTER
Теперь нажмите CTRL+SHIFT+ENTER. Почему? Поскольку функция ТРАНСП используется только в формулах массива, именно так вы завершаете формулу массива. Короче говоря, формула массива — это формула, которая применяется более чем к одной ячейке. Поскольку на шаге 1 вы выбрали более одной ячейки (вы это сделали, не так ли?), формула будет применена более чем к одной ячейке. Вот результат после нажатия CTRL+SHIFT+ENTER:
Советы
- org/ListItem»>
Вам не нужно вводить диапазон вручную. После ввода =ТРАНСП( вы можете использовать мышь, чтобы выбрать диапазон. Просто щелкните и перетащите от начала диапазона к концу. Но помните: нажмите CTRL+SHIFT+ENTER, когда закончите, а не ENTER сам по себе.
Технические характеристики
Функция ТРАНСП возвращает диапазон ячеек по вертикали как диапазон по горизонтали или наоборот. Функция ТРАНСП должна быть введена как формула массива в диапазоне, который имеет такое же количество строк и столбцов, соответственно, как исходный диапазон имеет столбцы и строки. Используйте TRANSPOSE для смещения вертикальной и горизонтальной ориентации массива или диапазона на рабочем листе.
Функция ТРАНСП должна быть введена как формула массива в диапазоне, который имеет такое же количество строк и столбцов, соответственно, как исходный диапазон имеет столбцы и строки. Используйте TRANSPOSE для смещения вертикальной и горизонтальной ориентации массива или диапазона на рабочем листе.
Синтаксис
ТРАНСП(массив)
Синтаксис функции ТРАНСП имеет следующий аргумент:
См. также
Транспонировать (повернуть) данные из строк в столбцы или наоборот
Создать формулу массива
Поворот или выравнивание данных ячеек
Рекомендации и примеры формул массива
9Н \) More…| void | magmablas_cgeam (magma_trans_t transA, magma_trans_t transB, magma_int_t m, magma_int_t n, magmaFloatComplex alpha, magmaFloatComplex_const_ptr dA, magma_int_t ldda, magmaFloatComplex beta, magmaFloatComplex_const_ptr dB, magma_int_t lddb, magmaFloatComplex_ptr dC, magma_int_t lddc, очередь magma_queue_t) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). Подробнее… Подробнее… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_ctranspose (magma_int_t m, magma_int_t n, magmaFloatComplex_const_ptr dA, magma_int_t ldda, magmaFloatComplex_ptr dAT, magma_int_t lddat, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ctranspose copies and transposes a matrix dA to matrix дАТ. More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_ctranspose_conj (magma_int_t m, magma_int_t n, magmaFloatComplex_const_ptr dA, magma_int_t ldda, magmaFloatComplex_ptr dAT, magma_int_t lddat, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ctranspose_conj_q копирует и транспонирует матрицу dA в матрицу dAT. More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_ctranspose_conj_inplace (magma_int_t n, magmaFloatComplex_ptr dA, magma_int_t ldda, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ctranspose_conj_inplace_q conjugate-transposes a square N-by-N matrix in- место. Подробнее… Подробнее… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| пустота | magmablas_ctranspose_inplace (magma_int_t n, magmaFloatComplex_ptr dA, magma_int_t ldda, magma_queue_t очередь) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_dgeam (magma_trans_t transA, magma_trans_t transB, magma_int_t m, magma_int_t n, double alpha, magmaDouble_const_ptr dA, magma_int_t ldda, double beta, magmaDouble_const_ptr dB, magma_int_t lddb, magmaDouble_ptr dC , magma_int_t lddc, очередь magma_queue_t) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| dgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_dtranspose (magma_int_t m, magma_int_t n, magmaDouble_const_ptr dA, magma_int_t ldda, magmaDouble_ptr dAT, magma_int_t lddat, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dtranspose copies and transposes a матрица dA в матрицу dAT. Подробнее… Подробнее… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_dtranspose_inplace (magma_int_t n, magmaDouble_ptr dA, magma_int_t ldda, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| dtranspose_inplace_q transposes a square N-by-N matrix in-place. More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_sgeam (magma_trans_t transA, magma_trans_t transB, magma_int_t m, magma_int_t n, float alpha, magmaFloat_const_ptr dA, magma_int_t ldda, float beta, magmaFloat_const_ptr dB, magma_int_t lddb, magmaFloat_ptr dC , magma_int_t lddc, очередь magma_queue_t) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_stranspose (magma_int_t m, magma_int_t n, magmaFloat_const_ptr dA, magma_int_t ldda, magmaFloat_ptr dAT, magma_int_t lddat, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
stranspose copies and transposes a матрица dA в матрицу dAT. Подробнее… Подробнее… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | Magmablas_Stranspose_inplace (magma_int_t n, magmafloat_ptr da, magma_int_t ldda, magma_queue_t Queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_zgeam (magma_trans_t transA, magma_trans_t transB, magma_int_t m, magma_int_t n, magmaDoubleComplex alpha, magmaDoubleComplex_const_ptr dA, magma_int_t ldda, magmaDoubleComplex beta, magmaDoubleComplex_const_ptr dB, magma_int_t lddb, magmaDoubleComplex_ptr dC , magma_int_t lddc, очередь magma_queue_t) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| zgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_ztranspose (magma_int_t m, magma_int_t n, magmaDoubleComplex_const_ptr dA, magma_int_t ldda, magmaDoubleComplex_ptr dAT, magma_int_t lddat, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ztranspose copies and transposes a матрица dA в матрицу dAT. Подробнее… Подробнее… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_ztranspose_conj (magma_int_t m, magma_int_t n, magmaDoubleComplex_const_ptr dA, magma_int_t ldda, magmaDoubleComplex_ptr dAT, magma_int_t lddat, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ztranspose_conj_q copies and conjugate-transposes a matrix dA to matrix dAT . Подробнее… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_ztranspose_conj_inplace (magma_int_t n, magmaDoubleComplex_ptr dA, magma_int_t ldda_quet9, magma_0779 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ztranspose_conj_inplace_q сопряженно-транспонирует квадратную матрицу размера N на N на месте. More… | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| void | magmablas_ztranspose_inplace (magma_int_t n, magmaDoubleComplex_ptr dA, magma_int_t ldda, magma_queue_t queue) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ztranspose_inplace_q transposes a square N-by-N matrix in-place. H \) H \)◆ magmablas_cgeam()
cgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). Операция также поддерживает следующие преобразования на месте C = alpha*C + beta*op( B ) C = alpha*op( A ) + beta*C ◆ magmablas_ctranspose()
ctranspose Копирует и транспонирует матрицу dA в матрицу dAT. То же, что и ctranspose, но добавляет аргумент очереди. ◆ magmablas_ctranspose_conj()
ctranspose_conj_q копирует и транспонирует матрицу dA в матрицу dAT. То же, что и ctranspose_conj, но добавляет аргумент очереди. ◆ magmablas_ctranspose_conj_inplace()
ctranspose_conj_inplace_q conjugate-транспонирует квадратную матрицу N на N на месте. То же, что и ctranspose_conj_inplace, но добавляет аргумент очереди. ◆ magmablas_ctranspose_inplace()
ctranspose_inplace_q транспонирует квадратную матрицу размера N на N на месте. То же, что и ctranspose_inplace, но добавляет аргумент очереди. ◆ magmablas_dgeam()
dgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). Операция также поддерживает следующие преобразования на месте C = alpha*C + beta*op( B ) C = alpha*op( A ) + beta*C ◆ magmablas_dtranspose()
dtranspose копирует и транспонирует матрицу dA в матрицу dAT. То же, что и dtranspose, но добавляет аргумент очереди. ◆ magmablas_dtranspose_inplace()
dtranspose_inplace_q транспонирует квадратную матрицу размера N на N на месте. То же, что и dtranspose_inplace, но добавляет аргумент очереди. ◆ magmablas_sgeam()
sgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). Операция также поддерживает следующие преобразования на месте C = alpha*C + beta*op( B ) C = alpha*op( A ) + beta*C ◆ magmablas_stranspose()
stranspose копирует и транспонирует матрицу dA в матрицу dAT. То же, что и stranspose, но добавляет аргумент очереди. ◆ magmablas_stranspose_inplace()
stranspose_inplace_q транспонирует квадратную матрицу размера N на N на месте. То же, что и stranspose_inplace, но добавляет аргумент очереди. ◆ magmablas_zgeam()
zgeam добавляет/переставляет матрицы: C = alpha*op(A) + beta*op(B). Операция также поддерживает следующие преобразования на месте C = alpha*C + beta*op( B ) C = alpha*op( A ) + beta*C ◆ magmablas_ztranspose()
ztranspose копирует и транспонирует матрицу dA в матрицу dAT. То же, что и ztranspose, но добавляет аргумент очереди. ◆ magmablas_ztranspose_conj()
ztranspose_conj_q копирует и транспонирует матрицу dA в матрицу dAT. То же, что и ztranspose_conj, но добавляет аргумент очереди. ◆ magmablas_ztranspose_conj_inplace()
ztranspose_conj_inplace_q conjugate-транспонирует квадратную матрицу N на N на месте. То же, что и ztranspose_conj_inplace, но добавляет аргумент очереди. ◆ magmablas_ztranspose_inplace()
ztranspose_inplace_q транспонирует квадратную матрицу размера N на N на месте. То же, что и ztranspose_inplace, но добавляет аргумент очереди. Транспонировать матрицуВ Python матрица состоит из строк и столбцов. Мы можем создать матрицу по-разному, но проще всего использовать список, как показано ниже: matrix = [[1, 2, 4], [31, 17, 15] ] Список внутри приведенного выше списка представляет собой строку, и каждый элемент внутри списка называется столбцом. Итак, в приведенном выше примере у нас есть две строки и три столбца [2 X 3]. А также, индексация Python начинается с нуля. Транспонирование матрицы означает, что мы меняем строки на столбцы или столбцы на строки. Давайте обсудим различные методы транспонирования матрицы. Метод 1: Транспонирование матрицы NumPy transpose()Первый метод, который мы собираемся обсудить, — это Numpy. Numpy в основном имеет дело с массивом в Python, и для транспонирования мы назвали метод транспонирования (). В номер ячейки [24]: Импортируем модуль NumPy как np. В ячейке номер [25]: Мы создаем массив NumPy с именем arr_matrix. В ячейке с номером [26]: мы вызываем метод transpose() и используем оператор точки с созданной ранее матрицей arr_matrix. В ячейке номер [27]: Печатаем исходную матрицу (arr_matrix). В ячейке номер [28]: Мы печатаем матрицу транспонирования (arr_transpose), и по результатам мы обнаружили, что наша матрица теперь транспонирована. Метод 2: Использование метода numpy. transpose() transpose()Мы также можем транспонировать матрицу в Python, используя numpy.transpose(). При этом мы передаем матрицу в метод transpose() в качестве параметра. В ячейке с номером [29] мы создаем матрицу, используя массив NumPy с именем arr_matrix. В ячейке номер [30]: Мы передали arr_matrix в метод transpose() и сохранили результаты обратно в новую переменную arr_transpose. В ячейке номер [31]: Печатаем исходную матрицу (arr_matrix). В ячейке номер [32]: Мы печатаем матрицу транспонирования (arr_transpose), и по результатам мы обнаружили, что наша матрица теперь транспонирована. Метод 3: Транспонирование матрицы с использованием библиотеки SympyБиблиотека Sympy — это еще один подход, который помогает нам транспонировать матрицу. Эта библиотека использует символическую математику для решения задач алгебры. В номер ячейки [33]: Импортируем библиотеку Sympy. Она не поставляется вместе с Python, поэтому вам необходимо установить ее в вашей системе, прежде чем использовать эту библиотеку; иначе вы получите ошибки. В ячейке номер [34]: Создаем матрицу с помощью библиотеки sympy. В ячейке с номером [35]: мы вызываем транспонирование (T) с помощью оператора точки и сохраняем результаты обратно в новую переменную sympy_transpose. В номер ячейки [36]: Печатаем исходную матрицу (matrix). В ячейке номер [37]: Мы печатаем матрицу транспонирования (sympy_transpose), и по результатам мы обнаружили, что наша матрица теперь транспонирована. Метод 4: транспонирование матрицы с использованием вложенного циклаТранспонирование матрицы без какой-либо библиотеки в Python представляет собой вложенный цикл. Мы создаем матрицу, а затем создаем другую матрицу того же размера, что и исходная матрица, чтобы сохранить результаты обратно после транспонирования. Мы не делаем жесткий код матрицы результатов, потому что мы не знаем размерность матрицы в будущем. Итак, мы создаем размер результирующей матрицы, используя сам исходный размер матрицы. В ячейке номер [38]: Мы создаем матрицу и печатаем эту матрицу. В ячейке номер [39]: Мы используем некоторые питонические способы, чтобы узнать размер транспонированной матрицы, используя исходную матрицу. Потому что если мы этого не сделаем, то придется упомянуть размерность транспонированной матрицы. Но при этом методе нам не важны размеры матрицы. В ячейке номер [40]: Выполняем две петли. Один верхний цикл предназначен для строк, а вложенный цикл — для столбцов. В номер ячейки [41]: Печатаем исходную матрицу (Matrix). В ячейке номер [42]: Мы печатаем матрицу транспонирования (trans_Matrix), и по результатам мы обнаружили, что наша матрица теперь транспонирована. Метод 5: Использование понимания списка Следующий метод, который мы собираемся обсудить, это метод понимания списка. Этот метод похож на обычный Python, использующий вложенные циклы, но более питоническим способом. Можно сказать, что у нас есть более продвинутый способ решения задачи транспонирования матрицы в одну строку кода без использования библиотеки. В ячейке номер [43]: Создаем матрицу m, используя вложенный список. В ячейке номер [44]: мы используем вложенный цикл, как мы обсуждали в предыдущем, но здесь в одной строке, и также нет необходимости упоминать противоположный индекс [j] [i], как мы делали в предыдущем вложенном цикле. В ячейке номер [45]: Печатаем исходную матрицу (m). В ячейке номер [42]: Мы печатаем матрицу транспонирования (trans_m), и по результатам мы обнаружили, что наша матрица теперь транспонирована. Способ 6. Транспонирование матрицы с помощью pymatrixpymatrix — еще одна облегченная библиотека для матричных операций в Python. Мы также можем выполнить транспонирование с помощью pymatrix. В номер ячейки [43]: Импортируем библиотеку pymatrix. Она не поставляется вместе с Python, поэтому вам необходимо установить ее в вашей системе, прежде чем использовать эту библиотеку; иначе вы получите ошибки. В ячейке номер [44]: Создаем матрицу с помощью библиотеки pymatrix. В ячейке с номером [45]: мы вызываем транспонирование (trans()) с помощью оператора точки и сохраняем результаты обратно в новую переменную pymatrix_transpose. В номер ячейки [46]: Печатаем исходную матрицу (matrix). В ячейке номер [47]: Мы печатаем матрицу транспонирования (pymatrix_transpose), и по результатам мы обнаружили, что наша матрица теперь транспонирована. Метод 7: использование метода zipzip — это еще один метод транспонирования матрицы. В ячейке номер [63]: Мы создали новую матрицу, используя список. В ячейке номер [64]: Мы передали матрицу в zip оператором *. Мы вызываем каждую строку, а затем преобразуем эту строку в новый список, который становится транспонированной матрицей. Заключение: Мы видели различные методы, которые могут помочь нам в транспонировании матрицы. В котором некоторые методы используют массив и список Numpy. Мы видели, что создание матрицы с использованием вложенного списка очень просто по сравнению с массивом Numpy. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Обозначение транспонированной матрицы , где a ik=aki для любых i и k.
Обозначение транспонированной матрицы , где a ik=aki для любых i и k.
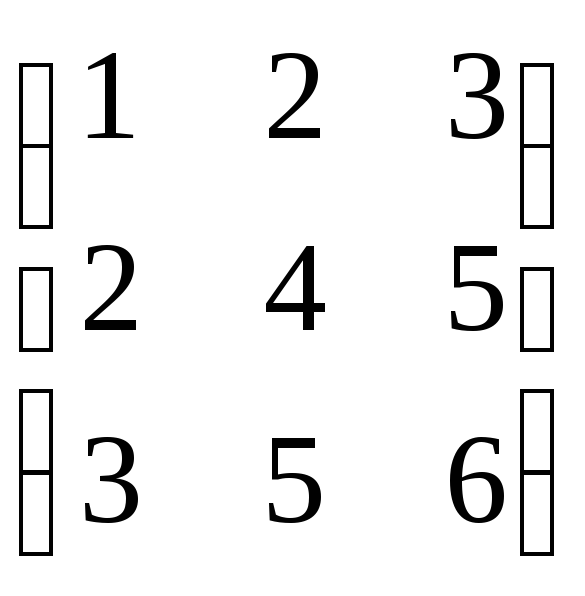 matrix('1 2 3; 4 5 6')
>>> k = 3
>>> L = (k * A).T
>>> R = k * (A.T)
>>> print(L)
[[ 3 12]
[ 6 15]
[ 9 18]]
>>> print(R)
[[ 3 12]
[ 6 15]
[ 9 18]]
matrix('1 2 3; 4 5 6')
>>> k = 3
>>> L = (k * A).T
>>> R = k * (A.T)
>>> print(L)
[[ 3 12]
[ 6 15]
[ 9 18]]
>>> print(R)
[[ 3 12]
[ 6 15]
[ 9 18]]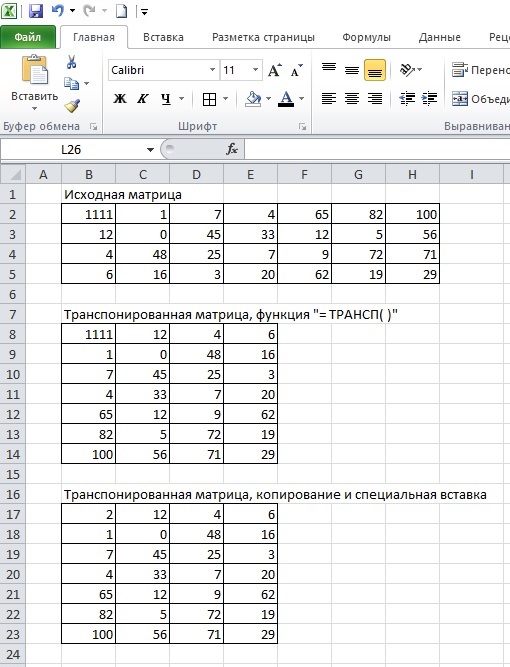 Увеличение объема продаж…
Увеличение объема продаж…


 ..
..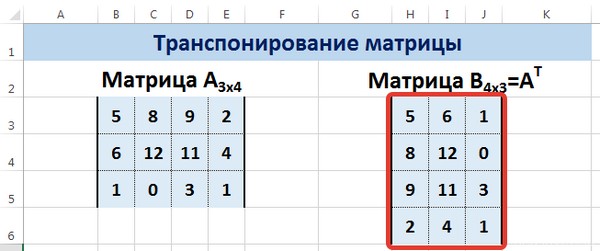
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
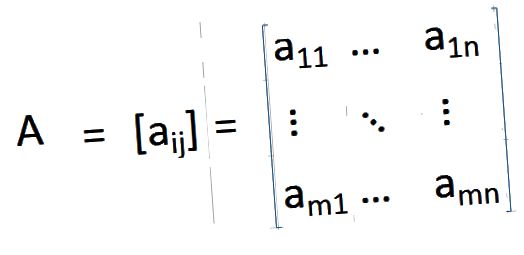
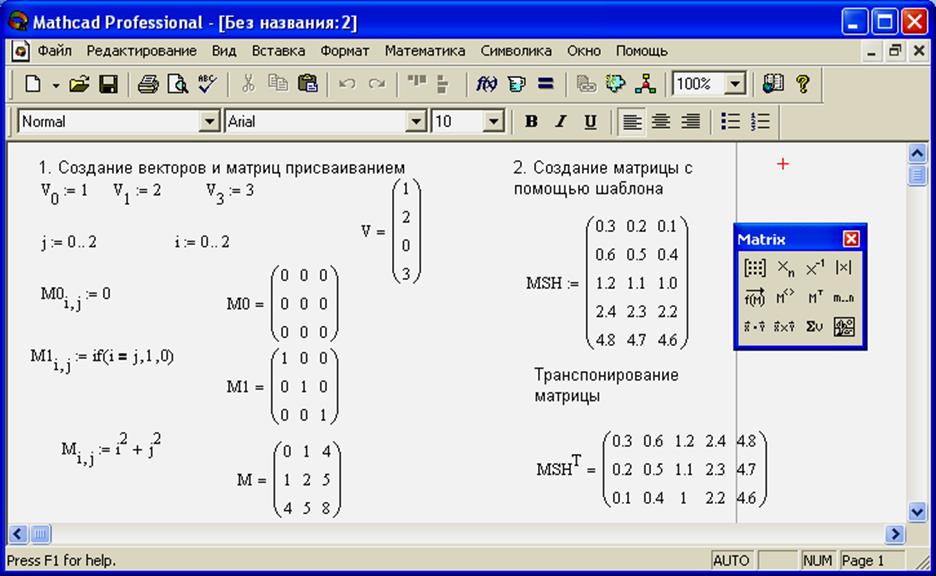 При этом если они равны числу неизвестных, то система определённая. Если <числа неизвестных, то система неопределённая.
При этом если они равны числу неизвестных, то система определённая. Если <числа неизвестных, то система неопределённая.


 е,
е,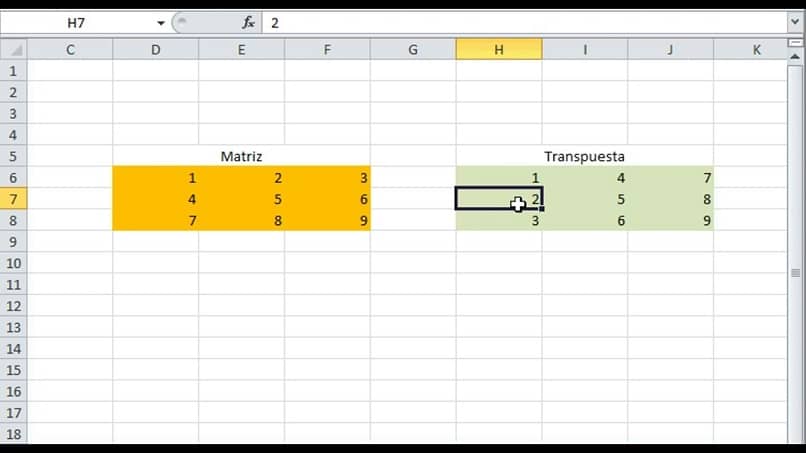
 Теорема о существовании обратной матрицы (с доказательством)
Теорема о существовании обратной матрицы (с доказательством)
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.02 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.02 с.) раздел Создание формулы массива.
раздел Создание формулы массива.
 N >= 0.
N >= 0. Матрица M-by-N dC.
Матрица M-by-N dC.




 N >= 0.
N >= 0. Можно ввести dC, выполняя операцию на месте, если dC передается как один из указателей на dA или dB. Матрица M-by-N dC.
Можно ввести dC, выполняя операцию на месте, если dC передается как один из указателей на dA или dB. Матрица M-by-N dC.

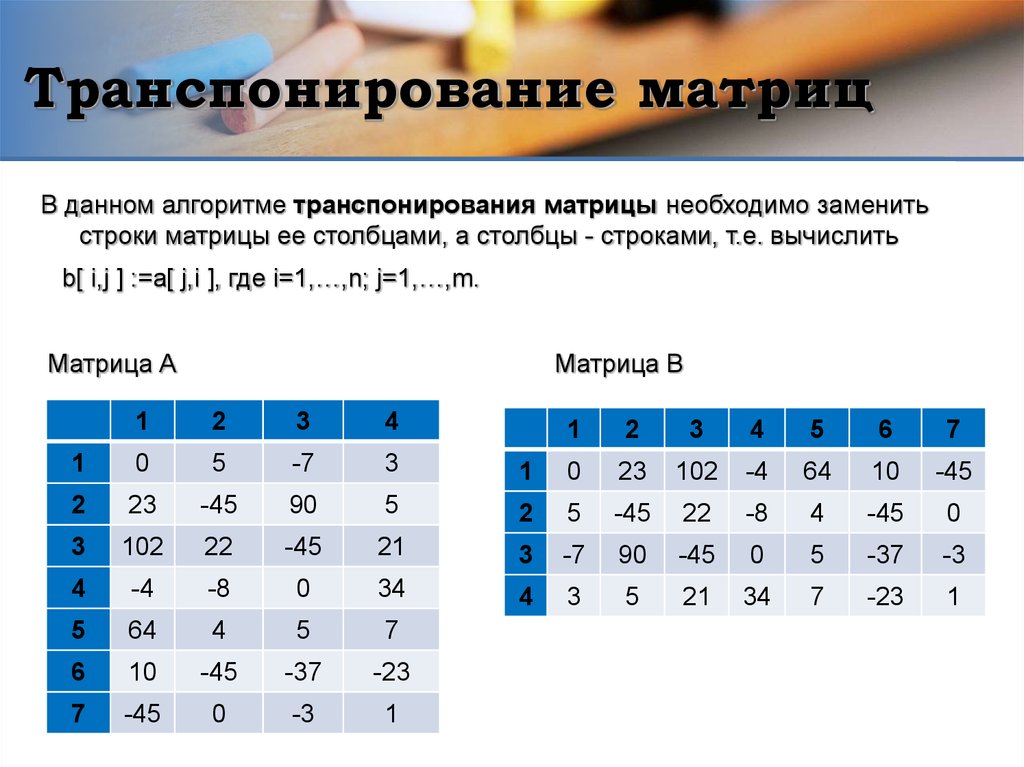
 N >= 0.
N >= 0. Матрица M-by-N dC.
Матрица M-by-N dC.

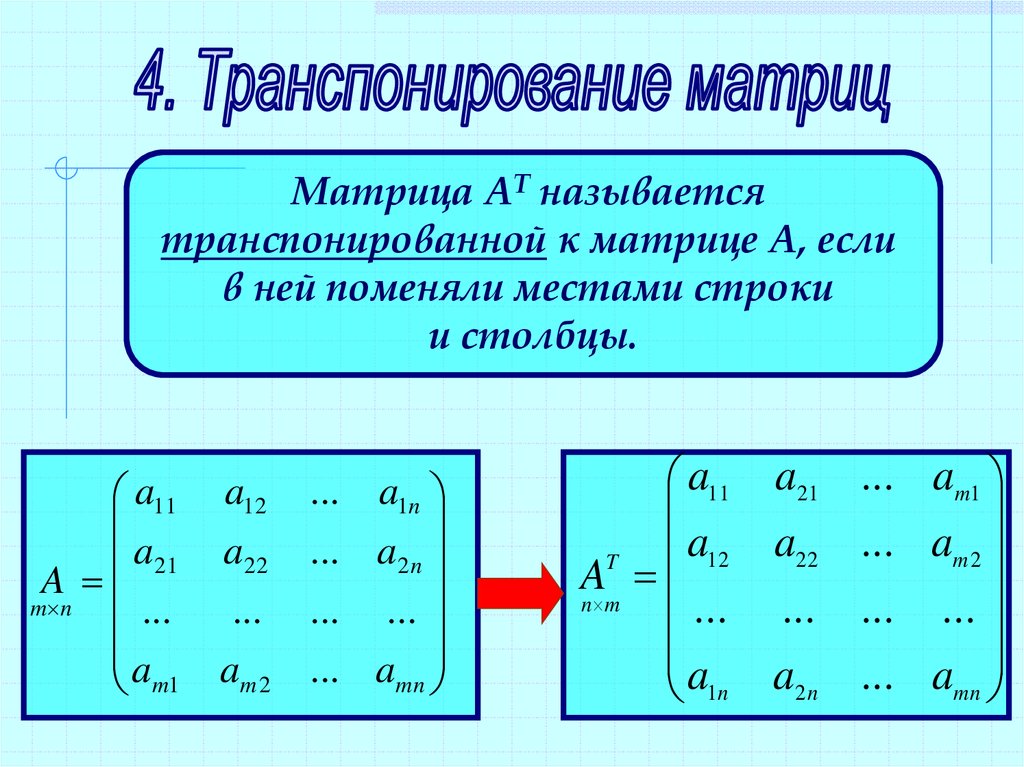
 N >= 0.
N >= 0. Матрица M-by-N dC.
Матрица M-by-N dC.