Задания по математике для 5 класса — интересные задачи по математике для 5 класса
Четыре причины изучать математику в 5 классе
Развитие логического мышления
Математика учит анализировать данные, устанавливать взаимосвязи и находить оптимальное решение. Эти навыки помогут справиться не с одной жизненной задачей.
Достижение успеха в любой профессии
Умение оперировать цифрами нужно не только экономистам. Математика необходима даже в таких творческих профессиях, как архитектор и фотограф.
Повышение авторитета в своем окружении
В школе разбирающийся в математике ребенок будет пользоваться уважением сверстников, а вне учебы не позволит обмануть себя, например, на кассе в магазине.
Развитие коммуникативных навыков
Неочевидно, но факт: те, у кого все хорошо с математикой, более стройно, логично и последовательно излагают свои мысли. А значит, с ними приятнее общаться.
Какой должна быть математика для учеников 5 класса?
Ребенок учится в удобное время
Каждый урок прокачивает знания по определенной теме и занимает около получаса. Но начать можно и с 5 минут в день! Доступ к курсу не ограничен: проходить уроки можно по несколько раз.
Ребенку интересно и хочется продолжать
Мудреных абстрактных заданий на этом курсе не встретишь — только конкретные жизненные ситуации и увлекательные математические задачи, развивающие логику и двигающие сюжет игры. Оторваться будет сложно!
Оторваться будет сложно!
Ребенок может заниматься углубленно
Курс дает возможность в интересной игровой форме потренироваться в решении сложных, продвинутых математических задач, которые в школе обычно не предлагают, и даже подготовиться к олимпиаде по математике.
Какие задачи по математике для 5 класса предлагает Умназия?
Задачи на классификацию
Поиск закономерностей
Математические задачи на логику
Задачи на истину и ложь
Волшебные квадраты
Математические ребусы
Задачи на переливание
Задачи на взвешивание
Задачи, решаемые с конца
Задачи на скорость
Задачи, решаемые методом перебора
Геометрические задачи
Начать заниматься?
Примеры заданий по математике для 5 класса
Задача 1
Ума-Коала едет на гироскутере на день рождения к своей подруге Сообразебре.
Ума-Коала знает, что скорость её передвижения составляет 12 км/час.
Можешь ли ты определить, сколько метров проезжает Ума-Коала за одну минуту?
Решить задачу
Задача 2
Три богатыря снарядились на битву. Каждый надел кольчугу, взял щит и меч. У каждого кольчуга, щит и меч были разного цвета: серебряного, золотого и бронзового. Добрыня Никитич взял серебряный меч, а Алёша Попович — золотую кольчугу.
Какого цвета было снаряжение у Ильи Муромца?
Решить задачу
Задача 3
Кощей Бессмертный похитил Василису Прекрасную. А чтобы красавица не сбежала, старик запер её в башне, а на дверь поставил кодовый замок. Каждая буква означает цифру. Одинаковые буквы — это одинаковые цифры, а разные — разные.
Василиса легко открыла дверь и сбежала от Кощея. А ты догадался, какой код придумал Кощей Бессмертный?
А ты догадался, какой код придумал Кощей Бессмертный?
Чему равна сумма А + Б + В, если известно, что она меньше 10?
Решить задачу
Решать задачи по математике для 5 класса
Познакомьтесь с форматом курса «Математическое мышление». Пройдите сюжетную игру и решите три математические задачи!
Решать задачи
В Умназии дети развивают логическое мышление, решая увлекательные сюжетные задачи по математике
Продуманная программа
Курсы математического мышления разработаны на базе множества источников, экспертизы методистов и педагогов, разделены на 10 тем с теорией и игровыми заданиями с объяснением
Увлекательные задания
Ребенок решает сюжетные игровые задачи по математике для изучения новых тем и закрепления пройденного по каждому курсу.
Дипломы и награды
В конце каждого курса ребенок решает тест или проходит игру, получая сертификат в случае успешного выполнения. Вы будете уверены в его знаниях!
Интересные задания по математике для учеников 5 класса
В пятом классе у школьника появляется немало новых предметов, и есть риск закопаться в учебниках на весь день. Тут-то и пригодится умение грамотно отбирать, анализировать и структурировать материал. Иными словами, поможет развитое логическое мышление.
Так что на этом этапе стоит уделить особое внимание решению логических и математических задач. А чтобы ребенок не заскучал, их стоит подавать в интересной форме, например, в виде игры.
Купите курс математики для детей со скидкой 40 % уже сейчас
Задания по математике для 3 класса — интересные задачи по математике для 3 класса
Четыре причины изучать математику в 3 классе
Развитие логического мышления
Математика учит анализировать данные, устанавливать взаимосвязи и находить оптимальное решение. Эти навыки помогут справиться не с одной жизненной задачей.
Эти навыки помогут справиться не с одной жизненной задачей.
Достижение успеха в любой профессии
Умение оперировать цифрами нужно не только экономистам. Математика необходима даже в таких творческих профессиях, как архитектор и фотограф.
Повышение авторитета в своем окружении
В школе разбирающийся в математике ребенок будет пользоваться уважением сверстников, а вне учебы не позволит обмануть себя, например, на кассе в магазине.
Развитие коммуникативных навыков
Неочевидно, но факт: те, у кого все хорошо с математикой, более стройно, логично и последовательно излагают свои мысли. А значит, с ними приятнее общаться.
А значит, с ними приятнее общаться.
Какой должна быть математика для учеников 3 класса?
Доступный игровой формат
Зубрежка таблицы умножения не научит рационально мыслить, а творческая задача или эксперимент в рамках увлекательной сюжетной истории — научат. Здесь уже придется включить логику. Но все это — в нескучной игровой форме.
Эффективное закрепление материала
Спеша подготовиться к следующему школьному занятию, можно забыть содержание предыдущего. На курсах Умназии этого точно не произойдет: пройденный на каждом уроке материал закрепляется с помощью интересных экспериментов в виртуальной лаборатории.
Развитие нестандартного мышления
Творческие математические задания учат школьников нешаблонно мыслить, не сдаваться и подбирать разные подходы к решению жизненных задач. А эти навыки пригодятся не только на уроках математики.
Какие задачи по математике для 3 класса предлагает Умназия?
Задачи на классификацию
Поиск закономерностей
Математические задачи на логику
Задачи на истину и ложь
Волшебные квадраты
Математические ребусы
Задачи на переливание
Задачи на взвешивание
Задачи, решаемые с конца
Задачи на скорость
Задачи, решаемые методом перебора
Геометрические задачи
Начать заниматься
Примеры заданий по математике для 3 класса
Задача 1
Царь подарил Шамаханской царице перстень. Перстень был золотой, с алмазом и гравировкой. Оказалось, что у Шамаханской царицы уже много таких украшений. Она хранит все свои перстни в шкатулке, которая имеет жёлтый, синий и красный отделы. В жёлтом отделе шкатулки хранятся только золотые перстни. В красном — только перстни с алмазами. А в синем — перстни с гравировкой.
Перстень был золотой, с алмазом и гравировкой. Оказалось, что у Шамаханской царицы уже много таких украшений. Она хранит все свои перстни в шкатулке, которая имеет жёлтый, синий и красный отделы. В жёлтом отделе шкатулки хранятся только золотые перстни. В красном — только перстни с алмазами. А в синем — перстни с гравировкой.
Посмотри на все перстни царицы, и скажи, в какой из частей шкатулки лежит больше всего перстней, а в какой части совсем нет колец.
Решить задачу
Задача 2
Маша, Полина и Федя сверяли часы. У Маши часы спешат на 8 минут, а у Феди они остановились 5 минут назад.
Можешь ли ты определить, на сколько минут или часов спешат часы Полины?
Решить задачу
Математические загадки на логику с ответами. Самые сложные задачи в мире
Содержание
- Польза занятий логикой и математикой
- Уроки-игры
- Математические задачи на логику для дошкольников
- Математические задачи на логику: 1-2 класс
- Математические задачи на логику: 3-4 класс
- Занимательные математические задачи для учащихся 5-х классов с ответами
- Математические головоломки
- Визуальная тренировка для мозга
- Загадки
- Логические задачки
- ПРАВИЛЬНЫЕ ОТВЕТЫ:
- Самая сложная задача в мире
Польза занятий логикой и математикой
Элементарные математические представления помогают сформировать в детском саду. Базовые математические способности развивают в школе.
Базовые математические способности развивают в школе.
А чтобы ребёнок научился рассуждать логически, мыслить нестандартно — обычных арифметических и геометрических задач недостаточно.
Уже в дошкольном возрасте желательно выработать привычку ежедневно выполнять задания и упражнения на развитие логического мышления.
Благодаря регулярным тренировкам:
- ребёнок учится рассуждать, анализировать и делать правильные выводы;
- развивает сообразительность, память, внимание и интеллект;
- успехи повышают самооценку, интерес к обучению в школе, вдохновляют на победы в математических олимпиадах и конкурсах.
Уроки-игры
В школьных учебниках занимательного материала недостаточно. Однако опытный педагог умеет сделать привычные задания по математике интересными. В 1 классе это особенно важно, так как дети лучше откликаются на игровую форму обучения. Им скучно решать примеры, но все меняется, если учитель принесет на урок мяч и будет спрашивать верный ответ у поймавшего его.
Повысить активность детей позволяет игровой сюжет, присутствующий на занятии. Вариантов может быть множество. Например, за каждое выполненное задание ребятишки получают кусочек паззла, и в конце урока из них собирается картинка. Или класс отправляется спасать героя, попавшего в беду. На пути они встречают различных злодеев и побеждают их, решая задачки и примеры. Очень нравятся детям соревнования, когда класс делится на команды и каждая набирает жетоны за работу. Победителей можно наградить бумажными медалями. Таким образом, не всегда нужно искать занимательный материал. Иногда достаточно изменить форму его подачи.
Математические задачи на логику для дошкольников
Начиная с 3 летнего возраста малыша, родители должны понемногу заниматься тренировкой логического мышления у своих детей. Детям это очень важно, ведь для них в таком возрасте многие очевидные вещи кажутся сложными, а непонятные для восприятия взрослым, напротив, очевидными. Представим несколько вариантов логических задач для детей 3-5 лет.
- На столе лежит 1 апельсин. Его разрезали на 2 части, сколько апельсинов лежит на столе? Ответ: 1, разрезанный.
- Собаку привязали к забору веревкой. Длина веревки составляет 10 метров, а собака прошла за день 100 метров. Как ей это удалось? Ответ: Собака ходила вдоль забора туда и обратно и «находила» целых 100 метров.
- Какой день недели соответствует числу 3? Ответ: среда, т.к. его порядковый номер в неделе – 3.Примечание: Про дни недели дошкольникам можно задавать различные варианты вопросов. Это поможет не только в развитии логического мышления, но и поможет скорее выучить дни недели.
- Посчитать, сколько людей в следующей строке: ты да я, да мы с тобой. Ответ: 2.
- Папа и сын, дедушка и внук, сын и папа. Сколько всего человек здесь отмечено? Ответ: 3, т.к. папа – сын дедушки, сын папы – внук дедушки.
- На опушке стояло 3 высоких сосны. На каждой сосне по 3 больших ветки и по 3 маленьких. На каждой маленькой ветке по яблоку. Сколько всего яблок на деревьях? Ответ: 0, на соснах яблоки не растут.

- Папу Антона зовут Андрей Викторович, а дедушку – Сергей Иванович. Какое отчество у мамы Антона? Ответ: Сергеевна, Потому что Сергей Иванович – это отец мамы Антона. Отца папы Антона зовут Виктор.
- У двух братьев по одной сестре. Сколько всего детей в семье? Ответ: 3. 2 брата и одна сестра на двоих.
- Какие камни есть в море? Ответ: мокрые.Примечание: аналогичная задача-загадка моет звучать так «Каких камней в море нет?» — ответ: сухих.
- Вася и Петя играли в морской бой и сыграли по 3 партии. Каждый выиграл по 3 раза. Это правда или ложь? Ответ: ложь. Во время одной партии выиграть может только один.
- В поле работали 5 тракторов. 2 трактора сломались и остановились. Сколько тракторов в поле? Ответ: 5, т.к. учитываются все тракторы, и рабочие, и сломанные.
- Одно яйцо варится 5 минут. Сколько времени нужно, чтобы сварить 2 яйца? Ответ: все те же 5 минут.
- Саша сидит в самолете. Впереди него машина, сзади – лошадь. Где находится Саша? Ответ: катается на карусели.

- Алена сидит, когда она встанет и уйдет, ее мама так и не сможет сесть на ее место. Где сидит Алена? Ответ: у мамы на коленях.
- Что все дети на земле делают одновременно? Ответ: взрослеют.
Опираясь на предложенные варианты заданий на развитие логического мышления, родители могут придумывать незамысловатые условия задач самостоятельно.
Математические задачи на логику: 1-2 класс
Но вот дети пошли в школу, буквально за первые месяцы учебы они начинают хорошо считать, ориентироваться в пространстве и времени. Задачки для дошкольников уже кажутся им простыми и неинтересными. Поэтому для таких деток мы приготовили несколько вариантов упражнений тренировки логики и смекалки, ориентируясь на их новые способности и возможности.
- Первоклассника попросили назвать самое большое число. Что он ответил?
Ответ: 31. Первоклассники каждый день записывают число месяца в тетрадь, самое большое число в месяце – 31. - На доске написаны два числа 4 и 5.
 Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая.
Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая. - По узкой дороге может проехать только одна машина. С одной стороны дороги находится гора. Одна машина едет с горы, другая – под гору. Как им разминуться? Ответ: обе машины едут в одном направлении и разминаться им не придется.
- Сколько раз из числа 10 можно отнять число 2? Ответ: один, т.к. уже после первого вычитания двойки останется число 8, а не 10.
- На столе стоят 6 стаканов: в первые три налили воду, вторые три – пустые. Нужно расставить стаканы так, чтобы чередовались пустые и полные стаканы, но при этом можно взять в руки только один стакан. Как поступить, чтобы выполнить условие? Ответ: Взять второй стакан и перелить из него воду в пятый стакан. Второй стакан поставить на прежнее место.
- За 10 часов 10 человек могут выкопать траншею длиной в 10 метров. Сколько нужно человек, чтобы они выкопали траншею диной в 100 метров за 100 часов? Ответ: 10 человек.
 На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров.
На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров. - Школьники участвуют в соревнованиях по бегу. Ваня занимает третью позицию, Антон занимает вторую позицию. Саша обгоняет Антона. Какую позицию занимает Саша? Ответ: вторую, т.к. впереди Антона тоже кто-то бежит и этот кто-то пока первый.
- Учитель положил на пол карандаш и попросил учеников перешагнуть через него, но никто не смог этого сделать. Почему? Ответ: карандаш лежит у стены и шагать детям некуда.
- Таня и Алиса пошли в магазин и нашли 2 рубля. Сколько бы денег они нашли, если бы с ними пошла еще и Марина? Ответ: 2 рубля, т.к. размер находки никак не зависит от количества ее нашедших.
- Из пункта А в пункт Б вышла кошка, а из пункта Б в пункт А вышла мышка. Когда они встретятся, кто из них будет ближе к пункту А, а кто к пункту Б? Ответ: они обе будут на одинаковом расстоянии от пункта А, и на одинаковом расстоянии от пункта Б.
- На столе стояли 3 чашки с чаем.
 Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись.
Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись. - Марина шла из дома в школу и встретила трех мужиков. У каждого за спиной был мешок. У первого мужика в мешке был один кот, у второго в мешке был один кот и один пес. У третьего в мешке было 2 пса. Сколько всего котов направлялось в школу? Ответ: один, сама Марина. Мужики с мешками шли в обратную от школы сторону.
- В классе стоял стол с четырехугольной крышкой. Ученики отпилили один угол, что стало со столом, сколько углов осталось на крышке? Ответ: 5. Если отпилить один угол, то получим на его месте 2 новых, поэтому всего 5 углов.Примечание: на самом деле количество углов может зависеть и от того, как размышляет ребенок. Если он «пилит» стол по углам диагонали, т.е. распиливает его пополам, то вполне возможно, что у стола будет 3 угла. Если же один распил приходится на угол, а второй на сторону крышки, то может остаться и 4 угла.
 Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол.
Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол. - На тарелке лежат 3 банана. Их нужно разделить между тремя девочками, чтобы на тарелке остался один банан. Ответ: одной девочке нужно отдать банан вместе с тарелкой.
- Какое слово зашифровано: ООО? Ответ: ТРИО, т.е. ТРИ О.
Родители тоже могут составлять свои задачи для детей, ориентируясь на предложенные варианты. Чем чаще ребенок будет заниматься упражнениями на логику, тем быстрее будет работать его мозг, тем выше будет успеваемость в школе.
Математические задачи на логику: 3-4 класс
Дальнейшее обучение в школе имеет свои особенности: дети научились складывать двузначные числа, совершать с ними различные математические операции, в том числе умножение, деление. Логические математические задачи для школьников 3-4 класса должны охватывать уже полученные знания и совершенствовать их качество.
- В кошельке лежит 15 копеек двумя монетами.
 Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком.
Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком. - Шла Маша в Волгоград, а навстречу ей 10 ребят. У каждого в руках по лукошку, в каждом лукошке по кошке, а у каждой кошки по котенку. Сколько всего ребят шло в Волгоград? Ответ: одна Маша. Все остальные, сколько бы их не перечисляли, шли навстречу девочке, а значит в противоположную сторону от Волгограда.
- Дедушка пилит бревна. Распил бревна пополам он делаем ан одну минуту. Сколько ему понадобится времени, чтобы распилить бревно на 10 частей? Ответ: 9 минут, т.к.чтобы распилить бревно на 10 частей, нужно сделать 9 распилов.
- Мальчик пришел в амбар. В каждом углу амбара стояло по 3 мешка. На каждом мешке сидело по кошке, у каждой кошки было по котенку. Сколько всего ног было в амбаре? Ответ: две, только мальчика.Примечание: Как бы долго дети не перемножали между собой числа-«ноги» кошек и котят, стоит помнить, что у кошек – лапы, а ноги – только у мальчика.
- Родители купили своим двум дочкам Маше и Лизе по коробке конфет.
 В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется.
В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется. - Из ГОРОНО в школу пришли проверяющие. Они выбрали класс для проверки, но не все дети были готовы отвечать урок. Тем не менее, на каждый вопрос учителя весь класс поднимал руку, и тот, кого учитель вызывал к доске, отвечал блестяще. Как получилось, что учитель угадывал, кого вызвать отвечать? Ответ: решением этой задачи есть небольшая хитрость. Перед уроком школьники и учитель договорились, что те, кто наверняка знают ответ на поставленный вопрос, будут поднимать правую руку.
 А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался.
А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался. - Что у коровы находится спереди, а у быка сзади? Ответ: буква «К». Корова, быК.
- Когда маме исполнилось 31 год, дочери было 8. Сейчас мама старше дочери ровно в 2 раза. Сколько их обеим лет? Ответ: дочке 23, маме 46. Когда дочь родилась, маме было 31-8 = 23 года. Чтобы быть старше дочки в два раза, маме должно быть 23*2 = 46 лет. За это время дочь доросла до 23 лет.
- Две одноклассницы Наташа и Лена живут в одном подъезде: Лена на втором этаже, а Наташа на четвертом. Наташа поднимается по ступенькам на четвертый этаж и проходит 60 ступенек. Сколько ступенек проходит Лена, которая поднимается на второй этаж? Ответ: 20. Чтобы подняться с первого этажа на четвертый, нужно пройти три пролета. 60_3=20 ступенек в одном пролете. А Лена поднимается с первого на второй этаж и проходит при этом только один пролет, все те же 20 ступенек.
- Может ли страус называть себя птицей? Ответ: нет, не может.
 Страусы не умеют разговаривать.
Страусы не умеют разговаривать. - Какая физическая величина не имеет ни высоты, ни глубины, ни ширины, ни длины, но ее можно измерить? Ответ: время, температура.
- Задание на логику из серии «Юный Шерлок». На вызов о самоубийстве были вызваны представители уголовного розыска. В кабинете жертвы они обнаружили диктофон и включили его. На диктофоне была записана следующая фраза: «В моей смерти прошу никого не винить, жизнь не имеет смысла…» далее раздался выстрел. Как следователи поняли, что убийство сфабриковано? Ответ: убитый не мог перемотать запись на начало, это сделал кто-то другой.
- Что не может поместиться даже в самую большую кастрюлю? Ответ: ее крышка.
- В кастрюле налита вода до самого верха. Как отмерять жидкость, не используя никаких мерительных приспособлений, чтобы в кастрюле осталась только половина жидкости. Ответ: нужно наклонить кастрюлю и выливать воду до тех пор, пока не покажется с боковой части дно. Это и будет половина кастрюли.
- Когда цифра «2» означает «10»? Ответ: на циферблате цифра «2» соответствует «10 минутам».

С каждым годом задания на развитие логики и смекалки должны становится все сложнее, иметь подвохи, хитрости, чтобы ребенок учился размышлять, уделять внимание деталям. А регулярные и систематические занятия обязательно принесут свои плоды.
Занимательные математические задачи для учащихся 5-х классов с ответами
Из гнезда вылетели три ласточки. Какова вероятность того, что через 15 секунд они будут находиться в одной плоскости? (Ответ: 100%, так как три точки всегда образуют одну плоскость)
На столе лежат две монеты, в сумме они дают 3 рубля. Одна из них — не 1 рубль. Какие это монеты? (Ответ: 2 рубля и 1 рубль. Одна то не 1 рубль, а вот другая — 1 рубль)
С какой скоростью должна бежать собака, чтобы не слышать звона сковородки, привязанной к ее хвосту? (Ответ: Если выдумаете, что ей нужно бежать со сверхзвуковой скоростью, то вы ошибаетесь — собаке достаточно стоять на месте)
Один оборот вокруг Земли спутник делает за 1 ч 40 мин, а другой — за 100 минут. Как это может быть? (Ответ: 1 ч 40 мин = 100 мин)
Как это может быть? (Ответ: 1 ч 40 мин = 100 мин)
Крыша одного дома несимметрична: один скат ее составляет с горизонталью угол 60 градусов, другой — угол 70 градусов. Предположим, что петух откладывает яйцо на гребень крыши. В какую сторону упадет яйцо — в сторону более пологого или крутого ската? (Ответ: Петухи не кладут яйца)
В 12-этажном доме есть лифт. На первом этаже живут всего 2 человека, от этажа к этажу количество жильцов увеличивается вдвое. Какая кнопка в лифте этого дома нажимается чаще других? (Ответ: Независимо от распределения жильцов по этажам, кнопка «1»)
В двух кошельках лежат две монеты, причем в одном кошельке монет вдвое больше, чем в другом. Как такое может быть? (Ответ: Один кошелек лежит внутри другого)
Сын отца профессора разговаривает с отцом сына профессора, причем сам профессор в разговоре не участвует. Может ли такое быть? (Ответ: Да, может, если профессор — женщина)
Два сына и два отца съели 3 яйца. Сколько яиц съел каждый? (По одному яйцу каждый)
На складе было 5 цистерн с горючим, по 6 т в каждой. Из двух цистерн горючее выдали. Сколько цистерн осталось? (5)
Из двух цистерн горючее выдали. Сколько цистерн осталось? (5)
Вообрази, что ты капитан футбольной команды. В районе 8 футбольных команд по 11 человек в каждой. Игроки вашей команды на 2 года моложе своего капитана, а игроки других — только на 1 год. Сколько лет капитану вашей команды? (Столько, сколько лет отвечающему)
Пара лошадей пробежала 20 км. Сколько километров пробежала каждая лошадь? (20 км)
Когда сороке исполнится 4 года, что с ней произойдет? (Будет жить пятый год)
Если в 11 часов ночи идет дождь, то возможно ли через 48 часов солнечная погода? (Нет, так как будет ночь)
Чтобы сварить 1 кг. мяса требуется один час. Сколько времени потребуется для варки ½ кг мяса? (1 час)
У Марины было целое яблоко, две половинки и 4 четвертинки. Сколько было у нее яблок? (3)
На грядке сидели 6 воробьев, к ним прилетели еще 5. Кот подкрался и схватил одного воробья. Сколько воробьев осталось на грядке? (Один, которого схватил кот. Остальные улетели)
Мальчик написал на бумажке число 86 и говорит своему товарищу: «Не производя никакой записи, увеличь это число на 12 и покажи мне ответ». Недолго думая, товарищ показал ответ. А вы это сделать сумеете? (Перевернуть бумажку «вверх ногами»)
Недолго думая, товарищ показал ответ. А вы это сделать сумеете? (Перевернуть бумажку «вверх ногами»)
В клетке находились 4 кролика. Четверо ребят купили по одному из этих кроликов и один кролик остался в клетке. Как это могло получиться? (Одного кролика купили вместе с клеткой)
Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Сколько всего летело уток? (Три утки, одна за другой)
У одного старика спросили, сколько ему лет. Он ответил, что ему сто лет и несколько месяцев, но дней рождения у него было всего 25. Как это могло быть? (Этот человек родился 29 февраля, т. е. день рождения у него бывает один раз в четыре года)
Что это такое: две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги, схватив три, бросили их в четыре, чтобы четыре оставили одну? (Повар сидел на стуле, имеющем три ножки, пришла собака и утащила куриную ногу. Повар бросил стул в собаку, чтобы она оставила куриную ногу)
Часы бьют каждый час и отбивают столько ударов, сколько показывает часовая стрелка. Сколько ударов отобьют часы в течение 12 часов? (Количество ударов равняется 1+2+3+…+12…= 78. Сумма членов, равноотстоящих от концов (1+12,2+11,3+10,…) равны между собой — 13. Таких пар равноотстоящих от концов чисел имеется 6. Значит, 1+2+3+…+12=6 13=78)
Сколько ударов отобьют часы в течение 12 часов? (Количество ударов равняется 1+2+3+…+12…= 78. Сумма членов, равноотстоящих от концов (1+12,2+11,3+10,…) равны между собой — 13. Таких пар равноотстоящих от концов чисел имеется 6. Значит, 1+2+3+…+12=6 13=78)
Летели скворцы и встретились им деревья. Когда сели они по одному на дерево, то одному скворцу не хватило дерева, а когда на каждое дерево сели по два скворца, то одно дерево осталось незанятым. Сколько было скворцов и сколько деревьев? (Предположим, что после того как скворцы сели на деревья по два, с каждого дерева взлетело по одному скворцу. Один из взлетевших скворцов может сесть на незанятое дерево, тогда на каждом дереве будет сидеть по одному скворцу. По условию, если на каждое дерево сядет по одному скворцу, то один скворец останется в воздухе. Значит, взлетело 2 скворца. Тогда общее число скворцов равно 4, а число деревьев З).
Математические головоломки
Вопрос 1. Какое число зашифровано?
Вопрос 2. Как поместить шары с цифрами, чтобы получить число 30?
Как поместить шары с цифрами, чтобы получить число 30?
Вопрос 3. Какая цифра получится в конце?
Замените знак вопроса числом, соответствующим приведенным ниже уравнениям. Найдите закономерность.
Визуальная тренировка для мозга
Вопрос 4. Разделите изображение на четыре части, которые сочетали бы всех видов насекомых:
Вопрос 5. Какой вид сверху на башню: А, В, С или D?
Вопрос 6. Каким образом представляются кубики для человека, который стоит в оранжевой точке и смотрит на фигуру в указанном направлении?
Вопрос 7. Быстро решите, какой фрукт необходимо добавить?
Вопрос 8. Смотрите внимательно и угадайте, кто вор?
Загадки
Вопрос 9. Примите жизненно важное решение. В комнате без света есть три двери: за первой спряталась ядовитая змея, за второй – лев, который не ел пару дней, в третьей вас ждет экзекуция на электрическом столе. Какую дверь безопаснее всего открыть?
Вопрос 10. Разминка на логику и память. В названии какого города спрятались имена ста девушек и одного парня?
Разминка на логику и память. В названии какого города спрятались имена ста девушек и одного парня?
Вопрос 11. Логическая загадка: у отца Фрэнка 5 сыновей. Имена его четырех сыновей — Фефе, Фифи, Фофо, Фуфу. Соответственно, как зовут его пятого сына?
Вопрос 12. Знаменитая загадка: по пути в Сент-Айвз я увидел мужчину с 7 женами. У каждой жены было 7 мешков. В каждом мешке было по 7 кошек. У каждого кота было 7 котят. Котенок, кошки, мешки, жены – сколько их направляются в Сент-Айвс?
Логические задачки
Вопрос 13. Как отмерить 4 литра воды, если есть 5-литровая и 3-х литровая емкости?
Вопрос 14. Как сделать цифру «4», но не сломать ни одну палочку.
Вопрос 15. В каком чайнике больше чая?
ПРАВИЛЬНЫЕ ОТВЕТЫ:
1-й Правильный ответ: 9.
2-й Правильный ответ:
Этот вопрос не может быть решен математически. Потому что сумма трех нечетных чисел не может быть четное число.
Но здесь важно ваше внимание. Если вы поместите шары с цифрами 11 и 13, то получите 24. Затем, если вы поместите шар с цифрой 9, но перевернете, то получите 24 + 6 = 30.
Если вы поместите шары с цифрами 11 и 13, то получите 24. Затем, если вы поместите шар с цифрой 9, но перевернете, то получите 24 + 6 = 30.
3-й Правильный ответ:
Если мы знаем, что каждое полученное число является степенью числа 4, получаем:
41 = 4
42 = 16
43 = 64
44 = 256
4-й Правильный ответ:
5-й Правильный ответ:
Если вы посмотрите на башню сверху, верхний слой будет оранжевым. Таким образом, ответ определенно не C.
Второй фиолетовый слой не будет виден сверху, потому что он такого же размера, как и верхний слой.
И третий слой также не будет виден, потому что он меньше, чем два верхних слоя.
Четвертый слой будет следующим, который будет виден сверху вокруг фиолетового слоя.
Последний будет самым крупным, и он оранжевый. В соответствии с этим, ответ будет A.
6-й Правильный ответ:
Пойдем шаг за шагом. Очевидно, что внизу 4 блока.
Над крайним правым блоком есть еще один. Таким образом, ответ определенно не C.
Самый высокий блок состоит из трех блоков в высоту.
Итак, ответ D.
7-й Правильный ответ:
Банан, Груша, Перец
8-й Правильные ответы:
9-й Правильные ответы:
С электрическим стулом. Палач скорее всего пойдет проверить, почему света нет, а вы сможете убежать.
10-й Правильный ответ:
Севастополь – Сева и 100 Поль.
11-й Правильный ответ:
Если у отца Фрэнка 5 сыновей, а имена 4 сыновей такие же, как указано выше, то Фрэнк уже 5-й сын.
12-й Правильный ответ:
Только я.
13-й Правильный ответ:
Налейте полную емкость в 5 литр;
Перелейте из нее в 3-х литровую емкость – получаем остаток 2 литра;
Выливаем 3 литра – остается только 2 литра воды;
Переливаем ее в 3-х литровую емкость;
Снова заполняем 5-ти литровую емкость
Переливаем в 3-х литровую емкость недостающий 1 литр воды и получаем остаток в 4 литра!
14-й Правильный ответ:
15-й Правильный ответ:
В первом. Нужно смотреть на положение носика.
Нужно смотреть на положение носика.
Самая сложная задача в мире
Самой сложной задачей в мире официально признали задание из итальянской газеты, опубликованное в 1992 году. Составил ее философ по имени Джордж Булос. Условия задачи следующие:
Имеются три божества. Одно из них ‒ покровитель правды (А), другое ‒ покровитель лжи (В), третье ‒ покровитель случайностей (С). И первый всегда отвечает исключительно правду, второй лжет, а вот третий может лгать или не лгать в произвольной последовательности. Богов нужно распознать, задав им в общей сложности 3 вопроса. Отвечать они могут лишь «нет» или «да», причем на своем собственном языке (Da и Ja), так что придется еще догадаться, которое из слов означает «да», а которое ‒ «нет». Не разрешается задавать нескольким божествам один и тот же вопрос. Зато одному можно сразу задать два или даже три вопроса, тогда остальные останутся вовсе без вопросов. Иногда ответ на какой-либо вопрос влияет на то, кому и какой следующий вопрос задать. Бог случайностей отвечает, словно в его голове подбрасывается воображаемая монетка, причем аверс ‒ правда, а реверс ‒ ложь. Запрещено задавать парадоксальные вопросы, на которые можно дать ответ как нет, так и да, или нельзя дать ответ вовсе.
Бог случайностей отвечает, словно в его голове подбрасывается воображаемая монетка, причем аверс ‒ правда, а реверс ‒ ложь. Запрещено задавать парадоксальные вопросы, на которые можно дать ответ как нет, так и да, или нельзя дать ответ вовсе.
Самая сложная логическая задача имеет следующее решение:
Первым же вопросом необходимо отыскать того, кто НЕ является божеством случайностей. Вариантов таких вопросов много, но главное условие ‒ наличие в вопросе некоторых логических связей. Например: «Если ты — божество правды, а В ‒ божество случайностей, то Da ‒ это означает да?» Можно упростить решение, применяя условные фразы, которые противоречат фактам. Суть в том, что на любой из возможных вопросов (Q), заданный божеству правды или божеству лжи («Если я задам некий вопрос Q, ответ будет звучать как Ja?»), ответят Ja в том случае, если ответ должен быть да, и Da ‒ если ответ должен быть нет. Чтобы это доказать, автор предложил целых восемь вариантов вопросов. В конце, после того, как выяснили, кто божество правды, а кто лжи, оставшийся бог будет опознан методом исключения.
Источники
- https://logiclike.com/math-logic
- https://FB.ru/article/390638/interesnyie-zadaniya-po-matematike-igryi-i-zadaniya-s-otvetami-dlya-shkolnikov
- https://ChildAge.ru/obuchenie-i-obrazovanie/nachalnaya-shkola/samostoyatelnaya-rabota/matematicheskie-zadachi-na-smekalku-s-otvetami.html
- https://ped-kopilka.ru/uchiteljam-predmetnikam/matematika/zanimatelnye-zadachi-po-matematike-s-otvetami-5-klas.html
- https://joy-pup.com/puzzle/15-novyh-zadach-na-logiku/
- https://megatopof.ru/prochee/slozhnye-zadachi.html
Интересные задачи по геометрии и геометрические головоломки ✅ Блог IQsha.ru
О чём вы думаете, когда слышите слово “геометрия”? Скорее всего, это будут мысли о треугольниках и квадратах, круге и ромбе. Но геометрия ─ это не только фигуры, но и весь окружающий мир, всё, что имеет структуру. Предлагаем познакомить малышей с этим увлекательным миром и предложить им интересные геометрические головоломки! Эти занимательные задачки подойдут и дошкольникам, и детям постарше и раскрасят череду повседневных игр.
Геометрические головоломки развивают абстрактное и логическое мышление, воображение, комбинаторные способности, а также терпение и усидчивость, ведь составление новых фигур требует времени.
Мы подобрали для вас 25 занимательных задач по геометрии и уверены, что их решение принесёт не только пользу, но и большое удовольствие вашему ребёнку.
Интересные задачи по геометрии
Задача 1
Посмотрите, сколько треугольников на этом рисунке? А четырёхугольников? И сколько фигур всего? Посчитайте их и запишите верные ответы.
Посмотреть ответ
4 треугольника, 1 четырехугольник ─ всего 5 фигур.
Задача 2
Посмотрите внимательно на домик. Назовите все фигуры, которые были использованы при его строительстве.
Посмотреть ответ
круг, треугольник, квадрат, прямоугольник и многоугольник.
Задача 3
Перед вами нелёгкая задача ─ посчитать все фигуры на рисунке. Сколько на нём четырёхугольников, а треугольников?
Посмотреть ответ
5 четырехугольников, 4 треугольника ─ всего 9 фигур.
Задача 4
Как вы думаете, сколько на рисунке треугольников? А четырёхугольников? Сможете их посчитать?
Посмотреть ответ
всего на рисунке 6 треугольников и 7 четырёхугольников.
Задача 5
Как вы думаете, возможно ли обычным циркулем начертить эллипс?
Посмотреть ответ
Это возможно, но с условием: бумага, на которой вы будете чертить, должна лежать на стороне цилиндра или любой трубы. Тогда оборотом обычного циркуля можно начертить эллипс.
Задача 6
На одной плоскости размещены 11 шестерёнок, которые соединены по цепочке. Как вы думаете, смогут ли все шестерёнки вращаться одновременно?
Посмотреть ответ
Давайте представим, что первая шестерёнка двигается по часовой стрелке. Тогда вторая должна двигаться против часовой. Третья ─ вновь по часовой стрелке, четвёртая ─ против и так далее. Получается, что «нечётные» шестерёнки вращаются по часовой стрелке, а «чётные» ─ против часовой. Тогда выходит, что первая и одиннадцатая двигаются одновременно по часовой стрелке, что невозможно. Значит, все шестерёнки одновременно вращаться не могут.
Тогда выходит, что первая и одиннадцатая двигаются одновременно по часовой стрелке, что невозможно. Значит, все шестерёнки одновременно вращаться не могут.
Задача 7
Внимательно посмотрите на фигуру и разделите её сначала на две равные части, затем на три.
Посмотреть ответ
Эту фигуру можно разделить на множество одинаковых частей вот таким образом. А у вас получились такие же части?
Задача 8
Вам нужно нужно разделить фигуру месяца на 6 частей, но провести можно только две прямые линии. Уже знаете, как это сделать?
Посмотреть ответ
Задача 9
Посмотрите внимательно и найдите на фигуре пять прямых углов. Как быстро вы справились с задачей?
Задача 10
Как называются фигуры ─ общая часть треугольников и четырёхугольников?
Посмотреть ответ
Слева изображён треугольник, а справа — пятиугольник.
Задача 11
Какие фигуры были использованы для строительства грузовика? Посчитайте их количество и запишите.
Посмотреть ответ
7
Задача 12
На дороге произошла авария, поэтому водителям приходится объезжать этот участок по другому пути. Он отмечен на картинке пунктирной линией. На сколько этот новый путь длиннее обычной дороги?
Посмотреть ответ
На 6 км. Потому что 5 км ─ это длина прежней дороги.
Задача 13
Как вы думаете, сколько квадратов изображено на рисунке?
Посмотреть ответ
на рисунке изображены 14 квадратов.
Задача 14
Посмотрите внимательно на чертёж и посчитайте количество четырехугольников.
Посмотреть ответ
4
Задача 15
Перед вами шесть фигур. Ваша задача ─ соединить их попарно непроизвольными и непрерывными линиями так, чтобы они не пересекались.
Посмотреть ответ
Задача 16
Посмотрите на рисунок и найдите на нём три одинаковые карточки.
Посмотреть ответ
чтобы легко найти карточки, их нужно было покрутить. На рисунке 3, 4, 5 карточки одинаковые.
На рисунке 3, 4, 5 карточки одинаковые.
Задача 17
К вам в гости пришли 8 гостей и вы хотите их напоить чаем с вкуснейшим тортом! Как поделить плоский круглый торт на 8 равных частей за три прямолинейных надреза ножа? При это перекладывать куски нельзя! Справитесь?
Посмотреть ответ
Задача 18
Посмотрите на чертёж и расположение девяти точек на нём: по три в каждом вертикальном и горизонтальном ряду. Ваша задача ─ нарисовать четырёхзвенную ломаную, не отрывая карандаша от бумаги. Эта ломаная должна проходить через все девять точек.
Посмотреть ответ
в условии задачи не было указано, что ломаная не может выходить за пределы рамки, в которой находятся все точки.
Выполните развивающие упражнения от Айкьюши
Задача 19
Перед вами ещё одна интересная задача! Давайте попробуем сделать из прямоугольника квадрат? Известно, что одна сторона прямоугольника равна 4, а другая 9 единицам длины. Этот прямоугольник разрешается разрезать только на две равные части.
Этот прямоугольник разрешается разрезать только на две равные части.
Посмотреть ответ
если разрезать лист лист бумаги так, можно сложить из полученных частей квадрат размером 6 × 6. Проверьте сами!
Задача 20
Как вы думаете, возможно ли сложить шесть карандашей так, чтобы каждый касался любого другого?
Посмотреть ответ
сначала расположим три карандаша, а следом за ними сверху ещё три, но в другом направлении. Посмотрите, каждый карандаш касается остальных. А у вас получилось?
Задача 21
Посмотрите, на картинке нарисован квадратный пруд. У каждого берега пруда растёт дерево. Строителям нужно расширить этот пруд в два раза таким образом, чтобы сохранить его квадратную форму и все деревья по берегам. Как это сделать?
Посмотреть ответ
Задача 22
Вам нужно разделить эту фигуру на 8 одинаковых по форме частей, каждая из которых имеет 4 угла.
Посмотреть ответ
Вот как нужно было разделить эту фигуру. Справились?
Справились?
Задача 23
А теперь попробуйте решить такую интересную задачку! Вам нужно разрезать шестиугольник на три части и из получившихся кусочков сложить ромб. Готовы попробовать?
Посмотреть ответ
Задача 24
Посмотрите внимательно на эти три квадрата. Сколько светлых маленьких квадратов останется, если наложить фигуры друг на друга.
Посмотреть ответ
останутся три маленьких квадрата. У вас получился тот же ответ?
Задача 25
Ваша задача ─ найти центр круга, используя лишь карандаш и угольника с прямым углом.
Посмотреть ответ
найти центр круга можно было так, как указано на рисунке. А вы смогли справиться с этой задачкой?
Геометрические головоломки
Пентамино
Это головоломка из плоских фигур, каждая из которых состоит из пяти одинаковых квадратов. Всего таких элементов в пентамино 12, и они обозначаются латинскими буквами, потому что по форме напоминают их. Именно пентамино вдохновила программистов на создание знаменитой компьютерной игры “Тетрис”! С помощью этих элементов вы сможете вместе с ребёнком создавать различные фигуры, проявляя смекалку и сообразительность.
Именно пентамино вдохновила программистов на создание знаменитой компьютерной игры “Тетрис”! С помощью этих элементов вы сможете вместе с ребёнком создавать различные фигуры, проявляя смекалку и сообразительность.
Колумбово яйцо
Это ещё одна популярная и довольно известная головоломка. Колумбово яйцо ─ это овал, который разрезан на 10 частей. С помощью такой головоломки ваш малыш также сможет создавать различные изображения и фигуры.
По легенде, эта головоломка был придумана китайскими мудрецами для сына императора, который хотел найти для ребёнка интересное и полезное занятие для развития ума и сообразительности. Неизвестно, правдива эта легенда или нет, но мы рады, что Колумбово яйцо сейчас доступно любому ребёнку!
Танграм
Это очень популярная и древняя китайская головоломка. Её называют ещё «семь дощечек мастерства», потому что состоит она из семи плоских фигур, которые складываются для получения более сложной фигуры. Так можно собрать изображения людей или животных, предметы быта, буквы алфавита, цифры и многое другое.
Так можно собрать изображения людей или животных, предметы быта, буквы алфавита, цифры и многое другое.
Складывая фигуры, нужно соблюдать всего два условия: использовать все 7 деталей танграма и не перекрывать их между собой.
Начинать знакомить малыша с танграмом можно уже с 2-3 лет. Для начала предложите потрогать детали, изучить их форму, величину и цвет. Затем научите ребёнка складывать простые фигуры из 2-4 элементов танграма, например, ёлочку. По мере взросления малыша и развития его познавательных способностей и логического мышления игры с танграмом будут так же усложняться.
Этапы освоения игры Танграм
- Ребёнок накладывает на готовую схему части танграма.
- Задача усложняется! Теперь малыш самостоятельно складывает фигуры из элементов по схемам.
- На этом этапе ребёнку нужно сложить фигуру танграма только по контурному изображению.
- Финальный этап ─ это то, к чему должен прийти малыш: он самостоятельно придумывает и составляет фигуры, развивая воображение.

Игры с танграмом совершенствуют не только воображение, но и память, улучшают у детей наглядно-образное мышление и внимание, а также умение выполнять задание инструкции.
Танграм ─ доступная игра, её можно приобрести в магазине или сделать самим из цветного картона или бумаги, фанеры или небольших дощечек. Детали головоломки можно сделать бесцветными, главное, чтобы элементы игры были безопасными.
Тетрамино
Элементы тетрамино известны многим: это те самые “падающие фигуры” в игре “Тетрис”. Узнали их? Если в пентамино фигуры состоят из пяти маленьких квадратов, то в тетрамино их 4.
Как играть? Из элементов тетрамино так же составляются различные фигуры. Можно пользоваться готовыми схемами или придумывать их самостоятельно.
Мы рассказали вам о самых интересных и известных геометрических задачках и головоломках для детей. Они помогут малышу представить себя математиком и мудрецом и весело и интересно провести время. Разгадывайте всей семьёй другие занимательные задания от Айкьюши и развивайте логику, мышление и кругозор!
Разгадывайте всей семьёй другие занимательные задания от Айкьюши и развивайте логику, мышление и кругозор!
Выполните упражнения от Айкьюши:
Соотносим фигуру с предметом
Изучаем фигуры
Соотносим фигуры
Екатерина Дорошина,
педагог, методист IQsha, автор статей и упражнений
игры и задания с ответами для школьников
Родители и воспитатели в детском саду часто используют интересные задания по математике. Для дошкольников это считается нормой, в то время как в школьных учебниках предлагаются длинные ряды однообразных примеров и сложные задачи. Именно поэтому большинство учеников считает математику скучным предметом. Для поддержания мотивации педагогам рекомендовано включить в привычные уроки элементы занимательности. Это позволяет заинтересовать детей, побудить их к активной работе на занятии и снизить утомляемость.
Уроки-игры
В школьных учебниках занимательного материала недостаточно. Однако опытный педагог умеет сделать привычные задания по математике интересными. В 1 классе это особенно важно, так как дети лучше откликаются на игровую форму обучения. Им скучно решать примеры, но все меняется, если учитель принесет на урок мяч и будет спрашивать верный ответ у поймавшего его.
Однако опытный педагог умеет сделать привычные задания по математике интересными. В 1 классе это особенно важно, так как дети лучше откликаются на игровую форму обучения. Им скучно решать примеры, но все меняется, если учитель принесет на урок мяч и будет спрашивать верный ответ у поймавшего его.
Повысить активность детей позволяет игровой сюжет, присутствующий на занятии. Вариантов может быть множество. Например, за каждое выполненное задание ребятишки получают кусочек паззла, и в конце урока из них собирается картинка. Или класс отправляется спасать героя, попавшего в беду. На пути они встречают различных злодеев и побеждают их, решая задачки и примеры. Очень нравятся детям соревнования, когда класс делится на команды и каждая набирает жетоны за работу. Победителей можно наградить бумажными медалями. Таким образом, не всегда нужно искать занимательный материал. Иногда достаточно изменить форму его подачи.
Игровые приемы
Необязательно придумывать сказочный сюжет для каждого занятия. Школьники должны привыкать и к серьезной работе. Однако во время урока неизбежно накапливается напряжение. Помочь его сбросить призваны различные игровые приемы, на которые не уходит много времени. Вот примеры подобных интересных заданий по математике:
Школьники должны привыкать и к серьезной работе. Однако во время урока неизбежно накапливается напряжение. Помочь его сбросить призваны различные игровые приемы, на которые не уходит много времени. Вот примеры подобных интересных заданий по математике:
- «Слепой счет». Попросите первоклассников закрыть глаза и поднять вверх руки. Учитель диктует примеры (счет ведется в пределах первого десятка). Дети на пальцах показывают ответ. Ребятишек постарше можно вызвать к доске и попросить с завязанными глазами выполнить в столбик любое действие с двумя двузначными числами.
- «Меткие стрелки». На доске написаны примеры, а справа от них — правильные ответы в произвольном порядке. Дети копируют это в тетради. Затем стрелочками соединяют примеры с правильными ответами.
- «Эстафета». На доске в три столбика выписаны примеры. Дети, сидящие в одном ряду, строятся в колонну. Стоящий первым бежит к доске и решает первый пример, затем возвращается к команде и передает мел следующему игроку.
 При выявлении победителя принимается во внимание правильность ответов и затраченное время.
При выявлении победителя принимается во внимание правильность ответов и затраченное время.
Смешные задачи
Задания, рассмотренные выше, считаются занимательными по своей форме. Помимо них выделяют упражнения, интересные своим содержанием. Ярким примером могут стать задачи Г. Остера, отличающиеся от других юмористической подачей материала. Приведем несколько интересных заданий по математики для 1 класса из его книги:
- Мама купила несколько кактусов. Трехлетняя Маша побрила половину из них папиной бритвой. Колючими остались 12 кактусов. Сколько побритых растений у мамы? (12)
- Курочка Ряба снесла яйцо, но мышка разбила его. Тогда добрая Ряба снесла еще три яйца, но мышка и их разбила. Курочка поднатужилась и дала пять яиц. Бессовестная мышка все их расколотила. Из скольких яиц дед с бабой смогли бы приготовить себе яичницу, если бы не разбаловали мышку? (9).
- У Сережи было 12 больших хрямзиков и 7 маленьких. Когда ему объяснили, что это такое, он все выкинул и отпрыгнул подальше.
 Сколько хрямзиков бросил Сережа? (19).
Сколько хрямзиков бросил Сережа? (19).
Задачи на логику
Очень полезно давать детям нестандартные задания, приучающие их рассуждать, а не отвечать бездумно. Решая подобные задачи, школьники развивают внимательность, сообразительность и гибкость мышления. Приведем примеры интересных заданий по математике, которые могут использоваться в начальных классах:
- На дереве было 40 ворон. Охотник выстрелил из ружья и убил 6 птиц. Сколько ворон осталось сидеть на дереве? (Ни одной, выжившие птицы улетели).
- Сколько концов у 32 с половиной палок? (66).
- Пастух вел гусей. Один гусь шел впереди трех, еще один подгонял трех птиц и два гуся бежали посередине. Сколько всего было гусей? (4).
- Упряжка из трех коней пробежала 60 км. Какое расстояние пробежал каждый конь? (60 км.)
- Что тяжелее — килограмм пуха или килограмм свинца? (Они весят одинаково).
- Чтобы пролететь от пункта А к пункту Б, самолету требуется 1 час 20 мин. На обратный путь тратится 80 минут.
 Как это может быть? (Это одинаковое время, так как 60 мин. + 20 мин. = 80 мин.)
Как это может быть? (Это одинаковое время, так как 60 мин. + 20 мин. = 80 мин.) - Папа пилит дрова. Распилить бревно пополам он может за 1 мин. Сколько времени ему нужно, чтобы распилить бревно на 8 частей? (7 минут, т. к. понадобится сделать 7 распилов).
- Мама купила по коробке конфет своим дочкам: Кате и Лене. В каждой коробке лежало 15 конфет. За день Катя съела несколько штук, а остальные оставила на завтра. Лена же съела столько конфет, сколько осталось у ее сестры, а другие отложила. Сколько сладостей мама насчитала вечером в обоих коробках? (У Кати осталось 15-a=b конфет. Значит, Лена съела b конфет. Т. к. в этом уравнении a+b=15, а всего конфет было 30, то мама насчитала 15 конфет в двух коробках).
Задания со сказочными персонажами
Первоклассники — это вчерашние дошкольники. Они любят, когда на занятии вводится какой-нибудь волшебный герой. Например, Незнайка, который допустил ошибки в решаемых примерах. Задачки со сказочным содержанием также уместны в 1 классе. Интересные задания по математике можно составить самостоятельно, ориентируясь на примеры, приведенные ниже:
Интересные задания по математике можно составить самостоятельно, ориентируясь на примеры, приведенные ниже:
- Серый волк на день рождения пообедал семерыми козлятами, тремя поросятами и одной Красной Шапочкой. Сколько всего животных у него в животе? (10).
- В корзинке у Красной Шапочки лежат пирожки с вареньем, капустой и мясом. Больше всего пирожков с вареньем, а с капустой меньше, чем с мясом. Сколько пирожков в корзинке, если с вареньем их ровно три штуки? (6).
- У Бабы Яги в избушки жило 17 животных, из них 2 говорящих кота, а остальные — мышки-норушки. 8 мышек бабушка подарила Кощею Бессмертному. Сколько грызунов осталось в избушке? (7).
- Карлсон съел 19 шоколадных конфет, а засахаренных орешков на 4 штуки меньше. Сколько засахаренных орешков съел Карлсон? (15).
Задачи в стихах
Внимание ребятишек привлекает все необычное. Рифмованные задачи они решают с большим удовольствием, воспринимая такое занятие как веселую игру. Ниже приведен пример интересного задания по математике для 2 класса, с помощью которого можно вспомнить таблицу умножения. Слова, заключенные в скобки, должны договаривать сами ребята:
Слова, заключенные в скобки, должны договаривать сами ребята:
Единожды один (один).
Жил у отца любимый сын.
Дважды четыре (восемь),
Когда настала осень,
Трижды два (шесть),
Стал кто-то в саду яблоки есть.
Четырежды три (двенадцать).
Сын пошел с вором повстречаться.
Пятью пять (двадцать пять).
Вдруг жар-птица влетела в сад.
Девятью пять (сорок пять).
Стала яблоки птица клевать.
Четырежды восемь (тридцать два).
Не стерпел молодец воровства.
Семью семь (сорок девять).
Да как схватит жар-птицу в гневе!
Семью девять (шестьдесят три).
Молит птица: «Меня отпусти».
Шестью четыре (двадцать четыре).
«Будешь счастливей всех в этом мире».
Семью четыре (двадцать восемь).
Молодец птицу в небо подбросил.
Трижды десять (тридцать).
А она вдруг стала девицей.
Семью пять (тридцать пять).
Красотой — что ни в сказке сказать!
Трижды девять (двадцать семь).
Эта свадьба запомнилась всем.
Пятью один (пять).
А их дочка умела летать.
Познавательные задачи
Чем старше дети, тем серьезней подбираемый материал. Не только решать задачки, но и одновременно расширять кругозор способны ученики 3-4 классов. Интересные задания по математике могут быть связаны с темами, изучаемыми на уроках истории или окружающего мира. Вот примеры подобных задач:
- Российский император Петр I ежедневно спал с 9 часов вечера до 2 часов ночи, а в другое время занимался делами. Сколько часов длился его рабочий день? (19).
- Император Александр II уменьшил срок службы в армии на 19 лет. При нем солдаты защищали Родину в течение 72 месяцев. Сколько лет служил русский солдат до этого? (25 лет).
- Большая комета Галилея появляется возле Земли каждые 76 лет. Последний раз это произошло в 1986 году. Когда комета прилетит снова? (В 2062 году).
- Землю заселяют 2 млн 500 тыс. различных видов животных. Из них 4/5 части занимают насекомые.
 Сколько видов насекомых обитает на нашей планете? (2 млн)
Сколько видов насекомых обитает на нашей планете? (2 млн)
Примеры с необычной структурой
Внимание детей привлекают задания, не вписывающиеся в привычный шаблон. Обычные примеры, в которых надо узнать результат по известным компонентам и действиям, быстро приедаются. Другое дело, если нужно расставить действия и скобки между цифрами, чтобы получился указанный результат. Приведем несколько подобных заданий по математике. В 4 классе дети вполне справятся с ними, а для школьников помладше примеры можно упростить:
8 8 8 8 = 0 Ответ: (8+8)-(8+8)=0.
8 8 8 8 = 1 Ответ: (8+8):(8+8)=1.
8 8 8 8 = 3 Ответ: (8+8+8):8=3.
8 8 8 8 = 7 Ответ: (8×8-8):8=7.
8 8 8 8 = 8 Ответ: (8-8)×8+8 =8.
8 8 8 8 = 9 Ответ: (8×8+8):8 =9.
8 8 8 8 = 10 Ответ: (8+8):8+8=10.
8 8 8 8 = 16 Ответ: 8×(8+8):8=16.
8 8 8 8 = 48 Ответ: 8×8-(8+8)=48.
8 8 8 8 = 56 Ответ: (8-8:8)×8=56.
Математические ребусы
Скучно решать уравнения. Другое дело, если назвать тот же самый пример загадкой или ребусом. Приведем примеры нескольких интересных заданий по математике. В 3 классе неизвестные можно обозначить буквами латинского алфавита или звездочками. В 1-2 классах детям больше нравятся изображения игрушек, фруктов или других реальных предметов. Мы рассмотрим вариант для ребятишек постарше:
Приведем примеры нескольких интересных заданий по математике. В 3 классе неизвестные можно обозначить буквами латинского алфавита или звездочками. В 1-2 классах детям больше нравятся изображения игрушек, фруктов или других реальных предметов. Мы рассмотрим вариант для ребятишек постарше:
- CN + NC = 33. Найди значение C и N. (В данном случае один из символов равен одному, а другой — двум).
- FFD + FDF + DFF= 444. Чему равны F и D? (F=1, D=2).
- Замени звездочки нужными цифрами: 1*9* + * 3 =4225. (Ответ: 1792+2433=4225).
- Восстанови пример, поставив вместо букв цифры: AA1 × AAA + AAA00=11211. (А=1).
Игры для будущих шифровальщиков
Другим интересным заданием по математике может стать разгадывание закодированных слов. В этом случае каждой букве соответствует свое число. Чтобы разгадать шифр, дети должны решить ряд примеров. Ниже представлено два таких задания.
- Отгадай сказочного персонажа:
| Цифры | 72 | 18 | 40 | 27 | 49 | 64 | 49 | 81 | 36 | 56 |
| Буквы |
М=9×3, О=7×7, В=8×8, Ю=6×3, Й=5×8, А=8×7, К=6×6, Д=9×8, Ч=9×9. (Дюймовочка).
(Дюймовочка).
- В январе он толстый, но с каждый прожитым днем становится все тоньше и тоньше.
| Цифры | 60 | 45 | 4 | 85 | 72 | 20 | 45 | 11 | 23 |
| Буквы |
Е=34+51, Р=74-63, А=57-12, ь=38-15, Д=4×5, Л=24:6, Н=46+14. (Календарь).
Математические фокусы
Чтобы привлечь внимание школьников, нужно их удивить. Специально для этой цели можно использовать интересные задания по математике с ответами, известными заранее. Лучше назвать их «фокусами». Дети загадывают произвольные числа, проводят с ними ряд операций. А потом учитель угадывает верный ответ, общий для всех присутствующих. Понять секрет такого «фокуса» наверняка захочется всем. Вот несколько подобных задач:
- Дети должны загадать любое число от 1 до 9 и умножить его на 2.
 Потом полученное число умножается на 5. К результату прибавляется 7, затем цифра, обозначающая десятки, отбрасывается. К оставшемуся числу прибавляют 3, отнимают 8, умножают на 4. И учитель называет ответ, общий для всех школьников: 8.
Потом полученное число умножается на 5. К результату прибавляется 7, затем цифра, обозначающая десятки, отбрасывается. К оставшемуся числу прибавляют 3, отнимают 8, умножают на 4. И учитель называет ответ, общий для всех школьников: 8. - Пусть дети возьмут три цифры, за исключением нуля, и составят из них все возможные трехзначные числа. Затем нужно узнать сумму этих чисел. Взятые цифры тоже складываются между собой. Сумма всех трехзначных чисел делится на сумму трех цифр. Педагог «угадывает» ответ: 222.
Интересные задания по математике позволяют сделать предмет более привлекательным для ребят начальных классов. К тому же, они заставляют школьников думать нестандартно, отходить от шаблонов. Таким образом развивается любознательность и творческое мышление.
Занимательные задачи
1 260
Занимательные задачи!
Чем хороши занимательные задачи — ими можно интересно занять детей по в дороге, по пути в школу или устроить конкурс на школьном празднике. Обратите внимание, что мало кто сможет дать правильный ответ сразу, потому не забывайте о маленьких подсказках, разгадывание задачек от этого будет не менее интересным.
Обратите внимание, что мало кто сможет дать правильный ответ сразу, потому не забывайте о маленьких подсказках, разгадывание задачек от этого будет не менее интересным.
1.В каждом из 4 углов комнаты сидит кошка. Напротив каждой из этих кошек сидят три кошки. Сколько всего в этой комнате кошек?
2. У отца шесть сыновей. Каждый сын имеет сестру. Сколько всего детей у этого отца?
3. В мастерской по пошиву одежды от куска сукна в 200 м ежедневно, начиная с 1 марта, отрезали по 20 м. Когда был отрезан последный кусок?
4. В клетке находятся 3 кролика. Три девочки попросили дать им по одному кролику. Каждой девочке дали кролика. И все же в клетке остался один кролик. Как так получилось?
5. 6 рыбаков съели 6 судаков за 6 дней. За сколько дней 10 рыбаков съедят 10 судаков?
6. На одном дереве сидело 40 сорок. Проходил охотник, выстрелил и убил 6 сорок. Сколько сорок осталось на дереве?
7. Два землекопа за 2 часа работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 часов работы выкопали 100 м такой же канавы?
Два землекопа за 2 часа работы выкопают 2 м канавы. Сколько нужно землекопов, чтобы они за 100 часов работы выкопали 100 м такой же канавы?
8. Два отца и два сына разделили между собой 3 апельсина так, что каждому досталось по одному апельсину. Как это могло получиться?
9. По стеблю растения, высота которого 1 м, от земли ползет гусеница. Днем она поднимается на 3 дм, а ночью опускается на 2 дм. Через сколько суток гусеница доползет до верхушки растения?
10. Есть два ведра емкостью 4 и 9 литров. Как с их помощью принести из речки ровно 6 литров воды?
Ответы:
1.4
2.Одной девочке дали клетку с кроликом.
3.9марта
4.7
5. 6 рыбаков за день едят 1 судака.
Один рыбак есть 1/6 судака в день.
10 рыбаков едят за день 10/6 судака.
10 судаков делим на 10/6 судака = 6 дней
6.Все улетели
7. 2
8. Дед, отец и внук = 2 отца и 2 сына
9.Через 7/12 суток.
10. Из полного девятилитрового ведра нужно вылить в реку 8литров воды, пользуясь ведром в 4 литра. Затем литр, оставшийся в большом ведре, нужно перелить в пустое четырехлитровое ведро. Если в него теперь добавить три литра из полного большого ведра, то в девятилитровом ведре как раз останется шесть литров воды.
Затем литр, оставшийся в большом ведре, нужно перелить в пустое четырехлитровое ведро. Если в него теперь добавить три литра из полного большого ведра, то в девятилитровом ведре как раз останется шесть литров воды.
Подумай и сосчитай
Чтоб одеть тепло сыночков,
Не хватает двух носочков.
Сколько же в семье сынков,
Если в доме шесть носков?
Ответ:четверо
Столько книжек у ребяток,
Сколько у Алеши пяток.
Принесла ребяткам Галя
Мячик, книжку, мишек.
Вы, ребята, посчитали,
Сколько стало книжек?
Ответ: три
******************
К трем лягушкам у болота
Прибежали два енота,
Прискакала тетя жаба
И пришла наседка Ряба.
Сколько в камышах болотных
Оказалось земноводных?
Ответ: четверо
Задачи на внимание
1. Подумай и скажи — кто быстрее переплывет речку — утята или цыплята?
2. Подумай и скажи — какого цвета волосы у колобка?
3. Отгадай загадку:
Лежали конфетки в кучке.
Две матери, две дочки
Да бабушка с внучкой
Взяли конфет по штучке,
И не стало этой кучки.
Сколько конфет было в кучке?
4. Росли 5 берез. На каждой березе по 5 больших веток. На каждой ветке по 5 маленьких веток. На каждой маленькой ветке — по 5 яблок. Сколько всего яблок?
5. Подумай и скажи — что помогает выжить белым медведям в пустыне, где нет воды?
6. На каких деревьях вьют свои гнезда страусы?
7. На столе лежит 2 яблока и 4 груши. Сколько всего овощей лежит на столе?
8. Подумай и скажи — кто громче рычит: тигр или буйвол?
9. Посмотрел Ваня утром в окно и говорит:
— А на улице, оказывается, очень сильный ветер. Нужно теплее одеваться.
Как он догадался, что на улице ветер? Что он увидел?
10. Пошли 2 девочки в лес за грибами, а навстречу 2 мальчика. Сколько всего детей идет в лес? (подсказка: 2 — остальные идут обратно)
11. В комнате горело 5 свечей. Зашел человек, потушил 2 свечи. Сколько осталось? ( подсказка: 2- остальные сгорели)
12. Бревно распилили на 4 части. Сколько сделали распилов?
Бревно распилили на 4 части. Сколько сделали распилов?
13. Прочитай слова и скажи — какое слово лишнее в каждом ряду?
— диван, стул, шкаф, конура, тумбочка,
— гвоздика, ромашка, камыш, лилия, астра,
— боровик, мухомор, сыроежка, подберезовик, лисичка.
14. Подумай и скажи — сколько земли будет в яме глубиной 1 метр, длиной 1 метр и шириной 1 метр?
15. У шестилетней девочки была кошка с коротким хвостом. Она съела мышку с длинным хвостом, а мышка проглотила 2 зернышка и съела тонкий кусочек сыра. Скажи, сколько лет было девочке, у которой была кошка?
16. На одном берегу реки стоит петух, а на другом индюк. Посреди реки — островок. Кто из этих птиц быстрее долетит до островка?
17. Скажи сколько грибов можно вырастить из 5 семечек?
18. Скажи, кто обитает в море на большей глубине: щука, рак или форель?
19. Гусь на двух ногах весит 2 кг. Сколько он будет весить, стоя на одной ноге?
20. На клене 5 веток. На каждой ветке по 2 яблока. Cколько яблок на клене?
Cколько яблок на клене?
Мой блог находят по следующим фразам
- kak opredelit pol rebenka
- позы при зачатии ребенка фото
- логические задания для детей 5-6 лет
- красивые картинки где дети играют с песком
- загадки для детей 13 лет с ответами
- интересные задания для детей
30 занимательных вопросов по математике с ответами
Математика может быть увлекательной, если к ней относиться правильно. Математика — это не что иное, как игра, игра, которая совершенствует ваш интеллект и повышает вашу концентрацию. По сравнению с прошлыми временами у людей более дружелюбный подход к математике, что делает ее более привлекательной. Золотое правило состоит в том, чтобы знать, что математика — это осознанная деятельность, а не задача.
Золотое правило состоит в том, чтобы знать, что математика — это осознанная деятельность, а не задача.
Нет ничего лучше сложных математических задач или хитрых математических вопросов, просто вы недостаточно хорошо изучили математику, чтобы понять ее легкость и взаимосвязь. Сложные математические вопросы и ответы могут быть преобразованы в забавные математические задачи, если вы посмотрите на это как на сеанс мозгового штурма. При правильном отношении, друзьях и учителях занятия математикой могут быть очень интересными и восхитительными.
Математика интересна тем, что несколько уравнений и диаграмм могут передавать огромные объемы информации. Относитесь к математике как к языку, переходя к строгому доказательству и используя логическое обоснование для выполнения определенного шага в доказательстве или выводе.
Отношение к математике как к языку полностью избавляет вас от понятия сложных математических задач или каверзных математических вопросов. Знакомство детей с забавными вопросами по математике может вызвать сильную любовь и признательность к математике в раннем возрасте. Таким образом вы создаете благополучное будущее ребенка. Забавные математические задачи побудят вашего ребенка решить их, а не играть в бинго или печь.
Знакомство детей с забавными вопросами по математике может вызвать сильную любовь и признательность к математике в раннем возрасте. Таким образом вы создаете благополучное будущее ребенка. Забавные математические задачи побудят вашего ребенка решить их, а не играть в бинго или печь.
По-видимому, существует бесчисленное множество способов сделать из простых математических задач сложные вопросы и ответы. Это включает в себя зарождение идеологии, что математика проще, чем их страх. Этого можно добиться, связав математику с повседневной жизнью. Упражнения в математике с помощью игральных костей, карт, головоломок и таблиц гарантируют, что ваш ребенок эффективно подходит к математике.
Если вы хотите добавить веселья и азарта в образовательные занятия, ознакомьтесь также с
Забавные вопросы по математике с ответами — PDF Вот загружаемый PDF-файл, состоящий из вопросов Fun Math. Нажмите кнопку «Загрузить», чтобы просмотреть их.
Вот несколько забавных, хитрых и сложных математических задач, которые бросят вызов вашему мышлению.
Если 1=3
2=3
3=5
4=4
3 5=4
Тогда 6=?
Ответ: равно 3, потому что «шесть» состоит из трех букв
Сколько парковочных мест занимает автомобиль?
Эта хитрая математическая задача стала популярной несколько лет назад после того, как появилась на вступительном экзамене в Гонконге… для шестилетних детей. Предположительно, у студентов было всего 20 секунд, чтобы решить задачу!
Предположительно, у студентов было всего 20 секунд, чтобы решить задачу!
Ответ:
Хотите верьте, хотите нет, но этот «математический» вопрос вообще не требует математики. Если вы перевернете изображение вверх ногами, то увидите, что имеете дело с простой числовой последовательностью.
Замените вопросительный знак в приведенной выше задаче соответствующим номером.
9(2)
Эта проблема возникает прямо из стандартизированного теста, приведенного в Нью -Йорке в 2014 году. На выставку заявлено 49 собак. Маленьких собак на 36 больше, чем крупных. Этот вопрос взят непосредственно из домашнего задания по математике второклассника. Ответ: Чтобы вычислить, сколько маленьких собак участвует в соревнованиях, вы должны вычесть 36 из 49, а затем разделить результат на 13 на 2, чтобы получить 6,5 собак или число. больших собак, конкурирующих. Но вы еще не закончили! Затем вам нужно прибавить 6,5 к 36, чтобы получить количество соревнующихся маленьких собак, которое равно 42,5. Конечно, на самом деле половина собаки не может участвовать в выставках собак, но ради решения этой математической задачи давайте предположим, что это возможно. Добавьте 8,563 и 4,8292. Ответ: Сложить два десятичных знака проще, чем кажется. Пусть вас не смущает тот факт, что число 8,563 меньше, чем число 4,8292. Все, что вам нужно сделать, это добавить 0 в конце 8,563, а затем добавить, как обычно. Я нечетное число. Убери одну букву и я стану квитком. Какой я номер? Ответ: Используя только сложение, как сложить восемь восьмерок и получить число 1000? Ответ: 888 + 88 + 8 + 8 + 8 = 1000 9005  Сколько маленьких собак записались на соревнования?
Сколько маленьких собак записались на соревнования? 
13,3922
Семь (убери букву «с» и станет «чет»).
Салли 54 года, а ее матери 80 лет, сколько лет назад мать Салли была умножена на ее возраст?
Ответ:
41 год назад, когда Салли было 13 лет, а ее матери 39 лет. .
.
| 41 год назад |
Ответы на какие 3 числа одинаковы при сложении или умножении?
Ответ:
| 1, 2 и 3 |
В корзине 5 яблок, как разделить яблоки между 5 детьми так, чтобы у каждого ребенка было по 1 яблоку, а в корзине осталось 1 яблоко?
Ответ:
4 ребенка получают по 1 яблоку, а пятый ребенок получает корзину с оставшимся яблоком.
Есть трехзначный номер. Вторая цифра в четыре раза больше третьей цифры, а первая цифра в три раза меньше второй цифры. Какой номер?
Ответ:
Заполните знак вопроса
Ответ:
Две девочки родились от одной матери, в одно и то же время, в один и тот же день, в один и тот же месяц и в один и тот же год, но почему-то они не близнецы.
 Почему бы и нет?
Почему бы и нет?
Ответ:
Потому что была третья девочка, что делает их тройняшками!
| Тройняшки |
Корабль, стоящий на якоре в порту, имеет лестницу, которая свисает с борта. Длина лестницы 200см, расстояние между каждой ступенькой 20см и нижняя ступенька касается воды. Приливы поднимаются со скоростью 10 см в час. Когда вода достигнет пятой ступени?
Ответ:
Прилив поднимает и воду, и лодку, так что вода никогда не достигает пятой ступеньки.
Позавчера мне было 25.
 В следующем году мне будет 28. Это правда только один день в году. В какой день у меня День Рождения?
В следующем году мне будет 28. Это правда только один день в году. В какой день у меня День Рождения?
Ответ:
| 31 декабря |
У вас есть 3-литровая бутылка и 5-литровая бутылка. Как отмерить 4 литра воды, используя 3-литровые и 5-литровые бутылки?
Ответ:
Решение 1 :
Сначала наполните 3-литровую бутылку и перелейте 3 литра в 5-литровую бутылку.
Снова наполните 3-литровую бутыль.
 Теперь налейте 2 литра в 5-литровую бутылку, пока она не наполнится.
Теперь налейте 2 литра в 5-литровую бутылку, пока она не наполнится.Пустая 5-литровая бутылка.
Перелейте оставшийся 1 литр из 3-литровой бутылки в 5-литровую бутылку.
Теперь снова наполните 3-литровую бутылку и перелейте 3 литра в 5-литровую бутылку.
Теперь в 5-литровой бутыли 4 литра. Вот и все.
Решение 2 :
Сначала наполните 5-литровую бутыль и перелейте 3 литра в 3-литровую.
Пустая 3-литровая бутылка.
Перелейте оставшиеся 2 литра из 5-литровой бутылки в 3-литровую бутыль.
Снова наполните 5-литровую бутыль и перелейте 1 литр в 3-литровую бутылку, пока она не наполнится.

Теперь в 5-литровой бутыли 4 литра. Вот и все.
3 Друзья пошли в магазин и купили 3 игрушки. Каждый человек заплатил 10 рупий, что составляет стоимость одной игрушки. Итак, они заплатили 30 рупий, т.е. общую сумму. Владелец магазина предоставил скидку в размере 5 рупий на общую покупку 3 игрушек за 30 рупий. Затем среди 5 рупий каждый человек взял 1 рупию, а оставшиеся 2 рупии отдали нищему возле магазина. Теперь фактическая сумма, выплачиваемая каждым человеком, составляет 9 рупий, а сумма, отдаваемая нищему, составляет 2 рупии. Таким образом, общая эффективная выплаченная сумма равна 9 * 3 = 27, а сумма, отданная нищему, равна 2 рупиям, таким образом, общая сумма составляет 29 рупий.. Куда делся другой Rs.1 от оригинальных Rs.30?
Ответ:
По логике платежи должны быть равны поступлениям. Мы не можем сложить сумму, уплаченную людьми, и сумму, отданную нищему, и сравнить ее с 30 рупиями. Общая выплаченная сумма составляет 27 рупий. Итак, из 27 рупий владелец магазина получил 25 рупий, а нищий — 2 рупии. Таким образом, платежи равны квитанциям.
Мы не можем сложить сумму, уплаченную людьми, и сумму, отданную нищему, и сравнить ее с 30 рупиями. Общая выплаченная сумма составляет 27 рупий. Итак, из 27 рупий владелец магазина получил 25 рупий, а нищий — 2 рупии. Таким образом, платежи равны квитанциям.
Как получить число 100, используя четыре семерки (7) и единицу (1)?
Ответ 1: 177 – 77 = 100 ;
Ответ 2: (7+7) * (7 + (1/7)) = 100
- 9002
Переместите любые четыре спички, чтобы получить только 3 равносторонних треугольника (спички не убирайте)
Ответ:
Найдите площадь красного треугольника.

Ответ:
Чтобы решить этот интересный математический вопрос, вам нужно понять, как работает площадь параллелограмма. Если вы уже знаете, как связаны площадь параллелограмма и площадь треугольника, то сложение 79 и 10, а затем вычитание 72 и 8, чтобы получить 9, должно иметь смысл.
Сколько футов в миле?
Ответ:
Решить — 15+ (-5x) = 0
Ответ:
Что такое 1,92÷3
Ответ:
Мужчина взбирается на наклонную гору.
 Ему нужно проехать 100 км, чтобы добраться до вершины горы. Каждый день Он поднимается на 2 км вперед в дневное время. Измученный, он отдыхает там ночью. Ночью, пока он спит, он соскальзывает на 1 км назад, потому что гора наклонена. Тогда сколько дней потребуется ему, чтобы достичь вершины горы?
Ему нужно проехать 100 км, чтобы добраться до вершины горы. Каждый день Он поднимается на 2 км вперед в дневное время. Измученный, он отдыхает там ночью. Ночью, пока он спит, он соскальзывает на 1 км назад, потому что гора наклонена. Тогда сколько дней потребуется ему, чтобы достичь вершины горы?
Ответ:
| 99 дней |
Если 72 x 96 = 6927, 58 x 87 = 7885, то 79 x 86 = ?
Ответ:
Посмотрите на этот ряд: 36, 34, 30, 28, 24, … Какое число должно быть следующим?
Ответ:
Посмотрите на этот ряд: 22, 21, 23, 22, 24, 23, … Какое число должно быть следующим?
Ответ:
Если 13 х 12 = 651 и 41 х 23 = 448, то 24 х 22 =?
Ответ:
Посмотрите на этот ряд: 53, 53, 40, 40, 27, 27, … Какое число должно быть следующим?
Ответ:
Заключение
Конечными целями обучения математике являются навыки понимания и запоминания представленного материала, его применения учащимися. Мало пользы от того, что учащиеся вспоминают формулу или процедуру для подготовки к завтрашнему оцениванию только для того, чтобы забыть основную концепцию к следующей неделе.
Мало пользы от того, что учащиеся вспоминают формулу или процедуру для подготовки к завтрашнему оцениванию только для того, чтобы забыть основную концепцию к следующей неделе.
Учителя должны сосредоточиться на том, чтобы учащиеся понимали материал, а не просто запоминали процедуры. После того, как вы узнаете ответы на забавный вопрос по математике, вы начинаете спрашивать себя, как вы могли так легко что-то упустить. Правда в том, что большинство вопросов с подвохом предназначены для того, чтобы обмануть ваш разум, поэтому ответы на забавные математические вопросы логичны и просты.
iOS и Android — это универсальное решение для развития у детей множества навыков. Ознакомьтесь со структурой комиссий Cuemath и подпишитесь на бесплатную пробную версию.
5 простых математических задач, которые никто не может решить
Введите ключевые слова для поискаГлавные новости дня
1
Первый в мире полностью электрический реактивный самолет Первый полет асов
2
Лучшие электромобили 2022 года
3
Помните, когда: Ральф Нейдер тащил Corvair
Chevy4
Первый взгляд: умные очки Viture One
5
Купить игры раннего доступа Amazon Prime уже сейчас
Редакторы, одержимые Gear, выбирают каждый продукт, который мы рассматриваем. Мы можем заработать комиссию, если вы покупаете по ссылке.
Как мы тестируем снаряжение.
Мы можем заработать комиссию, если вы покупаете по ссылке.
Как мы тестируем снаряжение.
Легко понять, в высшей степени трудно доказать.
По Эйвери Томпсон
Justin LewisGetty Images
Математика может быть довольно сложной. К счастью, не все математические задачи должны быть неразрешимыми. Вот пять актуальных задач в области математики, которые может понять каждый, но решить пока не удалось никому.
Гипотеза Коллатца
Джон МакЛун
Выберите любой номер. Если это число четное, разделите его на 2. Если оно нечетное, умножьте его на 3 и прибавьте 1. Теперь повторите процесс с новым числом. Если вы продолжите, вы в конечном итоге окажетесь на 1. Каждый раз.
Математики перепробовали миллионы чисел и так и не нашли ни одного, которое в конце концов не равнялось бы 1. Дело в том, что они никогда не могли доказать , что не существует особого числа, которое никогда не ведет к 1. Возможно, что есть какое-то действительно большое число, которое вместо этого стремится к бесконечности, или, может быть, число, которое получает застрял в петле и никогда не достигает 1. Но никто так и не смог доказать это наверняка.
Возможно, что есть какое-то действительно большое число, которое вместо этого стремится к бесконечности, или, может быть, число, которое получает застрял в петле и никогда не достигает 1. Но никто так и не смог доказать это наверняка.
Проблема с движущимся диваном
Claudio Rocchini
Итак, вы переезжаете в свою новую квартиру и пытаетесь привезти свой диван. Проблема в том, что коридор поворачивает, и вам нужно поставить диван за угол. Если это маленький диван, это может не быть проблемой, но действительно большой диван обязательно застрянет. Если вы математик, вы спросите себя: какой самый большой диван вы могли бы поставить за углом? Это не обязательно должен быть прямоугольный диван, он может быть любой формы.
Суть задачи о движущемся диване. Вот конкретика: вся задача в двух измерениях, угол — это угол 90 градусов, а ширина коридора равна 1. Какая наибольшая двумерная область может уместиться вокруг угла?
Самая большая площадь, которая может поместиться за углом, называется — я не шучу — диваном-константой. Никто точно не знает, насколько он велик, но у нас есть довольно большие диваны, которые работают, поэтому мы знаем, что он должен быть как минимум таким же большим, как они. У нас также есть несколько диванов, которые не работают, поэтому они должны быть меньше, чем те. Все вместе мы знаем, что константа дивана должна быть в пределах 2,219.5 и 2,8284.
Никто точно не знает, насколько он велик, но у нас есть довольно большие диваны, которые работают, поэтому мы знаем, что он должен быть как минимум таким же большим, как они. У нас также есть несколько диванов, которые не работают, поэтому они должны быть меньше, чем те. Все вместе мы знаем, что константа дивана должна быть в пределах 2,219.5 и 2,8284.
Идеальная прямоугольная задача
Gfis
Помните теорему Пифагора, A 2 + B 2 = C 2 ? Три буквы соответствуют трем сторонам прямоугольного треугольника. В треугольнике Пифагора все три стороны — целые числа. Давайте расширим эту идею до трех измерений. В трех измерениях есть четыре числа. На изображении выше это A, B, C и G. Первые три — это размеры коробки, а G — диагональ, идущая от одного из верхних углов к противоположному нижнему углу.
Точно так же, как есть некоторые треугольники, у которых все три стороны являются целыми числами, существуют также прямоугольники, у которых три стороны и пространственная диагональ (A, B, C и G) являются целыми числами. Но есть еще три диагонали на трех поверхностях (D, E и F), и это поднимает интересный вопрос: может ли существовать ящик, в котором все семь из этих длин являются целыми числами?
Но есть еще три диагонали на трех поверхностях (D, E и F), и это поднимает интересный вопрос: может ли существовать ящик, в котором все семь из этих длин являются целыми числами?
Цель состоит в том, чтобы найти ящик, в котором A 2 + B 2 + C 2 = G 2 , и где все семь чисел являются целыми числами. Это называется совершенным кубоидом. Математики испробовали множество различных возможностей, но пока не нашли ни одной, которая работает. Но они также не смогли доказать, что такого ящика не существует, поэтому идет охота за идеальным прямоугольным параллелепипедом.
Задача о вписанном квадрате
Клаудио Роккини
Нарисуйте замкнутую петлю. Петля не обязательно должна быть кругом, она может быть любой формы, которую вы хотите, но начало и конец должны встречаться, и петля не может пересекаться. Должна быть возможность нарисовать квадрат внутри петли так, чтобы все четыре угла квадрата касались петли. Согласно гипотезе вписанного квадрата, каждая замкнутая петля (в частности, каждая плоская простая замкнутая кривая) должна иметь вписанный квадрат, квадрат, все четыре угла которого лежат где-то на петле.
Должна быть возможность нарисовать квадрат внутри петли так, чтобы все четыре угла квадрата касались петли. Согласно гипотезе вписанного квадрата, каждая замкнутая петля (в частности, каждая плоская простая замкнутая кривая) должна иметь вписанный квадрат, квадрат, все четыре угла которого лежат где-то на петле.
Это уже решено для ряда других форм, таких как треугольники и прямоугольники. Но квадраты сложны, и до сих пор формальное доказательство ускользало от математиков.
Проблема со счастливым концом
Дэвид Эппштейн
Задача о счастливом конце названа так потому, что она привела к женитьбе двух математиков, которые работали над ней, Джорджа Секереса и Эстер Кляйн. По сути, проблема работает следующим образом:
Поставьте пять точек в случайных местах на листе бумаги. Предполагая, что точки не расположены преднамеренно, скажем, в линию, вы всегда должны быть в состоянии соединить четыре из них, чтобы создать выпуклый четырехугольник, который представляет собой форму с четырьмя сторонами, где все углы меньше 180 градусов. Суть этой теоремы в том, что вы всегда сможете создать выпуклый четырехугольник с пятью случайными точками, независимо от того, где эти точки расположены.
Суть этой теоремы в том, что вы всегда сможете создать выпуклый четырехугольник с пятью случайными точками, независимо от того, где эти точки расположены.
Вот как это работает для четырех сторон. Но для пятиугольника, пятиугольника, оказывается, нужно девять точек. Для шестиугольника это 17 точек. Но кроме этого мы не знаем. Остается загадкой, сколько точек требуется для создания семиугольника или любой другой формы большего размера. Что еще более важно, должна быть формула, чтобы сказать нам, сколько точек требуется для любой формы. Математики подозревают, что уравнение имеет вид M=1+2 N-2 , где M — количество точек, а N — количество сторон фигуры. Но пока им удалось доказать только то, что ответ по крайней мере такой же большой, как ответ, который вы получаете таким образом.
Эйвери Томпсон twitter.com/physicallyavery
Некоторые шары для боулинга плавают, а другие нет
Можете ли вы решить эту задачу вероятности?
Решение задачи о вероятности земного шара
3 лайфхака для улучшения общего состояния мозга
Родился первый клонированный арктический волк
Как приготовить сухой лед
Нил де Грасс Тайсон: наша хронология не особенная
Как работает лазерное удаление татуировок?
Как телескоп Уэбба помог улучшить зрение человека
Странный эксперимент с двумя щелями стал еще более странным
20 занимательных математических вопросов с решениями
Вы тоже боитесь математики? Математика всегда была для вас настоящей задачей? Считаете ли вы, что миф о математических генах реален?
Ну, поверьте нам, мы чувствуем вас, и мы здесь, чтобы разрушить этот миф о математических генах для вас. Математика может быть действительно веселой и занимательной, если на нее смотреть с правильной стороны.
Математика может быть действительно веселой и занимательной, если на нее смотреть с правильной стороны.
Все мы прошли через этот пугающий этап, когда мы ломали голову над пониманием математики и лежащей в ее основе логики, и все же в день экзамена мы не могли понять, к чему спрашивается вопрос. Но давайте подойдем к этому по-другому, давайте посмотрим на математику как на игру, и тогда математические вопросы никогда не будут казаться сложными. Математика становится намного интереснее, если к ней подходить с другой стороны. Каждый вопрос, уравнение и математическая диаграмма говорят о многом, и, как правило, большинство шагов вашего ответа находятся в самом вопросе.
Для начала возьми себе за правило ежедневно заниматься математикой, и уверяем тебя, через несколько дней это покажется проще твоего страха. Свяжите это со своей повседневной жизнью и осваивайте математику с практикой. Крайне важно разрушить мифы, связанные с математикой и математическими генами, с самого начала, потому что страх математики иногда становится единственной проблемой для нежелания попробовать.
Хотите знать, почему математика так важна? Самый простой ответ — потому что это важнейший жизненный навык, который поможет вам на каждом этапе вашей жизни, от самых простых вещей, таких как расчет вашего процента, до планирования бюджета в дальнейшей жизни. Давайте сломаем стереотип математического гена, решая несколько простых, кажущихся сложными, но тем не менее занимательных математических задач с их пошаговыми решениями. Благодаря этому вы столкнетесь с закономерностями, логикой и концепциями, которые помогут побороть ваш страх перед математикой и внутренние убеждения, поразив вас осознанием того, что не «математический ген», а практика делает вас мастером математики.
Пришло время провести мозговой штурм и активно поработать, чтобы бросить вызов своим мыслительным способностям и улучшить свои математические навыки, с помощью этих сложных, логических и, казалось бы, сложных математических вопросов.
Вопрос 1. Если 1=3, 2=3, 3=5, 4=4; 5=4, тогда 6=?
а. 2
2
б.5
в.3
г.4
Ответ. в. 3
Если вы заметили закономерность «один» = 3, «три» = 5 и т. д., в зависимости от количества букв выводится число. Итак, поскольку «шесть» состоит из трех букв, следовательно, 6 = 3.
Вопрос 2. У Джои было 6 братьев и сестер. Все они родились с разницей в 2 года. Младшей из них является Хлоя, которой всего 7 лет, а Джоуи — самая старшая. Вычислите возраст Джоуи.
a.12
b.18
c.22
d.19
Ответ. Возраст младшей сестры, Хлои, 7 лет. Всего 7 братьев и сестер, Джоуи плюс его 6 братьев и сестер. Принято считать, что все они родились с разницей в 2 года. Таким образом, возраст Джои будет
7 + 2 + 2 + 2 + 2 + 2 + 2 = 19
Вопрос 3. Всего 49собаки зарегистрировались для участия в выставке собак. Маленьких собак зарегистрировалось на 36 больше, чем крупных собак. Сколько маленьких собак заявлено для участия в соревнованиях?
a.13
b.42.5
c.6.5
d. 42
42
Ответ. Чтобы узнать количество соревнующихся собак, сначала нужно вычесть 36 из 49, а затем разделить результат на 2. То есть 13 разделить на 2, чтобы получить 6,5. 6,5 — это количество зарегистрировавшихся больших собак. Нет, это еще не окончательный ответ. Следующим шагом является прибавление 6,5 к 36. Таким образом, ответ равен 42,5, а поскольку мы все знаем, что полусобака не может участвовать, то это гипотетический вопрос, и мы должны принять 42,5 в качестве ответа.
Вопрос 4. Решите: 3 + 2 • (8 – 3)
a.13
b.24
c.15
d.17
Ответ. 3 + 2 • (8 – 3)
= 3 + 2 (5)
= 3 + 10
= 13
Вопрос 5. Проанализируйте закономерность и найдите пропущенное число:
а.9
б.5
c.6
d.1
Ответ. Если вы проанализируете узор в каждом из полных кругов, вы поймете, что числа в сумме дают 20. Следовательно, для неполного круга
2 + 9 + 8 + ? = 20.
19+? = 20
? = 20 – 19 = 1
Вопрос 6. Я нечетное число. Убери одну букву и я стану квитком. Какой я номер?
Я нечетное число. Убери одну букву и я стану квитком. Какой я номер?
Ответ. Ответ на этот вопрос — «семь», что является нечетным числом, а когда вы уберете «s» из «семерки», оно станет «четным».
Вопрос 7. Под каким номером стоит машина?
Ответ. Хотите верьте, хотите нет, но вам не понадобятся никакие расчеты и даже 5 секунд, чтобы решить этот вопрос, когда вы смотрите на картинку вверх ногами. Оказывается, это просто последовательность чисел и ответ 87.
Вопрос 8. Анкит посетил выставку возле своего дома. Он катался на своем новом велосипеде, подаренном его матерью за победу в научном конкурсе. Дойдя до выставки, Анкит увидел, что всего там 14 велосипедов и трехколесных велосипедов. Учитывая, что общее количество колес равно 38, найдите количество трехколесных велосипедов в парке.
Ответ. Общее количество циклов = 14
Каждый велосипед имеет не менее 2 колес.
14 x 2 = 28
Общее количество приведенных колес = 38
38 – 28 = 10
Это означает, что имеется 10 велосипедов с одним дополнительным колесом в каждом, поэтому общее количество трехколесных велосипедов в парке равно 10.
Вопрос 9. Какие три числа при сложении или умножении дают одинаковый ответ?
Ответ. 1 + 2 + 3 = 6 и 1 х 2 х 3 = 6; поэтому ответ равен 1, 2 и 3.
Вопрос 10. Решите следующее уравнение:
9 – 3 ÷ 1/3+ 1 =?
Ответ. Ответ на этот вопрос: 1. Все, что вам нужно сделать, это перевернуть дробь, чтобы превратить деление в умножение.
9 – 3 х 3 + 1 =?
9 – 9 + 1 = 1
Вопрос 11. Рис весом 33/4 фунта был разделен поровну и помещен в 4 контейнера. Сколько унций риса было в каждом?
Ответ. 33/4 ÷ 4 фунта.
= (4 × 3 + 3)/4 ÷ 4 фунта.
= 15/4 ÷ 4 фунта.
= 15/4 × 1/4 фунта.
= 15/16 фунтов.
Мы знаем, что 1 фунт = 16 унций.
Следовательно, 15/16 фунтов = 15/16 × 16 унций.
= 15 унций.
Вопрос 12. Джессика купила корзину с 5 яблоками. Если бы она должна была разделить яблоки так, чтобы каждый из ее 5 учеников получил по 1 яблоку и 1 яблоко осталось в корзине. Как она это сделает?
Как она это сделает?
Ответ. Джессика может раздать по 4 яблока 4 ученикам и дать пятому ученику корзину с яблоком.
Вопрос 13. Добавьте 8,254 и 4,2672.
Ответ. Сложение цифр с десятичной дробью так же просто, как и простое сложение. Тот факт, что 8,254 имеет меньше цифр, чем 4,2672, не имеет значения. Все, что вам нужно сделать, это просто добавить 0 в конце 8.254. Таким образом, ответ становится 12,5212.
Вопрос 14. Составьте уравнение, используя четыре семерки (7) и единицу (1), чтобы получить ответ как 100.
Ответ. 177 – 77 = 100
Вопрос 15. Если 1 = 5; 2 = 25; 3 = 325 и 4 = 4325; тогда 5 =?
Ответ. Немедленный ответ, который возникнет у вас в голове, глядя на паттерн, — 54325. Но это неправильный ответ. Правильный ответ дан в самом вопросе, так как вопрос гласит, что 1 = 5, тогда 5 = 1.
Вопрос 16. Предположим, что на складе находится 85 человек, из которых некоторые превратились в зомби, а некоторые еще в живых. Если соотношение зомби к количеству живых людей составляет 2:3, подсчитайте общее количество зомби.
Если соотношение зомби к количеству живых людей составляет 2:3, подсчитайте общее количество зомби.
Ответ. Нам дано, что на каждых 3 человек приходится 2 зомби.
2 + 3 = 5
Чтобы вычислить общее количество групп людей и зомби, делим общую силу на 5.
85/5 = 17.
Теперь, чтобы получить общую численность. зомби и людей, умножим 17 на 2 и 3 соответственно. Таким образом, ответ: 34 зомби и 51 человек.
Вопрос 17. Глядя на этот ряд: 22, 21, 23, 22, 24, 23, … Какое число должно быть следующим?
Ответ: Если вы заметили, чередующиеся числа в ряду создают последовательный шаблон чисел. Таким образом, следуя шаблону, ответ будет 25.
Вопрос 18. Найдите площадь красного треугольника.
Ответ: Для решения этого вопроса необходимо знать формулы нахождения площади треугольника и площади параллелограмма и соотношения между ними.
Так как площадь треугольника равна половине площади параллелограмма.
Теперь, когда вы это знаете, прибавив 79 и 10, а затем вычтя 72 и 8, вы получите ответ как 9.
Вопрос 19. Предположим, есть трехзначное число. Вторая цифра числа в четыре раза больше третьей, а первая в три раза меньше второй. Найдите число.
Ответ. Число 141, так как 4 в четыре раза больше 1, а также в три раза меньше 1.
Вопрос 20. Составьте правильное уравнение, используя числа 2, 3, 4 и 5 и символы = и +.
Ответ. Наилучшее возможное уравнение с использованием заданных чисел и символов будет таким:
5 + 2 = 3 + 4
Почему важно смотреть на математические задачи с забавной точки зрения?
Важно смотреть на математические задачи с интересной точки зрения и превращать математику в восхитительный опыт, потому что улучшение ваших математических навыков поможет вам в долгосрочной перспективе. Каждая область требует от человека знания базовой математики и простейших вопросов с подвохом. Большинство конкурсных экзаменов также внушают страх ученикам с математической частью, хотя на самом деле на этих экзаменах самые простые математические вопросы, которые порой даже не требуют вычислений, а просто логического мышления. Математика и ее практика делают вас более умным человеком, логическое мышление повышает способность к концентрации, помогает вам сосредоточиться и стать внимательным, тем самым совершенствуя свой интеллект и помогая вашему мозгу и общему развитию.
Математика и ее практика делают вас более умным человеком, логическое мышление повышает способность к концентрации, помогает вам сосредоточиться и стать внимательным, тем самым совершенствуя свой интеллект и помогая вашему мозгу и общему развитию.
Как превратить занятия математикой в веселое времяпрепровождение?
Несколько советов и приемов, которые с самого начала облегчат математические задачи, заключаются в том, чтобы заинтересовать их:
Первым и главным ключом к освоению математики является регулярная практика.
Относитесь к математике как к мозговому штурму и осознанной деятельности, а не рассматривайте ее как задачу.
Свяжите математические задачи с вашей повседневной жизнью и посмотрите на них с этой точки зрения. Чтобы было еще интереснее, попробуйте использовать кости, пазлы, карты и т. д.
Посмотрите на вопрос и поймите информацию, примените навыки и вспомните концепции.
Интересные математические задачи
Подборка интересных математических задач, используемых в реальной жизни. Это та математика, которую вам нужно увидеть, чтобы увидеть полезность математики и, как следствие, оценить математику.
Это та математика, которую вам нужно увидеть, чтобы увидеть полезность математики и, как следствие, оценить математику.
Эти математические задачи действительно помогут многим, особенно школьникам, понять, почему математика — это предмет, который нельзя воспринимать как должное.
Вы также можете прочитать, почему математика важна. Теперь давайте приступим сразу к этим проблемам.
Интересные математические задачи о бизнесе, экологии, инвестициях, индексе потребительских цен и демографии.
Инвестиции. Задача №1: Инвестор с $10000 вкладывает часть денег под 8%, а остальную часть под 12%. Сколько нужно инвестировать по каждой ставке, чтобы получить 11% от общей суммы?
базовые знания: Проценты и решение уравнений с дробями
Решение:
Пусть x будет той частью, которая вложена в 8%. Другая часть, вложенная под 12%, составляет 10000-х.
х × 8% + (10000 — х) × 12% = 10000 × 11%
х × 8 / 100 + | (10000 — х) × 12 / 100 знак равно | 10000 × 11 / 100 |
8x / 100 + | 120000 — 12x / 100 знак равно | 110000 / 100 |
Умножить обе стороны на 100
100 × 8x / 100 + | 100 × 120000 — 12x / 100 знак равно | 100 × 110000 / 100 |
.
х ×
8 / 100
+
(10000 — х) ×
12 / 100
знак равно
10000 × 11 / 100 |
8x / 100 + | 120000 — 12x / 100 знак равно | 110000 / 100 |
Умножить обе стороны на 100
100 × 8x / 100 + | 100 × 120000 — 12x / 100 знак равно |
100 × 110000 / 100 |
. инвестировано под 12%
инвестировано под 12%
Индекс потребительских цен. Задача № 2: Предположим, что в 1960 году индекс потребительских цен был равен 70, а в 2015 году – 280. Какая месячная зарплата в 2015 году будет иметь такую же покупательную способность, как месячная зарплата в 800 долларов в 1960 году?
базовые знания: Соотношение и пропорция
Решение:
Пусть x будет месячной зарплатой в 2015 году.
х / 800 знак равно | 280 / 70 |
х × 70 = 280 × 800
70х = 224000
70 / 70 Икс | знак равно 224000 / 70 |
х = 3200
х / 800 знак равно | 280 / 70 |
х × 70 = 280 × 800
70х = 224000
70 / 70 Икс | знак равно 224000 / 70 |
х = 3200
Бизнес. Задача №3: Книжный магазин заработал 11000 долларов, продав 3000 книг по математике и 1000 книг по физике. Клиент купил 1 книгу по математике и 1 книгу по физике и заплатил 7 долларов. Какова цена каждой книги?
Задача №3: Книжный магазин заработал 11000 долларов, продав 3000 книг по математике и 1000 книг по физике. Клиент купил 1 книгу по математике и 1 книгу по физике и заплатил 7 долларов. Какова цена каждой книги?
базовые знания: Система линейных уравнений
Решение:
Пусть x — цена учебника по математике, а y — цена учебника по физике
х + у = 7
3000 × x + 1000 × y = 11000
Используйте x + y = 7, чтобы найти y
x — x + y = 7 — x
y = 7 — x
Подставьте 7 — x вместо y в 3000 × x + 1000 × y = 11000
3000 × x + 1000 × (7 — x) = 11000
3000x + 7000 — 1000x = 11000
2000x = 11000 — 7000
2000x = 4000
x = 2 с 2000 года
× 2 = 4000Так как 2 + 5 = 7, y = 5
Цена книги по математике 2 доллара, а цена книги по физике 5 долларов.
Экология. Проблема № 4: Давление, которое испытывает человек, погружаясь все глубже и глубже в океан, возрастает линейно. На поверхности давление близко к 15 фунтам на квадратный дюйм. 33 фута ниже поверхности, давление 30 фунтов. Если 25000 фунтов на квадратный дюйм могут сломать ваши кости, то какая глубина чрезвычайно опасна для человека?
На поверхности давление близко к 15 фунтам на квадратный дюйм. 33 фута ниже поверхности, давление 30 фунтов. Если 25000 фунтов на квадратный дюйм могут сломать ваши кости, то какая глубина чрезвычайно опасна для человека?
базовые знания: Линейное уравнение
Решение:
Сначала смоделируйте давление ( p ) в зависимости от глубины ( d ) с помощью линейного уравнения.
Найдем уравнение p = md + b
Используя (0, 15) и (33, 30), найдем m
м =
30 — 15 / 33 — 0
м =
15 / 33
= 0,45
p = 0,45d + b
Используйте (0, 15), чтобы найти b
15 = 0,45 × 0 + b
15 = b
p = 0,45d + 15
+0,5
25000 — 15 = 0,45d + 15 — 15
24985 = 0,45d
д =
24985 / 0,45
= 55522 фута
Имейте в виду, что на глубине около 1000 футов под океаном уже очень опасно.
Демография. Проблема № 5: Население штата Флорида сейчас составляет 19,9 миллиона человек. Последний формат пассажирских номеров в штате Флорида — от AAA A00 до ZZZ Z99. Если букву о нельзя использовать при изготовлении номеров, хватит ли государству номерных знаков для своих жителей?
фоновые знания: Мультипликативный принцип (Счет)
Решение:
Формат показывает, что первые 4 символа — буквы, а последние 2 символа — цифры. В английском алфавите 26 символов. Поскольку букву «о» использовать нельзя, выбор теперь равен 25. Для цифр 0–9 имеется 10 символов.
Обратите внимание, что цифры и буквы могут повторяться!
Для первой буквы есть 25 вариантов
Для второй буквы есть 25 вариантов
Для третьей буквы есть 25 вариантов
Для четвертой буквы есть 25 вариантов
Для первого числа есть 10 вариантов
Для второго числа есть 10 вариантов
Принцип подсчета гласит, что нужно умножить все выбор
Количество номерных знаков = 25 × 25 × 25 × 25 × 10 × 10 = 39 062 500
Поэтому номерных знаков будет хоть отбавляй.
Приведенные выше интересные математические задачи были помещены здесь, чтобы показать вам, как математика применяется в реальной жизни. Я надеюсь, что вы полюбите математику, изучая ее. Я буду обновлять эту страницу все более и более интересными математическими задачами. Возвращайтесь, пожалуйста, чтобы я мог показать вам, как решать другие интересные математические задачи !
Более интересные математические задачи
Спрос и предложение. Задача № 6: Чтение задачи
Базовые знания: Обратная вариация, форма пересечения наклона, решение квадратных уравнений.
Применение наклона в реальной жизни
03, 22 октября 11:31
Каковы некоторые реальные применения наклона? Наклон имеет множество применений в реальном мире. Исследуйте их здесь!
Подробнее
14 интересных математических фактов. В этой статье я представляю 14… | by StephenwithaPhD
Умножение единиц всегда дает палиндромные числа.
В этой статье я представляю 14 интересных математических фактов, которые я собрал за последние несколько лет преподавания. Обычно я дарю коллекцию из них первокурсникам в первый день их учебы, чтобы облегчить им поступление в колледж, а также просто заставить их задуматься. Некоторые из них более интересны на уровне «о, хорошо», другие — на уровне «правда, как так получилось?» уровень. Я позволю тебе быть судьей. Некоторые из этих фактов не требуют пояснений и требуют лишь минутного размышления, другие требуют немного больше размышлений, поэтому я сделал несколько комментариев по ходу дела. Я надеюсь, что каждый может получить что-то из списка.
I) Числа на противоположных сторонах игральной кости всегда в сумме дают семь.
II) Ноль — четное число.
Для некоторых из нас это может быть фактом «да, я знаю», но многие люди никогда об этом не задумывались.
Каждый год я предлагаю определенный набор вопросов своим первокурсникам, чтобы заставить их задуматься, это один из них, поскольку он заставляет их подвергнуть сомнению свое определение того, что такое четное число. Я всегда получаю одни и те же результаты, все в классе готовы утверждать, что знают, что такое четное число, но очень немногие готовы встать и заявить, что считают ноль четным.
Я всегда получаю одни и те же результаты, все в классе готовы утверждать, что знают, что такое четное число, но очень немногие готовы встать и заявить, что считают ноль четным.
Для ясности хорошее определение четного числа звучит так: говорят, что число четное, если при делении на 2 оно остается целым числом. Нуль идеально подходит для этого, так как 0/2 = 0.
III) Полезный прием для процентов.
Знаете ли вы, что x% от y = y% от x?
Это может значительно упростить вычисление процентов. Например, попробуйте посчитать в уме 8% от 50. Не так просто право. А теперь переверните и вместо этого отработайте 50% от 8, думаю понятно, что проще.
Точно так же 32% от 75 может показаться трудным для вычисления, но 75% от 32 кажется гораздо более легкой задачей.
IV) Каждое нечетное число, написанное на английском языке, содержит букву «e».
V) «Четыре» — единственное число, написанное на английском языке, в написании которого содержится такое же количество букв, как и в самом числе.
VI) Если вы подсчитаете количество букв в 13 различных видах игральных карт (туз, два, три, четыре, пять, шесть, семь, восемь, девять, десять, валет, дама, король), вы обнаружит, что в колоде 52 буквы, ровно столько игральных карт (без джокеров).
VII) Единственное число, написанное на английском языке, которое пишется буквами в алфавитном порядке, — это «сорок». Единственное число, написанное на английском языке, которое пишется буквами в обратном алфавитном порядке, — это «один».
VIII) Вы можете разрезать торт на 8 равных частей, используя только 3 разреза.
Многие люди говорили мне, что многие компании использовали этот вопрос в качестве вопроса на собеседовании для проверки «нестандартного мышления».
«Фокус» здесь в том, чтобы не думать о торте как о двухмерном круге, как склонны большинство людей, а как о трехмерном цилиндре, которым он и является. Это позволяет нам не только делать обычные вертикальные разрезы, но теперь мы также можем делать горизонтальные разрезы. Таким образом, если вы используете два надреза, чтобы сформировать крест на верхней части торта, эффективно разделяя торт на четыре равные части, и используете свой третий разрез в качестве горизонтального разреза через центр торта, эффективно разделяя каждую из четырех частей. равные части пополам, вы получите свои 8 равных частей.
Таким образом, если вы используете два надреза, чтобы сформировать крест на верхней части торта, эффективно разделяя торт на четыре равные части, и используете свой третий разрез в качестве горизонтального разреза через центр торта, эффективно разделяя каждую из четырех частей. равные части пополам, вы получите свои 8 равных частей.
IX) В переполненном помещении два человека, вероятно, будут праздновать день рождения в один день.
Хорошо, это немного расплывчато. Что означает «переполненный зал» и насколько вероятно «вероятно». Очень хорошие вопросы!
Оказывается, и это на самом деле очень легко увидеть с некоторой базовой вероятностью, что если у вас всего 23 человека в комнате, то вероятность того, что у двоих из них дни рождения совпадают, составляет 50%.
Я знаю, это кажется совершенно нелогичным. Позвольте мне добавить к вашему нелогичному чувству: если в комнате будет 70 человек, у вас теперь будет 9 человек.Вероятность того, что двое из них родились в один день, составляет 9,9%!
Это известно как парадокс дня рождения (или проблема дня рождения), и я настоятельно рекомендую вам разобраться в этом подробнее. Я надеюсь написать короткую статью об этой проблеме очень скоро.
Я надеюсь написать короткую статью об этой проблеме очень скоро.
X) Их ровно 10! секунд за 6 недель.
Для тех, кто не знает, для любого положительного целого числа n, n!, читаемое как «n факториал», представляет собой произведение всех положительных целых чисел, меньших или равных n. Так, например, 5! = 5 × 4 × 3 × 2 × 1,
Итак, чтобы увидеть, что 10! секунды = 6 недель, давайте конвертируем шесть недель в секунды.
Теперь попробуем переписать это так, чтобы оно выглядело как 10!,
XI) Количество миллисекунд в сутках равно 5⁵× 4⁴ × 3³ × 2² × 1¹.
XII) Умножение единиц всегда дает палиндромные числа.
Для тех, кто не в курсе, палиндромное число — это просто число, которое в обратном направлении такое же, как и в прямом, например, 23432.
Итак, если вы посчитаете 1 × 1, мы получим 1. Хорошо, это немного ленивый палиндром, идем дальше.
11 × 11 = 121,
111 × 111 = 12321,
1111 × 1111 = 1234321,
и так далее. Если вы умножите 111111111 × 111111111, вы получите 12345678987654321.
Если вы умножите 111111111 × 111111111, вы получите 12345678987654321.
Кроме того, нет необходимости иметь одинаковое количество единиц в двух числах, которые вы умножаете. Например, 11 × 1111 = 12221 и
111111 × 1111 = 123444321.
XIII) 18 — единственное число, которое в два раза больше суммы своих цифр.
Хотя это легко проверить, верно ли это для 18, нужно немного подумать, чтобы доказать, что 18 — единственное число, для которого это верно.
XIV) Повторяющееся десятичное число 0,9999. . . точно равно 1.
Я могу привести довольно простое доказательство этого.
Пусть х = 0,9999. . . .
Тогда, умножив обе части уравнения на десять, мы получим
10x = 9,9999. . . .
Если теперь вычесть x = 0,9999. . . с обеих сторон имеем
10x − x = (9,9999…) − (0,9999…)
⇒ 9x = 9
⇒ x = 1,
Аналогичный факт имеет место для любого числа, содержащего бесконечную цепочку из девяток. Например 0,4999…. = 0,5, 19,999… = 20 и −2,999…= −3.
Например 0,4999…. = 0,5, 19,999… = 20 и −2,999…= −3.
Честно говоря, я никогда полностью не доволен этим доказательством. Это, безусловно, служит своей цели, чтобы подчеркнуть, что происходит, но для тех, кто изучал любой уровень реального анализа, вам может показаться, что это дешевый трюк. Я в чем-то согласен, а тем, кому интересно, стоит поискать, как доказать этот факт, используя пределы последовательностей! На самом деле, вы можете увидеть формальное доказательство прямо здесь
В этой статье я представляю формальное доказательство того, что повторяющееся десятичное число 0,999…. на самом деле равно 1.
stephenwithaphd.medium.com
Вот и все, 14 интересных математических фактов, которые сделают вас душой любой вечеринки, а если нет, то, возможно, вы пойдете не на ту вечеринку! Спасибо за чтение.
Четыре странные и интересные неразрешимые математические задачи | Самрат Дутта | август 2022 г.
Источник: Pexels. У всех нас была математика в школе, но некоторые из нас выбрали академические или карьерные пути, которые больше не нуждаются в математике, а для других математика стала неотъемлемой частью их жизни. Однако все, от новичка до знатного человека, которые когда-либо касались математической задачи, согласятся, что наиболее отличительной чертой интригующей задачи является ее сложность.
Однако все, от новичка до знатного человека, которые когда-либо касались математической задачи, согласятся, что наиболее отличительной чертой интригующей задачи является ее сложность.
По мере развития математика также становится все более и более сложной, но никогда не теряет своей первоначальной сущности. Однако даже величайшие математики сталкивались с проблемами, которые кажутся неразрешимыми и остаются таковыми до сих пор. Вот некоторые неразрешимые и почти мистические по своей сути проблемы.
Задача «Затерянный в лесу», впервые предложенная в 1955 году, была простой и полностью соответствовала названию.
Представьте, что вы путешественник, заблудившийся в лесу, и у вас есть карта леса определенной формы, однако вы не знаете, где вы находитесь и в каком направлении смотрите – каков же кратчайший путь из лес?
Что касается этой задачи, то математики оказались не лучше заблудившегося туриста. При отсутствии конкретных факторов и переменных, на которых можно было бы основывать расчеты, теряется процесс изучения.
Математическая логика и теоремы, необходимые для решения этой задачи, если они будут изобретены, могут значительно помочь другим разделам математики. Один исследователь назвал эту задачу «задачей на миллион долларов», подразумевая, что это, возможно, одна из самых дискретных, но важных математических проблем, которые ждут своего решения.
Обычно для решения этой проблемы предлагается просто идти по прямой. Это также эффективно в реальном лесу. Однако решения во многом зависят от формы леса. Например, в случае равностороннего треугольника наилучшим возможным маршрутом будет определенная зигзагообразная линия, которая, как доказано, всегда не может уместиться внутри такого треугольника.
Эта задача также имеет определенное отношение к задаче о червях, поскольку они обратны друг другу. Если вы найдете самую маленькую форму червя, которая не помещается внутри определенной формы одеяла, то это то же самое, что найти форму кратчайшего пути, который выведет вас из леса. По сути, то, что не работает с проблемой червя, работает с проблемой леса. Увлекательно, правда?
По сути, то, что не работает с проблемой червя, работает с проблемой леса. Увлекательно, правда?
Представьте, что вы двигаете диван по узкому коридору. Даже если вы не выполняли задачу самостоятельно, вы можете хотя бы представить, насколько это может быть утомительно. Юмор некоторых ситкомов 90-х, безусловно, помогает этому воображению.
В любом случае, вопрос –
Какой самый большой диван (по площади), который можно сдвинуть за угол 90°, не поднимая его?
Эта проблема была впервые предложена Лео Мозером в 1966 году и до сих пор остается нерешенной. Вам может быть интересно, почему это так, ведь проблема кажется довольно простой. Ответ кроется в объективной природе математической логики.
В 1992 году математик Джозеф Гервер придумал диван в форме телефона (📞), который, казалось, был ответом. Однако, согласно вопросу, необходимо объективно доказать, что никакой другой диван любой формы и размера не может заменить этот диван.
Это должен быть абсолютно герметичный, полностью логичный аргумент, а не просто идея с множеством доказательств в свою пользу. Это требует противопоставления этого дивана всем возможным врагам дивана.
Для этого ученые в настоящее время проводят симуляции, но до сих пор проблема не решена. Мы только пришли к выводу, что предложение Гервера — один из самых больших диванов, а самый большой диван может быть всего на несколько процентов больше.
Мозер не остановился на диване и добавил к списку нелепых и неразрешимых задач еще одну. Этот называется «Червь Мозера». Вопрос:
Если мы предположим, что червяк-мать хочет накрыть червяка-детеныша одеялом, то какое наименьшее возможное одеяло может покрыть всего червяка независимо от его положения?
Простой ответ, который можно было бы придумать, состоит в том, чтобы сделать квадратное одеяло, каждая сторона которого в два раза длиннее червяка. Это кажется полной защитой, но того же эффекта можно добиться с помощью круглого одеяла с размером червя в качестве диаметра.
Это новое одеяло занимает всего 79% площади квадратного одеяла. Ну тогда в чем, кажется, дело? То же, что и первая проблема. Пока не будут опробованы все размеры и формы, невозможно доказать, какой размер одеяла является наименьшим из возможных.
Даже тогда ученые проводят симуляции и предсказывают, что наименьший размер одеяла должен составлять от 6% до 6,5% от изначально предложенного квадратного одеяла. Мы, конечно, надеемся, что достаточно скоро найдем применимый ответ, чтобы червь-мать мог эффективно работать, чтобы защитить своих детенышей.
Думаю, многие из нас слышали о магических квадратах и даже видели некоторые из них. Они представляют собой сетку чисел 4×4, где каждая строка, столбец и диагональ составляют одно и то же число. Магические квадраты были обнаружены в древних текстах и реликвиях со всей Индии, Китая и других частей Юго-Восточной Азии и даже в некоторых частях Европы. Следовательно, это то же самое, что сказать, что это не ново.
Задача о магических квадратах здесь относится к задаче «квадрат квадратов». Это один магический квадрат 3×3, где каждый квадрат магического квадрата будет содержать квадратное число.
Это один магический квадрат 3×3, где каждый квадрат магического квадрата будет содержать квадратное число.
Задача состоит в том, чтобы найти работающий магический квадрат квадратов, т. е. каждая строка, столбец и диагональ в сумме дают одно и то же число. 1996 г. в одной из своих статей в журнале Scientific American. Вы можете найти эту точную проблему самостоятельно, но никто не смог ее решить.
Было несколько промахов, но это не помогает. Возможно, у этой проблемы нет ответа, и этот магический квадрат квадратов не может быть решен… из-за кажущейся недоступности квадратов. Но даже тогда это нужно доказать, а доказательства — это то, чего нам не хватает.
Немногие занимаются этими математическими задачами, а те, кто этим занимаются, в основном любители. Они надеются, что эти проблемы можно решить или, по крайней мере, доказать их неразрешимость.
Все в математике основано на доказательствах, которые можно получить откуда угодно. Даже любители могут попробовать и использовать его как ступеньку в своем путешествии с числами и проблемами.



 Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая.
Какой знак нужно поставить между ними, чтобы получился результат больше 4 и меньше 5. Ответ: запятая. На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров.
На 1 час 10 человек выкопают 1 метр траншеи, за 10 часов они выкапывают 10 метров траншеи, а за 100 часов – 100 метров. Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись.
Папа выпил чай из одной чашки и поставил ее на место. Мама выпила свой чай и тоже поставила чашку на место. Сколько чашек было на столе, когда пришел пить чай сын? Ответ: 3 чашки. Они хоть и пустые, но никуда со стола не делись. Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол.
Но это нюансы, которые лучше рассматривать, рисуя на листе бумаги, где ребенок собирается «пилить» стол. Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком.
Одна из монет не пятак, как такое может быть? Ответ: может, т.к. другая монета вполне может быть пятаком. В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется.
В каждой коробке было по 15 конфет. Маша съела несколько конфет и отложила коробку. А Лиза съела столько, сколько оставалось в коробке у Маши, и тоже отложила коробку. Вечером мама посчитала конфеты в коробках обеих девочек. Сколько конфет там было? Ответ: 15. Маша и Лиза съели вместе 15 конфет. Маша несколько (например, 15-х=у), а Лиза столько, сколько осталось у Маши (т.е. у конфет). Сумма х+у = 15. А у девочек было по 15 конфет, т.е. 2*15 = 30. Было 30, 15 съели, и 15 на двоих осталось. А сколько у кого – этого в задаче не уточняется. А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался.
А те, кто не знают – левую. Благодаря маленькой хитрости класс достойно прошел проверку и никто ни о чем не догадался. Страусы не умеют разговаривать.
Страусы не умеют разговаривать.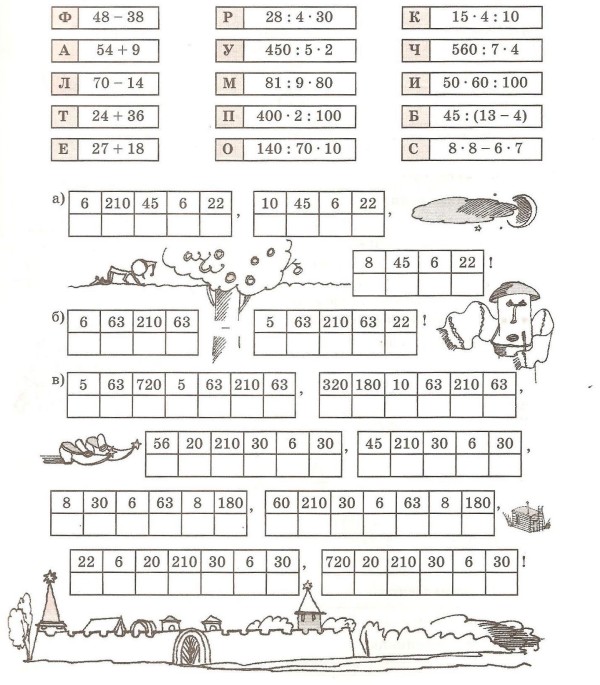

 При выявлении победителя принимается во внимание правильность ответов и затраченное время.
При выявлении победителя принимается во внимание правильность ответов и затраченное время. Сколько хрямзиков бросил Сережа? (19).
Сколько хрямзиков бросил Сережа? (19). Как это может быть? (Это одинаковое время, так как 60 мин. + 20 мин. = 80 мин.)
Как это может быть? (Это одинаковое время, так как 60 мин. + 20 мин. = 80 мин.) Сколько видов насекомых обитает на нашей планете? (2 млн)
Сколько видов насекомых обитает на нашей планете? (2 млн) Потом полученное число умножается на 5. К результату прибавляется 7, затем цифра, обозначающая десятки, отбрасывается. К оставшемуся числу прибавляют 3, отнимают 8, умножают на 4. И учитель называет ответ, общий для всех школьников: 8.
Потом полученное число умножается на 5. К результату прибавляется 7, затем цифра, обозначающая десятки, отбрасывается. К оставшемуся числу прибавляют 3, отнимают 8, умножают на 4. И учитель называет ответ, общий для всех школьников: 8. Почему бы и нет?
Почему бы и нет?  В следующем году мне будет 28. Это правда только один день в году. В какой день у меня День Рождения?
В следующем году мне будет 28. Это правда только один день в году. В какой день у меня День Рождения?  Теперь налейте 2 литра в 5-литровую бутылку, пока она не наполнится.
Теперь налейте 2 литра в 5-литровую бутылку, пока она не наполнится.

 Ему нужно проехать 100 км, чтобы добраться до вершины горы. Каждый день Он поднимается на 2 км вперед в дневное время. Измученный, он отдыхает там ночью. Ночью, пока он спит, он соскальзывает на 1 км назад, потому что гора наклонена. Тогда сколько дней потребуется ему, чтобы достичь вершины горы?
Ему нужно проехать 100 км, чтобы добраться до вершины горы. Каждый день Он поднимается на 2 км вперед в дневное время. Измученный, он отдыхает там ночью. Ночью, пока он спит, он соскальзывает на 1 км назад, потому что гора наклонена. Тогда сколько дней потребуется ему, чтобы достичь вершины горы?