Транспортная задача онлайн решение: Транспортная задача онлайн

Онлайн-калькулятор:Метод дифференциальных рент

Назначение. Онлайн-калькулятор предназначен для решения транспортной задачи методом дифференциальных рент (см. пример решения). Для этого выберите размерность матрицы тарифов (количество поставщиков и количество магазинов).

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Количество столбцов (магазины) 2345678910
Количество строк (поставщики) 2345678910

Если при определении оптимального плана ТЗ методом потенциалов сначала находился какой-нибудь опорный план, а затем он последовательно улучшался, то при нахождении решения ТЗ методом дифференциальных рент сначала распределяют между пунктами назначения часть груза (так называемое оптимальное распределение) и на последующих итерациях постепенно уменьшают общую величину нераспределенных поставок. Первоначальный вариант распределения груза определяют следующим образом.

В каждом из столбцов таблицы данных находят минимальный тариф. Найденные числа заключают в кружки, а клетки, в которых стоят указанные числа, заполняют. В них записывают максимально возможные числа. В результате получают некоторое распределение поставок груза в пункты назначения. Это распределение в общем случае не удовлетворяет ограничениям исходной транспортной задачи. Поэтому в результате последующих шагов следует постепенно сокращать нераспределенные поставки груза так, чтобы при этом общая стоимость перевозок оставалась минимальной. Для этого сначала определяют избыточные и недостаточные строки.

Строки, соответствующие поставщикам, запасы которых полностью распределены, а потребности пунктов назначения, связанных с данными потребителями запланированными поставками, не удовлетворены, считаются недостаточными. Эти строки иногда называют также отрицательными. Строки, запасы которых исчерпаны не полностью, считаются избыточными. Иногда их называют также положительными.

После того, как определены избыточные и недостаточные строки, для каждого из столбцов находят разности между числом в кружке и ближайшим к нему тарифом, записанным в избыточной строке. Если число в кружке находится в положительной строке, то разность не определяют. Среди полученных чисел находят наименьшее. Это число называется промежуточной рентой. После определения промежуточной ренты переходят к новой таблице. Эта таблица получается из предыдущей таблицы прибавлением к соответствующим тарифам, стоящим в отрицательных строках, промежуточной ренты. Остальные элементы остаются прежними. При этом все клетки новой таблицы считают свободными. После построения новой таблицы начинают заполнение ее клеток. Теперь уже число заполняемых клеток на одну больше, чем на предыдущем этапе. Эта дополнительная клетка находится в столбце, в котором была записана промежуточная рента. Все остальные клетки находятся по одной в каждом из столбцов, и в них записаны наименьшие для данного столбца числа, заключенные в кружки.

Заключены в кружки и два одинаковых числа, стоящих в столбце, в котором в предыдущей таблице была записана промежуточная рента.

Поскольку в новой таблице число заполняемых клеток больше, чем число столбцов, то при заполнении клеток следует пользоваться специальным правилом, которое состоит в следующем. Выбирают некоторый столбец (строку), в котором имеется одна клетка с помещенным в ней кружком. Эту клетку заполняют и исключают из рассмотрения данный столбец (строку). После этого берут некоторую строку (столбец), в которой имеется одна клетка с помещенным в ней кружком. Эту клетку заполняют и исключают из рассмотрения данную строку (столбец). Продолжая так, после конечного числа шагов заполняют все клетки, в которых помещены кружки с заключенными в них числами. Если к тому же удается распределить весь груз, то получают оптимальный план. Если же оптимальный план ТЗ не получен, то переходят к новой таблице. Для этого находят избыточные и недостаточные строки, промежуточную ренту и строят новую таблицу.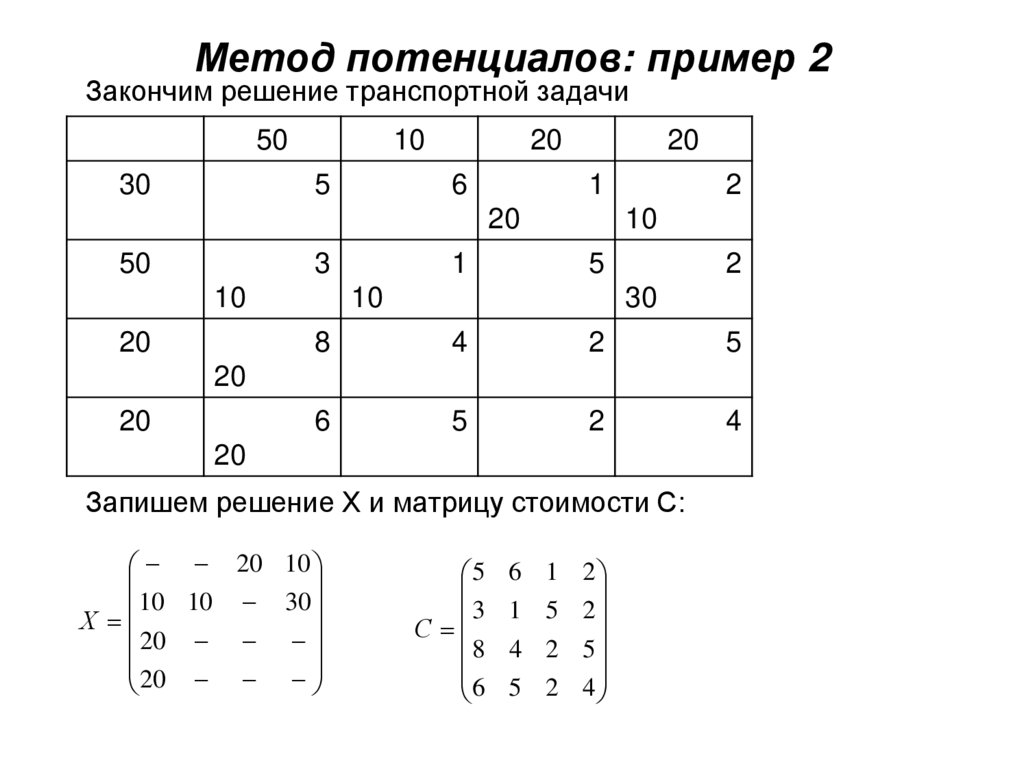

При этом могут возникнуть некоторые затруднения при определении знака строки, когда ее нераспределенный остаток равен нулю. В этом случае строку считают положительной при условии, что вторая заполненная клетка, стоящая в столбце, связанном с данной строкой еще одной заполненной клеткой, расположена в положительной строке.

После описанных выше итераций нераспределенный остаток становится равным нулю. В результате получается оптимальный план ТЗ.

Транспортная задача с ограничениями на пропускную способность

Пусть требуется при решении транспортной задачи ограничить перевозки от поставщика с номером l к потребителю с номером m.
Возможны ограничения двух типов:

1. x_lm > а;
2. x_lm < b,
3. x_lm = k,

где а и b— постоянные величины.

1. Если x_lm > a, то необходимо прежде, чем решать задачу, сократить (уменьшить) запасы l-го поставщика и запросы m-го потребителя на величину а (зарезервировать перевозку x_lm = а).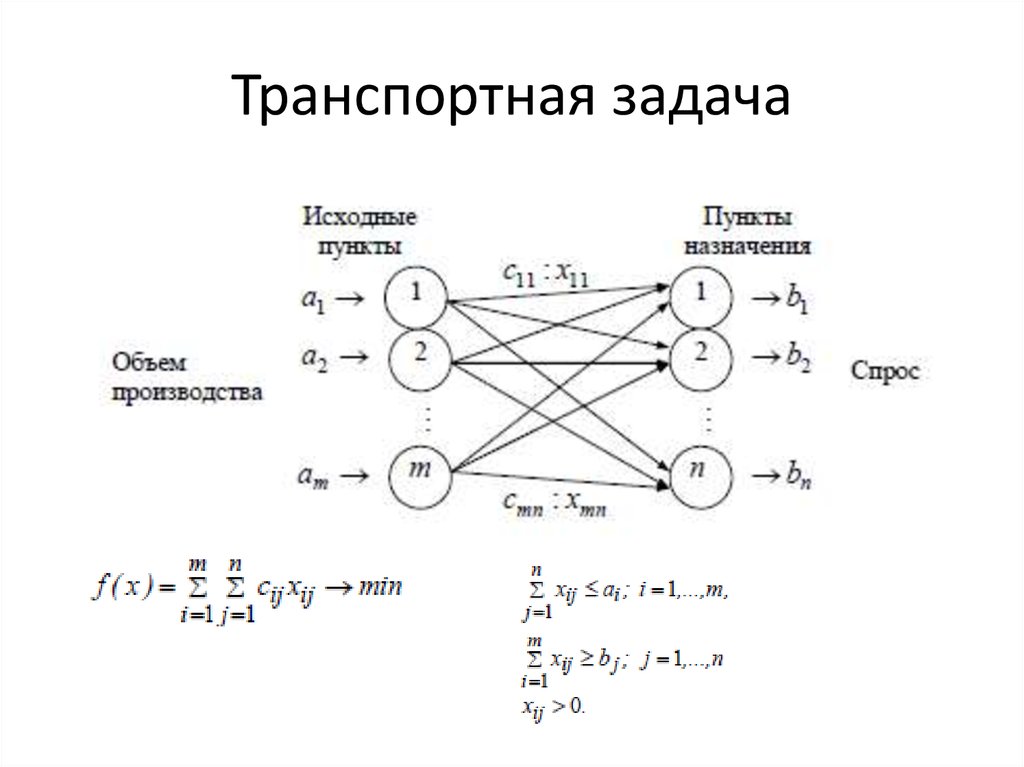 После решения задачи в оптимальном решении следует увеличить объем перевозки x_lm на величину а.

2. Если x_lm<b, то необходимо вместо

m-го потребителя с запросами b_m ввести двух других потребителей. Один из них с номером m должен иметь запросы b ‘_m=b, а другой с номером п + 1— запросы b_п+1= b_m — b. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости c_l(n+1) которая принимается равной сколь угодно большому числу М (М >> 1). После получения оптимального решения величины грузов, перевозимых к (n + 1)-му потребителю, прибавляются к величинам перевозок l-го потребителя. Так как c_l(n+1)) = М — самая большая стоимость перевозки, то в оптимальном решении клетка с номером (l, n+ 1) останется пустой, x_l{n+1) = 0 и объем перевозки х_lm не превзойдет b.

3. Если x_lm = k, то необходимо уменьшить запасы и потребности для номеров l и m на величину k. Стоимость перевозки c_lm назначают равной М >> 1.

4. В некоторых задачах требуется запретить перевозки от отдельных поставщиков отдельным потребителям. В таких случаях либо зачеркивают соответствующую клетку таблицы транспортной задачи, либо назначают соответствующую этой клетке стоимость перевозки единицы груза сколь угодно большой, равной М >> 1. В остальном задача решается обычным способом.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Инструкция. Для получения онлайн решения транспортной задачи выберите размерность матрицы тарифов. Количество столбцов (магазины) 2345678910

Количество строк (поставщики) 2345678910

Найти решение транспортной задачи, если из А₂ в В₄ перевозки запрещены, из А₁ в В₃ должно быть доставлено не менее n единиц груза, а из А₃ в В₁ не более m единиц груза.

Пример. В трех хранилищах горючего ежедневно хранится 175, 125 и 140 т бензина. Этот бензин ежедневно получают четыре заправочные станции в количествах, равных соответственно 180, 110, 90 и 40 т. Тарифы перевозок 1 т бензина с хранилищ к заправочным станциям задаются матрицей .
Составит такой план перевозок бензина, при котором общая стоимость перевозок является минимальной.

Рассмотрим первый вариант ограничения. Пусть требуется ограничить перевозки от поставщика с номером

2 к потребителю с номером 3 в размере не менее 40. Сокращаем запасы 2-го поставщика и запросы 3-го потребителя на величину а = 40. Решаем задачу с использованием калькулятора.

	1	2	3	4	Запасы
1	9	7	5	3	175
2	1	2	4	6	85
3	8	10	12	1	40
Потребности	180	110	50	40

В результате получим оптимальный план.

	1	2	3	4	Запасы
1	15	110	50		175
2	85				85
3				40	40
4	80				80
Потребности	180	110	50	40

Далее в оптимальном решении следует увеличить объем перевозки x₂₃ на величину а = 40.

	1	2	3	4	Запасы
1	15	110	50		175
2	85		40		125
3				40	40
4	80				80
Потребности	180	110	90	40

Рассмотрим второй вариант ограничения.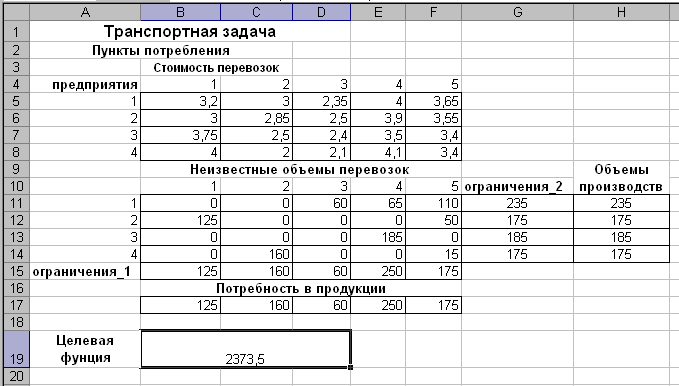 Пусть требуется ограничить перевозки от поставщика с номером 2 к потребителю с номером 3 в размере не более 30. Вместо 3-го потребителя с запросами 90 вводим двух других потребителей. Один из них с номером 3 должен иметь запросы b’₃=30, а другой с номером 4 + 1 — запросы b5 = 90 - 30 = 60. Стоимости перевозок для этих потребителей остаются прежними, за исключением стоимости c₂₅ которая принимается равной сколь угодно большому числу М (М >> 1).

	1	2	3	4	5	Запасы
1	9	7	5	3	5	175
2	1	2	4	6	—	125
3	8	10	12	1	12	140
Потребности	180	110	30	40	60

В результате получим опорный план.

	1	2	3	4	5	Запасы
1	9	7[85]	5[30]	3	5[60]	175
2	1[100]	2[25]	4	6	36	125
3	8[80]	10	12	1[40]	12	140
Потребности	180	110	30	40	60

После получения оптимального решения величины грузов, перевозимых к 5-му потребителю, прибавляются к величинам перевозок 2-го потребителя. 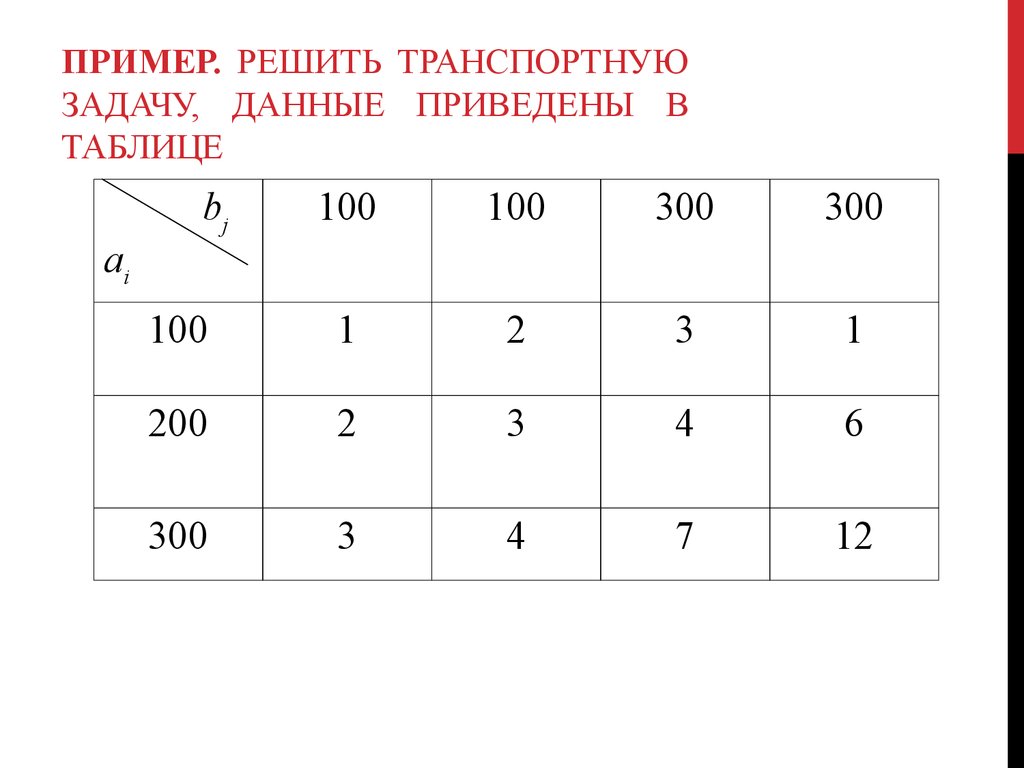Так как c₂₅ = М — самая большая стоимость перевозки, то в оптимальном решении клетка с номером (2, 5) останется пустой, x₂₅ = 0 и объем перевозки х₂₃ не превзойдет b = 30.

	1	2	3	4	Запасы
1		85	30+60		175
2	100	25	0 < 30		125
3	80			40	140
Потребности	180	110	90	40

Рассмотрим третий вариант ограничения.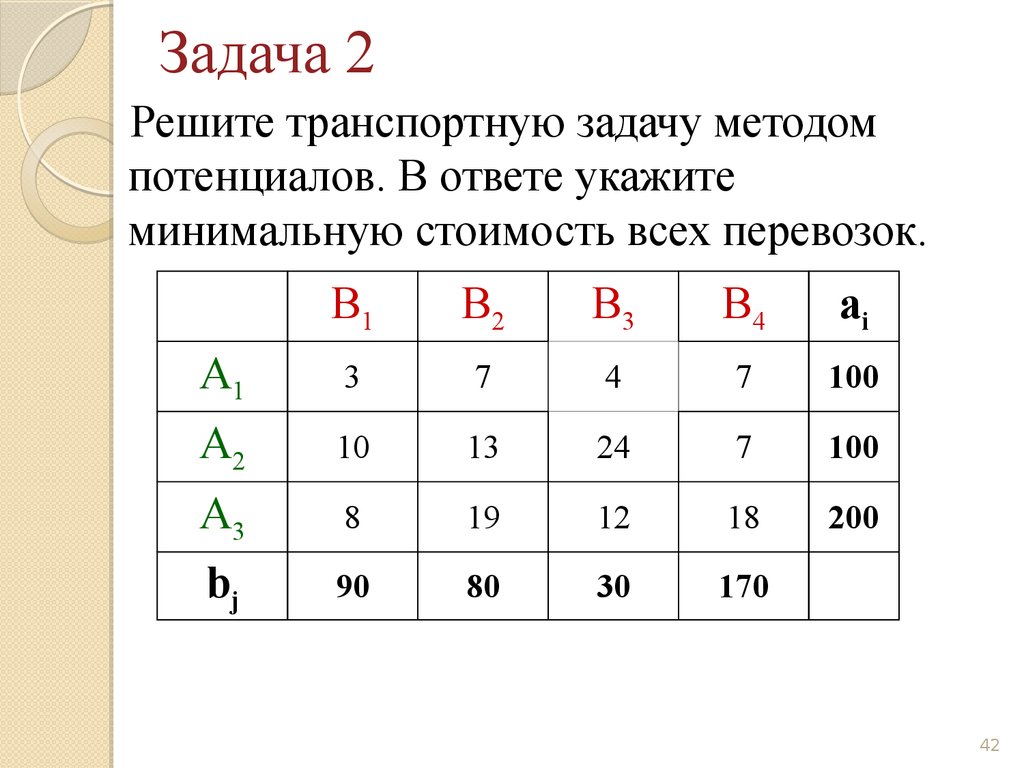 x₂₃ = 20. Модифицируем исходную матрицу:

	1	2	3	4	Запасы
1	9	7	5	3	175
2	1	2	M	6	85-20=65
3	8	10	12	1	40
Потребности	180	110	50-20=30	40

Решая методом потенциалов, получаем следующий оптимальный план:

	1	2	3	4	Запасы
1	9[35]	7[110]	5[30]	3	175
2	1[65]	2	36	6	65
3	8[0]	10	12	1[40]	40
4	0[80]	0	0	0	80
Потребности	180	110	30	40

Восстанавливаем исходную матрицу:

	1	2	3	4	Запасы
1	35	110	30		175
2	65		20		85=65+20
3				40	40
4	80	0	0	0	80
Потребности	180	110	50=30+20	40

Пример №1.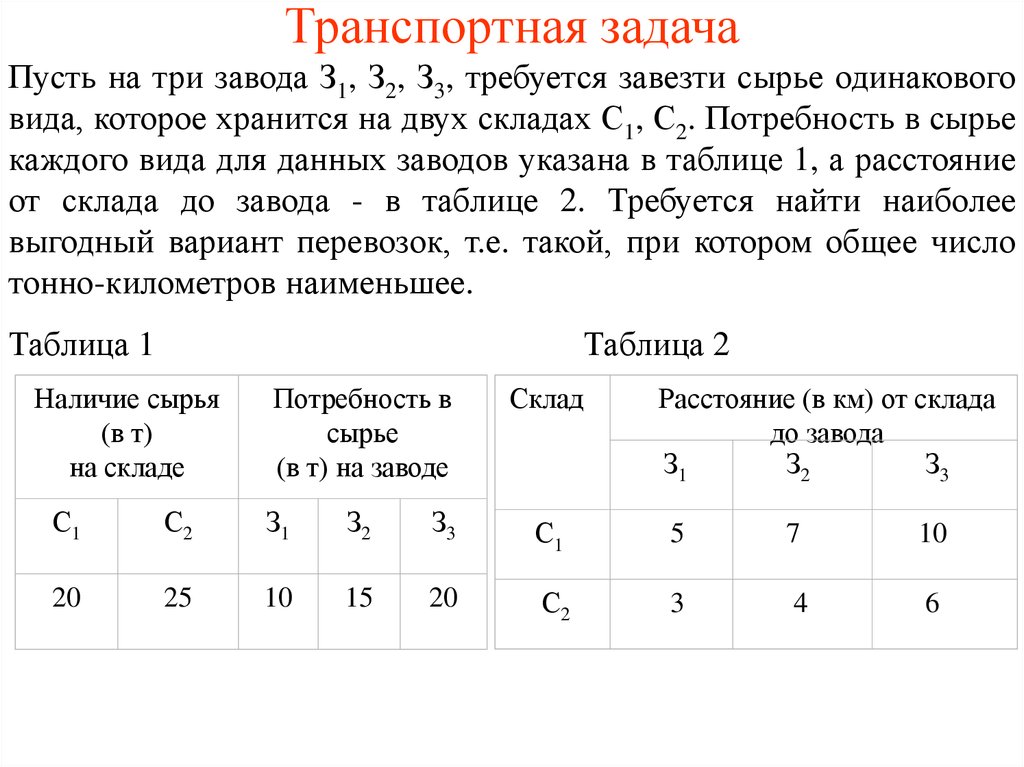 Транспортная задача с дополнительными ограничениями.
Скачать решение

Пример №2. Найти оптимальный план транспортной задачи, описываемой соответствующей таблицей, удовлетворяющим указанным условиям.

1. Потребности пунктов B₁ и B₃ удовлетворяются полностью.
2. Остаток груза в пункте A₁ не менее 10 ед., но не более 13 ед.
3. Суммарная вывозка из пунrта А₁ не менее 45 ед.
4. Суммарная поставка в пункт В₁ не более 70
5. Суммарная поставка в пункт В₂ не менее 100
6. В пункт В₂ должно быть завезено не менее 25 ед.
7. От второго поставщика должно быть вывезено не менее 50 ед.
8. x₁₂ ≤ 15
9. Суммарная вывозка из всех пунктов равна 75 ед.
10. Должен быть вывезен весь груз из пунктов А₃ и А₂.
11. Суммарная поставка в пункт В2 не превосходит 50 ед. , груза, но не менее 35 ед.
12. Из пункта А₁ нужно вывезти не менее 160 ед. груза, а в пункт В₁ завезти  не менее 70 ед. груза из пункта А₂.
13. x₁₁ + x₂₁ ≤ 35

Комбинация TDM и KSAM для определения начального возможного решения транспортных задач

Д. Априлианто, «Оптимизация SVM с оптимизацией роя бинарных частиц на основе выбора корреляционных признаков для диагностики хронического заболевания почек», J. Soft Comput. Исследовать., т. 2, с. 1, нет. 1, стр. 24–31, 2020.

Р. Х. Сапутра и Б. Прасетьо, «Повысить точность алгоритма c4.5 с помощью выбора функций оптимизации роя частиц ( pso ) и метода упаковки в диагностике рака молочной железы», J. Soft Comput . Исследовать., т. 2, с. 1, нет. 2020. Т. 1. С. 47–55.

И. Э. Тиффани, «Оптимизация наивного байесовского классификатора с помощью реализованной униграммы, биграммы, триграммы для анализа настроений в отзывах об отелях», J. Soft Comput. Исследовать., т. 2, с. 1, нет. 1, стр. 1–7, 2020.

А. Хан, «Решение транспортной проблемы: алгоритмический подход», Джахангирнагарский университет. J. Sci., vol. 34, стр. 49–62, 2011.

М. А. Ислам, М. М. Хак и М. С. Уддин, «Формула экстремальной разности по совокупным альтернативным издержкам: метод минимизации транспортных расходов», Prime Univ. Журнал, том. 6, нет. 2012. Т. 2. С. 125–130.

М. Ашрафул Бабу, М. Абу Хелал, М. С. Хасан и У. К. Дас, «Метод наименьшего распределения (LAM): новый подход к получению допустимого решения транспортной модели», Int. J. Sci. англ. Рез., том. 4, нет. 11, 2013.

У. Канти Дас, М. Ашрафул Бабу, А. Рахман Хан и Д. Шариф Уддин, «Усовершенствованный метод приближения Фогеля (AVAM): новый подход к определению штрафных затрат для более эффективного решения транспортной задачи. », Междунар. Дж. Инж. Рез. Техн., вып. 3, с. 182, 2014.

А. Р. Хан, В. Адриан, Н. Султана, С. С. Ахмед, «Определение начального базового допустимого решения транспортной задачи: подход TOCM-SUM», Бюл. Политехнический институт. Дин Яссы, том. 61, стр. 39–49, 2015.

Т. Кан, «Аппроксимационный метод Тункай Кана для получения начального базового допустимого решения транспортной задачи», Appl. вычисл. Матем., вып. 5, нет. 2, с. 78, 2016, doi: 10.11648/j.acm.20160502.17.

М. М. Ахмед, А. Р. Хан, Ф. Ахмед и М. С. Уддин, «Метод непрерывного распределения для решения транспортных задач», Am. Дж. Опер. Рез., том. 06, нет. 03. С. 236–244, 2016. doi: 10.4236/ajor.2016.63024.

М. М. Ахмед, А. Р. Хан, М. С. Уддин и Ф. Ахмед, «Новый подход к решению транспортных проблем», Open J. Optim., vol. 05, нет. 01, стр. 22–30, 2016, doi: 10.4236/ojop.2016.51003.

Э. Хоссейни, «Три новых метода поиска начального базового допустимого решения транспортных задач», Appl. Мат. наук, вып. 11, стр. 1803–1814, 2017, doi: 10.12988/ams.2017.75178.

Y. Harrath и J. Kaabi, «Новая эвристика для создания начального базового допустимого решения для сбалансированной транспортной задачи», Int. J. Ind. Syst. англ., вып. 30, нет. 2, с. 193, 2018 г., doi: 10.1504/ijise.2018.10016216.

С. М. Абул Калам Азад и М. Камрул Хасан, «Эффективный алгоритм решения транспортной задачи по минимизации затрат», Int. Дж. Матем. Опер. Рез., том. 15, нет. 2019. Т. 4. С. 434–445. doi: 10.1504/IJMOR.2019.103005.

ZH Radthy, FH Maghool и AH Khaleel, «Применение линейного программирования в соответствии с транспортной задачей на реальных данных», Int. J. Sci. Технол. Рез., том. 8, нет. 1, стр. 100–102, 2019 г.

Б. Амалия, К. Фатичах и Э. Сурьяни, «Матрица совокупных альтернативных издержек — минимальная сумма: новый подход к определению начального базового возможного решения транспортной задачи», Египет. . Информатика Ж., т. 1, с. 20, нет. 2, стр. 131–141, 2019 г., doi: 10.1016/j.eij.2019.01.002.

Б. Амалия, К. Фатичах, Э. Сурьяни и А. Мусвар, «Матрица совокупных альтернативных затрат — высшая ячейка: новый метод получения начального базового возможного решения транспортных задач», в серии материалов международной конференции ACM, 2020 г. , стр. 151–156, doi: 10.1145/3411174.3411198.

К. Карагул и Ю. Сахин, «Новый метод аппроксимации для получения начального базового допустимого решения транспортной задачи», J. King Saud Univ. — англ. наук, вып. 32, нет. 2020. Т. 3. С. 211–218. doi: 10.1016/j.jksues.2019..03.003.

ZU Rizqi, «Алгоритм Зака: эвристический подход к решению транспортной задачи», Материалы Международной конференции по промышленной инженерии и управлению операциями, 2019 г., стр. 1127–1131.

Л. Каур, М. Ракшит и С. Сингх, «Альтернативный подход к поиску начального базового допустимого решения транспортной задачи», Int. J. Sci. Технол. Рез., том. 8, нет. 9, стр. 442–447, 2019.

П. Сумати и К. В. Сатья Бама, «Инновационный маршрут для решения транспортных проблем с наименьшими затратами», Междунар. Дж. Инж. Доп. Техн., вып. 9, нет. 1, стр. 5368–5369, 2019, doi: 10.35940/ijeat.A3070.109119.

Б. Маллиа, М. Дас и К. Дас, «Новый алгоритм решения транспортной проблемы с узким местом», Int. Дж. Иннов. Технол. Исследуйте. англ., вып. 8, нет. 8, стр. 419–423, 2019.

Р. Муругесан и Т. Эсаккиаммал, «Определение наилучшего начального базового допустимого решения транспортной задачи: подход TOCM-ASM», Adv. Мат. науч. Дж., том. 9, нет. 7, стр. 4563–4577, 2020, doi: 10.37418/amsj.9.7.25.

R. Murugesan и T. Esakkiammal, «Улучшенный метод ASM для решения транспортной задачи», Adv. Мат. науч. Дж., том. 9, нет. 10, стр. 8259–8271, 2020, doi: 10.37418/amsj.9.10.55.

R. Murugesan и T. Esakkiammal, «Метод TOCM-VAM по сравнению с методом asm в транспортных задачах», Adv. Мат. науч. Дж., том. 9, нет. 6, стр. 3549–3566, 2020, doi: 10.37418/amsj.9.6.34.

Сравнение транспортных задач в исследовании операций

• На этой странице
• Аннотация
• Введение
• Заключение
• Каталожные номера
• Авторское право

Авторы: Дхивья Бхарати С. , М. Рамья

Ссылка DOI: https://doi.org/10.22214/ijraset.2022.40310

Сертификат: Посмотреть сертификат

Abstract

В исследовании операций транспортная проблема является одной из преобладающих областей и широко используется в качестве инструмента принятия решений во многих областях. Мы сообщаем об основном допустимом решении и, следовательно, о методах достижения оптимального решения сбалансированной транспортной задачи.

Введение

I. ВВЕДЕНИЕ

Транспортная задача в исследовании операций имеет широкое применение в управлении запасами, планировании производства, составлении графиков, личном распределении и т.д. Цель состоит в том, чтобы свести к минимуму затраты на распространение продукта из нескольких источников или мест происхождения в несколько пунктов назначения. Характеристика транспортной задачи такова, что она обычно решается специализированным методом, а не симплекс-методом.

II. ТРАНСПОРТНАЯ ЗАДАЧА

Транспортная задача в операционных исследованиях связана с нахождением минимальной стоимости транспортировки одного товара из заданного количества источников в заданное количество пунктов назначения. Эти типы задач могут быть решены общими сетевыми методами, но здесь мы используем определенный алгоритм транспортировки.

Данные модели включают

1. Уровень предложения в каждом источнике и объем спроса в каждом пункте назначения.
2. Удельная стоимость транспортировки товара из каждого источника в каждый пункт назначения.

Поскольку существует только один товар, пункт назначения может получать спрос из более чем одного источника. Цель состоит в том, чтобы определить, сколько должно быть отправлено из каждого источника в каждый пункт назначения, чтобы минимизировать общие транспортные расходы.

Типы транспортных задач в исследовании операций:          

a. Сбалансированная транспортная задача: В транспортной задаче, когда общее предложение из всех источников равно общему спросу во всех пунктах назначения, говорят, что транспортная задача сбалансирована     .

B. Несбалансированная транспортная задача: В транспортной задаче, когда сумма предложения, доступного из всех источников, не равна сумме потребностей всех пунктов назначения, говорят, что несбалансированная транспортная задача.

III. РЕШЕНИЕ ТРАНСПОРТНОЙ ЗАДАЧИ

1. Поиск начального базового допустимого решения.
2. Проверка на оптимальность.

Существует три метода нахождения начального базового допустимого решения:

A. Метод северо-западного угла

Метод начинается с ячейки северо-западного угла таблицы x 11 .

1. Выберите ячейку в северо-западном углу транспорта и распределите в ячейке как можно больше, чтобы либо была исчерпана вместимость первой строки, либо было исчерпано требование назначения первого столбца.
2. Если спрос исчерпан, переместите одну ячейку вправо по горизонтали во второй столбец и выделите как можно больше.
3. Если запас исчерпан, переместиться на одну ячейку вниз по вертикали ко второму ряду и выделить как можно больше. Если и предложение, и спрос исчерпаны, переместитесь на одну клетку по диагонали и распределите как можно больше.
4. Продолжайте описанную выше процедуру до тех пор, пока не будут выделены все ресурсы.

B. Метод наименьших затрат

Метод наименьших затрат путем присвоения возможности ячейке с наименьшей удельной стоимостью.

1. Найдите ячейку с наименьшей (минимальной) стоимостью в таблице перевозок.
2. Выделить максимально допустимое количество для ячейки.
3. Удалите строку или столбец, в которых выполняется выделение.
4. Повторяйте вышеуказанные шаги для сокращенной транспортной таблицы до тех пор, пока не будут выполнены все назначения.

C. Аппроксимативный метод Фогеля

Аппроксимационный метод Фогеля — это усовершенствованная версия метода наименьших затрат, который обычно дает лучшие исходные решения.

1. Рассчитайте штрафы для каждой строки и каждого столбца. Здесь штраф означает разницу между двумя последовательными наименьшими затратами в строке и в столбце.
2. Выберите строку или столбец с наибольшим штрафом.
3. В выбранной строке или столбце распределите максимально допустимое количество по ячейке с минимальной стоимостью.
4. Удалите строку или столбец, в которых выполняются все распределения.
5. Напишите сокращенную транспортную таблицу и повторите шаги с 1 по 4.
6. Повторяйте процедуру до тех пор, пока не будут выполнены все распределения.

IV. ИЛЛЮСТРАТИВНЫЙ ПРИМЕРЫ

A. Метод северо-западного угла

Пример: Определите начальное базовое допустимое решение следующей транспортной задачи.

Сравнение между тремя методами

Northwes цель завершения питания, а затем следующий. Преимуществом метода северо-западного угла является быстрое решение, потому что вычисления занимают мало времени, но дает плохое решение, потому что оно очень далеко от оптимального решения.

Метод аппроксимации Фогеля и метод наименьших затрат используются для получения кратчайшего маршрута. Преимущество метода аппроксимации Фогеля и метода наименьшей стоимости дает лучшее начальное базовое решение, поскольку дает начальное решение, близкое к оптимальному решению, но решение методов аппроксимации Фогеля медленное, поскольку вычисления занимают много времени. Стоимость перевозки по методу аппроксимации Фогеля и методу наименьших затрат меньше, чем по методу северо-западного угла.

Вывод

Транспортная задача — одно из наиболее часто встречающихся приложений в реальных жизненных ситуациях. Транспортная задача указывает количество груза, которое необходимо перевезти из разных пунктов отправления в разные пункты назначения, чтобы общая стоимость транспортировки была минимизирована без нарушения ограничений доступности и ограничений требований.

Литература

[1] Гасс С.И., О решении транспортной задачи, Журнал Оперативного Исследовательского Общества 35(12), 1113-1114, 1990. [2] Р.Р.К. Шарма и К. Д. Шарма, Новая двойная процедура для решения транспортной задачи, European Journal of Operations Research 144, 560-564, 2003. [3] Х. Вагнер, Принципы исследования операций, Нью-Джерси: Прентис-Холл, Энглвудские скалы, 1969. [4] У. Л. Уинстон, Приложения и алгоритмы исследования операций, Калифорния: Издательство Уодсворт, 1991. [5] П. К. Гупта и Д. С. Хира, Исследование операций, С. Чанд, Нью-Дели, Индия, 1992. [6] Хамди А. Таха, Исследование операций, введение, Арканзасский университет, Фейетвилл, 19.97. [7] В. Сундаресан, К.С. Ганапати Субраманиан, К. Ганесан, Методы управления ресурсами (исследование операций).