Транспозиция матрицы: определение, свойства и примеры решения задач

Содержание

Работа с матрицами в Mathcad 15, 14, 13. Матричные операции, транспонирование, обратные матрицы

В статье рассмотрены основные возможности mathcad 15 для работы с матрицами

Ввод матриц
Перемножение матриц
Транспонирование матриц
Обратные матрицы
Выделение строки и столбца матрицы

Ввод матрицы

Чтобы ввести матрицу в mathcad 15 нужно в свободном поле ввести с клавиатуры имя матрицы. Пусть это будет M. Затем на панели Matrix нужно нажать кнопку «Matrix or vector». В появившемся окне нужно ввести количество строк и столбцов и нажать OK

Рис. 1. Ввод матрицы

Затем появится заготовка матрицы с пустыми маркерами для ввода элементов вручную. См. рис. 2

Рис. 2. Заполнение матрицы

Перемножение матриц

Как известно, перемножение матриц осуществляется по правилу «строка на столбец». -1 является такая матрица, при умножении которой на исходную матрицу M получается единичная матрица. Существует множество аналитических способов нахождения обратной матрицы. В mathcad есть стандартная операция по определению обратной матрицы. Введите исходную матрицу M. Затем снова введите имя матрицы M и на панели Matrix нажмите кнопку «Invers». на рисунке 5 можно посмотреть синтаксис записи и убедиться в правильности определения обратной матрицы

Рис. 5. Обратная матрица

Выделение столбца и строки из матрицы

Для того чтобы «вытащить» столбец из матрицы можно воспользоваться стандартной функцией mathcad из панели matrix. Введите произвольную матрицу M и затем ниже в рабочем поле mathcad выполните операцию, как показано на рис. 6. Обратите внимание, что по умолчанию номера столбцов и строк индексируются с «нуля»

Рис. 6. Выделение столбца матрицы

Аналогичным способом можно выделить строку, но для этого матрицу предварительно нужно транспонировать.

При этом строка будет отображена в виде столбца. Если вы хотите получить результат в виде строки, то операцию транспонирования нужно провести 2 раза. Синтаксис будет выглядеть как на рисунке 7

Рис. 7. Выделение строки матрицы

Обратите внимание, что если при перемножении матриц их размерность «не совпадает» то mathcad выдаст ошибку
Обратите внимание, что обратная матрица не всегда может существовать для исходной матрицы

7.1.1. Транспонирование MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим.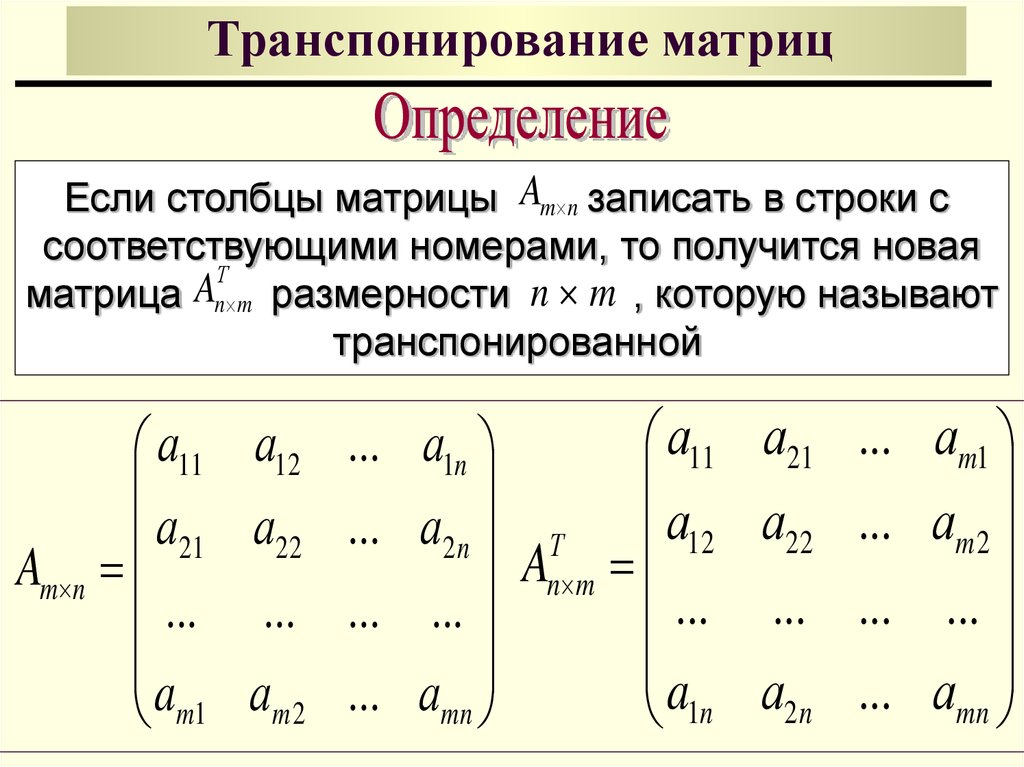

Однако поиск лучших телефонов на Android может быть сложной задачей.

1114 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

Главная
База знаний
CAD / CAM
MathCAD 12

Линейная алгебра
7.1. Простейшие матричные операции
- 7.1.1. Транспонирование
- 7.1.2. Сложение и вычитание
- 7.1.3. Умножение
7.2. Векторная алгебра
- 7.2.1. Модуль вектора
- 7.2.2. Скалярное произведение
- 7.2.3. Векторное произведение
- 7.2.4. Векторизация массива
7. 3. Вычисление определителей и обращение квадратных матриц
- 7.3.1. Определитель квадратной матрицы
- 7.3.2. Ранг матрицы
- 7.3.3. Обращение квадратной матрицы
- 7.3.4. Возведение квадратной матрицы в степень
- 7.3.5. Матричные нормы
- 7.3.6. Число обусловленности квадратной матрицы
7.4. Вспомогательные матричные функции
- 7.4.1. Автоматическая генерация матриц
- 7.4.2. Разбиение и слияние матриц
- 7.4.3. Сортировка элементов матриц
- 7.4.4. Вывод размера матрицы

Транспонированием называют операцию, переводящую матрицу размерности MxN в матрицу размерности NxM, делая столбцы исходной матрицы строками, а строки — столбцами. Несколько примеров транспонирования приведены в листинге 7.1. Ввод символа транспонирования (transpose) осуществляется с помощью панели инструментов Matrix (Матрица) или нажатием клавиш <Ctrl>+<!>.

He забывайте, что для вставки символа транспонирования матрица должна находиться между линиями ввода.

Рис. 7.1. Ввод матриц и основные операции над ними осуществляются при помощи панели Matrix

ПРИМЕЧАНИЕ

Все матричные и векторные операторы, о которых пойдет речь, допустимо использовать как в численных, так и в символьных расчетах. Мощь символьных операций заключается в возможности проводить их не только над конкретными числами, но и над переменными. Смело используйте символьный процессор в качестве мощного математического справочника, когда вы хотите вспомнить какое-либо определение из области линейной алгебры. Именно по этой причине мы прибегаем к примерам символьных расчетов в большинстве иллюстраций к данному разделу.

Листинг 7.1. Транспонирование векторов и матриц

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9965 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6976 0

Глава 2 Работа с файлами Mathcad 11

12520 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2255 s

11.3 Транспозиция матриц

Следующий: 11.4 Сортировка слиянием Up: 11 алгоритмов гиперкуба Предыдущий: 11.2 Векторное преобразование

Транспонирование двумерного N Н матрица А дает матрицу A’ того же размера, в котором . Если А и/или А’ распределяются между несколькими задачи, то выполнение операции транспонирования может потребовать коммуникация. Мы рассматриваем здесь одномерное столбцовое разложение входных и выходных матриц по Р задания. Обратите внимание, что эта транспозиция требует всеобщего общения.

Один широко используемый алгоритм перестановки продолжается в P-1 . шаги, при этом каждая задача обменивается данными с другой задачей в каждом шаг, при стоимости связи для каждого процессора

Этот алгоритм использовался в примере свертки в Раздел 4.4. Альтернативный алгоритм, описанный здесь используется коммуникационный шаблон гиперкуба, чтобы сократить сообщение начальные расходы за счет повышенных затрат на передачу данных. Основная идея аналогична этой используется в алгоритме рекурсивного сокращения вдвое, но поскольку оператор, используемый для объединения сообщений при транспонировании, называется «дополнение». а не «уменьшать», размеры сообщений не уменьшаются по мере транспонировать выручку.

Рисунок 11.3: Три этапа транспонирования матрицы алгоритм при P=N=8 . Изначально каждая задача имеет один столбец матрица. После транспонирования каждая задача имеет одну строку. В каждом шаг, каждая задача обменивается половиной своих данных; эти данные заштрихованы верхнюю часть фигуры.

Нижняя часть рисунка показывает происхождение восьми значений, удерживаемых задачей 0 на каждом шаге алгоритма. Задача 0 отправляет элементы 4-7 в своем первом сообщении и получает четыре элементы из задания 4; они хранятся в ячейках 4–7. в второй шаг, задача 0 меняет местами оба элемента 2-3 (свои) и 6-7 (из задачи 3) с задачей 2. На третьем шаге меняет местами элементы 1 (своего), 3 (из задачи 2), 5 (из задачи 4) и 7 (из задачи 6) с задание 1.

Алгоритм работает следующим образом. Задачи разбиты на две наборы. Соответствующие пары заданий в двух наборах меняются местами. половина их данных предназначена для задач в другом наборе. Задания 0..(P/2)-1 сообщают нижнюю половину своих данных, а задачи (P/2)..P-1 сообщить верхнюю половину. Это разделение и процесс обмена повторяется до тех пор, пока каждый набор не будет содержать одну задачу. См. рис. 11.3 для более подробной информации.

Поскольку каждое из сообщений имеет размер , стоимость связи составляет:

Сравнение уравнений 11. 3 и 11.4. показывает, что алгоритм гиперкуба отправляет примерно меньше сообщений, но в разы больше данных. В большинстве ситуаций, срок передачи данных преобладает, и алгоритм должен быть предпочтительно. Тем не менее, мы можем ожидать, что алгоритм будет конкурентоспособность при небольших проблемах и когда запуск сообщений стоит дорого и стоимость трансфера низкая.

Следующий: 11.4 Сортировка слиянием Up: 11 алгоритмов гиперкуба Предыдущий: 11.2 Векторное сокращение

Самый быстрый словарь в мире | Vocabulary.com

ПЕРЕЙТИ К СОДЕРЖАНИЮ

матричная транспозиция замена каждой строки квадратной матрицы на соответствующий столбец
69″>
настроение ваше обычное настроение
сопоставление акт расположения близко друг к другу
транспонировать акт изменения порядка или места
прямая передача Механизм передачи, при котором инфекционный агент передается непосредственно в организм при прикосновении, укусе, поцелуе, половом акте или воздушно-капельным путем, попадающим в глаза, нос или рот
машинный перевод использование компьютеров для перевода с одного языка на другой
экспозиция коллекция вещей для всеобщего обозрения
26″>
матричная операция математическая операция с матрицами
сложение матриц сложение матриц
обращение матрицы определение матрицы, которая при умножении на заданную матрицу дает единичную матрицу
неправильный перевод неправильный перевод
непрямая передача Механизм передачи, при котором возбудитель передается человеку фомитом переносчика
авиаперевозки авиаперевозки
военная позиция точка, занятая войсками по тактическим соображениям
No related posts.