Теорема по геометрии фалеса: Теорема Фалеса — урок. Геометрия, 8 класс.

Интегрированный урок (математика + информатика) по теме: «Теорема Фалеса»

Цели урока:

Образовательная: доказать теорему Фалеса, научить применять её при решении задач по математике и информатике.

Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.

Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.

Оборудование и материалы:

Компьютер, экран, проектор.
Проектная работа “Теорема Фалеса”.
Программа “Живая геометрия”.
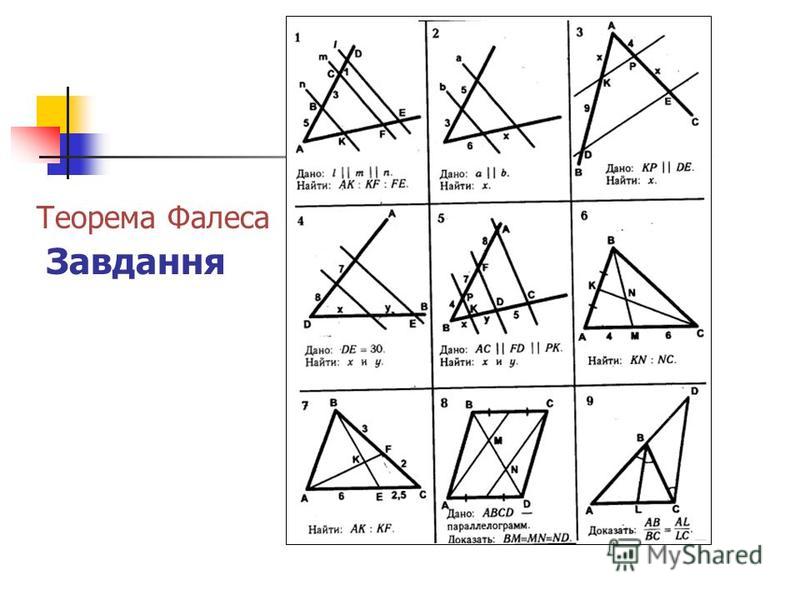
Плакат с рисунками 1,2,3.

Задачи учителей:

Показать практическое применение теоретических знаний учащихся при решении задач по геометрии и информатике.

Выявить глубокие связи между математикой и информатикой.

Ход урока:

Урок начинает учитель математики. Приветствие и вступительное слово о целях урока.

Фронтальный опрос учащихся:

1. Какие отрезки называются равными?

2. Какие прямые называются параллельными? На рис. 1 покажите параллельные прямые.

3. Какие углы называются вертикальными, внутренними накрест лежащими? Покажите их на рис.2

4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.

5. Сформулируйте признаки равенства треугольников. По каким признакам равны треугольники на рис 3?

Объяснение нового материала

Учитель математики объясняет новую тему с помощью просмотра проектной работы “Теорема Фалеса”.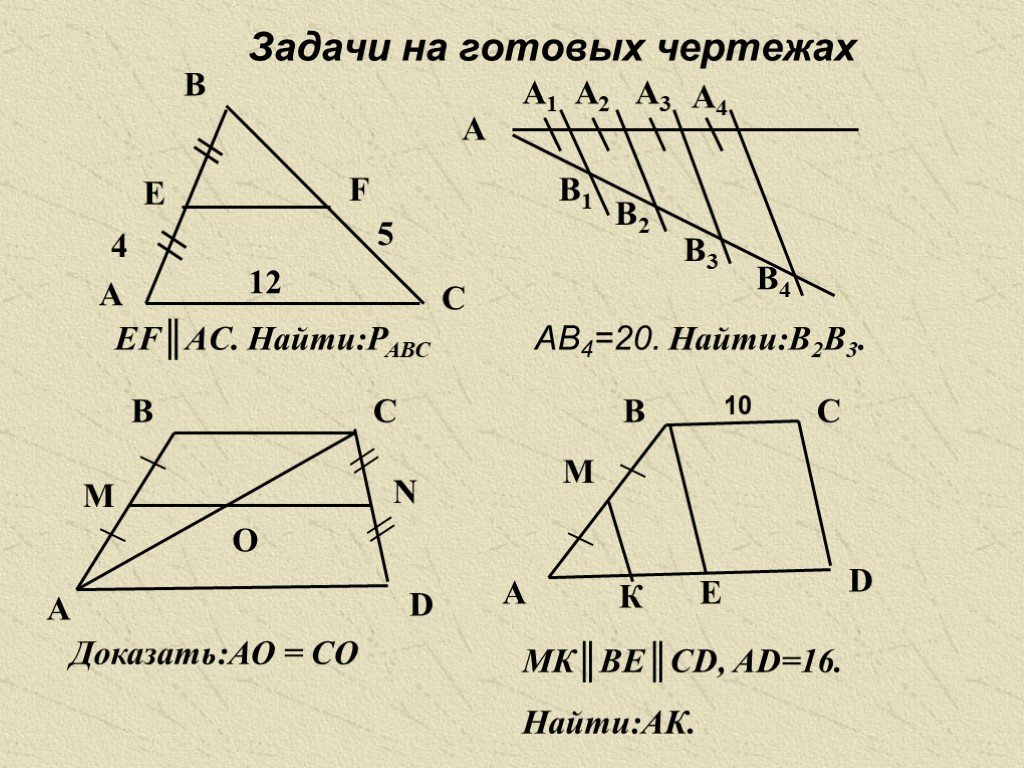

(Приложение 1)

Сегодня мы докажем теорему, носящую имя древнегреческого учёного Фалеса, который жил в 624-547г.г. до н.э.

 

• Великий учёный Фалес Милетский основал одну из прекраснейших наук — геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Короче: он был то же для Греции, что Ломоносов для России
.

Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.

Фалес — математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны.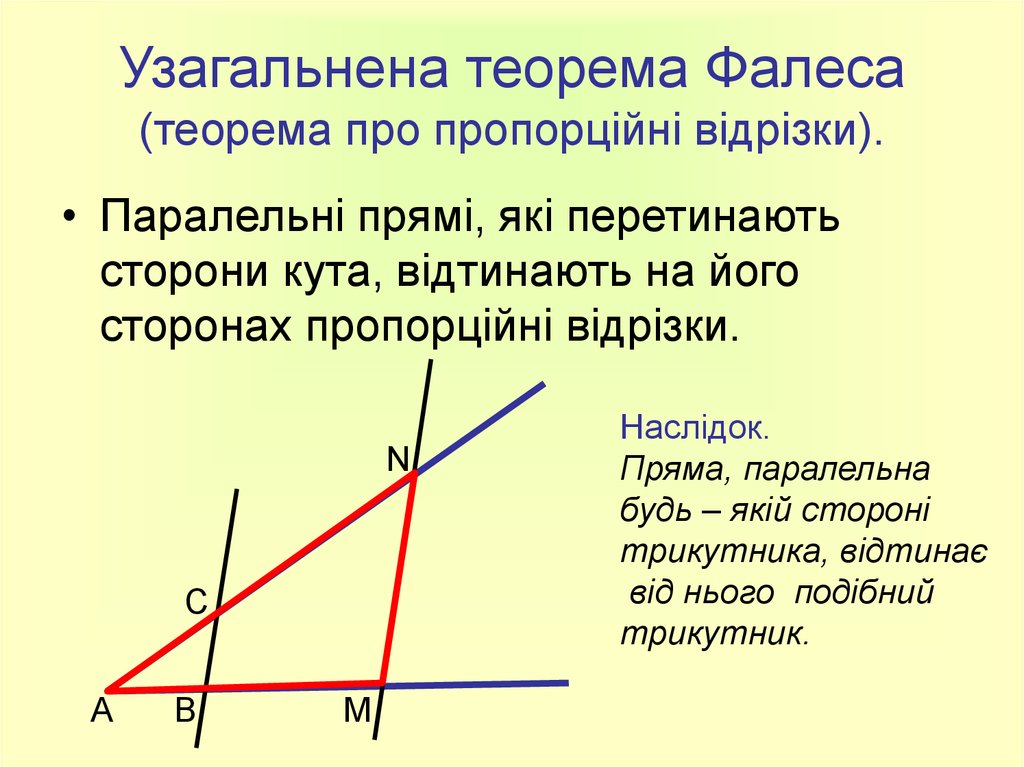 Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой.

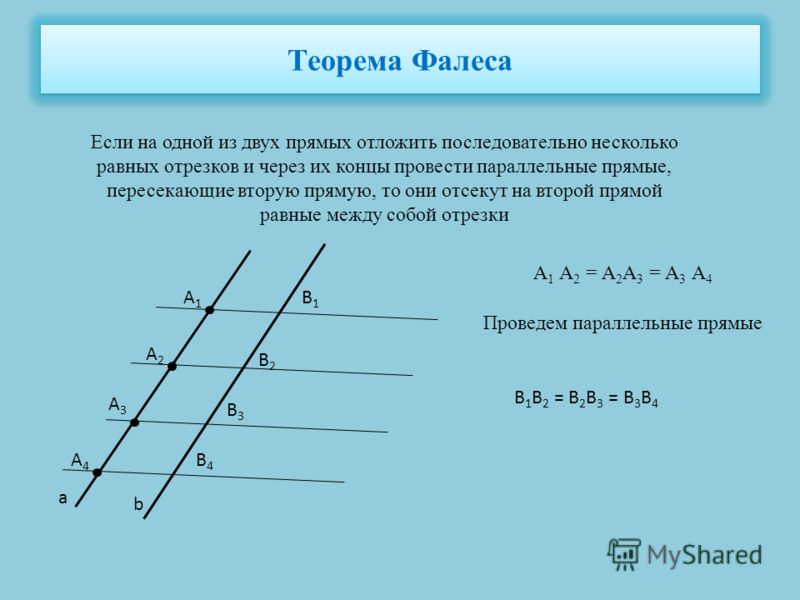
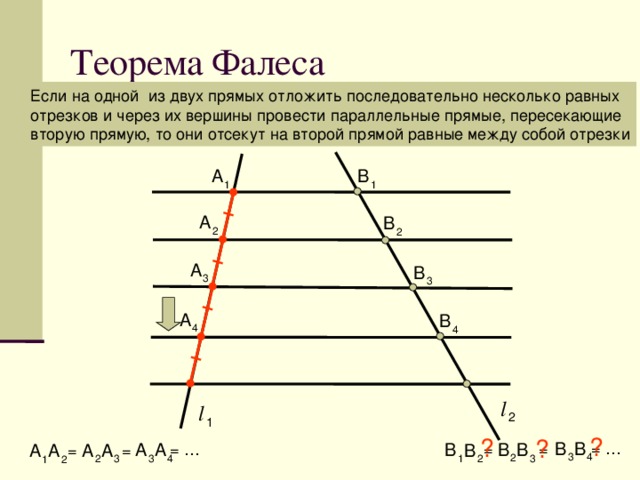
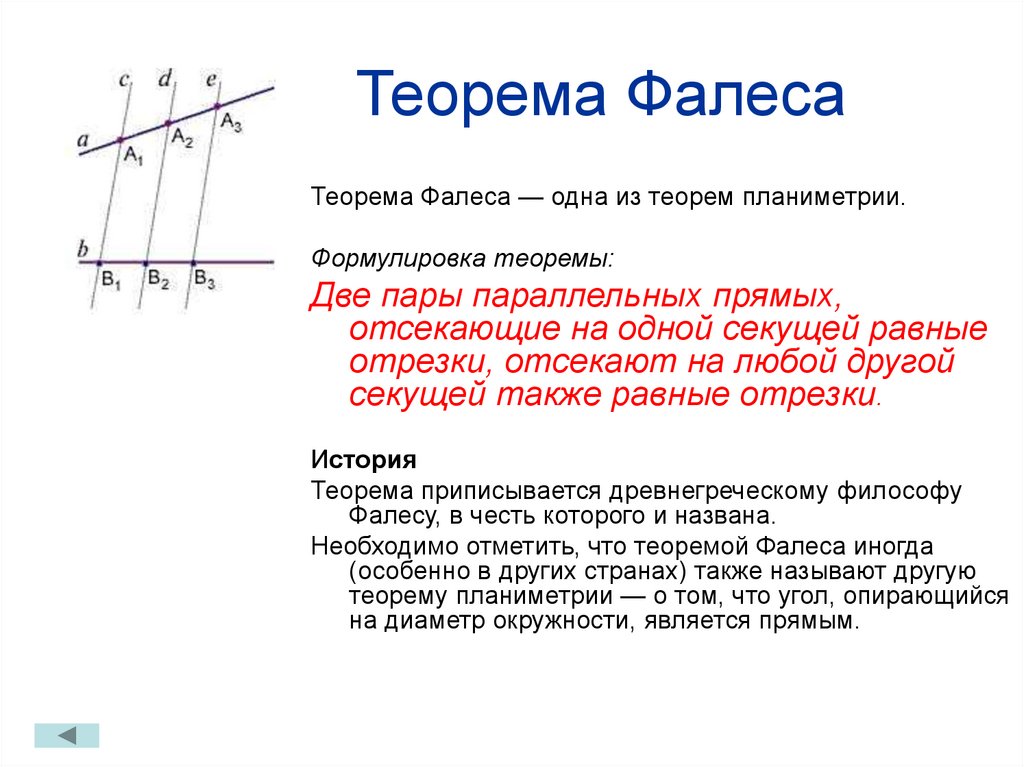
Фалес доказал теорему: “Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне”.

При активном участии учащихся разбирается доказательство теоремы с последовательным показом на экране каждого этапа построения чертежа и доказательства теоремы.

Из условия теоремы Фалеса делается вывод, что вместо сторон угла можно взять любые две прямые.

Затем ученики выполняют в тетрадях практическую задачу на деление отрезка длиной в 7см. на 6 равных частей.

Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.

Все этапы решения задачи учащиеся видят на экране. Это способствует зрительному запоминанию алгоритма решения данной задачи.

Показ проектной работы сопровождается музыкой- игрой на гитаре, что создаёт спокойную рабочую обстановку.

Вторую часть урока ведёт учитель информатики. С помощью программы “Живая геометрия” ученики вместе с учителем на компьютерах делят отрезок на три равные части.

Выполнение практического задания

Разделить данный отрезок на 3-равные части на компьютере с помощью программы “Живая геометрия”.

Используемые ИНСТРУМЕНТЫ “Живой геометрии”:

• стрелка;

• линейка (отрезок, луч).

Используемые КОМАНДЫ “Живой геометрии”:

• построения;

• правка;

Порядок работы:

1 .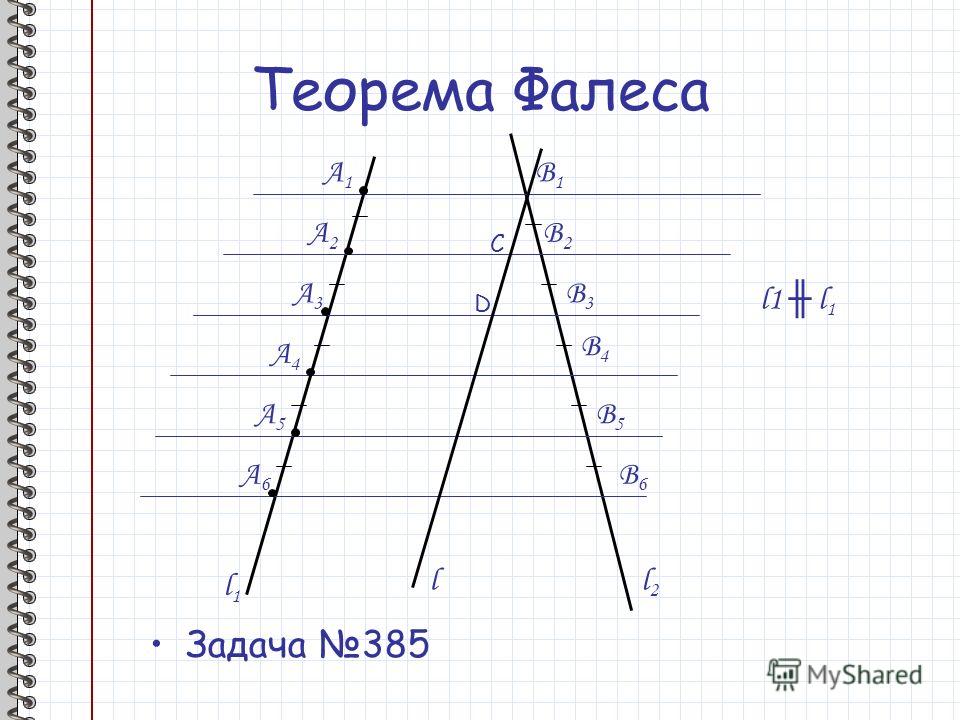 Построим данный отрезок АВ.

2.Проведем из т. А полупрямую а, не лежащую на прямой АВ.

3.Отложим на полупрямой а 3 равных отрезка.

Для этого используем команду ПОСТРОЕНИЯ— “окружность по центру и радиусу”; зададим произвольный радиус СО и построим на полупрямой а 3 окружности.

Они отсекают на полупрямой а равные отрезки АЕ=ЕР=РО.

4.Соединим точки В и О.

5. Проведем через точки Е и Р прямые, параллельные прямой ВО.

6. Они пересекают отрезок АВ в точках Н и I , которые делят отрезок АВ на 3 равные части; т.к. по теореме Фалеса:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Домашнее задание.

Задача: Разделить отрезок длиной 5 см. на 7 равных частей. Выучить теорему Фалеса.

Подведение итогов урока.

Приложение

Математика. Основы геометрии: Обобщенная теоремы Фалеса. Пропорции. Масштаб

<< Назад  |   Оглавление  |   Далее >>

Пропорции

Равенство вида

x1	=	y1
x2		y2

называется пропорцией. При этом говорят, что:

x₁ относится к x₂ как y₁ относится к y₂,

или

отношение чисел x₁ и x₂ равно отношению чисел y₁ и y₂,

или же

числа x₁ и x₂ соотносятся так же, как числа y₁ и y₂,

или, наконец,

числа x₁

и y₁ (!) пропорциональны числам x₂ и y₂ (то есть числители пропорциональны знаменателям).

Входящие сюда числа x₁, x₂, y₁ и y₂ называются членами пропорции. Обычно все они положительны, но это необязательно. Предполагается, однако, что ни одно из них не равно нулю. Особого названия это равенство удостоилось по той причине, что оно часто встречается при решении разных математических задач.

 

Пропорции можно преобразовывать, перенося члены «с верху» одной части равенства «в низ» другой части равенства и наоборот. Эту процедуру легко обосновать следующим образом. Допустим мы хотим перенести x₁ из левой части в правую. Для этого умножим обе части пропорции на 1/x₁:

1		x1	=	1		y1	.
x1		x2		x1		y2

В результате получаем

1	=	y1	,
x2		x1y2

то есть переменная x₁ у нас переместилась «по диагонали сверху вниз». Перенесем теперь «влево наверх» переменную y₂. Это достигается умножением на нее обеих частей данного равенства. В результате имеем

y2	=	y1	.
x2		x1

Мы получили новую пропорцию, которая отличается от исходной перестановкой членов, расположенных «по диагонали». Таким образом, в первоначальном равенстве

x1	=	y1
x2		y2

числители x₁ и y₁ соотносятся между собой точно так же, как и соответствующие им знаменатели x₂ и y₂.

Обобщенная теорема Фалеса

Теорема Фалеса, рассмотренная в прошлый раз, допускает следующее обобщение.

Пусть две произвольные прямые x и y пересекаются тремя параллельными прямыми n₁, n₂ и n₃ в точках X₁, X₂, X₃ и Y₁, Y₂, Y₃, как показано на рисунке:

 

Тогда длины отсекаемых отрезков образуют следующую пропорцию

|Y1Y2|	=	|X1X2|	.
|Y1Y3|		|X1X3|

Докажем эту теорему в случае, когда отношение длин

|X1X2|

|X1X3|

представляет собой рациональное число, то есть может быть выражено в виде несократимой дроби

|X1X2|	=	a	,
|X1X3|		b

где a и b — некоторые натуральные числа, a < b.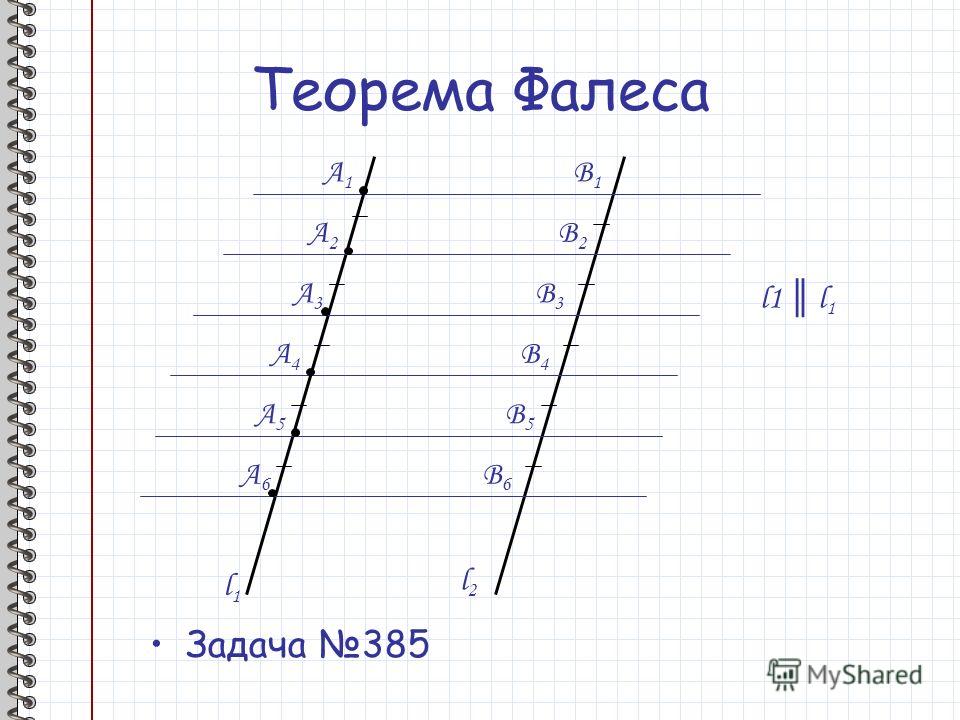 Разобьем отрезок X₁X₃ на b одинаковых частей. (При этом точка X₂ окажется одной из точек деления.) Проведем через каждую точку деления прямые, параллельные n₁, n₂ и n₃. (Одна из этих прямых совпадет с прямой n₂.)

 

По теореме Фалеса (в ее первоначальном варианте), отрезок Y₁Y₃ также делится этими прямыми на b равных частей, из которых a частей составляют отрезок Y₁Y₂. Следовательно,

|Y1Y2|	=	a	=	|X1X2|	,
|Y1Y3|		b		|X1X3|

что и требовалось доказать. Из нашего построения следует также, что

|Y2Y3|	=	b − a	=	|X2X3|
|Y1Y3|		b		|X1X3|

и

|Y2Y3|	=	b − a	=	|X2X3|	.
|Y1Y2|		a		|X1X2|

Пользуясь свойствами пропорций, эти равенства можно переписать в виде одной цепочки:

|Y1Y2|	=	|Y2Y3|	=	|Y1Y3|	.
|X1X2|		|X2X3|		|X1X3|

Таким образом, отрезки отсекаемые на прямой y пропорциональны соответствующим отрезкам на прямой x.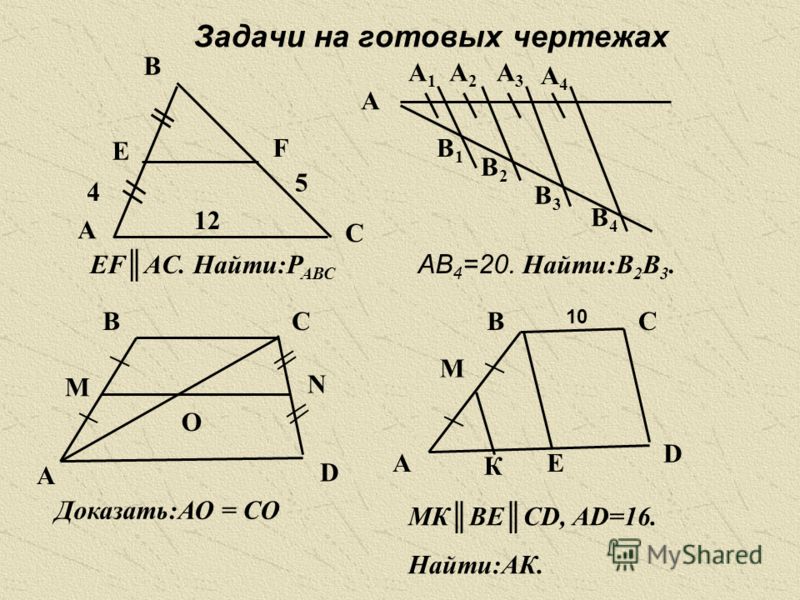

 

Теоретически возможна также ситуация, когда отношение длин

|X1X2|

|X1X3|

не является рациональным числом, поскольку длины отрезков |X₁X₂| и |X₁X₃| могут, в принципе, выражаться иррациональными числами. Однако на практике такой случай никогда не встречается. Для определения длин отрезков мы всегда пользуемся каким-либо измерительным прибором (например, школьной линейкой), который выдает лишь округленные результаты в виде конечной десятичной дроби.

Важное следствие

Пусть даны несовпадающие прямые x и y, которые пересекаются в точке O, и еще — две параллельные прямые n₁ и n₂, которые пересекают прямую x в точках X₁ и X₂ и прямую y в точках Y₁ и Y₂, как показано на рисунке.

 

Введем обозначения:

x₁ = |OX₁|, x₂ = |OX₂|;

y₁ = |OY₁|, y₂ = |OY₂|;

z₁ = |X₁Y₁|, z₂ = |X₂Y₂|.

Тогда

x1	=	y1	=	z1	.
x2		y2		z2

Действительно, оба равенства в этой цепочке непосредственно следует из обобщенной теоремы Фалеса. Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y₁ проведем прямую m, параллельную прямой x.

 

Верно и обратное утверждение. Пусть дана та же геометрическая конструкция и известно, что

x1	=	y1	.
x2		y2

Тогда прямые n₁ и n₂ параллельны. В самом деле, проведем через точку X₁ вспомогательную прямую, параллельную прямой n₂. По обобщенной теореме Фалеса, эта вспомогательная прямая проходит через точку Y₁.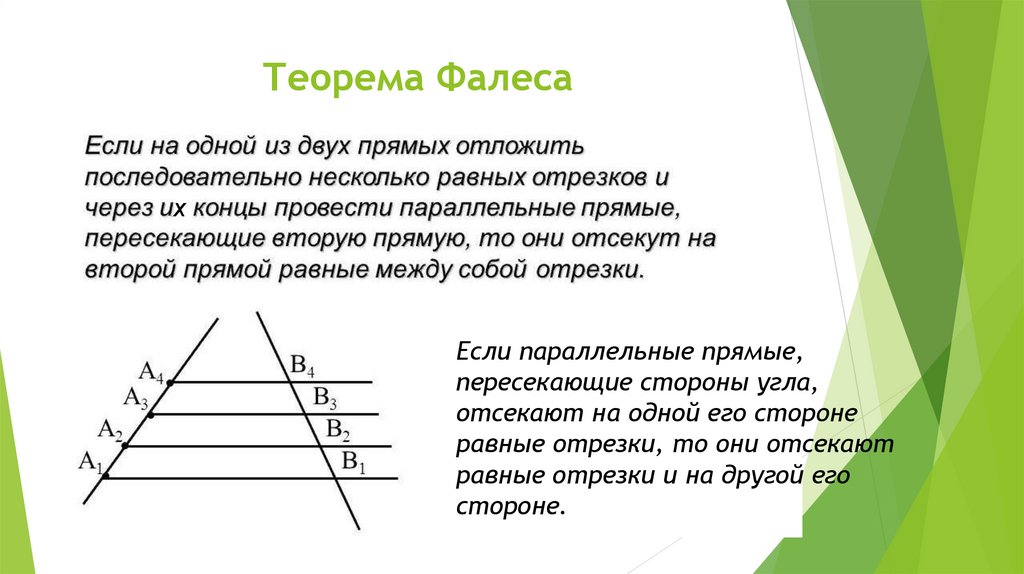 Следовательно, она совпадает с прямой n₁. Таким образом, прямая n₁ параллельна прямой n₂.

Масштаб

Выйдем на улицу, прихватив с собой лист бумаги и карандаш. Расположим наш лист горизонтально и поставим на нем приблизительно посередине точку O. Из этой точки проведем мысленно лучи в направлении различных примечательных точек на местности, расположенных в радиусе примерно ста метров, — деревьев, столбов, углов зданий и того подобного.

Допустим, у нас есть возможность измерить расстояния до этих примечательных точек. Пусть, например, расстояние до ближайшего дерева равно 10 м. Мысленно отложим от точки O в направлении этого дерева отрезок, длина которого в 1000 раз меньше данного расстояния, и отметим карандашом на бумаге положение второго его конца. Нетрудно рассчитать, что расстояние от точки O до отметки составит 10 м/1000 = 1 см.

Подобным же образом, пусть расстояние до какого-то другого примечательного объекта равно x₁.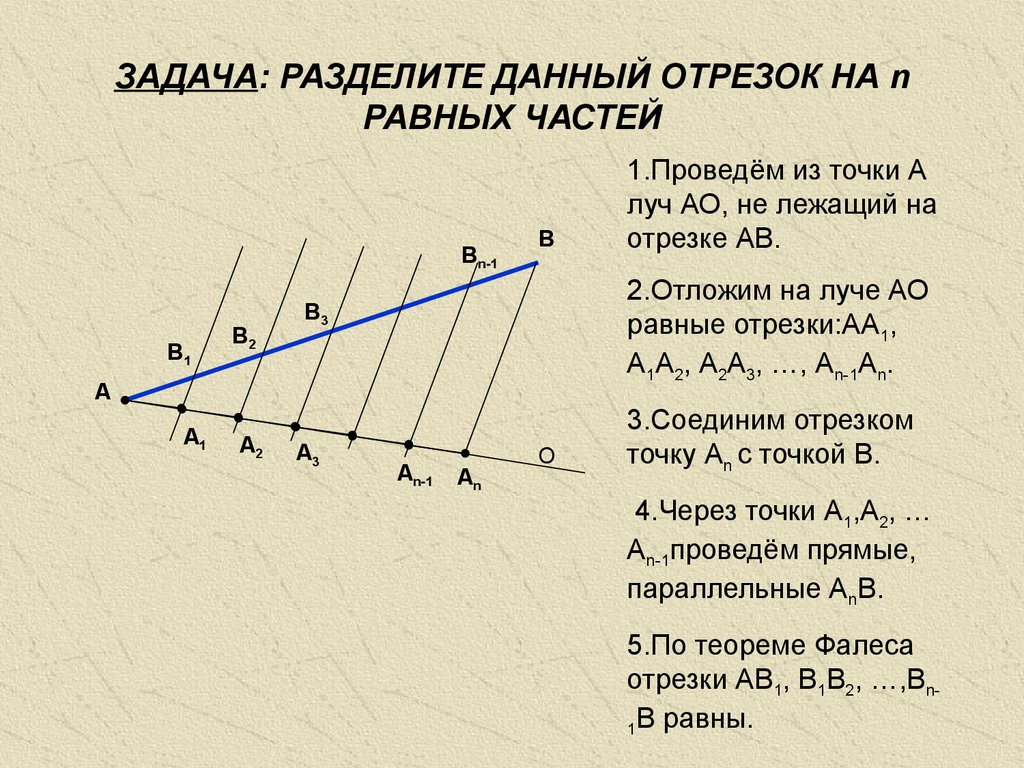 Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x₂ = kx₁ вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.

В результате на нашем листе бумаги получится карта местности. В силу теоремы Фалеса и свойств пропорций, все соотношения между расстояниями на бумаге будут в точности такими же, как и в действительности. Более того, все линии на бумаге окажутся параллельны соответствующим линиям на местности. Эта параллельность, конечно, нарушится, когда мы унесем наш лист куда-нибудь в другое место, однако углы между линиями сохранятся.

Параметр k, который мы использовали в нашем построении, называется масштабным коэффициентом или просто масштабом. Разумеется, он необязательно должен быть равен 1/1000. Он может, в принципе, принимать любое значение, важно лишь, чтобы это значение оставалось всё время неизменным в процессе построения карты.

На настоящих географических картах масштаб обязательно указывается в легенде, при этом вместо дробной черты обычно используется двоеточие. Например, масштаб 1:100 000 означает, что один сантиметр на карте соответствует 100000 сантиметрам (то есть одному километру) на местности.

Технические чертежи также всегда выполняются, как говорят,  в определенном масштабе. Масштаб 1:1 означает, что деталь начерчена в натуральную величину. А масштаб 10:1 говорит о том, что чертеж выполнен с десятикратным увеличением.

Замечание о параллельных прямых

Мы назвали параллельными такие несовпадающие прямые, угол между которыми равен нулю. Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.

Пусть на плоскости даны две прямые — x и n. Отметим на них произвольные точки — O и Y — и проведем через эти точки третью прямую — y. Если исходить из того, что угол между прямыми x и n не равен нулю, то смежные углы должны оказаться не равны друг другу. Пусть для определенности α₁ > α₂, как показано на рисунке.

 

Проведем через точку O прямую n₁, параллельную прямой n. Отметим на ней со стороны угла α₁ произвольную точку N₁ и проведем через эту точку прямую y₁, параллельную прямой y. При этом образуется параллелограмм, обозначенный на рисунке серым фоном.

 

Это значит, что прямая y₁ пересекает прямую n в некоторой точке, которую мы обозначим через N. Прямая x, заходя на «территорию» параллелограмма в точке O, обязательно должна где-то оттуда выйти. Она может это сделать либо через отрезок YN, либо через отрезок N₁N. В первом случае сразу становится очевидно, что прямая x пересекает прямую n. Рассмотрим второй случай. Обозначим точку пересечения прямой x и отрезка N₁N через X₁. Проведем через нее прямую n₂, параллельную прямой n. Эта прямая разбивает параллелограмм ON₁NY на два новых параллелограмма и пересекает прямую y в некоторой точке Y₁. Отметим на прямой x такую точку X, для которой выполняется соотношение

|OY1|	=	|OX1|	.
|OY|		|OX|

Проведем через точки X и Y прямую. Согласно рассмотренному выше следствию из теоремы Фалеса, эта прямая параллельна прямой n₂, а значит, образует нулевой угол с прямой n. Следовательно, новая прямая совпадает с прямой n, которая, таким образом, пересекает прямую x в точке X.

Мы теперь можем утверждать, что следующие три утверждения о несовпадающих прямых a и b, лежащих в одной плоскости, означают в точности одно и то же:

(1) Угол между прямыми a и b равен нулю.

(2) Прямые a и b нигде не пересекаются.

(3) Прямые a и b параллельны.

В традиционных курсах геометрии определением параллельности прямых служит утверждение 2. Мы выбрали для этих целей утверждение 1. Ведь гораздо проще определить угол между двумя прямыми, чем удостовериться, что они нигде не пересекаются на всём своем бесконечном протяжении.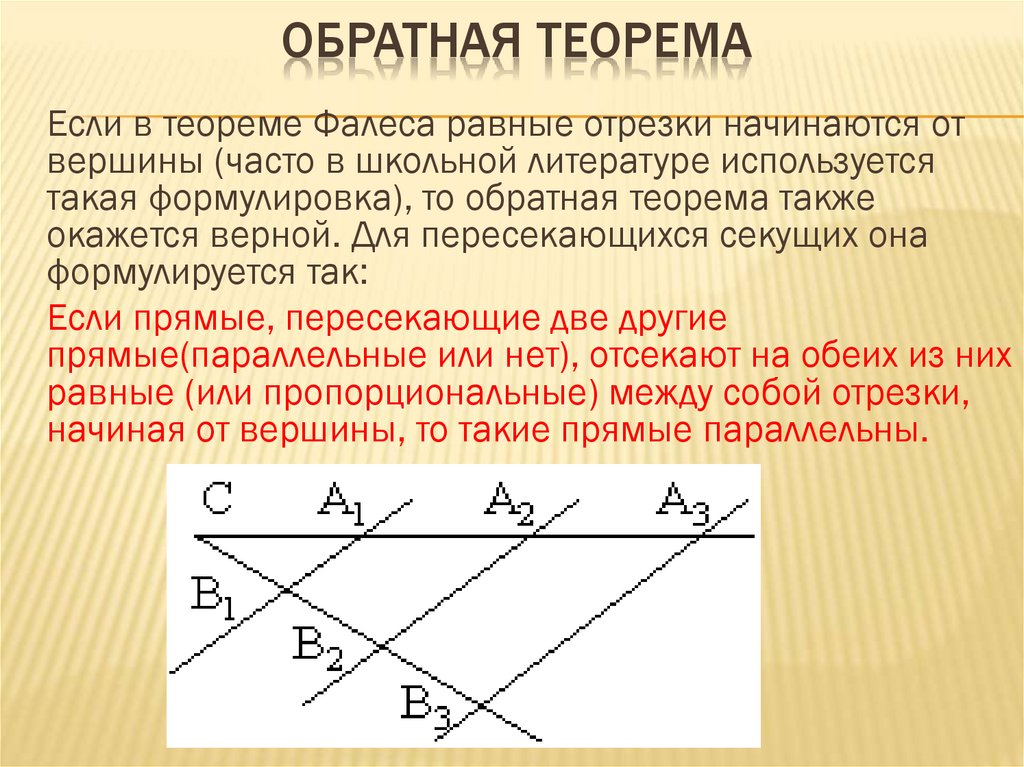

Конспект

1. Равенство вида x₁/x₂ = y₁/y₂ называется пропорцией. Числители пропорциональны знаменателям. Числитель и знаменатель одной дроби соотносятся так же, как числитель и знаменатель другой дроби. Эквивалентное равенство: x₁/y₁ = x₂/y₂.

2. Обобщенная теорема Фалеса. Пусть две произвольные прямые a и b пересекаются тремя параллельными прямыми. Тогда отрезки, отсекаемые на прямой a, пропорциональны соответствующим отрезкам, отсекаемым на прямой b.

3. Следствие 1. Пусть стороны угла с вершиной в точке O пересекаются двумя параллельными прямыми n₁ и n₂. Тогда отрезки, отсекаемые на прямых n₁ и n₂, соотносятся так же, как отрезки, отложенные на любой из сторон угла от точки O до соответствующих точек пересечения с прямыми n₁ и n₂.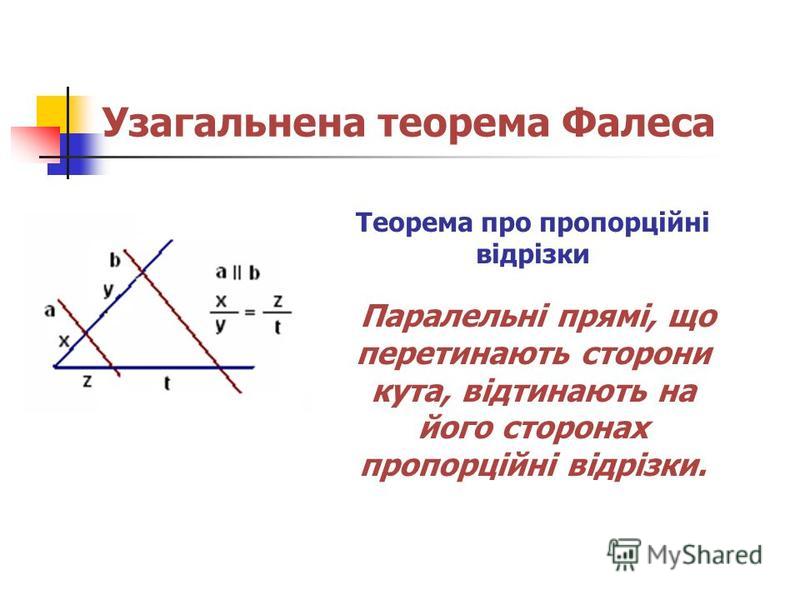

4. Следствие 2. Пусть на сторонах угла отложены от вершины отрезки таким образом, что отрезки на одной стороне пропорциональны отрезкам на другой. Тогда прямые, проходящие через соответствующие концы этих отрезков, параллельны друг другу.

5. На карте сохраняются все соотношения между расстояниями и все углы. Отношение расстояния между некоторыми двумя точками на карте к расстоянию между соответствующими точками на местности не зависит от выбора точек и называется масштабом.

6. Если угол между двумя прямыми, лежащими в одной плоскости, не равен нулю, то такие прямые обязательно пересекаются.

таил | Жизнь | Философия

Содержание

1.	Введение
2.	Личная жизнь Фалеса
3.	Какой вклад Фалес внес в философию?
4.	Геометрия
5.	Резюме
6.	Часто задаваемые вопросы о Фалесе Милетском
7.	Внешние ссылки

16 декабря 2020                

Время чтения: 3 минуты

Чем знаменит Фалес Милетский?

Фалес Милетский был греческим математиком, астрономом и досократическим философом. Он жил в 6-м и 5-м веках до нашей эры в Милете, который находится на территории современной Турции.

Он известен как один из легендарных Семи Волхвов. Известно, что он ввел идею научной философии.

Мало что известно о Фалесе, если не считать того, что говорили о нем другие философы, но он по-прежнему является важной фигурой как первый досократический философ.

Он также известен своим вкладом в математику. Он использовал геометрию для расчета высоты пирамид и расстояния между кораблем и берегом.

Его самое известное утверждение заключалось в том, что все в своей основе состоит из воды. Он считал, что Земля представляет собой плоскую массу, плавающую в огромном море.

Фалес проложил путь эпохе Сократа и классическим философам к установлению центральных тем западной философии.

Многие из его теорий и убеждений покажутся нам странными, но в то время они считались новаторскими.

 

Жизнь Фалеса — PDF

Если вы когда-нибудь захотите прочитать ее столько раз, сколько захотите, вот загружаемый PDF-файл, чтобы узнать больше.

📥

Жизнь Фалеса Милетского — PDF

Скачать

Читайте также:

• Гипатия Александрийская

---

Личная жизнь Фалеса

Даты жизни Фалеса неизвестны, но приблизительно оценены. Фалес, вероятно, родился около 625 г. до н.э. в Милете в Ионии, Малая Азия. (современная Турция)

Считается, что он никогда не был женат и не женился, потому что ему не нравилась мысль о детях. Хотя в более поздние годы, беспокоясь о семье, он усыновил своего племянника.

Говорят, что в какой-то момент своей жизни он посетил Египет, где узнал о геометрии. Его часто называют первым греческим математиком.

Он хотел оторваться от мифологии и объяснить мир естественными, практическими теориями и гипотезами.

Фалес также был наблюдательным ученым. Ему удалось успешно предсказать солнечное затмение 28 мая 585 г. до н.э., и по сей день мы не знаем, как он это сделал.

Фалес умер в возрасте 78 лет во время 58-й Олимпиады, где он перенес тепловой удар во время просмотра игр.

---

Какой вклад Фалес внес в философию?

Фалеса считали уникальным за то, что он отверг греческий пантеон богов и искал предсказуемые законы в природе, подобно современным ученым.

Другими словами, Фалес считал мир рациональным, упорядоченным и постижимым посредством исследования.

По его словам, под всем должно быть что-то объединяющее. Этим Фалес хотел объяснить жизнь.

Из всех элементов Фалес определил воду как объединяющую силу. Но почему вода? Мы подумаем.

В древние времена законы физики плохо понимались. Реки текут в моря, волны разбиваются, приливы и отливы приходят и отливают, а так как они не знали гравитации, вода, казалось, двигалась самостоятельно.

Кроме того, каждому живому существу нужна вода. Мы можем прожить месяцы без еды, но только три дня без воды.

Если все живое нуждается в воде, вода должна быть важным компонентом жизни. Таким образом, вода может объяснить движение, энергию, происхождение земли и способность веществ трансформироваться.

Большинство досократических философов, пришедших после него, последовали за ним в объяснении природы как проистекающей из единства всего, вместо того чтобы прибегать к мифологическим и сверхъестественным объяснениям.

Конечно, теперь мы знаем, что Фалес сильно ошибался. Тем не менее, он начал мыслить научно и рационально еще в те времена, когда люди считали, что за все несут ответственность боги.

Геометрия

Фалес также был известен своими нововведениями в области геометрии. У него были как теоретические, так и практические знания и понимание геометрии.

Фалес изучал и понимал прямоугольные треугольники и подобные им треугольники. Он также использовал свои знания на практике.

Фалес измерял высоту пирамид по их теням в тот момент, когда его собственная тень равнялась его высоте. Он также измерял расстояния кораблей в море с помощью геометрии.

 

Фалесу Милетскому приписывают открытие 5 геометрических теорем:

• Диаметр окружности делится пополам
• Углы, противолежащие двум равным сторонам треугольника, равны
• Противолежащие углы двух пересекающихся углов равны
• Угол, вписанный в полуокружность, является прямоугольным треугольником
• Мы можем определить треугольник, если у нас есть длина его основания и два угла при основании даны

Теорема Фалеса

Фалес очень хорошо известен своей теоремой Фалеса, которую до сих пор преподают в школах.

Теорема Фалеса утверждает, что если A, B и C являются различными точками на окружности, где прямая AC является диаметром, то угол \(∠ABC\) является прямым.

Один интересный факт заключается в том, что Фалес, как говорят, принес быка в жертву греческому богу в знак благодарности за открытие этой теоремы.

Основная теорема о пропорциональности

Фалес также ввел основную теорему о пропорциональности, которая является одним из широко используемых понятий в геометрии.

Он гласит, что если провести прямую, параллельную одной стороне треугольника, пересекающую две другие стороны в разных точках, то две другие стороны делятся в том же отношении.

На приведенном выше рисунке PQ проведен параллельно стороне YZ треугольника XYZ. Таким образом, согласно теореме, отношение XP и PY будет равно отношению XQ и QZ.

---

Резюме

Фалес считается заслуживающим доверия и вдумчивым человеком, несмотря на то, что он ошибался во многих вещах.

Фалес использовал свои небольшие знания, чтобы выдвинуть хорошие теории. Благодаря ему более поздние досократики сформировали новые представления о мире, что в конечном итоге привело к Сократу, человеку, навсегда изменившему западный мир. Изучение математики и ее истории — очень обогащающее путешествие. Присоединяйтесь к нам в обогащающем путешествии, подпишитесь на бесплатную пробную версию.

---

О Cuemath

Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-занятия для ученых и развития навыков, а их приложение Mental Math для iOS и Android представляет собой универсальное решение для дети для развития нескольких навыков. Ознакомьтесь со структурой оплаты Cuemath и подпишитесь на бесплатную пробную версию.

---

Часто задаваемые вопросы о Фалесе из Милета (FAQ)

Почему Фалес известен?

Фалес известен как один из семи мудрецов. Он известен главным образом своей космологией воды как сущности всей материи и тем, что Земля представляет собой плоский диск, плавающий в море.

Где учился Фалес?

Говорят, что в какой-то момент своей жизни Фалес посетил Египет, где узнал о геометрии. Его также часто называют первым греческим математиком и первым в мире философом.

Является ли Фалес первым философом?

Да, Фалес считается первым философом.

Что открыл Фалес?

Фалесу Милетскому приписывают открытие 5 геометрических теорем:

• Круг делится пополам своим диаметром
• Углы, противолежащие двум равным сторонам треугольника, равны
• Противолежащие углы двух пересекающихся углов равны
• Угол, вписанный в полуокружность, является прямоугольным треугольником
• Мы можем определить треугольник, если у нас есть длина его основания и два угла при основании даны

Талес | Природа математики

Фалес Милетский (624 – 546 до н.э.)

Фалес Милетский был одним из семи греческих мудрецов и считался Аристотелем первым философом греческой традиции. Философ ХХ века Бертран Рассел идет дальше и говорит, что западная философия начинается с Фалеса. Насколько нам известно, Фалес был первым математиком, увидевшим необходимость дедуктивных рассуждений. Другие жители древнего мира, например, вавилоняне и египтяне, определенно знали некоторые жемчужины геометрии и успешно использовали их в технике и промышленности. Однако именно Фалес хотел доказать эти факты с помощью дедуктивных рассуждений, начиная с набора аксиом и делая выводы посредством дедукции. Фалес тоже хотел понять мир не через мифологию, а через человеческий разум. Он часто ассоциируется с фразой «Все есть вода». Для современного уха это звучит нелепо и слишком упрощенно. Однако мы также можем рассматривать это выражение как означающее, что мир может быть понят людьми через несколько основных принципов. Это был огромный отход от мышления древнего мира. К сожалению, мы не можем прочитать ни одного из оригинальных сочинений Фалеса, так как они утеряны во времени. То, что мы знаем о нем и его работах, мы получили от других греческих философов. Узнайте больше о Фалесе.

Ниже приведены четыре элементарных факта, которые мы все изучаем в старшей школе и которые приписываются Фалесу, хотя есть некоторые споры о том, какие из этих фактов Фалес фактически доказал в деталях (см. книгу Хита, A History of Greek Mathematics, Vol I ). который является частью назначенного чтения). Эти факты были известны другим гораздо раньше, но Фалес видел необходимость поставить эти факты на прочную основу, т. е. доказать их!

• Круг делится любым диаметром на две равные части.

• Углы при основании равнобедренного треугольника равны .

• При пересечении двух прямых противоположные углы равны.

• Два треугольника равны, если у них одна сторона и два угла равны.

Следующая теорема о подобных треугольниках, которую вы изучаете в средней школе, также приписывается Фалесу.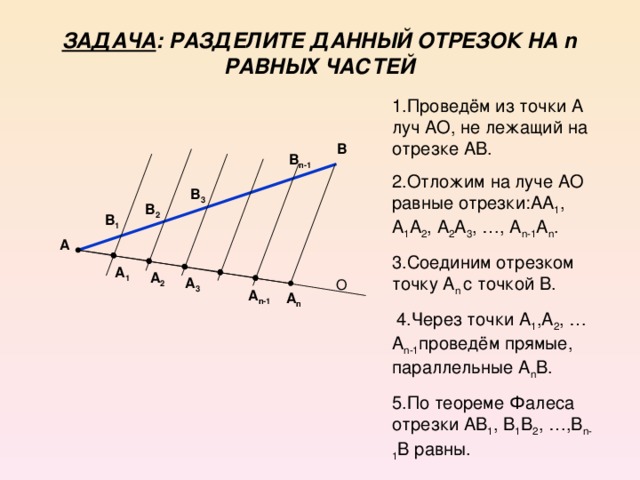

Теорема : Рассмотрим следующий треугольник ABC вместе с отрезком DE, параллельным BC. Тогда |AB|/|AD| = |AC|/|AE|.

Доказательство: Ссылка. Я привожу доказательство ниже.

Нарисуйте отрезок от B до E и еще один от C до E. Затем нарисуйте отрезок от E до F, перпендикулярный AB, и еще один отрезок от D до G, перпендикулярный AC. См. рисунок ниже.

Площадь(ADE) = 1/2 |AD| |ЭФ| = 1/2 |AE| |ДГ| (база умножается на высоту)

Площадь (BDE) = 1/2 |BD| |ЭФ|

Площадь (CDE) = 1/2 |CE| ГД|

Таким образом, площадь(ADE)/площадь(BDE) = |AD|/|BD| (1)

и площадь(ADE)/площадь(CDE) = |AE|/|CE| (2)

Также обратите внимание, что

Площадь(BDE) = Площадь(CDE) (3)

, поскольку эти два треугольника имеют одно и то же основание DE и, поскольку DE || до н.э. они имеют одинаковую высоту.

Комбинируя уравнения (1), (2), (3), мы видим, что

|AD|/|BD| = |AE|/|CE|

Выполняя обратные обе части, мы получаем

|BD|/|AD| = |CE|/|AE|

и так, прибавляя по 1 к обеим сторонам получаем

|BD|/|AD| + |AD/|AD| = |CE|/|AE| + |АЕ|/|АЕ|

, что означает, что

(|BD| + |AD|)/|AD| = (|CE| + |AE|)/|AE|

Но это означает, что

|AB|/|AD| = |AC|/|AE|

КЭД.

Вот еще одна жемчужина Фалеса.

Теорема : Если AC — диаметр окружности, а B — любая другая точка окружности (кроме A и C), то угол ABC — прямой угол.

Доказательство : Рассмотрим следующий рисунок:

Так как OB = OC (поскольку все они являются радиусами одной окружности), то треугольник OBC является равнобедренным треугольником и, таким образом, согласно одному из Фалесов ранее В результате углы OBC и OCB равны. Поскольку OB = OA, то, опять же по предыдущей теореме Фалеса, углы OAB и ABO равны. Поскольку сумма углов треугольника, в частности треугольника ABC, должна составлять 180 градусов, должно быть так, что a + (a + b) + b = 180. Это означает, что 2 a + 2 b = 180. или, что то же самое, a + b = 90. Это показывает, что угол при вершине B равен 90 градусов. КЭД .

Конечно, в доказательстве этой теоремы отсутствует доказательство того факта, что (внутренние) углы любого треугольника составляют в сумме 180 градусов (или, на языке Фалеса, «сумма двух прямых углов»).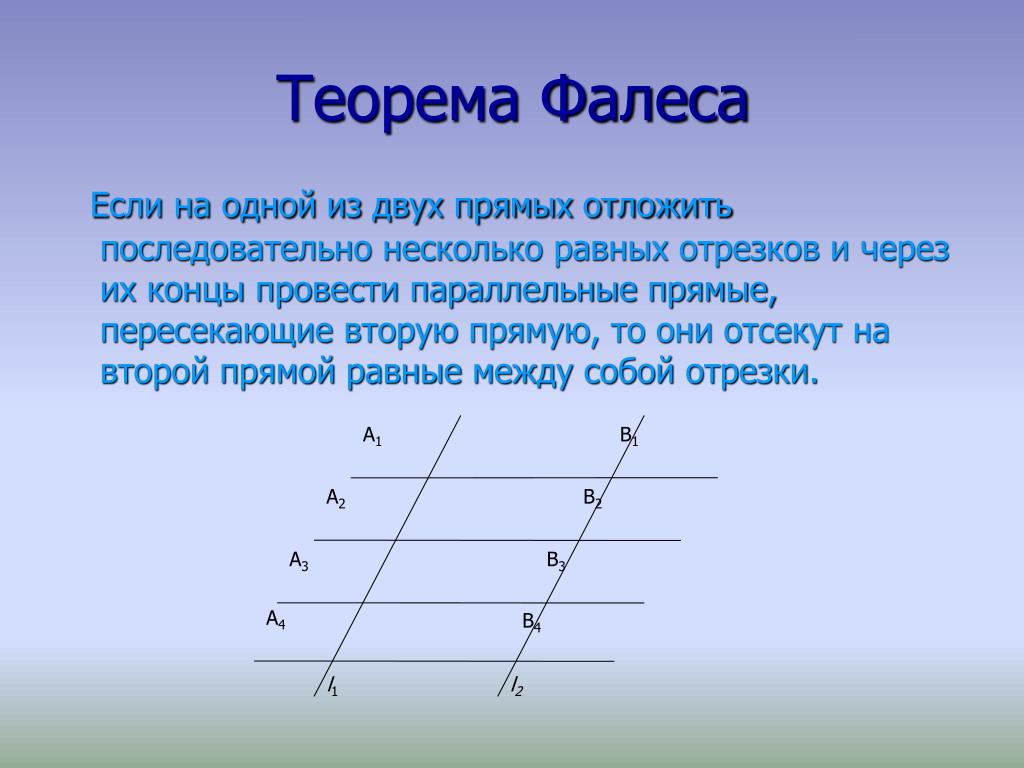 Вот доказательство этого драгоценного камня: обозначьте углы вашего треугольника A, B, C и нарисуйте параллельные линии L и M на изображении ниже

Теперь используйте некоторые основные факты об углах (заполните детали), и вы можете см., что A + B + C образует угол 180 градусов на приведенном выше рисунке.

Следует также отметить, что существует обратная теорема Фалеса.

Обратное к теореме Фалеса : Гипотенуза прямоугольного треугольника равна диаметру описанной окружности.

Доказательство . Возьмите прямоугольный треугольник и переверните его по диагонали, чтобы получился параллелограмм. Обратите внимание, что две диагонали будут пересекаться пополам. Точка пересечения этих двух диагоналей будет центром описанной окружности, очевидно, с гипотенузой в качестве диагонали. КЭД .

Вот хорошее следствие этой теоремы, которое говорит нам, как построить касательную к окружности, используя только линейку и циркуль. Мы поговорим об этом подробнее в разделе, посвященном делению угла пополам и трисечению угла позже или . Прямо сейчас просто вспомните, как разделить угол пополам с помощью линейки и циркуля. Возможно, вам придется просмотреть свои школьные заметки.

Следствие : Имея окружность C и точку P вне окружности, можно построить, используя только линейку и циркуль, касательную к этой окружности, которая проходит через P.

Proo f:

Проведите линию из центра O окружности C в точку P. Теперь с помощью линейки и циркуля проведите середину M линии OP. Теперь нарисуйте окружность с центром в точке M. Таким образом, окружность пересечет исходную окружность C в некоторой точке T. По теореме Фалеса (которую мы только что сделали) треугольник OTP имеет прямой угол в точке T. Согласно определению касательной, это говорит что линия PT касается нашей исходной окружности C. QED .

Мы закончим наш визит к Фалесу приписываемым ему прекрасным приложением, которое находит расстояние от положения на суше до корабля в море. Предположим, что мы находимся на суше в точке А, а корабль выходит в море в точке В.

Как найти расстояние от А до В. Вот остроумный способ сделать это.

– Выберите точку D (на берегу) так, чтобы AD была перпендикулярна AB. Базовая линейка и циркуль говорят, что мы можем это сделать.

– Выберите точку E (снова на берегу) так, чтобы ED был перпендикулярен AB. Опять же, базовая линейка и циркуль говорят, что мы можем это сделать.

–Найти середину M AD. Опять линейка и циркуль.

–Прямая, проходящая через M и B, пройдет через некоторую точку P на прямой ED.

–Рассмотрите треугольники PDM и MBA. Эти треугольники имеют прямые углы при D и A. Согласно Фалесу, эти треугольники имеют равные углы при вершине M. Поскольку M является серединой DA, мы имеем DM = MA. Таким образом, опять же по Фалесу, эти два треугольника конгруэнтны.

– Таким образом, расстояние от A до B (которое мы хотим вычислить) равно расстоянию от P до D (которое мы можем измерить).