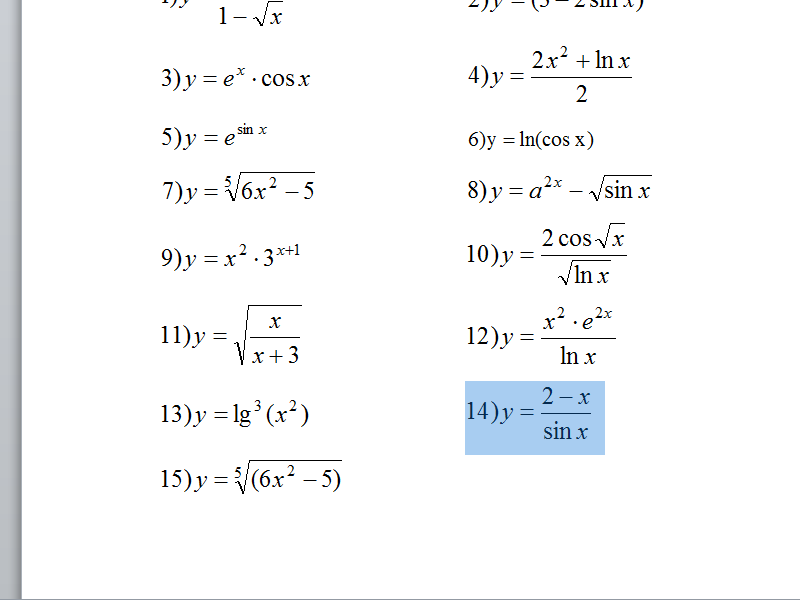Производная от 4х в квадрате
В течение урока предоставляются сведения о производных основных математических функций, свойствах производных, демонстрируется решение заданий с применением знаний о свойствах производных и производных основных функций. Видеоурок начинается с представления его темы. Вводится понятие формул дифференцирования — формул, необходимых для отыскания производных определенных функций. Далее демонстрируется применение изученных формул для нахождения значения производных функций. В примере 1 дается 6 функций, предел которых нужно определить:.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Квадрат производной
Производная арккотангенса - Вычисление производных
- Производная тангенса
- Найдите точку максимума функции у=корень из 4-4х-х^2
- Таблица производных простых функций
- Производная функции
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Производная 5 Экспонента и натуральный логарифм.
Квадрат производной
Математический Анализ. Определение производной. Процесс нахождения производной называется дифференцированием. Производная функции в некоторой точке характеризует скорость изменения функции в этой точке. Перейдем к более строгой формулировке: Определение производной.
Пример 1. Пример 2. Пример 3. Пример 4. Пример 5. Пример 6. Пример 7. Пример 8. Пример 9. Пример Математический анализ. Пределы и непрерывность. Приложения производной. Последовательности и ряды. Двойные интегралы. Тройные интегралы.
Криволинейные интегралы. Поверхностные интегралы. Ряды Фурье. Дифференциальные уравнения. Уравнения 1-го порядка. Уравнения 2-го порядка. Уравнения N -го порядка. Системы уравнений. Формулы и таблицы. В примерах ниже мы выведем производные основных элементарных функций, используя приведенное формальное определение производной.
Эти функции составляют основной костяк в том смысле, что производные других функций можно выразить уже через них, применяя правила действий с производными.
Найдем производную заданной функции, используя определение производной. Выведем производную логарифмической функции, пользуясь лишь определением и не применяя никаких других правил вычисления производной.
Производная арккотангенса
Данный онлайн калькулятор позволяет находить производную функции второго порядка. Производная служит обобщенным понятием скорости изменения функции. Нахождение производной функции называется дифференцированием функции. Так как производная функции также является функцией, то эту функцию можно дифференцировать еще раз. Вторая производная определяет скорость изменения скорости, другими словами, ускорение. Нахождение производной второго порядка может быть использовано, например, для анализа выпуклости функций.
Онлайн калькулятор. Вычисляет производную заданной функции.
Вычисление производных
Статья предоставлена специалистами сервиса Автор Автор24 — это сообщество учителей и преподавателей, к которым можно обратиться за помощью с выполнением учебных работ.
Квадратом производной является операция возведения результата вычисления производной в степень 2. Задай вопрос специалистам и получи ответ уже через 15 минут! Главная Методические указания Блог для фрилансеров Статьи о заработке онлайн Работа для репетиторов Работа для преподавателей Калькуляторы Мне нужна помощь с выполнением работы Вы будете перенаправлены на Автор Все предметы Математика Производная и дифференциал Квадрат производной. Статья предоставлена специалистами сервиса Автор24 Автор24 — это сообщество учителей и преподавателей, к которым можно обратиться за помощью с выполнением учебных работ. Прочитать как работает сервис.
Производная тангенса
Зарегистрироваться Забыли пароль? Воскресенье, 04 марта Помогите решить. URL Профиль. Ни о чем не нужно говорить, ничему не следует учить, и печальна так и хороша темная звериная душа.
Если аргумент арккотангенса отличен от , то производную ищем как производную сложной функции , то есть по формуле:. Найти производную функции.
2
Вы искали: производная функции онлайн. Исследовать функцию при помощи I производной. Артём Давыдов. Решено Производная функции. Спасибо всем ответившим. Вопрос задан анонимно.
Таблица производных простых функций
Разумеется, неплохо бы ещё иметь представление о производной вообще. О том, что такое производная, и как работать с таблицей производных — доступно рассказано в предыдущем уроке. Здесь же мы займёмся правилами дифференцирования. Дифференцирование — это операция нахождения производной. Более за этим термином ничего не кроется. Выражение «правила дифференцирования» относится к нахождению производной от арифметических операций.
f'(x) Найти производную функции онлайн. Помимо производной вы увидете на сравнение графика функции и графика производной функции.
Производная функции
Математический Анализ. Определение производной. Процесс нахождения производной называется дифференцированием. Производная функции в некоторой точке характеризует скорость изменения функции в этой точке.
Тогда предел разностного отношения. Таким образом,. Если функция f x имеет производную в точке x, то эта функция называется дифференциируемой в этой точке. Если функция f x имеет производную в каждой точке некоторого промежутка, то говорят, что эта функция дифференцируема на этом промежутке. Операция нахождения производной называется дифференцированием.
Account Options Войти.
Во вкладке «Записи курсов» можно скачать разборы ранних ларинских вариантов. Найдите наименьшее значение функции. Под знаком квадратного корня находится всегда положительный квадратный трёхчлен дискриминант отрицателен. Чем меньше его значение, тем меньше значение функции. Найдём наименьшее значение квадратного трёхчлена наша задача тремя способами.
Поиск по сайту. Главная страница. Лекционный материал. Лабораторный практикум.
10 класс. Алгебра. Производная. Применение производной к исследованию функции. — Исследование функции y=(x³-4)÷(x-1)³ и сопутствующие задачи.
Комментарии преподавателяИсследование функции и сопутствующие задачи
Дано: .
Надо исследовать эту функцию, построить график, найти промежутки монотонности, максимумы минимумы и какие задачи сопутствуют знанию об этой функции.
Сначала полностью воспользуемся той информацией, которая дает функция без производной.
1. Найдем интервалы знакопостоянства функции и построим эскиз графика функции:
1) Найдем .
2) Корни функции: , отсюда
3) Интервалы знакопостоянства функции (см. рис.1):
Рис. 1. Интервалы знакопостоянства функции.
Теперь знаем, что на промежутке и график находится над ось Х, на промежутке — под осью Х.
2. Построим график в окрестности каждого корня (см. рис.2).
Рис. 2. График функции в окрестности корня.
3. Построим график функции в окрестности каждой точки разрыва области определения. Область определения разрывается в точке . Если значение близко к точке , то значение функции стремится к (см. рис.3).
Рис. 3. График функции в окрестности точки разрыва.
4. Определим, как ведет график в окрестности бесконечно удаленных точек:
Запишем с помощью пределов
. Важно, что при очень больших , функция почти не отличается от единицы.
Найдем производную, интервалы ее знакопостоянства и они будут интервалами монотонности для функции, найдем те точки, в которых производная равна нулю, и выясним, где точка максимума, где точка минимума.
Отсюда, . Эти точки являются внутренними точками области определения. Выясним, какой знак производной на интервалах, и какая из этих точек является точкой максимума, а какая — точкой минимума (см.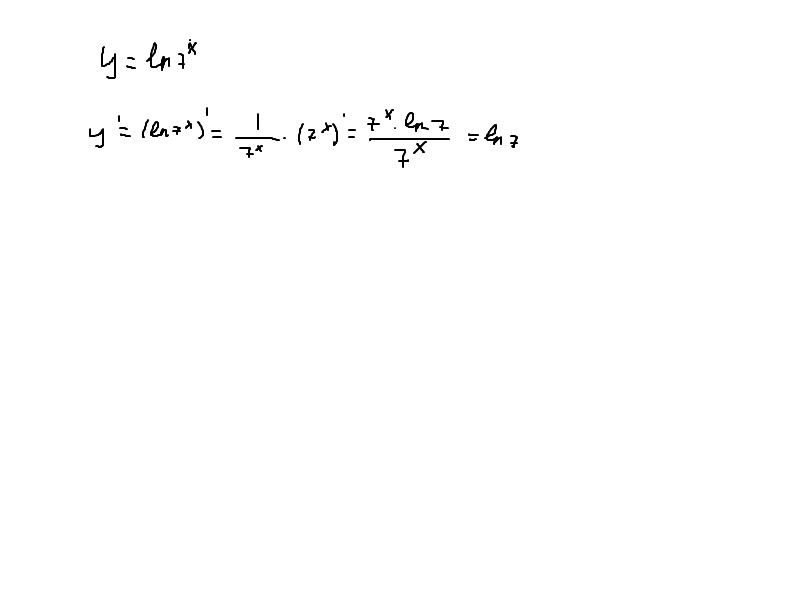
рис.4).
Рис. 4. Интервалы знакопостоянства производной.
Из рис. 4 видно, что точка — точка минимума, точка — точка максимума. Значение функции в точке равно . Значение функции в точке равно 4. Теперь построим график функции (см. рис.5).
Рис. 5. График функции .
Таким образом, построили график функции. Опишем его. Запишем интервалы, на которых функция монотонно убывает: , — это те интервалы, где производная отрицательна. Функция монотонно возрастает на интервалах и . — точка минимума, — точка максимума.
Задача.
Найти число корней уравнения в зависимости от значений параметра.
Решение.
1. Построить график функции. График этой функции построен выше (см. рис.5).
2. Рассечь график семейством прямых и выписать ответ (см. рис.6).
Рис. 6. Пересечение графика функции с прямыми .
Ответ:
1) При — одно решение.
2) При — два решения.
3) При — три решения.
4) При — два решения.
5) При — три решения.
6) При — два решения.
7) При — одно решение.
Таким образом, решили одну из важных задач, а именно, нахождение числа решений уравнения в зависимости от параметра . Могут быть разные частные случаи, например, при каком будет одно решение или два решения, или три решения. Заметим, что эти частные случаи, все ответы на эти частные случаи содержатся в общем ответе.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/issledovanie-funktsii-y-x-sup-3-sup-4-247-x-1-sup-3-sup-i-soputstvuyuschie-zadachi
http://www.youtube.com/watch?v=dU0kgE-XKV0
http://www.youtube.com/watch?v=Ig81GEJE2YI
http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf
http://vklasse.org/10-klass/reshebniki/algebra/ag-mordkovich-2009-zadachnik
http://ege-ok.
ru/2013/11/12/issledovanie-funktsii-i-postroenie-grafika
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Производная от ln(4x) — DerivativeIt
Производная от ln(4x) равна 1/x
Как вычислить производную от ln(4x)
используется для вычисления производной от ln(4x).
Первый метод заключается в использовании цепного правила для производных.
Второй метод заключается в использовании свойств журналов для записи ln(4x) в форме, которая дифференцируема без необходимости использования цепного правила.
Нахождение производной от ln(4x) с помощью цепного правила
Цепное правило полезно для нахождения производной выражения, которое можно было бы дифференцировать, если бы оно было выражено в x, но в форме другого выражения, которое могло бы также быть дифференцированным, если бы он стоял сам по себе.
В этом случае:
- Мы знаем, как дифференцировать 4x (ответ 4)
- Мы знаем, как дифференцировать ln(x) (ответ 1/x)
Это означает, что цепное правило позволит нам провести дифференцирование функции ln(4x).
Чтобы выполнить дифференцирование, цепное правило говорит, что мы должны дифференцировать выражение, как если бы оно было выражено только через x, если мы затем умножаем этот результат на производную того, чем на самом деле выражено выражение (в данном случае производная от 4x).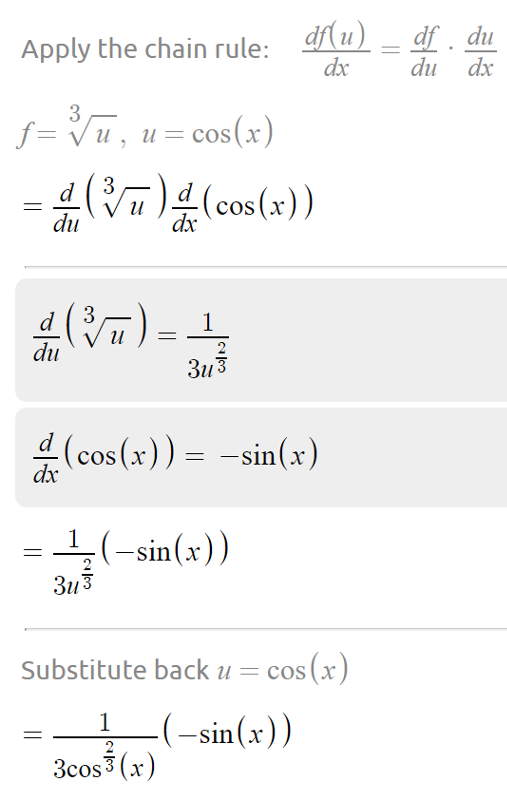
Использование цепного правила для нахождения производной от ln(4x)
ln(4x) представляет собой стандартную логарифмическую функцию ln(x), за исключением того, что у нее нет x в качестве аргумента, вместо этого она имеет другую функция х (4х).
Назовем функцию в аргументе g(x), что означает:
g(x) = 4x
Отсюда следует, что:
ln(4x) = ln(g(x))
Итак если функция f(x) = ln(x) и функция g(x) = 4x, то функция ln(4x) может быть записана как составная функция.
f(x) = ln(x)
f(g(x)) = ln(g(x)) (но g(x) = 4x)
f(g(x)) = ln(4x )
Определим эту составную функцию как F(x):
F(x) = f(g(x)) = ln(4x)
Мы можем найти производную от ln(4x) (F'(x)) с помощью цепного правила.
Цепное правило:
Для двух дифференцируемых функций f(x) и g(x)
Если F(x) = f(g(x))
Тогда производная F (x) есть F'(x) = f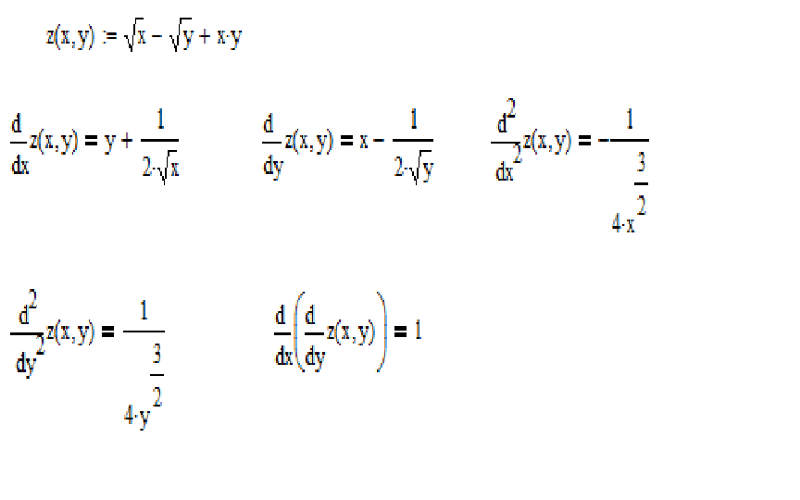'(g(x)).
g'(x)
Теперь мы можем просто подставить f(x) и g(x) в цепное правило.
Теперь мы можем просто подставить f(x) и g(x) в цепное правило. Но прежде чем мы это сделаем, кратко повторим производную натурального логарифма.
Производная ln(x) по x равна (1/x)
Производная ln(s) по s равна (1/s)
Аналогичным образом производная ln(4x ) по отношению к 4x составляет (1/4x).
Мы будем использовать этот факт как часть цепного правила, чтобы найти производную ln(4x) относительно x .
Как найти производную от ln(4x) с помощью цепного правила:
| F'(x) | = f'(g(x)).g'(x) | Определение цепного правила |
| = f'(g(x)).(4) | g(x) = 4x ⇒ g'(x) = 4 | 3 9 0 ( /4x).4 | f(g(x)) = ln(4x) ⇒ f'(g(x)) = 1/4x (производная ln(4x) по 4x равно (1/4x)) |
| = 1/x |
Используя цепное правило, мы находим, что производная ln(4x) равна 1/x
Наконец, небольшое замечание по синтаксису и обозначениям: ln(4x) иногда записывается в приведенных ниже формах (с производной согласно приведенным выше вычислениям).
Просто имейте в виду, что не все приведенные ниже формы математически правильны.
| LN4X | ► Производная LN4X = 1/x |
| LN 4x | ► Произволение LN 4x = 1/x |
| LN 4 x | ► x |
| LN 4 x | ► x19 /x |
Верхний наконечник
Производную от выражений можно обобщить в виде ln(ax) (где a — постоянное значение):
Производная ln(ax) = 1/x
константа, производная от ln(ax) всегда равна 1/x)
Нахождение производной от ln(4x) с использованием свойств логарифма
Поскольку ln — натуральный логарифм, применяются обычные свойства логарифмов.
Свойство произведения бревен утверждает, что ln(xy) = ln(x) + ln(y). Другими словами, получение журнала продукта равно суммированию журналов каждого члена продукта.
Поскольку 4x является произведением 4 и x, мы можем использовать свойства логарифмов, чтобы переписать ln(4x):
f(x) = ln(4x) = ln(4) + ln(x)
Как найти производную от ln(4x), используя свойство произведения бревен
Вторая производная ln(4x)
