Найти площадь трапеции онлайн
Пример решили: 1192 раза Сегодня решили: 0 раз
Введите длины сторон трапеции и высоту
Сторона a Сторона b Высота h
Вычисление площади трапеции по заданным основаниям и высоте
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Трапеция – это четырёхугольник, у которого противоположные стороны параллельны, а две другие
непараллельны. Параллельные стороны называются основаниями трапеции, а непараллельные – боковыми сторонами.
В любой трапеции середины оснований, пересечения диагоналей, пересечения продолжения боковых сторон лежат на одной прямой.
Существуют следующие виды трапеций (частные случаи):
- Равнобокая трапеция – трапеция, имеющая равные боковые стороны и углы при основаниях;
- Прямоугольная трапеция – трапеция, которая имеет прямой угол.

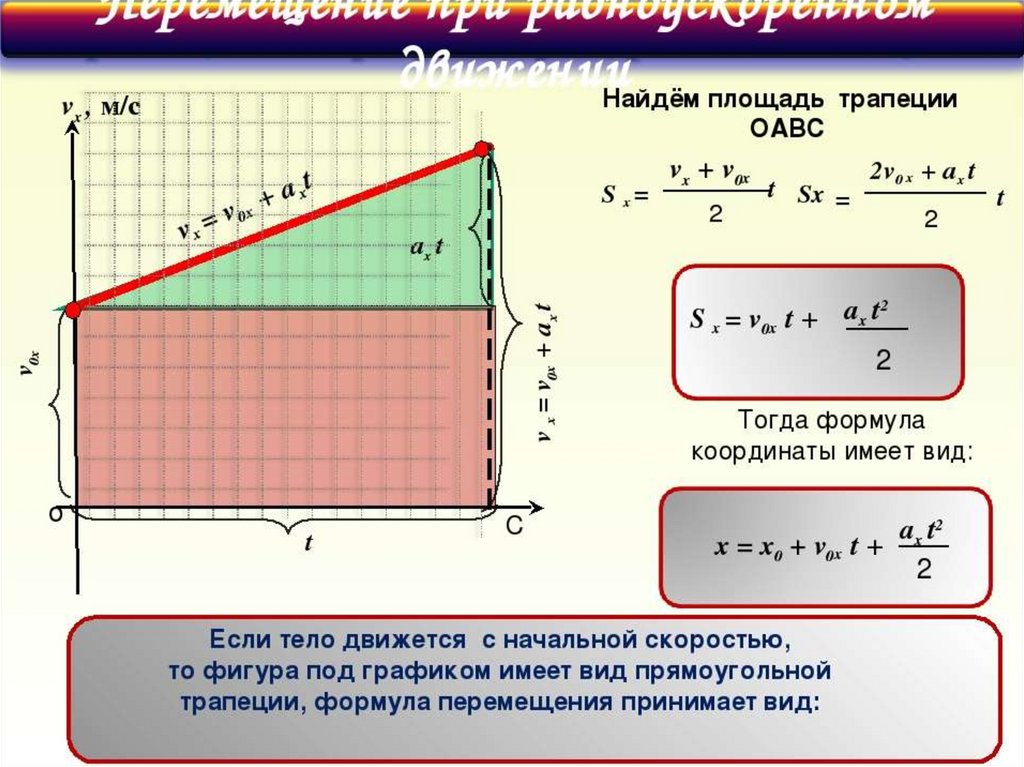
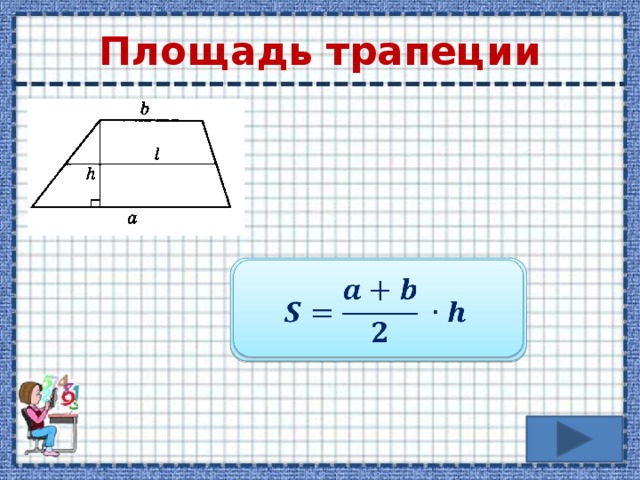
Площадь трапеции можно найти как произведение высоты на половину суммы оснований:
$$S = h \cdot {a + b \over 2}$$
Примеры решений
- Найти площадь трапеции с высотой 5 и длинами оснований 7 и 11
Посмотреть решениеДано:
$$ | BC | = 7 $$
$$ | AD | = 11 $$
$$ h = 5 $$
Решение:
$$ S = \frac{1}{2} \cdot h \cdot (|BC| + |AD|) = \frac{1}{2} \cdot 5 \cdot (7 + 11) = 45 $$
Ответ:
$$ S = 45 $$
- Найти площадь трапеции, если длины оснований равны 6 и 8, длина боковой стороны равна 10, а угол между основанием и боковой стороной равен 60°.
Посмотреть решениеДано:
$$ | BC | = 6 $$
$$ | AD | = 8 $$
$$ | AB | = 8 $$
$$ \angle BAD = 60^{ \circ }$$
Решение:
Предварительно вычислим высоту трапеции:
$$ h = |AB| \cdot sin \angle BAD = 10 \cdot sin 60^{ \circ } $$
Следовательно:
$$ S = \frac{1}{2} \cdot h \cdot (|BC| + |AD|) = \frac{1}{2} \cdot 8.
 {\circ} = 5 $$
{\circ} = 5 $$Следовательно:
$$ S = \frac{1}{2} \cdot h \cdot (|BC| + |AD|) = \frac{1}{2} \cdot 5 \cdot (8 + 12) = 50 $$
Ответ:
$$ S = 50 $$
- Найти площадь равнобокой трапеции, в которой боковая сторона равна 8. При этом, высота в два раза короче боковой стороны, боковая сторона в два раза короче короткого основания, а короткое основание в два раза короче длинного основания трапеции.
Посмотреть решениеДано:
$$ h = \frac{1}{2} \cdot |AB| $$
$$ | AB | = \frac{1}{2} \cdot |BC| $$
$$ | BC | = \frac{1}{2} \cdot |AD| $$
$$ | AB | = |CD| = 8 $$
Решение:
Предварительно вычислим длины оснований трапеции:
$$ |BC| = 2 \cdot |AB| = 16 $$
$$ |AD| = 2 \cdot |BC| = 32 $$
теперь найдем высоту трапеции:
$$ h = \frac{1}{2 } \cdot |AB| = 5 $$
Следовательно:
$$ S = \frac{1}{2} \cdot h \cdot (|BC| + |AD|) = \frac{1}{2} \cdot 4 \cdot (16 + 32) = 96 $$
Ответ:
$$ S = 96 $$
- Основания трапеции равны 10 и 20, соответственно.
 Площадь трапеции равняется 60. Чему равна высота трапеции?
Площадь трапеции равняется 60. Чему равна высота трапеции?
Посмотреть решениеДано:
$$ S = 60 $$
$$ | BC | = 10 $$
$$ | AD | = 20 $$
Решение:
Так как значения площади и длин оснований целочисленные значения, то можно предположить, что длина высоты тоже целое (точнее, натуральное) число.Подставляя последовательно в формулу вычисления площади трапеции
$$ S = \frac{1}{2} \cdot h \cdot (|BC| + |AD|) = 15 \cdot h $$
различные значения высоты, получим:
$$ 60 = 15 \cdot 1 $$
$$ 60 = 15 \cdot 2 $$
$$ 60 = 15 \cdot 3 $$
$$ 60 = 15 \cdot 4 $$
Так как последнее равенство верное, то высота трапеции равняется 4
Ответ:
$$ h = 4 $$
Попробуйте другие сервисы
Найти площадь треугольника
Найти площадь поверхности параллелепипеда
Найти площадь поверхности куба
Найти площадь ромба
Найти площадь кругового сектора
Расчет площади трапеции онлайн.
 Площадь трапеции
Площадь трапецииИ . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.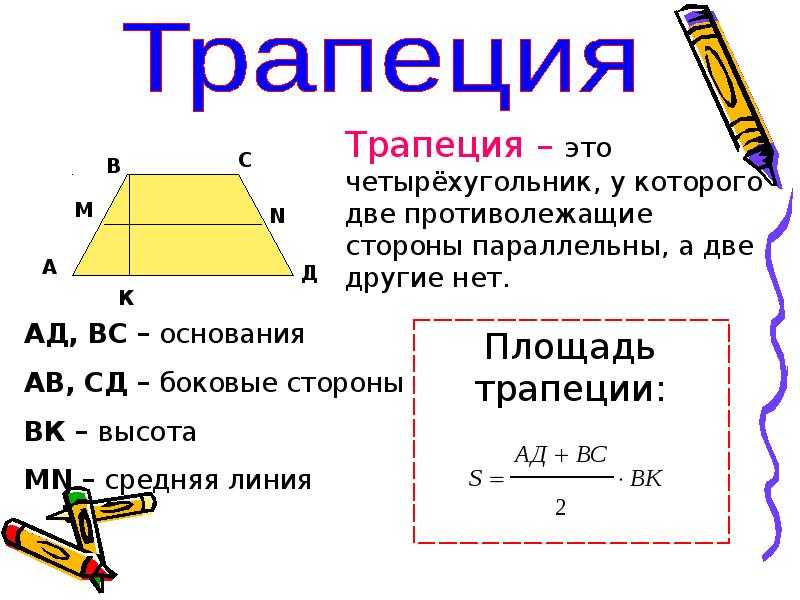
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.
- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
, где DP – внешняя высота в
Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:
Вынесем за скобку
Что и требовалось доказать.
Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то
2) Применение общей формулы площади четырехугольника .
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда
3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:
Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).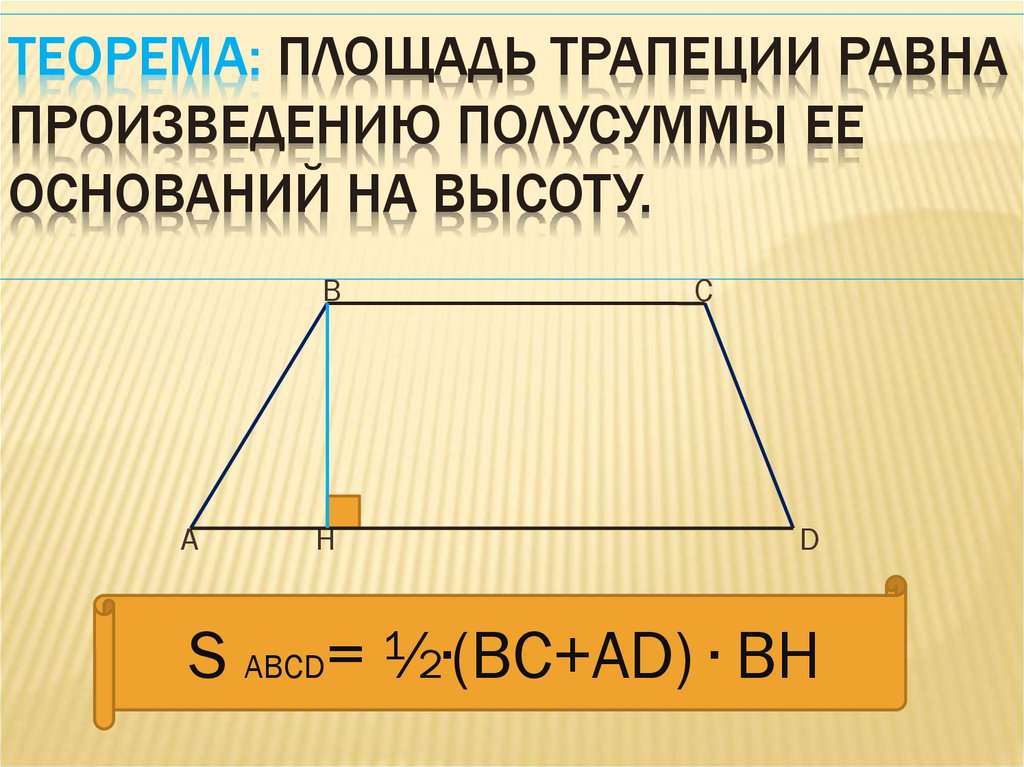
Спецприемы репетитора по математике.
Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:
Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:
Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.
В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы:). Приходите на занятия!
Приходите на занятия!
Задачи на площадь трапеции:
Замечание репетитора по математике : Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.
1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см.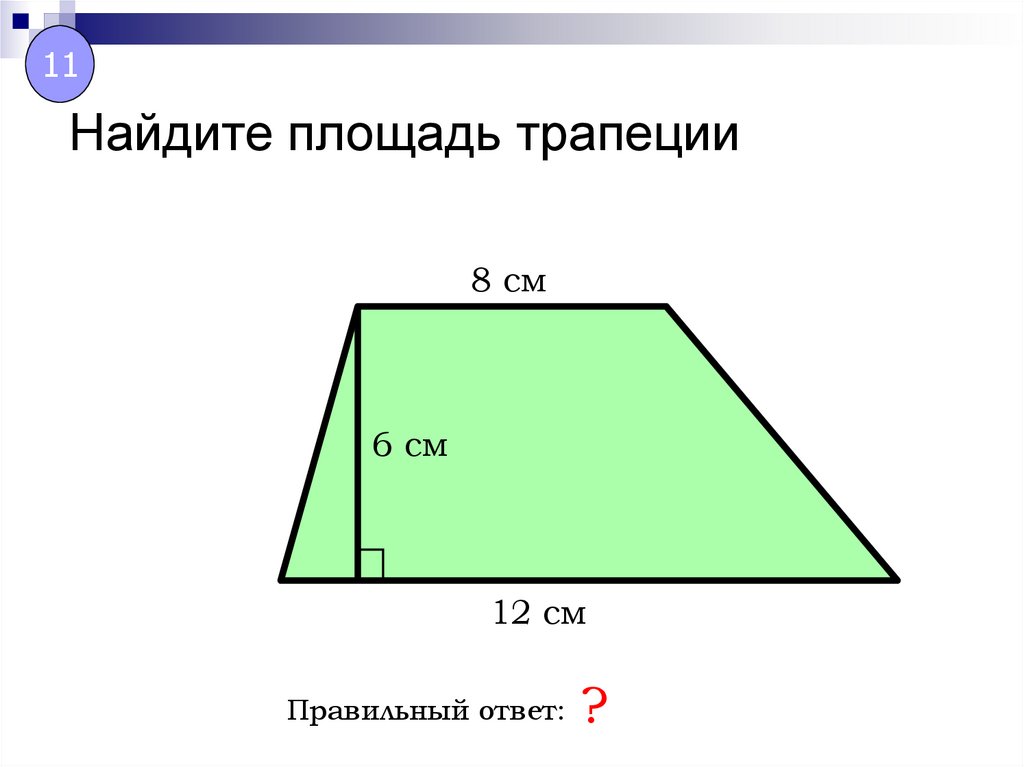
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).
Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.
Колпаков А.Н.
Репетитор по математике в Москве , подготовка к ЕГЭ в Строгино .
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
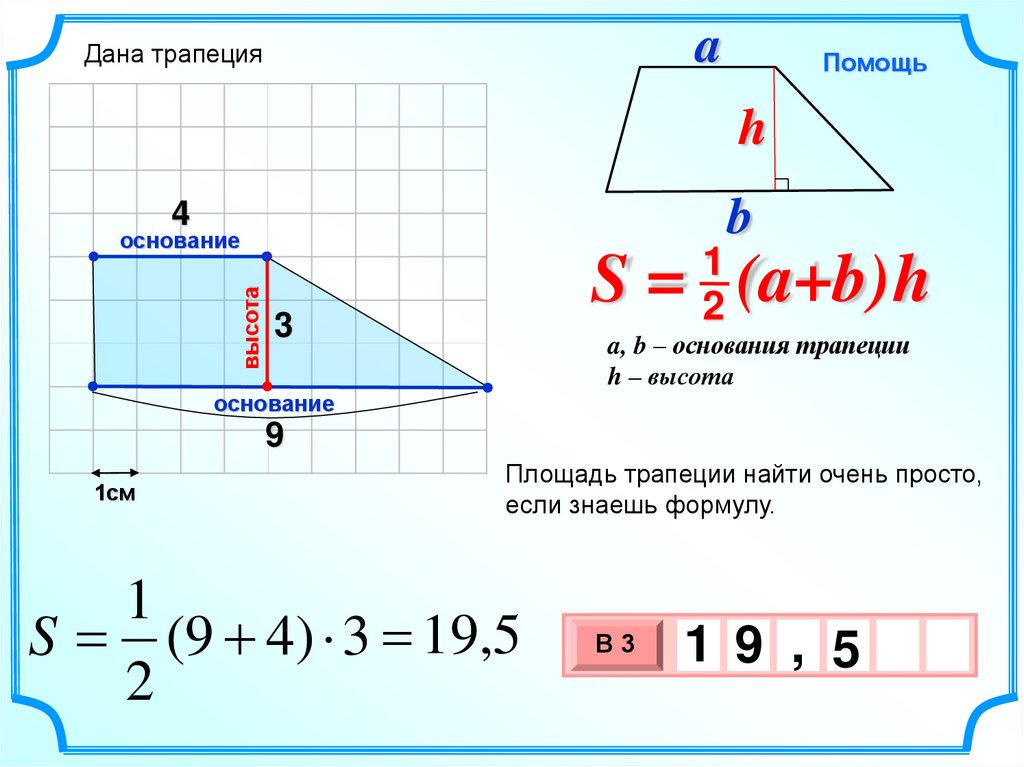
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
S = ½ * (a+b) * h
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали.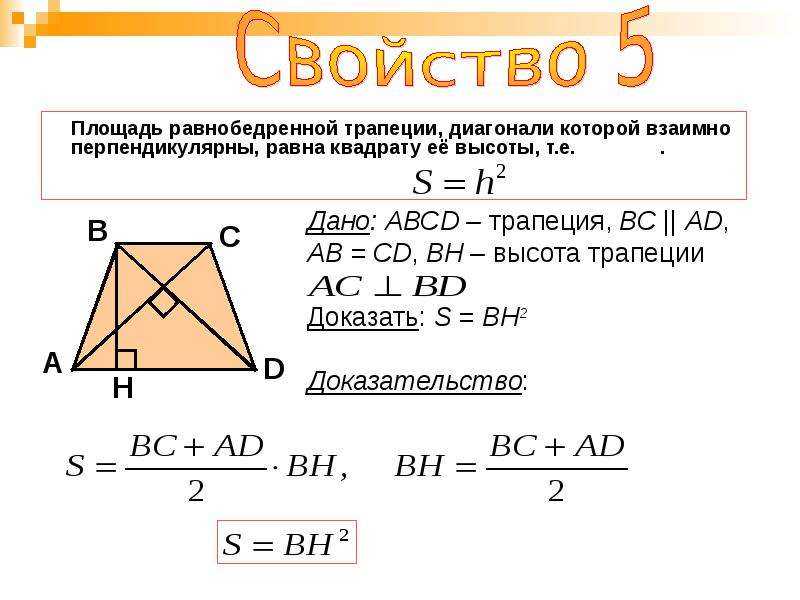 В данной формуле в расчете приводится синус угла.
В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.
Найти площадь равнобедренной трапеции можно несколькими способами.
- Через длины трех сторон. В этом случае длины боковых сторон будут совпадать, поэтому обозначены одной величиной — с, а и b — длины оснований:
- Если известна длина верхнего основания, боковой стороны и величина угла при нижнем основании, то площадь вычисляется так:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
- Если вместо верхнего основания известна длина нижнего – b, площадь рассчитывается по формуле:
S = c * sin α * (b – c * cos α)
- Если когда известны два основания и угол при нижнем основании, площадь вычисляется через тангенс угла:
S = ½ * (b2 – a2) * tg α
- Также площадь рассчитывается через диагонали и угол между ними.
 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
S = ½ * d2 * sin α
- Вычислим площадь трапеции, зная длину боковой стороны, средней линии и величину угла при нижнем основании.
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
S = m * c * sin α
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sin α
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
S = a * b / sin α
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям.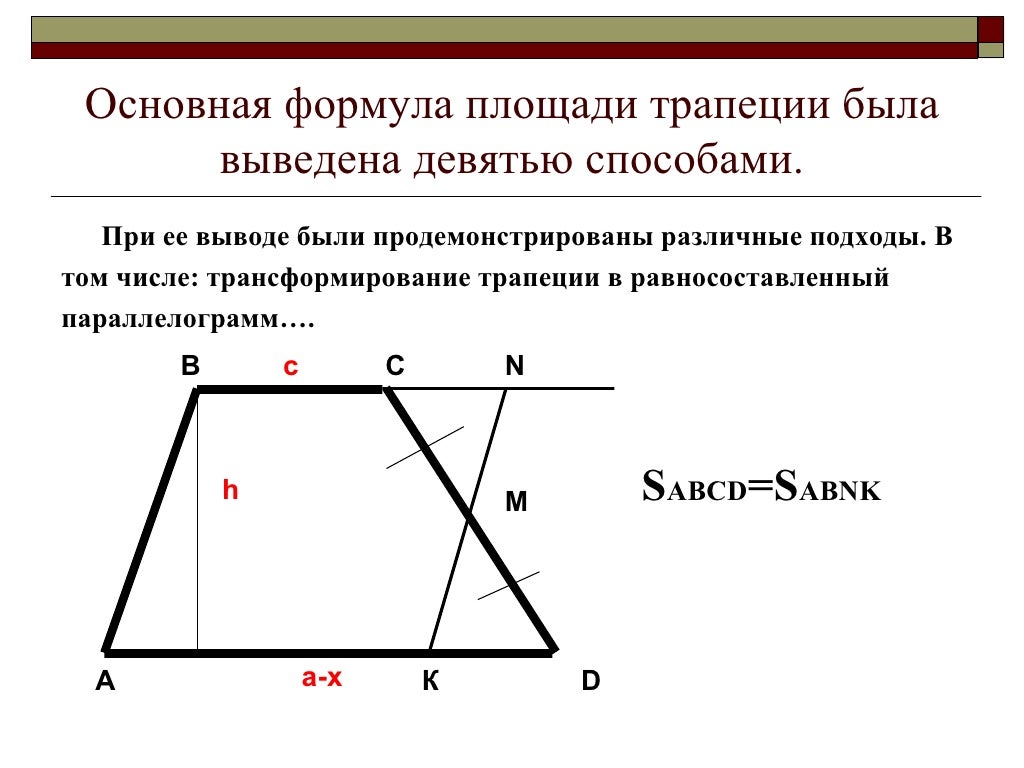 В этом случае боковая сторона по длине совпадает с высотой трапеции.
В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
- Если известны длины оснований и высота (или перпендикулярная боковая сторона), то площадь рассчитывается по формуле:
S = (a + b) * h / 2
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ рассчитать площадь — перемножить длину средней линии на высоту:
или на длину боковой перпендикулярной стороны:
- Следующий способ вычисления — через половину произведения диагоналей и синус угла между ними:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- Еще один способ вычисления — через полупериметр (сумма длин двух противоположных сторон) и радиус вписанной окружности.

Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов.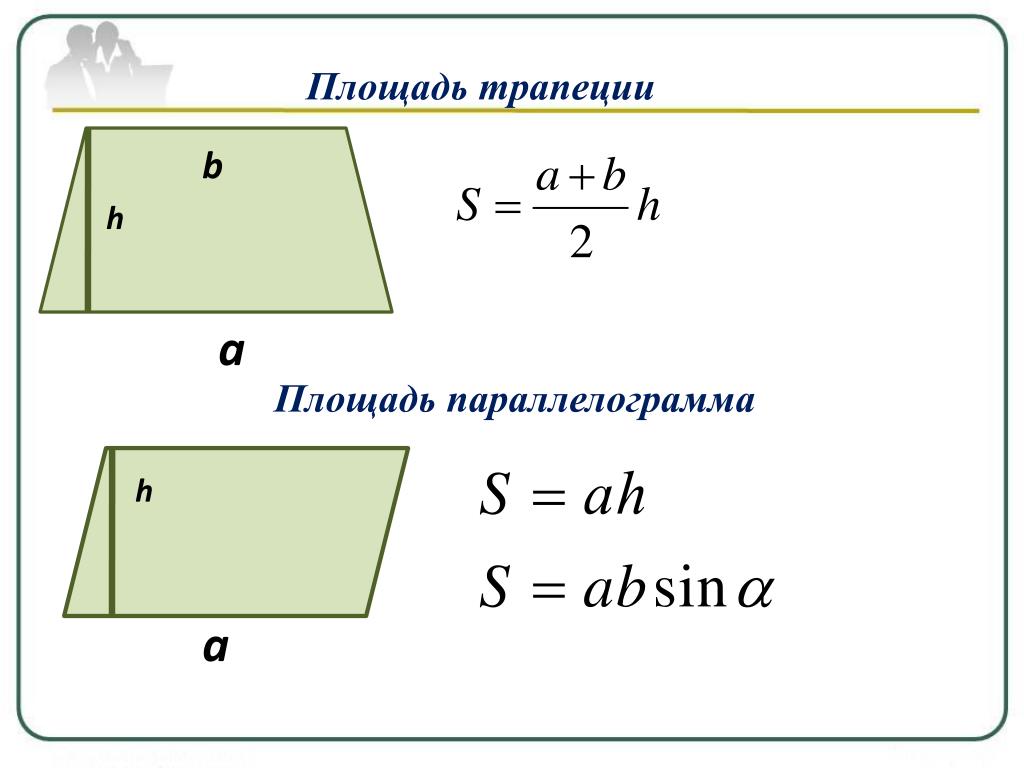 А сумма углов, прилежащих к боковой стороне, — 180 градусам.
А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Этот калькулятор рассчитал 2192 задачи на тему «Площадь трапеции»
ПЛОЩАДЬ ТРАПЕЦИИ
Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:
Общая теория для вычисления площади трапеции.
Трапеция — это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.
Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.
Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.
Две параллельные стороны трапеции называются основаниями трапеции .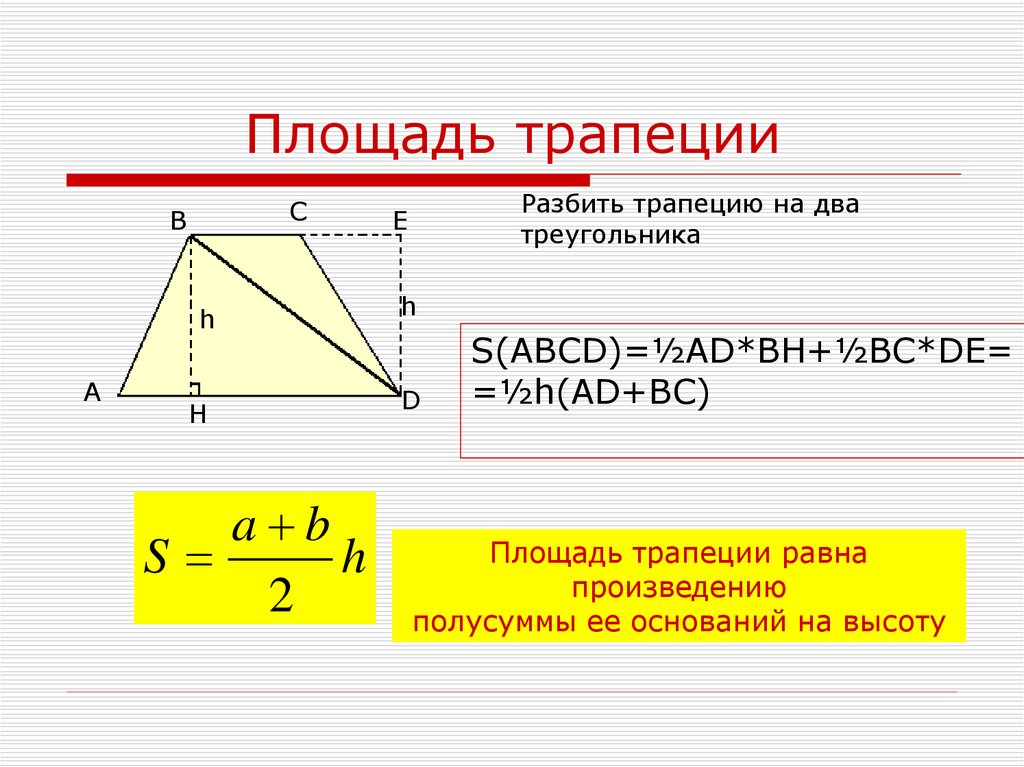
Две не параллельные стороны трапеции называются боковыми сторонами трапеции .
Рисунок №1: Трапеция ABCD
На рисунке №1 представлена трапеция ABCD с вершинами A,B ,C, D и сторонами AB, BC, CD, DA.
AB ǁ DC — основания трапеции ABCD.
AD, BC — боковые стороны трапеции ABCD.
Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.
Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.
Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.
Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.
Рисунок №2: Трапеция ABCD
На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.
То есть,.
Рисунок №3: Равнобедренная трапеция ABCD
На Рисунке №3, AD=BC.
Трапеция называется равнобедренной (равнобокой) , если ее боковые стороны равны.
Рисунок №4: Прямоугольная трапеция ABCD
На Рисунке №4 угол D — прямой (равен 90 о).
Трапеция называется прямоугольной, если угол при боковой стороне прямой.
Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.
Площадь обладает несколькими свойствами:
1. Она не может быть отрицательной.
2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.
3.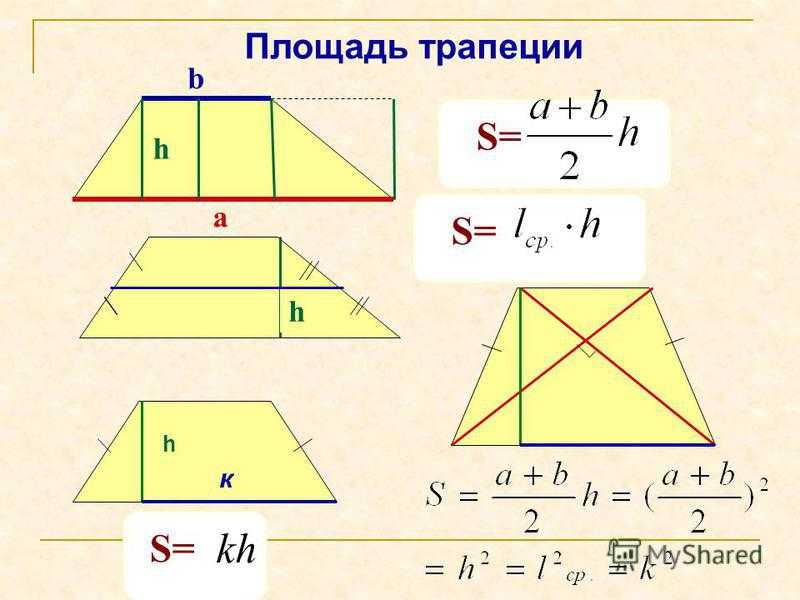 Если две фигуры равны, то и площади их равны.
Если две фигуры равны, то и площади их равны.
4. Площадь квадрата, который построен на единичном отрезке, равна единице.
За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.
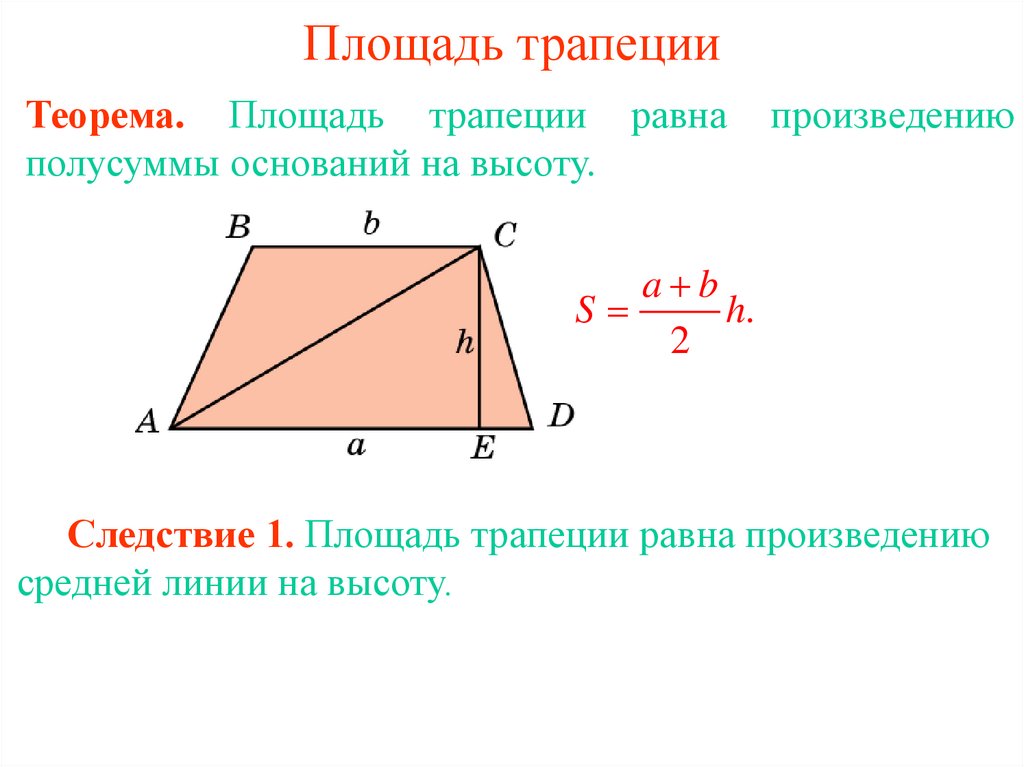
При решении задач часто используются следующие формулы вычисления площади трапеции:
1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:
2. Площадь трапеции равна произведению ее средней линии на высоту:
3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:
4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:
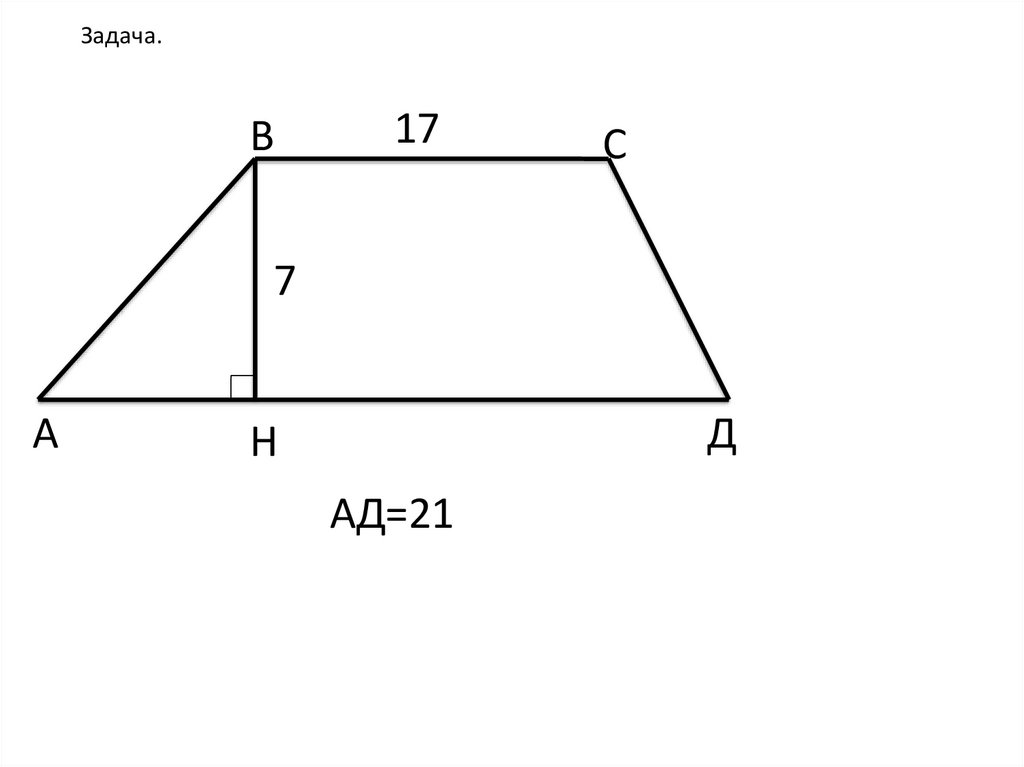
Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.
Решение:
Ответ:
Пример 2: Найти сторону основания трапеции с площадью S=35 см 2 , высотой h=7см и вторым основанием b = 2 см.
Решение:
Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:
Выразим из данной формулы сторону основания трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.
Решение:
Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:
Таким образом, имеем следующее:
Ответ:
Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.
Решение:
Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы высоту трапеции:
Таким образом, имеем следующее:
Ответ:
Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.
Решение:
Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:
Выразим из данной формулы среднюю линию трапеции:
Таким образом, имеем следующее.
Трапецией называется четырехугольник, у которого только две стороны параллельны между собой.
Они называются основаниями фигуры, оставшиеся – боковыми сторонами. Частными случаями фигуры считается параллелограмм. Также существует криволинейная трапеция, которая включает в себя график функции. Формулы площади трапеции включают в себя практически все ее элементы, и лучшее решение подбирается в зависимости от заданных величин.
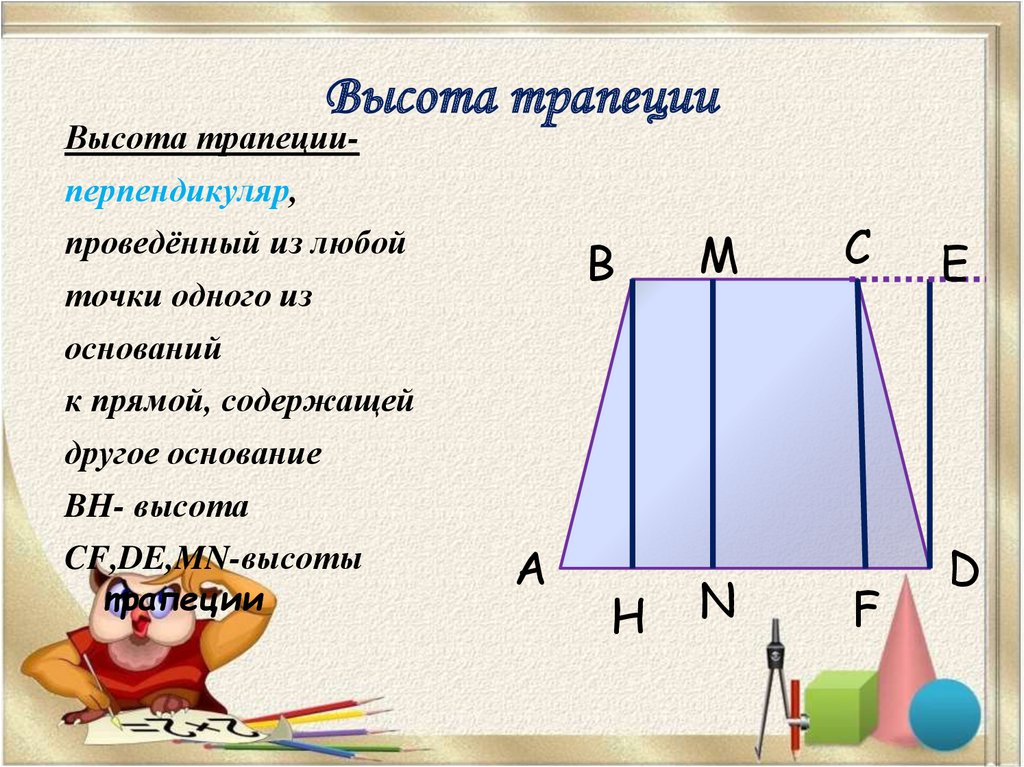
Основные роли в трапеции отводятся высоте и средней линии. Средняя линия – это линия, соединяющая середины боковых сторон. Высота трапеции проводится под прямым углом от верхнего угла к основанию.
Площадь трапеции через высоту равняется произведению полусуммы длин оснований, умноженному на высоту:
Если по условиям известна средняя линия, то эта формула значительно упрощается, так как она равна полусумме длин оснований :
Если по условиям даны длины всех сторон, то можно рассмотреть пример расчета площади трапеции через эти данные:
Допустим, дана трапеция с основаниями a
= 3 см, b
= 7 см и боковыми сторонами c
= 5 см, d
= 4 см.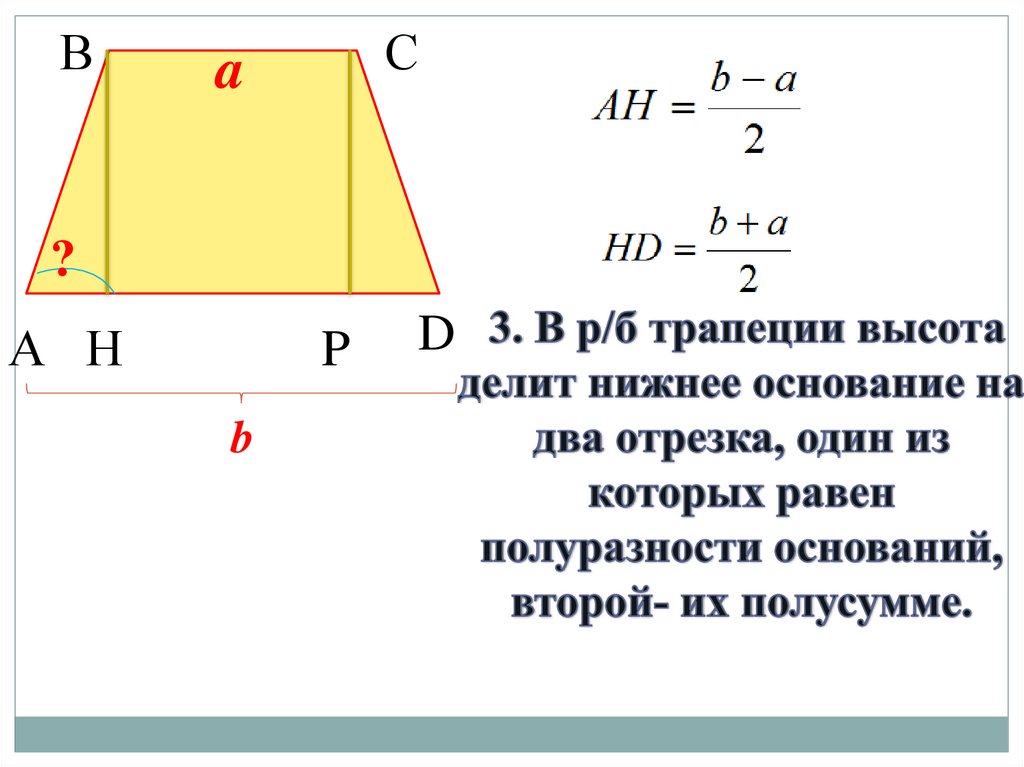 найдем площадь фигуры:
найдем площадь фигуры:
Площадь равнобокой трапеции
Отдельным случаем считается равнобокая или, как ее еще называют, равнобедренная трапеция.
Особым случаем является и нахождение площади равнобедренной (равнобокой) трапеции. Формула выводится различными способами – через диагонали, через углы, прилегающие к основанию и радиус вписанной окружности.
Если по условиям задана длина диагоналей и известен угол между ними можно использовать такую формулу:
Помните, что диагонали равнобокой трапеции равны между собой!
То есть, зная одно их оснований, сторону и угол, можно легко рассчитать площадь.
Площадь криволинейной трапеции
Отдельный случай – это криволинейная трапеция . Она располагается на оси координат и ограничивается графиком непрерывной положительной функции.
Ее основание располагает на оси X и ограничивается двумя точками:
Интегралы помогают вычислить площадь криволинейной трапеции.
Формула прописывается так:
Рассмотрим пример расчета площади криволинейной трапеции. Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Формула требует определенных знаний для работы с определенными интегралами. Для начала разберем значение определенного интеграла:
Здесь F(a)
– это значение первообразной функции f(x)
в точке a
, F(b)
– значение этой же функции f(x)
в точке b
.
Теперь решим задачу. На рисунке изображена криволинейная трапеция, ограниченная функцией . Функция
Нам необходимо найти площадь выделенной фигуры, которая является криволинейной трапецией, ограниченной сверху графиком , справа прямой x
={-8}, слева прямой x
={-10} и осью OX
снизу.
Площадь этой фигуры мы будем рассчитывать по формуле:
Условиями задачи нам задана функция. По ней мы найдем значения первообразной в каждой из наших точек:
Теперь
Ответ: площадь заданной криволинейной трапеции равняется 4.
Ничего сложного в расчетах этого значения нет. Важна только предельная внимательность в вычислениях.
Трапеция, Параллелограмм, Ромб, Квадрат, Прямоугольник
Тип многоугольника с 4 сторонами, 4 вершинами и 4 углами. Чтобы получить четырехугольник, нужно соединить четыре точки, не лежащие на одной прямой, и сумма всех внутренних и внешних углов всегда равна 360 градусам. -Слово «четырехугольник» произошло от латинских слов «Quadra» и «Latus», что означало четыре и стороны соответственно.
Чтобы получить четырехугольник, нужно соединить четыре точки, не лежащие на одной прямой, и сумма всех внутренних и внешних углов всегда равна 360 градусам. -Слово «четырехугольник» произошло от латинских слов «Quadra» и «Latus», что означало четыре и стороны соответственно.
Факты о четырехугольниках
Это замкнутая форма.
Это плоская фигура.
Имеет 4 ребра, вершины и стороны.
Чтобы получить диагонали четырехугольника, нужно соединить его противоположные стороны. Давайте проверим некоторые примеры четырехугольника.
Четырехугольник
Согласно евклидовой геометрии, четырехугольники можно определить как многоугольники с четырьмя сторонами и четырьмя вершинами. Все они являются двумерными структурами. Существует семь типов четырехугольников.
Все они являются двумерными структурами. Существует семь типов четырехугольников.
Трапеция
Трапеция не имеет сторон, параллельных друг другу. Равнобедренная трапеция имеет одну пару противоположных сторон, которые параллельны друг другу, а также их углы при основании равны друг другу.
Свойства трапеции
Основания трапеций параллельны друг другу. В приведенном выше случае AD // BC.
Ни одна из сторон, диагоналей и углов не равна друг другу.
Важные формулы, связанные с трапецией
Параллелограмм
Параллелограмм — это тип четырехугольника, в котором присутствуют две пары параллельных сторон. При этом противоположные стороны также равны друг другу. Параллелограммы также включают ромбы, ромбоиды и прямоугольники.
Свойства параллелограмма
Противоположные стороны параллелограмма параллельны и равны между собой.
Углы также равны.
Смежные углы являются дополнительными.
Диагонали делят друг друга пополам, а диагональ делит параллелограмм на два равных треугольника.
Если один из углов параллелограмма прямой, то все остальные углы прямые и параллелограмм становится прямоугольником.
Важные формулы, связанные с параллелограммами
Ромб
Ромб — это тип четырехугольника, в котором все четыре стороны имеют одинаковую длину.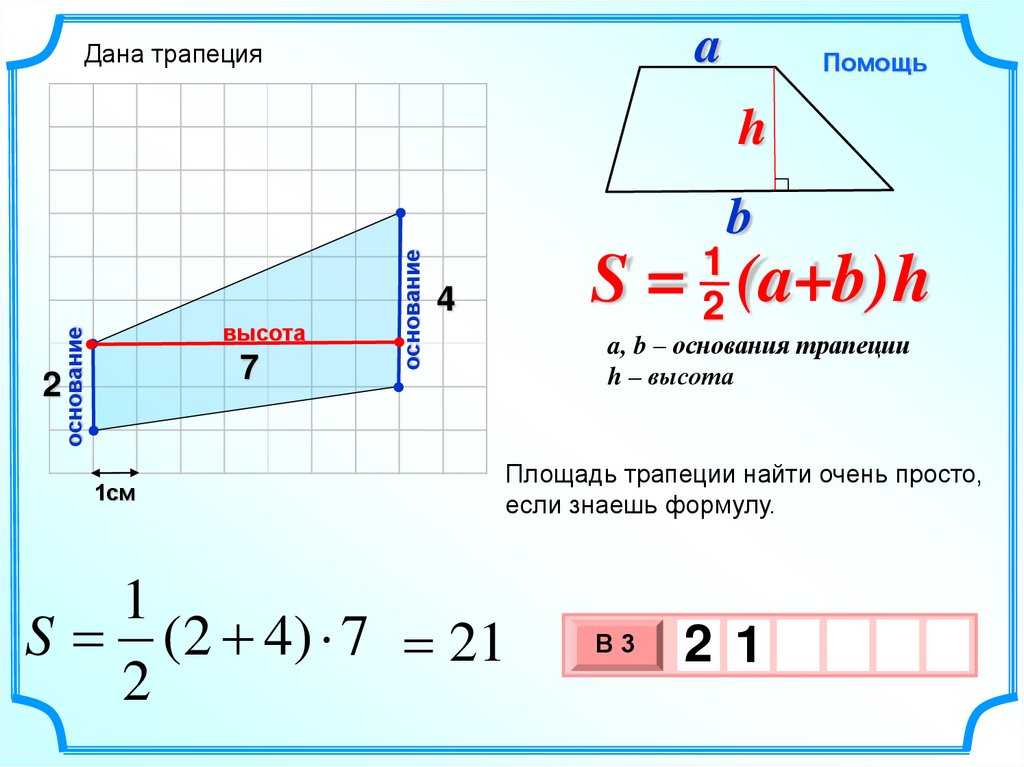 Кроме того, диагонали перпендикулярны друг другу и также делят друг друга пополам.
Кроме того, диагонали перпендикулярны друг другу и также делят друг друга пополам.
Свойства ромба
Все стороны ромба равны.
В ромбе противоположные углы также равны.
Диагонали ромба перпендикулярны друг другу и также делят друг друга пополам.
Смежные углы являются дополнительными.
Ромб также является параллелограммом, диагонали которого перпендикулярны друг другу.
Важные формулы для ромба
, если A и B являются диагонали ромба, затем
Площадь ромба = (A* B) / 2
Периметр Rombus = 4L
Rhombomboid
9000
Ромбоид — это в основном тип параллелограмма, в котором смежные стороны имеют неравную длину, а все присутствующие углы косые.
 Ромбоид — это параллелограмм, который не является ромбом.
Ромбоид — это параллелограмм, который не является ромбом.Прямоугольник
Прямоугольник — это параллелограмм, в котором все четыре угла эквивалентны прямым углам. Диагонали делят друг друга пополам и также равны по длине.
Свойства прямоугольника
Противоположные стороны прямоугольника параллельны и конгруэнтны.
Все углы прямые.
Диагонали равны и также делят друг друга пополам.
Противоположные углы, образованные в точке пересечения диагоналей, равны.
Прямоугольник — это уникальный тип параллелограмма, в котором все углы прямые.
Важные формулы для прямоугольника
Если ширина равна B, а длина L, то.

Длина диагонали прямоугольника равна √(L2 + B2).
Площадь прямоугольника L * B.
Периметр прямоугольника равен 2 (L+B).
Квадрат
Квадрат – это четырехугольник, у которого все четыре стороны равны по длине и все углы равны. Все углы равны 90 градусов, то есть углы прямые.
Квадрат также является параллелограммом, так как противоположные стороны параллельны друг другу. Кроме того, диагонали перпендикулярны друг другу и также имеют одинаковую длину. Четырехугольник можно назвать квадратом только в том случае, если он удовлетворяет свойствам прямоугольника и ромба.
Свойства квадрата
Все стороны и углы равны.
Противоположные стороны параллельны друг другу.

Диагонали равны.
Диагонали перпендикулярны и делят друг друга пополам.
Квадрат — это особый тип параллелограмма, у которого углы и стороны равны.
Также параллелограмм становится квадратом, когда диагонали равны и являются прямыми биссектрисами друг друга.
Важные формулы для квадратов
Воздушный змей
Из четырех сторон две смежные равны. Это означает, что две стороны равны и две другие стороны равны. Однако они не равны друг другу. Ни одна из сторон не параллельна. Диагонали не равны, но делят друг друга пополам под прямым углом.
Свойства воздушного змея
Две соседние стороны равны.

Диагонали не равны.
Диагонали перпендикулярны друг другу.
Одна диагональ делит воздушного змея на два равных треугольника. Отсюда следует, что углы, образованные равными сторонами, равны.
Важные формулы для воздушного змея
Классификация четырехугольника
Выпуклая: обе диагонали находятся внутри фигуры.
Вогнутая: В которой обе диагонали находятся вне фигуры.
Пересекающиеся: В котором пересекаются пары несмежных сторон. Они также известны как самопересекающиеся или скрещенные четырехугольники.

Важные факты о четырехугольниках
Если 2 стороны четырехугольника параллельны друг другу, он называется трапецией или трапецией.
Если две пары сторон параллельны друг другу, то это называется параллелограмм.
Некоторые особые типы параллелограммов — это квадраты и прямоугольники.
Если все стороны равны и две пары сторон параллельны друг другу, то ромб называется.
Четырехугольники (ромб, параллелограмм, трапеция) – Математика онлайн
В вашем браузере отключен JavaScript.
Чтобы в полной мере использовать наш веб-сайт,
включите JavaScript в вашем браузере.
Попробуйте 30 дней БЕСПЛАТНО
Узнайте, почему более 1,2 МИЛЛИОНА учеников выбирают диван-репетитор!
Хотите учиться быстрее и легче?
Тогда почему бы не использовать наши обучающие видео и не тренироваться в школе с обучающими играми.
Попробуйте бесплатно
Рейтинг
Будьте первым, чтобы дать оценку!
Вы должны войти в систему, чтобы иметь возможность дать оценку.
Вау, спасибо!
Пожалуйста, оцените нас и в Google! Мы с нетерпением ждем этого!
Перейти в Google
Авторы
Team Digital
Основы по теме
Четырехугольники (ромб, параллелограмм, трапеция)Содержимое
Четырехугольники (Ромб, Параллелограмм, Трапеция)
Нико и Ниа пробрались на кондитерскую фабрику, где запустили машину. Сладости спускаются по конвейерной ленте в разной форме, и им нужно рассортировать их по правильным коробкам, чтобы избежать неприятностей! Они узнают о форме ромба, форме параллелограмма и форме трапеции. Это означает, что они могут избежать неприятностей, потому что теперь они знают свойства ромба, свойства параллелограмма и свойства трапеции!
Сладости спускаются по конвейерной ленте в разной форме, и им нужно рассортировать их по правильным коробкам, чтобы избежать неприятностей! Они узнают о форме ромба, форме параллелограмма и форме трапеции. Это означает, что они могут избежать неприятностей, потому что теперь они знают свойства ромба, свойства параллелограмма и свойства трапеции!
Что такое параллелограмм?
Геометрия определения параллелограмма: Параллелограмм представляет собой четырехугольник с двумя парами параллельных сторон.
Свойства параллелограмма
Свойства параллелограмма:
- Противоположные углы равны
- Две пары параллельных сторон
На следующем рисунке показан пример параллелограмма со свойствами.
Вопросы и ответы о параллелограммах
Ниже вы найдете ответы на некоторые распространенные вопросы о параллелограммах!
- Что такое параллелограмм? Параллелограмм – это четырехугольник с равными противоположными углами и двумя парами параллельных сторон.

- Сколько сторон у параллелограмма? Параллелограмм — это четырехугольник, а значит, у него четыре стороны.
- Могут ли параллелограммы иметь прямые углы? Параллелограмм CAN имеет прямые углы, если выполняются все свойства параллелограмма.
Что такое ромб?
Геометрия определения ромба: Ромб – это четырехугольник, все стороны которого равны по длине.
Свойства ромба
Свойства ромба:
- Противоположные углы равны
- Четыре стороны ВСЕ одинаковой длины
- Две пары параллельных сторон
На следующем рисунке показан пример ромба со свойствами.
Вопросы и ответы о ромбах
Ниже вы найдете ответы на некоторые распространенные вопросы о ромбах!
- Сколько сторон у ромба? У ромба четыре стороны.
- Чем ромб отличается от параллелограмма? Ромб является параллелограммом, потому что у него две пары параллельных сторон.
 Однако ромб должен иметь четыре равные стороны.
Однако ромб должен иметь четыре равные стороны. - Является ли ромб четырехугольником? Ромб является четырехугольником, потому что у него четыре стороны.
- Есть ли у ромба прямые углы? Ромб CAN имеет прямые углы, но он не всегда должен иметь прямой угол, чтобы быть ромбом.
Что такое трапеция?
Геометрия определения трапеции: Трапеция – это четырехугольник с одной парой параллельных сторон.
Свойства трапеции
Свойства трапеции:
- Одна пара параллельных сторон
На следующем рисунке показан пример трапеции со свойствами.
Вопросы и ответы о трапециях
Ниже вы найдете несколько общих вопросов о трапециях с ответами!
- Может ли трапеция быть параллелограммом? Трапеция не является параллелограммом, потому что у нее только одна пара параллельных сторон, а у параллелограмма должно быть две пары параллельных сторон.

- Сколько сторон у трапеции? У трапеции четыре стороны, но только одна пара параллельных сторон.
Стенограмма
Четырехугольники (ромб, параллелограмм, трапеция)Нико и Ниа должны проникнуть на кондитерскую фабрику. К счастью, они находят открытое окно и забираются внутрь. Нико замечает на заводе большую кнопку, но для чего она?
Нет, Нико, не стоит. О, смотрите, теперь из машины выходят конфеты разной формы! Нико и Ниа должны узнать о параллелограммах, ромбах и трапециях, чтобы рассортировать сладости по нужным коробкам и избежать неприятностей!
«Четырехугольники (параллелограмм, ромб, трапеция)».
Параллелограмм, ромб и трапеция являются четырехугольниками.
«Четырехугольник» — это «многоугольник с четырьмя прямыми сторонами».
Параллелограммы, ромбы и трапеции — это четырехугольники, которые можно идентифицировать по их атрибутам или свойствам.
Давайте узнаем о свойствах параллелограммов, прежде чем помогать Нико и Ние.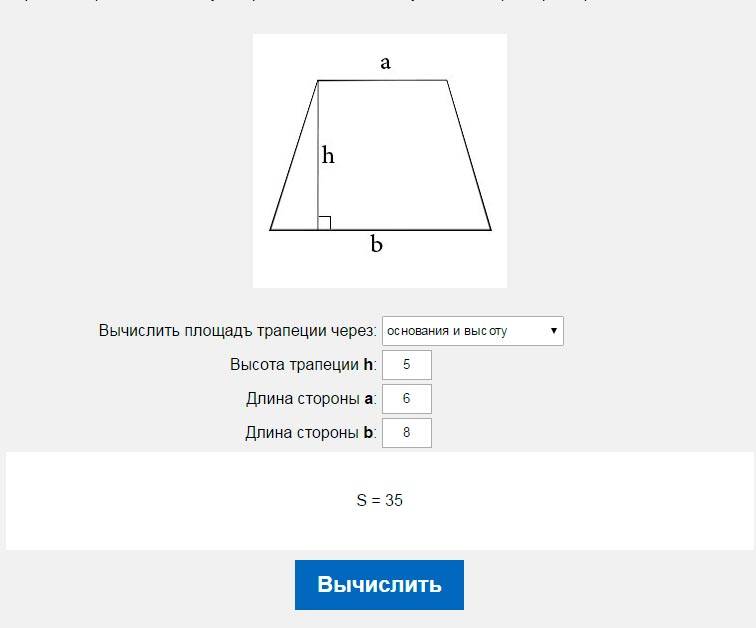 Как видите, параллелограмм может принимать разные формы, как вот ЭТИ фигуры.
Каким свойством, как вы заметили, обладают параллелограммы?
Как видите, параллелограмм может принимать разные формы, как вот ЭТИ фигуры.
Каким свойством, как вы заметили, обладают параллелограммы?
Все параллелограммы имеют «противоположные углы», которые «равны». ЭТИ два угла противоположны и равны, как и ЭТИ два. Параллелограммы также имеют «Две пары ПАРАЛЛЕЛЬНЫХ сторон». ПАРАЛЛЕЛЬНЫЕ прямые никогда не пересекаются и не пересекаются друг с другом. ЭТИ две линии параллельны. И ЭТИ две строчки. «Параллелограммы включают прямоугольники и квадраты», чтобы назвать некоторые фигуры, которые имеют две пары параллельных сторон. Теперь давайте посмотрим на ромб. Какие свойства, как мы заметили, есть у ромба?
Ромбы имеют «противоположные углы», которые «равны». ЭТИ два угла противоположны и равны, как и ЭТИ два. Ромбы также имеют «четыре стороны, ВСЕ равные по длине». ЭТИ четыре стороны равны по длине. Наконец, ромб также имеет «ДВЕ пары параллельных сторон». ЭТИ две линии параллельны. И то же ЗДЕСЬ.
Это означает, что ромб также может быть параллелограммом, потому что у него ДВЕ пары ПАРАЛЛЕЛЬНЫХ сторон!
Давайте посмотрим на нашу последнюю фигуру, трапецию. Какие свойства вы можете здесь выделить?
Какие свойства вы можете здесь выделить?
Трапеции имеют только «ОДНУ пару параллельных сторон». Можно ли найти параллельные стороны? ЭТИ две прямые параллельны, потому что они не пересекаются и не пересекаются! Трапеции НЕ являются типом параллелограмма, потому что ЭТИ две стороны в конечном итоге пересекутся или пересекутся друг с другом. Трапеция является разновидностью четырехугольника, потому что у нее ЧЕТЫРЕ стороны. Теперь мы можем идентифицировать параллелограммы, ромбы и трапеции на основе их свойств или атрибутов. Давайте поможем Нико и Ниа рассортировать конфеты трех форм, прежде чем они вызовут проблемы! Во-первых, мы начнем с ЭТОГО. Какие свойства мы замечаем?
Противоположные углы РАВНЫ и ДВЕ пары параллельных сторон, но НЕ все они равны по длине. В какую коробку он должен войти?
Он должен войти в поле ПАРАЛЛЕЛОГРАММА. Давайте посмотрим на вторую форму. Какие свойства вы здесь заметили?
У него есть только ОДНА пара параллельных сторон, потому что ЭТИ две стороны в конечном итоге пересекутся. Основываясь на свойстве, которое мы определили, в какую коробку следует положить это сладкое?
Основываясь на свойстве, которое мы определили, в какую коробку следует положить это сладкое?
Он должен быть в ячейке ТРАПЕЦИЯ, потому что у трапеции только ОДНА пара параллельных сторон. Наконец, мы можем отсортировать последнюю форму. Какие свойства вы заметили?
Противоположные углы РАВНЫ. Он также имеет четыре стороны, ВСЕ РАВНЫЕ по длине, плюс две пары ПАРАЛЛЕЛЬНЫХ сторон. В какую коробку следует положить это?
Он помещается в ячейку РОМБ, потому что у ромба противоположные углы равны, а четыре равные стороны параллельны. Помните, что параллелограммы, ромбы и трапеции являются четырехугольниками. У ПАРАЛЛЕЛОГРАММА противолежащие углы РАВНЫ и две пары сторон ПАРАЛЛЕЛЬНЫ. РОМБЫ имеют РАВНЫЕ противолежащие углы и две пары ПАРАЛЛЕЛЬНЫХ сторон. У них также есть четыре стороны, ВСЕ равные по длине. ТРАПЕЦИИ имеют только одну пару параллельных сторон. Уф, мы вовремя помогли Нико и Ние! «Ния, не подноси руку слишком близко к этой машине!» О, слишком поздно. Интересно, где окажется Ния?
Подождите, что делает Нико? — Ты определенно не подходящая фигура для этого, Ная!
Четырехугольники (ромб, параллелограмм, трапеция) упражнение
Хотите применить полученные знания? Вы можете повторить и попрактиковаться с заданиями к видео Четырехугольники (Ромб, Параллелограмм, Трапеция) .
Правильно определите четырехугольники.
Подсказки
У ромба 4 стороны одинаковой длины.
Трапеция имеет только один набор параллельных сторон.
Параллелограмм имеет 2 набора параллельных сторон и противоположные углы равны.
раствор
Rhombus
4 Стороны равной длины
2 Наборы параллельных сторон
ОПАСОВАЯ УГЛА
4-сторонняя форма
Трапеция
1 набор параллельных сторон
4-сторонняя форма
Воздушный змей
Без параллельных сторон
4-сторонняя форма
9003 2 равные по длине короткие стороны и 2 равные по длине короткие стороныВыделите правильные четырехугольники.
Подсказки
Помните, что у трапеции только одна пара параллельных сторон.

Попробуйте повернуть фигуру, чтобы определить особенности. Это трапеция. Он имеет один набор параллельных сторон.
Помните, что у трапеции только одна пара параллельных сторон. Эта форма имеет 2 набора параллельных сторон, поэтому НЕ является трапецией.
Решение
На картинке 3 трапеции.
Свойства фигур.
Подсказки
Пересечение означает, что стороны со временем встретятся, если продолжат движение.
Посмотрите на эти изображения трапеций. Что вы заметили в углах?
Параллелограмм, трапеция и ромб — все виды четырехугольников. Это означает, что они должны иметь 4 стороны и 4 угла.
Решение
1. Все параллелограммы имеют 4 угла. Истинный.
Параллелограмм является четырехугольником, а все четырехугольники имеют 4 стороны и 4 угла.
2. Трапеция может иметь два прямых угла. Истинный.

Некоторые трапеции не имеют прямых углов, однако трапеция может иметь 2 прямых угла.
3. Треугольник является разновидностью параллелограмма. ЛОЖЬ.
Треугольник не является параллелограммом, потому что у него 3 стороны, поэтому он не может быть четырехугольником.
4. У ромба есть стороны, которые со временем пересекутся. ЛОЖЬ.
У ромба две пары параллельных сторон. Пара параллельных сторон никогда не пересекутся — они продолжаются с расстоянием между ними.
Какая фигура лишняя?
Подсказки
На всех этих изображениях есть четырехугольники. Три одинаковых и один другой.
Параллелограмм имеет 2 пары параллельных сторон.
Трапеция имеет только 1 пару параллельных сторон.
Решение
Нечетным является каучук , потому что это параллелограмм .
Все остальные формы трапеции .

________________________________________________________
Мы знаем это, потому что параллелограмм имеет 2 пары параллельных сторон.
Трапеция имеет только 1 пару параллельных сторон.
Сопоставьте фигуры.
Подсказки
Конфеты в форме трапеции имеют только одну пару параллельных сторон.
Конфеты в форме ромба имеют 4 стороны одинаковой длины.
Прямоугольные конфеты имеют две пары параллельных сторон и 4 прямых угла.
Квадратные конфеты имеют 4 прямых угла.
Решение
Чтобы найти подходящие сладкие фигуры, не забудьте подумать о свойствах каждой фигуры.
Когда фигуры поворачиваются в различных направлениях , они могут выглядеть по-разному. Попробуйте визуализировать вращение фигур так, чтобы они были в другой ориентации, чтобы помочь вам сравнить их.

Назовите фигуру.
Подсказки
Форма может быть классифицирована более чем одним способом. Например, квадрат также может быть классифицирован как нечто другое.
Трапеция имеет только 1 набор параллельных сторон и всего 4 стороны.
Параллелограмм должен иметь 2 пары параллельных сторон и всего 4 стороны.
Параллелограммы и трапеции являются типами четырехугольников, это означает, что они должны иметь 4 стороны.
Решение
Параллелограмм — это четырехсторонняя фигура с двумя парами параллельных сторон. Квадрат, прямоугольник и ромб — это все виды параллелограмма.
Трапеция представляет собой четырехстороннюю фигуру с одной парой параллельных сторон. Трапеция может иметь 0 или 2 прямых угла.
Не параллелограмм и не трапеция.
Воздушный змей не имеет параллельных сторон.
Треугольник не является четырехугольником и, следовательно, не может быть параллелограммом или трапецией.

Куб — это трехмерная фигура. Хотя его грани квадратные (параллелограммы), сам куб не является таковым, поскольку не является двумерной формой.
Еще видео по теме 2D форма
Круги
Треугольники
Формы в мире — давайте попрактикуемся!
Рисование фигур — потренируемся
Квадраты и прямоугольники
Вершины и стороны (и их подсчет)
Пентагоны
Шестиугольники
Стороны и вершины фигур
Стороны и вершины 2D-фигур — давайте потренируемся!
Составление фигур — давайте потренируемся!
Четырехугольники (прямоугольник и квадрат)
Четырехугольники
Сравнение четырехугольников — давайте попрактикуемся!
Четырехугольники (ромб, параллелограмм, трапеция)
Start 30 Day Free Trial
Improve grades while having fun
and get full access to
4,106
Sofahero level
6,572
ready-made
vocabulary words
351
videos
1,482
упражнения
1,439
рабочие листы
круглосуточно
помощь от
учителей
материалы по всем предметам и классам.


 {\circ} = 5 $$
{\circ} = 5 $$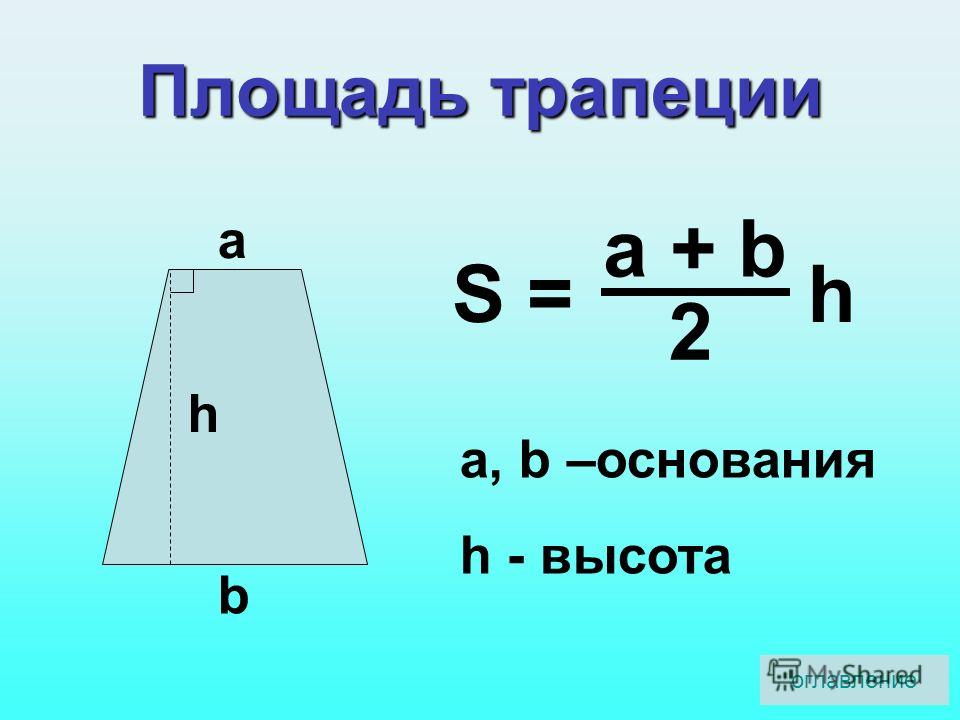 Площадь трапеции равняется 60. Чему равна высота трапеции?
Площадь трапеции равняется 60. Чему равна высота трапеции?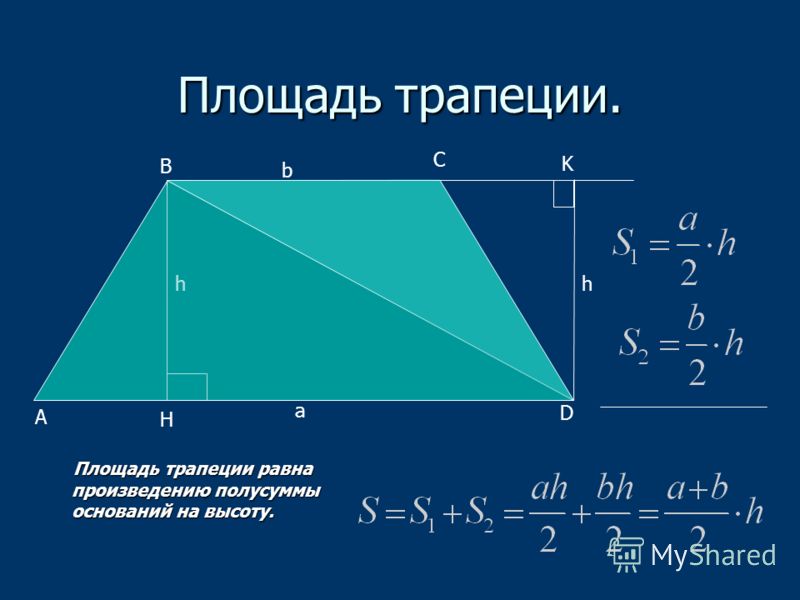 В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:
В этом случае диагонали по длине равны, поэтому каждую обозначаем буквой d без индексов:

 Однако ромб должен иметь четыре равные стороны.
Однако ромб должен иметь четыре равные стороны.