Средняя линия прямоугольной трапеции. Запоминаем и применяем свойства трапеции
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже .
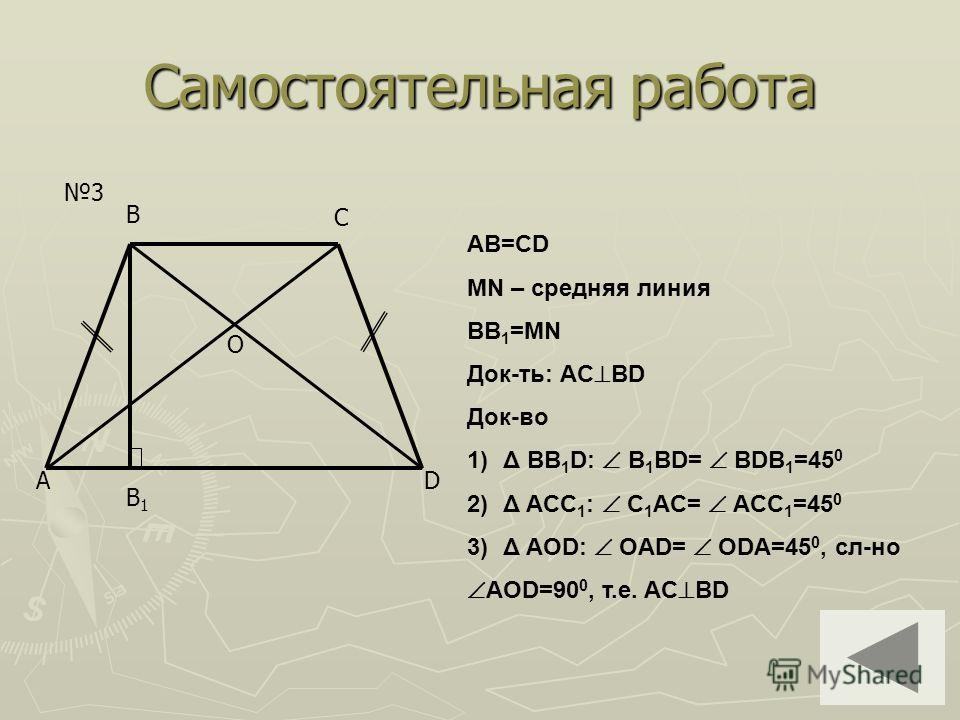
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу;
- боковые стороны AB и CD — два непараллельных элемента;
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
- высота трапеции CH — перпендикулярный основаниям отрезок;
- средняя линия EF — линия, соединяющая середины боковых сторон.
Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.

- При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2 .
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры.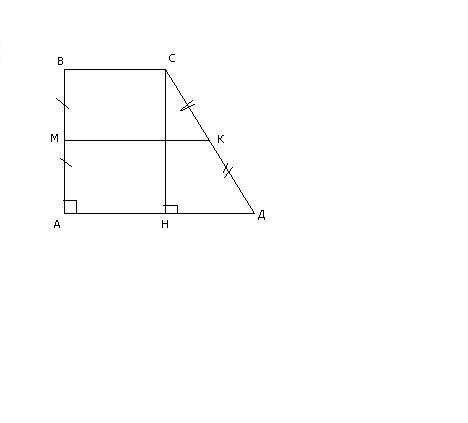 Радиус её можно найти через высоту, и он будет равен r = h/2.
Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов.
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a — b) * tg α;
c = √ (d 2 — (a — b) 2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны.
d = (a — b) /cosα;
d = c / sin α;
d = √ (c 2 + (а — b) 2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с 2 + b 2)
или по-другому, заменив «с» на «h»:
d1 = √ (h 2 + b 2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с 2 + b 2) или d 2 = √ (h 2 + а 2).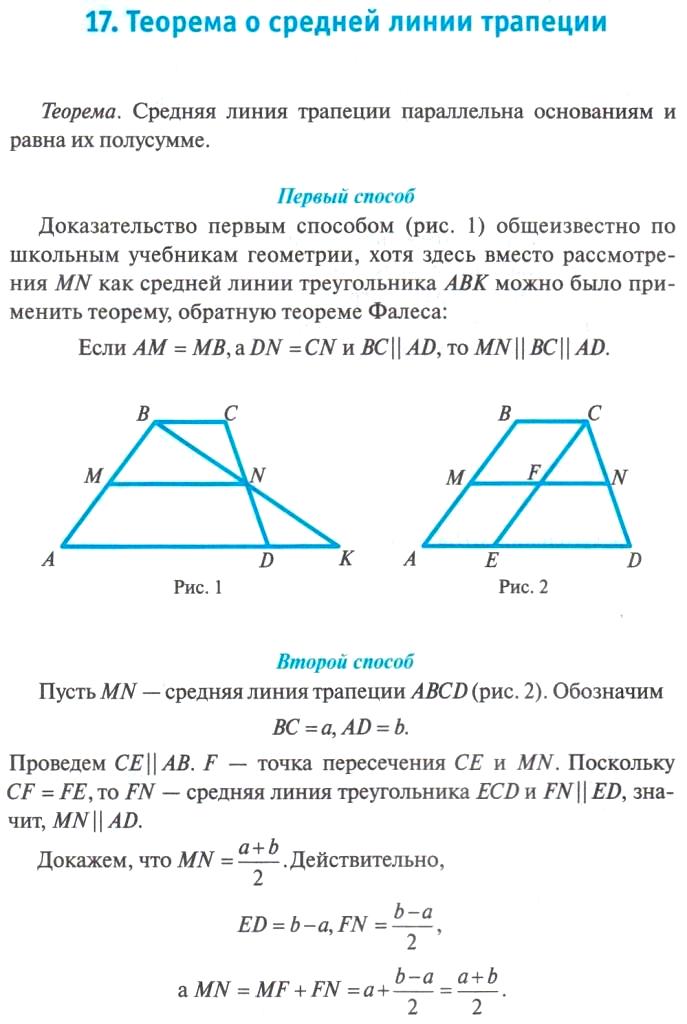
Задача №1
Условие . Площадь прямоугольной трапеции известна и равна 120 дм 2 . Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с 2 + (а — b) 2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а — b = 6.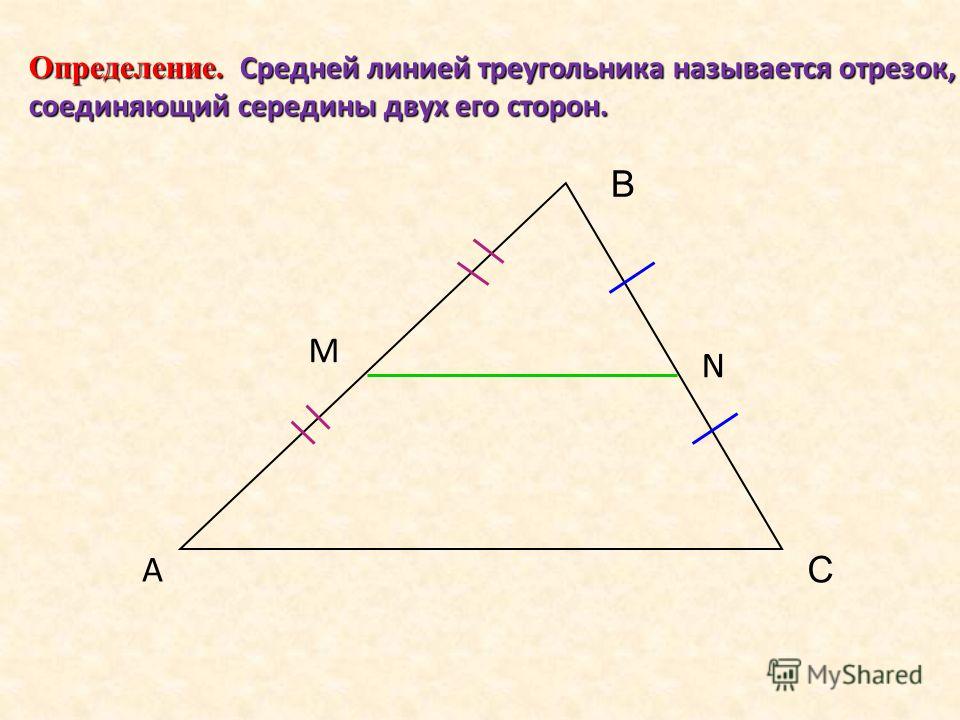
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d 2 = с 2 + (a — b) 2 или (a + b) 2 = с 2 + (a — b) 2 .
Необходимо сделать преобразования, подставив вместо с его значение из условия — 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см 2 .
Ответ. Искомая площадь 36 см 2 .
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции , которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Поэтому ознакомимся с ними более детально.
Вконтакте
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).
Если сложить все градусные меры внутренних , то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей. Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет . Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.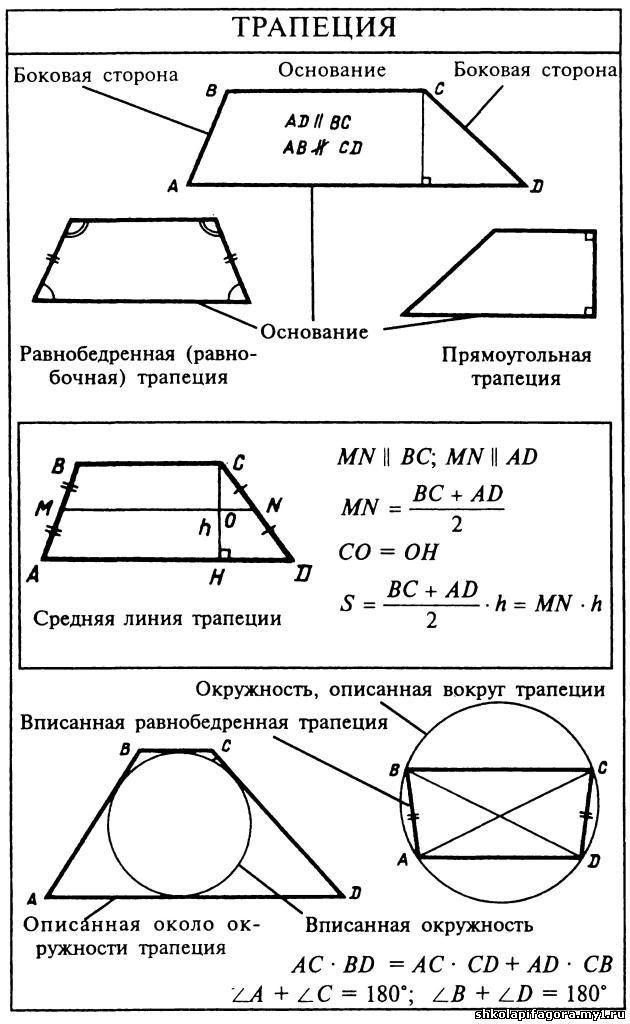
Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная . ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.
- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
- Вокруг любой правильной трапеции можно построить .
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции :
Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой.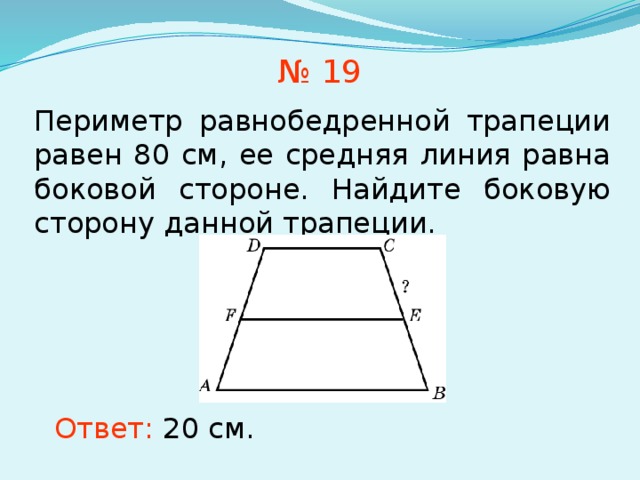 При этом, перпендикулярная сторона также будет являться и высотой.
При этом, перпендикулярная сторона также будет являться и высотой.
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур.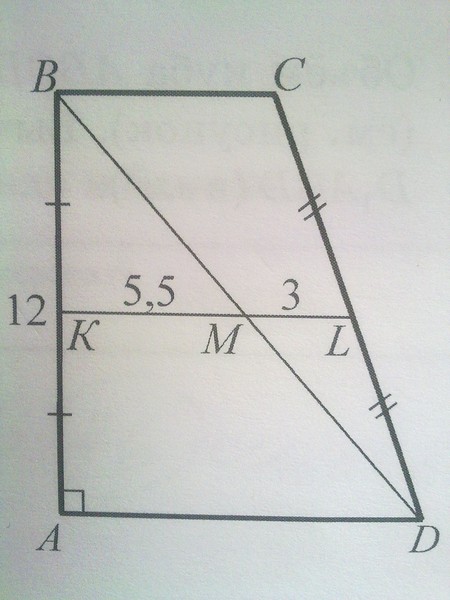 Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения. Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .
Как было установлено, DF=CH , отсюда .
Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как :
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.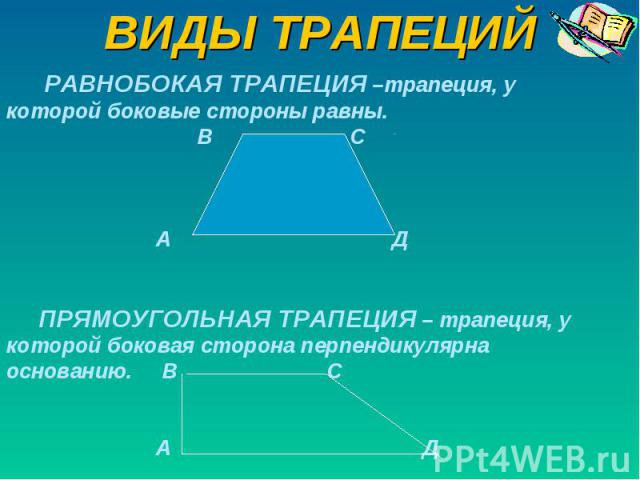
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ).
 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ . - А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.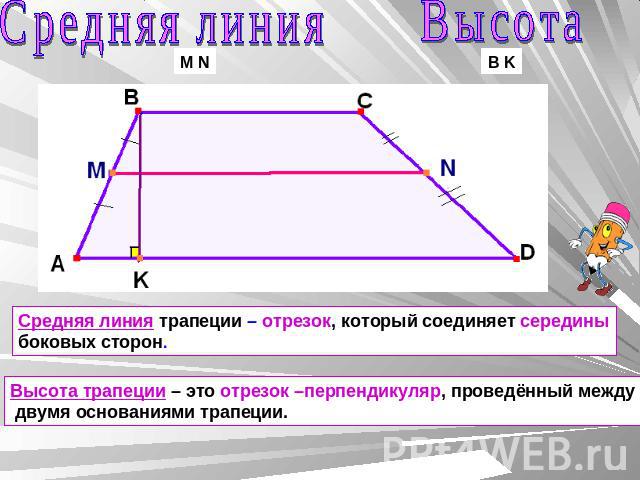
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.

- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка.
 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.

- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.

Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию.
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции
Навигация по странице: Определение прямоугольной трапеции Признаки прямоугольной трапеции Основные свойства прямоугольной трапеции Стороны прямоугольной трапеции Средняя линия прямоугольной трапеции
Определение.
Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.
| Рис.1 |
Признаки прямоугольной трапеции
Трапеция будет прямоугольной если выполняется одно из этих условий:
1. В тапеции есть два смежных прямых угла:
В тапеции есть два смежных прямых угла:
∠BAD = 90° и ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC, AB ┴ AD
Основные свойства прямоугольной трапеции
1. В трапеции есть два смежных прямых угла:
∠BAD = ∠ABC = 90°
2. Одна боковая сторона перпендикулярна основам:
AB ┴ BC ┴ AD
3. Высота равна меньшей боковой стороне:
h = AB
Стороны прямоугольной трапеции
Формулы длин сторон прямоугольной трапеции:
1. Формулы длины оснований через стороны и угол при нижнем основании:
a = b + d cos α = b + c ctg α = b + √d 2 — c2
b = a — d cos α = a — c ctg α = a — √d 2 — c2
2. Формулы длины оснований через стороны, диагонали и угол между ними:
| a = | d1d2 | · sin γ — b = | d1d2 | · sin δ — b |
| c | c |
| b = | d1d2 | · sin γ — a = | d1d2 | · sin δ — a |
| c | c |
3. Формулы длины оснований трапеции через площадь и другие стороны:
Формулы длины оснований трапеции через площадь и другие стороны:
| a = | 2S | — b b = | 2S | — a |
| c | c |
4. Формула боковой стороны через другие стороны и угол при нижнем основании:
c = √d 2 — (a — b)2 = (a — b) tg α = d sin α
5. Формулы боковой стороны через основы, диагонали и угол между ними:
| c = | d1d2 | · sin γ = | d1d2 | · sin δ |
| a + b | a + b |
6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:
| c = | S | = | 2S |
| m | a + b |
| d = | S | = | 2S |
| m sin α | (a + b) sin α |
7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:
Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:
| d = | a — b | = | c | = | h | = √c2 + (a — b)2 |
| cos α | sin α | sin α |
Средняя линия прямоугольной трапеции
Формулы длины средней линии прямоугольной трапеции:
1. Формулы средней линии через основание, высоту (она же равна стороне d ) и угол α при нижнем основании:
| m = | a — h · | ctg α | = | b + h · | ctg α |
| 2 | 2 |
2. Формулы средней линии через основания и боковые стороны сторону:
| m = | a — | √d 2 — c2 | = | b + | √d 2 — c2 |
| 2 | 2 |
Формулы по геометрии
Квадрат. Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм. Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Трапеция. Формулы и свойства трапеции
— Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
— Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
Формулы площади геометрических фигур
Формулы периметра геометрических фигур
Формулы объема геометрических фигур
Формулы площади поверхности геометрических фигур
Формулы и свойства квадрата
Прямоугольник. Формулы и свойства прямоугольника
Параллелограмм. Формулы и свойства параллелограмма
Ромб. Формулы и свойства ромба
Трапеция. Формулы и свойства трапеции
— Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
— Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
Формулы площади геометрических фигур
Формулы периметра геометрических фигур
Формулы объема геометрических фигур
Формулы площади поверхности геометрических фигур
Все таблицы и формулы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
все формулы и примеры задач. Видео «Площадь трапеции»
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним.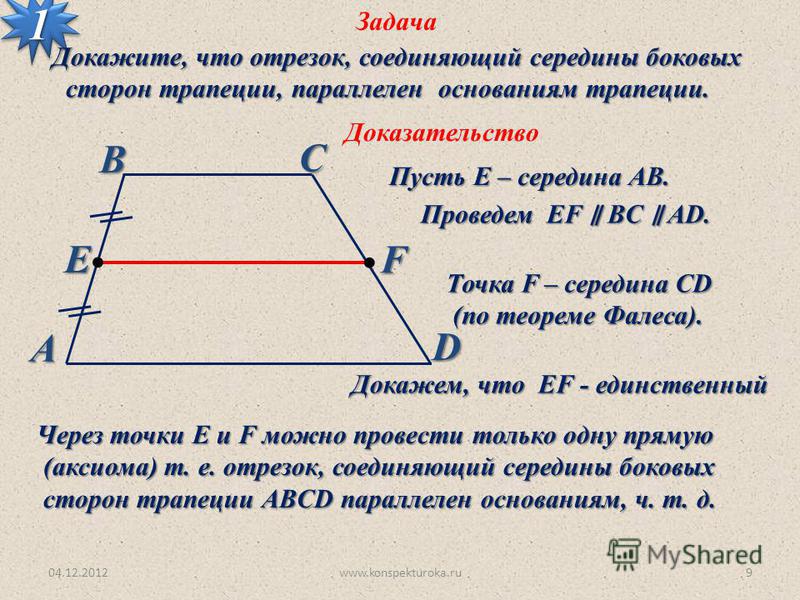 Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a — b) * tg α;
c = √ (d 2 — (a — b) 2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a — b) /cosα;
d = c / sin α;
d = √ (c 2 + (а — b) 2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно.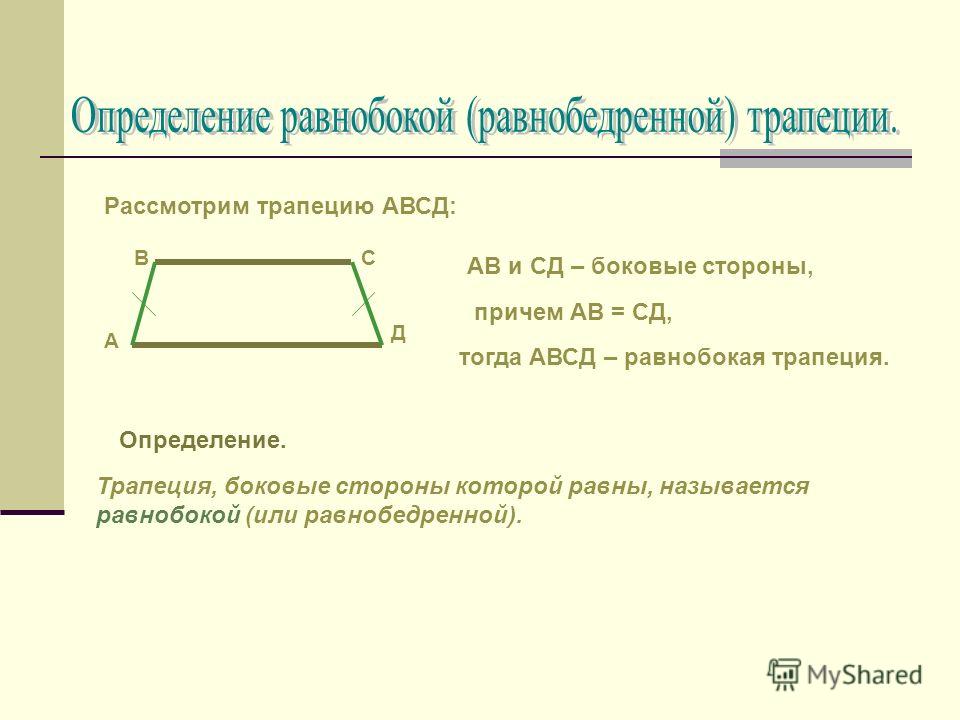 Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с 2 + b 2)
или по-другому, заменив «с» на «h»:
d1 = √ (h 2 + b 2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с 2 + b 2) или d 2 = √ (h 2 + а 2).
Задача №1
Условие . Площадь прямоугольной трапеции известна и равна 120 дм 2 . Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с 2 + (а — b) 2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а — b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d 2 = с 2 + (a — b) 2 или (a + b) 2 = с 2 + (a — b) 2 .
Необходимо сделать преобразования, подставив вместо с его значение из условия — 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см 2 .
Ответ. Искомая площадь 36 см 2 .
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см².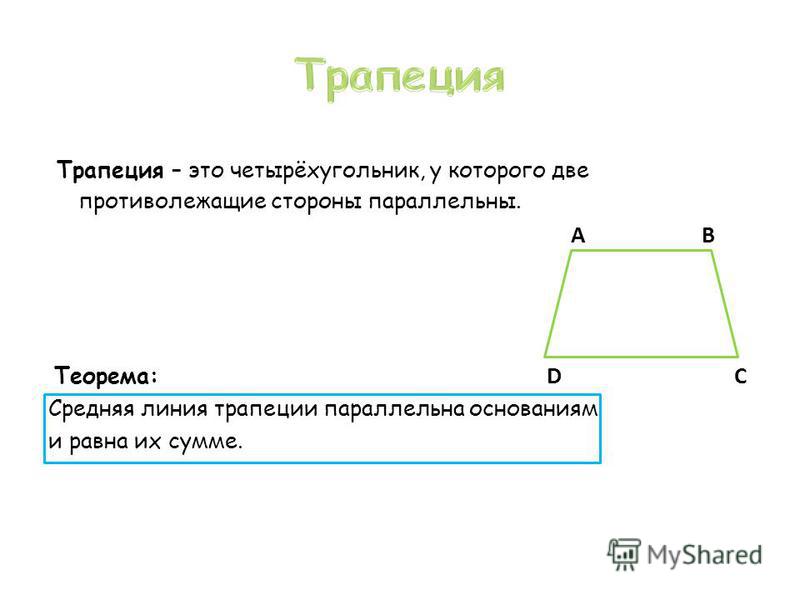 Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.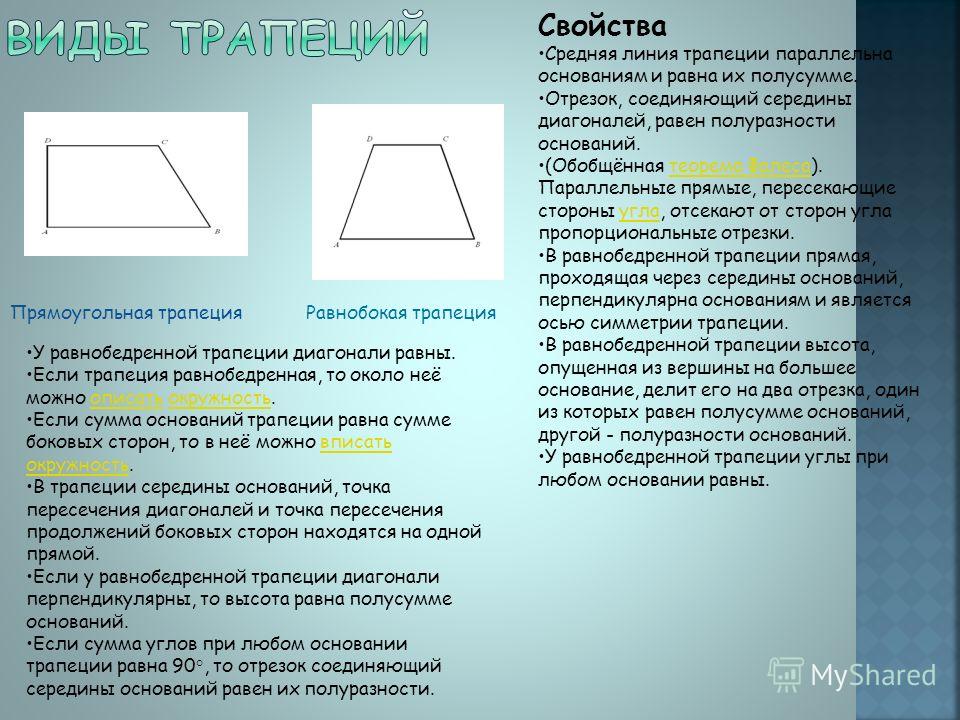
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
Добрый день, дорогие друзья! Сегодня у нас тема — трапеция решение задач по геометрии.
Прежде чем начинать разбирать задачи, давайте вспомним, что такое трапеция, и какие у неё есть элементы.
Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называют основаниями, а непараллельные — боковыми сторонами.
Трапеции бывают прямоугольные, равнобедренные и простые.
В прямоугольных трапециях есть 2 прямых угла.
В равнобедренных трапециях, как в равнобедренных треугольниках, углы при основаниях равны, равны так же и боковые стороны.
В трапеции имеется средняя линия, которая соединяет середины боковых сторон.
А теперь задачи.
Острый угол равнобедренной трапеции равен 60°. Доказать, что основание ВС = AD — AB.
Доказательство.
Опустим из вершин трапеции высоты BM и CN на нижнее основание AD.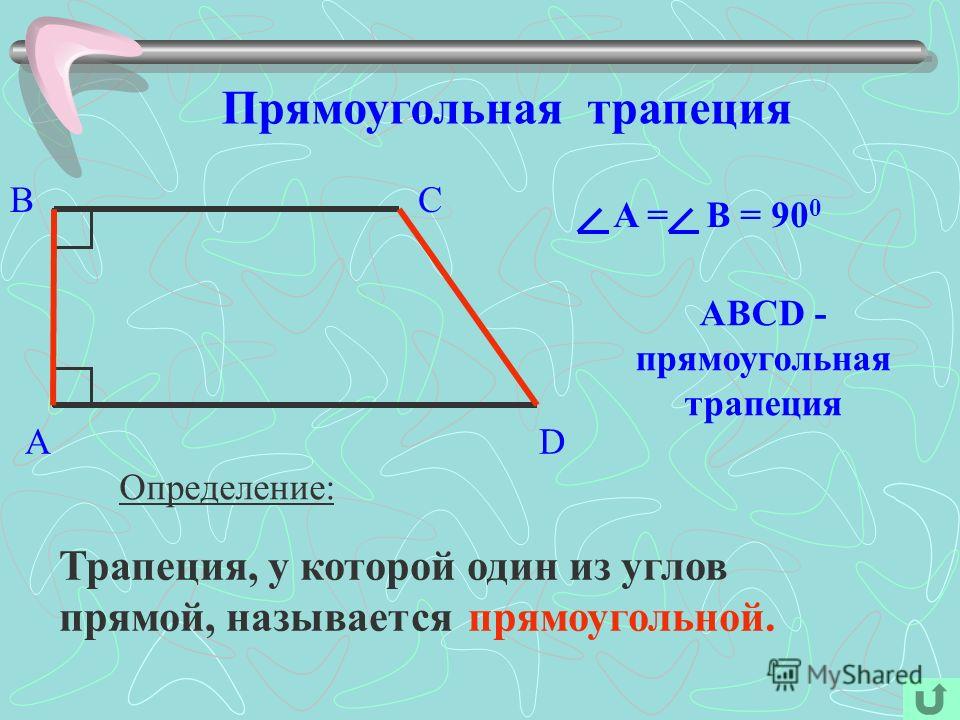
Получим два прямоугольных треугольника ABM и DCN, а также прямоугольник BCNM.
Поскольку в прямоугольных треугольниках один угол равен 60°, то второй, согласно следствию из теоремы о сумме внутренних углов треугольника,
равен 30°.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы.
Т.е. АМ= с/2.
То же самое и в правом треугольнике — ND = с/2.
Получается, что нижнее основание можно представить в виде суммы трёх отрезков, а именно AM, MN, ND, где AM=ND=c/2.
MN=BC, или верхнему основанию.
Отсюда можно написать MN=BC=AD — AM — ND = AD — c/2 — c/2 = AD — AB.
Мы доказали, что верхнее основание равно разности нижнего основания и боковой стороны.
Основания трапеции равны AD и BC. Найти длину отрезка KP, который соединяет середины диагоналей трапеции.
Решение:
На основании теоремы Фалеса отрезок KP принадлежит большему отрезку MN, который является средней линией трапеции.
Средняя линия трапеции
, как мы знаем, равна полу-сумме оснований трапеции
, или (AD+BC)/2.
В то же время, рассматривая треугольник ACD и его среднюю линию KN, можно понять, что KN=AD/2.
Рассматривая другой треугольник BCD и его среднюю линию PN, можно увидеть, что PN=BC/2.
Отсюда, KP=KN-PN = AD/2 — BC/2 = (AD-BC)/2.
Мы доказали, что отрезок, который соединяет середины диагоналей трапеции, равен полу-разности оснований данной трапеции
.
Задача 3.
Найти меньшее основание ВС равнобедренной трапеции, если высота СK, проведённая из конца C меньшего основания, делит большее основание на отрезки AK и KD, разность которых равна 8 см.
Решение:
Сделаем дополнительное построение. Проведём высоту ВМ.
Рассмотрим треугольники ABM и DCK. Они равны по гипотенузе и катету
— AB=CD, как боковые стороны равнобедренной трапеции.
Высоты трапеции BM и CK тоже равны, как перпендикуляры, расположенные между двумя параллельными прямыми
.
Следовательно, AM=KD. Получается, что разность между AK и KD равна разности между AK и AM.
А это есть отрезок MK. Но MK равен ВС, поскольку BCKM — прямоугольник.
Отсюда меньшее основание трапеции равно 8 см.
Задача 4.
Найти отношение оснований трапеции, если её средняя линия делится диагоналями на 3 равные части.
Решение:
Поскольку MN — средняя линия трапеции, то она параллельна основаниям и делит боковые стороны пополам
.
По теореме Фалеса MN делит также и стороны AC и BD пополам.
Рассматривая треугольник АВС можно видеть, что MO в нём — средняя линия. А средняя линия треугольника параллельна основанию и равна его половине
. Т.е. если MO=Х, то ВС=2Х.
Из треугольника ACD имеем ON — средняя линия.
Она тоже параллельна основанию и равна его половине.
Но, поскольку OP+PN= Х+Х=2Х, тогда AD=4Х.
Получается, что верхнее основание трапеции равно 2Х, а нижнее — 4Х.
Ответ: отношение оснований трапеции равно 1:2.
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания .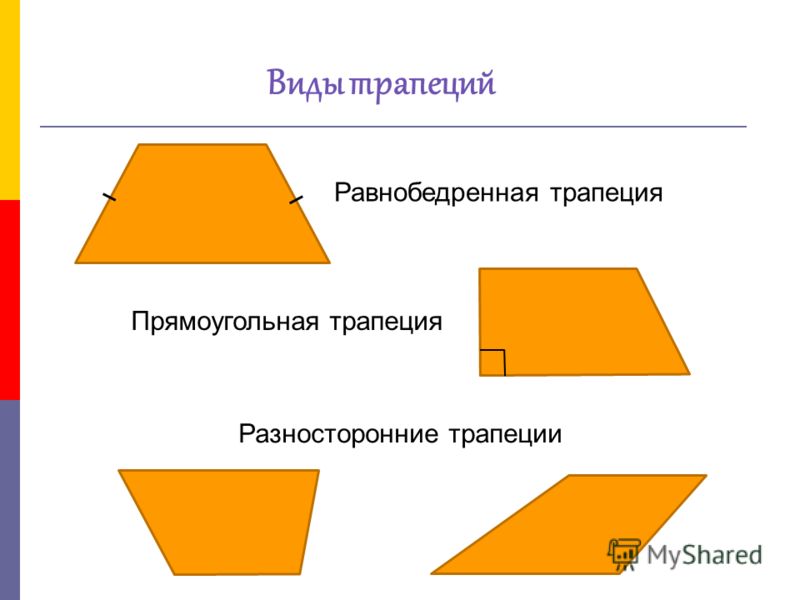 На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.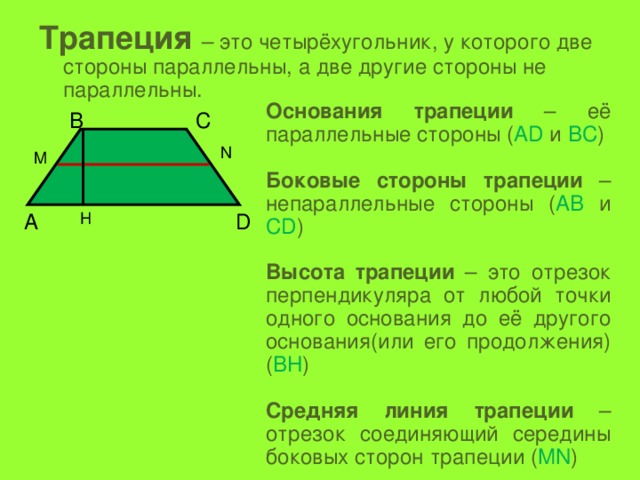
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне.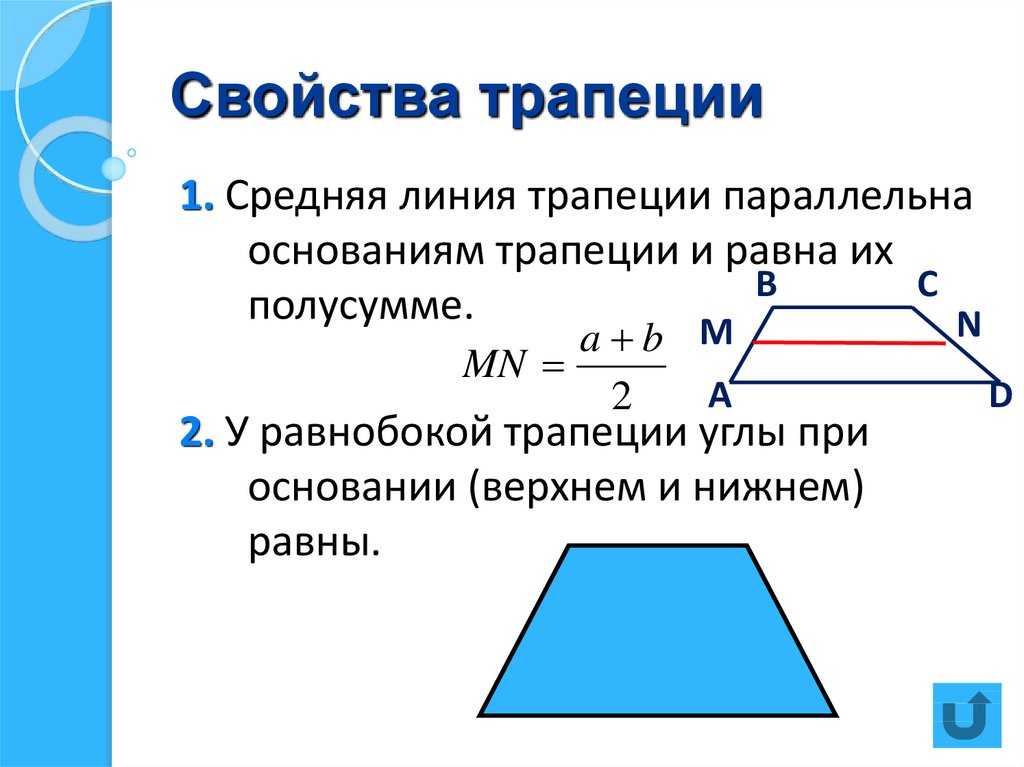 Найдите боковую сторону трапеции.
Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD , если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция».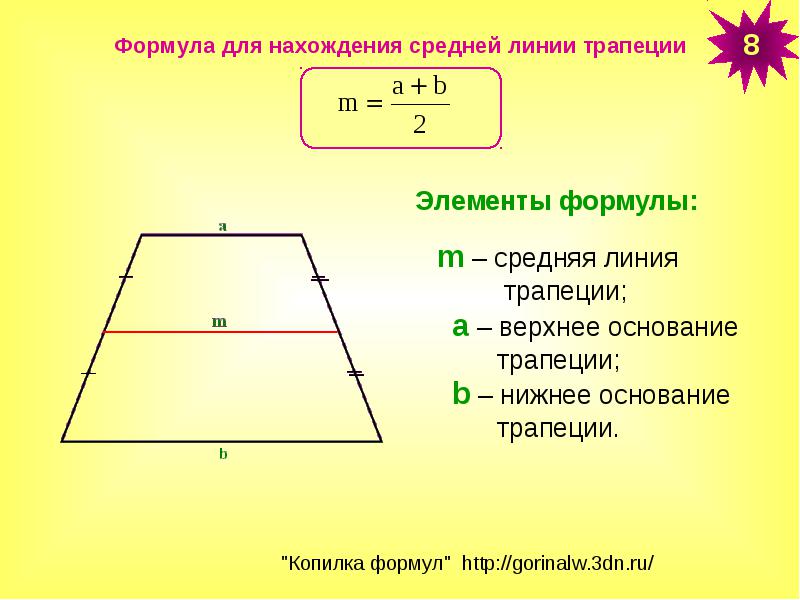 Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.
Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.
Как подготовиться к экзамену?
Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.
Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».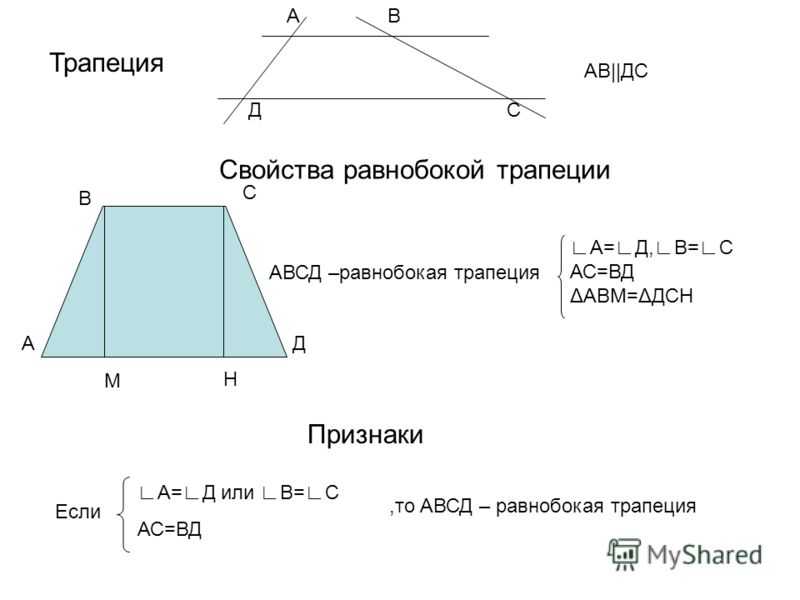
«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.
Как вычислить стороны трапеции. Площадь трапеции: как рассчитать, формула
И . Теперь можно приступить к рассмотрению вопроса, как найти площадь трапеции. Эта задача в быту встречается очень редко, но иногда возникает необходимость, например, найти площадь комнаты в форме трапеции, которая все чаще используется при строительстве современных квартир, или в дизайнерских проектах реконструкции.
Трапеция – геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны друг другу и называются основаниями трапеции. Два других сегмента называются сторонами трапеции. Кроме того, в дальнейшем нам понадобится еще одно определение. Это средняя линия трапеции, представляющая собой отрезок, соединяющий середины сторон и высоту трапеции, равную расстоянию между основаниями.
Два других сегмента называются сторонами трапеции. Кроме того, в дальнейшем нам понадобится еще одно определение. Это средняя линия трапеции, представляющая собой отрезок, соединяющий середины сторон и высоту трапеции, равную расстоянию между основаниями.
Как и треугольники, трапеция имеет отдельные виды в виде равнобедренной (равнобедренной) трапеции, у которой длины сторон одинаковы, и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна половине суммы оснований и параллельна им.
- Равнобедренные трапеции имеют равные стороны и углы, которые они образуют с основаниями.
- Середины диагоналей трапеции и точка пересечения ее диагоналей лежат на одной прямой.
- Если сумма сторон трапеции равна сумме оснований, то в нее можно вписать окружность
- Если сумма углов, образованных сторонами трапеции при любом ее основании равно 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.

- Равнобедренную трапецию можно описать окружностью. Наоборот. Если в окружность вписана трапеция, то она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции, будет перпендикулярен ее основаниям и представляет собой ось симметрии.
Как найти площадь трапеции .
Площадь трапеции будет равна половине суммы ее оснований, умноженной на ее высоту. В виде формулы это записывается как выражение:
где S — площадь трапеции, a,b — длина каждого из оснований трапеции, h — высота трапеции.
Вы можете понять и запомнить эту формулу следующим образом. Как следует из рисунка ниже, трапецию с помощью средней линии можно преобразовать в прямоугольник, длина которого будет равна половине суммы оснований.
Вы также можете разложить любую трапецию на более простые фигуры: прямоугольник и один или два треугольника, и если вам будет проще, то найти площадь трапеции как сумму площадей составляющих ее фигур.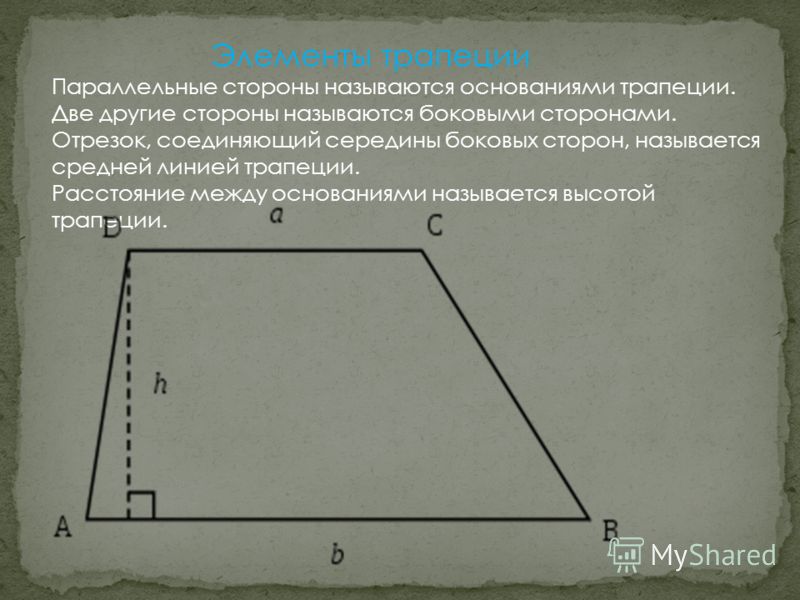
Есть еще одна простая формула для расчета его площади. Согласно ему площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается как: S = m * h, где S — площадь, m — длина средней линии, h — высота трапеции. Эта формула больше подходит для математических задач, чем для бытовых, так как в реальных условиях вы не узнаете длину средней линии без предварительных расчетов. И вы будете знать только длины оснований и сторон.
В этом случае площадь трапеции можно найти по формуле:
S = ((a + b) / 2) * √c 2 — ((b-a) 2 + c 2 -d 2 / 2 (b-a)) 2
где S – площадь, a,b – основания, c,d – стороны трапеции.
Есть еще несколько способов найти площадь трапеции. Но, они примерно так же неудобны, как и последняя формула, а значит, нет смысла на них останавливаться. Поэтому рекомендуем использовать первую формулу из статьи и желаем всегда получать точные результаты.
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм.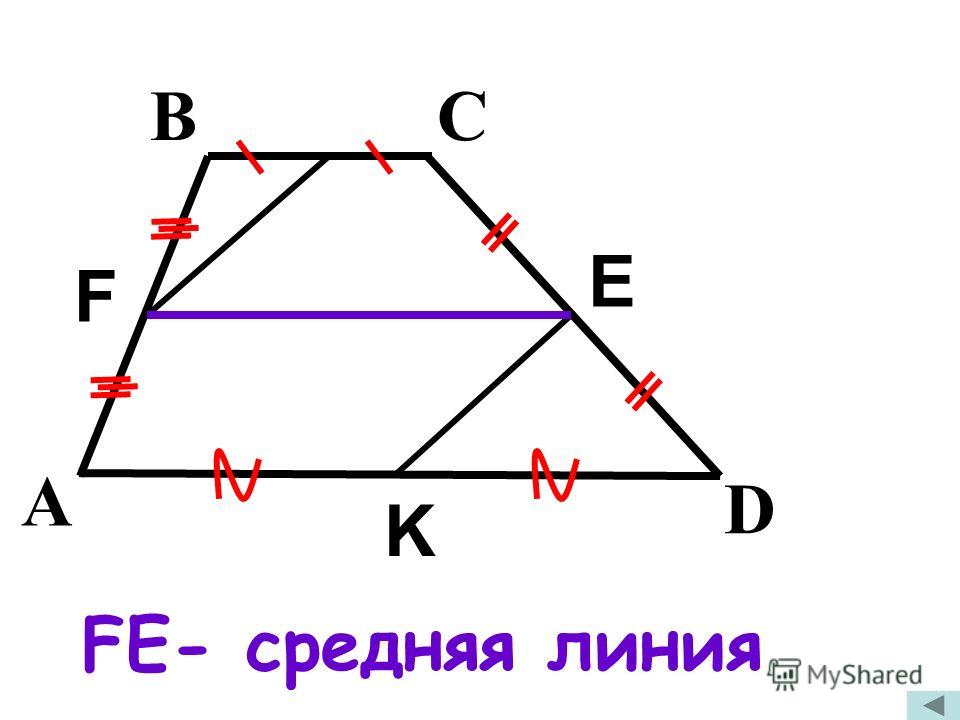 Среди них трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие — нет. Параллельные противоположные стороны называются основаниями, а две другие – сторонами трапеции. Отрезок, соединяющий середины сторон, называется средней линией. Трапеции бывают нескольких видов: равнобедренные, прямоугольные, криволинейные. Для каждого типа трапеций существуют формулы нахождения площади.
Среди них трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие — нет. Параллельные противоположные стороны называются основаниями, а две другие – сторонами трапеции. Отрезок, соединяющий середины сторон, называется средней линией. Трапеции бывают нескольких видов: равнобедренные, прямоугольные, криволинейные. Для каждого типа трапеций существуют формулы нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание равно a, нижнее — b, а высота — h. Тогда можно вычислить площадь S по формуле:
S = ½ * (a + b) * h
т.е. возьмите половину суммы оснований, умноженных на высоту.
Вы также можете вычислить площадь трапеции, если знаете значение высоты и средней линии. Обозначим среднюю линию — m. Затем
Решим задачу посложнее: нам известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь находится по формуле:
Тогда площадь находится по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sinα
где d с индексы 1 и 2 — диагонали. В этой формуле при расчете дается синус угла.
При известных длинах основания a и b и двух углах у нижнего основания площадь рассчитывается следующим образом:
S = ½ * (b2 — a2) * (sin α * sin β / sin(α + β))
Площадь равнобедренной трапеции
Равнобедренная трапеция является частным случаем трапеции. Отличие ее в том, что такая трапеция представляет собой выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Его стороны равны.
Есть несколько способов найти площадь равнобедренной трапеции.
- По трем сторонам. В этом случае длины сторон будут совпадать, поэтому они обозначаются одним значением — с, а и b — длины оснований:
- Если известны длина верхнего основания, боковой стороны и угол при нижнем основании, то площадь рассчитывается следующим образом:
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — сторона.
- Если вместо верхнего основания известна длина нижнего основания — b, то площадь рассчитывается по формуле:
S = c * sin α * (b — c * cos α)
- Если известны два основания и угол при нижнем основании, площадь вычисляется по тангенсу угла:
S = ½ * (b2 — a2) * tg α
- Также площадь вычисляется через диагонали и угол между ними. При этом диагонали равны по длине, поэтому каждая обозначается буквой d без индексов:
S = ½ * d2 * sinα
- Вычислите площадь трапеции, зная длину боковой стороны, среднюю линию и угол при нижнем основании.
Пусть сторона — с, средняя линия — м, угол — а, тогда:
S = m * c * sinα
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее сторон. Затем площадь находится через радиус вписанной окружности и угол при нижнем основании:
S = 4r2 / sinα
Такой же расчет производится через диаметр D вписанной окружности (кстати, он совпадает с высота трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется следующим образом:
S = a*b/sinα
(эта и последующие формулы справедливы только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется следующим образом:
Если известны только основания, то площадь вычисляется по формуле:
Через основания и боковую линию площадь площадь трапеции с вписанной окружностью и через основания и среднюю линию — m вычисляется следующим образом:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из сторон перпендикулярна основаниям. В этом случае длина стороны совпадает с высотой трапеции.
Прямоугольная трапеция состоит из квадрата и треугольника. Найдя площадь каждой из фигур, сложите результаты и получите общую площадь фигуры.
Также общие формулы расчета площади трапеции подходят для расчета площади прямоугольной трапеции.
- Если длины оснований и высота (или перпендикулярная сторона) известны, то площадь рассчитывается по формуле:
S = (a + b) * h / 2
Поскольку h (высота) может быть сторона с.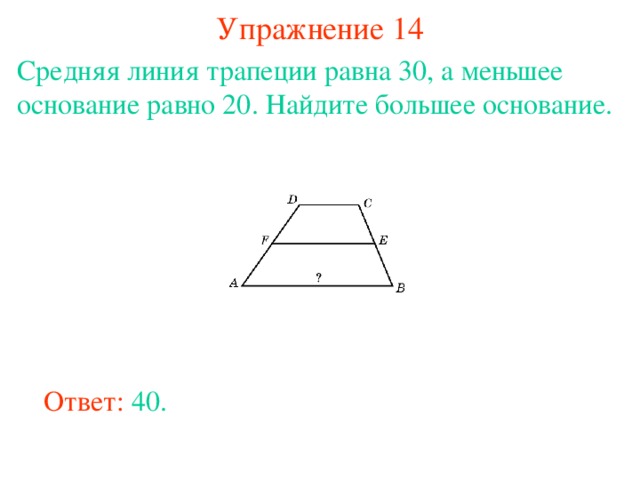 Тогда формула выглядит так:
Тогда формула выглядит так:
S = (a + b) * c / 2
- Другой способ вычисления площади — умножить длину средней линии на высоту:
или по длине боковой перпендикулярной стороны:
- Следующий метод расчета — через половину произведения диагоналей на синус угла между ними:
S = ½ * d1 * d2 * sinα
Если диагонали перпендикулярны, то формула упрощается до:
S = ½ * d1 * d2
- сумма длин двух противоположных сторон) и радиус вписанной окружности.
Эта формула действительна для оснований. Если взять длины сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
S = (2r + c) * r
- Если в трапецию вписана окружность, то площадь вычисляется так же:
где m — длина средней линии.
Площадь криволинейной трапеции
Криволинейная трапеция – плоская фигура, ограниченная графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке , оси x и прямых линиях x = а, х = б. На самом деле две его стороны параллельны друг другу (основаниям), третья сторона перпендикулярна основаниям, а четвертая представляет собой кривую, соответствующую графику функции.
На самом деле две его стороны параллельны друг другу (основаниям), третья сторона перпендикулярна основаниям, а четвертая представляет собой кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищется через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают такими же свойствами углов. Как и у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к стороне, равна 180 градусов.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают затруднения у многих школьников. Вы легко с ними справитесь, если запомните все необходимые формулы и потренируетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попадаться вам в КИМах на сертификационных экзаменах или на олимпиадах. Поэтому относитесь к ним бережно.
Что нужно знать о трапеции?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие нет.
В трапеции высоту (перпендикулярную основанию) также можно не указывать. Проводится средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в некоторых случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность вокруг него.
Формулы площади трапеции
Сначала рассмотрим стандартные формулы нахождения площади трапеции. Способы расчета площади равнобедренных и криволинейных трапеций будут рассмотрены ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, у которой высота h опущена к большему основанию. Вычислить площадь фигуры в этом случае несложно. Нужно просто разделить на два сумму длин оснований и умножить полученное на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, что помимо высоты трапеция имеет срединную линию m. Мы знаем формулу нахождения длины средней линии: m = 1/2(a + b). Поэтому мы с полным правом можем упростить формулу площади трапеции до следующего вида: S = м * ч . Другими словами, чтобы найти площадь трапеции, нужно среднюю линию умножить на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, нужно произведение диагоналей разделить пополам и полученное умножить на синус угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу нахождения площади трапеции, если о ней ничего не известно, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить ее на всякий случай: S = 1/2 (а + b) * √c 2 — ((1/2 (b — a)) * ((b — a) 2 + c 2 — d 2)) 2 .
Кстати, вышеприведенные примеры справедливы и для случая, когда нужна формула площади прямоугольной трапеции. Это трапеция, сторона которой примыкает к основаниям под прямым углом.
Это трапеция, сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда окружность радиуса r вписана внутрь равнобедренной трапеции, а боковая сторона и большее основание образуют острый угол α. В трапецию можно вписать окружность, если сумма длин ее оснований равна сумме длин сторон.
Площадь равнобедренной трапеции вычисляется следующим образом: квадрат радиуса вписанной окружности умножить на четыре и все это разделить на sinα: S = 4r 2 /sinα . Другая формула площади — это частный случай варианта, когда угол между большим основанием и стороной равен 30 0 : S = 8r2 .
Второй вариант: на этот раз берем равнобедренную трапецию, у которой, кроме того, проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота равна половине суммы оснований: h = 1/2 (a + b). Зная это, несложно преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h3 .
Зная это, несложно преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h3 .
Формула площади криволинейной трапеции
Начнем с понимания: что такое криволинейная трапеция. Представьте ось координат и график непрерывной и неотрицательной функции f, которая не меняет знак в пределах заданного отрезка по оси x. Криволинейная трапеция образована графиком функции у = f(x) — вверху, ось х — внизу (отрезок), а по бокам — прямыми линиями, проведенными между точками а и b и графиком функции.
Вычислить площадь такой нестандартной фигуры вышеуказанными методами невозможно. Здесь нужно применить математический анализ и использовать интеграл. А именно, формула Ньютона-Лейбница — S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F — первообразная нашей функции на выбранном интервале. А площадь криволинейной трапеции соответствует приращению первообразной на данном отрезке.
Примеры задач
Чтобы все эти формулы лучше укладывались в голове, вот несколько примеров задач на нахождение площади трапеции.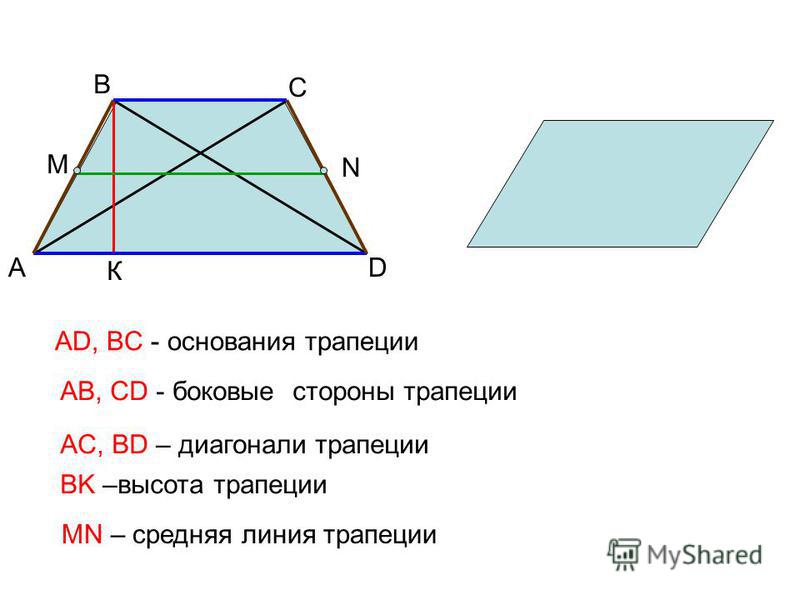 Будет лучше, если вы сначала сами попробуете решить задачи, а уже потом сверите полученный ответ с готовым решением.
Будет лучше, если вы сначала сами попробуете решить задачи, а уже потом сверите полученный ответ с готовым решением.
Задание №1: Дана трапеция. Его большее основание 11 см, меньшее 4 см. У трапеции есть диагонали, одна длиной 12 см, другая 9 см.
Решение: Построить трапециевидную АМРС. Проведите прямую RX через вершину P так, чтобы она была параллельна диагонали MC и пересекала прямую AC в точке X. Получился треугольник APX.
Рассмотрим две фигуры, полученные в результате этих манипуляций: треугольник APX и параллелограмм CMPX.
Благодаря параллелограмму узнаем, что РХ = МС = 12 см и СХ = MP = 4 см. Где можно вычислить сторону АХ треугольника АРКА: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник ARCH прямоугольный (для этого применим теорему Пифагора — AX 2 = AP 2 + PX 2). И вычислить его площадь: S APX = 1/2 (AP * PX) = 1/2 (9* 12) = 54 см 2 .
Далее нужно доказать, что треугольники AMP и PCX равны по площади.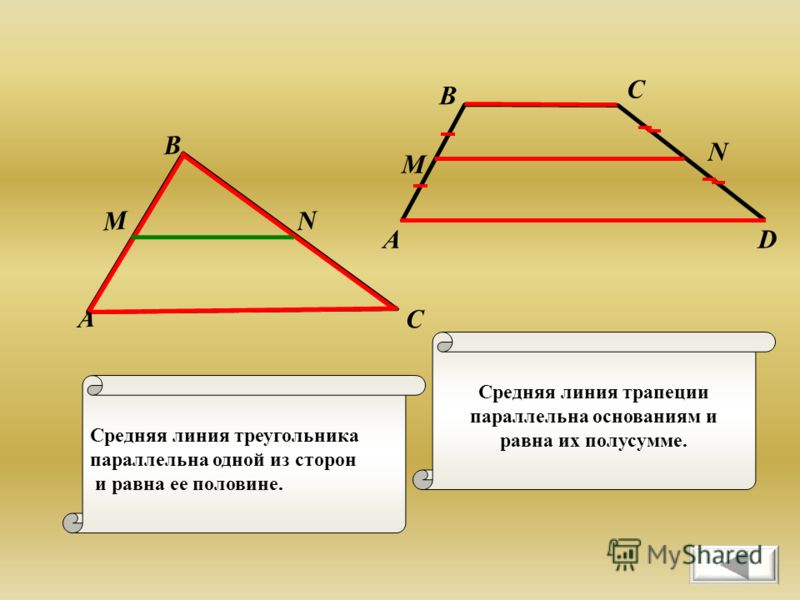 Основой будет равенство сторон MP и CX (уже доказано выше). А также высоты, которые вы опускаете по этим сторонам — они равны высоте трапеции АМРС.
Основой будет равенство сторон MP и CX (уже доказано выше). А также высоты, которые вы опускаете по этим сторонам — они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. Точки О и Е расположены на его боковых сторонах, а ОЕ и КС параллельны. Также известно, что площади трапеций ORME и OXE находятся в соотношении 1:5. ПМ = а и КС = b. Вам нужно найти ОЭ.
Решение: Проведите через точку М прямую, параллельную РК, и обозначьте точку ее пересечения с ОЕ как Т. А — точка пересечения прямой, проведенной через точку Е, параллельной РК, с основанием КС.
Введем еще одно обозначение — OE = x. А также высоту h 1 для треугольника TME и высоту h 2 для треугольника AEC (можно самостоятельно доказать подобие этих треугольников).
Предположим, что b > a. Площади трапеций ORME и OXE связаны как 1:5, что дает нам право составить следующее уравнение: (x + a) * h 1 = 1/5 (b + x) * h 2 . преобразуем и получаем: h 1 / h 2 = 1/5 * ((b + x) / (x + a)).
преобразуем и получаем: h 1 / h 2 = 1/5 * ((b + x) / (x + a)).
Так как треугольники TME и AEC подобны, то h 1 / h 2 = (x — a) / (b — x). Объедините обе записи и получите: (х — а) / (b — х) = 1/5 * ((b + х) / (х + а)) ↔ 5 (х — а) (х + а) = (b + x) (b — x) ↔ 5 (x 2 — a 2) = (b 2 — x 2) ↔ 6x 2 = b 2 + 5a 2 ↔ x = √ (5a 2 + b 2) / 6.
Таким образом, ОЕ = x = √ (5a 2 + b 2) / 6.
Заключение
Геометрия не самая легкая из наук, но с экзаменационными заданиями вы наверняка справитесь. Просто нужно немного терпения при подготовке. И, конечно же, запомнить все необходимые формулы.
Мы постарались собрать в одном месте все формулы расчета площади трапеции, чтобы вы могли использовать их при подготовке к экзаменам и повторении материала.
Обязательно поделитесь этой статьей со своими одноклассниками и друзьями в социальных сетях. Пусть хороших оценок за ЕГЭ и ГИА будет больше!
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Чтобы уверенно чувствовать себя и успешно решать задачи на уроках геометрии, недостаточно выучить формулы. Их нужно понять в первую очередь. Бояться, а тем более ненавидеть формул непродуктивно. В этой статье будут доступным языком разобраны различные способы нахождения площади трапеции. Для лучшего усвоения соответствующих правил и теорем обратим некоторое внимание на его свойства. Это поможет вам понять, как работают правила и в каких случаях следует применять те или иные формулы.
Определить трапецию
Что это за фигура вообще? Трапеция – это многоугольник с четырьмя углами и двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под разными углами. Его параллельные стороны называются основаниями, а для непараллельных сторон используется название «стороны» или «бедра». Такие фигуры довольно часто встречаются в быту. Контуры трапеции можно увидеть в силуэтах одежды, предметов интерьера, мебели, посуды и многих других. Трапеция может быть разных видов: разносторонняя, равнобедренная и прямоугольная. Более подробно их виды и свойства мы разберем далее в статье.
Более подробно их виды и свойства мы разберем далее в статье.
Свойства трапеции
Кратко остановимся на свойствах этой фигуры. Сумма углов, прилежащих к любой стороне, всегда равна 180°. Следует отметить, что все углы трапеции в сумме составляют 360°. Трапеция имеет понятие средней линии. Если соединить середины сторон отрезком, это будет средняя линия. Обозначается м.б. Средняя линия имеет важные свойства: она всегда параллельна основаниям (мы помним, что основания тоже параллельны друг другу) и равна их полусумме:
Это определение нужно выучить и понять, потому что оно является ключом к решению многих проблем!
У трапеции всегда можно уменьшить высоту до основания. Высота – это перпендикуляр, часто обозначаемый символом h, проведенный из любой точки одного основания к другому основанию или его продолжению. Средняя линия и высота помогут найти площадь трапеции. Такие задачи являются наиболее распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Простейшие формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых можно найти площадь трапеции. Достаточно умножить высоту на половину суммы оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства чтения в этой статье знаки умножения отмечены в формулах символом (*), хотя в официальных справочниках знак умножения обычно опускается.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высотой 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2=12. Значит, полусумма равна 12 см. Теперь умножаем полусумму на высоту: 12*7=84. Искомое найдено. Ответ: площадь трапеции 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически следует из предыдущей концепции средней линии: S=m*h.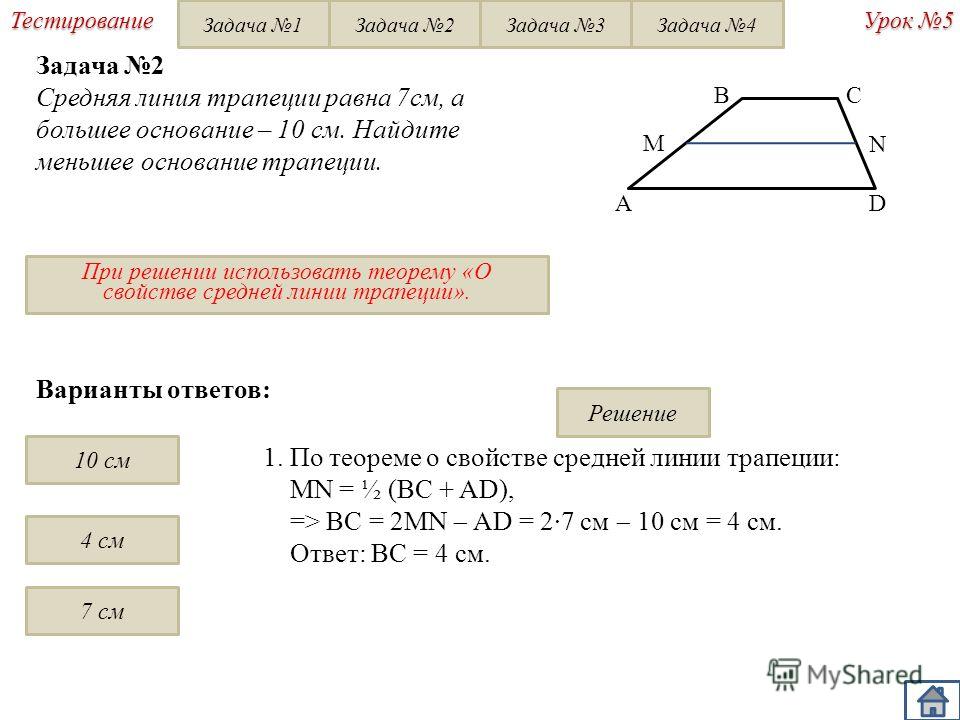
Использование диагоналей для расчетов
Другой способ найти площадь трапеции на самом деле не так уж сложен. Он связан со своими диагоналями. Согласно этой формуле, чтобы найти площадь, требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sin a.
Рассмотрим задачу, показывающую применение этого метода. Дано: трапеция с диагональю 8 и 13 см соответственно. Угол а между диагоналями равен 30°. Найдите площадь трапеции.
Раствор. Используя приведенную выше формулу, легко рассчитать, что требуется. Как известно, sin 30° равен 0,5. Следовательно, S = 8*13*0,5=52. Ответ: Площадь 52 квадратных метра. см.
Ищем площадь равнобедренной трапеции
Трапеция может быть равнобедренной (равнобедренной). Его стороны одинаковы И углы при основаниях равны, что хорошо показано на рисунке. Равнобедренная трапеция обладает теми же свойствами, что и обычная трапеция, плюс ряд специальных.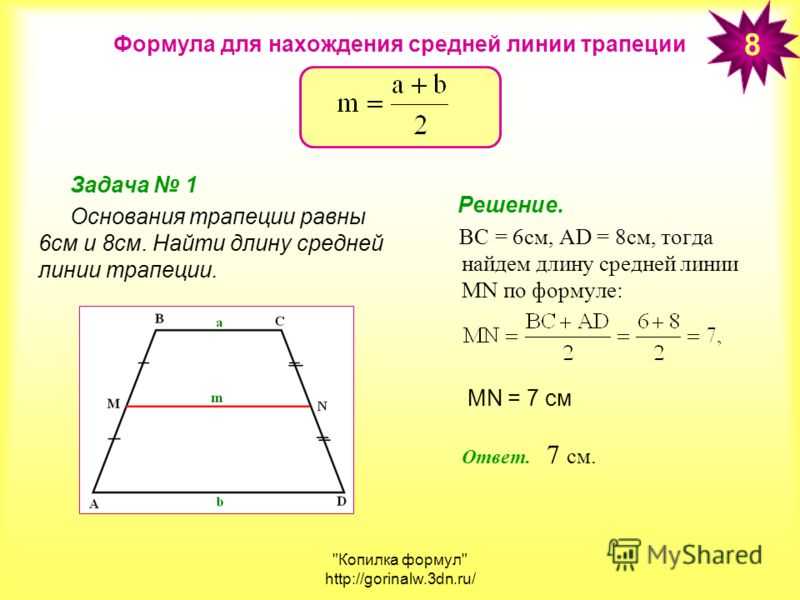 Вокруг равнобедренной трапеции можно описать окружность и вписать в нее окружность.
Вокруг равнобедренной трапеции можно описать окружность и вписать в нее окружность.
Какими способами можно вычислить площадь такой фигуры? Приведенный ниже метод потребует большого количества вычислений. Для его использования необходимо знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса, либо инженерный калькулятор. Вот формула:
S = c *sin a *( a — c * cos a ),
где С — латеральная поверхность бедра а — угол у нижнего основания.
У равнобедренной трапеции диагонали одинаковой длины. Верно и обратное: если диагонали трапеции равны, то она равнобедренная. Отсюда следующая формула, помогающая найти площадь трапеции – полупроизведение квадрата диагоналей и синуса угла между ними: S = ½ d 2 sin a.
Нахождение площади прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна сторона (ее бедро) примыкает к основаниям под прямым углом. Обладает свойствами обычной трапеции. Кроме того, у него есть очень интересная особенность. Разность площадей диагоналей такой трапеции равна разности площадей ее оснований. Для него используются все ранее приведенные способы расчета площади.
Это трапеция, у которой одна сторона (ее бедро) примыкает к основаниям под прямым углом. Обладает свойствами обычной трапеции. Кроме того, у него есть очень интересная особенность. Разность площадей диагоналей такой трапеции равна разности площадей ее оснований. Для него используются все ранее приведенные способы расчета площади.
Применение смекалки
Есть одна хитрость, которая может помочь в случае забывания конкретных формул. Рассмотрим подробнее, что такое трапеция. Если мы мысленно разделим его на части, то получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, а затем сложить все полученные значения.
Давайте проиллюстрируем это на следующем примере. Дана прямоугольная трапеция. Угол C = 45°, углы A, D равны 90°. Верхнее основание трапеции 20 см, высота 16 см. Требуется вычислить площадь фигуры.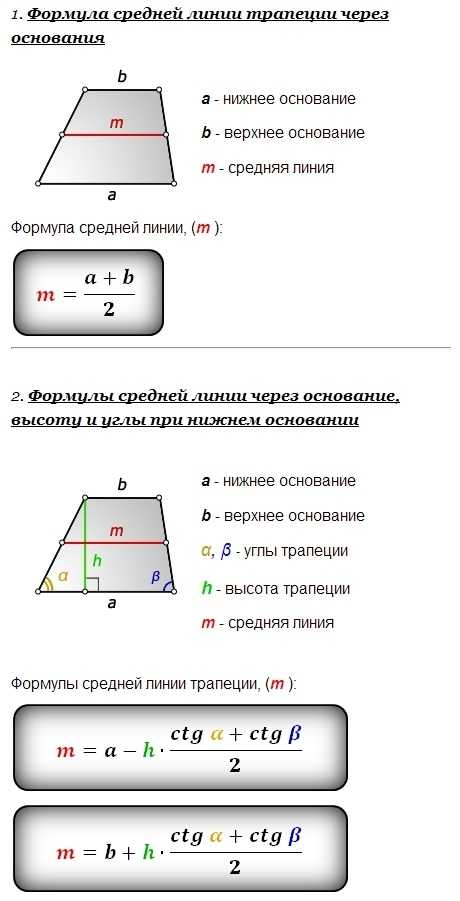
Эта фигура, очевидно, состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, то ее высота равна стороне, то есть 16 см. У нас есть прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона равна 16 см. Так как эта сторона также является высотой трапеции (а мы знаем, что высота падает на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Следовательно, оставшийся угол треугольника равен 45°. Вследствие этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны равны. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площади треугольника и прямоугольника и сложить полученные значения.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равна произведению его ширины на длину: S = 20*16 = 320. Нашли искомое: площадь трапеции S = 128 + 320 = 448 кв.см. Вы можете легко перепроверить себя, используя приведенные выше формулы, ответ будет идентичным.
Нашли искомое: площадь трапеции S = 128 + 320 = 448 кв.см. Вы можете легко перепроверить себя, используя приведенные выше формулы, ответ будет идентичным.
Используем формулу Пика
Наконец, приведем еще одну оригинальную формулу, помогающую найти площадь трапеции. Это называется формулой Пика. Его удобно использовать, когда трапецию рисуют на клетчатой бумаге. Подобные задания часто встречаются в материалах ГИА. Выглядит это так:
S = M/2 + N — 1,
в этой формуле М — количество узлов, т.е. пересечений линий рисунка с линиями ячейки на границах трапеции (оранжевые точки на рисунке), N — количество узлов внутри фигуры (синие точки). Его удобнее всего использовать при нахождении площади неправильного многоугольника. Однако чем больше арсенал используемых приемов, тем меньше ошибок и лучше результаты.
Конечно, приведенная информация далеко не исчерпывает видов и свойств трапеции, а также способов нахождения ее площади. В этой статье представлен обзор его наиболее важных характеристик. При решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
В этой статье представлен обзор его наиболее важных характеристик. При решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Наиболее распространенные формулы, составленные вместе, помогут учащимся сориентироваться в различных способах вычисления площади трапеции и лучше подготовиться к контрольным работам и контрольным работам по данной теме.
Площадь трапеции. Привет! В данной публикации мы рассмотрим эту формулу. Почему это так и как вы можете это понять? Если есть понимание, то учиться ему не нужно. Если просто хотите посмотреть эту формулу и что срочно, то можете сразу листать страницу вниз))
Теперь подробно и по порядку.
Трапеция — четырехугольник, две стороны которого параллельны, а две другие — нет. Те, которые не параллельны, являются основаниями трапеций. Два других называются сторонами.
Если стороны равны, то трапеция называется равнобедренной.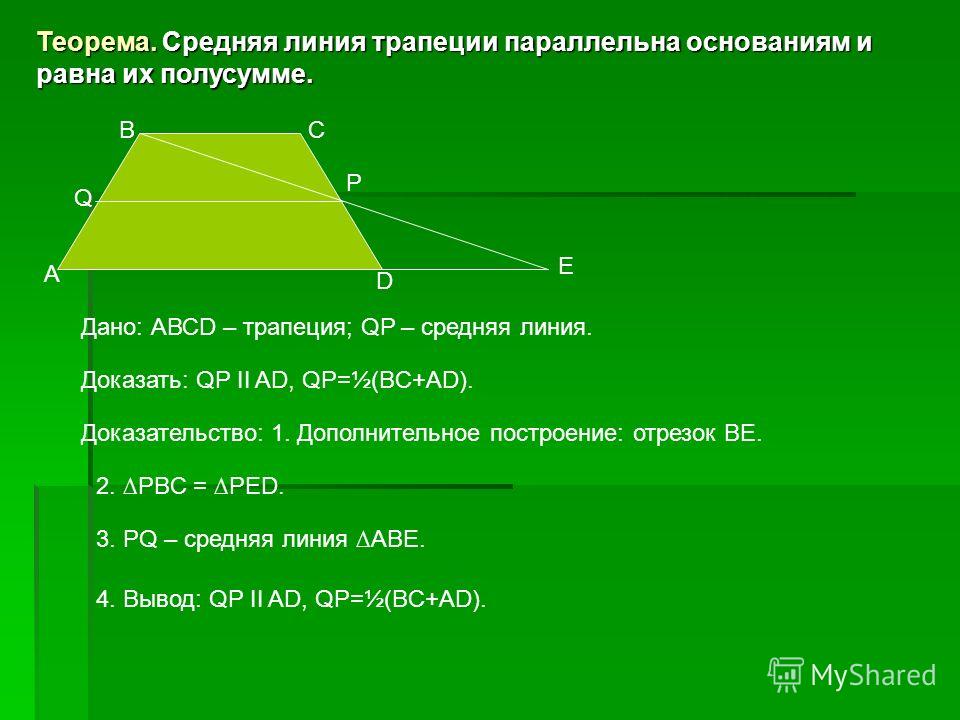 Если одна из сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
Если одна из сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапеция изображается так — большее основание внизу, соответственно меньшее вверху. Но никто не запрещает изображать его и наоборот. Вот скетчи:
Следующая важная концепция.
Срединная линия трапеции — это отрезок, соединяющий середины сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте углубимся. Почему именно?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и проведем дополнительные построения: проведем прямые через основания, а перпендикуляры через концы средней линии до пересечения с основаниями:
* Буквенные обозначения вершин и других точек намеренно не вводятся во избежание ненужных обозначений.
Смотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 равны.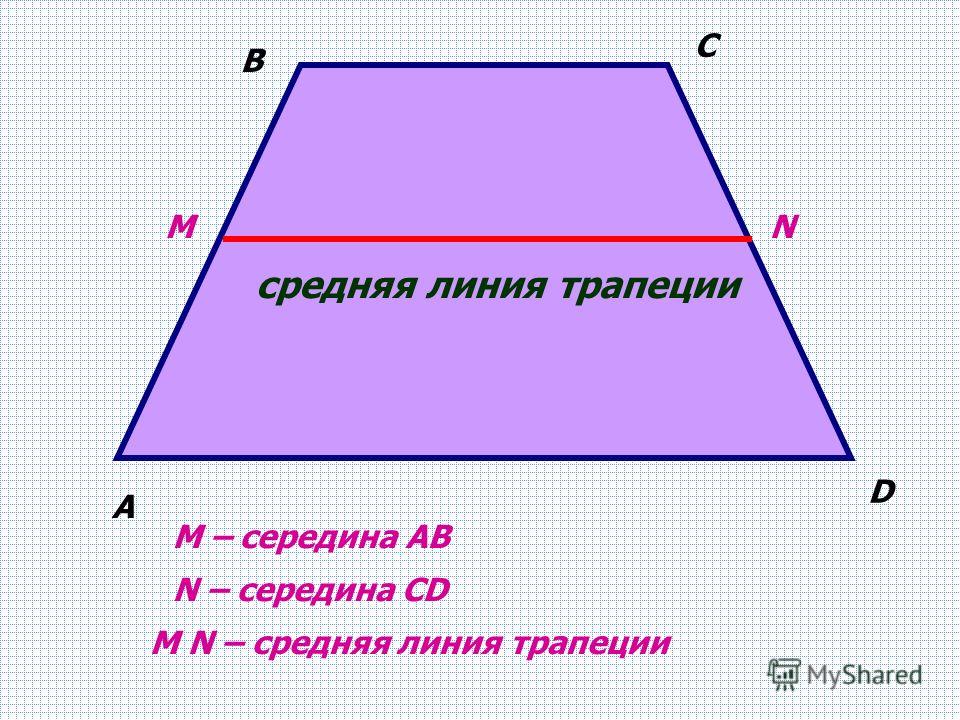 Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезки, то у нас получится отрезок (это сторона прямоугольника), равный средней линии. Далее, если «приклеить» отрезанные синий и красный отрезки к верхнему основанию трапеции, то у нас тоже получится отрезок (это тоже сторона прямоугольника), равный средней линии трапеции.
Понятно? Получается, что сумма оснований будет равна двум медианам трапеции:
См. другое объяснение
Сделаем следующее — построим прямую, проходящую через нижнее основание трапеции и прямая, которая пройдет через точки А и В:
Получаем треугольники 1 и 2, они равны по стороне и прилежащим углам (второй признак равенства треугольников). Это означает, что полученный отрезок (на эскизе он отмечен синим цветом) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия этой трапеции и средняя линия треугольника совпадают.
Известно, что треугольник равен половине параллельного ему основания, то есть:
Ладно, понял. Теперь о площади трапеции.
Формула площади трапеции:
Говорят: площадь трапеции равна произведению половины суммы ее оснований и высоты.
То есть получается, что он равен произведению средней линии на высоту:
Вы наверное уже заметили, что это очевидно. Геометрически это можно выразить так: если мысленно отрезать от трапеции треугольники 2 и 4 и положить их на треугольники 1 и 3 соответственно:
Тогда получится прямоугольник, площадь которого равна площади наша трапеция. Площадь этого прямоугольника будет равна произведению средней линии на высоту, то есть мы можем написать:
Но тут дело не в написании, конечно, а в понимании.
Скачать (просмотреть) материал статьи в формате *pdf
Вот и все. Удачи тебе!
С уважением, Александр.
чему равно, свойства, доказательство теоремы.
 Найдите среднюю линию трапеции с помощью высоты, диагоналей и углов
Найдите среднюю линию трапеции с помощью высоты, диагоналей и угловВ этой статье мы постараемся максимально полно отразить свойства трапеции. В частности, речь пойдет об общих признаках и свойствах трапеции, а также о свойствах вписанной трапеции и о окружности, вписанной в трапецию. Затронем также свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разобраться в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала вкратце вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – это четырехугольник, две стороны которого параллельны друг другу (это основания). А две не параллельны — это стороны.
В трапеции высоту можно не указывать — перпендикулярно основаниям. Проводятся средняя линия и диагонали. А также из любого угла трапеции можно провести биссектрису.
О различных свойствах, связанных со всеми этими элементами и их комбинациями, мы сейчас и поговорим.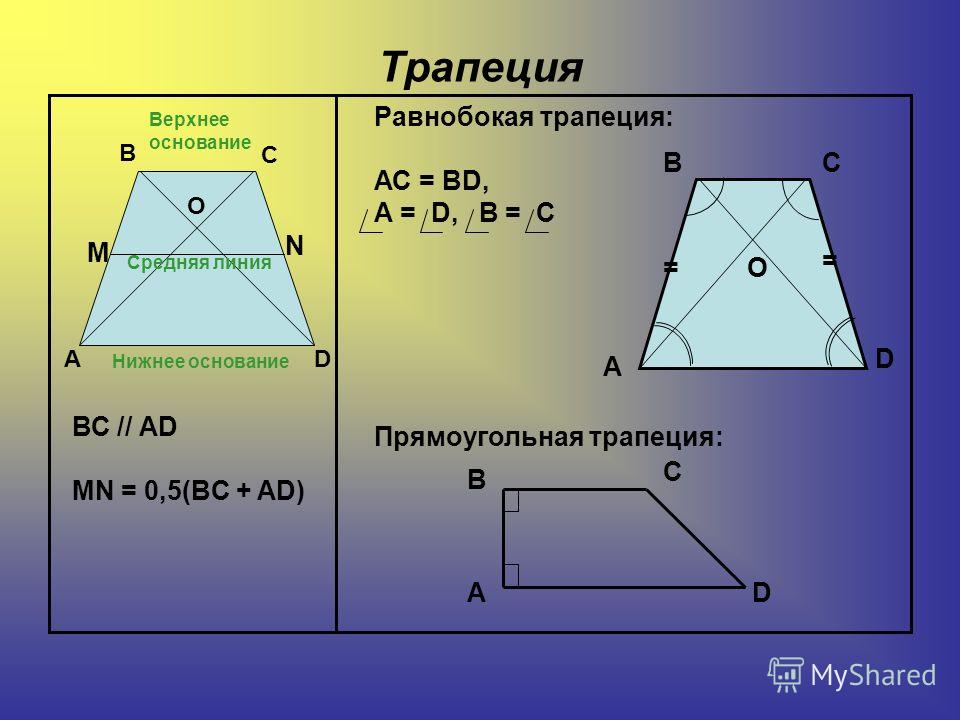
Свойства диагоналей трапеции
Чтобы было понятнее, при чтении начертите трапецию ACME на листе бумаги и проведите в ней диагонали.
- Если найти середины каждой из диагоналей (назовем эти точки X и T) и соединить их, получится отрезок. Одно из свойств диагоналей трапеции состоит в том, что отрезок XT лежит на средней линии. А его длину можно получить, разделив разность оснований на два: ХТ = (а — б) / 2 .
- Перед нами та самая трапеция ACME. Диагонали пересекаются в точке O. Рассмотрим треугольники AOE и IOC, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники подобны. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = AE/KM.
Отношение площадей треугольников AOE и IOC описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только на этот раз мы будем рассматривать треугольники, которые диагональные отрезки образовали вместе со сторонами трапеции.
 Площади треугольников АКО и ЭМО равны — их площади одинаковы.
Площади треугольников АКО и ЭМО равны — их площади одинаковы. - Еще одним свойством трапеции является построение диагоналей. Итак, если мы продолжим стороны АК и МЕ в сторону меньшего основания, то рано или поздно они пересекутся в какой-то точке. Далее проведите прямую линию через середины оснований трапеции. Он пересекает основания в точках X и T.
Если теперь продолжить линию XT, то она соединит точку пересечения диагоналей трапеции O, точку, в которой пересекаются продолжения сторон и середины оснований X и T. - Через точку пересечения диагоналей проводим отрезок, соединяющий основания трапеции (Т лежит на меньшем основании КМ, Х — на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОН = КМ/АЭ .
- А теперь через точку пересечения диагоналей проводим отрезок, параллельный основаниям трапеции (а и б). Точка пересечения разделит его на две равные части. Длину отрезка можно найти по формуле 2ab/(a + b) .

Свойства средней линии трапеции
Проведите среднюю линию трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, сложив длины оснований и разделив их пополам: м = (а + b)/2 .
- Если провести любой отрезок (высоту, например) через оба основания трапеции, то средняя линия разделит ее на две равные части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и начертите биссектрису. Возьмем, к примеру, угол КАЕ нашей трапеции АСМЕ. Выполнив построение самостоятельно, вы легко увидите, что биссектриса отсекает от основания (или его продолжения на прямой вне самой фигуры) отрезок такой же длины, как и сторона.
Свойства угла трапеции
- Какой бы из двух пар углов, примыкающих к стороне, вы ни выбрали, сумма углов в паре всегда равна 180 0 : α + β = 180 0 и γ + δ = 180 0 .
- Соедините середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции.
 Если сумма углов для любого из них равна 90 0 , длину отрезка ТХ легко вычислить по разнице длин оснований, деленной пополам: ТХ = (АЭ — КМ) / 2 .
Если сумма углов для любого из них равна 90 0 , длину отрезка ТХ легко вычислить по разнице длин оснований, деленной пополам: ТХ = (АЭ — КМ) / 2 . - Если провести параллельные линии через стороны угла трапеции, то они разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобедренной) трапеции
- У равнобедренной трапеции углы при любом из оснований равны.
- Теперь снова постройте трапецию, чтобы легче было представить, о чем она. Посмотрите внимательно на основание АЕ — вершина противоположного основания М проецируется в некоторую точку на прямой, содержащей АЕ. Расстояние от вершины А до точки проекции вершины М и средней линии равнобедренной трапеции равно.
- Несколько слов о свойстве диагоналей равнобедренной трапеции — их длины равны. А также углы наклона этих диагоналей к основанию трапеции одинаковы.
- Только вблизи равнобедренной трапеции можно описать окружность, так как обязательным условием для этого является сумма противоположных углов четырехугольника 180 0 .

- Свойство равнобедренной трапеции следует из предыдущего абзаца — если вокруг трапеции можно описать окружность, то она равнобедренная.
- Из особенностей равнобедренной трапеции следует свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + б)/2 .
- Снова проведите линию ТХ через середины оснований трапеции — в равнобедренной трапеции она перпендикулярна основаниям. И в то же время ТХ является осью симметрии равнобедренной трапеции.
- На этот раз опустите к большему основанию (назовем его а) высоту от противоположной вершины трапеции. Вы получите два разреза. Длину одного можно найти, если сложить длины оснований и разделить пополам: (а+б)/2 . Второе мы получим, если из большего основания вычтем меньшее и разделим полученную разницу на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Поскольку речь уже идет о трапеции, вписанной в окружность, остановимся на этом вопросе подробнее.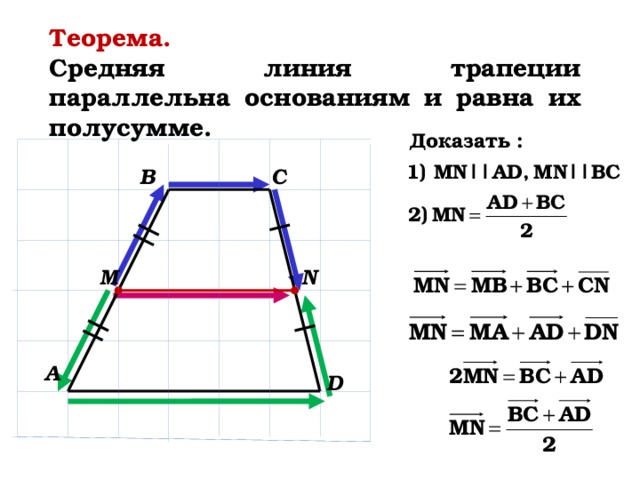 В частности, где находится центр окружности по отношению к трапеции. Здесь тоже рекомендуется не полениться взять в руки карандаш и нарисовать то, о чем пойдет речь ниже. Так вы быстрее поймете и лучше запомните.
В частности, где находится центр окружности по отношению к трапеции. Здесь тоже рекомендуется не полениться взять в руки карандаш и нарисовать то, о чем пойдет речь ниже. Так вы быстрее поймете и лучше запомните.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к стороне. В этом случае большее основание пересекает центр описанной окружности ровно посередине (R = ½AE).
- Диагональ и сторона могут встречаться и под острым углом — тогда центр окружности находится внутри трапеции.
- Центр описанной окружности может находиться вне трапеции, за ее большим основанием, если между диагональю трапеции и боковой стороной имеется тупой угол.
- Угол, образованный диагональю и большим основанием трапеции ACME (вписанный угол), равен половине соответствующего ей центрального угла: MAE = ½MY .
- Кратко о двух способах нахождения радиуса описанной окружности.
 Способ первый: внимательно посмотрите на свой рисунок — что вы видите? Вы легко заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противоположного угла, умноженное на два. Например, R = АЕ/2 * sinAME . Аналогично формулу можно записать для любой из сторон обоих треугольников.
Способ первый: внимательно посмотрите на свой рисунок — что вы видите? Вы легко заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противоположного угла, умноженное на два. Например, R = АЕ/2 * sinAME . Аналогично формулу можно записать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, стороной и основанием трапеции: R = AM * ME * AE / 4 * S AME .
Свойства трапеции, описанной около окружности
В трапецию можно вписать окружность, если выполняется одно условие. Подробнее об этом ниже. А вместе это сочетание фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, то длину ее средней линии легко найти, сложив длины сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- Для трапеции ACME, описанной около окружности, сумма длин оснований равна сумме длин сторон: AK + ME = KM + AE .

- Из этого свойства оснований трапеции следует обратное утверждение: в ту трапецию можно вписать окружность, сумма оснований которой равна сумме сторон.
- Точка касания окружности радиуса r, вписанной в трапецию, делит боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно рассчитать по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, нарисуйте этот пример сами. У нас есть старая добрая трапеция ACME, описанная вокруг окружности. В нем проведены диагонали, пересекающиеся в точке О. Треугольники АОК и ЕОМ, образованные отрезками диагоналей и сторон, прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т. е. стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции равна диаметру вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называется трапеция, один из углов которой прямой. И его свойства вытекают из этого обстоятельства.
- У прямоугольной трапеции одна сторона перпендикулярна основаниям.

- Высота и сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислить площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через сторону, примыкающую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы наверное уже догадались, что здесь нам снова понадобится трапеция ACME — нарисуйте равнобедренную трапецию. Из вершины M проведите прямую MT, параллельную стороне AK (MT || AK).
Получившийся четырехугольник АКМТ является параллелограммом (АК || МТ, КМ || АТ). Поскольку ME = KA = MT, ∆ MTE равнобедренный и MET = MTE.
АК || МТ, следовательно, МТЭ = КАЭ, МЭТ = МТЭ = КАЭ.
Где АКМ = 180 0 — МЕТ = 180 0 — КАЭ = КМЭ.
К.Э.Д.
Теперь, исходя из свойства равнобедренной трапеции (равенство диагоналей), докажем, что трапеция ACME равнобедренная :
- Для начала проведем прямую МХ – МХ || КЭ.
 Получаем параллелограмм КМНЕ (основание — МХ || КЕ и КМ || ЕХ).
Получаем параллелограмм КМНЕ (основание — МХ || КЕ и КМ || ЕХ).
∆AMH равнобедренный, так как AM = KE = MX и MAX = MEA.
МХ || KE, KEA = MXE, следовательно, MAE = MXE.
Оказалось, что треугольники АКЕ и ЕМА равны между собой, так как АМ = КЕ и АЕ — общая сторона двух треугольников. А также MAE=MXE. Можно заключить, что AK = ME, а значит, трапеция AKME равнобедренная.
Задание повторить
Основания трапеции АСМЕ равны 9 см и 21 см, сторона КА, равная 8 см, образует с меньшим основанием угол 150 0 . Вам нужно найти площадь трапеции.
Решение: Из вершины К опускаем высоту к большему основанию трапеции. И начнем смотреть на углы трапеции.
Уголки АЕМ и КАН односторонние. Значит, в сумме они составляют 1800. Следовательно, КАН = 30 0 (исходя из свойства углов трапеции).
Теперь рассмотрим прямоугольный ∆ANK (думаю, этот момент очевиден для читателей без дополнительных доказательств). Из него находим высоту трапеции КН — в треугольнике это катет, который лежит напротив угла 30 0 .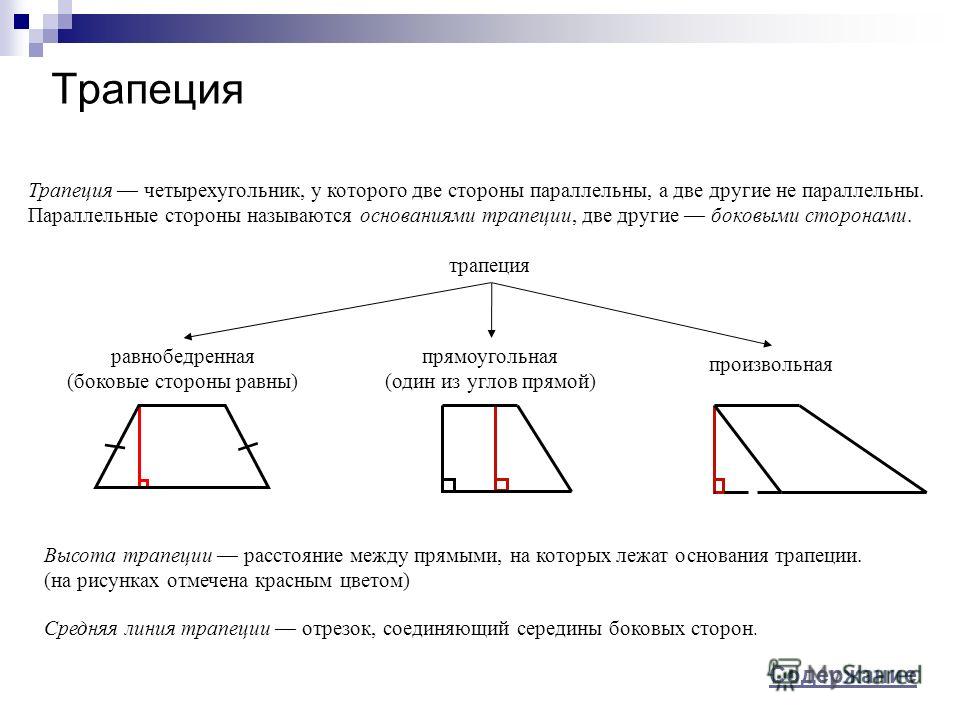 Следовательно, КН = ½АВ = 4 см.
Следовательно, КН = ½АВ = 4 см.
Площадь трапеции находится по формуле: S АКМЭ = (КМ + АЭ) * КН / 2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились нарисовать трапеции по всем вышеперечисленным свойствам с карандашом в руках и разобрать их на практике, вы должны были хорошо усвоить материал.
Конечно, информации здесь много, разнообразной и местами даже запутанной: не так уж сложно спутать свойства описываемой трапеции со свойствами вписанной. Но вы сами видели, что разница огромна.
Теперь у вас есть подробный обзор всех основных свойств трапеции. А также специфические свойства и особенности равнобедренных и прямоугольных трапеций. Очень удобно использовать для подготовки к зачетам и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайта, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Ваша конфиденциальность важна для нас.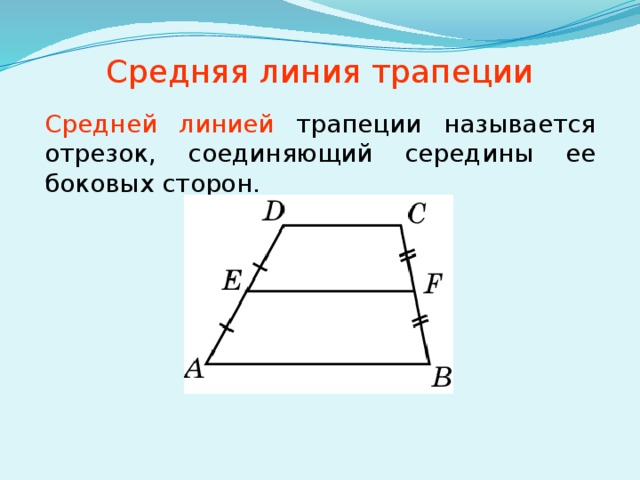 По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.
Сбор и использование личной информации
Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.
Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.
Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую информацию.
Какую личную информацию мы собираем:
- Когда вы подаете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т. д.
Как мы используем вашу личную информацию:
- Личная информация, которую мы собираем, позволяет нам связываться с вами и информировать вас об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.

- Время от времени мы можем использовать вашу личную информацию для отправки вам важных уведомлений и сообщений.
- Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
- Если вы участвуете в розыгрыше призов, конкурсе или аналогичном поощрении, мы можем использовать предоставленную вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от вас информацию третьим лицам.
Исключения:
- В случае необходимости — в соответствии с законом, судебным приказом, в порядке судопроизводства и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть свои Персональные данные. Мы также можем раскрыть информацию о вас, если решим, что такое раскрытие необходимо или уместно для обеспечения безопасности, правоохранительных органов или других целей, представляющих общественный интерес.

- В случае реорганизации, слияния или продажи мы можем передать личную информацию, которую мы собираем, соответствующему правопреемнику третьей стороны.
Защита личной информации
Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и неправомерного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Обеспечение конфиденциальности на уровне компании
Чтобы обеспечить безопасность вашей личной информации, мы сообщаем нашим сотрудникам о правилах конфиденциальности и безопасности и строго следим за соблюдением правил конфиденциальности.
Понятие средней линии трапеции
Для начала вспомним, какая фигура называется трапецией.
Определение 1
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
При этом параллельные стороны называются основаниями трапеции, а не параллельные — сторонами трапеции.
Определение 2
Средняя линия трапеции — это отрезок, соединяющий середины сторон трапеции.
Теорема о средней линии трапеции
Теперь введем теорему о средней линии трапеции и докажем ее векторным методом.
Теорема 1
Средняя линия трапеции параллельна основаниям и равна половине их суммы.
Доказательство.
Дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).
Рис. 1. Средняя линия трапеции
Докажем, что $MN||AD\ и \ MN=\frac(AD+BC)(2)$.
Рассмотрим вектор $\overrightarrow(MN)$. Далее мы используем правило многоугольника для сложения векторов. С одной стороны получаем, что
С другой стороны
Складывая два последних равенства, получаем
Так как $M$ и $N$ — середины сторон трапеции, то
Получаем :
Следовательно
Из того же равенства (поскольку $\overrightarrow(BC)$ и $\overrightarrow(AD)$ сонаправлены и, следовательно, коллинеарны), получаем, что $MN||AD$.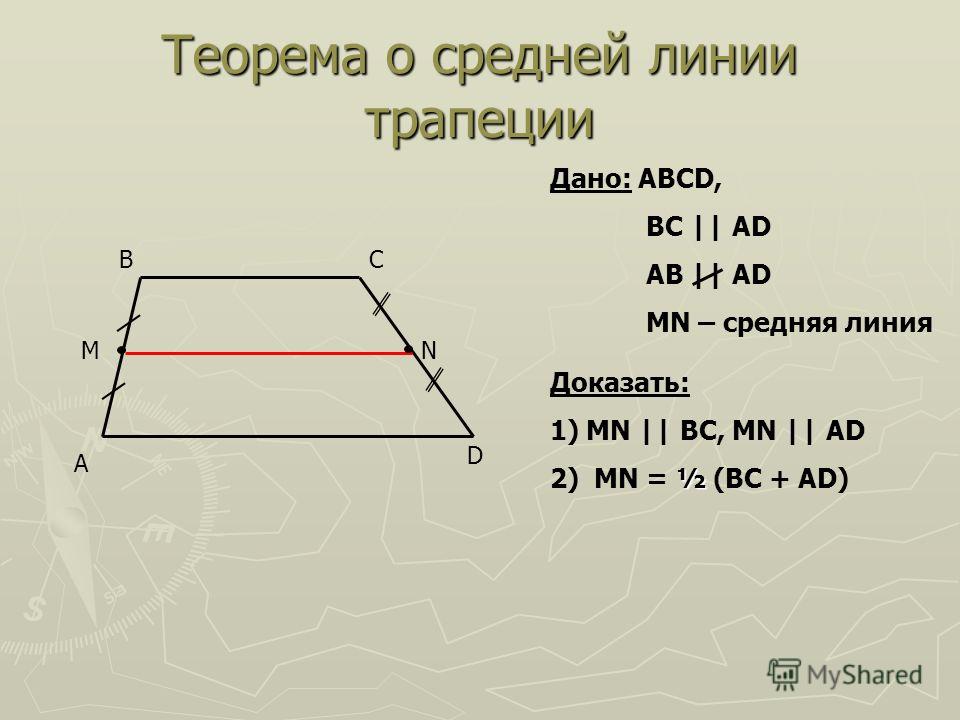
Теорема доказана.
Примеры задач на понятие средней линии трапеции
Пример 1
Стороны трапеции равны $15\см$ и $17\см$ соответственно. Периметр трапеции равен $52\см$. Найдите длину средней линии трапеции.
Раствор.
Обозначим среднюю линию трапеции через $n$.
Сумма сторон равна
Следовательно, поскольку периметр равен $52\см$, сумма оснований равна
Отсюда по теореме 1 получаем
Ответ: $10\cm$.
Пример 2
Концы окружности диаметром $9$ см и $5$ см соответственно от касательной. Найдите диаметр этого круга.
Раствор.
Дана окружность с центром $O$ и диаметром $AB$. Проведите касательную $l$ и постройте расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).
Рисунок 2.
Поскольку $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$, а поскольку $OH$ — радиус, то $OH\bot l$, следовательно, $ OH |\left|AD\right||BC$. Из всего этого получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
Из всего этого получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1 получаем
средней линии фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие используется для следующих фигур: треугольник, четырехугольник, трапеция.
Средняя линия треугольника
Свойства
- Средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвертой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или средним треугольником.
знаки
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок является средней линией.
- Площадь и, соответственно, объем треугольника, отсекаемого средней линией, равны 1/4 площади и, соответственно, объема всего данного треугольника.

Средняя линия четырехугольника
Средняя линия четырехугольника Отрезок, соединяющий середины противоположных сторон четырехугольника.
Свойства
Первая линия соединяет 2 противоположные стороны. Второй соединяет 2 другие противоположные стороны. Третий соединяет центры двух диагоналей (не во всех четырехугольниках диагонали делятся пополам точкой пересечения).
- Если в выпуклом четырехугольнике средняя линия образует равные углы с диагоналями четырехугольника, то диагонали равны.
- Длина средней линии четырехугольника меньше или равна половине суммы двух других сторон, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырехугольника — вершины параллелограмма. Его площадь равна половине площади четырехугольника, а его центр лежит в точке пересечения срединных линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последняя точка означает следующее: В выпуклом четырехугольнике четыре средних прямых второго рода .
 Средние линии второго рода — четыре отрезка внутри четырехугольника, проходящие через середины его смежных сторон, параллельных диагоналям. Четыре средние линии второго рода выпуклого четырехугольника разрезают его на четыре треугольника и один центральный четырехугольник. Этот центральный четырехугольник является параллелограммом Вариньона.
Средние линии второго рода — четыре отрезка внутри четырехугольника, проходящие через середины его смежных сторон, параллельных диагоналям. Четыре средние линии второго рода выпуклого четырехугольника разрезают его на четыре треугольника и один центральный четырехугольник. Этот центральный четырехугольник является параллелограммом Вариньона. - Точка пересечения средних линий четырехугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центром тяжести вершин четырехугольника.
- В произвольном четырехугольном векторе средняя линия равна половине суммы векторов основания.
Средняя линия трапеции
Средняя линия трапеции
Средняя линия трапеции — отрезок, соединяющий середины сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называется второй средней линией трапеции.
Рассчитывается по формуле: E F = A D + B C 2 (\displaystyle EF=(\frac (AD+BC)(2))), где AD А BC — основание трапеции.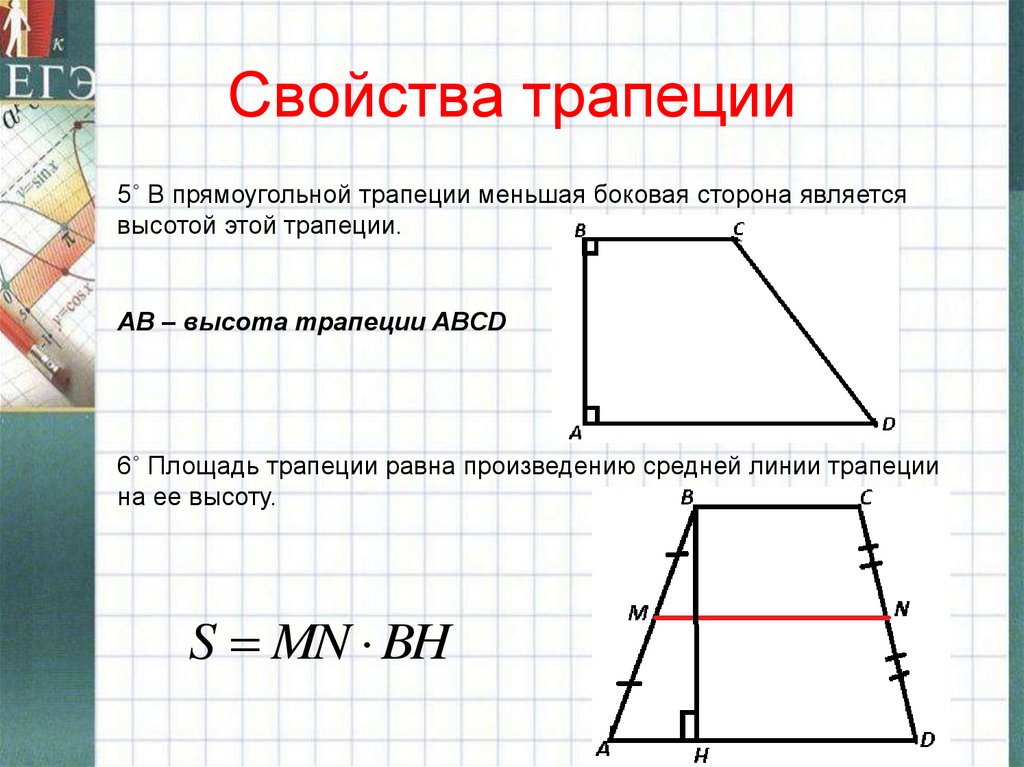
Диагонали прямоугольной трапеции взаимно перпендикулярны углу между ними. Диагонали трапеции
Опять пифагорейский треугольник :))) Если отрезок большой диагонали от большого основания до точки пересечения обозначить через x, то из очевидного подобия прямоугольных треугольников с одинаковыми углами это следует. х/64 = 36/х, следовательно, х = 48; 48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Единственным исключением является треугольник, образованный отрезками диагоналей и косой стороны, но он нас не интересует :). (Для ясности, рассматриваемое подобие — это просто ДРУГИЕ НАЗВАННЫЕ тригонометрические функции углов 🙂 мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, поэтому синус равен 3/5, а косинус 4/5 :)) можно сразу написать
Ответы. Нижнее основание 80, высота трапеции будет 60, а верхнее 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Смежные задачи:
1. Основанием призмы является треугольник, у которого одна сторона равна 2 см, а две другие по 3 см. Боковой край равен 4 см и образует с плоскостью основания угол 45°. Найдите ребро равнобедренного куба.
Основанием призмы является треугольник, у которого одна сторона равна 2 см, а две другие по 3 см. Боковой край равен 4 см и образует с плоскостью основания угол 45°. Найдите ребро равнобедренного куба.
2. Основанием наклонной призмы является равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, меньшая диагональ которого равна c. Найдите объем призмы.
3. У наклонной призмы основанием является прямоугольный треугольник, гипотенуза которого равна с, один острый угол равен 30, боковое ребро равно и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата, если его диагональ равна 10 см
2. В равнобедренной трапеции тупой угол на 135 градусов меньше, чем основание равно 4 см, а высота равна 2 см. Найдите площадь трапеция?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту, если площадь трапеции равна 168 см в квадрате?
4. В треугольнике ABC угол A = угол In = 75 градусов. Найдите ВС, если площадь треугольника равна 36 см в квадрате.
В треугольнике ABC угол A = угол In = 75 градусов. Найдите ВС, если площадь треугольника равна 36 см в квадрате.
1. Диагонали трапеции ABCD со сторонами AB и CD пересекаются в точке O
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите, что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эта высота делится биссектрисой угла при основании.
3. Линия АМ-касательная к окружности, АВ-хорда этой окружности. Докажите, что угол MAB измеряется половиной дуги AB, лежащей внутри угла MAB.
- Отрезок, соединяющий середины диагоналей трапеции, равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения, подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если мы продолжим стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной отношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции и проведенный через точку пересечения диагоналей, делится этой точкой пополам, и его длина равна 2ab/(a+b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединяем середины диагоналей трапеции ABCD, в результате чего у нас получится отрезок LM.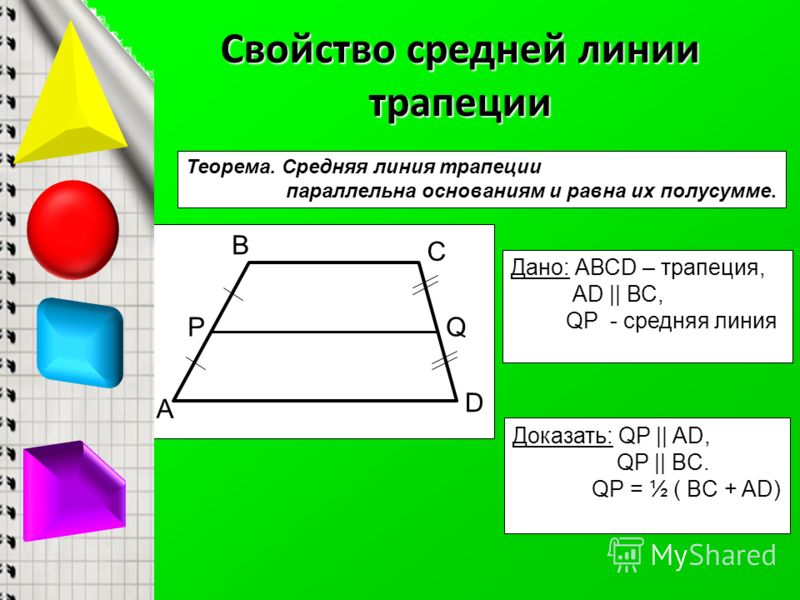
Отрезок, соединяющий середины диагоналей трапеции , лежит на средней линии трапеции .
Этот отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, образованные основаниями трапеции и точкой пересечения диагоналей трапеция — аналогичны .
Треугольники BOC и AOD подобны. Поскольку углы BOC и AOD вертикальны, они равны.
Углы OCB и OAD внутренние крест-накрест, лежащие на параллельных прямых AD и BC (основания трапеций параллельны друг другу) и секущей AC, следовательно, равны.
Углы OBC и ODA равны по той же причине (внутреннее пересечение).
Поскольку все три угла одного треугольника равны соответствующим углам другого треугольника, эти треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если известны длины двух соответствующих элементов подобных треугольников, то находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов связаны друг с другом точно такой же величиной.
Если известны длины двух соответствующих элементов подобных треугольников, то находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов связаны друг с другом точно такой же величиной.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на сторонах трапеции AB и CD. Это треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон этих треугольников могут быть совершенно разными, но площади треугольников, образованных сторонами и точкой пересечения диагоналей трапеции, равны , то есть треугольники равны.
Если стороны трапеции продолжить в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, проходящей через середины оснований .
Таким образом, любую трапецию можно продолжить до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продолженных сторон, подобны
- Прямая, соединяющая середины оснований трапеции, является одновременно медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, лежащей в точке пересечения диагоналей трапеции (КН), то отношение составляющих ее отрезков от стороны основания до точки пересечения диагоналей (КО/ОН) будет равно отношению оснований трапеции (ВС/АД).
КО/ОН=БК/АД
Это свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами :
- Заданное расстояние (км) делит пополам точку пересечения диагоналей трапеции
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна КМ = 2ab/(a + b)
A, B — основания трапеции
C, D — Стороны трапеции
D1 D2 — Диагональ — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.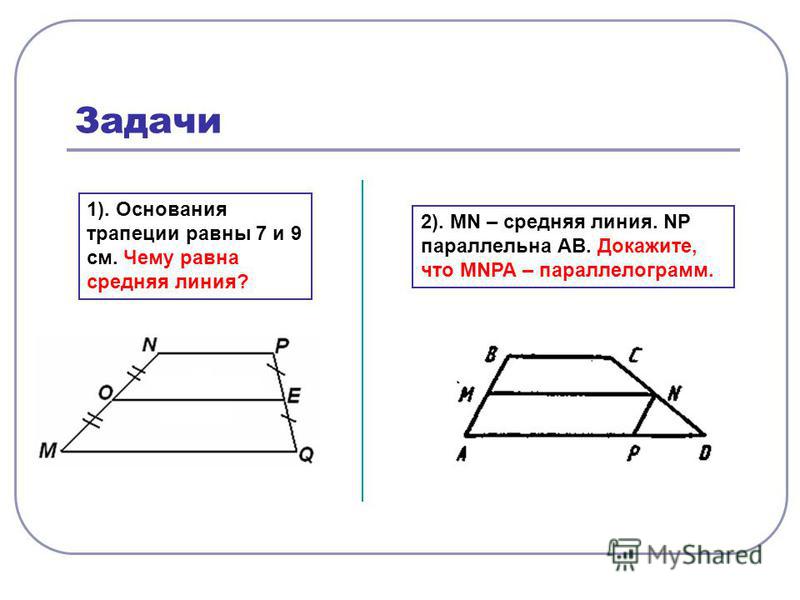 Сумма квадратов диагоналей трапеции равна сумме квадратов сторон плюс удвоенное произведение ее оснований. Это свойство диагоналей трапеции можно доказать как отдельную теорему
Сумма квадратов диагоналей трапеции равна сумме квадратов сторон плюс удвоенное произведение ее оснований. Это свойство диагоналей трапеции можно доказать как отдельную теорему
2 . Эта формула получается преобразованием предыдущей формулы. Квадрат второй диагонали набрасывается на знак равенства, после чего из левой и правой частей выражения извлекается квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с тем отличием, что в левой части выражения
оставлена еще одна диагональ. Следующая группа формул (4-5) аналогична по смыслу и выражает подобное отношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание . В этом уроке дается решение задач по геометрии о трапециях.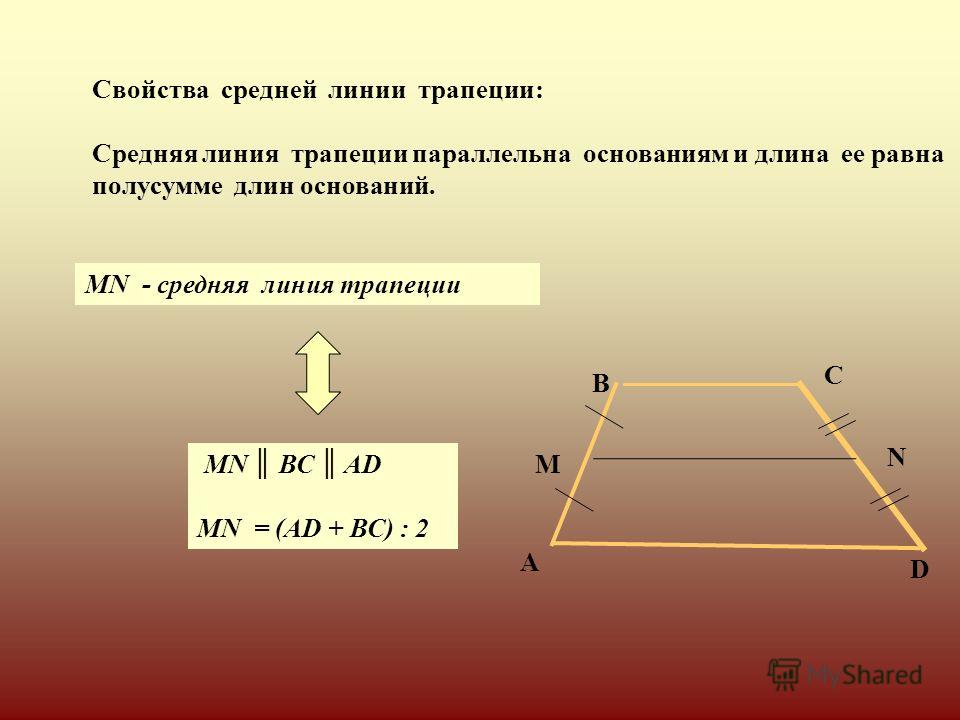 Если вы не нашли решение задачи по геометрии интересующего вас типа — задайте вопрос на форуме .
Если вы не нашли решение задачи по геометрии интересующего вас типа — задайте вопрос на форуме .
Задача .
Диагонали трапеции ABCD (AD | | BC) пересекаются в точке O. Найдите длину основания BC трапеции, если основание AD = 24 см, длина AO = 9 см, длина OS = 6 см.
Решение .
Решение этой задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC подобны по трем углам — AOD и BOC вертикальны, а остальные углы попарно равны, так как образованы пересечением одной прямой и двух параллельных прямых.
Так как треугольники подобны, то все их геометрические размеры связаны друг с другом, как известные нам по условию задачи геометрические размеры отрезков АО и ОС. то есть
AO/OC=AD/BC
9 / 6 = 24 / B.C.
БК = 24 * 6 / 9 = 16
Ответ : 16 см
Задание .
В трапеции ABCD известно, что AD=24, BC=8, AC=13, BD=5√17. Найдите площадь трапеции.
Решение .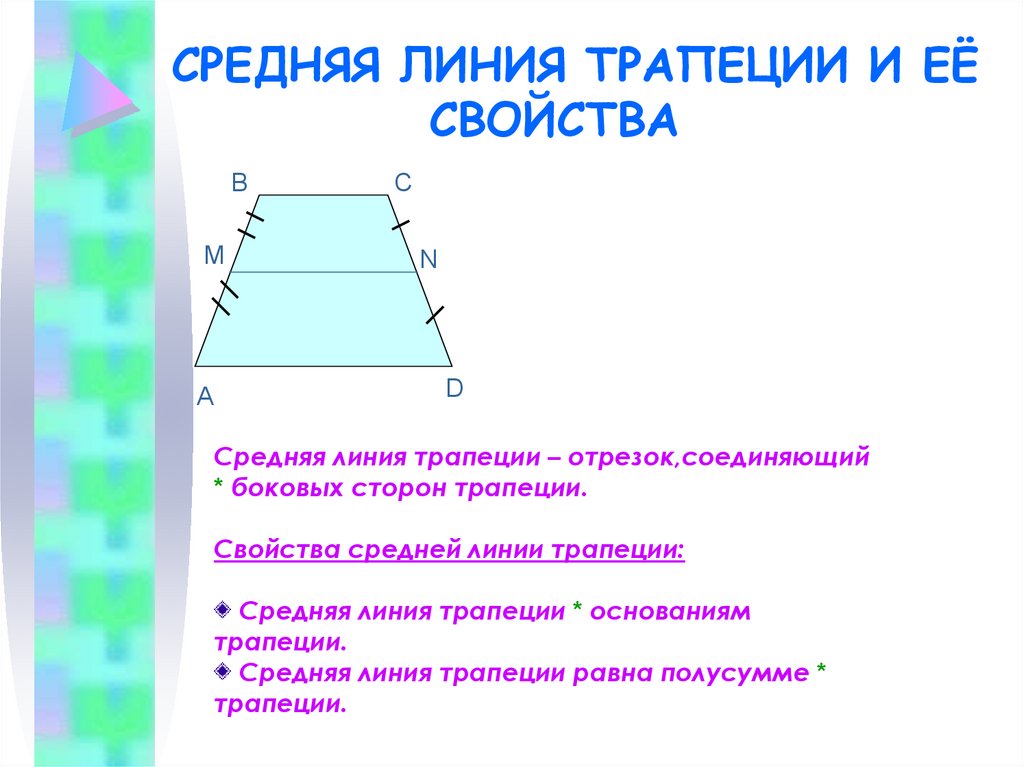
Чтобы найти высоту трапеции из вершин меньшего основания В и С, опускаем две высоты на большее основание. Так как трапеция неравнополочная, обозначим длину АМ = а, длину КД = b (не путать с символами в формуле нахождения площади трапеции). Так как основания трапеции параллельны и мы опустили две высоты, перпендикулярные большему основанию, то MBCK является прямоугольником.
Значит
AD=AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK прямоугольные, поэтому их прямые углы образованы высотами трапеций. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Считаем, что a = 16 — b , то в первом уравнении
ч 2 + (24 — 16 + b) 2 = 425
ч 2 = 425 — (8 + b) 2
Подставляем значение квадрата высоты во второе уравнение, полученное по теореме Пифагора. Получаем:
425 — (8 + b) 2 + (24 — b) 2 = 169
— (64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Где
ч 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдите площадь трапеции, используя ее высоту и половину суммы оснований
, где а b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5/2 = 80 см 2
Ответ : площадь трапеции равна 80 см2.
Если диагонали в равнобедренной трапеции перпендикулярны, то при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, то высота трапеции равна половине суммы оснований.
Проведем прямую CF через точку C параллельно BD и продолжим прямую AD до пересечения с CF.
Четырехугольник BCFD является параллелограммом (BC∥ DF как основание трапеции, BD∥ CF по построению). Итак, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Так как в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF равнобедренный с основанием AF. Следовательно, его высота CN также является медианой. А так как медиана прямоугольного треугольника, проведенного к гипотенузе, равна ее половине, то
, что можно записать в общем виде как
, где h — высота трапеции, a и b — ее основания.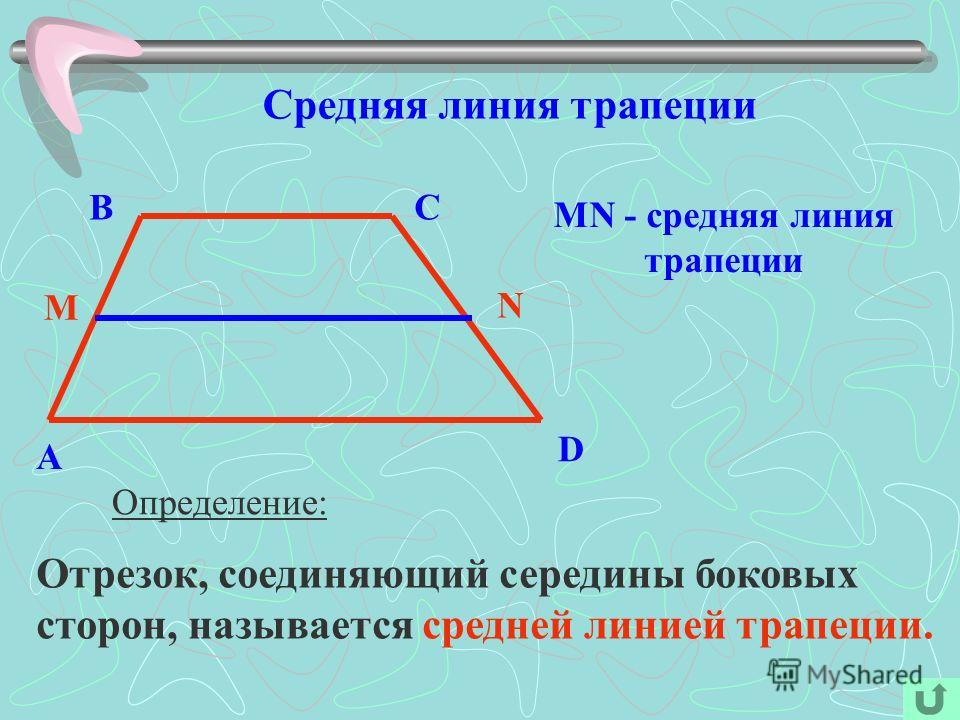

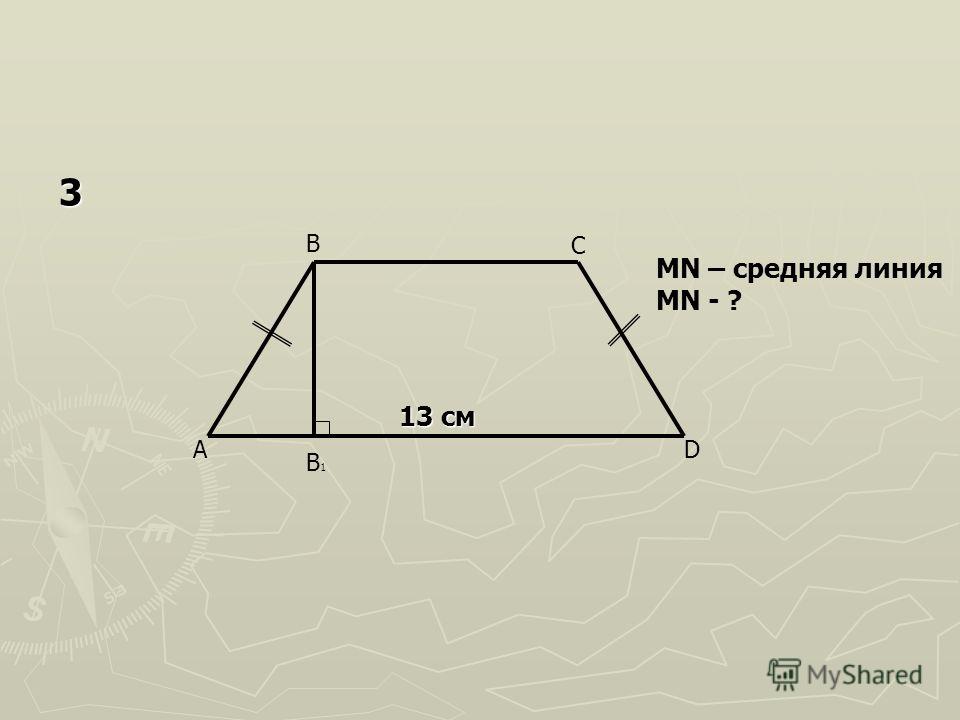
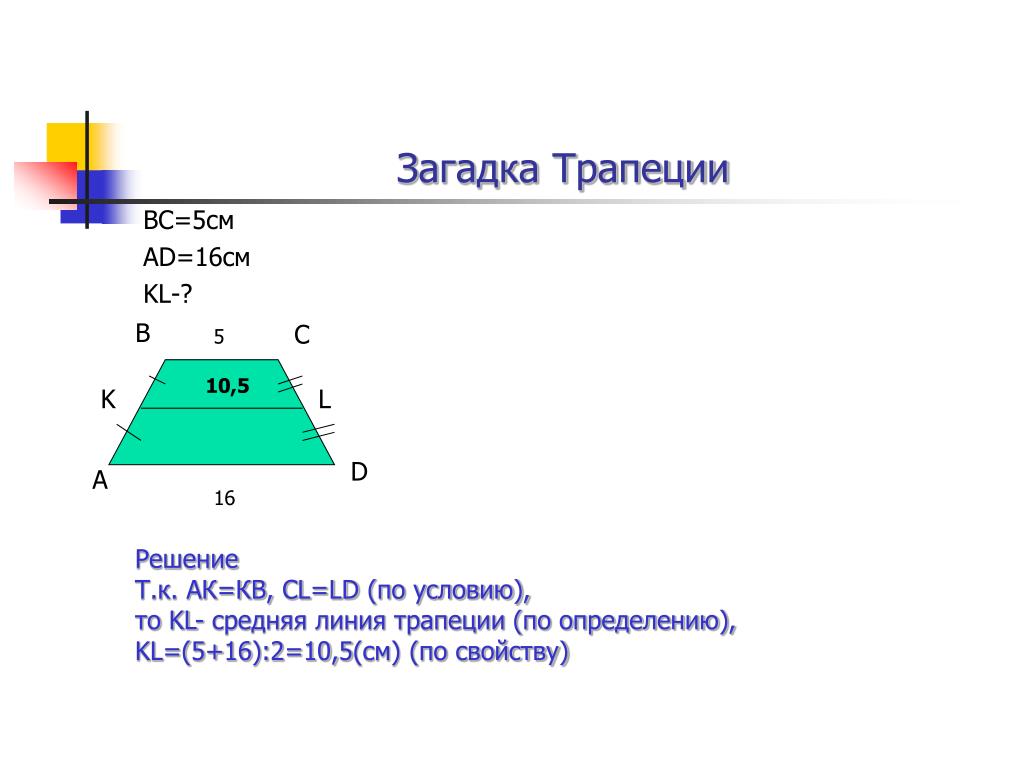
 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .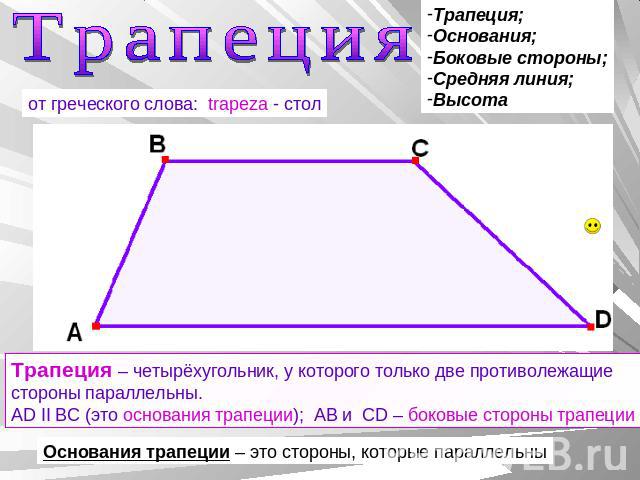
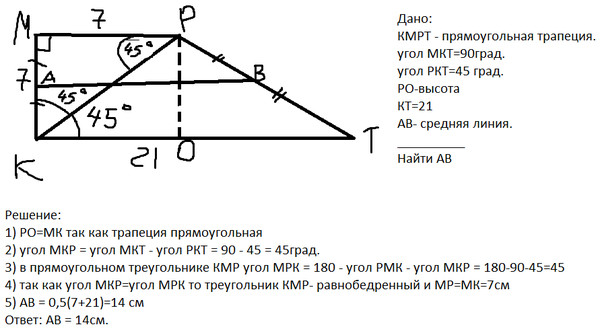
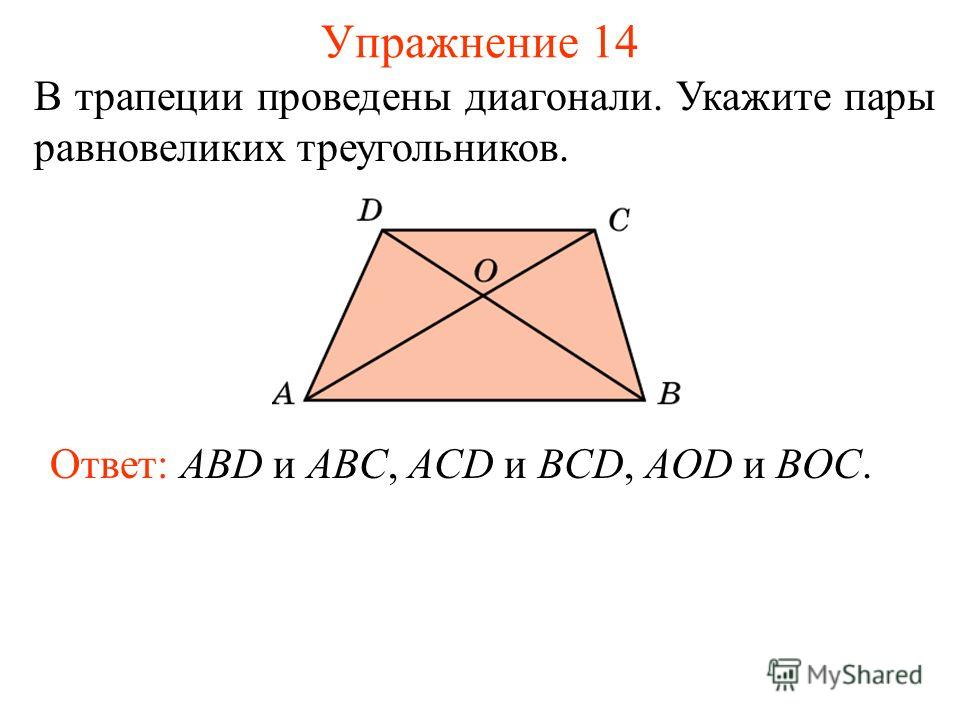 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).

 Площади треугольников АКО и ЭМО равны — их площади одинаковы.
Площади треугольников АКО и ЭМО равны — их площади одинаковы.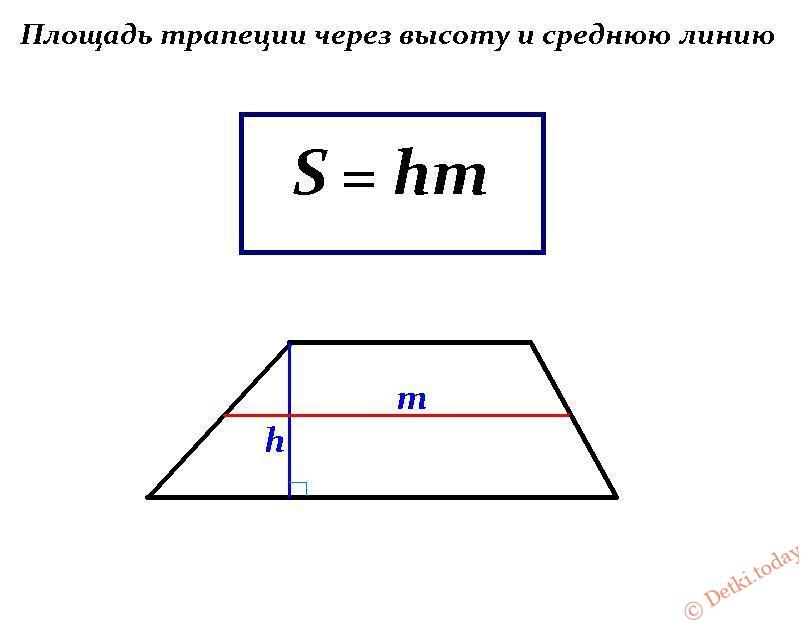
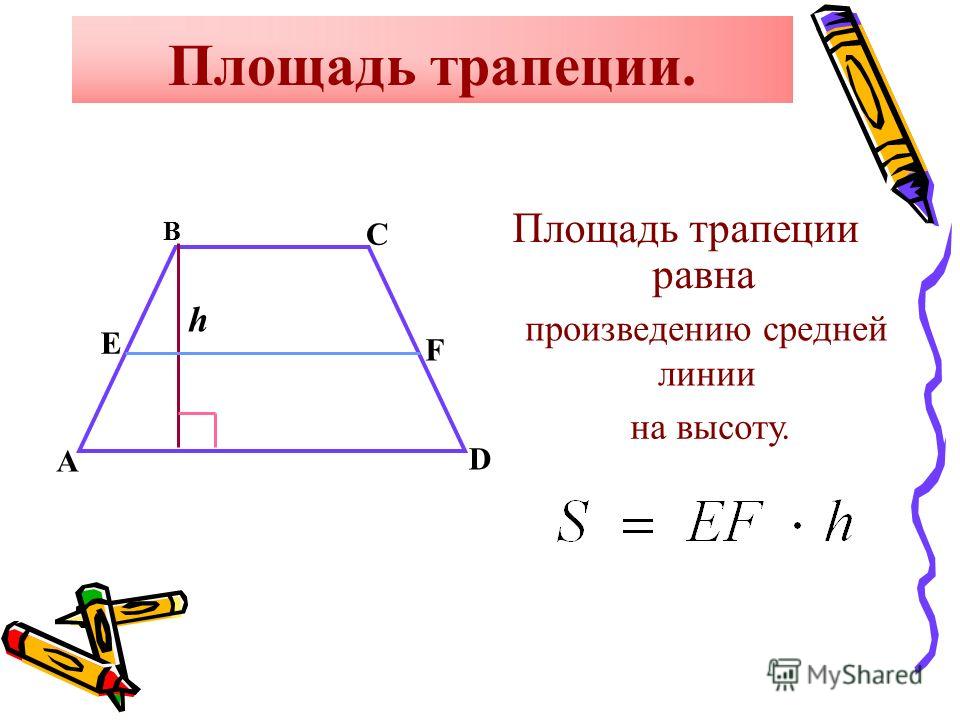 Если сумма углов для любого из них равна 90 0 , длину отрезка ТХ легко вычислить по разнице длин оснований, деленной пополам: ТХ = (АЭ — КМ) / 2 .
Если сумма углов для любого из них равна 90 0 , длину отрезка ТХ легко вычислить по разнице длин оснований, деленной пополам: ТХ = (АЭ — КМ) / 2 .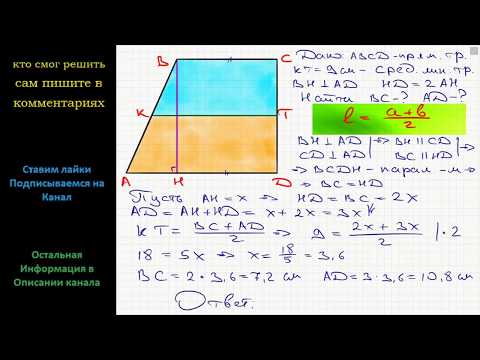
 Способ первый: внимательно посмотрите на свой рисунок — что вы видите? Вы легко заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противоположного угла, умноженное на два. Например, R = АЕ/2 * sinAME . Аналогично формулу можно записать для любой из сторон обоих треугольников.
Способ первый: внимательно посмотрите на свой рисунок — что вы видите? Вы легко заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противоположного угла, умноженное на два. Например, R = АЕ/2 * sinAME . Аналогично формулу можно записать для любой из сторон обоих треугольников.
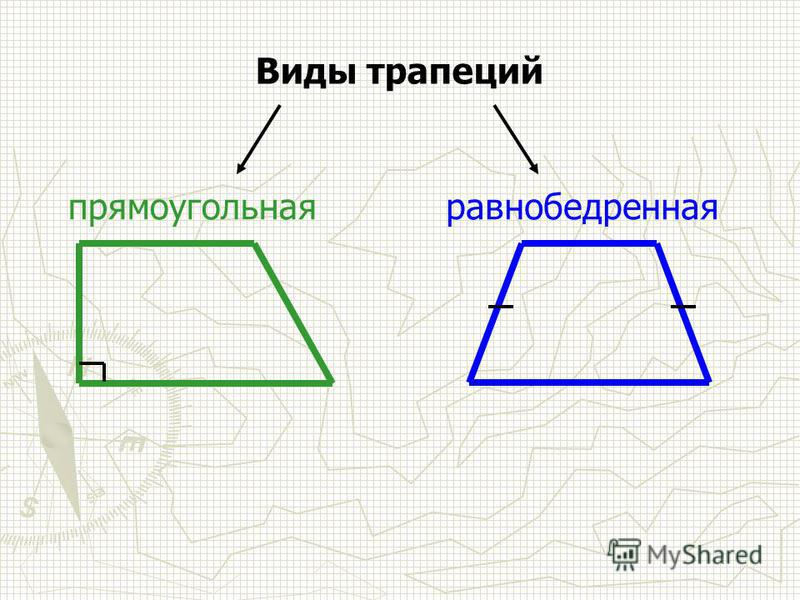
 Получаем параллелограмм КМНЕ (основание — МХ || КЕ и КМ || ЕХ).
Получаем параллелограмм КМНЕ (основание — МХ || КЕ и КМ || ЕХ).
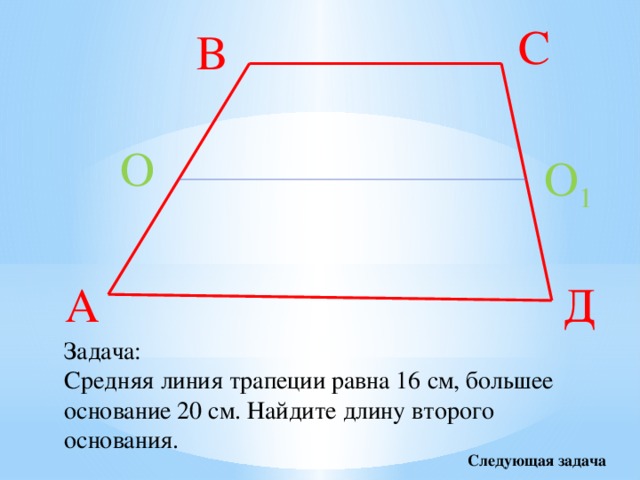

 Средние линии второго рода — четыре отрезка внутри четырехугольника, проходящие через середины его смежных сторон, параллельных диагоналям. Четыре средние линии второго рода выпуклого четырехугольника разрезают его на четыре треугольника и один центральный четырехугольник. Этот центральный четырехугольник является параллелограммом Вариньона.
Средние линии второго рода — четыре отрезка внутри четырехугольника, проходящие через середины его смежных сторон, параллельных диагоналям. Четыре средние линии второго рода выпуклого четырехугольника разрезают его на четыре треугольника и один центральный четырехугольник. Этот центральный четырехугольник является параллелограммом Вариньона.