В треугольнике медианы: Свойства медиан треугольника — подготовка к ЕГЭ по Математике

Свойства медианы треугольника — справочник для студентов и школьников

ОПРЕДЕЛЕНИЕ

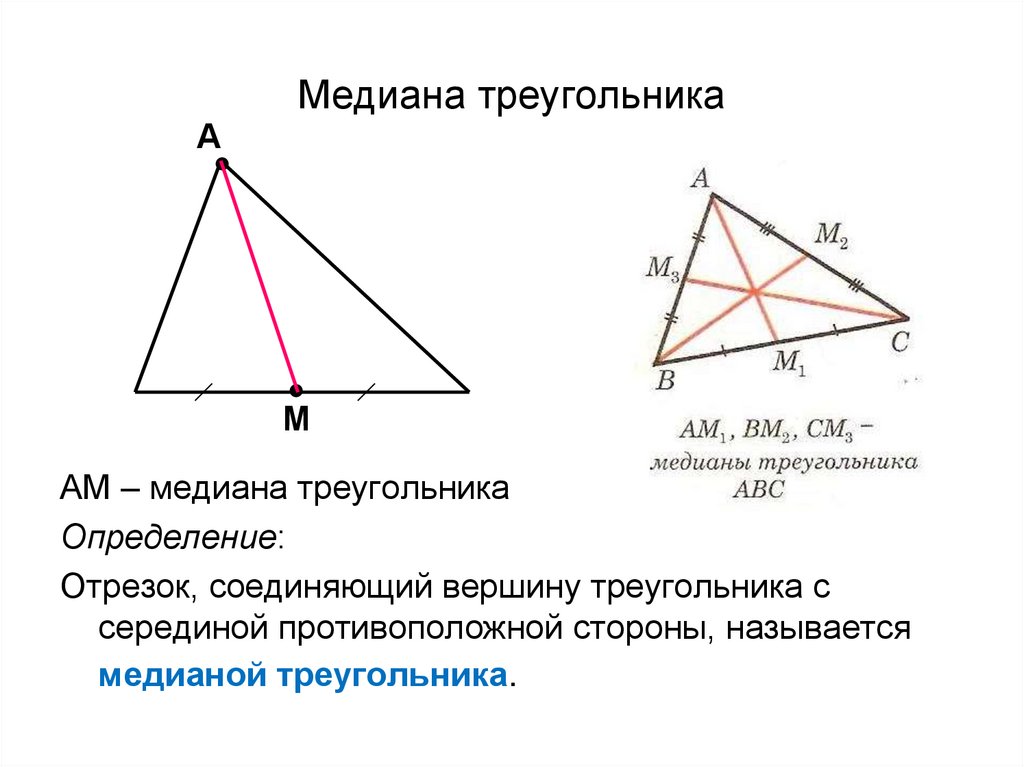
Медиана треугольника — это сегмент, соединяющий вершину треугольника с серединой противоположной стороны.

Свойства медианов треугольника

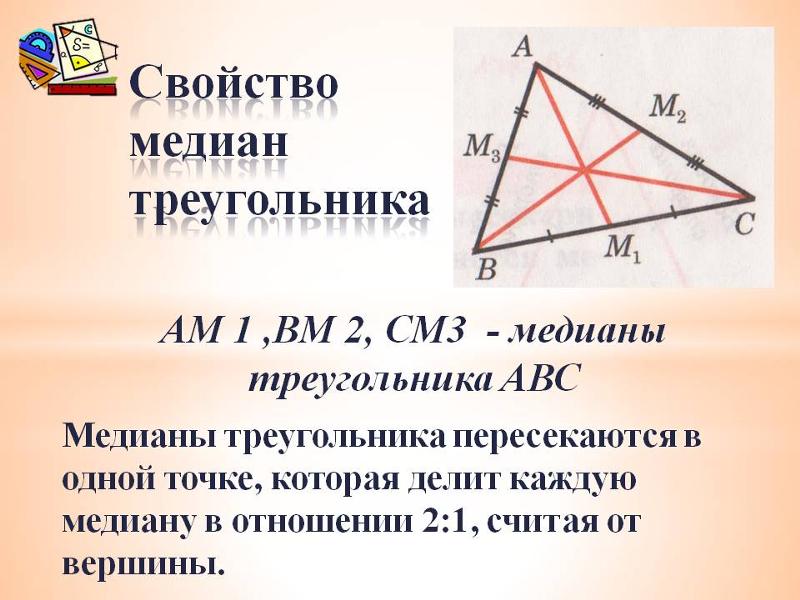
Медиана делит треугольник на два треугольника равного размера (то есть на треугольники с одинаковой площадью).

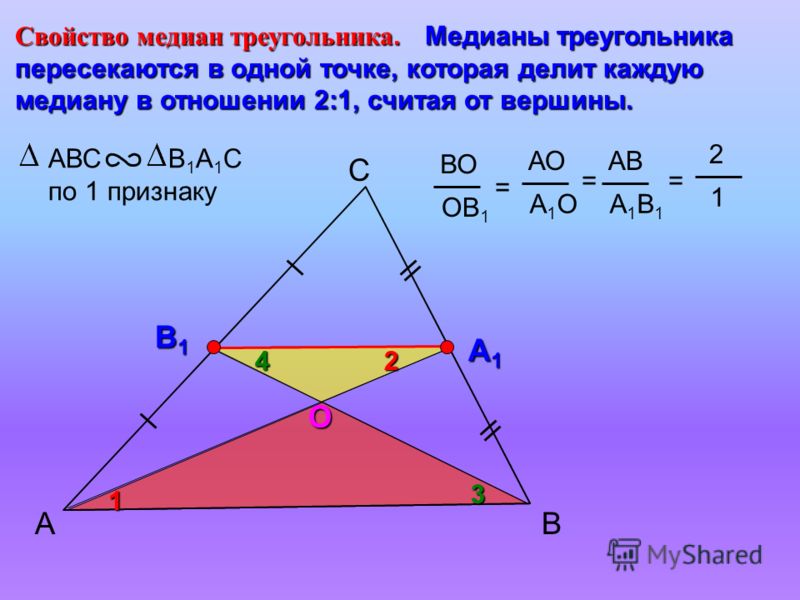
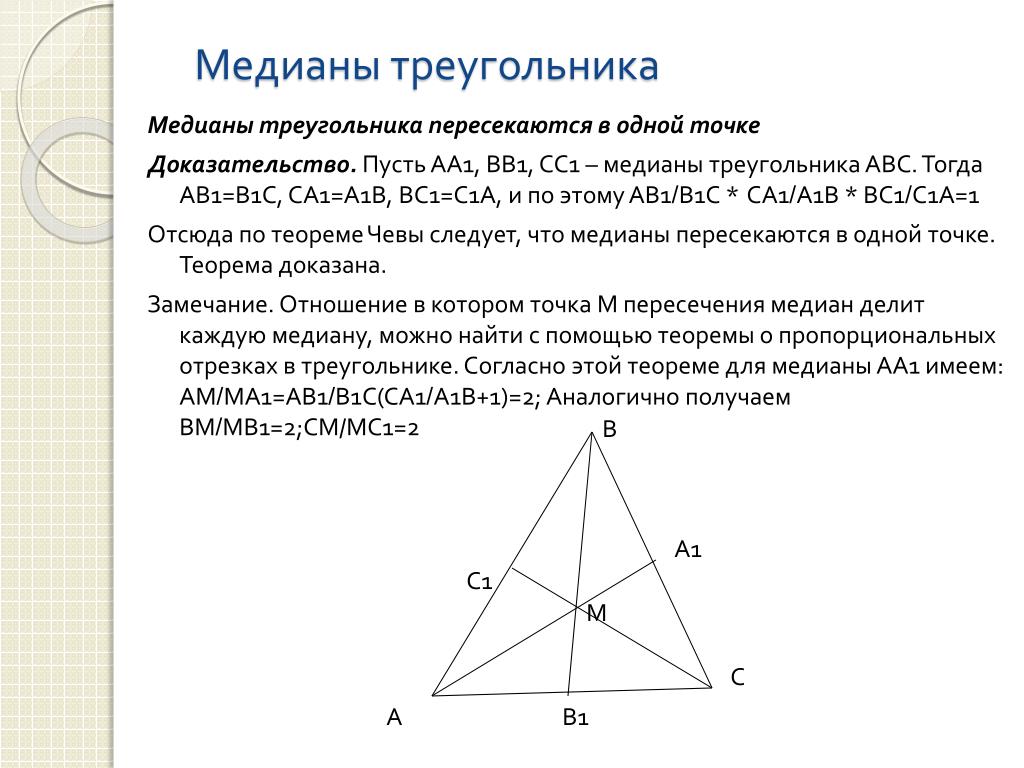
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в соотношении 2: 1, начиная с вершины. Эта точка называется центром тяжести треугольника.

Весь треугольник делится на его медианы на шесть треугольников равного размера.

В равнобедренном треугольнике медиана, опустившаяся до основания, является биссектрисой и высотой.

В равностороннем треугольнике любая медиана — это высота и биссектриса.

Примеры решения проблем

ПРИМЕР 1

Задача

В равнобедренном треугольнике \(\ \mathrm{ABC} \) со стороной \(\ A B=5 \mathrm{см} \) медиана была \(\ B L=4 \mathrm{см} \). {2}-2 A B \cdot A L \cos \angle A}=\sqrt{16+9-2 \cdot 4 \cdot 3 \cdot \frac{1}{2}}=\sqrt{13} \mathrm{см} \)

Медианы \(\ \mathrm{AK} \) и \(\ BL \) пересекаются в точке, которая делит каждую из них в соотношении 2: 1, начиная с вершины, т.е.

$\(\ B O=\frac{2}{3} B L=\frac{2 \sqrt{13}}{3} \mathrm{cm} \)

Ответ

\(\ B O=\frac{2 \sqrt{13}}{3} \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Свойства биссектрисы треугольника Свойства прямоугольного треугольника Свойства равностороннего треугольника Свойства равнобедренного треугольника

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Свойства медианы в прямоугольном треугольнике с доказательствами

В этой статье мы рассмотрим свойства медианы в прямоугольном треугольнике, а также их доказательства.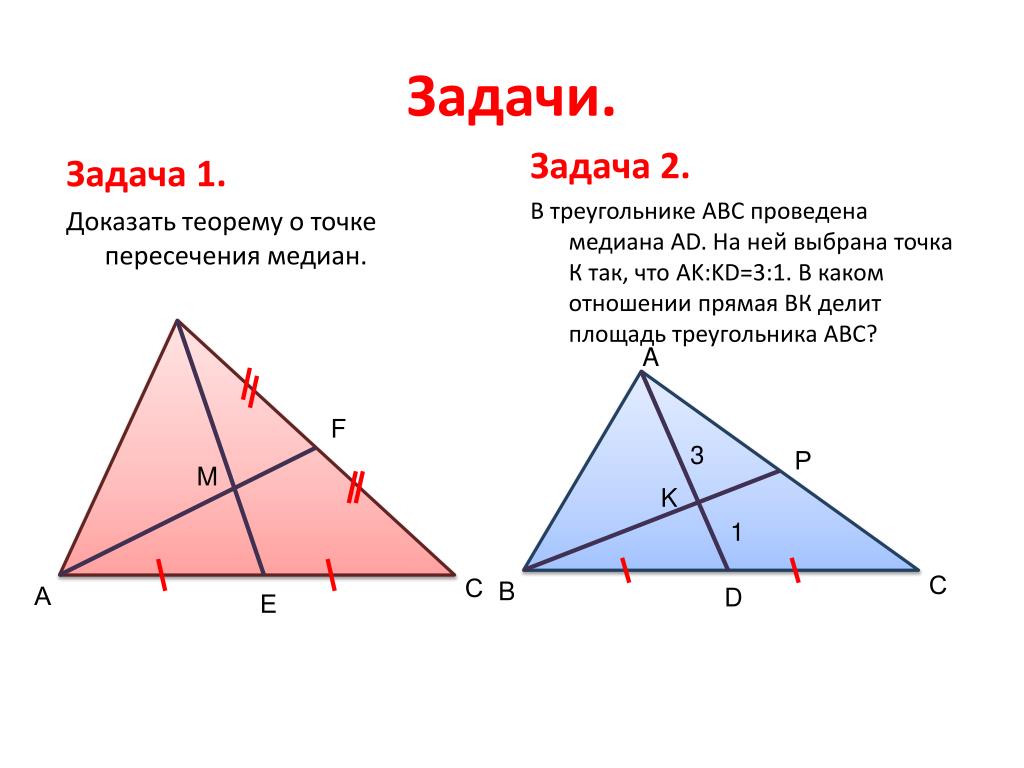

Медиана — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Для прямоугольного треугольника это будут медианы, проведённые с острого угла к серединам катетов или с прямого к центру гипотенузы (рис. 1).

Рисунок 1

Свойства медианы в прямоугольном треугольнике

1. Медианы в прямоугольном треугольнике пересекаются в одной точке, а точка пересечения делит их в соотношении два к одному считая от вершины, из которой проведена медиана.
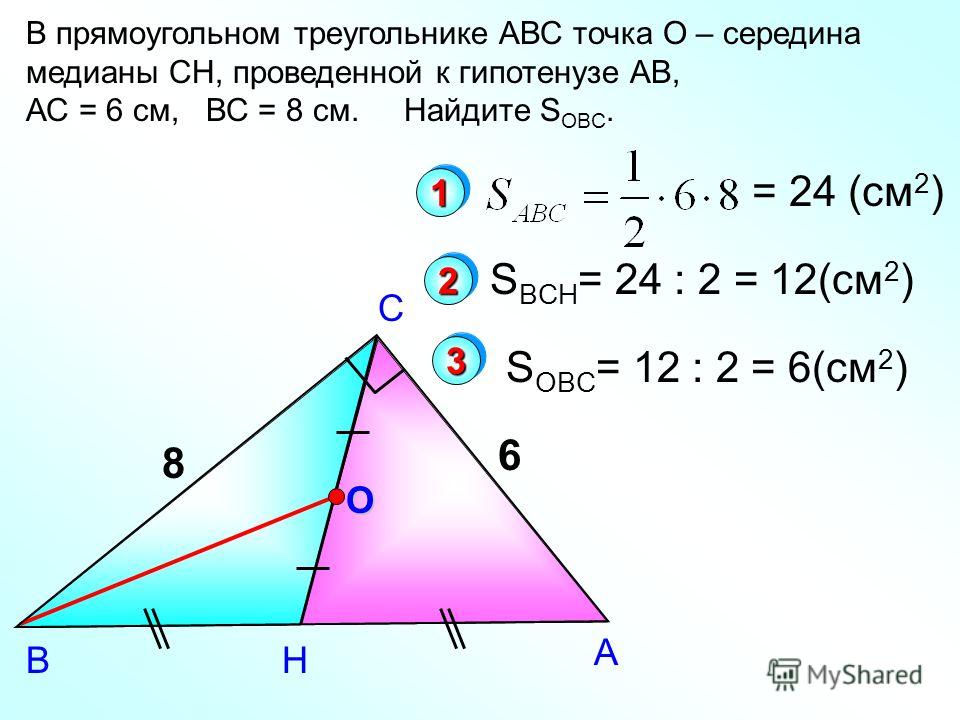
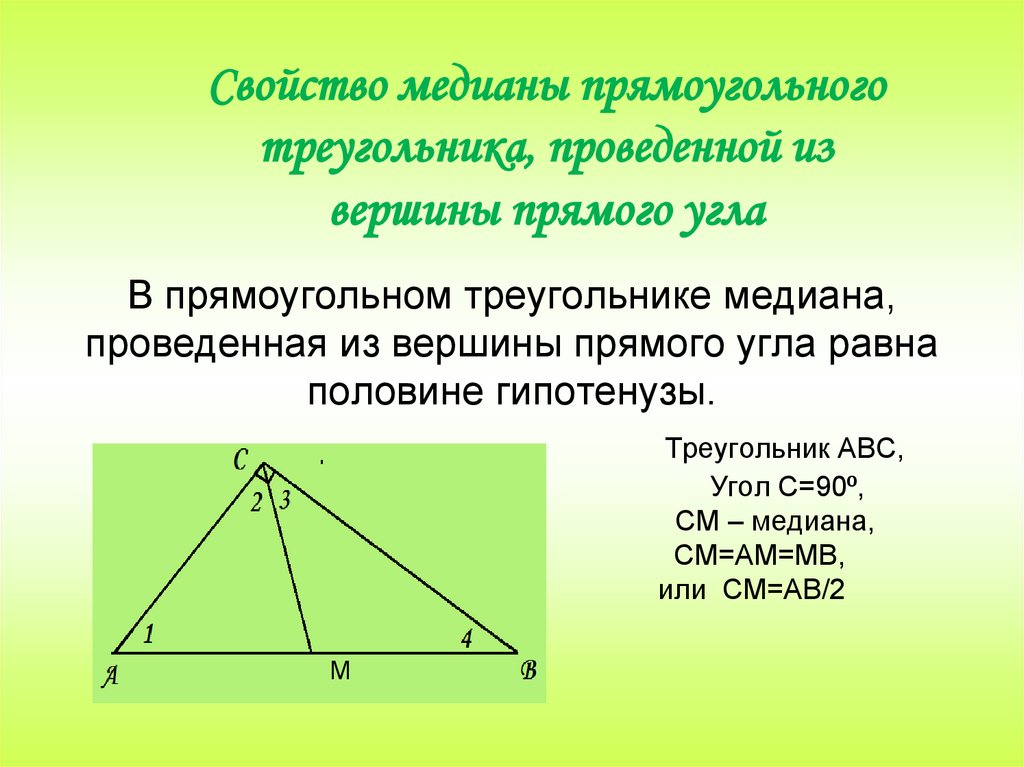
2. Медиана, проведённая из вершины прямого угла к гипотенузе, равна половине гипотенузы.
3. Медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательства свойств

Первое свойство

Доказать, что медианы в прямоугольном треугольнике пересекаются в одной точке и делятся в пропорции 2:1, считая от вершины.

Доказательство:

1. Рассмотрим прямоугольный треугольник ABC. Проведем две медианы AE и BD, которые пересекаются в точке X (рис. 2).

   Рисунок 2

2. Середины отрезков AX и BX обозначим, соответственно, буквами F и G (рисунок 3).
   Рисунок 3

3. Соединим между собой точки (D, F, G и E) и получим четырёхугольник DFGE (рис. 4).

   Рисунок 4

4. Сторона DE этого четырёхугольника будет средней линией треугольника ABC. Согласно определению: отрезок, соединяющий середины двух сторон треугольника, является его средней линией. При этом по свойству средняя линия параллельна не пересекающейся с ней стороне и равна половине этой стороны, то есть.
   DE || AB и DE = AB / 2.
5. Аналогично сторона FG треугольника AXB будет его средней линией.
   FG || AB и FG = AB / 2
6. Отсюда следует, что отрезки DE и FG являются параллельными и равными. Следовательно, четырехугольник DFGE – параллелограмм (по признаку параллелограмма).
7. Так как диагонали параллелограмма в точке пересечения делятся пополам, то
   FX=XE, GX=XD

   Рисунок 5

8. Так как AF = FX (по построению), то и AF = FX = XE, аналогично DX = XG = GB.
9. Получается, что точка X делит обе медианы AE и BD в соотношении 2 к 1 считая от вершины треугольника.
10. Аналогично, мы сможем доказать, что точка пересечения 3-ей медианы, проведенной из прямого угла к гипотенузе, с медианой AE (или BD) будет делить ее в соотношении 2 к 1, считая от вершины. То есть наша 3-я медиана также пройдет через точку X. Отсюда следует, что все 3 наши медианы пересекаются в одной точке.

Что и требовалось доказать.

Второе свойство

Доказать, что медиана, проведённая с вершины прямого угла к гипотенузе, равна половине гипотенузы.

Доказательство:

1. Чтобы доказать это свойство рассмотрим прямоугольный треугольник ABC и проведём медиану к гипотенузе. Точку ее пересечения с гипотенузой обозначим буквой D (рис. 6).

   Рисунок 6

2. Отразим симметрично наш треугольник ABC относительно отрезка AB (рисунок 7). В результате получим четырёхугольник AEBC, в котором AD=DB (поскольку CD медиана к стороне AB) и CD=DE (по построению). То есть диагонали четырехугольника AEBC пересекаются и точкой пересечения делятся пополам. Отсюда следует, что AEBC является параллелограммом (по признаку параллелограмма).

   Рисунок 7

3. Один из признаков прямоугольника говорит о том, что параллелограмм является прямоугольником, если хотя бы один из его углов прямой. Поскольку ∠ACB прямой (по построению), то AEBC — прямоугольник.
4. Поскольку диагонали прямоугольника равны и в точке пересечения делятся пополам (свойство прямоугольника), то AB = CE и AD = DB = CD = DE.

   Рисунок 8

5. Так как AB = AD + DB, AD = BD и СD = AD = BD, то получается, что медиана AD, проведенная к гипотенузе AB равна половине ее длины.

Что и требовалось доказать.

Третье свойство

Доказать, что медиана, проведённая к гипотенузе прямоугольного треугольника, является радиусом описанной окружности.

Доказательство:

1. Опишем вокруг прямоугольного треугольника ABC окружность.

   Рисунок 9

2. Поскольку точка C уже лежит на окружности, то для того, чтобы доказать, что медиана CM является радиусом, нам надо доказать, что точка M – центр описанной окружности (т.е. равноудалена от нее).
3. Так как медиана делит отрезок пополам, а медиана проведенная к гипотенузе равна ее половине (согласно доказанному выше свойству), то точка M будет равноудалена от всех вершин треугольника, которые в свою очередь касаются окружности (рисунок 8).
4. Отсюда следует, что окружность, описанная вокруг прямоугольного треугольника ABC будет иметь центр на середине гипотенузы (в точке M), а медиана CM будет радиусом описанной окружности.

Что и требовалось доказать.

Скорее всего, Вам будет интересно:

• Свойства вписанной в треугольник окружности
• Средняя линия трапеции: чему равна, свойства, доказательство теоремы
• Свойства прямоугольной трапеции
• Третий признак равенства треугольников формулировка и доказательство
• Первый признак равенства треугольников: формулировка и доказательство (7 класс)
• Таблица прямых и обратных тригонометрических функций, онлайн калькулятор
• Состав служебного программного обеспечения
• Как найти область определения функции онлайн
• Закон Кулона: формулировка, определение, формула
• Основные положения молекулярно-кинетической теории (МКТ), формулы МКТ

Определение и свойства медианы треугольника. Как найти медиана треугольника

Автор Historian Просмотров 46 Опубликовано

23. 08.2022

Для закрепления теоретического материала преподаватель просит студентов решить ряд задач. Преподаватель предоставляет студентам серию задач для закрепления теоретического материала. Такие задачи предназначены для учащихся средней школы.

Содержание

1. Виды треугольников по углам
2. Виды треугольников по сторонам
3. Медиана, биссектриса, высота, средняя линия треугольника
4. Определение и свойства медианы треугольника
5. Свойства медианы
6. Свойство 1 (основное)
7. Свойство 2
8. Свойство 3
9. Свойство 4
10. Свойство 5
11. Примеры задач
12. Медиана треугольника.
13. Определение
14. Задачи
15. Как найти медиана треугольника
16. Свойства медианы треугольника
17. Средняя линия треугольника
18. Теорема о трех медианах треугольника
19. Доказательство теоремы о трех медианах треугольника
20. Открыть ответы…
21. Треугольник

Виды треугольников по углам

Треугольники расположены в соответствии с их углами: кислородный — тупоугольный — прямоугольный.

Остроугольные	Тупоугольные	Прямоугольные
Остроугольным треугольником называется треугольник, у которого все три угла острые. На рисунке показан такой остроугольный треугольник АВС.	Тупоугольным называется треугольник, у которого есть тупой угол. В треугольнике может быть только один тупой угол. На рисунке показан треугольник такого вида, где угол М – тупой.	Прямоугольным называется треугольник, у которого есть угол, равный 90 0 (прямой угол). На рисунке угол С равен 90 0. Такой угол в любом прямоугольном треугольнике – единственный.

Виды треугольников по сторонам

Треугольники расположены в соответствии с их сторонами: односторонний — равнобедренный — равнобедренный треугольник.

Разносторонний	Равнобедренный	Равносторонний
Треугольник называется разносторонним, если у него длины всех сторон разные.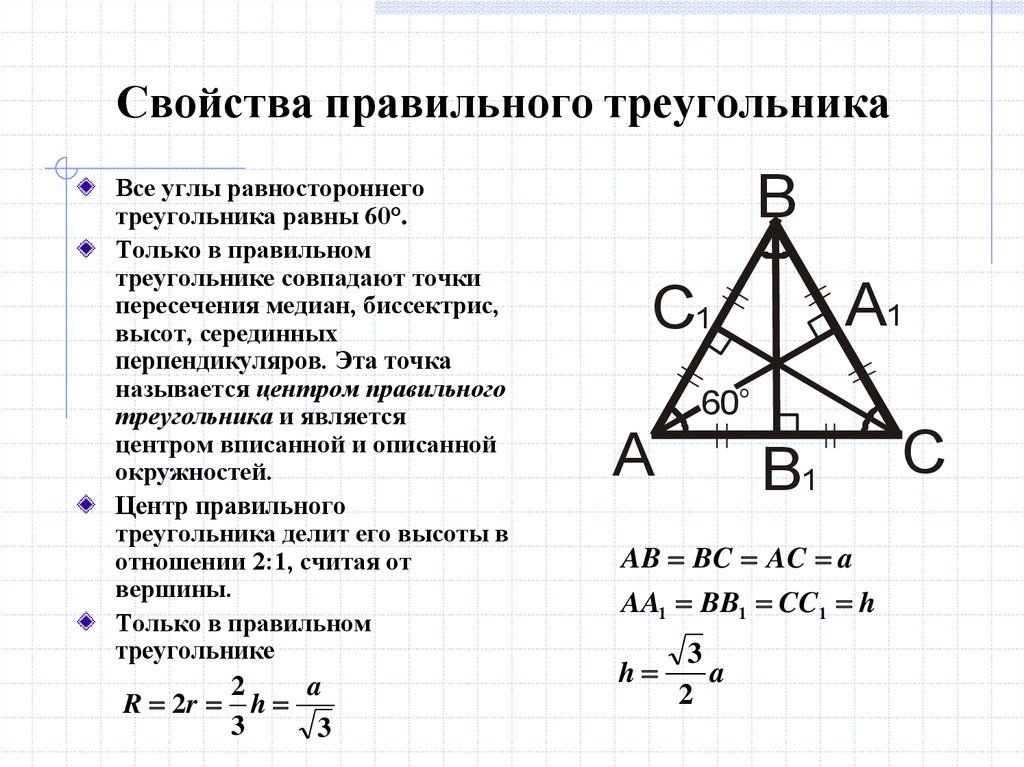 На рисунке показан такого вида треугольник АВС.	Треугольник называется равнобедренным, если у него две стороны равны. На рисунке показан равнобедренный треугольник АВС, у которого АВ=ВС.	Треугольник называется равносторонним, если у него все стороны равны. На рисунке показан такой треугольник, у него АВ=ВС=АС.

Медиана, биссектриса, высота, средняя линия треугольника

Часть треугольника, соединяющая вершину и центр противоположной стороны, называется центром треугольника.

Поскольку сторон три, для любого треугольника можно построить три медианы. На этой диаграмме показаны медианы (AF, EC и BD) треугольника ABC.

Это также показывает, что медианы пересекаются в точке O. Это справедливо для всех треугольников.

Прямоугольные треугольники — это треугольники с углом 90°, если кто-то забыл об этом. И в такой форме медиана обладает уникальными свойствами.

Определение и свойства медианы треугольника

В этой статье рассматривается определение треугольника и перечисляются его свойства.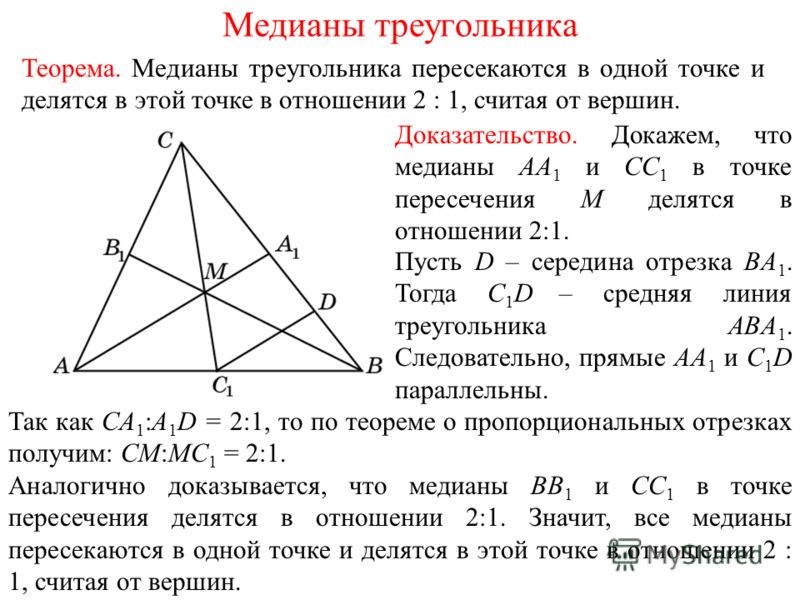 В нем также рассматриваются примеры задач для закрепления теоретического материала.

Медиана — это часть треугольника, соединяющая вершину с центром стороны, противоположной этой вершине.

Основанием медианы является точка пересечения медианы и одной из сторон треугольника, центр этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Поскольку треугольник имеет три вершины и три стороны, в нем есть три медианы. Все они пересекаются в одной точке (O). Это называется центром тяжести или центром масс треугольника.

При пересечении перпендикулярных линий каждая из них отсчитывается сверху и делится на 2:1. То есть:.

Свойство 2

Медиана делит треугольник на два равных (одинаковой площади) треугольника.

Свойство 3

Три медианы делят треугольник на шесть равных треугольников.

Свойство 4

Наименьшая медиана соответствует наибольшей стороне треугольника и наоборот.

• AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
• AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Предположим, что все стороны треугольника известны (a, b, c).

Длина медианы m_a заданный уравнением, можно найти из следующего уравнения.

Примеры задач

Площадь одной из фигур, образованных пересечениями трех перпендикулярных линий треугольника из задачи 1, равна 5 см2. Найдите площадь треугольника.

Решение В соответствии со свойством 3 выше, в результате пересечения трех перпендикулярных линий получается шесть треугольников равной площади. Поэтому: s_△ = 5 см2 и 6 = 30 см2.

Задача 2: Стороны треугольника равны 6, 8 и 10 см. Найдите середину стороны длиной 6 см.

Однако урок по этой теме показывает, что это действительно так. Это правда, что сложные проблемы редко решаются одной теоремой — почти всегда они разбиваются на несколько более мелких проблем.

Медиана треугольника.

Медиана и высота треугольника выступают в качестве графических параметров, определяющих величину всего треугольника, его сторон и углов.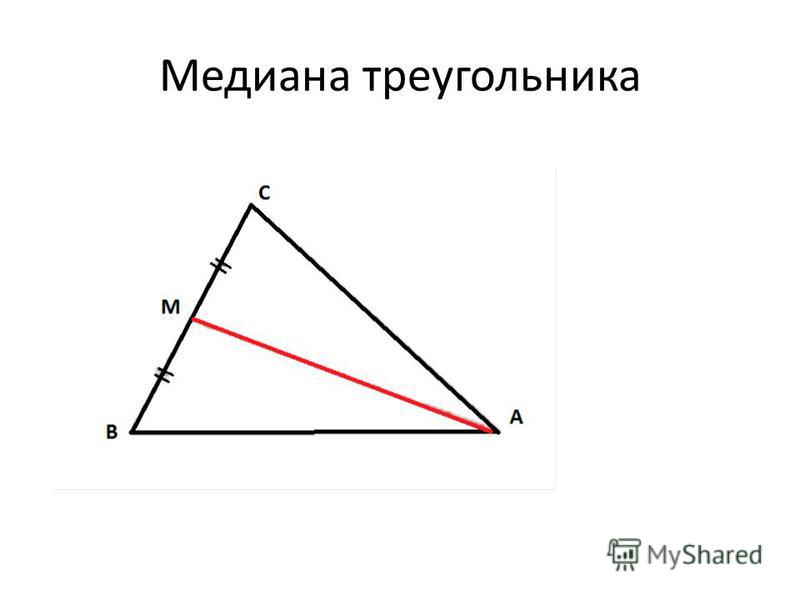 Три значения — медиана, высота и биссектриса — подобны штрих-коду продукта. Наша задача — уметь их измерять.

Определение

Медиана — это соединение между высотой и серединой на другой стороне. Поскольку треугольник имеет три вершины, медиана равна трем. Медиана не обязательно совпадает с высотой или биссектрисой. В большинстве случаев это отдельные разделы.

• Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
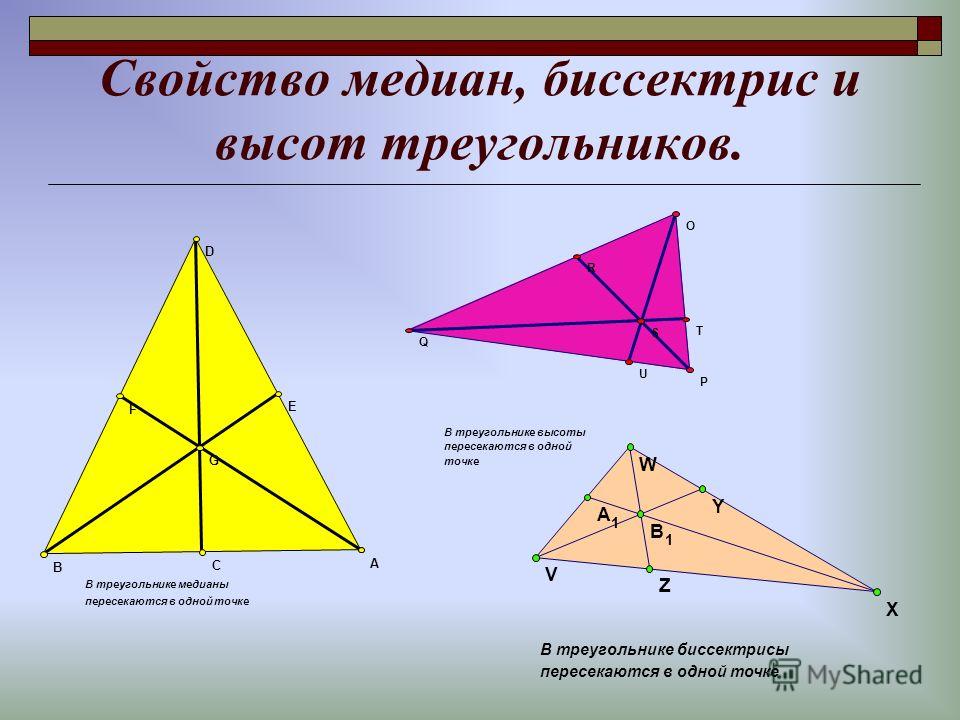
• Все медианы треугольника пересекаются в одной точке.
• Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольников.

• Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
• Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.

Задачи

Все эти качества легко запомнить и практиковать. Чтобы лучше понять проблему, давайте разберемся в некоторых вопросах.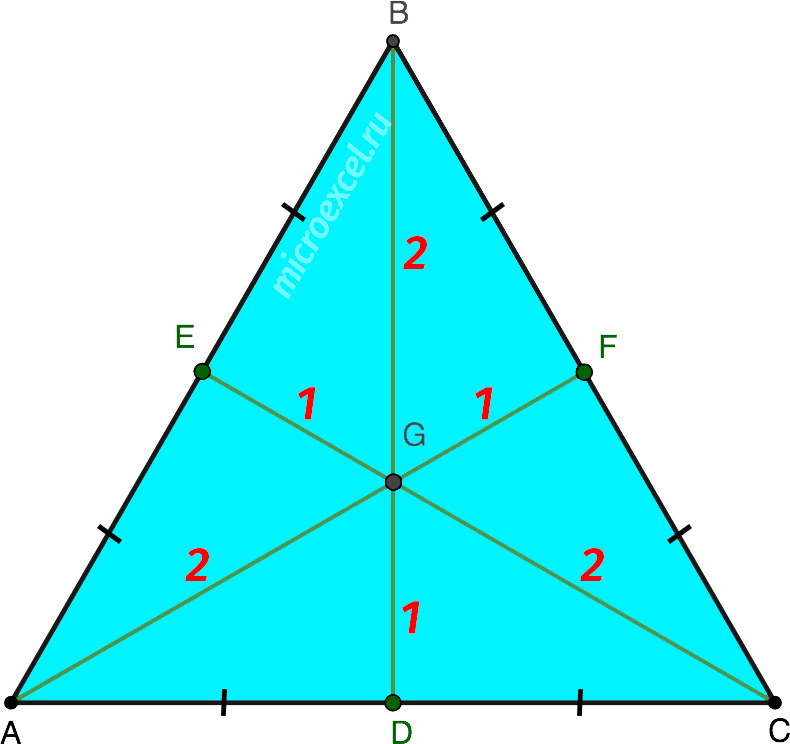 2)> $

$ m = \ sqrt*(49+81-64)> = \ sqrt $ — корень из результата.

• В равнобедренном треугольнике медиана, проведенная к основанию равна 8, а само основание – 6. Вместе с оставшимися двумя, эта медиана делит треугольник на 6 треугольников. Найти площадь каждого из них.

Посредник делит треугольник на шесть равносторонних треугольников. Поэтому площади меньших треугольников равны между собой. Достаточно найти наибольшую площадь и разделить ее на 6.

Учитывая медиану, проведенную к основанию, равнобедренные треугольники являются биссектрисой и высотой. Таким образом, основание и высота треугольника известны. Поиск района.

Площадь каждого из меньших треугольников: $= 4 $

Однако на практике исходные данные, используемые для нахождения через, могут представлять собой радикальные, динамические и дробные выражения и поэтому требуют выполнения длительных и сложных вычислений. Существует риск совершения ошибок, которые могут привести к неправильным ответам.

Как найти медиана треугольника

Термин «медиана» переводится как «на равной стороне». Для построения медианы центр одной стороны треугольника должен быть соединен с противоположной стороной треугольника. Полученное сечение представляет собой медиану треугольника.

Медиана треугольника. — Это отрезок, вписанный в вершину треугольника и соединяющий эту вершину с медианой центра противоположной стороны треугольника.

Интерстициальный CK показан красным цветом. Сторона AB центрального треугольника делится AK = KB.

Свойства медианы треугольника

Все они пересекаются друг с другом в общей точке на уровне треугольника.Центр тяжести. .

Для определения этой точки достаточно построить две медианы треугольника, а точкой пересечения будет третья медиана треугольника.

Используя пересечение промежуточных треугольников, каждая медиана измеряется от вершины треугольника и делится на 2:1. То есть длина средней части от вершины треугольника до пересечения с межвершинным расстоянием равна 2/3 его длины, а длина от пересечения межвершинного расстояния до стороны треугольника равна 1/3 его длины.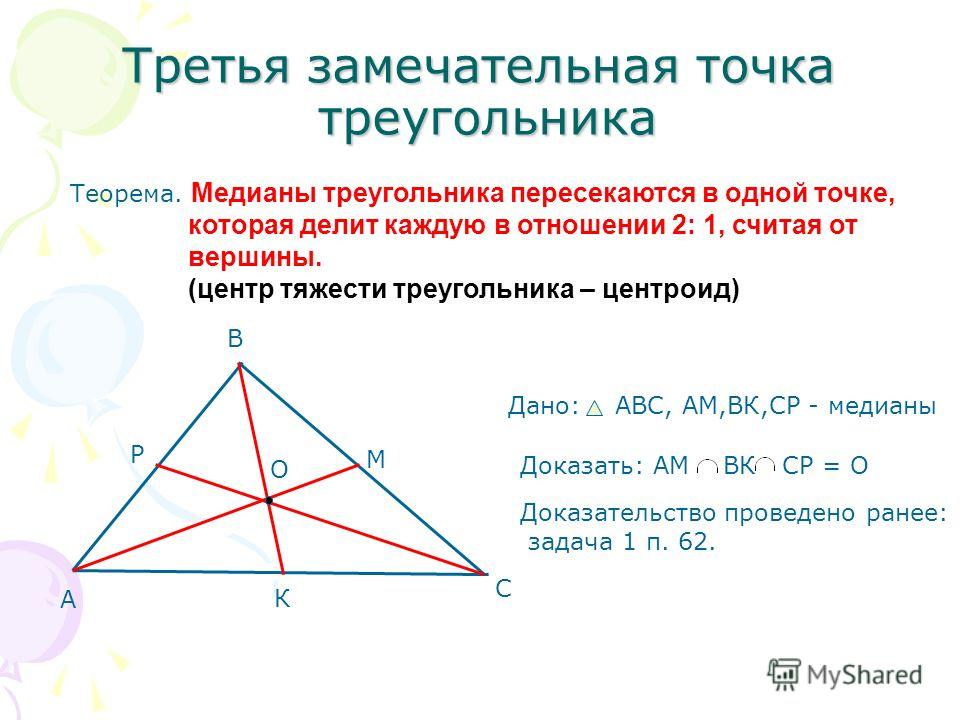

Медиана делит треугольник на два равных (по площади) треугольника.

Треугольник разделен на шесть равных треугольников с тремя медианными дисками.

Из отрезков, образующих медиану, можно построить треугольник, площадь которого равна 3/4 площади всего треугольника. Длина медианы удовлетворяет неравенству треугольника.

В прямоугольном треугольнике медиана, полученная из вершин прямых углов, равна половине предметов.

Большая сторона треугольника соответствует наименьшей медиане.

В равнобедренных треугольниках биссектрисы и высоты медиан, проведенных к основанию треугольника, совпадают.

В правильном женском треугольнике три «примечательные» линии (высота, дихотомос и медиана) совпадают, а три «примечательные» точки (ортографическая точка, центр тяжести и эндоциклический центр и периферия) находятся в «примечательных» местах.

Средняя линия треугольника

Сечение, проходящее через два основания среднего треугольника, является центральным классом треугольника.

Средняя линия треугольника всегда параллельна сторонам треугольника, где нет общей точки. Средняя линия треугольника равна половине длины стороны треугольника, к которой она параллельна.

Медиана — это соединение между высотой и серединой на другой стороне. Поскольку треугольник имеет три вершины, медиана равна трем. Медиана не обязательно совпадает с высотой или биссектрисой. В большинстве случаев это отдельные разделы.

Теорема о трех медианах треугольника

Три точки пересечения треугольника пересекаются в некоторой точке, от этой точки они делятся на ዄ (ዄ displaystyle 2:1 \) и измеряются сверху.

Что это значит? Рисунок. На самом деле, в этой теореме есть два утверждения. Вы заметили это?

1. медианы треугольников пересекаются в одной точке.

2. точка пересечения делит интерстиций на \ (\ displaystyle 2:1 \) и измеряется сверху.

Поясним секрет этой теоремы, т.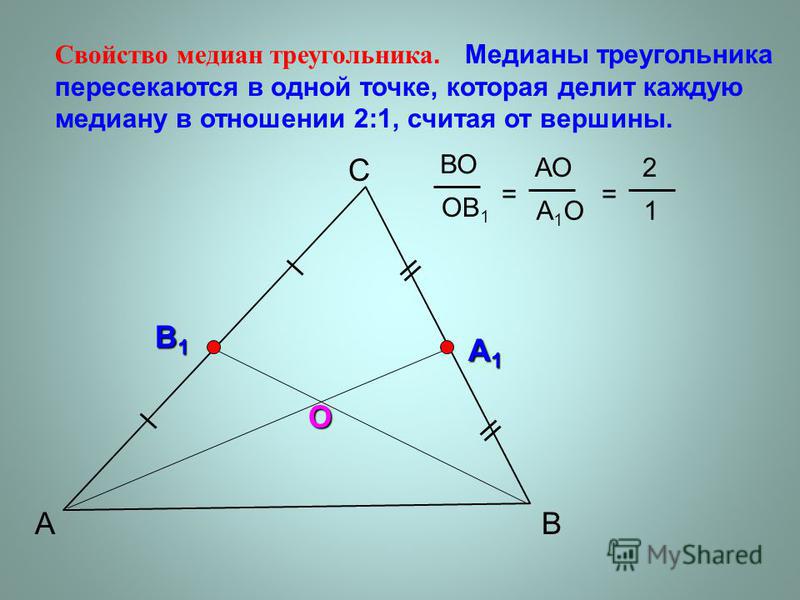 е. докажем ее.

Доказательство теоремы о трех медианах треугольника

Сначала спроектируйте только две медианы, а не все три. Они определенно пересекаются, не так ли? \Показать их пересечение с \(⌘ displaystyle e \).

Соединим точки ⌘ (⌘ displaystyle n \) и ߡ (ߡ displaystyle k \). Что у нас есть.

Конечно, ⌘ (⌘ displaystyle nk \) — это средняя линия ߡ (ߡ displaystyle \ треугольника abc \). Помните, что это значит?

Далее построим еще одну среднюю линию: отметим талию {{displaystyle ae \) — поставьте точку Ǿ (⌘ displaystyle f \) и отметим середину Ǿ (⌘ displaystyle ec \) — поставьте точку Ǿ (⌘ displaystyle g \). .

Теперь \ (⌘ displaystyle fg \) — средняя линия \ (⌘ displaystyle \ треугольник aec \). Среднее:.

Вы смотрели матч? И NK, и FG параллельны AC. и ዄ (ዄ displaystyle nk = ዄ frac \) и ዄ (ዄ displaystyle fg = ዄ frac \).

Далее рассмотрим четырехугольник ɑ (ɑ displaystyle nkgf \). Существуют ли параллельные и равные противоположности (⌘ (⌘ displaystyle nk) и 섹 (⌘ displaystyle fg \))?

Конечно, только в прямоугольниках!

Поэтому ɛ (ɛ displaystyle nkgf \) — это прямоугольник.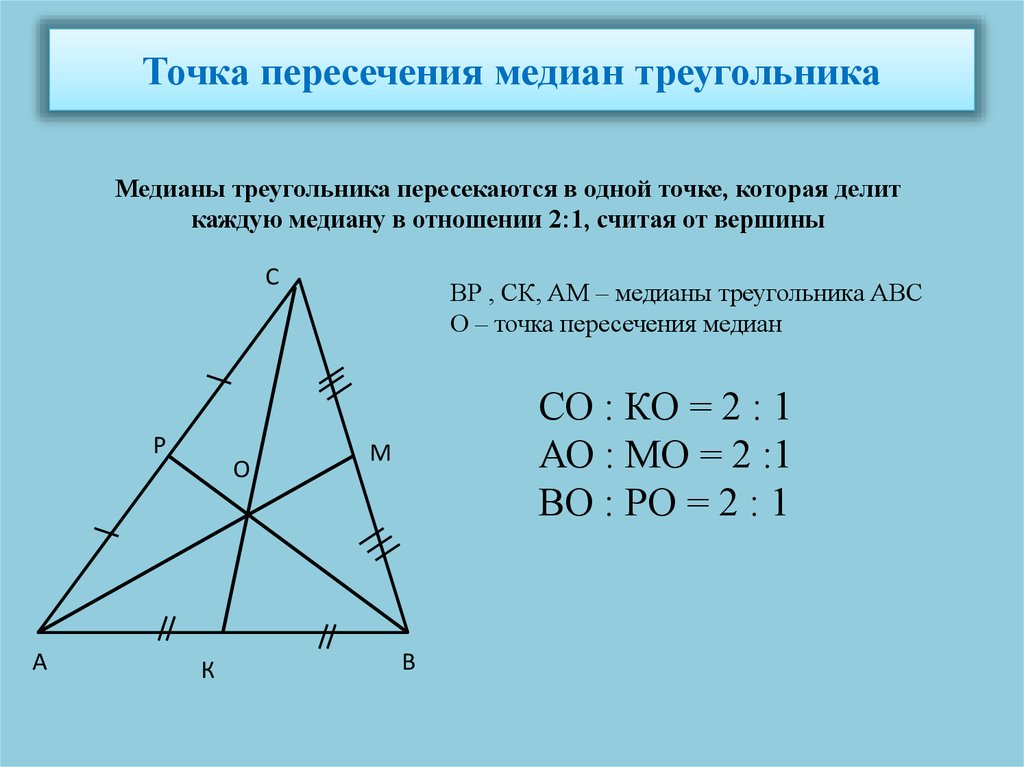 Так что

Теперь давайте вспомним свойства прямоугольника. Например, что вы знаете о диагоналях прямоугольника? Он разделен с правым, центральным перекрестком.

Открыть ответы…

Мы постоянно совершенствуем этот семинар, и вы можете помочь в этом. Доступ и использование руководства «Юклава» без ограничений (все темы по использованию и применению, 2000+ решенных задач, 20+ онлайн-семинаров, 100+ статей по образовательным программам).

Мы постоянно совершенствуем этот семинар, и вы можете помочь в этом. Доступ и использование руководства «Юклава» без ограничений (все темы по использованию и применению, 2000+ решенных задач, 20+ онлайн-семинаров, 100+ статей по образовательным программам).

Треугольник

Рисунок 1. Треугольник (общий случай).

Так, треугольник, в котором длины всех сторон различны и ни один из углов не равен, называется произвольным (рис. 1).

• В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным .
• В случае, если у треугольника все стороны одинаковы, он называется равносторонним .
• В случае, если у треугольника один и углов прямой (), он называется прямоугольным .
• Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:

Для разных типов треугольников поиск параметров треугольника может осуществляться по-разному. Для естественных проблем использование того или иного типа определяется конкретными данными проблемы.

Рисунок 2.Треугольники (рассекающие полосы)

Биссектриса угла — это геометрическое положение знака, равного стороне этого угла. Другими словами, биссектриса — это линия, делящая угол центрального треугольника (рис. 2). Известно, что биссектрисы внутренних углов треугольника делят противоположную сторону на отрезки в соответствии с прилежащей стороной.

Для нахождения частей углов через различные данные можно использовать следующие соотношения

Медиана треугольника — это часть, соединяющая вершину треугольника с центром противоположной стороны.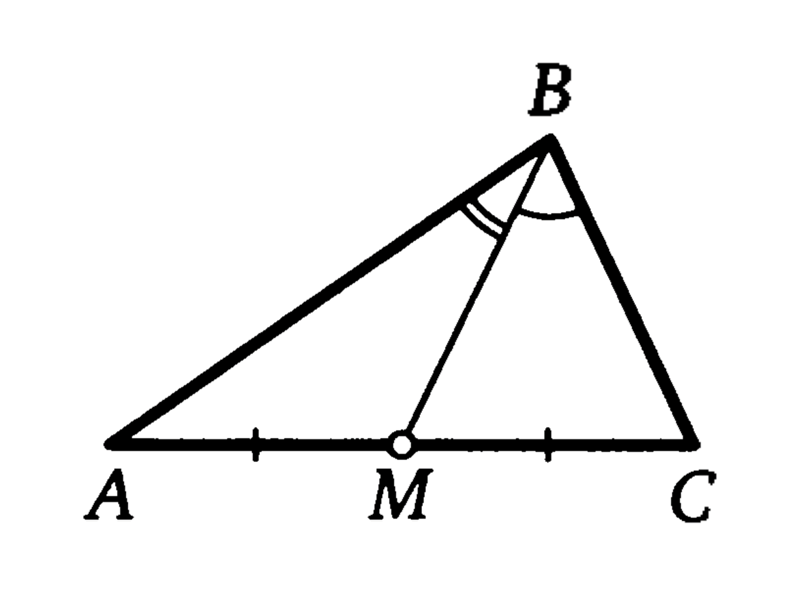 Все промежутки в треугольнике пересекаются в одной точке. Эта точка делит медиану в соотношении 2:1, измеряя от вершины (рис. 3).

Рис. 3. треугольник (медиана)

Для нахождения медианы треугольника по различным данным можно использовать следующие пропорции

Высота треугольника вертикальна, падает из вершины противоположного треугольника или его продолжения (рис. 4).

Вы можете найти высоту треугольника по различным данным, используя следующие пропорции

Важно: Тип, выбранный для решения конкретной задачи, зависит от того, что легче найти из данного

Среднее значение треугольника

Среднее значение треугольника

ПРЕДУПРЕЖДЕНИЕ. В вашем браузере отсутствует Javascript или он не включен. Это означает, что вы не увидите уравнений или фильмов.

Р. Адам Молнар

Первые три исследования по логарифмам и параболам были сосредоточены главным образом на алгебре. Мы построили декартову геометрию с помощью точек и кривых, но основное внимание уделялось символьной математике.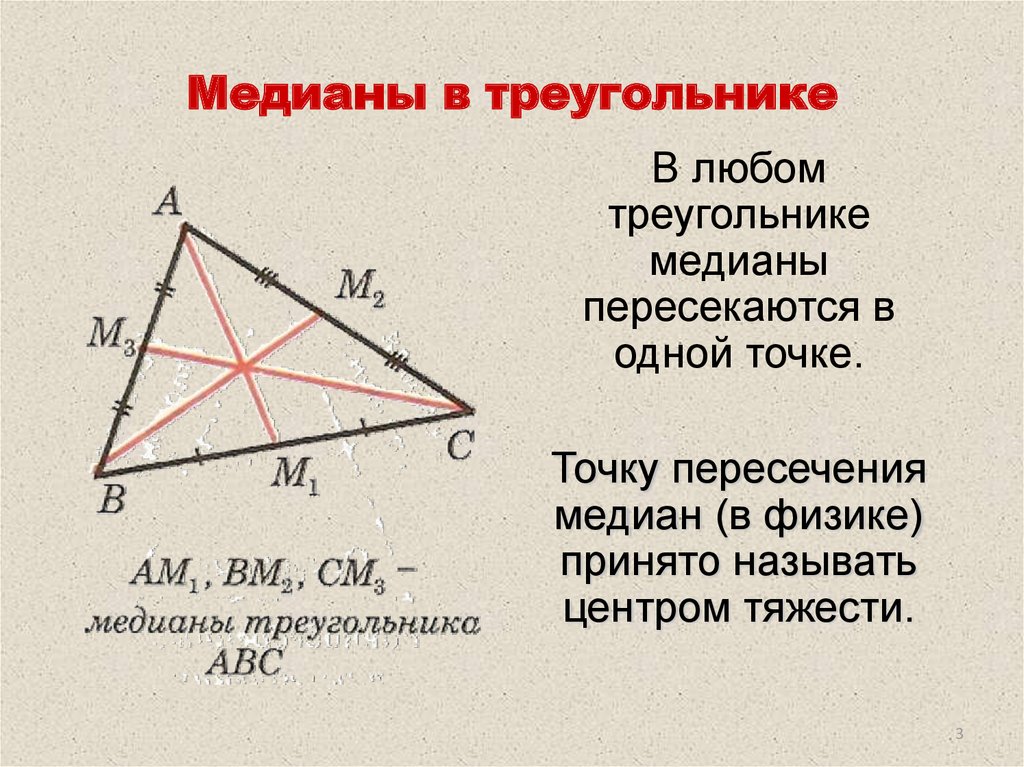 Это исследование начинает наш переход к геометрии, основанной на фигурах, хотя мы сохраним некоторые алгебраические шаги. Он предназначен для учащихся начальных классов средней школы, таких как Джорджия Математика 1 или начальная геометрия.

Определение треугольника и медианы

Хотя более серьезные математики, вроде тех, кто работает в Wolfram Mathworld, могут съёжиться при таком определении, мы могли бы назвать геометрию изучением форм. Геометрия имеет долгую историю. Платон и Сократ говорили о геометрии. Чуть позже, в III веке до нашей эры, были написаны «Начала» Евклида. Книги по-прежнему доступны и полезны сегодня. Для сравнения, наши более ранние темы (логарифмы и декартовы координаты) были впервые опубликованы примерно в 1615 году нашей эры. Большинство статистических тем касаются относительных детей за последние 100 лет!

Элементы начинаются с некоторых определений. В этой записи мы рассмотрим одну из основных фигур, определяемую тремя прямыми линиями. Книга I, определение 19 называет это трехугольником по количеству сторон. На современном языке мы называем это треугольником, потому что фигура имеет три внутренних угла. На рисунке ниже показаны некоторые распространенные типы треугольников. В частности, нам нужно помнить, что некоторые треугольники тупоугольные, у которых один угол больше прямого. Иногда они выглядят не так аккуратно, как нетупые остроугольные треугольники (не только потому, что я покрасил этот треугольник в коричневый цвет).

Мы можем нарисовать много вещей, используя треугольник. В этом задании мы сосредоточимся на отрезках, называемых медианами. Медиана треугольника соединяет одну из угловых точек треугольника, называемую вершиной, с серединой противоположной стороны. Внутри каждого треугольника есть три медианы, по одной из каждой вершины.

Построим медианы треугольника. Я продемонстрирую на картинках из бесплатного Java-пакета GeoGebra. Мы начнем с треугольника в системе координат, обозначив вершины A, B и C.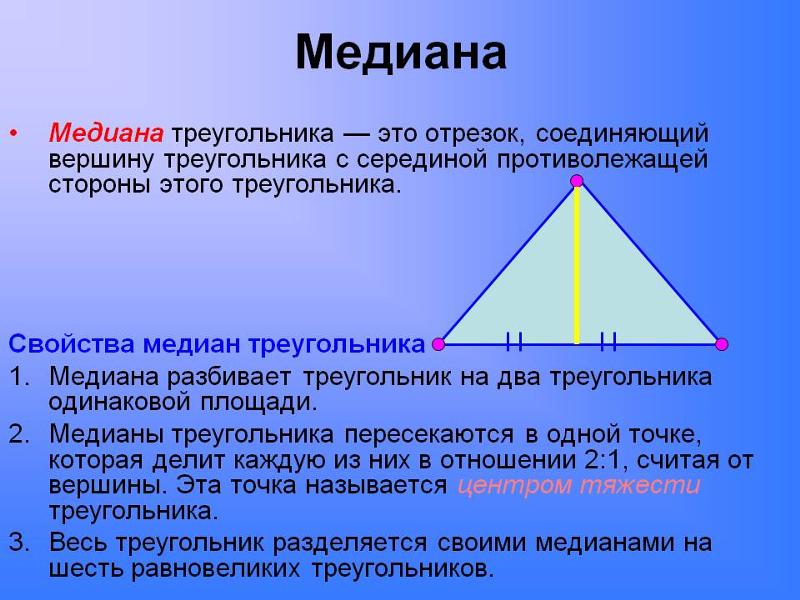 Чтобы упростить задачу, я зафиксирую точку A в начале координат (0, 0). Мы можем составить любой треугольник, перемещая B и C.

У греков, включая Евклида, были правила, касающиеся того, что можно строить. В их конструкциях разрешалось использовать только циркуль и линейку без опознавательных знаков. Если вы хотите увидеть, как они построили медиану, вы можете изучить эту страницу в Math Open Reference. Вместо этого подхода мы будем использовать свойства системы координат.

Обозначим координаты точки B как (b_x, b_y). Середина стороны AB находится на полпути между A и B. В горизонтальном направлении x это \frac{0 + b_x}{2} = \frac{b_x}{2}. В вертикальном направлении Y средняя точка будет находиться в точке \frac{0 + b_y}{2} = \frac{b_y}{2}. Точно так же, если координаты точки C равны (c_x, c_y). середина стороны AC равна \left( \frac{c_x}{2}, \frac{c_y}{2} \right) . Середина стороны BC равна \left( \frac{b_x + c_x}{2} , \frac{b_y + c_y}{2} \right) . В GeoGebra мы будем называть эти точки midAB, midAC и midBC соответственно.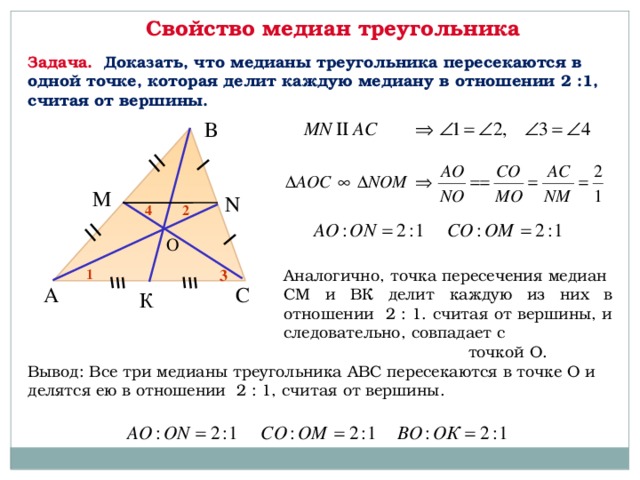 Медианы соединяют эти средние точки с противоположной вершиной, например, от середины АВ до С. На рисунке каждая медиана показана своим цветом — фиолетовым, зеленым и черным.

Триколор Перекресток

Интересно, что лиловая, зеленая и черная срединные линии пересекаются в одной и той же точке. Это правда, или они просто рядом? Пройдемся по математике и покажем, не обманывают нас глаза, что все три медианы соединены.

На плоскости любые две непараллельные прямые имеют точку пересечения. Нам нужно найти уравнения для срединных линий, а затем найти пересечение. Чтобы найти уравнения линии, мы найдем наклон линии. На основании двух точек (x_1, y_1), (x_2, y_2) наклон m равен изменению y, деленному на изменение x, m = \frac{y_2 — y_1}{x_2 — x_1}. (Есть особый случай, который мы не можем игнорировать. Если линия вертикальная, две координаты x будут одинаковыми, и мы попытаемся разделить на ноль. Поскольку это бесполезно, мы не забудем правильно писать вертикальные линии.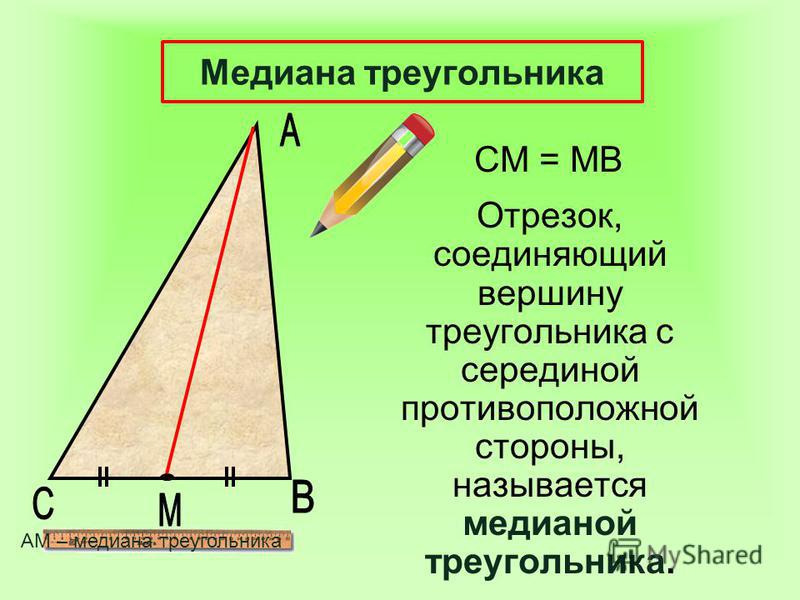 как x = x_1 = x_2, если необходимо.) Учитывая наклон, мы можем указать линию, используя точку и наклон.

y — y_1 = m (x — x_1) ~~ = \frac{y_2 — y_1}{x_2 — x_1} (x — x_1)

Так как мы знаем координаты вершин и средних точек, мы подставляем, чтобы найти уравнения прямой. Немного алгебры находит следующие уравнения:

\mbox{Фиолетовая медиана от C}: y = \frac{b_y — 2 c_y}{b_x — 2 c_x} (x — c_x) + c_y

\mbox{Зеленая медиана от B}: y = \frac{c_y — 2 b_y}{c_x — 2 b_x} (x — b_x) + b_y

\mbox{Черная медиана от A}: y = \frac{b_y + c_y}{b_x + c_x} ~ x

Чтобы найти пересечение фиолетовой и зеленой медиан, поскольку они у нас есть в форме ( y = something ), мы устанавливаем y = y и находим x.

\frac{b_y — 2 c_y}{b_x — 2 c_x} (x — c_x) + c_y ~~ = ~~ \frac{c_y — 2 b_y}{c_x — 2 b_x} (x — b_x) + b_y

Цель состоит в том, чтобы изолировать два термина, включающих x, с одной стороны и терминов, не включающих x, с другой стороны, а затем выполнить необходимое деление. Есть несколько алгебраических шагов, но в итоге мы приходим к результату

х = \ гидроразрыва {b_x + c_x} {3}

, а затем подставив это значение x обратно в любую строку, мы получим координату y y = \frac{b_y + c_y}{3} . Точка \left( \frac{b_x + c_x}{3} , \frac{b_y + c_y}{3} \right) лежит на фиолетовом и зеленом сегментах. Он также лежит на третьей медиане? Для проверки попробуем подставить точку в уравнение для черной медианы от A.

\left( \frac{b_y + c_y}{3} \right) = \frac{b_y + c_y}{b_x + c_x} ~ \left( \frac{b_x + c_x}{3} \right)

\left( \frac{b_y + c_y}{3} \right) = \frac{b_y + c_y}{3}

Две стороны совпадают, что означает, что точка действительно лежит на медиане из A. Поскольку мы нашли эту точку как пересечение медиан из B и C, все три медианы имеют общее пересечение. Эта точка имеет специальное название — центроид. На этом рисунке я добавил числовые метки к точкам.

Волшебные две трети

В предыдущей части мы видели, что в состав дробей входят числа 2 и 3.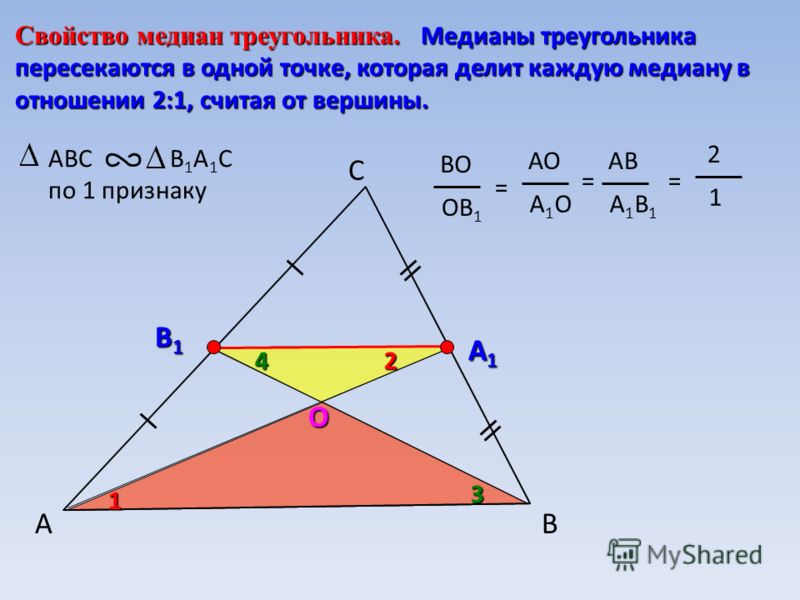 Оказывается, центр тяжести имеет особое положение. Он не только пересекает все три медианы, но и проходит две трети пути от вершины до середины. Например, расстояние от А до центроида в два раза больше расстояния от центроида до середины ВС. Есть несколько способов продемонстрировать это. Невероятная Академия Хана предоставляет Youtube видео двух подходов. Можно использовать подобные треугольники или применить трехмерное расстояние. Чтобы показать что-то другое, я собираюсь применить формулу расстояния в двух измерениях. 9{2} }

Расстояние до центроида равно одной трети квадратного корня, а более длинное второе расстояние равно половине квадратного корня. Отношение \frac{1/3}{1/2} = \frac{2}{3} , как и было заявлено.

Я только что показал вычисления для черной медианы от A. Процедура такая же для двух других медиан, просто вычисления немного длиннее. Для экспериментов с манипуляциями я предлагаю перейти на страницу centroid.html для апплета GeoGebra. Вы можете щелкнуть и переместить все три вершины треугольника — A, B и C. Апплет автоматически обновляет средние точки, медианы и расстояния.

Теорема о центроиде

Теорема о центроиде

Этот урок противопоставляет два метода доказательства геометрических теорем и мотивировать основную теорему этого курса.

Медианы встречаются в своих нижних трисекторах.

(Щелкните изображение, чтобы загрузить centroid.seg для KSEG.)

Доказательство в стиле Евклида

Пусть $ G $ будет точкой, где медианы $ B B’ $ и $ C C’ $ $\треугольника ABC$ пересекаются. Мы покажем, что $ G $ делит две медианы в в том смысле, что $BG:GB’ = 2:1$ и $CG:GC’ = 2:1$. Этот означает, что любые две медианы пересекаются в своей точке на расстоянии двух третей пути от вершину к середине противоположной стороны. Так делают все трое.

До места в «Началах» Евклида стоят теоремы о подобных треугольники и углы, образованные секущими двух параллельных прямых. Здесь мы будем использовать

• simAAA Два треугольника подобны тогда и только тогда, когда их углы равны попарно равны.

• simSAS Два треугольника подобны тогда и только тогда, когда две пары соответствующих стороны равны, а прилежащие углы равны.

• altIA Две прямые параллельны тогда и только тогда, когда два противоположных внутренних угла они делают с поперечной равными.

• sameSA Две прямые параллельны тогда и только тогда, когда соответствующие углы на одинаковые стороны секущей равны.

Шаг 1: Примените simSAS к $ \треугольнику AC’B’ $ и $ \triangle ABC $, заметив, что они имеют $ \угол A $ в общие, а смежные стороны находятся в соотношении $1:2$. Так два треугольника подобны.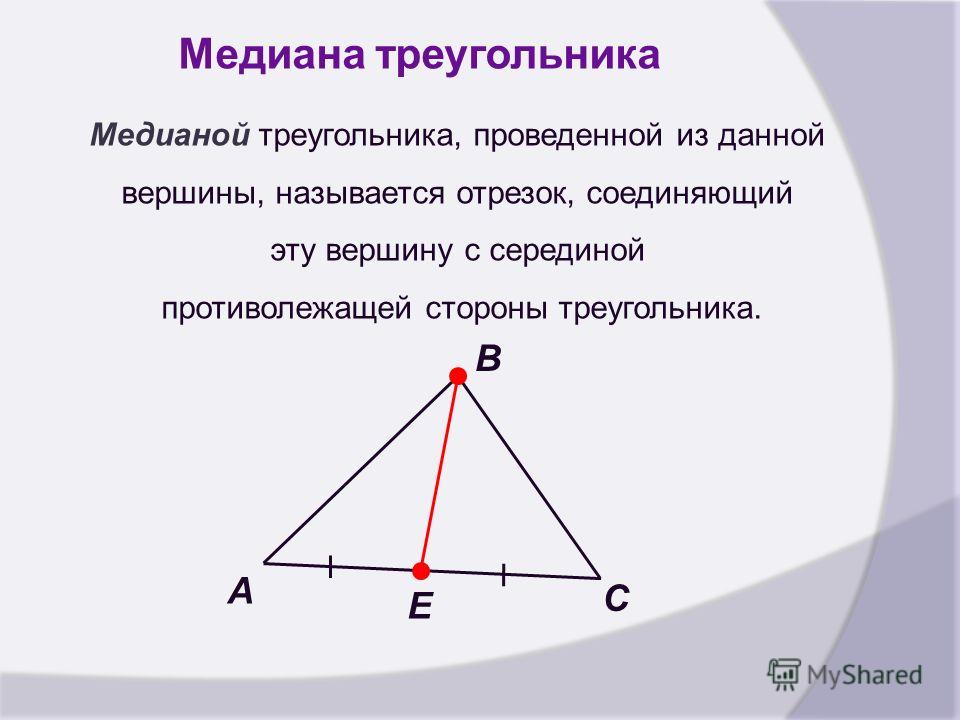 Что, по определению подобия, подразумевает, что $ \угол B’C’A = \угол CBA $ и $ C’B’:BC = 1:2 $.

Шаг 2: Примените тот же SA к двум строкам $C’B’$ и $BC$ к первому следствию: $ \угол B’C’A = \угол CBA $. Следовательно $ С’В’ \|\| БК $. Это, в свою очередь, означает, что sameSA $ \угол GC’B’ = \угол GCB $ и $ \угол C’B’G = \угол CBG $

Шаг 3: Примените simAAA к двум треугольникам $ \triangle GB’C’ $ и $GBC$. Две пары их углов уже показаны быть равным. Третья пара, $ \angle B’GC’ $ и $ \angle BGC $, равны, потому что это «противоположные углы». Таким образом, два треугольника подобны.

Шаг 4: Из второго вывода на шаге 1 мы знаем отношение к быть $2:1$. Таким образом, $1:2 = GB’:GB$ и $1:2 = GC’:GC$. Таким образом, $ G $ «рассекает» две медианы, как и предсказывалось.

Медианы треугольника совпадают в центре треугольника.

Доказательство в стиле Декарта

Непосредственное наблюдение нескольких примеров позволяет предположить, что медианы треугольника не только встречаются в одной и той же точке, но что эта точка составляет две трети путь от вершины до середины противоположной стороны на каждой медианы. Для краткости назовите эту точку «нижним трисектором».

Шаг 1: Нижний трисектор медианы от вершина $ A $ есть $ G = \frac{1}{3}A + \frac{2}{3}A’ $

Шаг 2: Середина стороны, противоположной $ A $, равна $ A’ = \frac{1}{2}B + \frac{1}{2}C $.

Шаг 3: Подставляя и упрощая получаем $ G = \frac{1}{3}A + \frac{1}{3}B + \frac{1}{3}C $.

Шаг 4: Выражение для $G$ логически симметрично в все три вершины, т.е. нельзя сказать, попали ли вы на шаг 4 начиная с вершины $A$ или либо $B,C$. Таким образом, $ G $ должен быть нижним трисектором на каждой медиане.

Одним из способов развития математики является обобщение теоремы.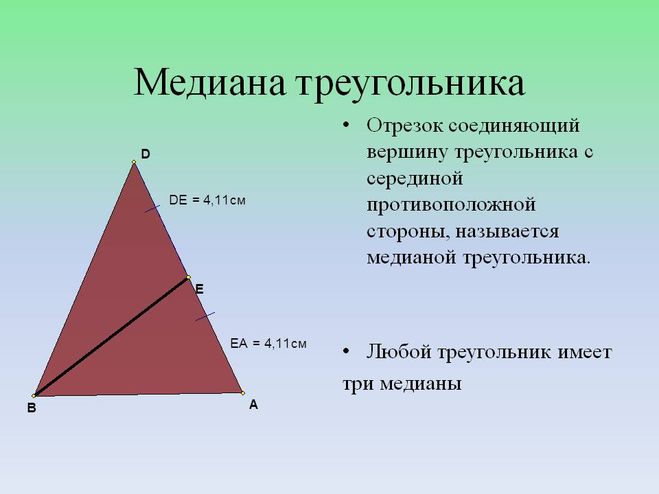 Этот влечет за собой ослабление гипотез и/или усиление выводов. Выше мы уже видели, как можно усилить вывод Теорема о центроиде, сформулированная в начале. Не только медианы одновременно, мы точно знаем, где на каждой медиане находится общая точка расположен.

В рамках подготовки к уроку по теореме Чевы давайте посмотрим, как мы могли бы ослабить гипотезы. Вы должны использовать KSEG, чтобы следить за этим обсуждением. Сначала мы переформулируем теорему таким образом, чтобы стало ясно, что гипотезы и выводы.

Мы не хотели бы ослаблять гипотезу о том, что $ \треугольник ABC $ опуская его. Ибо единственной альтернативой было бы для $ (ABC) $ до быть коллинеарной, и понятие «медиана» не имело бы особого смысла.

Мы могли бы исследовать случай, когда треугольник становится более общим многоугольник, например четырехугольник. Или мы могли бы рассмотреть, что происходит если треугольник приобретает другое измерение и становится тетраэдром. Вы можете поэкспериментировать с KSEG, чтобы увидеть, сможете ли вы обнаружить какие-либо теоремы.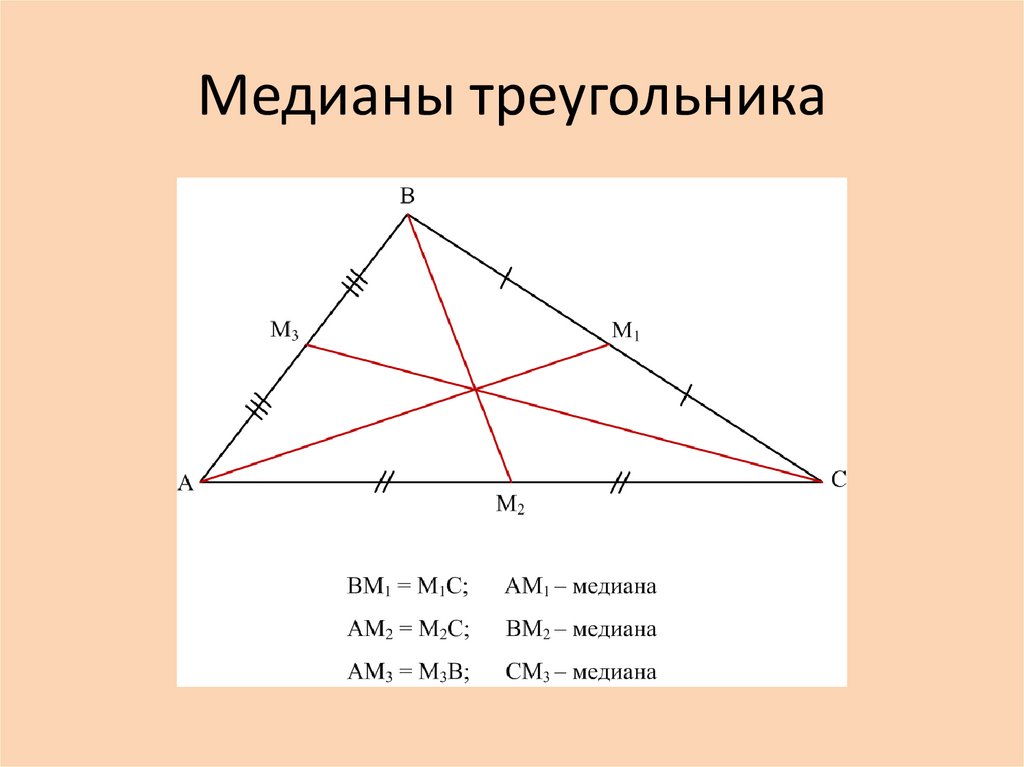 о «медианах». Конечно, нужно также обобщить понятие медиана.

Сохраняя треугольник, предположим, что мы ослабили потребность в точках $ A’, B’, C’ $ должны быть серединами на противоположной стороне. Если мы переедем $A’$ вдоль $(BC)$ параллелизм уничтожается немедленно. Но если вы затем осторожно переместите $ B’ $, это может быть восстановлен. Что вы изменили, так это долю сегментов от $A’$ в $B$ и $C$. Выразим это соотношение как $ \frac{A’-B}{A’-C}$. Таких отношений три, и вы может никогда не догадаться, какая связь между ними, когда параллелизм бывает.

Мы развиваем эти идеи на следующих уроках.

Исправлено 10 сентября 2009 г. WYS.

Урок Медиана, проведенная к гипотенузе прямоугольного треугольника

This Lesson (Медиана, проведенная к гипотенузе прямоугольного треугольника ) была создана пользователем ikleyn(45987)   : Просмотр исходного кода, Показать
О ikleyn 3 :

Теорема 1
В прямоугольном треугольнике медиана, проведенная к гипотенузе, имеет меру половины гипотенузы.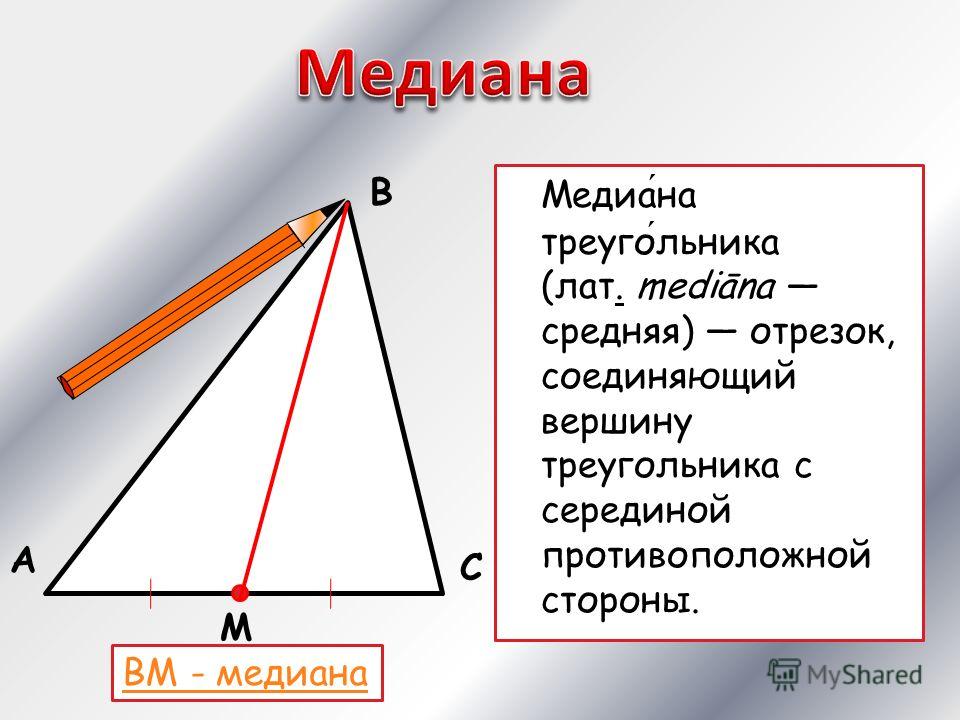

Доказательство Рассмотрим прямоугольный треугольник ABC с прямым углом A ( рис. 1 ),             , и пусть AD будет медианой, проведенной из вершины A 20 8 к гипотенузе . Нам нужно доказать, что длина медианы г. н.э. г. составляет половину -й длины гипотенузы г. до н.э. г. . Проведите прямую линию DE , проходящую через середину D параллельно отрезку AC до пересечения с другим отрезком AB в точке E ( Рисунок 2 ). Угол BAC прямой по условию. Углы BED и BAC равны, так как они являются соответствующими углами при параллельных прямых

Рисунок 1 . К теореме 1

Рисунок 2 . К доказательству теоремы 1

АС и ЭД и поперечная АВ (см.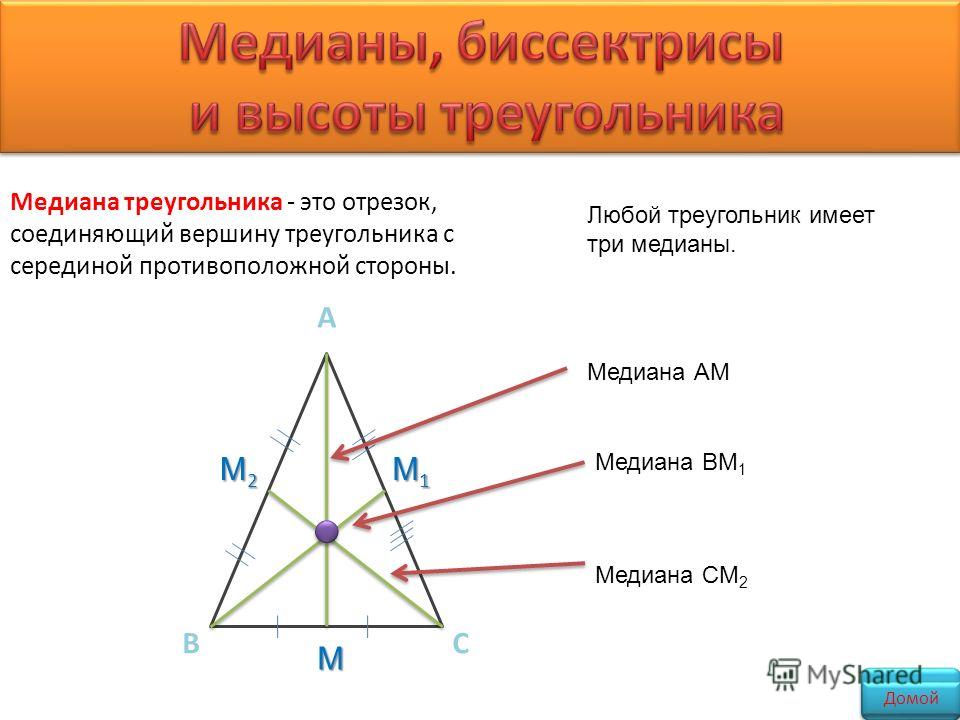 урок Параллельные прямые в теме Углы, комплементарные, дополнительные углы в разделе Геометрия на этом сайте).
Следовательно, угол BED является прямым углом.

Теперь, начиная с прямой линии DE проходит через середину D и параллельна AC , она разрезает сторону AB на два конгруэнтных отрезка равной длины: AE = EB (см. урок Отрезок, соединяющий середины двух сторон треугольника в теме Треугольники в разделе Геометрия на этом сайте).
Итак, треугольники AED и BED являются прямоугольными треугольниками, имеющими конгруэнтные катеты AE и EB и общая ветвь DE . Следовательно, эти треугольники конгруэнтны в соответствии с постулатом 1 (SAS) урока Проверка соответствия треугольников в теме Треугольники в разделе Геометрия на этом сайте.
Из этого следует, что отрезки AD и DB конгруэнтны как соответствующие стороны этих треугольников.
Поскольку DB имеет длину, равную половине длины гипотенузы BC , мы доказали, что медиана AD имеет длину, равную половине длины гипотенузы.

Теорема 1 доказана.

Примечание
В ходе доказательства Теоремы 1 мы фактически доказали также следующее утверждение:
В прямоугольном треугольнике медиана, проведенная к гипотенузе, делит треугольник на два равнобедренных треугольника .

Верно и обратное утверждение теоремы 1 .

Теорема 2
Если в треугольнике медиана имеет меру, равную половине длины проведенной стороны, то этот треугольник является прямоугольным.

Доказательство Дан треугольник ABC ( Рисунок 3 ) с медианой AD , проведенной                     из вершины A в сторону BC . Мы знаем, что длина медианы н. 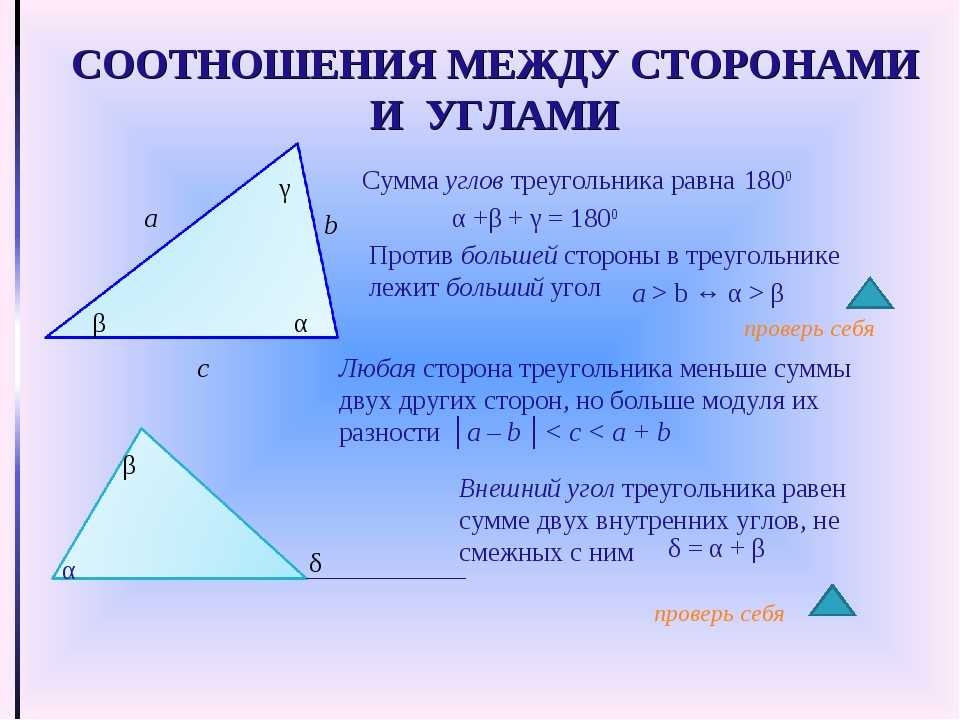э. составляет половину длины стороны г. до н.э. . Нам нужно доказать, что треугольник ABC прямоугольный. Сегменты AD и BD имеют одинаковую длину, по условию. Это означает, что треугольник ADB равнобедренный. Отсюда следует, что углы ABD и BAD ( рисунок 4 ) равны как углы при основании равнобедренного треугольника (см. урок Равнобедренные треугольники в теме Треугольники раздела Геометрия на этом сайте). Итак, мы обозначили оба угла ABD и BAD одним и тем же символом .

Рисунок 3 . К теореме 2

Рисунок 4 . К доказательству теоремы 2

Аналогичные рассуждения показывают, что углы ACD и CAD равны как углы при основании равнобедренного треугольника ACD (отрезки AD и CD имеют одинаковую длину по условию).