Определенные интегралы как решать: Как решать интегралы для чайников, примеры решений

как решать, правила вычисления, объяснение. Замена переменной в определенном интеграле

>> >> >> Методы интегрирования

Определение интеграла, определенного и неопределенного, таблица интегралов, формула Ньютона-Лейбница, интегрирование по частям, примеры вычисления интегралов.

Неопределенный интеграл

Пусть u = f(x) и v = g(x) — функции, имеющие непрерывные . Тогда, по произведения,

d(uv))= udv + vdu или udv = d(uv) — vdu.

Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:

∫ udv = uv — ∫ vdu (8.4.)

Эта формула выражает правило интегрирования по частям . Оно приводит интегрирование выражения udv=uv»dx к интегрированию выражения vdu=vu»dx.

Пусть, например, требуется найти ∫xcosx dx. Положим u = x, dv = cosxdx, так что du=dx, v=sinx. Тогда

∫xcosxdx = ∫x d(sin x) = x sin x — ∫sin x dx = x sin x + cosx + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например, ∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax и другие, которые вычисляются именно с помощью интегрирования по частям.

Определенный интеграл

Методы интегрирования , понятие определенного интеграла вводится следующим образом. Пусть на отрезке определена функция f(x). Разобьем отрезок [ a,b] на n частей точками a= x 0 Δ x i =x i — x i-1 . Сумма вида f(ξ i)Δ x i называется интегральной суммой, а ее предел при λ = maxΔx i → 0, если он существует и конечен, называется определенным интегралом функции f(x) от a до b и обозначается:

F(ξ i)Δx i (8.5).

Функция f(x) в этом случае называется интегрируемой на отрезке , числа a и b носят название нижнего и верхнего предела интеграла .

Методы интегрирования имеют следующие свойства:

Последнее свойство называется теоремой о среднем значении .

Пусть f(x) непрерывна на . Тогда на этом отрезке существует неопределенный интеграл

∫f(x)dx = F(x) + C

и имеет место формула Ньютона-Лейбница , cвязывающая определенный интеграл с неопределенным:

F(b) — F(a). (8.6)

Геометрическая интерпретация: представляет собой площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), прямыми x = a и x = b и отрезком оси Ox.

Несобственные интегралы

Интегралы с бесконечными пределами и интегралы от разрывных (неограниченных) функций называются несобственными. Несобственные интегралы I рода — это интегралы на бесконечном промежутке, определяемые следующим образом:

(8.7)

Если этот предел существует и конечен, то называется сходящимся несобственным интегралом от f(x) на интервале [а,+ ∞), а функцию f(x) называют интегрируемой на бесконечном промежутке [а,+ ∞). В противном случае про интеграл говорят, что он не существует или расходится.

Аналогично определяются несобственные интегралы на интервалах (-∞,b] и (-∞, + ∞):

Определим понятие интеграла от неограниченной функции. Если f(x) непрерывна для всех значений x отрезка , кроме точки с, в которой f(x) имеет бесконечный разрыв, то несобственным интегралом II рода от f(x) в пределах от a до b называется сумма:

если эти пределы существуют и конечны. Обозначение:

Примеры вычисления интегралов

Пример 3.30. Вычислить ∫dx/(x+2).

Решение. Обозначим t = x+2, тогда dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| + C .

Пример 3.31 . Найти ∫ tgxdx.

Решение.∫ tgxdx = ∫sinx/cosxdx = — ∫dcosx/cosx. Пусть t=cosx, тогда ∫ tgxdx = -∫ dt/t = — ln|t| + C = -ln|cosx|+C.

Пример 3.32 . Найти ∫dx/sinx

Пример 3.33. Найти .

Решение. =

.

Пример

3.34 . Найти ∫arctgxdx.

Решение. Интегрируем по частям. Обозначим u=arctgx, dv=dx. Тогда du = dx/(x 2 +1), v=x, откуда ∫arctgxdx = xarctgx — ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; так как
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Пример 3.35 . Вычислить ∫lnxdx.

Решение. Применяя формулу интегрирования по частям, получим:
u=lnx, dv=dx, du=1/x dx, v=x. Тогда ∫lnxdx = xlnx — ∫x 1/x dx =
= xlnx — ∫dx + C= xlnx — x + C.

Пример 3.36 . Вычислить ∫e x sinxdx.

Решение. Применим формулу интегрирования по частям. Обозначим u = e x , dv = sinxdx, тогда du = e x dx, v =∫sinxdx= — cosx → ∫ e x sinxdx = — e x cosx + ∫ e x cosxdx. ∫e x cosxdx также интегрируем по частям: u = e x , dv = cosxdx, du=e x dx, v=sinx. Имеем:
∫ e x cosxdx = e x sinx — ∫ e x sinxdx. Получили соотношение ∫e x sinxdx = — e x cosx + e x sinx — ∫ e x sinxdx, откуда 2∫e x sinx dx = — e x cosx + e x sinx + С.

Пример 3.37. Вычислить J = ∫cos(lnx)dx/x.

Решение.Так как dx/x = dlnx, то J= ∫cos(lnx)d(lnx). Заменяя lnx через t, приходим к табличному интегралу J = ∫ costdt = sint + C = sin(lnx) + C.

Пример 3.38 . Вычислить J = .

Решение. Учитывая, что = d(lnx), производим подстановку lnx = t. Тогда J = .

Пример 3.39 . Вычислить J = .

Решение. Имеем: . Поэтому =

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Изучаем понятие « интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о , необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

« Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Если определения из учебника слишком сложны и непонятны, прочитайте нашу статью. Мы постараемся максимально просто, “на пальцах” объяснить основные моменты такого раздела математики, как определенные интегралы. Как вычисляется интеграл, читайте в данной инструкции.

С геометрической точки зрения интеграл функции – это площадь фигуры, образуемой графиком данной функции и осью в пределах интегрирования. Запишите интеграл, проанализируйте функцию под интегралом: если подынтегральное выражение возможно упростить (сократить, вынести множитель на знак интеграла, разбить на два простых интеграла), сделайте это. Откройте таблицу интегралов, чтобы определить, производная какой функции стоит под интегралом. Ответ найден? Выпишете множитель, вынесенный за интеграл (если это имело место), запишите найденную из таблицы функцию, подставьте границы интеграла.

Для вычисления значения интеграла рассчитайте его значение в верхней границе и вычтите его значение в нижней границе. Разница – и есть искомая величина.

Чтобы проверить себя или хотя бы уяснить ход решения задачи на интегралы, удобно пользоваться онлайн-сервисом нахождения интегралов , однако прежде чем приступать к решению, ознакомьтесь с правилами ввода функций . Огромнейшее его преимущество в том, что здесь пошагово расписывается все решение задачи с интегралом.

Конечно, здесь рассмотрены лишь самые простые варианты интегралов – определенные, на самом деле разновидностей интегралов великое множество, изучаются они в курсе высшей математики, математического анализа и дифференциальных уравнений в ВУЗах для студентов технических специальностей.

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Изучаем понятие « интеграл»

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных , необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x) .

Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

« Интеграл»

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

• Производная от интеграла равна подынтегральной функции:

• Константу можно выносить из-под знака интеграла:

• Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

• Линейность:

• Знак интеграла изменяется, если поменять местами пределы интегрирования:

• При любых точках a , b и с :

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

В каждой главе будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Понятие определённого интеграла и формула Ньютона-Лейбница

Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) — F (a )).

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.

Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,

(38)

Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

(39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому

Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b , далее — значение нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет определённым интегралом. .

При a = b по определению принимается

Пример 1.

Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной

(при С = 0), получим

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).

Пример 2. Вычислить определённый интеграл

Решение. Используя формулу

Найти определённый интеграл самостоятельно, а затем посмотреть решение

Свойства определённого интеграла

Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.

(40)

Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,

На основании формулы (39) последнее равенство означает равенство интегралов

Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.

(41)

Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.

(42)

Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т.е. если

(43)

Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т. е.

(44)

Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.

(45)

Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство

можно почленно интегрировать , т.е.

(46)

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.

Пример 5. Вычислить определённый интеграл

Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим

Определённый интеграл с переменным верхним пределом

Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл

(47)

а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.

(48)

Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим

так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.

Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.

Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной

где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной

то в соответствии с формулой (16) можно записать

В этом выражении

первообразная функция для

В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна

Пусть α и β – значения переменной t , при которых функция

принимает соответственно значения a и b , т.е.

Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть

Тургенев

§3. Методические рекомендации по решению задач с помощью определенного интеграла. Методика формирования у учащихся средней школы обобщенных умений и навыков при изучении определенного интеграла в процессе решения задач

Методика формирования у учащихся средней школы обобщенных умений и навыков при изучении определенного интеграла в процессе решения задач

дипломная работа

Часто при изучении интегрального исчисления в школе рассматриваются лишь основные моменты данного раздела: нахождение первообразных функции, вычисление определённых интегралов, отыскание площадей плоских фигур и объёмов тел вращения. Данные вопросы являются базовыми и необходимыми, ведь именно они раскрывают основную суть процесса интегрирования, но где же творческий подход в обучении математике? Где он? Порой мы просто-напросто ограничиваем тему «Интеграл» учебников и делаем её недоступной для другого математического материала, входящего в рамки школьной программы. Многие из учителей забывают, что, используя несложные конструкции, содержащие определённые интегралы, можно составить прекрасные уравнения, неравенства, их системы, различные задачи с параметрами, решение которых вызовет лишь положительное одобрение со стороны школьников. И это действительно так. Решая достаточно большое количество стандартизованных задач, учащиеся вскоре приходят к усталости, усталости решать «одно и тоже». В этот момент «мозговой штурм» сменяется «мозговым спадом», что на наш взгляд, не хотел бы наблюдать на своём уроке каждый учитель. И вот тогда на помощь могут прийти всё те же конструкции. Благодаря им, учащиеся будут стремиться вычислить не только сам интеграл, но и применить полученные в ходе вычисления результаты к решению конкретной задачи, которая в свою очередь вызовет интерес у школьников. Таким образом, удастся восстановить атмосферу сотрудничества на уроке и локализовать «штурм» в каждом из учеников. Составляя конструкции, можно осуществить внутриматематическое моделирование, которое позволит доказать учащимся то, что тема «Интеграл» не существует сама по себе, автономно, а великолепно и в полном объёме используется при решении задач ранее изученных тем.

Также одним из существенных моментов при решении задач, содержащих конструкции, является то, что учащиеся сталкиваются с тем, что в пределах интегрирования появляются переменные (до этого были лишь постоянные), для которых чаще всего приходится проводить анализ и находить их ОДЗ. Ведь вне ОДЗ многие определённые интегралы не вычислимы, тогда сталкиваемся с несобственными интегралами, решение которых не предусматривается школьной программой. Поэтому при составлении любых конструкций данный факт должен обязательно учитываться. Именно анализ заставляет учащихся сомневаться, делает процесс вычисления познавательным и привлекает к себе класс. Заинтересованный ученик всегда активен. Он стремится решить, понять, осознать. Поддержание данного стремления — основная задача учителя, его мастерство и профессионализм. Приведём примеры некоторых из конструкций, которые могут быть использованы в конкретных ситуациях. К каждому заданию прилагается по два варианта с решениями.

I. Решить уравнения.

А) ,

Решение. Вычислим интеграл:

Тогда

Решая полученное уравнение, находим, что x = 0, x = + 1, x = — 2.

Ответ: — 2, — 1, 0, 1.

Следует отметить, что в данном задании ничего не потребовалось, кроме техники нахождения простейших интегралов и решения уравнения, в том числе кубического.

Б) .

Решение. (В силу того, что интеграл неопределён при , то подобные точки выколоты из области задания). Вычислим значение интеграла:

.

Для удобства проведём вычисления по отдельности:

,

Приравнивая левую и правую часть равенства, получим:

.

Решая полученное тригонометрическое уравнение, имеем , где .

Но так как (по условию), то подбором устанавливаем, что .

Ответ: .

В данном задании учащимся приходится проводить исследовательскую работу с целью нахождения ОДЗ, решением тригонометрического уравнения, отбором корней. Здесь же они сталкиваются с вычислением нетабличного интеграла, для решения которого применяется подстановка, с которой многие учителя сталкиваются в своей преподавательской практике. Только правильный выбор подстановки и её использование приведёт к желаемому результату.

II. Решить неравенства.

А) ,

Решение. Вычислим определённый интеграл:

Тогда .Приравняем многочлен, стоящий в левой части к нулю и находим корни уравнения . Откуда . Методом интервалов решаем неравенство : откуда

Ответ: .

Б) .

Решение. По отдельности вычислим интеграл, стоящий в левой части и интеграл, стоящий в правой части неравенства:

; .

Тогда

Ответ: .

Существенных трудностей задания А) и Б) не вызывают.

III. Оцените последовательности.

А) ,

Решение. Вычислим данный интеграл:

.

Пользуясь неравенством Коши для двух неотрицательных чисел, оценим выражение

.

Прибавив к обеим частям данного неравенства — 2, получим оценку (an):

.

Ответ: .

Б) .

Решение. Вычислим определённый интеграл:

Тогда .

Используя неравенство Коши для трёх неотрицательных чисел, оценим (bn):

.

Ответ: .

Вся трудность заданий А) и Б) заключается лишь в том, на сколько хорошо учащиеся помнят неравенство Коши.

IV. На координатной плоскости изобразите множество точек (область), удовлетворяющих следующим условиям.

А)

Решение. Преобразуем каждое неравенство системы по отдельности:

.

С учётом вычислений данная система примет вид:

На координатной плоскости заштриховываем множества точек, удовлетворяющих каждому из неравенств системы:

Закрашенная часть — искомая область.

Б)

(данную конструкцию уместно предложить после изучения показательной функции).

Решение. Преобразуем каждое из неравенств системы по отдельности:

Тогда с учётом вычислений данная система примет вид:

.

На координатной плоскости заштриховываем множества точек, удовлетворяющих каждому из неравенств системы:

Закрашенная часть — искомая область.

Сложность заданий А) и Б) заключается лишь в том, на сколько правильно учащиеся могут решать неравенства с двумя переменными.

V. При всех значениях параметра решить уравнения.

А)

Решение. Для начала вычислим предложенный интеграл:

.

Тогда .

определенный интеграл задача

Решая данное уравнение относительно параметра а, имеем:

1. если a = — 1: — 3 = 0, сл., решений нет; если a = 1: получим линейное уравнение 2x — 3 = 0, сл., ;

2. если

2.1. если , то решений нет;

2.2. если

Произведя отбор, запишем ответ.

Ответ: при :

при : решений нет

при a = 1: .

Б).

Решение. Вычислим предложенные определённые интегралы:

;

.

С учётом полученных вычислений имеем:

Во избежание ошибок при решении данного задания, необходимо заранее вспомнить с учащимися основные свойства тригонометрических функций (особенно области значений синуса и косинуса), а также правила решения отдельных задач с параметрами (это касается и задания А). Добиться максимальной работоспособности учащихся на уроке можно лишь при постановке таких проблемных ситуаций, которые будут создавать у школьников стремление их разрешить. На мой взгляд, одной из таких ситуаций будет использование предложенных конструкций, которые и осуществят творческий подход при обучении математике.

Изучение темы «Определенный интеграл» представляет собой сложный процесс, основными компонентами которого являются:

— приобретение учащимися определенной системы знаний, умений, навыков;

— овладение определенной системой фактов, идей.

Целью занятий по решению определенного интеграла является расширение и углубление знаний, развитие интереса учащихся к предмету, а также развитие их математических способностей, формирование у учащихся понятий и методов решения систем уравнений различной сложности.

Положение школьного курса алгебры в системе математических предметов имеет свою специфику. Прежде всего, курс алгебры девятилетней школы, по своему содержанию, носит преимущественно прикладной и практический характер. При его изучении учащиеся овладевают определенными знаниями, умениями и навыками, составляющими существенное звено математического аппарата, который активно применяется при решении разнообразных математических и нематематических задач. При этом следует отметить то, что обучение в VII -IX классе представляет не завершающий, а промежуточный этап в системе математического образования каждого школьника. На базе, полученной учеником математической подготовки, строится его дальнейшее обучение в X — XI классах. В XI классе вводится понятие определенного интеграла, и рассматриваются методы его решения.

Исходя из вышесказанного, следует отметить, важность изучения темы «Определенный интеграл». Основное место в данной теме занимают методы решения интеграла; замена переменной и интегрирование по частям.

Как же сконцентрировать внимание учащихся при изучении определенного интеграла? Эту проблему можно решать разными способами. При закреплении и тренировке в применении изученного материала полезен следующий прием. После предъявления первого задания учитель, не решая и не разъясняя его, просит учащихся составить аналогичное упражнение. Уже одно это заставляет школьников сосредоточиться, так как понять аналогию можно только тогда, когда хорошо проанализировал условие исходного примера.

Рассмотрим урок, на котором отрабатывается метод решения определенного интеграла способом подстановки. Учащимся предлагается вычислить следующий интеграл:

.

Решение. Воспользуемся подстановкой , роль и играют значения 0 и . Имеем

.

Это задание ученики должны выполнить самостоятельно. При этом они имеют право задавать учителю вопросы по поводу возникающих трудностей.

Следующее задание уже более сложнее. Например:

.

Решение. Подстановка (где t изменяется от до 0) приводит к равенству

или

.

Перенося последний интеграл налево, получаем

.

Описанный метод очень удобен для рассмотрения различных случаев вычисления интегралов. Описанная работа занимает обычно весь урок. Естественно, что более сильные учащиеся опережают класс. Для того чтобы они не дезорганизовывались, ожидая новых заданий, учитель предлагает им решать упражнения из учебника. Можно отметить и еще один недостаток таких уроков. Учащиеся одного и того же класса в одно и то же время распадаются на две большие группы, которым нет дела друг до друга. Такое отчуждение вредно влияет на внимание учащихся. Объединить класс можно несколько иным построением урока. Учитель вначале рассматривает не одно задание, а сразу два или три. Разъяснив задание, он стирает его с доски. Закончив объяснения, учитель составляет на доске три задания для самостоятельной работы.

Ребята приступают к самостоятельной работе. Тот, кто выполнит все задания первым, подходит к учителю, который быстро проверяет работу ученика и выставляет за нее оценку. Несколько человек, получившие хорошие оценки, объявляются консультантами. Они должны проверить работы своих товарищей и выставить в их тетрадях свои оценки. Разрешение на выставление оценок мобилизует проверяющих. Они с большой ответственностью приступают к проверке. Учитель же может проконтролировать проверяющих, собрав тетради и просмотрев их после урока.

Такие уроки требуют от учителя максимума внимания и умения владеть классом, но и учащимся они приносят большую пользу как в учебном, так и в воспитательном плане.

Система упражнений для изучения интеграла в учебном пособии недостаточно совершенна. Задания здесь в основном сводятся к вычислению площадей фигур и интеграла, т.е. имеют тренировочный характер. На уроках в 10 классе будут полезны задачи, в которых вычислению интеграла предшествовало бы упрощение или преобразование формулы, задающей функцию. Таковы следующие задачи:

1. Вычислите интеграл, предварительно выполнив необходимые преобразования подынтегральной функции:

а) ;

б) ;

в) .

Дополнительного времени, как и дополнительных знаний, для рассмотрения приведенных задач фактически не требуется: их решение целесообразно связать с повторением.

Можно предлагать и такие задачи на вычисления интегралов, которые требуют более сложных преобразований тригонометрических выражений.

2. Вычислите интеграл:

а) ;

б) ;

в) :

Решение.

.

Задачи 1-2 полезно рассмотреть на внеклассных и факультативных занятиях.

До сих пор рассматривались упражнения, в которых требовалось вычислить интеграл, привлекая для этого сведения из предшествующего курса алгебры и начал анализа. Но и задачам, в которых интеграл играет вспомогательную роль, надо отвести время на уроках или внеклассных занятиях. Вот примеры таких упражнений.

3.Решить уравнение:

а) ; б) ;

Найти все значения t такие, что и является корнем уравнения:

а) ; б) .

Найти множество неотрицательных корней уравнения:

.

Предложенные задачи, несомненно, будут способствовать сознательному усвоению понятия интеграла. Необходимо предупреждать возможность формального подхода к вычислению интегралов. Прежде чем вычислять интеграл, нужно убедиться, что на отрезке интегрирования существует первообразная подынтегральной функции: формула Ньютона-Лейбница применима лишь для непрерывных функций, а они имеют первообразную. Чтобы избежать недоразумений, полезно приучать десятиклассников перед формальным интегрированием устанавливать, непрерывна ли заданная (под интегралом) функция. В этих целях полезно рассмотреть следующую задачу:

Вычисляя и , ученик нашел, что

.

Верны ли эти равенства? Если нет, то в чем заключается ошибка?

Анализ ошибки полезно связать с геометрическими иллюстрациями и убедиться, что в точке x=2 функция не определена. Следовательно, на промежутке [0;3] функция не является непрерывной.

Методические разработки уроков по теме «Определенный интеграл»

С учетом методических рекомендаций приведенных выше и на основании учебника “Алгебра и начала анализа 10-11” (авторы А. Н. Колмогоров, А.М. Абрамов) были разработаны уроки по теме «Понятие определенного интеграла. Формула Ньютона-Лейбница».

Конспект урока по алгебре (11 класс)

Урок-лекция №1

Тема урока:

Понятие интеграла.

Тип урока:

Изучение нового материала.

Цели урока:

— «открыть», что такое интеграл;

— учить решать интеграл;

— развивать интерес к математике, показав на историческом материале значимость интеграла;

— воспитывать самостоятельность и аккуратность.

Ход урока

I. Организационный момент:

— приветствие класса;

— проверить готовность класса к уроку;

— сообщить тему урока и цели.

II. Изучение нового материала.

а) учитель, для того, чтобы заинтересовать учащихся новым материалом, приводит исторические данные.

История понятия интеграла связана с задачами нахождения квадратур. Задачами о квадратуре той или иной плоской фигуры математики Древней Греции и Рима называли задачи, которые мы сейчас относим к задачам на вычисление площадей. Символ введен Лейбницем ( 1675 г.). Этот знак является изменением латинской буквы S ( первой буквы слова summa). Само слово интеграл придумал Я. Бернулли (1690 г.), которое происходит от латинского integer означает целый.

б) Открытие нового знания происходит в виде обыкновенного урока, где ученику будут представлены основные положения определенного интеграла и способы его решения.

Необходимо сказать учащимся, что основные моменты необходимо записать и рассмотреть следующий материал: (см. глава 1 §1)

III. Домашнее задание.

Рассмотреть и проработать основные положения по изученному материалу, а именно:

— выучить определения;

— выучить запись определенного интеграла (уметь читать определенный интеграл).

IV. Подведение итогов.

Итак, давайте вспомним, что сегодня мы узнали (учитель с помощью учащихся):

— что такое определенный интеграл;

— как записывается определенный интеграл;

А сейчас прошу задать вопросы, если что-то непонятно.

Урок №2

Тема урока:

Формула Ньютона-Лейбница.

Тип урока:

Изучение нового материала.

Цели урока:

1. Образовательная:

— ввести понятие формулы Ньютона-Лейбница;

— рассмотреть способы решения определенного интеграла, сводящегося к формуле Ньютона-Лейбница.

2. Развивающая:

— развивать память учащихся;

— развивать логическое и абстрактное мышление.

3. Воспитательная

— прививать интерес к математике;

— воспитывать положительное отношение к процессу обучения.

Ход урока

I. Организационный момент:

— приветствие класса;

— проверить готовность класса к уроку;

— сообщить тему урока и цели.

II. Изучение нового материала.

Данный пункт урока рекомендуется начать с беседы: повторение опорных знаний о интеграле.

Необходимо повторить основные понятия интеграла, вспомнить: основные способы и методы решения определенного интеграла в зависимости от его вида. А затем плавно перейти к изложению нового материала.

Рассмотрим интеграл, применяя формулу Ньютона-Лейбница. В подинтегральном выражении находим первообразную, а затем вместо неизвестного подставляем пределы интегрирования.

А сейчас рассмотрим пример, который поможет осмыслить выше сказанное.

Пример 1

.

Решение.

Поскольку для x одной из первообразных является ,

III. Первичное осмысление и закрепление нового материала через практику (учащиеся работают у доски).

Пример 2

Решение.

.

Пример 3

.

Решение.

Пример 4

.

Решение.

.

IV. Постановка домашнего задания.

Продиктовать примеры три — четыре (использовать материал, содержащийся в приложении).

V. Подведение итогов.

Ребята, сегодня мы познакомились с определенными интегралами, сводящиеся к формуле Ньютона-Лейбница, а также узнали способы их решения. Есть что-нибудь непонятное в этой теме?

Если есть, то учитель ещё раз повторяет непонятные положения.

Урок №3

Тема урока:

Свойства определенного интеграла.

высшая математика для чайников интегралы

Вы искали высшая математика для чайников интегралы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и высшая математика интегралы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «высшая математика для чайников интегралы».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как высшая математика для чайников интегралы,высшая математика интегралы,высшая математика интегралы для чайников,вычислить интеграл примеры решений,вычислить неопределенный интеграл примеры решений,задания интегралы,интеграл как брать,интеграл как находить,интеграл как решать,интеграл как решать примеры,интеграл матпрофи,интеграл пример,интеграл примеры,интеграл примеры решения,интегралы высшая математика,интегралы высшая математика для чайников,интегралы для чайников,интегралы для чайников как решать,интегралы для чайников примеры решения,интегралы задания,интегралы задачи,интегралы как находить,интегралы как решать,интегралы как решать примеры,интегралы неопределенные,интегралы неопределенные примеры решений,интегралы определенные примеры,интегралы примеры,интегралы примеры решения,интегралы примеры решения для чайников,интегралы примеры с решением,интегралы простые,интегралы с нуля,интегралы с нуля простым языком,интегрирование примеры,интегрирование сложной функции,интегрирование сложных функций,интегрирования примеры,как брать интеграл,как вычислить интеграл для чайников,как интегрировать,как найти неопределенный интеграл примеры,как находить интеграл,как находить интегралы,как решать интеграл примеры,как решать интегралы для чайников,как решать интегралы неопределенные,как решать интегралы определенные,как решать интегралы примеры,как решать интегралы примеры решения,как решать неопределенные интегралы,как решать неопределенные интегралы для чайников,как решать неопределенный интеграл,как решать определенные интегралы,как решать определенные интегралы примеры решения,как решать определенный интеграл,как решать первообразные,как решить интеграл определенный,как решить определенный интеграл,матпрофи интегралы,методы решения интегралов,неопределенные интегралы,неопределенные интегралы как решать,неопределенные интегралы примеры,неопределенные интегралы примеры с решением,неопределенные интегралы сложные,неопределенный интеграл для чайников,неопределенный интеграл как решать,неопределенный интеграл примеры,неопределенный интеграл примеры решений,неопределенный интеграл примеры решения,неопределенный интеграл примеры с решениями,неопределенный интеграл решения примеры,неопределенный интеграл формулы,определенные интегралы для чайников,определенные интегралы как решать,определенные интегралы примеры с решением,определенный интеграл для чайников,определенный интеграл как решать,определенных интегралов примеры с решением,первообразная примеры,первообразная примеры решения,первообразная примеры с решением,первообразные как решать,правила интегрирования неопределенного интеграла,пример интеграл,примеры интегралов,примеры интегралов неопределенных,примеры интегралов с решением,примеры интегралов с решением для студентов,примеры интегралы с решением,примеры интегрирования,примеры неопределенные интегралы,примеры неопределенных интегралов,примеры неопределенных интегралов с решением,примеры первообразных с решением,примеры решений интегралов,примеры решений неопределенный интеграл,примеры решений неопределенных интегралов,примеры решения интегралов,примеры решения интегралов неопределенных,примеры решения интегралов с ответами,примеры решения неопределенных интегралов,примеры с решением интегралов,примеры с решением неопределенных интегралов,примеры с решением определенных интегралов,примеры с решением первообразных,примеры с решениями определенный интеграл,простейшие интегралы,решение интегралов для чайников,решение интегралов определенных примеры,решение интегралов примеры,решение определенных интегралов примеры с решением,сложные неопределенные интегралы,способы решения интегралов,формулы неопределенный интеграл. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и высшая математика для чайников интегралы. Просто введите задачу в окошко и нажмите «решить» здесь (например, высшая математика интегралы для чайников).

Где можно решить любую задачу по математике, а так же высшая математика для чайников интегралы Онлайн?

Решить задачу высшая математика для чайников интегралы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Определенный интеграл | Как вычислить определенный интеграл?

EПусть p(x) — первопроизводная непрерывной функции f(x), определенной на [a, b], тогда определенный интеграл от f(x) по [a, b] обозначается через  и равен [p (б) – р(а)].

   = P(b) – P(a)

Числа a и b называются пределами интегрирования, где a называется нижним пределом, а b называется верхним пределом. Интервал [a, b] называется интервалом интегрирования.

Примечание

• Постоянное интегрирование не включается в вычисление определенного интеграла.
•  читается как «интеграл от f(x) от a до b»

Шаги для нахождения определенных интегралов

Чтобы найти определенный интеграл от f(x) по интервалу [a, b], т.е.  у нас есть следующие шаги:

 

1. Найдите неопределенный интеграл ∫f(x)dx .
2. Вычислить P(a) и P(b), где P(x) — первообразная f(x), P(a) — значение первообразной при x=a, а P(b) — значение первообразной при x=b .
3. Рассчитать P(b) – P(a).
4. Результатом является желаемое значение определенного интеграла.

Определенные интегралы путем замены

Для интеграла . Пусть g(x) = t, тогда g'(x) dx = dt, где при x = a t = g(a) и при x = b t = g(b).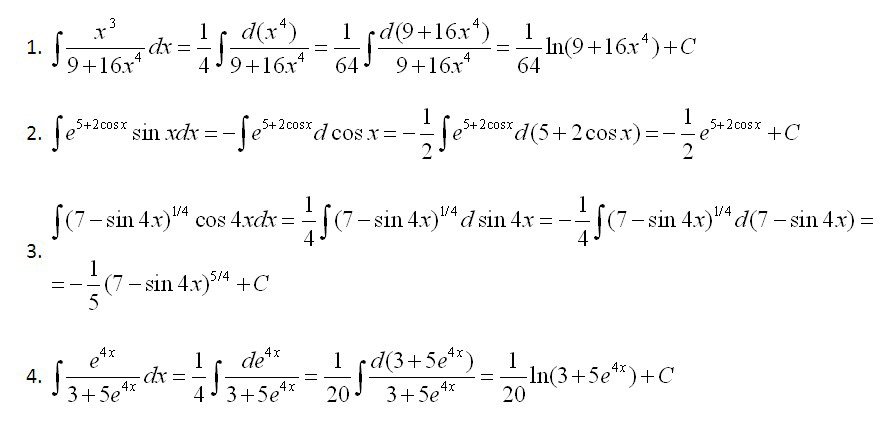

Если переменная изменяется в определенном интеграле, то замена новой переменной влияет на подынтегральную функцию, дифференциал (т.е. dx) и пределы.

Пределами новой переменной t являются значения t, соответствующие значениям исходной переменной x. Его можно получить, подставив значения x в отношение подстановки x и t.

Свойства определенного интеграла

Свойство 1)

Доказательство:

Пусть p(x) — первообразная f(x). Затем

и = p (b)-p (a) ——————- (ii)

от (i) и (ii)

Свойство 2)

, если ограничения определенные интегралы меняются местами, его значение меняется только на знак минус.

Доказательство:

Пусть p(x) будет первообразной f(x). Тогда

 = p(b) – p(a)  

и  = -[p(a) – p(b)]  = p(b) – p(a)  

Свойство 3) где a < c < b

Доказательство:

Пусть p(x) — первопроизводная f(x). Тогда

 = p(b) – p(a)                                                                                               ——————0003

 = [p(c) – p(a)] + [p(b) – p(c)] = p(b) – p(a)             ——————(ii)

Из (i ) и (ii)

Свойство 4)  

Доказательство:

Пусть x = a – t . Затем dx = d (a -t) ⇒ dx = -dt

Когда x = 0 ⇒ t = a и x = a ⇒ t = 0

⇒ [по вторым свойству]

⇒ [по первым свойствам ]

Собственность 5)

Доказательство:

Использование третьего свойства

—————– x = -a ⇒ t = a и x = 0 ⇒ t = 0

[по второму свойству]

⇒ [по первым свойствам] ———– (ii)

от (i) и (ii)

⇒

⇒

⇒ 

Property 6) If f(x) is a continuous function defined on [0, 2a],

Proof:

Using third property

                               —————–(

Рассмотрим

⇒                                        [ Используя второе свойство]

⇒                                         [ Используя первое свойство]

замены в (I)

Свойство 7)

Доказательство

Пусть t = a + b -x ⇒ dt = -dx

Ограничения: x = a, y = y = dt = -dx

b и x = b, y = a

после положения значения и предела t в

⇒

⇒ [Используя второе свойство]

⇒ [Использование первого свойства]

Решаемый пример на определенных интегралах

Задача 1: Оценка:

(I)

(II)

(III)

(III) 9

9: 9:

.

(I) =

= [2 ³ — 1 ³ ]

= 8 — 1

DX = 7

(ii)     =  

                                      = (1/2)[log|-1| – лог|-3| ]

= (1/2) [log 1 — log 3]

= (1/2) [0 — log 3]

= (1/2) log 3

(III) = (SEC ² x — 1) DX

=

= [TAN (π/4) — (π/4)] — [TAN 0 — 0]

= 1 — (π/4)

Задача 2: вычислить:  

Решение:

Пусть 5x ² + 1 = t. Тогда d(5x ² + 1) = dt ⇒ 10 x dx = dt

 Для пределов: нижний предел ⇒ x = 0, тогда t = 5x ² +1 = 1, и верхний предел ⇒ x = 1, тогда t = 5x ² + 1 = 6

=

=

= (1/5) [log 6 — log 1]

= (1/5) log 6

Задача 3: Оценка:

Решение:

[Использование определения F (x)]

= [0 -(-1 -1)] + [ (1 + 1) — (0)]

Проблема 4: Оценка:

Решение:

⇒

⇒

= 1 + 1

⇒

⇒

= 1 + 1

⇒

⇒

= 1. 0003

Задачи 5: Оценить:

Решение:

I = —————— (i)

I =

Использование

I =—————————————————————————————————————————————————————————————————————— -(ii)

Добавление (i) и (ii)

2i =

2i =

2i =

2i =

I = 0

Задача 6: Оценка:

Решение: Решение: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение:: Решение: Решение:: Решение: Решение:: Решение: Решение:: Решение: Решение:: Решение: Решение:: Решение:: Решение:

I =                  ——————(i)

Использование свойства

I =

I = ————— (ii)

Добавление (i) и (ii)

2i =

2i =

2i = 2 — 1

2i = 1

I = 1/2

Часто задаваемые вопросы по определенным интегралам

Вопрос 1: Что понимается под определенными интегралами?

Ответ:

Определенные интегралы — это интегралы, которые определены в соответствующих пределах, т. е. указаны их верхний и нижний пределы. Он представлен как ∫ _b ^a f(x) dx, где a — верхний предел, а b — нижний предел интегрирования.

Вопрос 2: Как упрощаются определенные интегралы?

Ответ:

Для упрощения определенных интегралов используйте следующие шаги:

• Упростите интеграл как обычно.
• Подставьте верхний и нижний пределы в ответ интегрирования.
• Вычтите оба ответа, полученные на шаге 2

Вопрос 3: Напишите формулу решения определенных интегралов.

Ответ:

Предположим, что требуется определенный интеграл от функции f(x) в интервале [a, b], тогда

∫ _b ^a dx = F(a) – F(b)  

где ∫ f(x) dx = F(x) + C

Вопрос 4: Что представляет собой значение, полученное при решении определенного интеграла? Может ли он быть отрицательным?

Ответ:

Значение, полученное при решении определенного интеграла, представляет собой площадь. Да, он может быть и отрицательным.

Определенные интегралы: формула, примеры и свойства

Для функции f (x), непрерывной на отрезке [a, b], можно вычислить интеграл между пределами a и b. Интеграл, вычисленный между двумя пределами, называется определенным интегралом.

Определенные интегралы – обозначение

Определенный интеграл обычно дает значение, в отличие от неопределенного интеграла, который дает функцию.

Определенные интегралы изображаются так же, как изображаются неопределенные интегралы, с той лишь разницей, что пределы добавляются в виде нижнего и верхнего индекса к знаку интегрирования. Например, если мы хотим интегрировать в пределах от 5 до 8, соответствующие обозначения будут

Решение определенных интегралов

Как вы решаете определенные интегралы? Чтобы найти определенные интегралы, следуйте следующей процедуре:

1) Запишите определенный интеграл с его пределами в виде

2) Проинтегрируйте функцию f ‘(x) так же, как и для неопределенного интеграла, чтобы найти f (x). Не включайте постоянную интегрирования C. Запишите результат в форме

3) Теперь оцените f (x) между заданными пределами: f (b) — f (a). Это даст вам окончательное значение.

Вам интересно, почему мы не включили здесь константу интегрирования? Предположим, мы включили C в нашу оценку f (x). Назовем это g(x). В этом случае значение g (x) = f (x) + C.

Тогда мы бы оценили g (x) между заданными пределами:

g (b) — g (a) = (f (b) + C) — (f (a) + C)

= f ( b) — f (a)

Таким образом, вы можете видеть, что константа интегрирования в конце концов аннулируется. Именно поэтому мы не включаем его в расчеты в первую очередь.

Пример 1

Оценка

Решение 1

=

= (5/3 × 7³) — (5/3 × 1³)

= 570

0021

Интеграция — очень полезный инструмент для нахождения площади под графиком. В приведенном выше примере мы находим площадь, заключенную между осью x и кривой f (x) = 5x² между x = 1 и x = 7. Мы можем представить приведенный выше пример графически.

График, изображающий f (x) = 5x², чтобы найти площадь, заключенную между x = 1 и x = 7, Nilabhro Datta — StudySmarter Originals

Кривая на приведенном выше графике представляет f (x) = 5x². Как уже упоминалось, значение определенного интеграла между 1 и 7 дает площадь, заключенную между кривой и осью x между x = 1 и x = 7.

Пример 2

Оценка ПРИМЕЧАНИЕ — x IS в Radians

Раствор 2

=

= SIN (1) — SIN (0,5)

= 0,841-0,479

= 0,3653

= 0,841-0,479

. предыдущем примере приведенное выше значение дает нам площадь, заключенную между кривой y = cos (x) и осью x между x = 0,5 и x = 1. Посмотрите на следующее изображение для наглядной демонстрации.

График, изображающий f (x) = cos (x), для нахождения площади, заключенной между x = 0,5 и x = 1, Нилабхро Датта — StudySmarter Originals

Пример 3

Учитывая (2Px + 7) dx = 4P², покажите, что есть два возможных значения P. Найдите эти значения.

Решение 3

(2Px + 7) dx

= (25P + 35) — (P + 7)

= 24P + 28

Теперь,

257 > 067 > 04P² = P²

=>

=> (P + 1) (P — 7) = 0

Следовательно, значение P может быть либо -1, либо 7.

Пример 4

Найти замкнутую область, ограниченную кривая y = x (x — 5) и ось x.

Решение 4

Чтобы найти площадь, ограниченную кривой и осью x, найдем точки, в которых кривая пересекается с осью, т.е. где y = f (x) = 0

f (x) = x (x — 5) = 0

=> x = 0 или x = 5.

Таким образом, кривая пересекает ось x в точке (0, 0) и (5, 0).

0 и 5 служат нижней и верхней границами нашего определенного интеграла.

Итак, общая площадь = (x) (x — 5) dx

Отрицательная площадь, ограниченная кривой

В приведенном выше примере площадь получается отрицательной. Что это значит?

Это означает, что площадь, ограниченная кривой и осью x, находится ниже оси x, т. е. отрицательной стороны оси x.

Если мы нарисуем кривую y = f (x) = x (x — 5), мы получим следующую кривую.

График, изображающий f (x) = x (x — 5), для нахождения площади, заключенной между кривой и осью x, Nilabhro Datta — StudySmarter Originals

Как мы видим здесь, область, ограниченная кривой, находится ниже оси x.

Площадь, ограниченная кривой, и ось x, расположенная выше оси x, дает положительное значение для ∫f (x) dx, а площадь, ограниченная кривой, и ось x, опускающаяся ниже оси x, дает отрицательное значение для ∫ f (x) dx.

Что, если мы хотим найти полную величину площади, заключенной между кривой и осью x, когда часть ее находится выше оси x, а часть — ниже оси x? В этих случаях нам нужно было бы найти обе площади по отдельности и сложить их величины, не принимая во внимание их знак.

Если мы возьмем один определенный интеграл по всей площади, результирующее значение будет [(площадь, заключенная над осью x) — (площадь, заключенная под осью x)]).

Определенные интегралы — ключевые выводы

• Для функции f (x), непрерывной в замкнутом интервале [a, b], можно вычислить интеграл между пределами a и b. Интеграл, вычисленный между двумя пределами, называется определенным интегралом. Он выражается как f(x)dx.
• Определенный интеграл обычно дает значение, в отличие от неопределенного интеграла, который дает функцию.
• Значение f (x) dx дает нам площадь, заключенную между кривой f (x) и осью x в интервале x = a и x = b.
• Если площадь, ограниченная кривой f (x), и ось х находится выше оси абсцисс, это дает положительное значение для ∫f (x) dx, а если площадь падает ниже оси абсцисс, дает отрицательное значение для ∫f (x) dx.

Формулы определенных интегралов — объяснение, свойства, примеры решений и важные часто задаваемые вопросы

Понятие определенных интегралов

Определенный интеграл тесно связан с первообразной и неопределенным интегралом данной функции. Введение понятия определенного интеграла данной функции начинается с функции f(x), непрерывной на отрезке (a,b). Приведенный интервал делится на «n» подынтервалов, которые, хотя и не обязательно, могут считаться равными по длине (Δx). В каждом подинтервале выбирается произвольное значение домена xi, вычисляется соответствующая длина подинтервала, и эти «n» произведений добавляются для вычисления их сумм. Сумма известна как сумма Римана и может быть положительной, отрицательной или нулевой в зависимости от поведения функции на замкнутом интервале. 9{n}\] (fxi ) Δx

Что такое интегрирование в математике?

В математике интегрирование — это процесс суммирования частей для определения целого. Это обратный процесс дифференцирования, когда мы можем разделить функцию на части. Интегрирование используется для определения суммирования в очень больших масштабах. Вычисление суммы небольших чисел является простой задачей и может быть выполнено даже вручную, но вычисление суммы больших чисел, где предел может достигать бесконечности, является сложной задачей. В таком случае используется метод интегрирования. Интеграция и дифференцирование являются важными концепциями исчисления. Существует два различных типа интеграции, а именно:

В этой статье содержится информация о концепциях определенных интегралов, уравнений определенных интегралов, свойствах определенных интегралов, формуле определенного интегрирования по частям, формулах приведения в определенном интегрировании и т. д.

Определенное интегральное уравнение

Интеграл, включающий верхний и нижний пределы рассматривается как определенный интеграл. Интеграл Римана рассматривается как определенный интеграл, в котором x ограничен вещественной линией.

No related posts.