Тригонометрический вид комплексного числа: Представьте комплексное чтсло в тригонометрической форме z=2i

Комплексные числа в электротехнике

Господа, в сегодняшней статье я хотел бы вам немного рассказать про комплексные числа и сигналы. Данная статья будет в основном теоретической. Ее задача – подготовить некоторый фундамент для возможности понимания дальнейших статей. Просто когда речь заходит про фазу или, допустим, про поведение конденсатора в цепи переменного тока, так сразу и начинаю лезть все эти комплексности. А про фазу все-таки хочется поговорить, штука важная. Нет, эта статья ни в коем случае не будет кратким курсом ТФКП, мы рассмотрим только лишь очень узкую область из этой вне всякого сомнения интересной и обширной темы. Итак, поехали!

Но прежде чем начать говорить непосредственно про комплексные числа, я бы хотел еще рассказать про такую любопытную штуку, как тригонометрический круг. Господа, вот мы с вами уже на протяжении аж трех (раз, два, три) статей говорим про синусоидальный ток. Но как вообще формируется функция синуса? Да и косинуса тоже? Можно по-разному ответить на этот вопрос, но в контексте данной статьи я выбрал следующее объяснение.

Взгляните, пожалуйста, на рисунок 1. На нем изображен так называемый тригонометрический круг.

Рисунок 1 – Тригонометрический круг

Там много всего намалевано, поэтому давайте разбираться постепенно что там есть что. Во-первых, там есть, собственно, некоторая окружность, центр которой совпадает с центром системы координат с осями Х и Y. Радиус этой окружности равен единице. Просто единице, без всяких вольт, ампер и прочего. Далее из центра этой окружности проведены два радиус-вектора ОА и ОЕ. Очевидно, длина этих векторов равна единице, потому что у нас окружность единичного радиуса. Угол между вектором ОА и осью Х равен φ₁, угол между вектором ОЕ и осью Х равен φ₂

А теперь самое интересное, господа. Давайте рассмотрим, чему равны проекции

этих векторов на оси Х и Y. Проекция вектора ОА на ось Х – это отрезок ОВ, а на ось Y – это отрезок ОС. И все вместе (сам вектор ОА и его проекции ОВ и ОС) образует прямоугольный треугольник ОАВ. По правилам работы с прямоугольным треугольником мы можем найти его стороны ОВ и ОС, то есть проекции радиус вектора ОА на оси Х и Y:

Абсолютно аналогично можно найти соотношения для вектора OE:

Если не понятно почему так, советую погуглить про соотношения сторон в прямоугольном треугольнике. Ну а мы для себя сейчас выносим один немаловажный вывод – проекция единичного вектора на ось Х равна косинусу угла между вектором и осью Х, а проекция на ось Y – синусу этого угла.

А теперь давайте начнем вращать радиус-вектор против часовой стрелки с некоторой частотой. Ну, так, чтобы он своим концом вычерчивал окружность. И, как вы уже, вероятно, догадались, при таком вращении проекция вектора на ось Х будет вырисовывать функцию косинуса, а проекция на ось Y – функцию синуса.

То есть, если этот наш радиус-вектор делает за секунду, например, 50 оборотов (то есть вращается с частотой 50 Гц), то это значит, что его проекция на ось Х формирует функцию

а его проекция на ось Y – вырисовывает функцию

Довольно интересный факт на мой взгляд. И вообще тригонометрический круг – любопытная штука. Рекомендую познакомиться с ним поближе, погуглив на эту тему. Он позволяет многое лучше понять. Мы же сейчас рассмотрели только немногие из фич, которые нам будут нужны. Сейчас давайте пока временно оставим этот факт и поговорим непосредственно про комплексные числа.

Итак, господа, комплексное число – это выражение вида

a – это действительная часть комплексного числа z.

b – это мнимая часть комплексного числа z.

На самом деле в серьезных книжках по математике комплексное число определяют несколько по-другому, однако нас вполне устроит и такой вариант.

По-научному – это алгебраическая форма записи комплексного числа. Есть еще и другие, с ними познакомимся чуть позже.

а и b – это обычные числа, к которым мы с вами все привыкли. Например, 42, 18, -94, 100500, 1.87 ну и так далее. То есть абсолютно любые. Например, могут иметь место вот такие записи

А число

j – это так называемая мнимая единица. Часто ее обозначают не j, а i, но i – это обычно ток в электротехнике, поэтому мы будем использовать буковку j. Что это такое? Формально, это можно записать так

Немного не понятно, как это может быть корень из отрицательного числа . Все мы с детства привыкли, что под корнем у нас только лишь положительные числа. Но математики ввели вот такую вот абстракцию, которая позволяет извлечь корень и из отрицательных чисел. И, как ни странно, подобная абстракция неплохо помогает описывать вполне себе реальные, а вовсе никакие не абстрактные процессы в электротехнике.

То есть мы видим, что комплексное число само по себе как бы просто состоит из двух самых обычных чисел. Да, перед втором стоит некоторое мифическое j, но сути дела это не меняет.

Давайте теперь познакомимся с

графическим представление комплексных чисел.

Господа, взгляните на рисунок 2. Там как раз-таки это представление и изображено.

Рисунок 2 – Комплексная плоскость

Итак, в чем здесь, собственно, фишка? А фишка в том, что мы берем и рисуем систему координат. В ней мы ось Х обзываем Re, а ось Y – Im. Re – это ось действительных чисел, а Im – это ось мнимых чисел. Теперь на оси Re мы откладываем величину a, а на оси Im – величину b нашего комплексного числа z. В итоге мы получаем точку на комплексной плоскости с координатами (а, b). И теперь можно провести радиус вектор из начала координат в эту точку. Собственно, этот вектор и можно считать комплексным числом.

Интересный факт: давайте представим, что b равно 0. Тогда получается, что комплексное число вырождается в самое обыкновенно, «одномерное»: мнимая часть просто обнуляется. И, естественно, вектор в этом случае будет лежать на оси

Re. То есть, можно сказать, что все числа, которые нас окружают в обычной жизни, находятся на оси Re, а комплексное число – это выход за пределы этой оси, в некотором роде расширение границ. Ну да не будем углубляться в это .

Давайте лучше углубимся в другое. А именно в то, как еще можно представить комплексные числа. Только что мы пришли к выводу, что комплексное число – по сути это вектор. А вектор можно характеризовать длинной и углом наклона, например, к оси Х. Действительно, эти два параметра полностью определяют любой вектор при условии, что у нас двумерное пространство, само собой. Для объема или какого-нибудь многомерного пространства (ужас какой) это не верно, а для двумерного – это так. Давайте теперь выразим сказанное математически.

Итак, давайте теперь исходить из того, что нам известна длина вектора (обзовем ее |z|) и угол φ₁.

Что мы можем найти, исходя из этих знаний? Да вообще говоря, довольно много. По сути нам известна гипотенуза прямоугольного треугольника и один из его углов, то есть, согласно каким-то там теоремам геометрии, прямоугольный треугольник полностью определен. Поэтому давайте найдем его катеты а и b:

А теперь, господа, можно сделать небольшой финт ушами? Помните алгебраическую запись комплексного числа? Ну, вот эту

Давайте-ка подставим сюда a и b, представленные через синусы с косинусами. Получим

Мы получили интересное выражение. Выражение вида

называется тригонометрической формой записи комплексного числа. Она хороша, если нам известна длина нашего вектора

|z| и угол его наклона φ₁. Когда речь пойдет об электротехнике, длина вектора внезапно превратится в амлитуду сиганала, а угол наклона – в фазу сигнала. Кстати, обратите внимание, что тригонометрическая форма записи комплексного числа чем-то близка к тригонометрическому кругу, который мы нарисовали в начале статьи. Но к этому сходству мы вернемся чуть позже.

Господа, теперь нам осталось познакомиться с последней формой записи комплексного числа – показательной. Для этого необходимо знать так называемую формулу Эйлера. С вашего позволения я не буду затрагивать вывод этой формулы и рассматривать, откуда она взялась. Это немного выходит за рамки статьи и, к тому же, есть много источников, где, вне всякого сомнения, вам расскажут про вывод этой формулы гораздо более профессионально, чем это смогу сделать я. Мы же просто приведем готовый результат. Итак, формула Эйлера имеет вид

где е – это экспонента или, как ее еще называют, показательная функция. Для математиков это некоторый предел при стремлении чего-то там к бесконечности, а если по-простому – обычное число

Да, просто две целых и семь десятых .

А теперь сравните формулу Эйлера и тригонометрической записью комплексного числа. Не замечаете интереснейшего сходства? Скрестив эти два выражения, можно получить как раз-таки показательную форму записи комплексного числа:

Как ни странно, эта мудреная запись используется в электротехнике не так уж и редко.

Итак, мы познакомились с основными вариантами записи комплексных числе. Теперь давайте постепенно продвигаться к нашей любимой электротехнике. Запишем закон изменения косинусоидального напряжения.

Мы уже записывали этот закон неоднократно, например, в самой первой статье, посвященной переменному току. Правда, там был синус, а здесь косинус, но это абсолютно ничего не меняет по сути, просто тут косинус немного удобнее для объяснения.

А сейчас внимание, господа. Очень хитрая последовательность действий.

Во-первых, никто нам не мешает рассмотреть косинус, который стоит в этом выражении, на тригонометрическом круге, который мы чертили на рисунке 1 в самом начале статьи. А что? Почему нет? Будем представлять себе, что некоторый вектор Á_m, равный амплитуде нашего косинусоидального напряжения, вращается в прямоугольной системе координат с круговой частотой ω. И тогда в силу выше изложенных обстоятельств его проекция на оси Х будет вырисовывать как раз наш закон v(t). Вроде бы никакого подвоха пока нет.

Смотрим дальше. На оси Х проекция рисует нашу функцию времени, а ось Y пока что вообще не при делах. А что б она просто так не простаивала – давайте-ка считать, что это не просто абы какая ось Y, а ось мнимых чисел. То есть мы сейчас вводим то самое комплексное пространство. В этом пространстве при вращении вектора Á_m (вектора обычно обозначаются буквой с точкой или стрелочкой сверху) в то время как его проекция на оси Х рисует косинус, на оси Y у нас будет рисоваться функция синуса. Вся фишка в том, что мы сейчас как бы скрещиваем тригонометрический круг с комплексной плоскостью. И в результате получаем что-то типа того, что показано на рисунке 3 (картинка кликабельна).

Рисунок 3 – Представление напряжения на комплексной плоскости

Что мы на нем видим? Собственно, то, о чем только что говорили. Вектор, равный по длине амплитуде нашего напряжения, вращается в системе координат, на оси Х (которая Re) вырисовывается закон косинуса (он полностью совпадает нашим сигналом v(t)). А на оси Y (которая Im) вырисовывается закон синуса. Итого на основе вышесказанного наш исходный сигнал

мы можем представить в тригонометрической форме вот так

или в показательной форме вот так

Давайте представим теперь, что у нас не косинусоидальный сигнал, а синусоидальный. К нему мы как-то больше привыкли. То есть, пусть напряжение изменяется вот по такому закону

Проведем все рассуждения аналогичным образом. Единственное отличие будет в том, что теперь наш сигнал «рисуется» на мнимой оси Im, а ось Re как бы не при делах. Но вводя комплексное пространство, мы внезапно получаем, что комплексная запись сигнала для данного случая точно такая же, как и для случая косинуса. То есть и для сигнала

мы можем записать комплексное представление в тригонометрической форме вот так

или в показательной форме вот так

Выходит, что комплексное представление для случая синусоидального и косинусоидального сигнала имеет один и тот же вид. Кстати, это довольно очевидно, если вспомнить, что при вращении вектора по окружности и синус и косинус вырисовываются одновременно на разных осях. А само комплексное число описывает именно этот вращающийся вектор и, таким образом, содержит в себе инфу как про ось Х, так и про ось Y.

Давайте теперь пойдем от обратного и представим, что у нас есть запись некоторого комплексного сигнала в виде

Или, например, в таком виде

Как понять – что он описывает: синус или косинус? Ответ – да никак. Он описывает и то, и то одновременно. И если мы имеем косинусоидальный сигнал, то мы должны взять действительную часть этого комплексного сигнала, а если синусоидальный – мнимую. То есть для случая косинуса это выглядит как-то так:

или так

А для случая синуса это выглядит вот так

или так

Здесь Re() и Im() – функции взятия действительной или мнимой части комплексного числа. Кстати, они определены во многих математических САПРах и их можно прям вот в таком виде использовать. То есть передавать им комплексное число, а на выходе получать дейтсвительную или мнимую часть.

Возможно, вы спросите: а зачем так все усложнять? Какая с этого выгода? В чем профит? Профит, безусловно, есть, но о нем мы поговорим чуть позже, в следующих статьях. На сегодня пока все, господа. Спсибо что прочитали и пока!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Social button for Joomla

Тригонометрическая форма — комплексное число

Cтраница 1

Тригонометрическая форма комплексного числа Выражение комплексного числа а а 0г называется алгебраической формой его записи.  [1]

Тригонометрическая форма комплексного числа, отличного от 1уля, определена однозначно: это запись комплексного числа z в виде ( 1), где г — положительное число, равное модулю числа г, косинус и синус берутся от одного и того же угла ф, равного аргументу числа г, при этом между косинусом и синусом стоит знак плюс.  [2]

Тригонометрическая форма комплексных чисел приводит к простому правилу извлечения корней из комплексных чисел. Корень ге-й степени из комплексного числа z f 1 О имеет п значений.  [3]

Тригонометрическая форма комплексного числа удобна для того, чтобы находить произведение и частное комплексных чисел, возводить в степень и извлекать корни.  [4]

Тригонометрическая форма комплексного числа, отличного от нуля, определена однозначно: это запись комплексного числа z в виде ( 1), где г-положительное число, равное модулю числа 2, косинус и синус берутся от одного и того же угла ф, равного аргументу числа z, при этом между косинусом и синусом стоит знак плюс.  [5]

Тригонометрическую форму комплексного числа удобно также использовать при решении уравнений вида z z0, где z0 — заданное комплексное число, п — натуральное число.  [6]

Тригонометрическую форму комплексного числа рекомендуется изложить в следующем порядке: дать определение аргумента комплексного числа, вывести формулу и привести определение тригонометрической формы комплексного числа. Затем рассмотреть переход от алгебраической формы комплексного числа к тригонометрической и обратно.  [7]

Переход от тригонометрической формы комплексного числа к алгебраической производится подстановкой в выражение 2 г ( со8ф 1эшф) числовых значений созф и зшф, затем раскрываются скобки и производятся упрощения.  [8]

Понятия аргумента и тригонометрической формы комплексного числа разбираются, например, в 1 гл.  [9]

Удача с находкой тригонометрической формы комплексного числа — далеко не рядовое событие. Это пример маленького чуда, которое изредка происходит примерно по такой схеме.  [10]

Понятия аргумента и тригонометрической формы комплексного числа разбираются, например, в § 1 гл.  [11]

Понятия аргумента и тригонометрической формы комплексного числа разбираются, например, в § 1 гл.  [12]

Понятия аргумента и тригонометрической формы комплексного числа разбираются, например, в § 1 гл.  [13]

Дать понятие о тригонометрической форме комплексного числа, выработать у учащихся навыки перехода от алгебраической формы комплексного числа к тригонометрической и обратно.  [14]

Эта запись называется тригонометрической формой комплексного числа.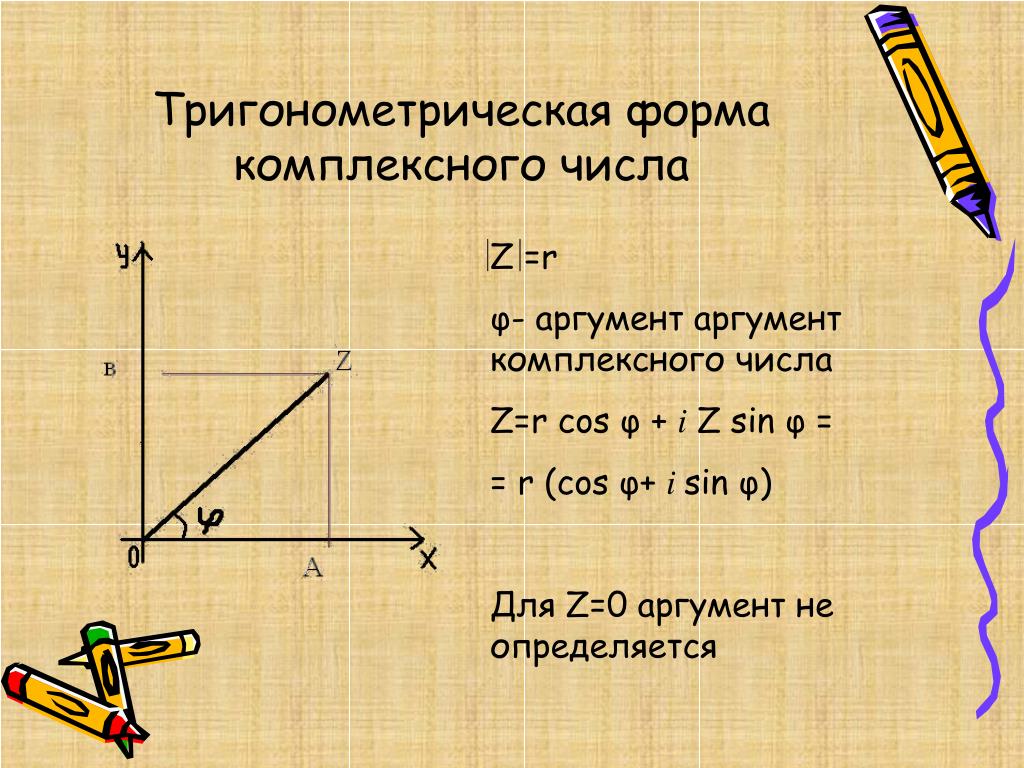  [15]

Страницы:      1    2    3

Тригонометрическая форма комплексных чисел — Концепция

Удобная форма для чисел в комплексной плоскости, отличная от прямоугольной формы, — это тригонометрическая форма комплексных чисел. Тригонометрическая форма комплексных чисел использует модуль и угол для описания местоположения комплексного числа. Важно уметь преобразовывать комплексные числа из прямоугольной в тригонометрическую и из тригонометрической в ​​прямоугольную.

комплексные числа сложная плоскость аргумент модуля синус косинус касательная прямоугольная форма тригонометрическая форма

Мы говорим о комплексной плоскости, и позвольте мне напомнить вам, что способ, которым мы визуализируем комплексные числа, заключается в построении графика на плоскости, мы графически изображаем число z равным a+bi, нанося точку a coma b и, таким образом, это означает что эта точка находится на единицах вправо и на единицах вверх от начала координат. В комплексной плоскости это реальная ось, а это воображаемая ось.
Я хочу определить термин как абсолютное значение или модуль z. Это комплексное число определяется как абсолютное значение z, равное квадратному корню из квадрата a плюс b в квадрате. Теперь это следует прямо из теоремы Пифагора. Эта величина в точности равна длине этого красного сегмента. Это расстояние z от начала координат, и это именно то, чем является абсолютное значение для действительных чисел, расстояние от начала координат. Так что для комплексных чисел это означает то же самое. Иногда термин модуль используется для абсолютного значения, но это означает абсолютное значение z.
Вдобавок к такой форме для комплексных чисел есть еще одна форма, чем-то напоминающая полярные координаты. Теперь, если мы назовем эту длину r и измерим угол от действительной оси тета, мы можем фактически представить z через r и тета следующим образом. Прежде всего заметим, что r в точности равно модулю z. r равно квадратному корню из квадрата a плюс b в квадрате, и, во-вторых, давайте заметим, что косинус тета равен a над r. Таким образом, a равно r косинус-тета, а синус-тета равен b больше r. Таким образом, b равно r sine theta, и поэтому мы можем переписать эту форму, которая на самом деле называется прямоугольной формой, по-другому, z можно записать. Поскольку a — это наш косинус тета, я поставлю r косинус тета вместо плюса b — это наш синус тета. Я положил r синус тета умножить на i. Теперь соглашение состоит в том, чтобы вытащить r и поставить круглые скобки. Косинус тета плюс, и вы ставите i впереди, вы не хотите, чтобы это выглядело так, как будто вы берете синус тета, умноженный на i. Итак, я синус тета. Эта форма называется «Тригонометрическая форма». иногда называемая «полярной формой», и она действительно полезна, как вы увидите в одном или двух уроках. Но мы будем часто использовать тригонометрическую форму, и в ближайшем будущем мы собираемся научиться преобразовывать туда и обратно тригонометрическую форму и прямоугольную форму.

тригонометрия — нахождение тригонометрической формы комплексного числа

Задай вопрос

спросил 7 лет, 7 месяцев назад

Изменено 7 лет, 7 месяцев назад

Просмотрено 329 раз

$\begingroup$

Мне нужно найти тригонометрическую форму комплексного числа: $1-i\sqrt{3}$

Я нашел, что

$r = 2$

, что означает, что тригонометрическая форма равна $2 ( \cos \alpha — i\sin\alpha)$ и мне нужно найти альфу.