Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
Другие ответы
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
 ru 🎓
ru 🎓1
Первый слайд презентации
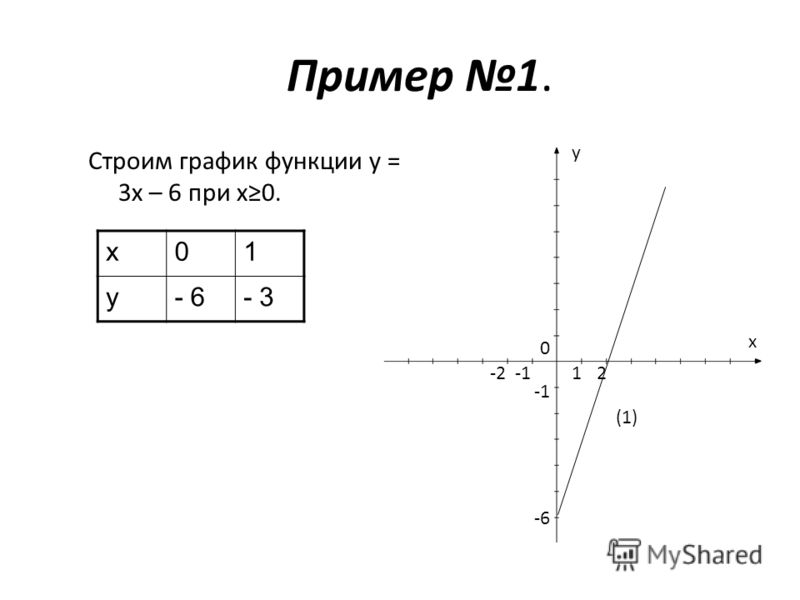
=х(х+1) =х 2 +х Задание 2 2 Постройте график функции y = и определите при каких значениях параметра с прямая y = с имеет с графиком ровно одну общую точку. x 3 – x х–1 x= 1. D(y): Построим график y= x 2 + x 1). a=1 > 0, ветви направ. вверх 2). 4). Точки пересечения с осью О x, y=0. x 2 + x =0 х(х+1)=0 x= –1, x= 0 точки (–1;0), (0;0) -3 -2 1 2 3 4 х -1 — 0,25 Если x = 1, то y = 1 2 + 1 = 2 Исключаем точку (1; 2). y = 2 y = – 0,2 5 7 6 5 4 3 2 1 -1 -2 -3 -4 Построим график функции y = х 3 – x х–1 х(х 2 –1) х–1 = х(х–1)(х+1) (х–1) = у=х 2 +х 2 b x 0 = – a 1 2 1 x 0 = – = –0,5 y 0 = (–0,5) 2 +(–0,5) = 0,25–0,5 = –0,25 Вершина параболы (–0,5;–0,25) 3). Ось симметрии x = –0,5. Ответ : – 0,25; 2. — 1 2 Нет общих точек Одна общая точка Две общих точки Две общих точки Одна общая точка 5). х=2, то у=2 2 +2=6,точка (2; 6)
Изображение слайда
2
Слайд 2
–2
y = m
Задание 2 2
1 2 3
-1
3
2
1
–1
–2
–3
–4
–5
–6
–7
–8
Постройте график функции
и определите, при каких значениях m прямая
имеет с графиком ровно две
общие точки.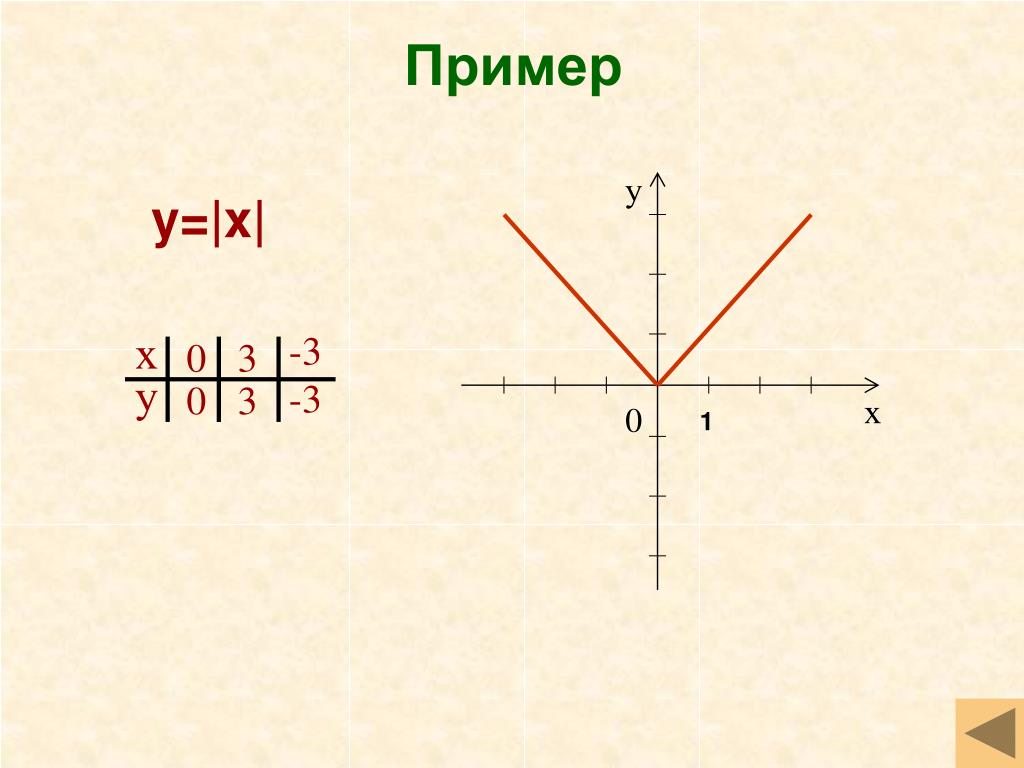 Две общих точки
–3
Нет общих точек
1 общая точка
y=m – это прямая, параллельная оси О x.
2
x=0, x= -3
2 общие точки
Построим параболу с помощью сдвига на 2 ед. отрезка вверх
Если x = 0, то y = 2
x = –3, то y = –(–3) 2 +2 = – 7
Исключаем две точки (0;2) и (–3; – 7).
Две общих точки
–3
Нет общих точек
1 общая точка
y=m – это прямая, параллельная оси О x.
2
x=0, x= -3
2 общие точки
Построим параболу с помощью сдвига на 2 ед. отрезка вверх
Если x = 0, то y = 2
x = –3, то y = –(–3) 2 +2 = – 7
Исключаем две точки (0;2) и (–3; – 7).
Изображение слайда
3
Слайд 3
–2
y = m
Задание 2 2
1 2
-1
3
2
1
–1
–2
–3
Постройте график функции
и определите, при каких значениях m прямая
имеет с графиком ровно одну
общую точку.
y = m
Используем формулу для разложения квадратного трехчлена на множители
ax 2 +bx+c=a(x- x 1 )(x- x 2 )
Построим параболу с помощью сдвига на 1 ед. отрезок вниз
Если x = – 2, то y = ( – 2) 2 – 1 = 3
Исключаем точку (–2; 3)!!!
y= 3
Ответ: m= –1, m=3.
Нет общих точек
y=m – это прямая, параллельная оси О x.
1 общая точка
2 общие точки
y= -1
При m = 3 прямая проходит через проколотую точку и имеет с параболой одну общую точку.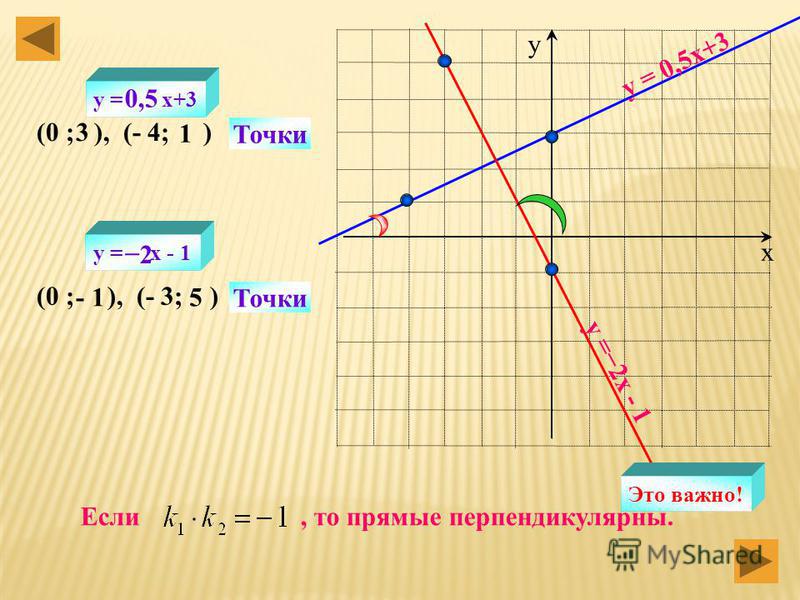
Изображение слайда
4
Слайд 4
–2
y = m
-1
5
4
3
2
1
–1
–2
–3
Постройте график функции
и определите, при каких значениях m прямая
имеет с графиком ровно одну
общую точку.
y = m
Используем формулу для разложения квадратного трехчлена на множители
ax 2 +b+c=a(x- x 1 )(x- x 2 )
x= 2 ; x= –2
Построим график y= x 2 –2x – 3
1). a=1 > 0, ветви направ. вверх
2). x 0 = – = 1
y o =1 2 – 2*1 – 3 = 1 – 2 – 3 = – 4
Вершина параболы ( 1 ;– 4 )
3). Ось симметрии x = 1.
–2
2*1
4). Точки пересечения с осью О x, y=0.
x 2 –2x – 3=0 x 1 +x 2 = 2
x 1 x 2 = –3
x= – 1, x= 3 точки (– 1 ;0), ( 3 ;0)
5). Если x=0, то
у = 0 2 –2*0 – 3 = – 3. Точка ( 0 ; – 3 )
Если x= – 2, то y= ( – 2) 2 – 2 * (–2)–3 = 5
Если x= 2, то у = 2 2 – 2*2 – 3 = –3
Исключаем точки (–2; 5), (2; –3)
1 2
Нет общих точек
Одна общая точка
Две общих точки
y = – 3
y = – 4
y = 5
Ответ: – 4 ; – 3; 5.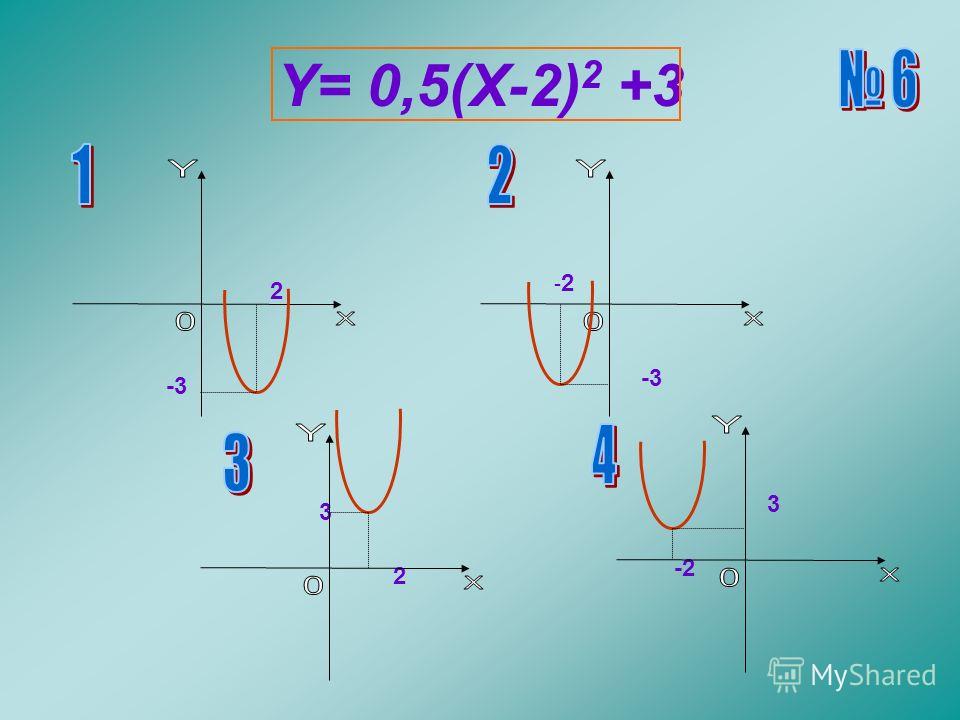
Изображение слайда
5
Слайд 5
x 4 – 13 x 2 + 36 ( x –3)( x+2) y = Постройте график функции y = и определите при каких значениях параметра m прямая y = m имеет с графиком ровно одну общую точку. x 4 – 13 x 2 + 36 ( x –3)( x+2) Задание 2 2 t 2 – 13 t + 36 = 0 Пусть x 2 = t t 1 + t 2 = 13 t 1 t 2 = 36 t 2 – 13 t + 36 = Разложим трёхчлен на множители по формуле a ( x – x 1 )( x – x 2 ) (t – 9)(t – 4) = (x 2 – 9)(x 2 – 4) = (x – 3)(x+3)(x–2)(x+2) ( x –3)( x+2) = (x – 3)(x+3)(x–2)(x+2) x= – 2 x= 3 = ( x+3)(x–2) = x 2 + x –6 Это приведённое квадратное уравнение (старший коэффициент равен 1). Найдем корни по теореме Виета. y = x 2 + x –6 Построим график функции x= – 2 x= 3, D(y): Вернёмся к замене, разложим двучлены по формуле a 2 – b 2 = (a – b)(a+b) t 1 = 9 t 2 = 4 5 x y ОГЭ ГОТОВИМСЯ К
Изображение слайда
6
Слайд 6
Задание 2 2
Постройте график функции
y =
и определите при каких значениях параметра m прямая y = m имеет с графиком ровно одну общую точку.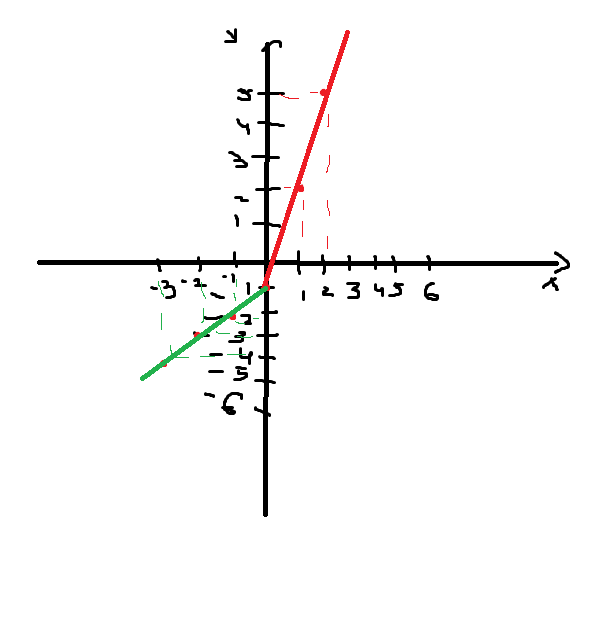 x 4 – 13 x 2 + 36
( x – 3)( x + 2)
y = x 2 + x –6
Построим график функции
x= – 2
x= 3,
D(y):
Построим график y= x 2 + x –6
1). a=1 > 0, ветви направ. вверх
2). x 0 = – = –0,5
y o = (–0,5) 2 –0,5–6 = 0,25–6,5 = –6,25
Вершина параболы (–0,5;–6,25)
3). Ось симметрии x = –0,5.
1
2*1
5). Если x=0, то
у = 0 2 + 0 – 6 = – 6
Точка ( 0 ; – 6 )
4). Точки пересечения с осью О x, y=0.
x 2 + x – 6=0 x 1 +x 2 = – 1
x 1 x 2 = –6
x= – 3, x= 2 точки (– 3 ;0), ( 2 ;0)
-3 -2 -1 1 2 3 4
– 0,5
–6,25
Если x = 3, то y = 3 2 + 3 – 6 = 6
Если x =–2, то у =(–2) 2 +(–2)–6= –4
Исключаем точки (3; 6), ( – 2; –4 ).
Нет общих точек
Одна общая точка
Две общих точки
Одна общая точка
Две общих точки
Одна общая точка
y = –4
y = –6,2 5
y = 6
7
6
5
4
3
2
1
-1
-2
-3
-4
Ответ: –6,25; –4 ; 6.
x 4 – 13 x 2 + 36
( x – 3)( x + 2)
y = x 2 + x –6
Построим график функции
x= – 2
x= 3,
D(y):
Построим график y= x 2 + x –6
1). a=1 > 0, ветви направ. вверх
2). x 0 = – = –0,5
y o = (–0,5) 2 –0,5–6 = 0,25–6,5 = –6,25
Вершина параболы (–0,5;–6,25)
3). Ось симметрии x = –0,5.
1
2*1
5). Если x=0, то
у = 0 2 + 0 – 6 = – 6
Точка ( 0 ; – 6 )
4). Точки пересечения с осью О x, y=0.
x 2 + x – 6=0 x 1 +x 2 = – 1
x 1 x 2 = –6
x= – 3, x= 2 точки (– 3 ;0), ( 2 ;0)
-3 -2 -1 1 2 3 4
– 0,5
–6,25
Если x = 3, то y = 3 2 + 3 – 6 = 6
Если x =–2, то у =(–2) 2 +(–2)–6= –4
Исключаем точки (3; 6), ( – 2; –4 ).
Нет общих точек
Одна общая точка
Две общих точки
Одна общая точка
Две общих точки
Одна общая точка
y = –4
y = –6,2 5
y = 6
7
6
5
4
3
2
1
-1
-2
-3
-4
Ответ: –6,25; –4 ; 6.
Изображение слайда
7
Слайд 7
= – 5
-2
2
=–4
Вершина
( – 5 ;–4)
y(–5)=(-5+3)(-5+7)
x 0 =
– 7+(–3)
2
Постройте график функции
и определите, при каких значениях m прямая y = m
имеет с графиком ровно одну
общую точку.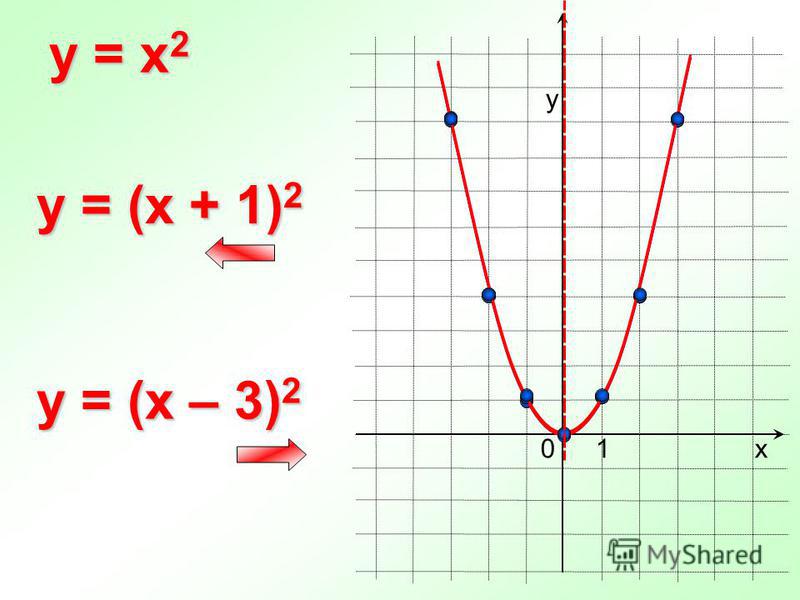 –2
-1
5
4
3
2
1
–1
–2
–3
–4
–5
–3
Задание 2 2
y
x
– 7
Найдем нули функции
( x+3)(x+7)=0
x= –3, x= –7.
– 5
y= ( x+3)(x+7)
D(y): x= –2.
Если x= – 2, то y= ( – 2+3)( – 2+7)=5
Исключаем точку (–2; 5)
= ( x+3)(x+7)
( x+3)(x 2 +9x+14)
y=
( x+2)
=
( x+2)
( x+3)(x )(x )
+7
+2
–
–
Используем формулу для разложения квадратного трехчлена на множители
ax 2 +bx+c=a(x- x 1 )(x- x 2 )
x 2 +9x+14=0
х 1 = –7 х 2 = – 2
х 1 +х 2 = – 9 х 1 х 2 = 14
x 2 +9x+14=(x+7)(x+2)
Нет общих точек
Две общих точки
Одна общая точка
Две общих точки
Одна общая точка
y = –4
y = 5
Ответ: m= –4, m=5.
–2
-1
5
4
3
2
1
–1
–2
–3
–4
–5
–3
Задание 2 2
y
x
– 7
Найдем нули функции
( x+3)(x+7)=0
x= –3, x= –7.
– 5
y= ( x+3)(x+7)
D(y): x= –2.
Если x= – 2, то y= ( – 2+3)( – 2+7)=5
Исключаем точку (–2; 5)
= ( x+3)(x+7)
( x+3)(x 2 +9x+14)
y=
( x+2)
=
( x+2)
( x+3)(x )(x )
+7
+2
–
–
Используем формулу для разложения квадратного трехчлена на множители
ax 2 +bx+c=a(x- x 1 )(x- x 2 )
x 2 +9x+14=0
х 1 = –7 х 2 = – 2
х 1 +х 2 = – 9 х 1 х 2 = 14
x 2 +9x+14=(x+7)(x+2)
Нет общих точек
Две общих точки
Одна общая точка
Две общих точки
Одна общая точка
y = –4
y = 5
Ответ: m= –4, m=5.
Изображение слайда
8
Слайд 8
–
–
–
Постройте график функции
и определите, при каких значениях m прямая y = m
имеет с графиком ровно одну
общую точку.
Задание 2 2
= ( x+ 5 )(x –2 )
( x 2 + 9х+20 )(x 2 –3 x+ 2 )
y=
x 2 + 3х–4
=
( x ) (х )
( x ) (х ) (x )(x )
+ 4
+ 5
Используем формулу для разложения квадратного трехчлена на множители
ax 2 +bx+c=a(x- x 1 )(x- x 2 )
x 2 +9x+ 20 =0
х 1 = – 4 х 2 = – 5
х 1 +х 2 = – 9 х 1 х 2 =20
x 2 +9x+ 20 =(x+ 4 )(x+ 5 )
–
–
–
х 2 –3 x+ 2 =0
х 1 =1 х 2 =2
х 1 +х 2 = 3 х 1 х 2 =2
х 2 –3 x+ 2 =(x –1 )(x –2 )
1
2
х 2 +3 x –4 =0
х 1 =1 х 2 =–4
х 1 +х 2 =–3 х 1 х 2 =–4
х 2 +3х–4 =(x –1 )(x +4 )
1
+4
y= ( x+ 5 )(x –2 )
D(y): x= 1, х= – 4.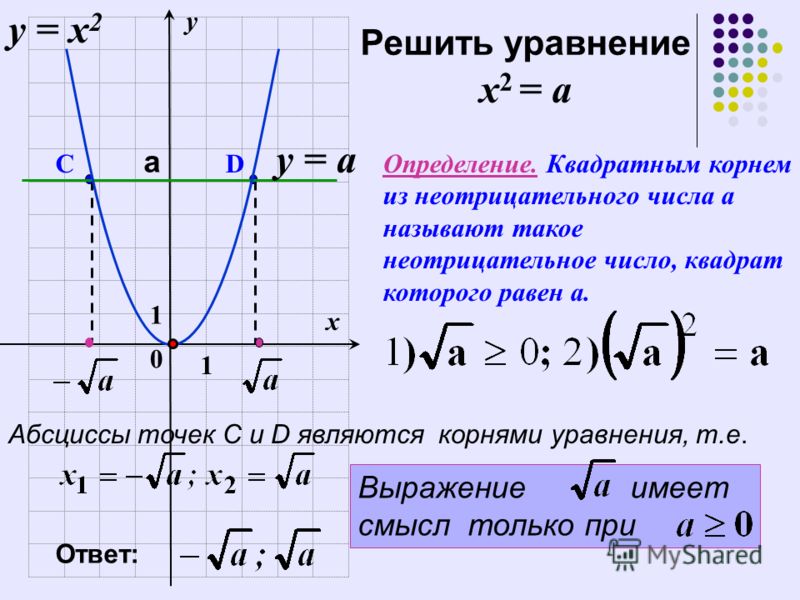 5
x
y
ОГЭ
ГОТОВИМСЯ
К
5
x
y
ОГЭ
ГОТОВИМСЯ
К
Изображение слайда
9
Последний слайд презентации: х(х+1) =х 2 +х Задание 2 2 Постройте график функции y = и определите при каких
–6 Постройте график функции и определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку. –10 = –1,5 3,5 -3,5 =– 12,25 Вершина ( –1,5;–12,25) y(– 1, 5)=(- 1, 5+ 5 )(- 1, 5 -2 ) x 0 = –5 + 2 2 2 –1,5 Задание 2 2 y x –5 Найдем нули функции ( x+ 5 )(x –2 )=0 x= – 5, x= 2. Если x= – 4, то y= ( – 4+5)( – 4–2)=–6 Исключаем точку (–4; –6) Нет общих точек Две общих точки Две общих точки Одна общая точка y = – 12,25 Ответ: m= – 12,25. y= ( x+ 5 )(x –2 ) D(y): x= –4, х=1. 1 –12,2 5 Точка пересечения с осью Оу, х=0, у(0)=(0+5)(0–2)=–10 ( 0;–10) –4 Если x= 1, то y= ( 1 +5)( 1 –2)=–6 Исключаем точку (1; –6) Нет общих точек
Изображение слайда
Вентилятор осевой настенный и потолочный ВЕНТС 100 Х1
Описание
Описание
| ПРИМЕНЕНИЕ | |
|
|
| КОНСТРУКЦИЯ | |
|
|
| ЭЛЕКТРОДВИГАТЕЛЬ | |
|
|
| УПРАВЛЕНИЕ | |
|
Ручное:
|
Автоматическое:
|
| МОНТАЖНЫЕ ОСОБЕННОСТИ | |
|
|
| ПРИМЕР МОНТАЖА | |
Характеристики
Характеристики
| Параметр | ВЕНТС 100 Х1 | ВЕНТС 100 Х1Т | ВЕНТС 100 Х1ТН | ВЕНТС 100 Х1В | ВЕНТС 100 Х1ВТ | ВЕНТС 100 Х1ВТН | ВЕНТС 100 Х1 Л | ВЕНТС 100 Х1В Л | ВЕНТС 100 Х1 К | ВЕНТС 100 Х1Т К | ВЕНТС 100 Х1 К Л | Единица измерения |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Напряжение | 220-240 | 220-240 | 220-240 | 220-240 | 220-240 | 220-240 | 220-240 | 220-240 | 220-240 | 220-240 | 220-240 | В |
| Частота тока | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | Гц |
| Потребляемая мощность | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | 14 | Вт |
| Производительность | 99 | 99 | 99 | 99 | 99 | 99 | 99 | 99 | 99 | 99 | 99 | м³/ч |
| Ток | 0.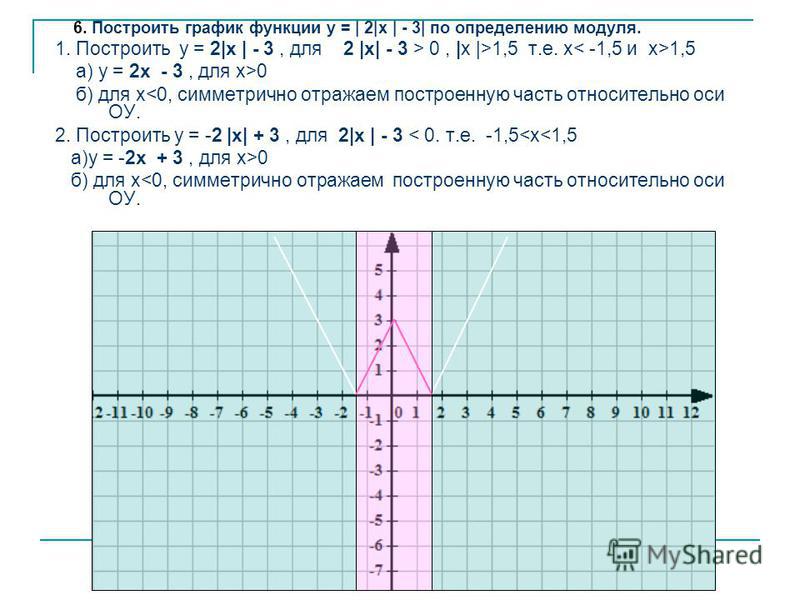 085 085 | 0.085 | 0.085 | 0.085 | 0. 085 085 | 0.085 | 0.085 | 0.085 | 0.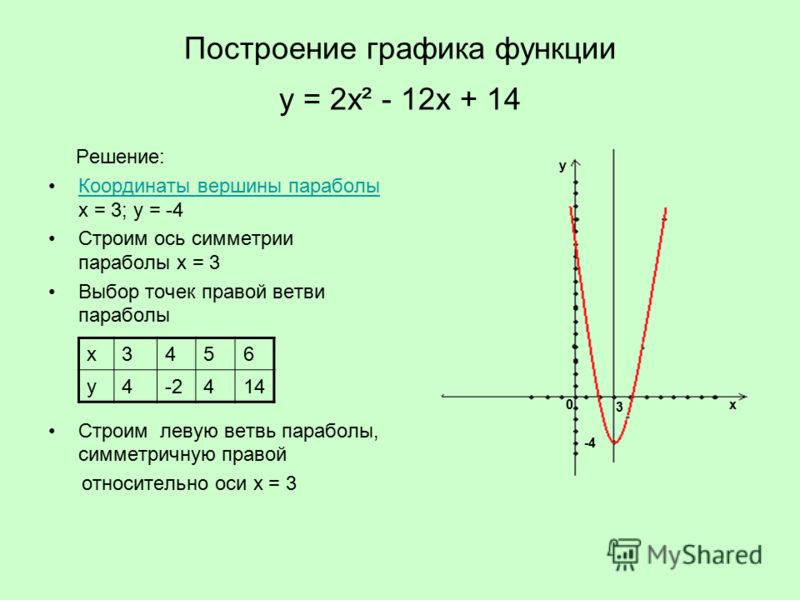 085 085 | 0.085 | 0.085 | А |
| Частота вращения | 2300 | 2300 | 2300 | 2300 | 2300 | 2300 | 2300 | 2300 | 2300 | 2300 | 2300 | мин-1 |
Уровень звукового давления на расст. 3 м 3 м | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | 33 | дБА |
| Вес | 0. 6 6 | 0.6 | 0.6 | 0.6 | 0. 6 6 | 0.6 | 0.6 | 0.6 | 0. 6 6 | 0.6 | 0.6 | кг |
| Размер патрубка | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | мм |
| Тип мотора | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | 220-240В / 50Гц | — |
| Диаметр воздуховода | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | мм |
| Конструкция | осевой | осевой | осевой | осевой | осевой | осевой | осевой | осевой | осевой | осевой | осевой | — |
| Степень защиты | IP 24 | IP 24 | IP 24 | IP 24 | IP 24 | IP 24 | IP 24 | IP 24 | IP 24 | IP 24 | IP 24 | — |
| Тип | вытяжной | вытяжной | вытяжной | вытяжной | вытяжной | вытяжной | вытяжной | вытяжной | вытяжной | вытяжной | вытяжной | — |
| Монтаж | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | настенный, потолочный | — |
График производительности
График производительности
- Метод подбора: Характеристика сети Постоянный расход Статическое давление
- Производительность: м³/ч л/с cfm
- Давление:
Па мБар дюйм вод.
 ст.
ст.
Рабочая точка
- Производительность: —
- Давление: —
Центр загрузок
Загрузки
Выберите тип документа
Название
Скачать
Смотреть
Декларация соответствия «Бытовые вентиляторы» (pdf 423.74Kb)
«ВЕНТС Х1» описание продукта 02-2020 (pdf 3.9Mb)
Сертификат GS «Х,Х1» (pdf 506.28Kb)
Скачать изображение товара в высоком качестве «ВЕНТС Х1» (psd 2.6Mb)
Сертификат GS «Х,Х1,Модерн,ЛД, ЛД Фреш тайм» (pdf 166. 94Kb)
94Kb)
Сертификат LVD «Х,Х1,Модерн,ЛД,ЛД Фреш тайм» (pdf 205.34Kb)
Скачать изображение «ВЕНТС Х1» для Вашего сайта (png 553.42Kb)
Сертификат ГЗ «Бытовые вентиляторы ВЕНТС» (pdf 1.27Mb)
Сертификат УкрСЕПРО «Бытовые вентиляторы ВЕНТС 1» (pdf 500.97Kb)
«Бытовые вентиляторы ВЕНТС» паспорт 01-2022 (V01RU_16-01) (pdf 3.91Mb)
Модификации
| Наименование модификации |
|---|
| ВЕНТС 100 Х1 |
| ВЕНТС 100 Х1Т |
| ВЕНТС 100 Х1ТН |
| ВЕНТС 100 Х1В |
| ВЕНТС 100 Х1ВТ |
| ВЕНТС 100 Х1ВТН |
| ВЕНТС 100 Х1 Л |
| ВЕНТС 100 Х1В Л |
| ВЕНТС 100 Х1 К |
| ВЕНТС 100 Х1Т К |
| ВЕНТС 100 Х1 К Л |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
Размеры
Характеристики
| Параметр | Величина | Единица измерения |
|---|---|---|
| ∅D | 100 | мм |
| B | 152 | мм |
| H | 120 | мм |
| L | 108 | мм |
| L1 | 12 | мм |
Условные обозначения
Условные обозначения
| ПИКТОГРАММА | УСЛОВНОЕ ОБОЗНАЧЕНИЕ | ОПИСАНИЕ МОДИФИКАЦИИ |
| Х1 К | Вентилятор оборудован обратным клапаном для предотвращения обратной тяги. |
|
| Х1 Л | Двигатель оборудован подшипниками качения для увеличения срока службы (около 40 000 рабочих часов) и установки вентилятора под любым углом. Подшипники не требуют обслуживания и имеют запас смазочного материала, достаточный для всего срока эксплуатации. | |
| Х1 турбо | Двигатель с повышенной производительностью. | |
| Х1 12 | Исполнение с безопасным двигателем низкого напряжения 12 В переменного тока. | |
| Х1T | Оборудован регулируемым таймером. Время срабатывания от 2 до 30 минут. | |
| Х1TH | Оборудован регулируемым таймером (время срабатывания от 2 до 30 минут) и реле влажности (порог срабатывания 60-90%). | |
| Х1В | Оборудован шнурковым выключателем. |
|
| Х1ВТ | Оборудован шнурковым выключателем и регулируемым таймером (время срабатывания от 2 до 30 минут). | |
| Х1ВТН | Оборудован шнурковым выключателем, регулируемым таймером (время срабатывания от 2 до 30 минут) и реле влажности (порог срабатывания 60-90%). |
Вычисление первообразной функции — что это такое?
Поговорим мы сегодня именно об этой прекрасной даме: узнаем, что такое первообразная, как она связана с интегралами и производными, и что самое важное, как её рассчитать без особого труда.
Дифференцирование и интегрирование
Если проанализировать все математические действия, то большинству из них будет соответствовать какое-то обратное:
сложение обратно вычитанию,
умножение — делению,
возведение в степень — извлечению арифметического корня.

С производной то же самое: мы можем продифференцировать функцию, а можем произвести обратный процесс — интегрирование.
Дифференциация — операция взятия полной или частной производной функции.
Интегрирование — процесс поиска интеграла; восстановление функции по её производной.
Нахождение производной от функции обозначается знаком ′. Так, если исходная функция — y, то её производная будет обозначаться y′.
Чтобы взять производную от функции, мы воспользуемся таблицей производных и правилами дифференцирования.
Функция f (x) | Производная f’ (х) |
|---|---|
С (т. е. константа, любое число) | 0 |
х | 1 |
xn | nxn-1 |
√x | 1/(2√x) |
sin x | cos x |
cos x | -sin x |
tg x | 1/cos2(х) |
ctg x | -1/sin2x |
ex | ex |
ax | ax * ln a |
ln x | 1/x |
logax | 1/(x * ln a) |
Правила дифференцирования
(c ⋅ f)′ = c ⋅ f′
(u + v)′ = u′ + v′
(u — v)′ = u′ — v′
(u ⋅ v)′ = u′v + v′u
(u/v)’ = (u’v — v’u)/v2
u, v, f — это функции, а c — константа (любое число).
У интегрирования тоже есть своё обозначение — ∫. То есть если мы хотим взять интеграл от функции f(x), мы запишем это так: ∫f(x) dx.
Внимательные заметили в записи интегрирования непривычное для нас «dx». Что это такое? Зачем добавлять эти буквы в выражение для интеграла? Сейчас во всём разберёмся!
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Дифференциал
Разберём буквы dx по отдельности:
d — это дифференциал,
х — функция, по которой будет произведено дифференцирование.
Так, если мы дифференцируем функции y, f, m, то их дифференциалы запишем соответственно как dy, df, dm.
Дифференциал в математике (от лат. differentia — разность, различие) — линейная часть приращения функции.
То есть это понятие родственно производной — но для чего его записывать рядом с интегралом?
Для понимания важности дифференциала в записи рассмотрим рисунок:
Геометрический смысл интеграла — это площадь фигуры под кривой функции. Если поместить график в декартову систему координат OХY, то эту площадь можно рассчитать относительно и оси ОХ, и оси ОУ, и именно дифференциал вносит ясность в выбор.
Понятие дифференциала в математике очень важное, глубокое, имеет множество нюансов использования, но сейчас нам важно понимать две вещи:
Что такое первообразная?
Пришло время познакомиться с её величеством первообразной! Начнём с определения.
Первообразная для функции f(x) — это такая функция F(x), производная которой равна f(x). То есть выполняется равенство F'(x) = f(x).
Пример 1: мы знаем, что ускорение является производной от скорости. Тогда по нему можно найти скорость, восстановив функцию и найдя его первообразную.
Пример 2: производная функции –sin(x). Посмотрим внимательно в таблицу производных: cos'(x) = –sin(x). Тогда первообразная функции sin(x) будет равна –cos(x) + С с учётом постоянной величины.
Константа
Зачем добавлять константу к первообразной?
Представьте, что нам необходимо найти производную функций:
−cos(x) + 3,
−cos(x) + 5,
−cos(x) − 6.
Тогда производная будет равна sin(x) для всех трёх вариантов, так как производная любого числа равна нулю:
(−cos(x) + 3)’ = sin (x),
(−cos(x) + 5)’ = sin (x),
(−cos(x) − 6)’ = sin (x).
Выходит, что получить исходную функцию в первозданном виде невозможно, но учесть дополнительное слагаемое в виде числа нам нужно. Именно поэтому в первообразной добавляют константу «+ С». Выражение, которое имеет общий вид F(x) + С, называется множеством первообразных функции.
Отсюда вытекает свойство первообразной: любые две первообразные одной и той же функции отличаются друг от друга не более чем на постоянную величину C.
Правила нахождения первообразной
Нахождение первообразной функции технически связано с поиском неопределённого интеграла функции.
Неопределённый интеграл — это интеграл, для которого не задан промежуток интегрирования.
Важный момент: если продифференцировать можно любую функцию, то найти первообразную функции можно не всегда.
Об этом говорит достаточное условие интегрируемости: если на некотором промежутке функция непрерывна, то она интегрируема на нём.
Каким образом можно найти первообразную функцию? Всё просто! Как и в случае с производной, мы можем воспользоваться готовой таблицей первообразных и свойствами неопределённого интеграла!
«Высокий» логарифм:
«Длинный» логарифм:
Свойства неопределённого интеграла
Свойства неопределённого интеграла можно назвать правилами интегрирования — основываясь на них, мы сможем находить первообразную сложных функций, сводя их к лёгким.
Производная от неопределённого интеграла равна подынтегральной функции; дифференциал от неопределённого интеграла равен подынтегральному выражению:
Неопределённый интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
Константу можно вынести из-под знака интеграла: то есть, если , то .
Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов:
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Примеры решения заданий
Задание 1
Найди первообразную функции
Записываем неопределённый интеграл:
Применяем свойство неопределённого интеграла об алгебраической сумме функций:
Выносим константы за знак интеграла:
Проводим интегрирование согласно таблице первообразных:
Задание 2
Вычисли неопределенный интеграл
Раскрываем скобку по формуле квадрата суммы и вносим х в скобку:
Воспользуемся свойством неопределенного интеграла об алгебраической сумме функций, выносим константы за знак интеграла и находим первообразную:
Интегрирование и нахождение первообразной — одна из самых сложных, но одновременно интересных тем алгебры. Иногда задания похожи на головоломку: необходимо выбрать верный способ решения, учесть все нюансы, выполнить верные вычисления. Научиться выполнять такие задания можно на уроках онлайн-курса математики в школе Skysmart: там вы не только подготовитесь к экзаменам, но и научитесь находить нестандартные решения, мыслить логически и строить самые неопровержимые доказательства.
Иногда задания похожи на головоломку: необходимо выбрать верный способ решения, учесть все нюансы, выполнить верные вычисления. Научиться выполнять такие задания можно на уроках онлайн-курса математики в школе Skysmart: там вы не только подготовитесь к экзаменам, но и научитесь находить нестандартные решения, мыслить логически и строить самые неопровержимые доказательства.
ООО «Авиакомпания «Победа», Группа «Аэрофлот»
- Home
- Информация
- Путешествие
- Багаж
Максимальные габариты
В сумме трёх измерений (длина+высота+ширина) должны составлять не более 203 см:
Вес и стоимость
- От 899 ₽* за 1 место багажа
- В рамках тарифа «Выгодный» можно заменить на лыжи/сноуборд (1 комплект) вместе с дополнительным снаряжением (ботинки, шлем, очки), упакованные в один общий или два отдельных чехла
- От 1199 ₽* за 1 место багажа
- В рамках тарифа «Максимум» можно заменить на лыжи/сноуборд (1 комплект) вместе с дополнительным снаряжением (ботинки, шлем, очки), упакованные в один общий или два отдельных чехла
- От 2399 ₽* за 1 место багажа
- Приобретается как дополнительная услуга
*Стоимость багажа формируется согласно установленным тарифам
Как купить?
- Выгоднее всего на сайте pobeda.
 aero и в мобильном приложении:
aero и в мобильном приложении:— при бронировании билетов
— добавить в существующее бронирование через Управление бронированием, Личный кабинет или Колл-центр — не позднее 4-х часов до вылета и прохождения онлайн-регистрации - На стойке регистрации в аэропорту
Как купить?
- Выгоднее всего на сайте pobeda.aero или в мобильном приложении:
— при бронировании билетов
— в процессе онлайн-регистрации - Вы также можете добавить багаж в своё бронирование:
— через Колл-центр — если до вылета более 4-х часов и не пройдена онлайн-регистрация
— на стойке регистрации в аэропорту — до окончания регистрации на рейс и до прохождения онлайн-регистрации
Как купить?
- Выгоднее всего на сайте pobeda.aero или в мобильном приложении:
— при бронировании билетов
— через Управление бронированием не позднее 1 часа до вылета
— в процессе Онлайн-регистрации не ранее 24 часов и не позднее 4 часов до вылета - Также добавить багаж в существующее бронирование можно:
— через Колл-центр не позднее 4 часов до вылета и прохождения онлайн-регистрации
— на стойке регистрации в аэропорту до окончания регистрации на рейс
Сколько стоит перевес?
За каждый килограмм перевеса (до 3 кг):
- 500 ₽ в аэропортах РФ
- 10 € или 11 $ в зарубежных аэропортах
За перевес от 4 до 9 кг:
- 1599-2599 ₽ в аэропортах РФ
- 31 € или 35 $ в зарубежных аэропортах
Подробнее о тарифах
Услуга «Дополнительное место»
- Свободное соседнее кресло
- Подходит для хрупкого багажа весом до 32 кг и с максимальными габаритами до 38х40х110 см (длина, ширина и высота)
Подробнее об услуге
Страхование багажа
- От задержки, повреждения и потери
- Выплаты до 60 000 ₽
- Если чемодан повреждён и не подлежит ремонту, вы можете купить новый и оформить выплату до 15 000 ₽ по фотографиям
Подробнее об услуге
Вы можете оформить ваш багаж сразу до конечного пункта перелёта, если вы летите:
- из России за границу, кроме стыковочных рейсов через Санкт-Петербург
- из зарубежных аэропортов стыковочным рейсом через аэропорт Внуково
Обращаем ваше внимание, багаж может быть оформлен трансфером до конечного пункта следования только при условии отсутствия в нем товаров, подлежащих таможенному декларированию в письменной форме. При наличии в вашем багаже таких товаров багаж оформляется только до пункта трансфера. Вам нужно получить багаж в транзитном аэропорту, пройти таможенный контроль и заново оформить багаж на стойке регистрации.
При наличии в вашем багаже таких товаров багаж оформляется только до пункта трансфера. Вам нужно получить багаж в транзитном аэропорту, пройти таможенный контроль и заново оформить багаж на стойке регистрации.
Правила и условия перевозки, доставки и получения трансферного багажа определены в Приложении 2 к Правилам перевозки.
За дополнительную плату вы можете оформить некоторый спортивный инвентарь как специальный багаж.
Каждый клиент может провозить:
Лыжное оборудование*
Один комплект лыж или сноуборд c дополнительным снаряжением (ботинки, шлем, очки), упакованные в один общий или два отдельных чехла
Не более двух комплектов на человека
*В рамках включённой нормы провоза багажа для тарифов «Выгодный» и «Максимум» возможна замена одного места багажа на:
- лыжи/сноуборд (1 комплект) вместе с дополнительным снаряжением (ботинки, шлем, очки), упакованным в один общий или два отдельных чехла
Общий вес и размер лыжного оборудования:
- для тарифа «Выгодный» вес до 10 кг, размер не более 203 см по сумме трёх измерений
- для тарифа «Максимум» вес до 20 кг, размер не более 203 см по сумме трёх измерений
Общее количество мест багажа в рамках пакетного тарифного предложения с учётом лыжного оборудования – не более двух.
Велосипед
В чехле или упаковке суммарным весом не более 20 кг и размером не более 203 см по сумме трёх измерений
Необходимо предварительное бронирование
Рыболовное оборудование
Упакованное в один контейнер (чехол)
Две удочки, один комплект снастей на человека
Весь остальной спортинвентарь, за исключением описанного выше, оформляется как обычный или негабаритный багаж.
Все виды шлемов, которые не помещаются в габариты ручной клади 36х30х27 см (общий размер всех предметов), перевозятся в багаже.
Детские коляски и люльки перевозятся в багаже бесплатно. Вы можете сдать их в багаж на регистрации или при посадке в самолёт. Регистрация детских колясок и люлек на стойке регистрации обязательна. По прилёте детские коляски и люльки получают только в зоне выдачи багажа или в зоне выдачи негабаритного багажа. Санки-коляски и автокресла перевозятся только в багаже за дополнительную плату.
В салон самолёта допускаются мягкая люлька (если можно сложить) и переноска «Кенгуру». Авиакомпания не предоставляет люльки для младенцев.
Авиакомпания не предоставляет люльки для младенцев.
Кресла-коляски с электрическим приводом оформляются для провоза исключительно в качестве зарегистрированного багажа на стойке регистрации в аэропорту вылета в порядке, установленном приложением 3 к Правилам перевозки.
Негабаритный багаж – это багаж, размеры которого превышают 203 см по сумме трёх измерений (длина+ширина+высота). Максимальный вес одного места негабаритного багажа – 32 кг. Такой багаж оплачивается отдельно по установленным тарифам в аэропорту на стойке регистрации.
Совместно с компанией «UTG-EXPRESS» мы предлагаем услуги по перевозке грузов и доставке экспресс-корреспонденции, подробнее по ссылке.
Багаж утерян
Не покидая зал выдачи багажа, обратитесь на стойку «Утерянный багаж» или «Востребование багажа». Там необходимо заполнить акт об утере или повреждении багажа. После заполнения акта заявке присвоят номер и расскажут, что делать дальше. Если в течение 5 дней вы не получили обратной связи, заполните специальную форму.
Если в течение 5 дней вы не получили обратной связи, заполните специальную форму.
Багаж повреждён
Не покидая зал выдачи багажа, обратитесь на стойку «Утерянный багаж» или «Востребование багажа». Там необходимо заполнить акт об утере или повреждении багажа. Право на предъявление претензии имеет клиент авиакомпании «Победа» или уполномоченное им лицо. Для этого необходимо отправить следующие документы на почтовый адрес (108811, Российская Федерация, г. Москва, пос. Московский, 22-й км. Киевского шоссе, 4/1):
- заявление в свободной форме с указанием адреса, номера телефона и электронной почты
- акт о неисправностях при перевозке багажа (PIR – оригинал)
- чеки, подтверждающие расходы (оригиналы)
- багажная бирка-оригинал
- маршрут-квитанция или посадочный талон (оригинал)
- полные банковские реквизиты для перечисления компенсации
Вы также можете оформить претензию и выслать документы онлайн, заполнив специальную форму.
Что нельзя провозить в багаже
Подробнее в правилах перевозки
3-8YX ONE — электрическая доска повышенной проходимости
Представляем
YX ONE
Смотреть видео Предзаказ
60 км/37 миль
АССОРТИМЕНТ
Большие литий-ионные аккумуляторы, способные проехать до 60 км без подзарядки, вы устанете раньше, чем ваш YX ONE! (до 60 км на одной зарядке в зависимости от массы тела и состояния водителя).
40 км/25 миль в час
МАКСИМАЛЬНАЯ СКОРОСТЬ
С максимальной скоростью 40 км/ч. три диапазона мощности предлагают выбор стиля езды. от низкой контролируемой скорости до более высоких скоростей, максимальная стабильность и впечатляющая сила подъема без рывков и колебаний.
ВЫДАЮЩАЯСЯ ПРОИЗВОДИТЕЛЬНОСТЬ НА ЛЮБОЙ МЕСТНОСТИ
- Максимальная скорость до 40 км/ч — 25 миль
- Максимальная дальность действия до 60 км / 37 миль
- Двигатель 750 Вт / Пиковая мощность 1500 Вт
- Аккумулятор 624 Втч / 48 В / 13 Ач
- Длина 980 мм
- Макс.
 подъем на 15 градусов
подъем на 15 градусов - Максимальная нагрузка 120 кг
- Передняя шина 10 дюймов
- Задняя шина 13 дюймов
- Вес 20 кг
- Торможение ДИСКОВЫЙ ТОРМОЗ
- АМОРТИЗАТОРЫ ПРУЖИН ПОДВЕСКИ
- Степень защиты IP65
- Вход зарядного устройства 110-240 В
- Напряжение 48 В
- Сила тока 2,9 А / 14,5 А·ч
- Время зарядки 3 ЧАСА ДО 80%
ОДНОКОЛЕСНОЕ
МОТОР ОБЕСПЕЧИВАЕТ
МАКСИМАЛЬНУЮ В
МОЩНОСТЬ И УПРАВЛЕНИЕ
Расположение передних и задних колес обеспечивает потрясающую маневренность и управляемость на всех скоростях и на любой местности.
 Всадник перемещает вес тела для контроля, наклоняя вес вперед-назад, носки-пятки, чтобы задать направление.
Всадник перемещает вес тела для контроля, наклоняя вес вперед-назад, носки-пятки, чтобы задать направление.Самое большое колесо, которое когда-либо использовалось на электрическом скейтборде.
Единая точка силового контакта с землей.
Быстро останавливается, включает шестипенсовик.
Галерея YX ONE
RIDE BY WIRE УВЕРЕННО НАКЛОНЯЙТЕСЬ В ПОВОРОТЫ
Изменяйте направление, наклоняясь и меняя баланс, делая поездку естественной и интуитивно понятной.
Управляйте своей скоростью с помощью рукоятки и троса, соединенных с досками, обеспечивая более безопасную и контролируемую езду, поддерживая баланс и контроль направления на высокой скорости.
YX One Timeline
AUG 19
Soft launch
Reservation Open
OCT 19
Gen 2 Prototype Testing
Enhancements
MARCH 20
Tooling
Commences
MAY 20
Production
Commences
20 ИЮНЯ
Доставка
Начало
YX One Timeline
ОФОРМИТЕ ПРЕДЗАКАЗ СЕГОДНЯ!
YX One
ЗАБРОНИРОВАТЬ СЕГОДНЯ И ПЛАТИТЬ МЕНЬШЕ.

Ограниченная партия первого тиража закрыта для бронирования. Доступно для предзаказа исключительно на Indiegogo до декабря 2019 г. перед окончательным производством.
Часто задаваемые вопросы
Q. Зачем бронировать сейчас?
Предварительное бронирование закрыто. YX ONE доступен исключительно на Indiegogo
909:20 Вопрос. Когда я получу свой YX ONE?В настоящее время мы работаем над графиком производства. Актуальную информацию о сроках и поставках см. на indiegogo
Q. Сколько стоит доставка?
В настоящее время мы согласовываем варианты доставки и стоимость с нашими партнерами по логистике. Учитывая большую батарею и вес YX ONE, имейте в виду, что окончательная доставка может стоить 100–200 долларов США для доставки в США / ЕС. Покупателям из ЕС, вероятно, придется платить НДС при импорте. Мы сообщим вам об окончательной стоимости доставки заранее и выставим окончательный счет через PayPal перед импортом.
В. Есть ли гарантия?
Да, на неизнашиваемые детали предоставляется 12-месячная гарантия. Если в течение этого времени вы обнаружите заводской брак, связанный с производством, мы заменим или отремонтируем его по гарантии.
Свяжитесь с нами
YX ONE
YX ONE
DOGPATCH LABS
ДУБЛИН 1
ИРЛАНДИЯ
Зарезервируйте
YX One
Способы оплаты
| Ранняя пташка | Поздняя пташка | |
| МРРП | 2 290,00 $ | 2 290,00 $ |
| Скидка | 44% | 40% |
| Вы экономите | 1 008,00 $ | $916,00 |
| Цена по предварительному заказу | 1 282,00 $ | 1 374,00 $ |
(Доставка и применимые налоги взимаются перед доставкой, подробности см. в разделе часто задаваемых вопросов.)
в разделе часто задаваемых вопросов.)
НАША ИСТОРИЯ
СОЗДАНА, ЧТОБЫ ПОДАРИТЬ ВПЕЧАТЛЯЮЩИЕ ВПЕЧАТЛЕНИЯ НА ЛЮБОЙ МЕСТНОСТИ. ОТ БЕЗДОРОЖЬЯ, ДО ПЕСЧАНОГО ДО ПЛЯЖА, ТРАВЯНЫХ ПОЛЕЙ.
МОЩНЫЙ МОТОР, БОЛЬШАЯ ШИРОКАЯ ШИНА, ПОЗВОЛЯЕТ ПОЕХАТЬ ТУДА, ЧТО БОЛЬШИНСТВО ПОЕЗДОК НА ЭЛЕКТРОМОБИЛЬНИКЕ НЕ ДОСТУПНО.
ВПЕРВЫЕ ЗАДУМАННЫЙ В ИЗРАИЛЕ ИЗОБРЕТАТЕЛЬ ЭЯЛЬ АЛОНИ, ТЕПЕРЬ ЭЛЕКТРИФИЦИРОВАННЫЙ И ПЕРЕОСНОВАННЫЙ КОМПАНИЕЙ MOBY В ДУБЛИНЕ. YX ONE – ЭТО МЕЖДУНАРОДНОЕ СОТРУДНИЧЕСТВО, КОТОРОЕ ЗАПУСКАЕТСЯ ПО ВСЕМУ МИРУ В КОНЦЕ 2019 Г., НАЧАЛЕ 2020 Г.
доказательство проверки — Натуральное число между двумя действительными числами $y,x$ такое, что $y-x > 1$
Задавать вопрос
Спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 565 раз
$\begingroup$
Докажите, что для $x,y \in \mathbb{R}$, таких что $y-x>1$, существует натуральное число $n$ такое, что $x < n < y$.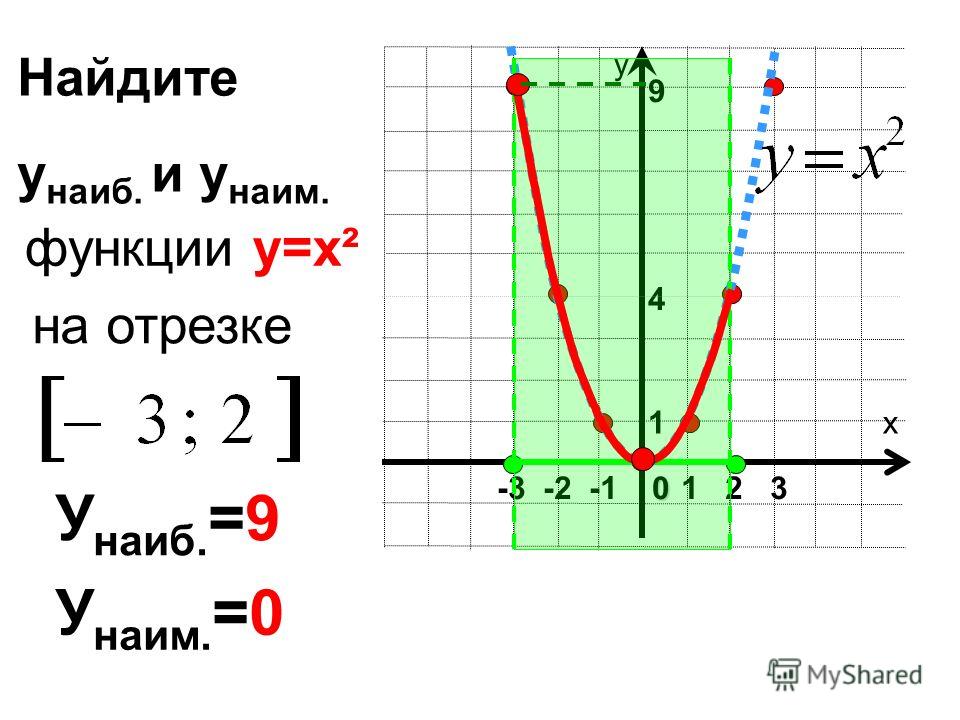
Рассмотрим следующий набор:
$$ S := \{n \in \mathbb{N} | х < п < у\} $$
Предположим, что $S = \emptyset$, поэтому $\forall n \in \mathbb{N}$ $n \leq x$ или $n \geq y$. Пусть $n_1$ — первое натуральное число перед $x$. Поэтому $n_1 < x < n_1 + 1$.
Теперь покажем, что $n_1+1 < y$. Предположим, что нет. Следовательно, $n_1 $$ 1 = n_1 + 1 — n_1 > y-x > 1$$ Отсюда противоречие, $x Вот что я думаю о своем доказательстве: я не использовал тот факт, что $x,y$ — действительные числа… Может быть, я не должен был так доказывать? Может ли кто-нибудь указать другое доказательство, если мое не подходит для этого случая? Я не знаю, просто странно что-то доказывать и не использовать все наши предпосылки. Спасибо! $\endgroup$ 3 $\begingroup$ Ваше доказательство верно, и вы неявно используете два важных свойства $\mathbb{R}$ и $\mathbb{N}$. Первое свойство, о котором я говорю, это архимедово свойство вещественных чисел (как упорядоченного поля). По сути, это говорит о том, что для каждого действительного числа $x$ существует некоторое натуральное число $n > x$. Другое свойство состоит в том, что натуральные числа хорошо упорядочены. Это означает, что каждое непустое подмножество натуральных чисел имеет наименьший элемент. Вы неявно используете правильный порядок натуральных чисел для нахождения максимального $n_1$ такого, что $n_1 \leq x$, а затем используете свойство Архимеда, чтобы сделать вывод, что $n_1 + 1 > x$. Прежде всего, как уже упоминалось в комментариях, нам явно нужно принять $0 \leq x$, иначе утверждение просто неверно. Пусть $y-x > 1$, тогда $y > x + 1 > x \geq 0$. По архимедову свойству существует некоторое $n \geq y$. Таким образом, множество $A = \{n \in \mathbb{N} : n \geq y\}$ всех натуральных чисел больше (или равных) $y$ непусто. Тогда из хорошо упорядоченных натуральных чисел должен быть наименьший элемент $n_1 \in A$. Так как $y > 1$, мы получаем, что $n_1 > 1$ и, следовательно, $n_1 — 1 > 0$ — натуральное число. Мы должны иметь $y > n_1 — 1$, так как иначе $n_1 — 1 \geq y$ и, следовательно, $n_1 — 1 \in A$, но $n_1$ был наименьшим элементом $A$. Тогда наличие $y-x>1$ означает, что они обязательно должны находиться в разных корзинах. Другими словами, для натуральных чисел $m Но так как $y-x>1$, то $y>m+1$. А именно
$$ x \in [m,m+1) \quad и \quad y \in (m+1,n+1) $$
$$ \ подразумевает x (как упоминалось в других ответах, нет ничего особенного в том, что Y и X реальны. Это сработало бы, если бы рациональные числа были натуральными числами) $\endgroup$ Зарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и пароль Электронная почта Требуется, но никогда не отображается Электронная почта Требуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie . 2008 г., июль; 99 (10): 4315-20. doi: 10.1016/j.biortech.2007.08.040.
Epub 2007 24 октября. Сюй Дун Лю 1 , Ян Сюй Сюй Донг Лю и др.
Биоресурсная технология.
2008 июль . 2008 г., июль; 99 (10): 4315-20. doi: 10.1016/j.biortech.2007.08.040.
Epub 2007 24 октября. Сюй Дун Лю 1 , Ян Сюй В этом исследовании сообщается об очистке и характеристике новой альфа-амилазы, расщепляющей сырой крахмал, из недавно выделенного Bacillus sp. YX-1. Максимальная активность альфа-амилазы (53 ед. мл(-1)) была достигнута при 45°С через 44 часа инкубации. Фермент очищали с использованием преципитации сульфатом аммония, ионообменной и гель-фильтрационной хроматографии и показали молекулярную массу 56 кДа с помощью SDS-PAGE. Этот фермент проявлял максимальную активность при рН 5,0, проявлял стабильность в широком диапазоне рН 4,5-11,0 и был оптимально активен при 40-50°С. Ферментный препарат обладал сильной способностью переваривать различные сырые крахмалы и эффективно гидролизовать сырой кукурузный крахмал. при концентрации 20% и рН 5,0, которые обычно используются в крахмальной промышленности, в течение 12 часов. Путем анализа его частичных аминокислотных последовательностей было высказано предположение, что этот фермент представляет собой новую альфа-амилазу. Биохимическая характеристика альфа-амилазы, переваривающей сырой крахмал, очищенной от Bacillus amyloliquefaciens. Гангадхаран Д., Нампутири К.М., Шиварамакришнан С., Пандей А.
Гангадхаран Д. и соавт.
Заявл. Биохим Биотехнолог. 2009 г., сен; 158 (3): 653–62. doi: 10.1007/s12010-008-8347-4. Epub 2008, 4 сентября.
Заявл. Биохим Биотехнолог. 2009.
PMID: 18769877 Производство изоформы α-амилазы, расщепляющей сырой крахмал, из Bacillus sp. при твердофазной ферментации и биохимической характеристике. Божич Н., Славич М.Ш., Гаврилович А., Вуйчич З.
Божич Н. и соавт.
Биопроцесс Биосист Инж. 2014 июль; 37 (7): 1353-60. doi: 10.1007/s00449-013-1105-1. Epub 2013 20 декабря.
Биопроцесс Биосист Инж. Новая α-амилаза, расщепляющая сырой крахмал: производство при твердофазной ферментации сырого проса и биохимическая характеристика. Мактуф С., Камун А., Мулис С., Ремо-Симеон М., Гриби Д., Чаабуни С.Е.
Мактуф С. и др.
J Microbiol Biotechnol. 2013 апр; 23 (4): 489-98. doi: 10.4014/jmb.1211.11027.
J Microbiol Biotechnol. 2013.
PMID: 23568203 Очистка и характеристика термостабильной α-амилазы, продуцируемой грибком Paecilomyces variotii. Michelin M, Silva TM, Benassi VM, Peixoto-Nogueira SC, Moraes LA, Leão JM, Jorge JA, Terenzi HF, Polizeli Mde L.
Мишлен М. и др.
Карбогид Рез. 2010 2 ноября; 345 (16): 2348-53. doi: 10.1016/j.carres.2010.08.013. Epub 2010 25 августа.
Карбогид Рез. Очистка и характеристика амилазы, переваривающей сырой крахмал, из почвенной бактерии — Cytophaga sp. Джинг С.Л., Ли Ю.Х., Чанг Л.В.
Джин С.Л. и соавт.
Биохим Мол Биол Инт. 1995 март; 35 (3): 549-57.
Биохим Мол Биол Инт. 1995.
PMID: 7539663 Посмотреть все похожие статьи Новые адаптированные к холоду α-амилазы, переваривающие сырой крахмал из Eisenia fetida : клонирование, экспрессия и характеристика генов. Цукамото К., Арики С., Наказава М., Сакамото Т., Уэда М.
Цукамото К. и др.
Представитель биотехнологии (Амст). 2021 17 августа; 31:e00662. doi: 10.1016/j.btre.2021.e00662. электронная коллекция 2021 сент. Аспекты и последние тенденции в микробной α-амилазе: обзор. Пол Дж.С., Гупта Н., Белия Э., Тивари С., Джадхав С.К.
Пол Дж.С. и др.
Заявл. Биохим Биотехнолог. 2021 авг;193(8):2649-2698. doi: 10.1007/s12010-021-03546-4. Epub 2021 14 марта.
Заявл. Биохим Биотехнолог. 2021.
PMID: 33715051
Обзор. Новая пищеварительная α-амилаза синего краба ( Portunus segnis ) Внутренности: очистка, биохимическая характеристика и применение для улучшения антиоксидантного потенциала овсяной муки. Маалей Х., Маалей А., Аффес С., Хмидет Н., Насри М.
Маалей Х. и др.
Int J Mol Sci. 2021 22 января; 22 (3): 1070. Идентификация и характеристика термофильной амилазы, продуцирующей бактериальные изоляты из почвы кирпичной печи. Улла И., Хан М.С., Хан С.С., Ахмад В., Женг Л., Шах Суа, Улла М., Икбал А.
Улла I и др.
Саудовская J Biol Sci. 2021 Январь; 28 (1): 970-979. doi: 10.1016/j.sjbs.2020.11.017. Epub 2020 11 ноября.
Саудовская J Biol Sci. 2021.
PMID: 33424389Бесплатная статья ЧВК. Метагеном почвы антарктической тундры как полезный природный ресурс холодоактивных лигноцеллюлозолитических ферментов. О Х.Н., Пак Д., Сон Х.Дж., Ким Д., Сул В.Дж.
О HN и др.
J микробиол. 2019 окт; 57 (10): 865-873. doi: 10.1007/s12275-019-9217-1. Просмотреть все статьи «Цитируется по» Наведите курсор на изображение, чтобы увеличить
Нажмите на изображение, чтобы увеличить Этот бронзовый горизонтальный обратный клапан NIBCO имеет Y-образную конструкцию с заменяемым седлом и диском. Поворотный обратный клапан предотвращает обратный поток, автоматически закрываясь, когда поток меняет направление. Обратный клапан из бронзы имеет резьбовые торцевые соединения для простоты установки. Особенности Гарантия на клапаны NIBCO с номинальным давлением Бронзовые обратные клапаны NIBCO T-413 и S-413 класса 125 Представление NIBCO является признанным производителем и лидером в области клапанов, фитингов и продуктов для регулирования расхода. Страна США Почтовый индекс Liberty Supply принимает возврат в течение 90 дней после даты выставления счета. Все возвраты должны иметь номер RMA. Запросы RMA можно отправить по электронной почте support@libertysupply. Плата за повторное хранение товаров, возвращенных в течение 30 дней, не взимается, если они находятся в оригинальной невскрытой упаковке. Предметы, открытые и возвращенные до 9Через 0 дней после даты выставления счета взимается комиссия в размере 20 % за пополнение запасов, если они находятся в неизмененном и пригодном для продажи состоянии. Ранее использованные/установленные элементы не подлежат возврату, за исключением случаев, когда на них распространяется гарантия. Возврат изделий по специальному заказу или модифицированных изделий (таких как отделка крыльчатки) оценивается в каждом конкретном случае. Если возврат разрешен, товары по специальному заказу будут облагаться переменной комиссией за пополнение запасов в размере до 50%. Клиенты могут отправить возвращенные товары обратно в Liberty Supply или попросить Liberty Supply организовать их получение. Стоимость обратной доставки, оплаченная Liberty Supply, будет вычтена из кредитованной суммы, если мы не виноваты. Ответственность за все подразумеваемые гарантии на продукцию ложится на производителя. Если товар возвращается по гарантии производителя, Liberty Supply направит возвращенный товар производителю для проверки и принятия решения, что может занять до 5 недель. Окончательное решение о гарантии остается на усмотрение производителя. Дата последнего обновления: 4 марта 2022 г. Зачем доверять DWYM? DWYM — ваш надежный источник отзывов о продуктах. Вместе с нашими штатными экспертами наша команда анализирует тысячи отзывов о продуктах с самых надежных веб-сайтов. Затем мы создаем один простой для понимания обзор. Учить больше. Показать содержимое Содержание Мы просмотрели лучшие записки и просмотрели обзоры с некоторых из самых популярных обзорных сайтов. Обновление от 29 сентября 2022 г. : В нашем анализе 14 обзоров экспертов YX-1 Multifunctional Handmade Scrapbook занял 12-е место , когда мы рассмотрели 16 лучших продуктов в категории. Полный рейтинг смотрите ниже. Каждое прекрасное мгновение жизни нужно запечатлеть и сохранить, чтобы поделиться с семьей и друзьями. Чтобы записать каждое фото и передать словами свои мысли и чувства, мы сблизимся друг с другом, любовь должна быть выражена! Этот фотоальбом для вырезок станет лучшим подарком на выбор! 762 отзыва пользователей Общий балл: 9,8 Общий балл: 9,7 Общий балл: 9.5 Общий балл: 9,4 Общий балл: 9,3 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Общий балл: 9,2 Цифровые фотографии пришли на смену печатным. В отпуске вы, скорее всего, поделитесь всеми своими фотографиями в Интернете, чем будете ждать, пока вы вернетесь, чтобы показать их своим друзьям. Хотя вам больше не нужно нести свою пленку в фотопроявитель и ждать печатных копий, есть что-то особенное в том, чтобы хранить фотографии в альбоме, который вы оставляете на полке и хвастаетесь перед гостями. Это может быть причиной возвращения фотоальбомов и альбомов для вырезок в последние годы. Это началось с повального увлечения скрапбукингом пару десятилетий назад, когда люди использовали бумагу и декоративные надписи для украшения своих страниц с фотографиями. Однако, когда вы покупаете фотоальбомы, подумайте, как вы будете прикреплять свои фотографии. Альбомы с защитной пленкой, как правило, самоклеящиеся, а это значит, что вам просто нужно прижать фотографии на место. Многие другие, однако, требуют, чтобы вы использовали клей для рукоделия, чтобы прикрепить свои фотографии. Если все ваши фотографии цифровые, возможно, вы захотите создать фотоальбом в Интернете. Затем вы можете распечатать фотографии на самой странице, а затем переплести их в книгу, которая будет отправлена вам для демонстрации и использования. Но одна проблема с этим подходом заключается в том, что вы не можете удалить и добавить фотографии позже. Что касается печати фотографий, если вы печатаете довольно много, вы можете подумать о покупке фотопринтера. Хотя, чтобы сделать использование этих свойств более явным, я бы представил доказательство несколько иначе, взяв $n_1$ за наименьшее $n$ большее, чем $y$. Давайте посмотрим, как это будет выглядеть, но прежде чем углубиться в это, я хочу повторить, что ваше доказательство полностью верно. Я просто буду очень точен здесь, чтобы показать, где вы неявно используете определенные свойства, которые вы могли бы (по праву) считать очевидными.
Хотя, чтобы сделать использование этих свойств более явным, я бы представил доказательство несколько иначе, взяв $n_1$ за наименьшее $n$ большее, чем $y$. Давайте посмотрим, как это будет выглядеть, но прежде чем углубиться в это, я хочу повторить, что ваше доказательство полностью верно. Я просто буду очень точен здесь, чтобы показать, где вы неявно используете определенные свойства, которые вы могли бы (по праву) считать очевидными. Может быть не совсем ясно, как здесь используются эти свойства, потому что мы не можем напрямую использовать их определения в этой формулировке. Позвольте мне немного изменить ваше доказательство, чтобы было понятнее, где мы используем эти свойства (также обратите внимание, что нет необходимости в доказательстве от противного, мы действительно можем построить требуемое натуральное число).
Может быть не совсем ясно, как здесь используются эти свойства, потому что мы не можем напрямую использовать их определения в этой формулировке. Позвольте мне немного изменить ваше доказательство, чтобы было понятнее, где мы используем эти свойства (также обратите внимание, что нет необходимости в доказательстве от противного, мы действительно можем построить требуемое натуральное число). {\infty} [n,n+1) $$
{\infty} [n,n+1) $$ Твой ответ
Зарегистрируйтесь или войдите в систему
Опубликовать как гость
Опубликовать как гость
Новая альфа-амилаза, расщепляющая необработанный крахмал из недавно выделенного Bacillus sp. YX-1: очистка и характеристика
принадлежность
 1016/j.biortech.2007.08.040
1016/j.biortech.2007.08.040 Авторы
принадлежность
 1016/j.biortech.2007.08.040
1016/j.biortech.2007.08.040 Абстрактный
Похожие статьи
 2014.
PMID: 24385152
2014.
PMID: 24385152 2010.
PMID: 20850111
2010.
PMID: 20850111 Цитируется
 Представитель биотехнологии (Амст). 2021.
PMID: 34557389
Бесплатная статья ЧВК.
Представитель биотехнологии (Амст). 2021.
PMID: 34557389
Бесплатная статья ЧВК. дои: 10.3390/ijms22031070.
Int J Mol Sci. 2021.
PMID: 33499004
Бесплатная статья ЧВК.
дои: 10.3390/ijms22031070.
Int J Mol Sci. 2021.
PMID: 33499004
Бесплатная статья ЧВК. Epub 2019 30 сентября.
J микробиол. 2019.
PMID: 31571125
Epub 2019 30 сентября.
J микробиол. 2019.
PMID: 31571125 Типы публикаций
термины MeSH
вещества
Поворотный бронзовый обратный клапан NIBCO T-413-Y-X 1-1/2 дюйма FIPT NL7402C
 Обратный клапан рекомендуется для коммерческого и промышленного пара, воды, нефти и газа. Этот обратный клапан NIBCO имеет ввинчивающуюся крышку для доступа к ремонту или замене деталей. Поворотные обратные клапаны могут быть установлены в горизонтальном положении (или вертикальном при движении потока вверх). Пожалуйста, обратитесь к техническим паспортам NIBCO, руководствам по химической стойкости и каталогам для получения информации по проектированию и установке. Выбирайте обратные клапаны NIBCO, чтобы выбрать наиболее подходящий, универсальный и экономичный вариант клапана для коммерческого, механического и промышленного применения. На обратные клапаны NIBCO распространяется 5-летняя ограниченная гарантия NIBCO 125%.
Обратный клапан рекомендуется для коммерческого и промышленного пара, воды, нефти и газа. Этот обратный клапан NIBCO имеет ввинчивающуюся крышку для доступа к ремонту или замене деталей. Поворотные обратные клапаны могут быть установлены в горизонтальном положении (или вертикальном при движении потока вверх). Пожалуйста, обратитесь к техническим паспортам NIBCO, руководствам по химической стойкости и каталогам для получения информации по проектированию и установке. Выбирайте обратные клапаны NIBCO, чтобы выбрать наиболее подходящий, универсальный и экономичный вариант клапана для коммерческого, механического и промышленного применения. На обратные клапаны NIBCO распространяется 5-летняя ограниченная гарантия NIBCO 125%.
Производитель НИБКО Номер детали НЛ7402К Модель Т-413-У-Х Тип клапана Чек Серия Т-413-Ю Тип обратного клапана Качели Номинальный размер трубы 1-1/2″ Тип торцевого соединения T — Внутренняя резьба NPT (FIPT) Материал Бронза Материал уплотнения седла ПТФЭ Специальные опции Кислородная служба Повороты Неручной Многооборотная конструкция крышки Ввинчиваемая крышка Номинальное давление (CWP) 200 фунтов на кв.  дюйм/13,8 бар CWP
дюйм/13,8 бар CWP Номинальное давление (SWP) 125 фунтов на кв. дюйм/8,6 бар SWP Код СКП 039923635112 Длина 4,49″ Ширина 4,43 дюйма Высота 2,43 дюйма Страна происхождения США Код питьевой воды Not LL Comp не предназначен для питья CA Предложение 65 Предупреждение Заявление ПРЕДУПРЕЖДЕНИЕ.  Этот продукт может подвергнуть вас воздействию химических веществ, включая свинец, который, как известно в штате Калифорния, вызывает рак и врожденные дефекты или другой вред репродуктивной системе. Для получения дополнительной информации посетите веб-сайт www.P65Warnings.ca.gov.
Этот продукт может подвергнуть вас воздействию химических веществ, включая свинец, который, как известно в штате Калифорния, вызывает рак и врожденные дефекты или другой вред репродуктивной системе. Для получения дополнительной информации посетите веб-сайт www.P65Warnings.ca.gov. com.
com.
Многофункциональный альбом ручной работы YX-1
Оценка DWYM
 Благодаря этому анализу мы определили лучший альбом для вырезок, который вы должны купить.
Благодаря этому анализу мы определили лучший альбом для вырезок, который вы должны купить.
Оформить заказ The Best Scrapbook для подробного обзора всех лучших вырезок. Общая сумма
От производителя
Обзоры экспертов
Суммарная оценка пользователей
Что понравилось экспертам
Что не понравилось экспертам
1.
 BBwill «Наше приключение»: плотный альбом для вырезок из крафт-бумаги
BBwill «Наше приключение»: плотный альбом для вырезок из крафт-бумаги 2. Альбом Vienrose по бескислотному льну
3. Самоклеящийся магнитный двухсторонний фотоальбом Potricher
4. Бескислотный альбом для вырезок на спирали Bstorify
5. Набор для вырезок со спиральными наклейками bemece
6. Обложка Pioneer из искусственной кожи и альбом Jumbo Page
7. MCS 848115 Gloss Expressions Vinyl Scrapbook
8. Деревянный альбом для вырезок «Сделай сам» PartyKindom «Наше приключение»
9. Христианский кожаный альбом ручной работы SEEHAN
10. MCS 848121 Gloss Expressions Page Protection Scrapbook
11. Подарочный альбом YX-1 Easy Open в твердом переплете
12.
 Многофункциональный альбом ручной работы YX-1
Многофункциональный альбом ручной работы YX-1 13. Альбом памяти Vienrose из льняной обложки без ПВХ
14. Записки Pioneer Classic Crafting
15. Очень большой альбом Transworld из искусственной кожи
16. Спиральный альбом Gotideal Tie Closure
 Но эта тенденция превратилась в нечто гораздо более простое. Сегодняшние фотоальбомы часто содержат фотографии на простой, но прочной бумаге, но некоторые даже идут по старинке, покупая фотоальбомы с традиционной защитной пленкой, покрывающей каждую страницу с фотографиями.
Но эта тенденция превратилась в нечто гораздо более простое. Сегодняшние фотоальбомы часто содержат фотографии на простой, но прочной бумаге, но некоторые даже идут по старинке, покупая фотоальбомы с традиционной защитной пленкой, покрывающей каждую страницу с фотографиями. Они относительно недороги, если вы печатаете достаточное количество изображений, чтобы быстро окупить затраты. Но для тех, кто лишь изредка печатает фотографии, оплата услуг онлайн-сервиса или местного магазина, вероятно, будет наиболее экономически выгодным вариантом.
Они относительно недороги, если вы печатаете достаточное количество изображений, чтобы быстро окупить затраты. Но для тех, кто лишь изредка печатает фотографии, оплата услуг онлайн-сервиса или местного магазина, вероятно, будет наиболее экономически выгодным вариантом. Храните свои альбомы в прохладном, сухом месте, и они должны быть защищены в течение десятилетий.
Храните свои альбомы в прохладном, сухом месте, и они должны быть защищены в течение десятилетий.

 11.16
11.16 11.16
11.16

 Блок управления поставляется отдельно.
Блок управления поставляется отдельно.
 ст.
ст.
 aero и в мобильном приложении:
aero и в мобильном приложении: подъем на 15 градусов
подъем на 15 градусов