Вектор Без Направления 6 Букв
Решение этого кроссворда состоит из 6 букв длиной и начинается с буквы С
Ниже вы найдете правильный ответ на Вектор без направления 6 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Четверг, 24 Октября 2019 Г.
СКАЛЯР
предыдущий следующий
другие решения
СКАЛЯР
ты знаешь ответ ?
ответ:
связанные кроссворды
- Скаляр
- Величина, значение которой характеризуется одним действительным числом
- Скаляр
- Величина, значение которой характеризуется одним действительным числом 6 букв
- Величина, каждое значение которой может быть выражено одним числом 6 букв
- Величина, характеризующаяся только числовым значением (мат.
 ) 6 букв
) 6 букв - Физическая величина 6 букв
похожие кроссворды
- Вектор 8 букв
- Матричный вектор 6 букв
- Геометрическое место концов вектор-функции 8 букв
- Математический вектор 8 букв
- Геометрическое место концов вектор-функции
- Четырехмерный вектор
- Единичный вектор 3 буквы
- Единичн.
 вектор или рос. т/канал 3 буквы
вектор или рос. т/канал 3 буквы - И вектор, и горная выработка 3 буквы
- Вектор, поделённый на длину 3 буквы
- Вектор с нормой равной единице 3 буквы
- Вектор единичной длины 3 буквы
- Вектор, указывающий направление наибольшего роста
- Математический вектор
- Осевой вектор
Системы линейных уравнений — презентация онлайн
1.
 ЛИНЕЙНАЯ АЛГЕБРАЛекция 6
ЛИНЕЙНАЯ АЛГЕБРАЛекция 6СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
(продолжение)
Экономическое приложение систем
уравнений
§ 1. ЭКОНОМИЧЕСКИЕ УРАВНЕНИЯ
Пример 1. Предположим, что некоторое предприятие выпускает
три вида продукции, при этом, используя сырье трех видов.
Необходимые характеристики производства указаны в таблице 1.
Требуется определить объем выпуска продукции каждого вида при
заданных запасах сырья.
Задачи такого рода типичны при прогнозах и оценках
функционирования предприятий, экспертных оценках проектов
освоения месторождения полезных ископаемых, а также в
планировании микроэкономики предприятий.
Решение. Обозначим неизвестные объемы выпуска продукции
через x1, x2 и x3. Тогда, при условии полного расхода запасов
каждого вида сырья можно записать балансовое соотношение,
которое образует систему трех уравнений с тремя
неизвестными
Решая эту систему уравнений любым способом, находим,
что при заданных запасах сырья объемы выпуска продукции
составляют по каждому виду соответствие (в условных
единицах):
• x1=150, x2 = 250, x3 =100.

Лекция 7
ЭЛЕМЕНТЫ ВЕКТОРНОЙ ЛГЕБРЫ
• § 1. ПОНЯТИЕ ВЕКТОРА
Различают величины скалярные и векторные.
Величина, которая полностью характеризуется одним
числовым значением, выражающим отношение этой
величины к соответствующей единице измерения,
называется скалярной величиной или скаляром.
Таковы, например, масса тела, температура среды и т.п.
Величина, которая кроме числового значения
характеризуется еще и направлением, называется векторной
величиной или вектором.
К числу их относятся сила, перемещение, скорость.
Вектор определяется числом и направлением.
Векторы будем обозначать a или a.
Геометрически вектор изображается
направленным отрезком пространства;
при этом используется обозначение a AB
• Под модулем (длиной) вектора a a
• понимается его численное значение, без учета направления.
• Вектор, модуль которого равен нулю, называется нулевым
или нуль-вектором. Направление нулевого вектора
произвольно.
• Два вектора a и b считаются равными, если они
расположены на параллельных или совпадающих прямых,
имеют одинаковую длину и одинаково направлены.
• Мы условимся не различать равные векторы и, таким образом,
приходим к понятию свободного вектора. Иными словами,
свободный вектор допускает перенос его в любую точку
пространства, при условии сохранения длины и направления.
В частности, для свободных векторов всегда можно
обеспечить их общую начальную точку.
• § 2. ДЕЙСТВИЯ НАД ВЕКТОРАМИ
• Сумма векторов
Суммой нескольких векторов, например,a, b, c, d называется вектор
s a b c d
по величине и направлению равный замыкающей
пространственной ломаной линии, построенной на данных
векторах.
s a b c d
• Для случая двух векторов s a b их суммой является
диагональ параллелограмма, построенного на этих векторах,
исходящая из общей точки их приложения (правило
параллелограмма).
Так как в любом треугольнике длина одной
стороны не превышает суммы длин двух
других сторон, то из рис.
 следует
следует• Для случая трех векторов s a b c их суммой является
диагональ ОМ параллелепипеда, построенного на этих
векторах (правило параллелепипеда).
Легко проверить, что для
векторного сложения справедливы
следующие свойства:
• 1) переместительное свойство:
• 2) сочетательное свойство:
• Для каждого вектора a OA существует противоположный
вектор, a AO имеющий ту же длину, но противоположное
направление
По правилу параллелограмма имеем a ( a ) 0, где 0 — нульвектор. Легко проверить, что a ( a ) 0
Разность векторов
Под разностью векторов a и b будем понимать вектор
d = a — b , такой что b + d = a .
Отметим, что в параллелограмме, построенном на данных
векторах a и b , их разностью является соответственно
направленная вторая диагональ параллелограмма.
Легко проверить, что справедливо следующее правило
вычитания:
Умножение вектора на скаляр.
• Определение. Произведением вектора a на скаляр k
• называется вектор, имеющий длину b = k a , направление,
которого:
• 1) совпадает с направлением вектора a , если k > 0;
• 2) противоположно ему, если k < 0;
• 3) произвольно, если k = 0.

• Нетрудно убедиться, что данная векторная операция
обладает следующими свойствами:
Если ненулевой вектор a разделить на его длину a = a , то
мы получим единичный вектор e , так называемый орт, того же
направления: e = a / a
Отсюда имеем стандартную формулу вектора: a = ae.
§ 3. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ВЕКТОРОВ
Определение. Два вектора a и b называются коллинеарными,
если они расположены или на параллельных прямых, или же
на одной и той же прямой.
Так как направление нулевого вектора произвольно, то можно
считать, что нулевой вектор коллинеарен любому вектору.
Справедлива Теорема 1. Два ненулевых вектора a и b
коллинеарны тогда и только тогда, когда они пропорциональны,
т. е. b = ka, где k — скаляр.
1) Пусть векторы a и b ( а ≠ 0, b ≠ 0 ) коллинеарны и e,e′—
их орты. Имеем a = ae и b = be′, где e′ = ±e .
Знак плюс соответствует векторам a и b одинакового
направления, а знак минус — векторам a и b противоположного
направления.

Тогда получаем, что b = ±be = ±b/a (ae)= ± (b/a) a
Отсюда вытекает формула b = ka где k = ±b / a .
2) Если выполнено равенство, то коллинеарность векторов a
и b непосредственно следует из смысла умножения вектора на
скаляр.
Определение. Три вектора a, b и c называются
компланарными, если они параллельны некоторой плоскости
или лежат в ней.
Тогда можно сказать также, что векторы a, b и c компланарны
тогда и только тогда, когда после приведения их к общему
началу они лежат в одной плоскости.
По смыслу определения тройка векторов, среди
которых имеется хотя бы один нулевой вектор,
компланарна.
• Теорема 2. Три ненулевых вектора a, b и c
компланарны тогда и только тогда, когда один из
векторов является линейной комбинацией других, т. е.,
например c = ka + lb .
• Доказательство. 1)Пусть векторы a, b и c
компланарны, расположены в плоскости Р и имеют общую
точку приложения О. Предположим сначала, что эти векторы
не все попарно коллинеарны, например,
векторы a и b неколлинеарны.
 Тогда,
Тогда,производя разложение вектора c в
сумму векторов ca и cb коллинеарных,
соответственно, векторам a и b, будем
иметь, c= ca + cb = ka+lb где k и l —
соответствующие скаляры.
• Если же векторы a, b, c попарно коллинеарны, то можно
написать
• c = k a = k a + 0b , и таким образом, снова вы полнено
условие теоремы
• 2) Обратно, если для векторов a = OA, b = OB и c = OC
выполнено условие теоремы, то, на основании смысла
соответствующих векторных операций, вектор c
расположен в плоскости, содержащей векторы a и b, т. е.
эти векторы компланарны.
Глава 4. Едем по указателям – FIZI4KA
Физика с формулами ›
В этой главе…
- Изучаем сложение и вычитание векторов
- Выражаем векторы через координаты
- Разбиваем векторы на компоненты
- Выражаем перемещение, ускорение и скорость в виде векторов
- Определяем изменение скорости под действием тяготения
Довольно трудно добраться в место назначения — пешком ли, на велосипеде ли, на автомобиле ли, на самолете ли — если вы не знаете направления движения. 2+v_0t \). С помощью таких соотношений можно получить значения для ускорения, например 27 метров в секунду в квадрате, или для скорости, например 42,7 мили в час. Конечно, полезно знать эти параметры движения, но что можно сказать о направлении движения?
2+v_0t \). С помощью таких соотношений можно получить значения для ускорения, например 27 метров в секунду в квадрате, или для скорости, например 42,7 мили в час. Конечно, полезно знать эти параметры движения, но что можно сказать о направлении движения?
В реальном мире просто необходимо знать направление движения. Именно векторы обозначают такое направление. Очень многие люди ошибочно считают векторы очень сложными объектами, но это совсем не так. В этой главе вы узнаете, насколько легко и просто можно обращаться с ними при решении задач.
Содержание
- Осваиваем векторы
- Определяем направление: основные свойства векторов
- Комбинируем направления: сложение векторов
- Вычисляем разницу расстояний: разность векторов
- Облекаем векторы в числа
- Разбиение вектора на компоненты
- Ищем компоненты вектора по заданной величине и углу
- Находим величину и направление вектора по его компонентам
- Срываем покров с векторов
- Перемещение — тоже вектор
- Скорость — еще один вектор
- Ускорение — еще один вектор
- Упражнение со скоростью: скользим по радуге
Осваиваем векторы
В главе 3 мы работали с простыми числами или измерениями, которые в физике называются величинами. Например, в результате измерения перемещения на 3 метра получена величина перемещения 3 метра. Вектор отличается от величины еще и наличием направления. В повседневной жизни на вопрос о пути понятие “вектор” возникает в виде следующего ответа встречного человека: “Это в 15 милях отсюда”. При этом величина вектора равна 15 милям, а направление вектора определяется взмахом руки. Когда вы навешиваете дверь на петли, то порой слышите совет: “Толкните сильнее влево”. Вот вам еще один вектор! Когда вы объезжаете препятствие на дороге, вам приходится ускоряться и замедляться в разных направлениях. Вот еще несколько векторов!
Например, в результате измерения перемещения на 3 метра получена величина перемещения 3 метра. Вектор отличается от величины еще и наличием направления. В повседневной жизни на вопрос о пути понятие “вектор” возникает в виде следующего ответа встречного человека: “Это в 15 милях отсюда”. При этом величина вектора равна 15 милям, а направление вектора определяется взмахом руки. Когда вы навешиваете дверь на петли, то порой слышите совет: “Толкните сильнее влево”. Вот вам еще один вектор! Когда вы объезжаете препятствие на дороге, вам приходится ускоряться и замедляться в разных направлениях. Вот еще несколько векторов!
Векторы встречаются в обыденных ситуациях, например в дорожных указателях, инструкциях по сборке или даже при попытке избежать столкновения со встречным. Поскольку физика стоит за всеми событиями повседневной жизни, то не удивительно, что многие физические концепции, например скорость, ускорение, сила, являются векторами. По этой причине следует поближе познакомиться с векторами, поскольку они присутствуют во всех разделах физики.
Вектор — это фундаментальное понятие физики.
Определяем направление: основные свойства векторов
При работе с векторами нужно иметь в виду его направление и величину. Физический параметр без направления, а только с величиной называется скаляром. Если к скаляру добавить направление, то получим вектор.
Визуально в физических задачах вектор отображается в виде стрелки. Действительно, стрелка имеет величину (т.е. длину) и направление (т.е. острие). Взгляните на рис. 4.1. Эта стрелка и есть вектор с началом в тупом конце и с окончанием — в заостренном конце.
Векторы можно использовать для представления силы, ускорения, скорости и других физических параметров. В физике для обозначения векторов используют полужирное начертание, например A. В некоторых книгах векторы обозначают стрелкой над символом, например \( \overrightarrow{A} \) . Стрелка обозначает, что у данного параметра A, помимо величины, есть также направление.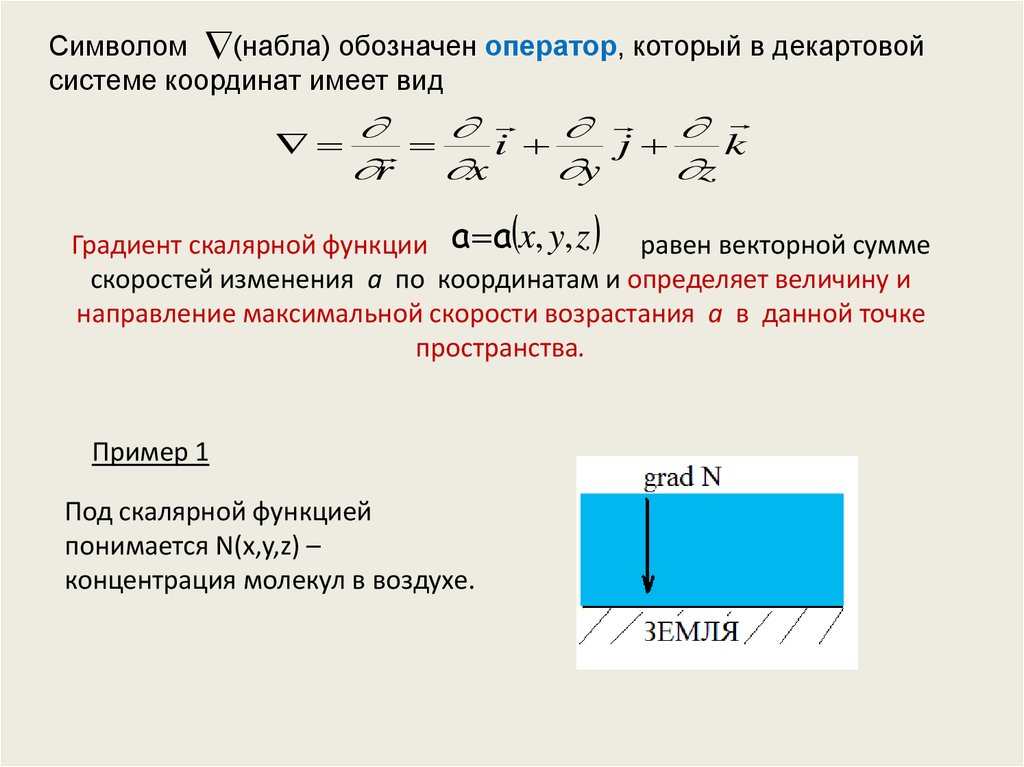
Допустим, какой-то умник предложит вам дать пример вектора. Проще простого! Достаточно сказать, что у некого вектора А есть некая величина и некоторое направление. Убежден, что это произведет на умника оглушительное впечатление! Например, скажите, что вектор А направлен под углом 15° к горизонтали и имеет величину 12 метров в секунду. Итак, любопытный умник получит исчерпывающую информацию о векторе А.
На рис. 4.2 показаны два вектора, А и В. Они очень похожи, поскольку обладают одинаковой длиной и направлением. Фактически оба эти вектора равны. Если два вектора равны по величине и направлению, то они считаются равными, т.е. А = В.
Очень скоро читатель станет настоящим экспертом в области векторов. Уже сейчас нам известно, что, когда мы встречаемся с символом А, это значит, что данный параметр обладает величиной и направлением, т.е. является вектором, а два вектора считаются равными, если они имеют одинаковую величину и направление. Но это еще далеко не все. Допустим, чтобы найти нужный вам отель, нужно проехать 20 миль к северу, а потом 20 миль на восток. Так насколько далеко и в каком направлении находится этот отель?
Но это еще далеко не все. Допустим, чтобы найти нужный вам отель, нужно проехать 20 миль к северу, а потом 20 миль на восток. Так насколько далеко и в каком направлении находится этот отель?
Комбинируем направления: сложение векторов
Два вектора можно сложить и получить результирующий вектор, который является суммой обоих векторов и определяет расстояние и направление до цели.
Допустим, что прохожий говорит вам, что для достижения пункта назначения вам нужно сначала следовать вектору А, а потом вектору В. Так где же находится в этом случае ваш пункт назначения? Сначала нужно проехать по пути, указанному вектором А, а потом по пути, указанному вектором В, как показано на рис. 4.3.
Когда вы доберетесь до конца вектора В, насколько далеко вы будете находиться от исходной точки? Для ответа на этот вопрос начертим еще один вектор С от исходной точки и до конечной точки путешествия, как показано на рис. 4.4.
4.4.
Новый вектор С представляет собой результат всего путешествия от начала и до самого конца. Все, что нужно сделать, чтобы получить его, так это начертить оба вектора А и В и соединить новым результирующим вектором С.
Сумма векторов достигается за счет того, что начало одного вектора помещается в конец другого, т.е. суммарный вектор проходит от начала одного до конца другого вектора. Иначе говоря, С = А + В. При этом С называется суммой векторов, результатом сложения векторов, или результирующим вектором. Не думайте, что этим ограничиваются возможности комбинирования векторов, ведь векторы можно и вычитать.
Вычисляем разницу расстояний: разность векторов
А что если некто предложит вам векторы С и А, показанные на рис. 4.4, и попросит найти их разность? Их разностью является вектор В, поскольку при сложении векторов А и В получается вектор С. Чтобы объяснить эту мысль, нужно прояснить смысл вычитания вектора А из вектора С: т.е. смысл операции С — А.
Чтобы объяснить эту мысль, нужно прояснить смысл вычитания вектора А из вектора С: т.е. смысл операции С — А.
Для вычитания двух векторов нужно расположить вместе основания векторов (т.е. концы векторов без остриев), а не совмещать основание одного вектора и острие другого вектора, как при сложении векторов. Затем нужно провести результирующий вектор, который является разностью двух векторов, от острия вычитающего вектора (А) к острию вычитаемого вектора (С). На рис. 4.5 показан пример вычитания вектора А из вектора С (иначе говоря, приведен пример С — А). Как видите, результат такого вычитания равен вектору В, поскольку С = А + В.
Еще один (и для некоторых более простой) способ вычитания векторов заключается в обращении направления второго вектора (т.е. вектора А в разности С — А) и сложении двух векторов: вектора С и обращенного вектора А (т.
е. совмещении острия обращенного вектора А с основанием вектора С с последующим проведением результирующего вектора от основания обращенного вектора А к острию вектора С).
Как видите, сложение и вычитание векторов может происходить с одними и теми же векторами в одной задаче. На самом деле с векторами можно выполнять и некоторые другие математические операции. Изложенный выше материал означает, что с векторами можно оперировать так же, как со скалярами, например С = А + В, С — А = В и т.д. Как видите, векторы очень похожи на числа.
Облекаем векторы в числа
Векторы удобно представлять в виде стрелок, но это не всегда самый точный способ работы с ними. Векторы гораздо точнее можно характеризовать числами. Рассмотрим пример сложения векторов А + В, показанных на рис. 4.6.
Предположим, что измерения на рис. 4.6 даны в метрах. Это значит, что вектор А направлен на 1 метр вверх и на 5 метров вправо, а вектор В направлен на 1 метр вправо и на 4 метра вверх. Для получения параметров результирующего вектора С нужно сложить горизонтальные измерения обоих векторов и отдельно сложить вертикальные измерения обоих векторов.
Для получения параметров результирующего вектора С нужно сложить горизонтальные измерения обоих векторов и отдельно сложить вертикальные измерения обоих векторов.
Результирующий вектор С направлен на 6 метров вправо и на 5 метров вверх. Как видите, для получения вертикального измерения вектора С нужно сложить вертикальное измерение вектора А и вертикальное измерение вектора В. А для получения горизонтального измерения вектора С нужно сложить горизонтальное измерение вектора А и горизонтальное измерение вектора В.
Если процедура сложения векторов все еще очень туманна для вас, то тогда можно использовать другую систему обозначений векторов. Поскольку вектор А “простирается” на 5 метров вправо (в положительном направлении оси X) и на 1 метр вверх (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например А = (5;1).
Аналогично, поскольку вектор В “простирается” на 1 метр вверх (в положительном направлении оси X) и на 4 метра вправо (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например В = (1;4).
С помощью такой системы обозначений сложение векторов существенно упрощается. Итак, для сложения двух векторов достаточно сложить их координаты по осям X и Y, чтобы получить координаты результирующего вектора по осям X и Y:
Получается, что весь секрет сложения векторов заключается в разбиении каждого вектора на координаты по осям X и Y с последующим их сложением, чтобы соответственно получить координаты X и Y результирующего вектора? Конечно, работа с этими числами для получения координат X и Y результирующего вектора требует некоторых усилий, но они достаточно просты, чтобы с успехом их выполнить.
Допустим, что нужный вам отель находится на расстоянии 20 миль к северу и на расстоянии 20 миль на восток. Как будет выглядеть вектор, направленный из исходной точки к этому отелю? С помощью координатного представления эта задача решается очень легко. Допустим, что положительное направление оси X направлено на восток, а положительное направление оси Y — на север. На первом этапе нужно проехать 20 миль на север, а на втором этапе — 20 миль на восток. В векторном представлении эта задача формулируется следующим образом (восток [X]; север [Y]):
Как будет выглядеть вектор, направленный из исходной точки к этому отелю? С помощью координатного представления эта задача решается очень легко. Допустим, что положительное направление оси X направлено на восток, а положительное направление оси Y — на север. На первом этапе нужно проехать 20 миль на север, а на втором этапе — 20 миль на восток. В векторном представлении эта задача формулируется следующим образом (восток [X]; север [Y]):
Чтобы сложить эти два вектора, нужно сложить их координаты по соответствующим осям:
Результирующий вектор, который указывает на отель, имеет вид (20; 20).
Рассмотрим еще один пример удачного применения такого представления векторов. Допустим, что вы едете на гоночном автомобиле со скоростью 150 миль в час на восток и видите в зеркало заднего вида приближающегося соперника. Нет проблем, нужно лишь удвоить скорость:
Теперь вы уже не едете, а почти “летите” со скоростью 300 миль в час, но в том же направлении. Итак, в этой задаче демонстрируется процедура умножения вектора на скаляр.
Итак, в этой задаче демонстрируется процедура умножения вектора на скаляр.
Разбиение вектора на компоненты
Формулировки задач по физике с использованием векторов не всегда так просты, как предыдущие примеры с манипуляциями векторов. Рассмотрим первый вектор на рис. 4.1 с координатами (4; 1) и сравним его со следующей типичной формулировкой физической задачи: найти время перемещения шара со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. С помощью дальнейшей информации в этом разделе вы научитесь находить компоненты векторов и легко и просто манипулировать ими.
Ищем компоненты вектора по заданной величине и углу
Чтобы определить координаты вектора, нужно научиться разбивать векторы на части, которые называются компонентами. Например для вектора (4; 1) Х-компонентой является число 4, а Y-компонентой — число 1.
Часто в физической задаче задается угол и величина вектора, а его компоненты нужно определить. В предыдущем примере известно, что шар катится со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. Для определения времени перемещения шара от одного конца плоскости к другому нам потребуется разобраться только с Х-компонентой. То есть, задача сводится к определению времени перемещения на расстояние 1 метр вдоль оси X. Для ответа на этот вопрос нужно определить скорость перемещения шара по оси X.
В предыдущем примере известно, что шар катится со скоростью 7 метров в секунду по наклонной плоскости с длиной основания 1 м, расположенной под углом 15°. Для определения времени перемещения шара от одного конца плоскости к другому нам потребуется разобраться только с Х-компонентой. То есть, задача сводится к определению времени перемещения на расстояние 1 метр вдоль оси X. Для ответа на этот вопрос нужно определить скорость перемещения шара по оси X.
Итак, нам известно, что шар движется со скоростью 7 метров в секунду под углом 15° к горизонтали (т.е. положительного направления оси X). В данной формулировке скорость является вектором \( \mathbf{v} \) с величиной 7 метров в секунду и направлением 15° к горизонтали.
Теперь нам нужно определить Х-компоненту вектора скорости шара, чтобы определить скорость перемещения шара вдоль основания наклонной плоскости. Х-компонента скорости является скаляром (т.е. имеет только значение, а не значение, направление и точку приложения, как вектор) и обозначается как \( v_x \). Аналогично, Y-компонента скорости шара также является скаляром и обозначается как \( v_y \). Итак, вектор скорости можно выразить через его компоненты:
Аналогично, Y-компонента скорости шара также является скаляром и обозначается как \( v_y \). Итак, вектор скорости можно выразить через его компоненты:
Именно так выражается разложение вектора на компоненты. Так чему же равны компонента \( v_x \) и компонента \( v_y \)? Скорость имеет величину \( v \) (7 метров в секунду) и направление \( \theta \) (угол 15° к горизонтали). Также нам известна длина основания наклонной плоскости (1,0 метр). На рис. 4.7 показана схема тригонометрических функций (о, Боже, только не это!), которые описывают направление вектора скорости и помогут нам определить его компоненты. Не стоит волноваться: тригонометрические соотношения не так уж и сложны, если известен угол \( \theta \), показанный на рис. 4.7. Величина (или модуль) вектора \( \mathbf{v} \) равна \( v \) (иногда если вектор обозначается символом \( v \), то его модуль обозначают символом \( \overline{v} \)), а его компоненты определяются с помощью рис. 4.7:
Рекомендуется хорошенько запомнить указанные выше выражения для компонент вектора, поскольку нам придется довольно часто встречаться с ними в курсе физики.
Теперь можно пойти немного дальше и попробовать связать отдельные стороны треугольника на рис. 4.7. Это можно легко сделать, если вспомнить соотношение для тангенса \( tg\,\theta=\sin\theta/\cos\theta \) и воспользоваться соотношениями для компонент скорости:
Зная соотношение \( v_x=v\cos\theta \), можно найти величину Х-компоненты скорости шара \( v_x=v\cos\theta \):
Подставляя числа, получим
Итак, теперь мы знаем, что горизонтальная скорость шара равна 6,7 метров в секунду. Поскольку длина основания наклонной плоскости равна 1,0 метра, то это расстояние шар преодолеет за время:
Таким образом, благодаря тому, что мы научились определять компоненту скорости, нам удалось легко найти решение все задачи: шару потребуется 0,15 секунды для перемещения вдоль наклонной плоскости. А чему равна Y-компонента скорости? Это можно очень легко определить, поступая аналогично:
Находим величину и направление вектора по его компонентам
Иногда требуется определить угол наклона вектора, если известны его компоненты.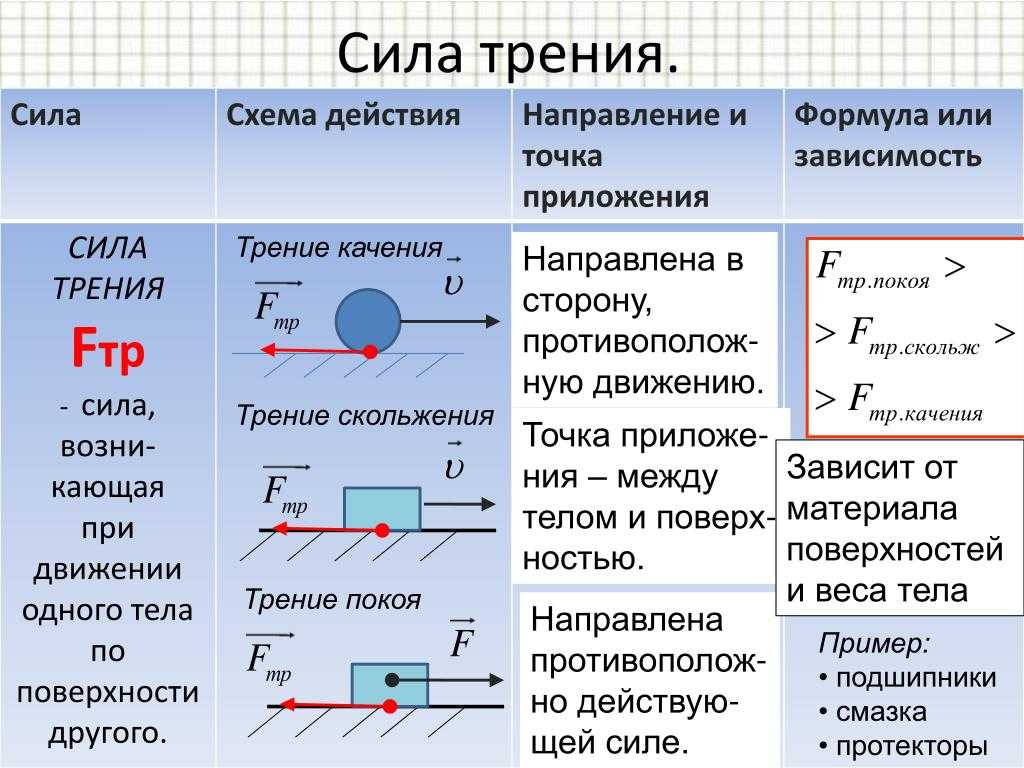 Например, предположим, что вы ищите отель, расположенный на 20 миль к северу и на 20 миль к востоку. Под каким углом нужно двигаться к нему и насколько далеко он находится? Условия этой задачи можно записать с помощью уже известных нам векторных обозначений (см. предыдущий раздел):
Например, предположим, что вы ищите отель, расположенный на 20 миль к северу и на 20 миль к востоку. Под каким углом нужно двигаться к нему и насколько далеко он находится? Условия этой задачи можно записать с помощью уже известных нам векторных обозначений (см. предыдущий раздел):
После сложения этих двух векторов получим следующий результат:
Результирующий вектор, который указывает на отель, имеет вид (20; 20). Это еще один способ указания вектора с помощью его компонент. Итак, вернемся к прежнему вопросу: под каким углом нужно двигаться к отелю и насколько далеко он находится от текущего положения? Иначе говоря, глядя на рис. 4.8, прежний вопрос теперь звучит так: “Чему равны \( h \) и \( \theta \)?”
Найти \( h \) не так уж и трудно, пользуясь теоремой Пифагора:
Подставляя численные значения, получим:
Итак, отель находится на расстоянии 28,3 мили. А под каким углом \( \theta \) нужно ехать к нему по прямой? Пользуясь основными тригонометрическими соотношениями, можно записать:
Иначе говоря:
Теперь для определения угла нужно использовать функции, обратные синусу и косинусу:
(Строго говоря, обратной синусу функцией является функция “арксинус”, или \( arcsin(x) \), а обратной косинусу — “арккосинус”, или \( arccos(x) \). {-1}(x) \) часто используется для обозначения функции “арктангенс”, но его не рекомендуется употреблять, чтобы не путать с функцией \( 1/tg(x) \). — Примеч. ред.)
{-1}(x) \) часто используется для обозначения функции “арктангенс”, но его не рекомендуется употреблять, чтобы не путать с функцией \( 1/tg(x) \). — Примеч. ред.)
Срываем покров с векторов
У нас есть два способа описания векторов для решения физических задач. Первый основан на использовании компонент по осям X и Y, а второй — на величине (модуле) и направлении вектора (угол обычно задается в градусах от 0° до 360°, где угол 0° соответствует направлению вдоль положительного направления оси X). Знание правил взаимного преобразования этих двух способов описания имеет очень большое значение, поскольку для операций с векторами удобно использовать компоненты вектора, а в формулировке физических задач обычно задаются величины и углы векторов.
Вот как выглядит формула преобразования двух способов описания векторов:
В этом уравнении предполагается, что \( \theta \) — это угол между горизонтальной компонентой и гипотенузой \( h \) (т.
е. самой длинной стороной прямоугольного треугольника, расположенного напротив прямого угла), как показано на рис. 4.8. Если угол не известен, то его можно вывести, если запомнить, что сумма всех углов треугольника равна 180°, а в прямоугольном треугольнике, если вычесть величину прямого угла 90°, то сумма остальных двух углов равна 90°.
Если вам известны компоненты (х,у), то его величину и направление можно определить по следующим формулам:
Такого рода преобразования нужно уметь легко выполнять, поскольку они довольно часто встречаются в задачах. На этом месте часто многие приходят в растерянность и не могут освоить дальнейший материал именно потому, что не овладели простыми правилами разложения вектора на компоненты.
Перемещение — тоже вектор
Перемещение \( s \) следует обозначать \( \mathbf{s} \), как вектор с определенной величиной и направлением (для обозначения векторов иногда используют стрелку, которая располагается над именем переменной, например \( \overrightarrow{s} \) ). В реальном мире очень важно знать не только величину, но и направление перемещения.
В реальном мире очень важно знать не только величину, но и направление перемещения.
Допустим, что сбылись ваши детские мечты и вы стали звездой бейсбола. Вот вам нужно стремглав бежать к первой базе на расстоянии 90 футов по прямой. Но в каком направлении находится первая база? Допустим, что она находится под углом 45°, как показано на рис. 4.9. Тогда вектор вашего перемещения \( \mathbf{s} \) имеет величину 90 футов и направление 45°. А какими будут компоненты этого вектора? Это очень просто:
Скорость — еще один вектор
Представьте себе, что вы бежите к первой базе с вектором перемещения s с величиной 90 футов и направлением 45° по отношению к оси X. Тут стоило бы задаться вопросом: “Позволит мне моя скорость опередить игрока на первой базе?” Хороший вопрос. Достанем калькулятор и подсчитаем скорость, если известно, что для достижения первой базы вам требуется 3 секунды. Для определения скорости нужно поделить величину вектора \( \mathbf{s} \) на это время:
В этом выражении вектор перемещения делится на скаляр времени. Результатом такого деления является тоже вектор, а именно вектор скорости:
Результатом такого деления является тоже вектор, а именно вектор скорости:
Итак, ваша скорость равна 30 футам в секунду под углом 45° и эта скорость является вектором \( \mathbf{v} \). Деление вектора на скаляр дает вектор другой величины, но такого же направления. В данном примере деление вектора перемещения \( \mathbf{s} \) на скаляр времени дает в результате вектор \( \mathbf{v} \). Он имеет такую же величину, что и величина перемещения, деленная на величину времени, но теперь вектор \( \mathbf{v} \) также имеет определенное направление, которое определяется направлением вектора перемещения \( \mathbf{s} \). Итак, в данном примере мы научились манипулировать с векторами, как со скалярами в главе 3, и получать вектор в результате этих манипуляций.
Допустим, что после этих вычислений вы пришли к выводу, что такой скорости недостаточно, чтобы опередить соперника. Ну что ж, нужно срочно изменить направление!
Ускорение — еще один вектор
Что произойдет, если в процессе движения внезапно изменить направление? Вы сразу же почувствуете изменение скорости, а значит, ощутите ускорение. Как и скорость, ускорение \( \mathbf{a} \) является вектором.
Как и скорость, ускорение \( \mathbf{a} \) является вектором.
Предположим, что в предыдущем примере нужно изменить скорость Y-компоненты скорости до величины 25 футов в секунду, чтобы избежать встречи с соперником, причем вам известно, что вы способны отклониться от курса на 90° с ускорением 60 футов в секунду в квадрате (в отчаянной попытке увильнуть от соперника). Достаточно ли этого ускорения для изменения скорости за ту долю секунды, которая отделяет вас от встречи с соперником?
Разница конечного \( t_1 \) и начального \( t_0 \) момента времени равняется изменению времени \( \Delta t \). Теперь изменение скорости легко найти по следующей формуле:
Теперь попробуем вычислить изменение скорости от исходной скорости на основе данных на рис. 4.10.
Для поиска конечного значения скорости \( \mathbf{v_1} \) нужно выполнить операцию сложения векторов. Это значит, что нужно разложить на компоненты вектор исходной скорости \( \mathbf{v_0} \) и вектор изменения скорости \( \Delta v \). Вот как выглядят компоненты исходной скорости \( \mathbf{v_0} \):
Вот как выглядят компоненты исходной скорости \( \mathbf{v_0} \):
Полпути пройдено. Итак, чему равно изменение скорости \( \Delta\!\mathbf{v} \)? Известно, что \( \Delta\!\mathbf{v}=\mathbf{a}\Delta\mathbf{t} \), а \( \mathbf{a} \) = 60 футов в секунду2 под углом 90° к прежнему направлению движения, как показано на рис. 4.10. Итак, подсчитаем величину изменения скорости \( \Delta\!\mathbf{v} \) по формуле \( \Delta\!\mathbf{v}=\mathbf{a}\Delta\mathbf{t} \):
Но что можно сказать о направлении \( \Delta\!\mathbf{v} \)? Если взглянуть на рис. 4.10, то можно увидеть, что изменение скорости \( \Delta\!\mathbf{v} \) направлено под углом 90° к текущему направлению движения, которое ориентировано под углом 45° к положительному направлению оси X. Следовательно, изменение скорости \( \Delta\!\mathbf{v} \) направлено под углом 135° к положительному направлению оси X. Теперь можно получить выражение для компонент вектора изменения скорости \( \Delta\!\mathbf{v} \):
Теперь остается только выполнить сложение векторов для поиска конечной скорости:
Итак, получен результат \( \mathbf{v_1} \) = (17,0 фута в секунду; 25,4 фута в секунду).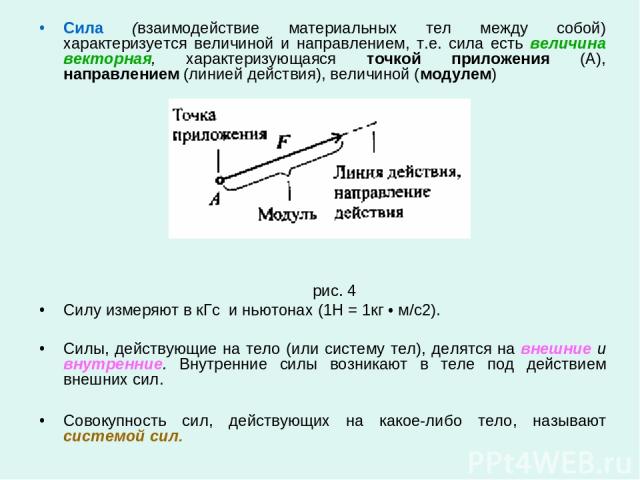 Y-компонента конечной скорости больше необходимой величины, которая равна 25,0 фута в секунду. После завершения этих вычислений можно спрятать калькулятор и смело выполнить запланированный вираж. Представьте себе, что к изумлению окружающих вам удалось уклониться от соперника и успешно достигнуть места назначения — первой базы (какой крутой поворот вам пришлось для этого выполнить!). Болельщики изумлены и приветствуют вас, а вы, небрежно касаясь кепки кончиками пальцев, отдаете им честь, зная, что все это стало возможным благодаря превосходному знанию физики. После затишья вы украдкой бросаете взгляд на вторую базу: а не закрепить ли успех и попробовать добежать до второй базы? Для этого снова придется достать калькулятор и определить компоненты векторов.
Y-компонента конечной скорости больше необходимой величины, которая равна 25,0 фута в секунду. После завершения этих вычислений можно спрятать калькулятор и смело выполнить запланированный вираж. Представьте себе, что к изумлению окружающих вам удалось уклониться от соперника и успешно достигнуть места назначения — первой базы (какой крутой поворот вам пришлось для этого выполнить!). Болельщики изумлены и приветствуют вас, а вы, небрежно касаясь кепки кончиками пальцев, отдаете им честь, зная, что все это стало возможным благодаря превосходному знанию физики. После затишья вы украдкой бросаете взгляд на вторую базу: а не закрепить ли успех и попробовать добежать до второй базы? Для этого снова придется достать калькулятор и определить компоненты векторов.
Именно так нужно работать с векторами разных физических параметров: перемещения, скорости и ускорения. Теперь, обладая такими знаниями, можно перевести скалярные уравнения из главы 3 в векторную форму, например, вот так:
Обратите внимание, что полный вектор перемещения — это комбинация перемещения с начальной скоростью и перемещения с постоянным ускорением.
Упражнение со скоростью: скользим по радуге
Хотя сила гравитации подробно описывается в главе 6, но здесь мы рассмотрим результат действия этой силы на небольшом примере с векторами в двух измерениях. Представьте себе, что мячик для игры в гольф движется по горизонтальной вершине скалы со скоростью 1,0 м/с и вскоре сорвется с края скалы на высоте 5 метров от поверхности Земли, как показано на рис. 4.11. Насколько далеко улетит мячик и с какой скоростью он столкнется с поверхностью Земли? В этой задаче прежде всего нужно определить время движения мячика.
Приступим к сбору фактов. Нам известно, что компоненты скорости мячика равны (1; 0), и он находится на высоте 5 метров от поверхности Земли. В процессе падения под действием силы тяготения Земли он движется с постоянным ускорением, \( g \), величина которого равна около 9,8 м/с2.
Итак, как определить, насколько далеко он упадет от края скалы? Один из способов решения этой задачи основан на определении времени движения мячика до столкновения с поверхностью Земли. Поскольку мячик ускоряется только в направлении оси Y (т.е. вертикально вниз), а его компонента скорости по оси X, \( v_x \), не меняется, то пройденное по горизонтали расстояние до столкновения будет равно \( v_xt \), где \( t \) — время движения мячика до столкновения. Сила тяготения ускоряет мячик по вертикали, а значит, перемещение по вертикали (т.е. вдоль оси Y) равно:
Поскольку мячик ускоряется только в направлении оси Y (т.е. вертикально вниз), а его компонента скорости по оси X, \( v_x \), не меняется, то пройденное по горизонтали расстояние до столкновения будет равно \( v_xt \), где \( t \) — время движения мячика до столкновения. Сила тяготения ускоряет мячик по вертикали, а значит, перемещение по вертикали (т.е. вдоль оси Y) равно:
В данном случае перемещение по вертикали \( s_y \) = 5 метров, а ускорение \( a_y \) = \( g \) = 9,8 м/с2. Поэтому предыдущее уравнение принимает вид:
Это значит, что время движения мячика до столкновения равно:
Итак, мы вычислили, что мячик будет находиться в полете 1,0 секунды. Отлично, явный прогресс! Поскольку компонента скорости мячика по оси X не изменялась в течение этого времени, то можно легко вычислить расстояние, которое пролетит мячик по горизонтали (т.е. вдоль оси X) за это время:
Подставляем числа и получаем:
Итак, мячик столкнется с поверхностью Земли на расстоянии 1,0 метра по горизонтали.
Теперь можно приступать ко второму вопросу задачи: попробуем определить скорость мячика в момент столкновения с поверхностью Земли. Частично ответ на этот вопрос мы уже знаем, поскольку компонента скорости мячика по оси X не изменялась. Однако по вертикали сила тяготения ускорила мячик по вертикали (т.е. вдоль оси Y), а потому компоненты конечной скорости имеют следующий вид: (1,0; ?). Итак, нам нужно определить величину компоненты скорости мячика по оси Y, обозначенной вопросительным знаком. Воспользуемся следующим соотношением для компоненты скорости по вертикали:
В данном случае начальная скорость \( v_{y0} \) = 0, постоянное ускорение \( a_y=g \) и нужно определить только конечную скорость \( v_{y1} \). Поэтому предыдущее уравнение приобретает следующий вид:
Подставляем числа и получаем:
Ускорение свободного падения, \( g \), также является вектором \( \mathbf{g} \). Он направлен к центру Земли, т.е. в отрицательном направлении оси Y, а на поверхности Земли его величина равна около -9,8 м/с2.
Отрицательный знак здесь обозначает направление вниз вектора \( \mathbf{g} \), т.е. в отрицательном направлении оси Y. Итак, подставляем обновленное значение ускорения и получаем:
Итак, компоненты конечной скорости мячика равны (1,0; -9,8) м/с. Чтобы найти величину вектора скорости (а не его отдельных компонент) в момент столкновения с поверхностью Земли, выполним следующие вычисления:
Триумфальный финал! Мячик пролетит 1,0 метра по горизонтали и столкнется с поверхностью Земли со скоростью 9,9 м/с. Совсем неплохо для начала.
Глава 5. Толкаем, чтобы привести в действие: сила →
← Глава 3. Утоляем жажду скорости
12. СКАЛЯРЫ и ВЕКТОРЫ — Физика это просто!!! 2016
В физике существуют скалярные величины (скаляры) и векторные величины (векторы). Хотя, правильнее в последнем случае все-таки говорить векторная величина, часто говорят, например, «вектор скорости». Упрощенно можно сказать, что скаляр — это просто число. Векторная величина — это когда есть число, которое имеет еще и направление в пространстве. Вектор в трехмерном пространстве можно представить в виде тройки чисел, каждое из которых есть компонента вектора относительно соответствующей координаты в трехмерной системе координат. Запутанно? Чтобы совсем запутаться, рекомендую обратиться к Википедии: https://ru.wikipedia.org/wiki/Векторная_величина. Для тех, кто любит попроще — первый том Фейнмановских лекций по физике. Для нас важно понять два момента: 1) Примерами скаляров являются: длина, площадь, время, масса, плотность, температура и т.п. Для наших задач достаточно понимания скаляра, как величины (числа с размерностью) без направления. 2) Под вектором мы будем понимать направленный отрезок. То есть три числа (мы ведь живем в трехмерном пространстве), которые преобразуются по определенным правилам при переходе от одной системы координат к другой. Попробуем обойтись без математических формул этих правил. Просто представим в нашем трехмерном пространстве направленный отрезок. Некую стрелку, которая, для простоты, неподвижна, неизменна, и имеет направление от одного конца к другому. Или даже представим, что у нас есть определенная операция перемещения в пространстве. У нее есть величина (расстояние перемещения по прямой из начальной точки в конечную) и направление. И представим систему координат (например, прямоугольную), которая неподвижна относительно нас, и начало отсчета которой совпадает с началом нашего направленного отрезка. Представили? Отлично! Тогда координаты «заостренного» конца нашего «направленного» отрезка с началом в точке (0,0,0) в этой системе координат будут выражаться тремя числами (Ах, Аy, Аz). Будет ли эта тройка чисел вектором? Будет! Мы же сами задали эти три числа, как координаты вектора. Теперь мы берем и поворачиваем произвольно нашу систему координат (но пока не сдвигаем начало координат). А теперь вывод. То, что важно для физики! Если у нас есть три какие-то величины (возможно, мы даже не знаем, связаны ли они между собой), которые изменяются с изменением системы координат, по такому же закону, по которому изменяются компоненты вектора из предыдущего абзаца ((Ах, Аy, Аz) —> (Аx’, Аy’, Аz’)), то мы можем смело утверждать, что эти три величины представляют собой компоненты какого-то вектора. Формулы можно посмотреть у Фейнмана или еще где-нибудь. Рассмотрим подробнее физические величины в нашем трехмерном пространстве. Зададим прямоугольную систему координат X, Y, Z. Помним, что у нас есть еще время t. Теперь посмотрим, что есть что. Путь вектор или скаляр? Скаляр. Почему? Перемещение — вектор. У перемещения есть начало и конец, есть величина перемещения и направление перемещения. Таким образом, у него три компоненты — три величины, по одной на каждую из координат. Далее сами перебираем физические величины и определяем, что есть скаляр, а что вектор!
|
Закон Гука, сила упругости — определение, формулы
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или замедляется, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которая является мерой действия одного тела на другое.
Она измеряется в ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат действия этой силы.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу сил. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Деформация растяжения
Деформация сжатия
Деформация сдвига
Деформация при кручении
Деформация при изгибе
Сила упругости: Закон Гука
Давайте займемся баскетболом. Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.
Такой удар будет называться абсолютно неупругим.
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не может вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Какой буквой обозначается сила упругости?
Закон Гука —сила упругости [Н] k — коэффициент жесткости [Н/м] х — изменение длины (деформация) [м] |
Важно раз
Изменение длины может обозначаться по-разному в различных источниках.
Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Важно два
Поскольку сила упругости всегда направлена против деформации (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при равномерном (без ускорения) поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу тяжести. Не забываем массу представить в единицах СИ – килограммах.
СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
m = 300 г = 0,3 кг
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
F = mg = 0,3*10 = 3 Н.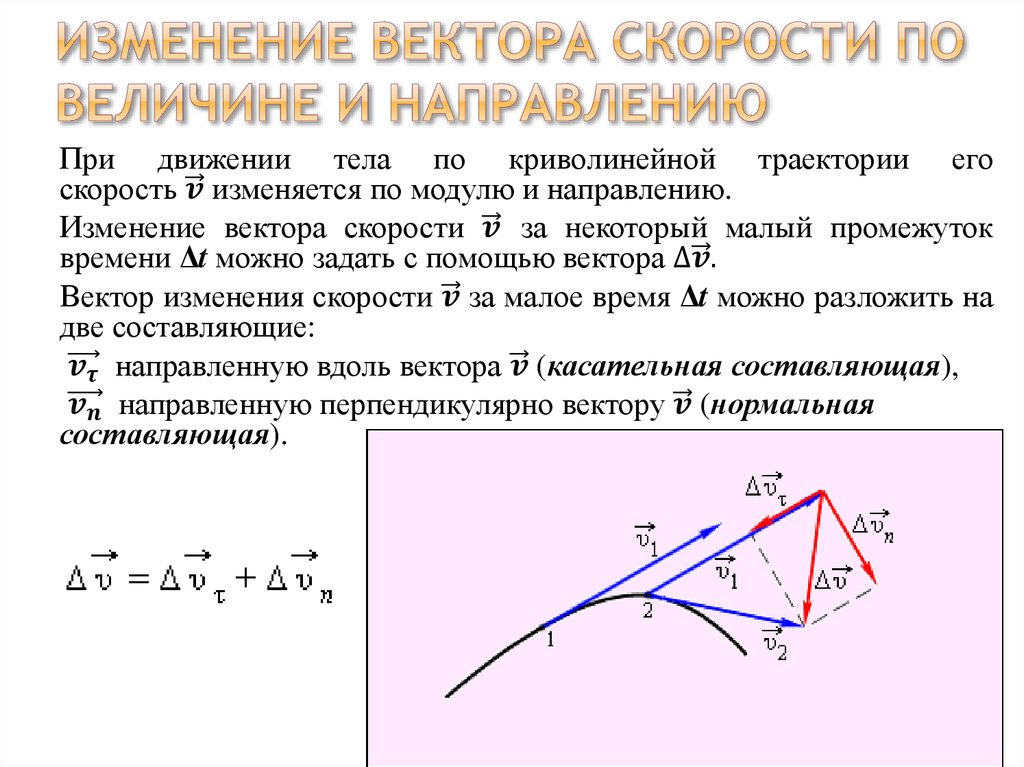
Вспомним закон Гука:
И выразим из него модуль удлинения лески:
Так как одна сила уравновешивает другую, мы можем их приравнять:
Подставим числа, жесткость лески при этом выражаем в ньютонах:
= 0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента жесткости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Задачка
Какова жесткость системы из двух пружин, жесткости которых k1 = 100 Н/м, k2 = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
66,7 Н/м
Очень-очень важно!
Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
F = kx
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры:
2 см = 0,02 м
И подставим в формулу:
=100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Что такое сила трения, виды силы трения; силы трения покоя и скольжения, законы и модуль силы трения
Определение силы трения
Когда мы говорим «абсолютно гладкая поверхность» — это значит, что между ней и телом нет трения. Такая ситуация в реальной жизни практически невозможна. Избавиться от трения полностью невероятно трудно.
Избавиться от трения полностью невероятно трудно.
Чаще при слове «трение» нам приходит в голову его «тёмная» сторона — из-за трения скрипят и прекращают качаться качели, изнашиваются детали машин. Но представьте, что вы стоите на идеально гладкой поверхности, и вам надо идти или бежать. Вот тут трение бы, несомненно, пригодилось. Без него вы не сможете сделать ни шагу, ведь между ботинком и поверхностью нет сцепления, и вам не от чего оттолкнуться, чтобы двигаться вперёд.
Трение — это взаимодействие, которое возникает в плоскости контакта поверхностей соприкасающихся тел.Сила трения — это величина, которая характеризует это взаимодействие по величине и направлению.
Основная особенность: сила трения приложена к обоим телам, поверхности которых соприкасаются, и направлена в сторону, противоположную мгновенной скорости движения тел друг относительно друга. Поэтому тела, свободно скользящие по какой-либо горизонтальной поверхности, в конце концов остановятся. Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.
Чтобы тело двигалось по горизонтальной поверхности без торможения, к нему надо прикладывать усилие, противоположное и хотя бы равное силе трения. В этом заключается суть силы трения.
Откуда берётся трение
Трение возникает по двум причинам:
- Все тела имеют шероховатости. Даже у очень хорошо отшлифованных металлов в электронный микроскоп видны неровности. Абсолютно гладкие поверхности бывают только в идеальном мире задач, в которых трением можно пренебречь. Именно упругие и неупругие деформации неровностей при контакте трущихся поверхностей формируют силу трения.
- Между атомами и молекулами поверхностей тел действуют электромагнитные силы притяжения и отталкивания. Таким образом, сила трения имеет электромагнитную природу.
Виды силы трения
В зависимости от вида трущихся поверхностей, различают сухое и вязкое трение. В свою очередь, оба подразделяются на другие виды силы трения.
- Сухое трение возникает в области контакта поверхностей твёрдых тел в отсутствие жидкой или газообразной прослойки.
 Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:
Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:
- трение скольжения,
- трение покоя,
- трение качения.
- Вязкое трение возникает при движении твёрдого тела в жидкости или газе. Оно препятствует движению лодки, которая скользит по реке, или воздействует на летящий самолёт со стороны воздуха. Интересная особенность вязкого трения в том, что отсутствует трение покоя. Попробуйте сдвинуть пальцем лежащий на земле деревянный брус и проделайте тот же эксперимент, опустив брус на воду. Чтобы сдвинуть брус с места в воде, будет достаточно сколь угодно малой силы. Однако по мере роста скорости силы вязкого трения сильно увеличиваются.
Сила трения покоя
Рассмотрим силу трения покоя подробнее.
Обычная ситуация: на кухне имеется холодильник, его нужно переставить на другое место.
Когда никто не пытается двигать холодильник, стоящий на горизонтальном полу, трения между ним и полом нет. Но как только его начинают толкать, коварная сила трения покоя тут же возникает и полностью компенсирует усилие. Причина её возникновения — те самые неровности соприкасающихся поверхностей, которые деформируясь, препятствуют движению холодильника. Поднатужились, увеличили силу, приложенную к холодильнику, но он не поддался и остался на месте. Это означает, что сила трения покоя возрастает вместе с увеличением внешнего воздействия, оставаясь равной по модулю приложенной силе, ведь увеличиваются деформации неровностей.
Пока силы равны, холодильник остаётся на месте:
Сила трения, которая действует между поверхностями покоящихся тел и препятствует возникновению движения, называется силой трения покоя
Сила трения скольжения
Что же делать с холодильником и можно ли победить силу трения покоя? Не будет же она расти до бесконечности?
Зовём на помощь друга, и вдвоём уже удаётся передвинуть холодильник. Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:
Получается, чтобы тело двигалось, нужно приложить силу, большую, чем самая большая сила трения покоя:
Теперь на движущийся холодильник действует сила трения скольжения. Она возникает при относительном движении контактирующих твёрдых тел.
Итак, сила трения покоя может меняться от нуля до некоторого максимального значения — Fтр. пок. макс И если приложенная сила больше, чем Fтр. пок. макс, то у холодильника появляется шанс сдвинуться с места.
Теперь, после начала движения, можно прекратить наращивать усилие и ещё одного друга можно не звать. Чтобы холодильник продолжал двигаться равномерно, достаточно прикладывать силу, равную силе трения скольжения:
Как рассчитать и измерить силу трения
Чтобы понять, как измеряется сила трения, нужно понять, какие факторы влияют на величину силы трения. Почему так трудно двигать холодильник?
Самое очевидное — его масса играет первостепенную роль. Можно вытащить из него все продукты и тем самым уменьшить его массу, и, следовательно, силу давления холодильника на опору (пол). Пустой холодильник сдвинуть с места гораздо легче!
Пустой холодильник сдвинуть с места гораздо легче!
Следовательно, чем меньше сила нормального давления тела на поверхность опоры, тем меньше и сила трения. Опора действует на тело с точно такой же силой, что и тело на опору, только направленной в противоположную сторону.
Сила реакции опоры обозначается N. Можно сделать вывод
Второй фактор, влияющий на величину силы трения, — материал и степень обработки соприкасающихся поверхностей. Так, двигать холодильник по бетонному полу гораздо тяжелее, чем по ламинату. Зависимость силы трения от рода и качества обработки материала обеих соприкасающихся поверхностей выражают через коэффициент трения.
<<Форма демодоступа>>
Коэффициент трения обозначается буквой μ (греческая буква «мю»). Коэффициент определяется отношением силы трения к силе нормального давления.
Он чаще всего попадает в интервал от нуля до единицы, не имеет размерности и определяется экспериментально.
Можно предположить, что сила трения зависит также от площади соприкасающихся поверхностей. Однако, положив холодильник набок, мы не облегчим себе задачу.
Ещё Леонардо да Винчи экспериментально доказал, что сила трения не зависит от площади соприкасающихся поверхностей при прочих равных условиях.
Сила трения скольжения, возникающая при контакте твёрдого тела с поверхностью другого твёрдого тела прямо пропорциональна силе нормального давления и не зависит от площади контакта.
Этот факт отражён в законе Амонтона-Кулона, который можно записать формулой:
где μ — коэффициент трения, N — сила нормальной реакции опоры.
Для тела, движущегося по горизонтальной поверхности, сила реакции опоры по модулю равна весу тела:
Сила трения качения
Ещё древние строители заметили, что если тяжёлый предмет водрузить на колёсики, то сдвинуть с места и затем катить его будет гораздо легче, чем тянуть волоком. Вот бы пригодилась эта древняя мудрость, когда мы тянули холодильник! Однако всё равно нужно толкать или тянуть тело, чтобы оно не остановилось. Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Значит, на него действует сила трения качения. Это сила сопротивления движению при перекатывании одного тела по поверхности другого.
Причина трения качения — деформация катка и опорной поверхности. Сила трения качения может быть в сотни раз меньше силы трения скольжения при той же силе давления на поверхность. Примерами уменьшения силы трения за счёт подмены трения скольжения на трение качения служат такие приспособления, как подшипники, колёсики у чемоданов и сумок, ролики на прокатных станах.
Направление силы трения
Сила трения скольжения всегда направлена противоположно скорости относительного движения соприкасающихся тел. Важно помнить, что на каждое из соприкасающихся тел действует своя сила трения.
Бывают ситуации, когда сила трения не препятствует движению, а совсем наоборот.
Представьте, что на ленте транспортёра лежит чемодан. Лента трогается с места, и чемодан движется вместе с ней. Сила трения между лентой и чемоданом оказалась достаточной, чтобы преодолеть инерцию чемодана, и эти тела движутся как одно целое. На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.
На чемодан действует сила трения покоя, возникающая при взаимодействии соприкасающихся поверхностей, которая направлена по ходу движения ленты транспортёра.
Если бы лента была абсолютно гладкой, то чемодан начал бы скользить по ней, стремясь сохранить своё состояние покоя. Напомним, что это явление называется инерцией.
Сила трения покоя, помогающая нам ходить и бегать, также направлена не против движения, а вперёд по ходу перемещения. При повороте же автомобиля сила трения покоя и вовсе направлена к центру окружности.
Для того чтобы понять, как направлена сила трения покоя, нужно предположить, в каком направлении стало бы двигаться тело, будь поверхность идеально гладкой. Сила трения покоя в этом случае будет направлена как раз в противоположную сторону. Пример, лестница у стены.
Подведём итоги
- Сила трения покоя меняется от нуля до максимального значения 0 < Fтр.покоя < Fтр.пок.макс в зависимости от внешнего воздействия.

- Максимальная сила трения покоя почти равна силе трения скольжения, лишь немного её превышая. Можно приближенно считать, что Fтр. = Fтр.пок.макс
- Силу трения скольжения можно рассчитать по формуле Fтр. = μ ⋅ N, где μ — коэффициент трения, N — сила нормальной реакции опоры.
- При равномерном прямолинейном скольжении по горизонтальной поверхности сила тяги равна силе трения скольжения Fтр. = Fтяги.
- Коэффициент трения μ зависит от рода и степени обработки поверхностей 0 < μ < 1 .
- При одинаковых силе нормального давления и коэффициенте трения сила трения качения всегда меньше силы трения скольжения.
Учите физику вместе с домашней онлайн-школой «Фоксфорда»! По промокоду PHYSICS72021 вы получите
бесплатный доступ к курсу физики 7 класса, в котором изучается закон силы трения.Задачи на силу трения
Проверьте, насколько хорошо вы разобрались в теме «Сила трения», — решите несколько задач. Решение — приведено ниже. Но чур не смотреть, пока не попробуете разобраться сами.
Решение — приведено ниже. Но чур не смотреть, пока не попробуете разобраться сами.
- Однажды в день открытия железной дороги произошёл конфуз: угодливый чиновник, желая выслужиться перед Николаем I, приказал выкрасить рельсы белой масляной краской. Какая возникла проблема и как её удалось решить с помощью сажи?
- В один зимний день бабушка Нюра катала внука Алексея по заснеженной горизонтальной дороге. Чему равен коэффициент трения полозьев о снег, если сила трения, действующая на санки, равна 250 Н, а их масса вместе с Алексеем составляет 50 кг?
- На брусок массой m = 5 кг, находящийся на горизонтальной шероховатой поверхности μ = 0,7, начинает действовать сила F = 25 Н, направленная вдоль плоскости. Чему при этом равна сила трения, действующая на брусок?
Решения
- Масляная краска снизила коэффициент трения между колёсами и рельсами, что привело к пробуксовке, поезд не смог двигаться вперёд. Посыпав рельсы сажей, удалось решить проблему, так как коэффициент трения увеличился, и колёса перестали буксовать.

- Санки находятся в движении, следовательно, на них будет действовать сила трения скольжения, численно равная Fтр. = μ ⋅ N, где N — сила реакции опоры, которая, при условии горизонтальной поверхности, равняется весу санок с мальчиком: N = m ⋅ g. Получаем формулу Fтр. = μ ⋅ m ⋅ g , откуда выразим искомую величину
Ответ задачи зависит от того, сдвинется ли брусок под действием внешнего воздействия. Поэтому вначале узнаем значение силы, которую нужно приложить к бруску для скольжения. Это будет максимально возможная сила трения покоя, определяющаяся по формуле Fтр. = μ ⋅ N , где N = m ⋅ g (при условии горизонтальной поверхности). Подставляя значения, получаем, что Fтр. = 35 Н. Данное значение больше прикладываемой силы, следовательно брусок не сдвинется с места. Тогда сила трения покоя будет равна внешней силе: Fтр. = F = 25 H .
векторов, скаляров и систем координат | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Определять и различать скалярные и векторные величины.

- Назначение системы координат для сценария с одномерным движением.
Рис. 1. Движение струи Eclipse Concept можно описать с точки зрения пройденного им расстояния (скалярная величина) или его смещения в определенном направлении (векторная величина). Чтобы указать направление движения, его перемещение должно быть описано на основе системы координат. В этом случае может быть удобно выбрать движение влево как положительное движение (это прямое направление для плоскости), хотя во многих случаях координата x идет слева направо, а движение вправо — как положительное. и движение влево как отрицательное. (кредит: кресло «Авиатор», Flickr)
В чем разница между расстоянием и перемещением? В то время как смещение определяется как направлением, так и величиной, расстояние определяется только величиной. Перемещение является примером векторной величины. Расстояние является примером скалярной величины. Вектор — это любая величина с величиной и направлением . Другие примеры векторов включают скорость 90 км/ч на восток и силу 500 ньютонов прямо вниз.
Другие примеры векторов включают скорость 90 км/ч на восток и силу 500 ньютонов прямо вниз.
Направление вектора в одномерном движении задается просто знаком плюс (+) или минус (-). Векторы представлены графически стрелками. Стрелка, используемая для представления вектора, имеет длину, пропорциональную величине вектора (например, чем больше величина, тем больше длина вектора) и указывает в том же направлении, что и вектор.
Некоторые физические величины, такие как расстояние, либо не имеют направления, либо не указываются. Скаляр — это любая величина, имеющая величину, но не имеющую направления. Например, температура 20ºC, 250 килокалорий (250 калорий) энергии в шоколадном батончике, ограничение скорости 90 км/ч, рост человека 1,8 м и расстояние 2,0 м — все это скаляры — величины без определенного направления. . Обратите внимание, однако, что скаляр может быть отрицательным, например, температура -20ºC. В этом случае знак минус указывает точку на шкале, а не направление. Скаляры никогда не изображаются стрелками.
Скаляры никогда не изображаются стрелками.
Системы координат для одномерного движения
Чтобы описать направление векторной величины, вы должны указать систему координат в системе отсчета. Для одномерного движения это простая система координат, состоящая из одномерной координатной линии. В общем, при описании горизонтального движения движение вправо обычно считается положительным, а движение влево считается отрицательным. При вертикальном движении движение вверх обычно положительное, а движение вниз отрицательное. Однако в некоторых случаях, как в случае со струей на рис. 1, может быть удобнее поменять местами положительное и отрицательное направления. Например, если вы анализируете движение падающих объектов, может быть полезно определить положительное направление вниз. Если люди в гонке бегут налево, полезно определить лево как положительное направление. Это не имеет значения, пока система ясна и последовательна. Как только вы задаете положительное направление и начинаете решать проблему, вы не можете изменить его.
Рис. 2. Обычно удобно рассматривать движение вверх или вправо как положительное (+), а движение вниз или влево как отрицательное (−).
Проверьте свое понимание
Скорость человека может оставаться неизменной, когда он или она поворачивает за угол и меняет направление. Учитывая эту информацию, является ли скорость скалярной или векторной величиной? Объяснять.
РешениеСкорость является скалярной величиной. Он совсем не меняется при смене направления; следовательно, он имеет только величину. Если бы это была векторная величина, она менялась бы при изменении направления (даже если бы ее величина оставалась постоянной).
Концептуальные вопросы
1. Студент пишет: « Птица, ныряющая за добычей, имеет скорость -10 м/с ». Что не так с заявлением ученика? Что на самом деле описал студент? Объяснять.
2. Какова скорость птицы?
3. Ускорение – это изменение скорости во времени. Учитывая эту информацию, является ли ускорение векторной или скалярной величиной? Объяснять.
Ускорение – это изменение скорости во времени. Учитывая эту информацию, является ли ускорение векторной или скалярной величиной? Объяснять.
4. В прогнозе погоды говорится, что на следующий день ожидается температура -5ºC . Является ли эта температура векторной или скалярной величиной? Объяснять.
Глоссарий
- скаляр:
- величина, описываемая величиной, но не направлением
- вектор:
- величина, описываемая и величиной, и направлением
Лицензии и атрибуции
Контент по лицензии CC, совместно используемый ранее
- College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в Лицензии
Направление вектора указывает величину вектора.
 ?
?Что такое определение силовых линий магнитного поля?
Линии магнитного поля показывают величину и направление магнитного поля Когда линии магнитного поля расположены близко друг к другу, магнитное поле сильное. В области, где плотность линий высока, говорят, что они имеют большую интенсивность или силу. Технически плотность линий пропорциональна величине поля. Направление, в котором ориентированы линии магнитного поля, предоставляет информацию о направлении поля, при условии, что линии имеют стрелки, нарисованные таким образом, что линии выходят из северного полюса. постоянного магнита, или, что то же самое, стрелки указывают в том направлении, куда указывал бы северный конец стрелки компаса, если бы он был помещен на линию. являются чрезвычайно ценными представлениями о силе и направлении магнитных (или электрических) полей. (Изображения силовых линий являются человеческими творениями, помогающими понять поля, но изображения силовых линий, которые правильно нарисованы, обеспечивают точное представление математического описания поля. ) Когда кто-то говорит, что магнитное поле «сильно», это не так. означают, что он оказывает большую силу на другой магнитный объект. Сила магнитного поля определяется крутящим моментом, а не силой. Вот как это сделать. Определение векторного магнитного поля. Если магнитное поле существует в определенной точке, то его характеризуют силой и направлением. В самом деле, это можно сделать во всех точках и знать величину и направление поля во всех точках. Поскольку векторы имеют величину и направление, мы можем связать вектор с магнитным полем в любой точке, и поэтому говорят, что магнитное поле является векторным полем. Направление магнитного поля: мы определяем силу или величину поля, используя классическое поведение. которые мы видим, когда пользуемся компасом. Поле оказывает крутящий момент на стрелку компаса, чтобы сориентировать ее. Один конец компаса помечен как «Север», потому что при отсутствии какого-либо другого поля стрелка компаса указывает на «Северный» географический полюс Земли.
) Когда кто-то говорит, что магнитное поле «сильно», это не так. означают, что он оказывает большую силу на другой магнитный объект. Сила магнитного поля определяется крутящим моментом, а не силой. Вот как это сделать. Определение векторного магнитного поля. Если магнитное поле существует в определенной точке, то его характеризуют силой и направлением. В самом деле, это можно сделать во всех точках и знать величину и направление поля во всех точках. Поскольку векторы имеют величину и направление, мы можем связать вектор с магнитным полем в любой точке, и поэтому говорят, что магнитное поле является векторным полем. Направление магнитного поля: мы определяем силу или величину поля, используя классическое поведение. которые мы видим, когда пользуемся компасом. Поле оказывает крутящий момент на стрелку компаса, чтобы сориентировать ее. Один конец компаса помечен как «Север», потому что при отсутствии какого-либо другого поля стрелка компаса указывает на «Северный» географический полюс Земли. Используя это определение, когда компас подносят к постоянному магниту, говорят, что северный конец компаса указывает на южный конец магнита. (Северные полюса притягивают южные полюса.) Это направление можно нанести на карту во всем пространстве вокруг стержневого магнита, ориентируя компас не только плоско или горизонтально, но и во всех направлениях, чтобы определить, куда указывает магнитное поле для всех положений. в пространстве вокруг постоянного магнита. (Это одинаково хорошо работает для электромагнитов, но мы опишем это для самой простой ситуации.) Напряженность магнитного поля: направление поля в каждой точке, как описано выше, является направлением, на которое указывает северный конец стрелки компаса, когда есть ноль. крутящий момент на игле. Если повернуть иглу так, чтобы она была перпендикулярна направлению поля, то игла испытывает максимальный крутящий момент. Этот крутящий момент измеряет силу или величину поля. Таким образом, как только вы зададите шкалу напряженности, назначив одно значение напряженности поля для одного конкретного компаса, вы сможете нанести на карту напряженность поля во всех точках с помощью одного и того же компаса и везде получите величину и направление магнитного поля.
Используя это определение, когда компас подносят к постоянному магниту, говорят, что северный конец компаса указывает на южный конец магнита. (Северные полюса притягивают южные полюса.) Это направление можно нанести на карту во всем пространстве вокруг стержневого магнита, ориентируя компас не только плоско или горизонтально, но и во всех направлениях, чтобы определить, куда указывает магнитное поле для всех положений. в пространстве вокруг постоянного магнита. (Это одинаково хорошо работает для электромагнитов, но мы опишем это для самой простой ситуации.) Напряженность магнитного поля: направление поля в каждой точке, как описано выше, является направлением, на которое указывает северный конец стрелки компаса, когда есть ноль. крутящий момент на игле. Если повернуть иглу так, чтобы она была перпендикулярна направлению поля, то игла испытывает максимальный крутящий момент. Этот крутящий момент измеряет силу или величину поля. Таким образом, как только вы зададите шкалу напряженности, назначив одно значение напряженности поля для одного конкретного компаса, вы сможете нанести на карту напряженность поля во всех точках с помощью одного и того же компаса и везде получите величину и направление магнитного поля. Магнитное поле Линии: Описанный выше процесс создает векторное поле, что означает, что в каждой точке пространства можно нарисовать маленькую стрелку с величиной и направлением, указывающим поле. Такой рисунок создает изображение пучка стрелок в пространстве вокруг магнита, представляющего магнитное поле. Это совершенно хорошее представление векторного поля. Можно также создать линейное представление векторного поля, магнитного, электрического или другого. Для магнита выше, если вы начнете с точки на северном конце магнита и проведете линию в направлении стрелки, вы сразу же столкнетесь с другой стрелкой. В точке новой стрелки вы продолжаете рисовать линию в направлении этой стрелки, пока не дойдете до следующей стрелки, которая указывает следующее направление, и так далее и так далее. По сути, если вы начнете с северного конца магнита и нарисуете линию в направлении, указанном стрелками, эта линия закончится на южном конце магнита. Можно выбрать новую начальную позицию на поверхности магнита и повторить процесс.
Магнитное поле Линии: Описанный выше процесс создает векторное поле, что означает, что в каждой точке пространства можно нарисовать маленькую стрелку с величиной и направлением, указывающим поле. Такой рисунок создает изображение пучка стрелок в пространстве вокруг магнита, представляющего магнитное поле. Это совершенно хорошее представление векторного поля. Можно также создать линейное представление векторного поля, магнитного, электрического или другого. Для магнита выше, если вы начнете с точки на северном конце магнита и проведете линию в направлении стрелки, вы сразу же столкнетесь с другой стрелкой. В точке новой стрелки вы продолжаете рисовать линию в направлении этой стрелки, пока не дойдете до следующей стрелки, которая указывает следующее направление, и так далее и так далее. По сути, если вы начнете с северного конца магнита и нарисуете линию в направлении, указанном стрелками, эта линия закончится на южном конце магнита. Можно выбрать новую начальную позицию на поверхности магнита и повторить процесс.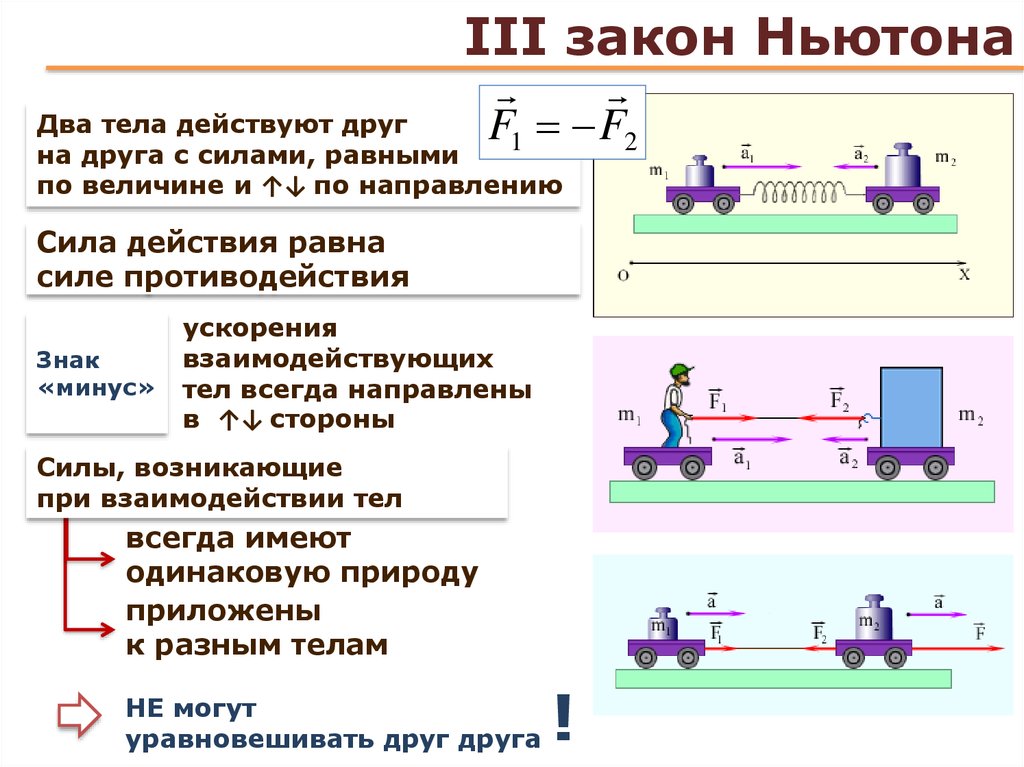 Делая это снова и снова, мы получаем целый набор линий, которые в конечном итоге заполняют все пространство вокруг магнита. Набор нарисованных линий не является линиями магнитного поля. Но каждая из нарисованных линий соответствует линии магнитного поля. Звучит странно, но чтобы точно представить силу поля, необходимо применить еще одно условие, определяющее, сколько линий будет нарисовано. Это условие состоит в том, что количество линий в любой области пространства пропорционально силе поля в этой области. Это требует некоторого дополнительного правила, потому что количество или плотность линий не будут сообщать о напряженности поля, если просто рисовать линии где угодно. Плотность линий магнитного поля: при использовании линий поля для представления векторного поля (электрического, магнитного или любого другого). нужна информация как о величине, так и о направлении, а отдельные линии дают только направление. Таким образом, принято считать, что количество линий, которые вы рисуете в любой конкретной области пространства, пропорционально силе (величине) поля в этой области.
Делая это снова и снова, мы получаем целый набор линий, которые в конечном итоге заполняют все пространство вокруг магнита. Набор нарисованных линий не является линиями магнитного поля. Но каждая из нарисованных линий соответствует линии магнитного поля. Звучит странно, но чтобы точно представить силу поля, необходимо применить еще одно условие, определяющее, сколько линий будет нарисовано. Это условие состоит в том, что количество линий в любой области пространства пропорционально силе поля в этой области. Это требует некоторого дополнительного правила, потому что количество или плотность линий не будут сообщать о напряженности поля, если просто рисовать линии где угодно. Плотность линий магнитного поля: при использовании линий поля для представления векторного поля (электрического, магнитного или любого другого). нужна информация как о величине, так и о направлении, а отдельные линии дают только направление. Таким образом, принято считать, что количество линий, которые вы рисуете в любой конкретной области пространства, пропорционально силе (величине) поля в этой области.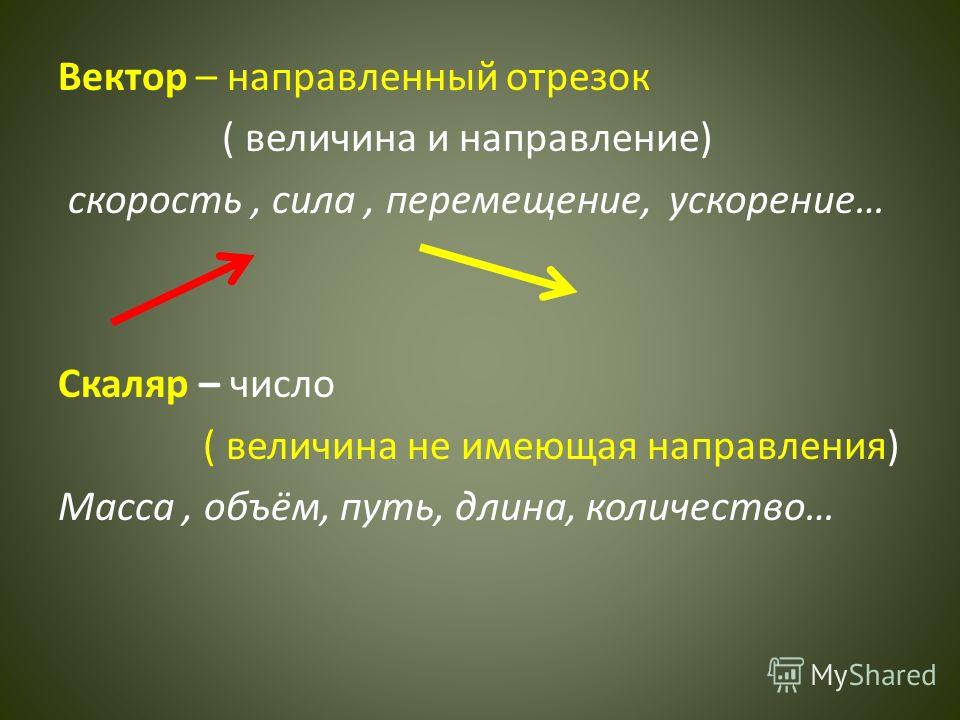 Это трудно сделать. К счастью, линии магнитного поля обладают особым свойством, облегчающим эту задачу. Линии магнитного поля никогда не начинаются и не заканчиваются. Линии на изображении стержневого магнита выглядят так, будто линии выходят из северного конца и входят в южный конец, и это так, но это так. они продолжают проходить внутри и выходят с противоположного конца, образуя замкнутые петли. Обычно часть петель внутри магнита не нарисована, но они есть. Это более понятно для электромагнитов, где на чертеже видна внутренняя часть. Рисование линий: технические аспекты рисования линий слишком сложны, чтобы объяснять их подробно, но вот простой и правильный подход. Во-первых, решите, сколько линий должно быть. нарисовано. Лучше больше, но пока допустим 100. Это означает, что все 100 должны выйти из частей магнита, которые считаются северными, и в части, определенные как южные. Это включает в себя концы и стороны и все области поверхности, куда линии могут входить или выходить. Нарисуйте больше линий в области, где напряженность поля у поверхности высока, и меньше вне областей, где напряженность низкая.
Это трудно сделать. К счастью, линии магнитного поля обладают особым свойством, облегчающим эту задачу. Линии магнитного поля никогда не начинаются и не заканчиваются. Линии на изображении стержневого магнита выглядят так, будто линии выходят из северного конца и входят в южный конец, и это так, но это так. они продолжают проходить внутри и выходят с противоположного конца, образуя замкнутые петли. Обычно часть петель внутри магнита не нарисована, но они есть. Это более понятно для электромагнитов, где на чертеже видна внутренняя часть. Рисование линий: технические аспекты рисования линий слишком сложны, чтобы объяснять их подробно, но вот простой и правильный подход. Во-первых, решите, сколько линий должно быть. нарисовано. Лучше больше, но пока допустим 100. Это означает, что все 100 должны выйти из частей магнита, которые считаются северными, и в части, определенные как южные. Это включает в себя концы и стороны и все области поверхности, куда линии могут входить или выходить. Нарисуйте больше линий в области, где напряженность поля у поверхности высока, и меньше вне областей, где напряженность низкая. Вы расположили линии с нужной плотностью, когда поместите свой воображаемый компас в область с некоторой плотностью линий, что создаст максимальный крутящий момент, соответствующий напряженности поля. Все это звучит намного проще, чем есть на самом деле. Не существует определения «силовых линий магнитного поля», но это определение магнитного поля: область вокруг магнитного материала или движущегося электрического заряда, внутри которой действует сила магнетизма.
Вы расположили линии с нужной плотностью, когда поместите свой воображаемый компас в область с некоторой плотностью линий, что создаст максимальный крутящий момент, соответствующий напряженности поля. Все это звучит намного проще, чем есть на самом деле. Не существует определения «силовых линий магнитного поля», но это определение магнитного поля: область вокруг магнитного материала или движущегося электрического заряда, внутри которой действует сила магнетизма.
Имея только величину%2c, но без направления — ответы на кроссворды
Разгадка кроссворда Имеющая только величину, но без направления с 6 буквами в последний раз видели 01 января 2004 года . Мы думаем, что наиболее вероятным ответом на эту подсказку будет SCALAR . Ниже приведены все возможные ответы на эту подсказку, упорядоченные по рангу. Вы можете легко улучшить поиск, указав количество букв в ответе.
| Ранг | Слово | Подсказка |
|---|---|---|
| 92% | СКАЛЯР | Имея только величину, но не направление |
| 69% | ОГРОМНОСТЬ | Величина |
| 69% | РАЗМЕР | Величина |
| 67% | ПРОСТРАНСТВО | Величина |
| 58% | РОСТ | Увеличение величины |
| 58% | УНИПОЛЯРНЫЙ | Наличие только одного полюса |
| 58% | СИГАРА | «Близко, но нет ___» |
| 55% | ВОСТОК | Направление |
| 55% | БЕЗЦЕЛЬ | Не имея направления |
| 53% | РАЗРЕШИТЬ | Подведи всех, не имея ограничений |
| 53% | АТЕ | Была печень, но не лук |
| 50% | ЗАДЕРЖКА | Короткое нижнее белье не годится, но остается |
| 50% | ИЖЕЛАНИЕ | ‘Если только!’ |
| 50% | ПОТЕРЯН | Не хватает направления? |
| 50% | ВНЕДУХ | В депрессии, не осталось крепких напитков? |
| 50% | ГРУППА | Направление |
| 47% | ДВА | Имея длину и ширину, но не глубину, для краткости |
| 47% | ПОТОКИ | «Нет __, нет славы» |
| 47% | ПОДОШВА | Только |
| 47% | ОБЫЧНЫЙ | «Для 2с ___» |
Уточните результаты поиска, указав количество букв.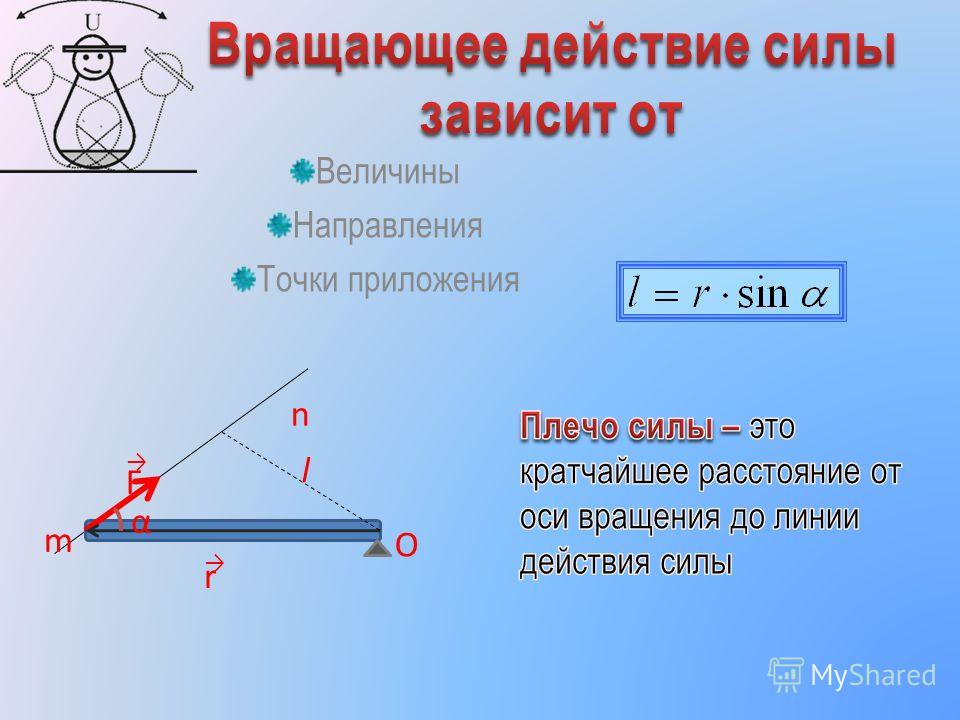 Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».
Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».
- Они назвали это прекращением кроссворда
- Звезда «Ковбоя Бибопа» Джон Кроссворд
- Режиссер фильма «Свидетель» Питер Кроссворд.
- Доктор-зоотехник держит подсказку кроссворда одежды сына
- Воины банту: Два хватающих члена парламента Кроссворд
- Припарковаться рядом с магазинами, прямо на улице и уйти? Кроссворд
- Забранные из класса, мужчины плохо себя ведут Кроссворд
- Чувство сожаления после того, как вы приняли решение кроссворда Variable Cornish Resort
- Посол бежит с северо-востока в Турцию? Кроссворд
- Умереть без похорон? Кроссворд
- Кольцевая дорога построена над Ист-Ривер.
- Шекспировский персонаж в машине, по телефону? Кроссворд
- Постройте зубчатые стены, когда голова Нормана будет найдена в корзине, Подсказка мертвого кроссворда
- Перевозит члена семьи, автомобиль перевернут вокруг поворота Кроссворд
- Кроссворд Tout’s Calculation Clive
- — Вторник Кроссворд
- Политик первым получил право на погоню за деньгами Кроссворд
- — Кроссворд понедельника
- — Кроссворд по средам
- — Четверг Кроссворд
- Очень многие поддерживают призыв к кроссворду промышленных действий
- Мягкое движение воздуха Кроссворд
- Обидчивая чувственная часть перед новостной статьей? Кроссворд
- Сладкая красавица сопровождает епископа на азиатском фестивале Кроссворд
- Кроссворд Дика Баха «Необычная птица»
- Кот из железного кабеля Кроссворд
- Приемлемо для уборки, как еда осталась? Кроссворд
- Храбрый — очаровательный кроссворд
- Путеводитель Посещение Австралии Кроссворд Подсказка
- Я не решаюсь сказать, что некоторые поэтические строки носят ключ к кроссворду
- Звук лавочника в подвале Кроссворд
- Spooner’s Suspended Herb In Filthy Place Кроссворд
- Кроссворд для пирсинга
- Проглотить в одном черновике Кроссворд
- Двенадцать месяцев — это долго, бесконечный кроссворд
- Кое-что, используемое альпинистами, носильщиками колледжей и бобрами.

- Разгадка кроссворда Smarter (Anag)
- Кроссворд Уолта Диснея (Глупый?) Летающий слон
- Автомобиль, не шикарный, хорошая сделка Кроссворд
- Задняя машина, вокруг которой наконец-то ночью отправились ходячие с факелами? Кроссворд
- Связь с правилом взлома оружия, я подозреваю, кроссворд
- Ингредиент для сухого супа (Se Ed?) Кроссворд
- Услышав машину, кто-то склоняется к правильному кроссворду
- Бросьте сына в ягуара, например, разгадывайте кроссворд
- Гол ни для одной из сторон? Кроссворд
- Еда в персонаже кокни, в основном разгадка кроссворда
- Mean Sort разорил банки во Флориде.
- Навязчивый член профсоюза в основном превращается в свинью, когда выпивает кроссворд
- Кроссворд «Закуска Ехидны»
- Cbs Crime Show Spinoff, семейный кроссворд
Мы нашли 1 решений для Имея только величину%2c, но без направления . Лучшие решения определяются по популярности, рейтингу и частоте поиска. Наиболее вероятный ответ на подсказку: SCALAR .
Лучшие решения определяются по популярности, рейтингу и частоте поиска. Наиболее вероятный ответ на подсказку: SCALAR .
С crossword-solver.io вы найдете 1 решения. Мы используем исторические головоломки, чтобы найти наилучшие ответы на ваш вопрос. Мы добавляем много новых подсказок на ежедневной основе.
С нашей поисковой системой для решения кроссвордов у вас есть доступ к более чем 7 миллионам подсказок. Вы можете сузить возможные ответы, указав количество букв, которые он содержит. Мы нашли более 16 ответов для Иметь только величину%2c, но без направления.
Любая ли величина имеет величину, но не имеет направления?
Содержание
- Как графически сложить два вектора?
- Когда два вектора складываются графически, можно ли перетаскивать?
- Как сложить два вектора в физике?
- Имеет ли значение порядок добавления векторов?
- Что получится в результате сложения векторов?
- Является ли аналитический или графический метод более точным?
- Является ли таблица Force более точной, чем графический метод?
- Что получится, если умножить два вектора?
- Могут ли единичные векторы быть отрицательными?
- Каково направление единичного вектора?
- По какой формуле найти величину вектора?
- Что такое вектор в математике?
- Кто отец вектора?
- Векторы сложные?
- Что называется вектором приведите два примера?
В отличие от векторов, обычные величины, имеющие величину, но не направление, называются скалярами.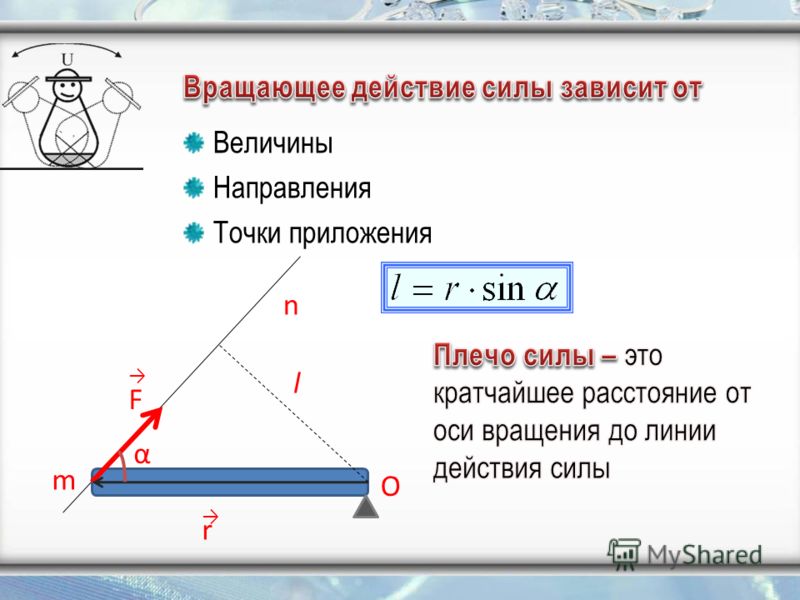 Например, перемещение, скорость и ускорение являются векторными величинами, а скорость (величина скорости), время и масса являются скалярными величинами.
Например, перемещение, скорость и ускорение являются векторными величинами, а скорость (величина скорости), время и масса являются скалярными величинами.
Как графически сложить два вектора?
Резюме
- Графический метод сложения векторов A и B включает в себя нанесение векторов на график и сложение их методом «голова к хвосту».
- Графический метод вычитания вектора B из A включает добавление противоположного вектора B, который определяется как -B.
- Сложение векторов коммутативно, так что A + B = B + A.
Когда два вектора складываются графически, можно ли их перетаскивать?
Вопрос: Векторы складываются графически. Можно перетаскивать векторы (сохраняя направление) так, чтобы кончик одного вектора касался кончика другого.
Как сложить два вектора в физике?
Чтобы сложить векторы, положите первый на набор осей хвостом в начале координат. Поместите следующий вектор хвостом в голову предыдущего вектора. Когда больше нет векторов, проведите прямую линию от начала координат до начала последнего вектора. Эта линия является суммой векторов.
Когда больше нет векторов, проведите прямую линию от начала координат до начала последнего вектора. Эта линия является суммой векторов.
Имеет ли значение порядок добавления векторов?
Суммарный результат двух или более векторов может быть определен в процессе сложения векторов. Наиболее распространенным методом сложения векторов является графический метод сложения «голова к хвосту».
Что получится в результате сложения векторов?
Результат представляет собой векторную сумму двух или более векторов. Это результат сложения двух или более векторов вместе. Если добавляются два или более векторов скорости, результатом является результирующая скорость. Если добавить два или более векторов силы, то результатом будет равнодействующая сила.
Является ли аналитический или графический метод более точным?
Аналитический метод более точен, чем графический метод, который ограничен точностью чертежа.
Является ли таблица Force более точной, чем графический метод?
Применяя все три метода, мы смогли увидеть, как каждый из них создает немного отличающуюся результирующую силу (Н) и результирующее направление (в градусах). Это видно из таблиц данных. Согласно нашим расчетам процентной ошибки, графический метод более точен, чем экспериментальный.
Это видно из таблиц данных. Согласно нашим расчетам процентной ошибки, графический метод более точен, чем экспериментальный.
Что получится, если умножить два вектора?
Скалярное произведение — также известное как «скалярное произведение», операция, которая берет два вектора и возвращает скалярную величину. Скалярное произведение двух векторов можно определить как произведение модулей двух векторов и косинуса угла между двумя векторами.
Могут ли единичные векторы быть отрицательными?
Ответ. Два вектора равны, если они имеют одинаковую величину и одно и то же направление. Точно так же, как скаляры, которые могут иметь положительные или отрицательные значения, векторы также могут быть положительными или отрицательными.
Каково направление единичного вектора?
Единичный вектор содержит информацию о направлении. Если вы умножаете положительную скалярную величину на единичный вектор, то вы получаете вектор с величиной, равной этой скалярной величине в направлении единичного вектора.
По какой формуле найти величину вектора?
Формулу для величины вектора можно обобщить на произвольные измерения. Например, если a=(a1,a2,a3,a4) — четырехмерный вектор, формула для его величины будет следующей: ∥a∥=√a21+a22+a23+a24.
Что такое вектор в математике?
Вектор — это объект, который имеет как величину, так и направление. Геометрически мы можем изобразить вектор как направленный отрезок, длина которого равна величине вектора и со стрелкой, указывающей направление. Направление вектора от хвоста к голове.
Кто отец вектора?
В современном виде векторы появились в конце XIX века, когда Джозайя Уиллард Гиббс и Оливер Хевисайд (соответственно из США и Великобритании) независимо друг от друга разработали векторный анализ для выражения новых законов электромагнетизма, открытых шотландским физиком Джеймсом Клерком Максвеллом. .
Векторы сложные?
Однако, возможно, в стандартных учебных программах по математике векторы являются первым таким «интересным» объектом, с которым сталкиваются студенты. Потратив (предположительно) более десяти лет на преподавание математики очень жестким и четко определенным образом, это довольно сложное переключение передач.
Потратив (предположительно) более десяти лет на преподавание математики очень жестким и четко определенным образом, это довольно сложное переключение передач.
Что называется вектором приведите два примера?
Вектор — это величина или явление, обладающее двумя независимыми свойствами: величиной и направлением. Термин также обозначает математическое или геометрическое представление такой величины. Примерами векторов в природе являются скорость, импульс, сила, электромагнитные поля и вес.
Поделиться Твитнуть Приколи это LinkedIn
Как найти величину и направление силы по компонентам x и y
Иногда у нас есть компоненты x и y силы, и мы хотим найти модуль и направление силы.
Давайте посмотрим, как мы можем это сделать.
Можно рассмотреть три возможных случая:
• Оба компонента отличны от нуля
Если у силы F компоненты x и y отличны от нуля, то для нахождения F мы начнем с , приблизительно представляющего компоненты на плоскости xy (на основе величины компонентов и их знака).
Если, например, оба компонента положительны, а компонент x немного больше по величине, мы могли бы представить их примерно так:
Компоненты x и y силы, обе отличные от zeroxyxFyFЗатем мы рисуем прямоугольник с F x и F y в качестве двух сторон:
Прямоугольник, у которого Fx и Fy являются двумя сторонами xyxFyFДиагональ прямоугольника, идущего из начала координат, представляет собой силу F:
Сила F является диагональю прямоугольника FxyxFyFМы можем найти величину F, применяя теорему Пифагора :
F = √F x 2 + Ф г 2
А как насчет направления F?
Направление часто выражается углом направления , то есть углом против часовой стрелки, который F образует с положительной осью x .
Посмотрим, как мы можем его найти:
Сначала найдем θ, угол F образует со своей составляющей F x :
Угол тета, образованный F и его составляющей x FxθyxFyFСогласно тригонометрии:
| F y |
| F x |
После того, как мы нашли θ, мы можем легко определить угол направления.
Иногда θ уже будет углом направления, в других случаях вам нужно будет прибавить θ к 180° или вычесть его из 180° и т. д., это зависит от того, в каком квадранте находится ваша сила.
Ознакомьтесь с приведенными ниже упражнениями, чтобы увидеть несколько примеров.
• Один из двух компонентов равен нулю
Часто компонент силы x или y равен нулю, а другой компонент отличен от нуля.
В этом случае величина и направление силы равны величине и направлению ненулевой составляющей :
Например, предположим, что сила F имеет нулевую составляющую y, а составляющую x > 0:
F x > 0
F y = 0
Если мы представим эти два компонента графически, мы должны увидеть что-то вроде этого:
Компонент x силы F больше 0xFxyF y равен нулю, поэтому мы не можем его увидеть.
Ясно, что F будет направлена в сторону положительной оси x и будет иметь ту же величину, что и F x :
Сила F направлена в сторону положительной оси xFxyF = F x
С другой стороны, если x-компонента F отрицательна,
F x < 0
F y = 0
x-компонент силы F меньше 0xFxy F будет в отрицательном направлении оси x, а величина будет такой же, как у F x .
А так как F x отрицательно, величина будет -F x (помните, что величина всегда положительна ), поэтому: F x
Таким образом, если F x равно −10 Н, то F имеет величину 10 Н.
То же самое можно показать для силы, у которой компонент x равен нулю, а компонент y отличен от нуля. .
• Оба компонента равны нулю
Если оба компонента равны нулю, то сила также равна нулю:
F x = 0
F y = 0
↓
F = 0
Чтобы проверить свое понимание, обязательно выполните приведенные ниже упражнения.
Упражнения
#1
Компонент x силы равен −7,0 Н, компонент y равен 0 Н. Найдите величину и направление силы.
Решение
F x = -7,0 Н
F y = 0 Н
Компонент x силы указывает в отрицательном направлении, компонент y равен zeroxyxFF будет в отрицательном направлении x и будет иметь ту же величину как компонент x:
точек F в отрицательном направлении xFxyF = −F x = 7,0 N
Это −F x , потому что F x отрицательно, а величина должна быть положительной.
#2
Найдите силу, зная, что ее компоненты x и y равны 50,0 Н и 21,2 Н соответственно.
Решение
Сначала мы грубо представим F x и F y на плоскости xy, и из этого мы нарисуем прямоугольник и F. 21.2 N
Force with Fx 50.0N and Fy 21.2NFxθyxFyFLet’s find the magnitude of F applying Pythagoras’ Theorem:
F = √F x 2 + F y 2
F = √50,0 2 + 21,2 2 N
F = √2949 N
F = 54.3 N
Next we find θ:
| θ = tan -1 | F y |
| F x |
| θ = TAN -1 | 21,2 N |
| 50,0 N |
θ = TAN -1
θ = TAN -1
θ = TAN -1
. угол направления F. Действительно, θ — это угол против часовой стрелки, который F образует с положительной осью x.
угол направления F. Действительно, θ — это угол против часовой стрелки, который F образует с положительной осью x.
Следовательно, величина силы равна 54,3 Н, а угол направления равен 23,0°.
#3
Предполагая, что сила имеет компонент x -387 Н и компонент y -532 Н, найдите модуль и направление силы.
Решение
F x = −387 N
F y = −532 N
Сила с компонентами: x -387n и y -532nfxθyxfyfLet’s определяет Malgitud of F:
F:
F:
F:
F:
F:
F:
F:
F:
F:
F:
F:
F:
900FX
let х 2 + F у 2
F = √ (−387) 2 + (−532) 2 N
F = 658 N
и затем θ:
| F x |
| θ = tan -1 | −532 N |
| −387 N |
θ = tan -1 1,37
θ = 53,9°
Нам нужен направляющий угол F, т. е. угол F против часовой стрелки образует с положительной осью x.
е. угол F против часовой стрелки образует с положительной осью x.
Глядя на плоскость xy выше, мы видим, что нам просто нужно добавить 180° к θ. Следовательно, угол направления силы будет 53,9° + 180° = 233,9°:
. Сила образует против часовой стрелки угол 233,9° с положительной осью x FxyxFyF233,9°Следовательно, величина равна 658 Н, а направленный угол равен 233,9. °.
#4
Найдите F, зная, что F x равно −9,48 N и F y 5,67 N.
Решение
F x = −9,45 N
F y = 5.67 N
Force with components: Fx -9.48N and Fy -5.67NFxθyxFyFThe magnitude of F will be:
F = √F x 2 + F y 2
F = √ (−9,48) 2 + (5,67) 2 N
F = √122 N
F = 11,0 N
и θ:
и θ:
|

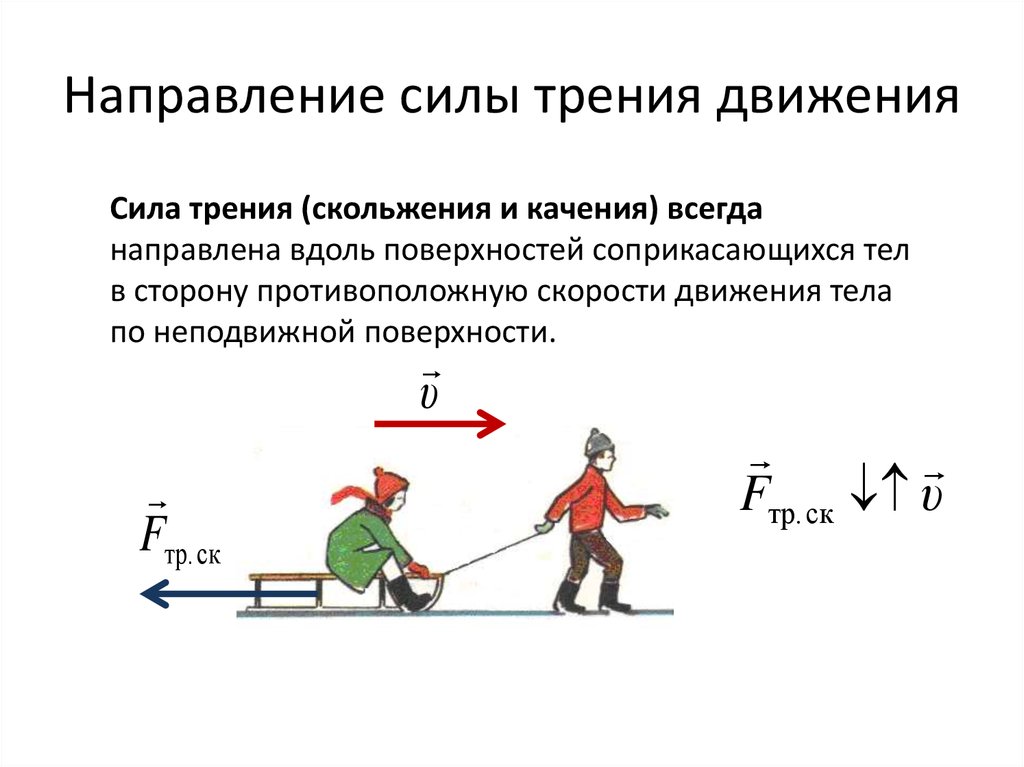 ) 6 букв
) 6 букв вектор или рос. т/канал 3 буквы
вектор или рос. т/канал 3 буквы Вектор — это фундаментальное понятие физики.
Вектор — это фундаментальное понятие физики. е. совмещении острия обращенного вектора А с основанием вектора С с последующим проведением результирующего вектора от основания обращенного вектора А к острию вектора С).
е. совмещении острия обращенного вектора А с основанием вектора С с последующим проведением результирующего вектора от основания обращенного вектора А к острию вектора С). Аналогично, поскольку вектор В “простирается” на 1 метр вверх (в положительном направлении оси X) и на 4 метра вправо (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например В = (1;4).
Аналогично, поскольку вектор В “простирается” на 1 метр вверх (в положительном направлении оси X) и на 4 метра вправо (в положительном направлении оси Y), то его можно выразить в координатах (х,у), например В = (1;4).
 е. самой длинной стороной прямоугольного треугольника, расположенного напротив прямого угла), как показано на рис. 4.8. Если угол не известен, то его можно вывести, если запомнить, что сумма всех углов треугольника равна 180°, а в прямоугольном треугольнике, если вычесть величину прямого угла 90°, то сумма остальных двух углов равна 90°.
е. самой длинной стороной прямоугольного треугольника, расположенного напротив прямого угла), как показано на рис. 4.8. Если угол не известен, то его можно вывести, если запомнить, что сумма всех углов треугольника равна 180°, а в прямоугольном треугольнике, если вычесть величину прямого угла 90°, то сумма остальных двух углов равна 90°.

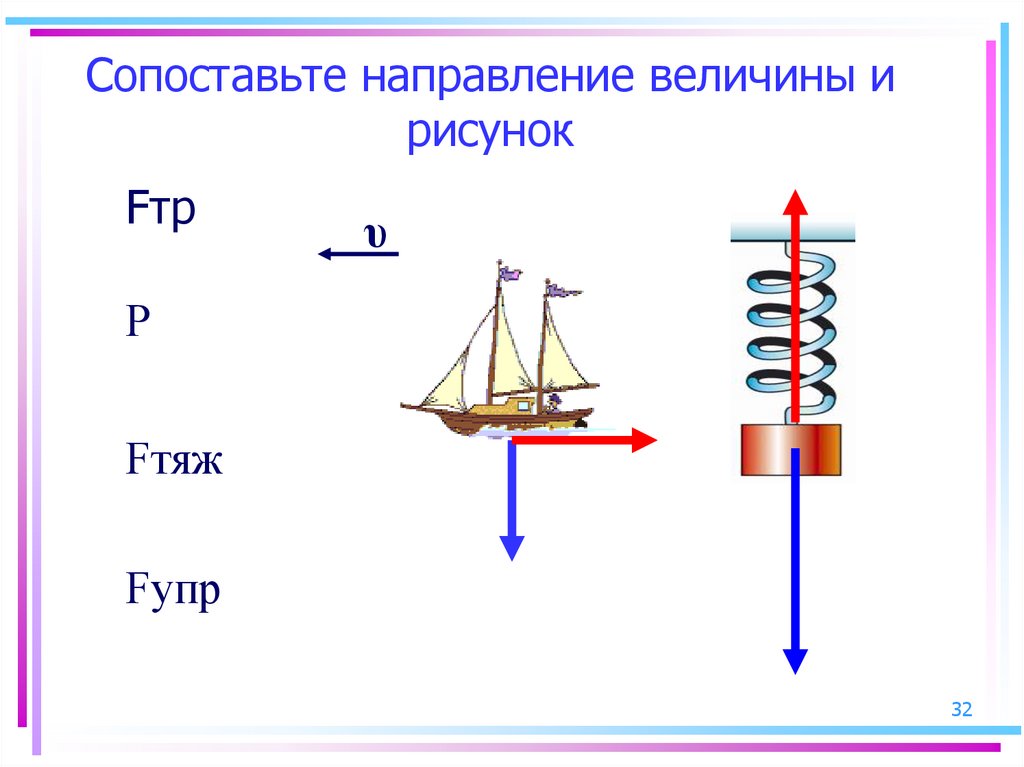

 Тогда в новой системе координат координаты нашего вектора будут (Аx’, Аy’, Аz’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат.
Тогда в новой системе координат координаты нашего вектора будут (Аx’, Аy’, Аz’). Заметьте, сам наш вектор (направленный отрезок в трехмерном пространстве) не изменился. Как бы мы не вращали систему координат, тройка чисел будет меняться, но вектор (в смысле направленного отрезка) останется на своем месте. Он смотрит в одну и ту же «точку вселенной». О как! И длина его не меняется из-за вращения системы координат. Они пока для понимания не столь важны. А важно следующее!
Они пока для понимания не столь важны. А важно следующее! поле
поле тока
тока Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:
Этот вид трения может возникать даже в состоянии покоя или в результате перекатывания одного тела по другому, поэтому здесь выделяют три вида силы трения:


