Калькулятор деления столбиком с остатком
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Данный калькулятор выполнит деление двух целых чисел с остатком и отобразит запись деления столбиком.
Введите целые неотрицательные числа
÷
Как оформлять деление столбиком
- Делимое располагается слева от вертикальной черты, под ним следует записать промежуточное решение, а в конце остаток.

- Справа от вертикальной черты записывается делитель, под ним находится горизонтальная черта.
- Под горизонтальной чертой записывается частное .
Как делить столбиком
Приведем правила деления в столбик с остатком на примере. Разделим 453 на 2.
Первое, что необходимо сделать – это определить неполное делимое. Неполное делимое должно быть меньше делителя. В нашем случае это число 4, выделим это число зеленым цвет
Теперь определим сколько раз число 2 содержится в числе 4. Число 2 содержится в числе 4 два раза. Следовательно, умножаем 2 на 2 и вычитаем результат произведения из неполного делимого 4 – 4 = 0. В результате вычитания у нас получился ноль, поэтому сносим следующую цифру 5 из числа 453 и выделим ее зеленым цветом. Запишем 2 под горизонтальной чертой и выделим синем цветом.
354_
4
50
Далее снова определяем сколько раз делитель – число 2 содержится теперь уже в числе 5. Число 2 содержится в числе 5 два раза.
354_
4
50_
4
1
Сносим последнее число 3, в результате имеем число 13. В числе 13 число 2 содержится 6 раз. Запишем число 6 под горизонтальной чертой. Умножим 6 на 2, получим 12. Вычтем из 13 число 12. 13 – 12 = 1. Остаток от деления = 1.
354_
4
50_
4
31_
21
1
| Вам могут также быть полезны следующие сервисы |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Показать больше |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора.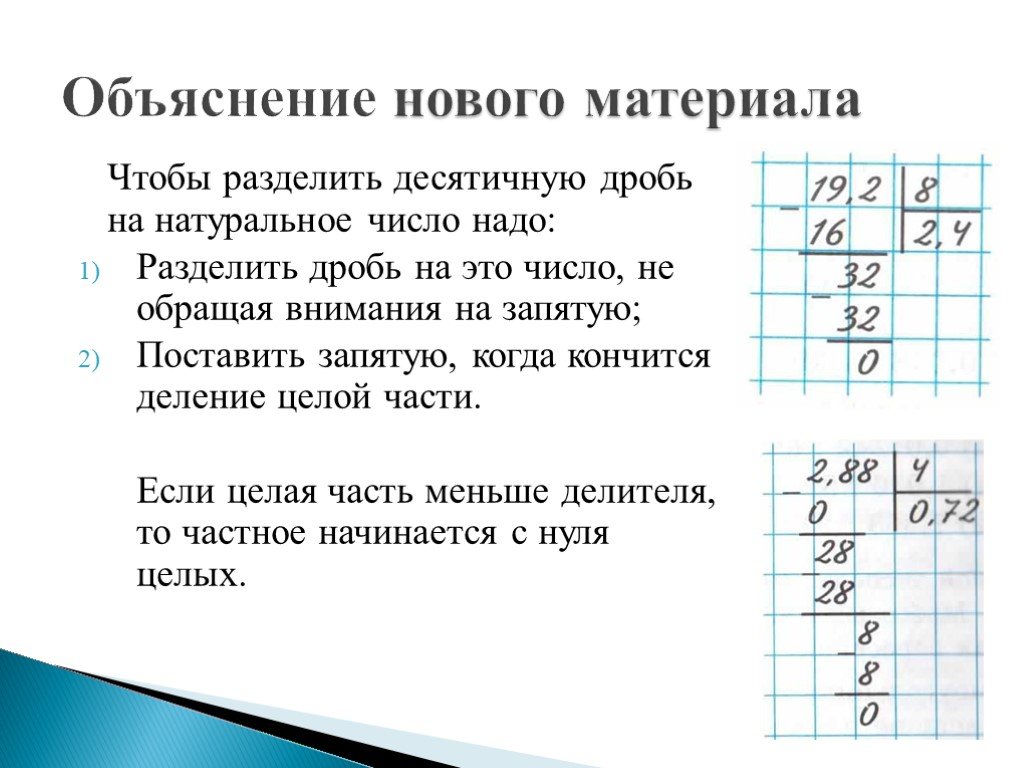 Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Онлайн калькулятор. Деление столбиком. — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
§ Деление в столбик. Как делить столбиком без остатка
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
Математика 5 класс
Математика 6 класс
Алгебра 7 класс
Геометрия 7 класс
Алгебра 8 класс
Алгебра 9 класс
Алгебра 10 класс
Алгебра 11 класс
Когда некто тебе противный что-то тебе доказывает, это и есть доказательство от противного. Это шутка :)Дон-Аминадо
Это шутка :)Дон-Аминадо
Записываем цифру «6» в частное.
Записываем «48» под «51».
Запомните!При записи под неполном частным самая правая цифра неполного частного должна стоять над самой правой цифрой произведения.
Между «51» и «48» слева поставим «−» (минус). Вычтем по правилам вычитания в столбик «48» и под чертой запишем результат.
Если остаток получился больше делителя, значит мы ошиблись в расчете и есть произведение более близкое, чем то, которое взяли мы.
Спишем из делимого «512» цифру «2» к «3».
Число «32» больше «8».
И опять по таблице умножения на «8», найдем ближайшее произведение.
8 · 4 = 32
В остатке получился ноль. Значит числа разделились нацело (без остатка).
Деление столбиком на двузначное число.
 Видео #
Видео #Деление столбиком или, правильнее сказать, письменный прием деления уголком, школьники проходят уже в третьем классе начальной школы, но зачастую этой теме уделяется так мало внимания, что к 9-11 классу не все ученики могут им свободно пользоваться.
Деление столбиком на двузначное число проходят в 4 классе, как и деление на трехзначное число, а далее этот прием используется только как вспомогательный при решении каких-либо уравнений или нахождении значения выражения.
Очевидно, что уделив делению столбиком больше внимания, чем заложено в школьной программе, ребенок облегчит себе выполнение заданий по математике вплоть до 11 класса. А для этого нужно немногое — понять тему и позаниматься, порешать, держа алгоритм в голове, довести навык вычисления до автоматизма.
Для начала повторим кратко, как делить столбиком на однозначное число:
А что если деление с остатком? Смотрим в следующем видео:
youtube.com/embed/Tn-W851Arxs» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Алгоритм деления столбиком на двузначное число
Как и при делении на однозначное число, будем последовательно переходить от деления более крупных счетных единиц к делению более мелких единиц.
1. Находим первое неполное делимое. Это число, которое делится на делитель с получением числа больше или равного 1. Это значит, что первое неполное делимое всегда больше делителя. При делении на двузначное число в первом неполном делимом минимум 2 знака.
Примеры 768:24. Первое неполное делимое 76
265:53 26 меньше 53, значит не подходит. Нужно добавить следующую цифру (5). Первое неполное делимое 265.
2. Определяем количество цифр в частном. Для определения числа цифр в частном следует помнить, что неполному делимому соответствует одна цифра частного, а всем остальным цифрам делимого — еще по одной цифре частного.
Примеры 768:24. Первое неполное делимое 76. Ему соответствует 1 цифра частного. После первого неполного делителя есть еще одна цифра. Значит в частном будет всего 2 цифры.
265:53. Первое неполное делимое 265. Оно даст 1 цифру частного. Больше в делимом цифр нет. Значит в частном будет всего 1 цифра.
15344:56. Первое неполное делимое 153, а после него еще 2 цифры. Значит в частном будет всего 3 цифры.
3. Находим цифры в каждом разряде частного. Сначала найдем первую цифру частного. Подбираем такое целое число, чтобы при умножении его на наш делитель получилось число, максимально приближенное к первому неполному делимому. Цифру частного записываем под уголок, а значение произведения вычитаем столбиком из неполного делителя. Записываем остаток. Проверяем, что он меньше делителя.
Затем находим вторую цифру частного. Переписываем в строку с остатком цифру, следующую за первым неполным делителем в делимом. Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
Полученное неполное делимое снова делим на делитель и так находим каждое последующее число частного, пока не закончатся цифры делителя.
4. Находим остаток (если есть).
Если цифры частного закончились и получился остаток 0, то деление выполнено без остатка. В ином случае значение частного записывается с остатком.
Так же выполняется деление на любое многозначное число (трехзначное, четырехзначное и т. д.)
Разбор примеров на деление столбиком на двузначное число
Сначала рассмотрим простые случаи деления, когда в частном получается однозначное число.
— Найдем значение частного чисел 265 и 53.
Первое неполное делимое 265. Больше в делимом цифр нет. Значит в частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 265 не на 53, а на близкое круглое число 50. Для этого 265 разделим на 10, будет 26 (остаток 5). И 26 разделим на 5, будет 5 (остаток 1). Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Цифру 5 нельзя сразу записывать в частном, поскольку это пробная цифра. Сначала нужно проверить, подойдет ли она. Умножим 53*5=265. Мы видим, что цифра 5 подошла. И теперь можем ее записать в частном под уголок. 265-265=0. Деление выполнено без остатка.
Значение частного чисел 265 и 53 равно 5.
Иногда при делении пробная цифра частного не подходит, и тогда ее нужно менять.
— Найдем значение частного чисел 184 и 23.
В частном будет однозначное число.
Чтобы было легче подобрать цифру частного, разделим 184 не на 23, а на 20. Для этого разделим 184 на 10, будет 18 (остаток 4). И 18 разделим на 2, будет 9. 9 – это пробная цифра, мы ее сразу писать в частном не будем, а проверим, подойдет ли она. Умножим 23*9=207. 207 больше, чем 184. Мы видим, что цифра 9 не подходит. В частном будет меньше 9. Попробуем, подойдет ли цифра 8. Умножим 23*8=184. Мы видим, что цифра 8 подходит. Можем ее записать в частном. 184-184=0. Деление выполнено без остатка.
Значение частного чисел 184 и 23 равно 8.
Рассмотрим более сложные случаи деления.
— Найдем значение частного чисел 768 и 24.
Первое неполное делимое – 76 десятков. Значит, в частном будут 2 цифры.
Определим первую цифру частного. Разделим 76 на 24. Чтобы легче было подобрать цифру частного, разделим 76 не на 24, а на 20. То есть нужно 76 разделить на 10, будет 7 (остаток 6). И 7 разделим на 2, получится 3 (остаток 1). 3 – это пробная цифра частного. Сначала проверим, подойдет ли она. Умножим 24*3=72 . 76-72=4. Остаток меньше делителя. Значит, цифра 3 подошла и теперь мы ее можем записать на месте десятков частного. 72 пишем под первым неполным делимым, между ними ставим знак минус, под чертой записываем остаток.
Продолжим деление. Перепишем в строку с остатком цифру 8, следующую за первым неполным делимым. Получим следующее неполное делимое – 48 единиц. Разделим 48 на 24. Чтобы было легче подобрать цифру частного, разделим 48 не на 24, а на 20. То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
То есть разделим 48 на 10, будет 4 (остаток 8). И 4 разделим на 2, будет 2. Это пробная цифра частного. Мы должны сначала проверить, подойдет ли она. Умножим 24*2=48. Мы видим, что цифра 2 подошла и, значит, можем ее записать на месте единиц частного. 48-48=0, деление выполнено без остатка.
Значение частного чисел 768 и 24 равно 32.
— Найдем значение частного чисел 15344 и 56.
Первое неполное делимое – 153 сотни, значит, в частном будут три цифры.
Определим первую цифру частного. Разделим 153 на 56. Чтобы легче было подобрать цифру частного, разделим 153 не на 56, а на 50. Для этого разделим 153 на 10, будет 15 (остаток 3). И 15 разделим на 5, будет 3. 3 – это пробная цифра частного. Помните: ее нельзя сразу записывать в частном, а нужно сначала проверить, подойдет ли она. Умножим 56*3=168. 168 больше, чем 153. Значит, в частном будет меньше, чем 3. Проверим, подойдет ли цифра 2. Умножим 56*2=112. 153-112=41. Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Остаток меньше делителя, значит, цифра 2 подходит, ее можно записать на месте сотен в частном.
Образуем следующее неполное делимое. 153-112=41. Переписываем в ту же строку цифру 4, следующую за первым неполным делимым. Получаем второе неполное делимое 414 десятков. Разделим 414 на 56. Чтобы удобнее было подобрать цифру частного, разделим 414 не на 56, а на 50. 414:10=41(ост.4). 41:5=8(ост.1). Помните: 8 – это пробная цифра. Проверим ее. 56*8=448. 448 больше, чем 414, значит, в частном будет меньше, чем 8. Проверим, подойдет ли цифра 7. Умножим 56 на 7, получится 392. 414-392=22. Остаток меньше делителя. Значит, цифра подошла и в частном на месте десятков можем записать 7.
Пишем в строку с новым остатком 4 единицы. Значит следующее неполное делимое – 224 единицы. Продолжим деление. Разделим 224 на 56. Чтобы легче было подобрать цифру частного, разделим 224 на 50. То есть сначала на 10, будет 22 (остаток 4). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 224-224=0, деление выполнено без остатка.
Значение частного чисел 15344 и 56 равно 274.
Пример на деление с остатком
Чтобы провести аналогию, возьмем пример, похожий на пример выше, и отличающийся лишь последней цифрой
— Найдем значение частного чисел 15345:56
Делим сначала точно так же, как в примере 15344:56, пока не дойдем до последнего неполного делимого 225. Разделим 225 на 56. Чтобы легче было подобрать цифру частного, разделим 225 на 50. То есть сначала на 10, будет 22 (остаток 5). И 22 разделим на 5, будет 4 (остаток 2). 4 – это пробная цифра, проверим ее, подойдет ли она. 56*4=224. И мы видим, что цифра подошла. Запишем 4 на месте единиц в частном. 225-224=1, деление выполнено с остатком.
Значение частного чисел 15345 и 56 равно 274 (остаток 1).
Деление с нулем в частном
Иногда в частном одним из чисел получается 0, и дети зачастую пропускают его, отсюда неправильное решение. Разберем, откуда может взяться 0 и как его не забыть.
Разберем, откуда может взяться 0 и как его не забыть.
— Найдем значение частного чисел 2870:14
Первое неполное делимое — 28 сотен. Значит в частном будет 3 цифры. Ставим под уголок три точки. Это важный момент. Если ребенок потеряет ноль, останется лишняя точка, которая заставит задуматься, что где-то упущена цифра.
Определим первую цифру частного. Разделим 28 на 14. Подбором получается 2. Проверим, подойдет ли цифра 2. Умножим 14*2=28. Цифра 2 подходит, ее можно записать на месте сотен в частном. 28-28=0.
Получился нулевой остаток. Мы обозначили его розовым для наглядности, но записывать его не нужно. Переписываем в строку с остатком цифру 7 из делимого. Но 7 не делится на 14 с получением целого числа, поэтому записываем на месте десятков в частном 0.
Теперь переписываем в ту же строку последнюю цифру делимого (количество единиц).
70:14=5 Записываем вместо последней точки в частном цифру 5. 70-70=0. Остатка нет.
Значение частного чисел 2870 и 14 равно 205.
Деление нужно непременно проверить умножением.
Примеры на деление для самопроверки
Найдите первое неполное делимое и определите количество цифр в частном.
3432:66 2450:98 15145:65 18354:42 17323:17
Усвоили тему, а теперь потренируйтесь решить несколько примеров столбиком самостоятельно.
1428 : 42 30296 : 56 254415 : 35 16514 : 718
2924 : 68 136576 : 64 710278 : 91 15830 : 293
Математика. Деление уголком | Сайт Леонида Некина
Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Деление «уголком» — это, на мой взгляд, самая тяжелая, самая нудная тема во всей школьной математике. Тут нам придется всерьез поднапрячься. Пусть, однако, нас вдохновляет мысль, что весь последующий материал будет значительно легче и приятнее.
Прежде всего, рассмотрим деление на однозначное число. Допустим, мы хотим вычислить значение выражения
Допустим, мы хотим вычислить значение выражения
648 / 2.
Пользуясь свойствами умножения, мы можем расписать делимое таким образом:
648 =
6 ∙ 100 + 4 ∙ 10 + 8 =
3 ∙ 2 ∙ 100 + 2 ∙ 2 ∙ 10 + 4 ∙ 2 =
( 3 ∙ 100 + 2 ∙ 10 + 4 ) ∙ 2 =
324 ∙ 2 .
После этого становится очевидно, что частное от деления равно
648 / 2 = 324.
Но это мы взяли самый что ни на есть простейший случай, когда каждую отдельно взятую цифру делимого можно поделить на делитель. А вот пример несколько посложнее:
156 / 2 = ?
Здесь первая цифра оказалась меньше делителя. Поэтому, расписывая делимое, мы не будем отрывать ее от второй цифры:
156 =
15 ∙ 10 + 6 .
Поскольку число 15 не делится нацело на 2, придется нам прибегнуть к делению с остатком. Представим результат такого деления в виде:
15 = 7 ∙ 2 + 1 = 14 + 1 .
Теперь мы можем продолжать расписывать наше делимое дальше:
156 =
15 ∙ 10 + 6 =
( 14 + 1 ) ∙ 10 + 6 =
14 ∙ 10 + 1 ∙ 10 + 6 =
14 ∙ 10 + 16 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 =
( 7 ∙ 10 + 8 ) ∙ 2 =
78 ∙ 2 .
Отсюда моментально получаем ответ:
156 / 2 = 78.
Такого рода расчеты можно проводить в уме и сразу же писать ответ. Но мы сейчас перепишем их в виде краткой таблицы. Умение составлять такие таблицы нам пригодится, когда мы займемся делением на многозначные числа, когда всё окажется не так просто. Делимое и делитель запишем так:
1 | 5 | 6 | 2 |
|
|
|
|
|
|
При делении первых двух разрядов ( 15 ) на двойку получается 7 плюс еще какой-то остаток. С этим остатком мы разберемся чуть позже, а пока запишем семерку под чертой снизу от делителя (здесь у нас со временем будет выписан полный ответ):
1 | 5 | 6 | 2 |
|
|
|
| 7 |
|
Умножаем на эту семерку наш делитель ( 2 ) и записываем ответ ( 14 ) под первыми двумя разрядами делимого ( 15 ):
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
Теперь настало время вычислить остаток от деления 15-ти на 2 .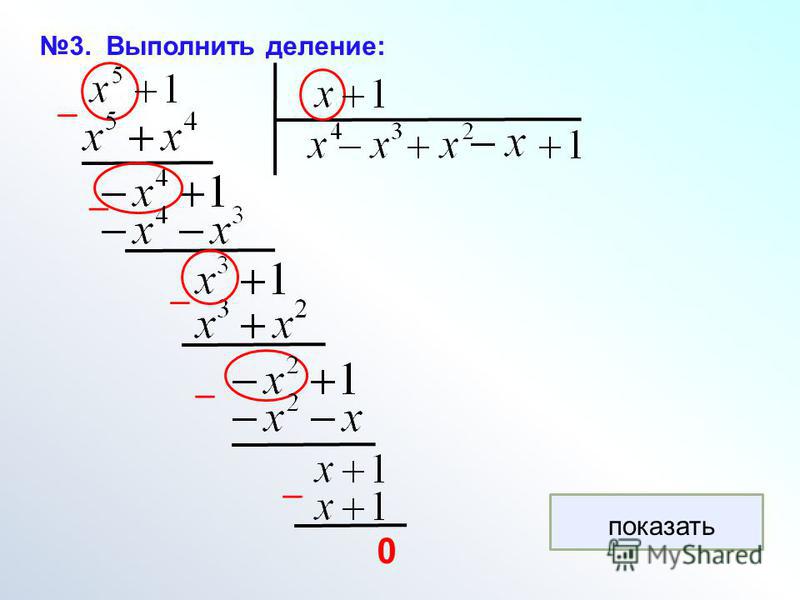 Он равен, очевидно,
Он равен, очевидно,
15 − 2 ∙ 7 = 15 − 14 .
У нас уже всё подготовлено, чтобы выполнить это вычитание «столбиком»:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
| 1 |
|
|
|
У нас получается единица , к которой мы приписываем шестерку из следующего разряда делимого:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 |
|
| 1 | 6 |
|
|
В результате такого приписывания у нас получается число 16 . Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
Мы делим его на наш делитеть ( 2 ) и получаем 8 . Эту восьмерку пишем в строке ответа, под чертой снизу от делителя:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
Ответ мы получили, однако правила составления таблицы таковы, что нам надо добавить в нее еще две строки. Мы должны формальным образом убедиться, что не потеряли остаток от деления. Умножаем делитель ( 2 ) на последнюю цифру ответа ( 8 ), приписываем результат ( 16 ) снизу к нашей таблице в последние два разряда делимого:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
| 1 | 6 |
|
|
Вычитаем последнюю строку из предпоследней и получаем 0:
1 | 5 | 6 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 6 |
|
|
| 1 | 6 |
|
|
|
| 0 |
|
|
Этот последний нуль есть не что иное, как остаток от деления, который образовался бы в том случае, если бы мы рассматривали деление с остатком:
156 : 2 = 78 (ост. 0).
0).
Чтобы получше это понять, возьмем похожий пример, в котором, однако, остаток не равен нулю:
157 : 2 = 78 (ост. 1).
Таблица для этого примера выглядит так:
1 | 5 | 7 | 2 |
|
1 | 4 |
| 7 | 8 |
| 1 | 7 |
|
|
| 1 | 6 |
|
|
|
| 1 |
|
|
Здесь, опять-таки, остаток стоит в последней строке. Для полноты картины распишем наше делимое в таком виде:
157 =
14 ∙ 10 + 17 =
7 ∙ 2 ∙ 10 + 8 ∙ 2 + 1 =
( 7 ∙ 10 + 8 ) ∙ 2 + 1 =
7 8 ∙ 2 + 1
Теперь мы готовы к тому, чтобы делить (нацело или с остатком) на многозначные числа. Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
Это делается при помощи подобной же таблицы (именно из-за ее особого вида данная процедура получила название деление «уголком»). Допустим, требуется выполнить деление с остатком:
135674 : 259 = ?
Приступаем к заполнению таблицы:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
|
|
|
|
|
|
|
|
|
|
В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого ( 1356 ) и получившееся число поделить (с остатком) на делитель ( 259 ). Почему надо взять именно первые четыре цифры делимого? Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число ( 135 ) оказалось бы меньше делителя ( 259 ), а это совсем не то, из чего можно было бы извечь полезную информацию. Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
Итак, возьмем первые четыре цифры делимого и рассмотрим следующее деление с остатком:
1356 : 259 = ?
Тут нам помогут приближенные вычисления, для которых, как мы знаем, вовсе необязательно, чтобы числа делились друг на друга нацело:
1356 / 259 ≈ 1356 / 300 ≈ 1500 / 300 = 15 / 3 = 5 .
Зная результат приближенного деления, мы можем предположить, что, скорее всего,
1356 : 259 = 5 (остаток — пока неважно какой).
Конечно, абсолютной уверенности у нас нет. Здесь вместо пятерки вполне может стоять четверка или шестерка , однако вряд ли мы ошиблись больше, чем на одну единицу. Имея это в виду, тем не менее берем эту пятерку и заносим ее в нашу таблицу в строку ответа. После этого умножаем на нее делитель ( 259 ) и при этом записываем ответ под делимым в подходящие разряды:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 |
|
|
Здесь «маленькие» цифры — это побочный продукт процедуры умножения: мы познакомились с ними, когда учились умножать «в столбик». После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
После того как умножение выполнено, они становятся больше не нужны: на них можно просто не обращать внимания. Выражение 259 ∙ 5 , написанное слева от таблицы, помещено сюда только ради пояснения того, что мы делаем. К таблице оно, собственно, не принадлежит, и в будущем мы такие пояснения выписывать не будем. Тут важно отметить, что результат нашего умножения ( 1295 ) оказался меньше записанного над ним числа 1356 , составленного из первых четырех цифр делимого. Если бы это было не так, то это означало бы, что приближенное деление дало нам завышенный результат. Нам надо было бы тогда зачеркнуть пятерку в строке ответа, на ее место поставить четверку — после чего зачеркнуть и переделать все наши последующие вычисления. Но нам на этот раз повезло, и ничего переделывать не требуется.
Теперь выполняем вычитание в столбик и получаем:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 |
|
|
|
|
| 6 | 1 |
|
|
|
|
|
Внимательно приглядимся к полученной разности ( 61 ). Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
Очень важно, что она оказалась меньше делителя ( 259 ). В противном случае мы пришли бы к выводу, что приближенное деление дало нам заниженный результат и нам пришлось бы теперь исправлять в строке ответа пятерку на шестерку , а также переделывать все последующие вычисления. К счастью, этого не случилось. Приближенное вычисление нас не подвело, и мы теперь совершенно точно знаем, что,
1356 : 259 = 5 (ост. 61 ).
Возвращаемся к таблице. К нашему остатку ( 61 ) приписываем семерку из следующего разряда делимого и приступаем к нахождению второй цифры ответа. Это делается с помощью точно такой же процедуры, что и раньше. Потом — очередь за третьей цифрой. В конце концов таблица принимает такой вид:
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | 5 | 9 |
| 1 | 2 | 4 |
|
|
|
|
|
|
259 ∙ 5 = | 1 | 2 | 9 | 5 |
|
| 5 | 2 | 3 |
|
|
| 6 | 1 | 7 |
|
|
|
|
|
|
| 1 | 1 |
|
|
|
|
|
259 ∙ 2 = |
|
| 5 | 1 | 8 |
|
|
|
|
|
|
|
| 9 | 9 | 4 |
|
|
|
|
|
|
| 1 | 2 |
|
|
|
|
259 ∙ 3 = |
|
|
| 7 | 7 | 7 |
|
|
|
|
|
|
| 2 | 1 | 7 |
|
|
|
Можно выписывать окончательный ответ:
135674 : 259 = 523 (ост. 217).
217).
Самая большая неприятность в делении «уголком» состоит в том, что приближенные вычисления, к которым приходится прибегать по ходу дела, не дают сразу гарантированно правильного результата и нуждаются иногда в последующей коррекции. Впрочем, по мере тренировки, у нас выработается особое чутье и мы будем уже сразу почти наверняка знать, какие цифры следует писать в строке ответа, чтобы потом ничего больше не надо было исправлять и переделывать.
Разумеется, нам будут попадаться случаи, когда частное содержит нули. Каждый такой нуль позволит сделать в таблице небольшие сокращения. Вот пример такой таблицы:
2 | 6 | 2 | 7 | 4 | 0 | 8 | 7 |
|
|
2 | 2 |
|
|
|
|
|
|
|
|
2 | 6 | 1 |
|
|
| 3 | 0 | 2 | 0 |
|
| 1 | 7 | 4 |
|
|
|
|
|
|
| 1 | 1 |
|
|
|
|
|
|
|
| 1 | 7 | 4 |
|
|
|
|
|
|
|
|
| 0 |
|
|
|
|
|
Как и в случае умножения «в столбик», для того чтобы было удобнее писать «маленькие» цифры, нам может понадобиться
лист со специальной линовкой для вычислений (формат pdf).
Теперь остается только тренироваться, тренироваться и тренироваться.
Из «бесконечного» сборника типовых упражнений
Деление нацело на однозначное число
Деление с остатком на однозначное число
Деление с остатком на однозначное число с возможным «приписыванием» нулей
Деление нацело на двузначное число
Деление с остатком на двузначное число
Деление нацело на трехзначное число
Деление с остатком на трехзначное число
как объяснить ребенку деление в столбик
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.

- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.
- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.

- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.
- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Конечно же, дети постигают азы математики на уроках в школе. Но не всегда малышу бывают понятны объяснения учителя. А может ребенок заболел и пропустил тему. В таких случаях родителям стоит вспомнить свои школьные годы, для того чтобы помочь ребенку не упустить важную информацию, без которой дальнейшее обучение будет нереально.
Учить ребенка столбиком начинают в третьем классе. К этому времени таблицей умножения школьник должен уже пользоваться с легкостью. Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Но если существуют с этим проблемы, стоит немедленно ведь перед тем, как научить ребенка делить столбиком, не должно возникать никаких сложностей с умножением.
Как научить делить столбиком?
Возьмем для примера трехзначное число 372 и поделим его на 6. Выбирайте любую комбинацию, но так, чтобы деление прошло без остатка. На первых порах это может запутать юного математика.
Записываем числа, разделяя их уголком, и поясняем ребенку, что данное большое число мы будем постепенно делить на шесть равных частей. Попробуем сначала разделить первую цифру 3 на 6.
Она не делится, а значит, добавляем вторую, то есть попробуем, получится ли поделить 37.
Необходимо спросить у ребенка сколько раз шестерка поместится в цифре 37. Тот, кто без проблем знает математику, сразу догадается, что методом подбора можно подобрать нужный множитель. Итак, давайте подбирать, возьмем, к примеру, 5 и умножим на 6 – получается 30, вроде бы результат недалеко от 37, но стоит попробовать еще раз. Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Для этого 6 множим на 6 – равно 36. Вот это нам подходит, и первая цифра частного уже найдена – записываем ее под делителем, за линией.
Число 36 записываем под 37 и при вычитании получаем единицу. Она опять не делится на 6, а значит, к ней сносим оставшуюся наверху двойку. Теперь число 12 очень легко разделить на 6. В результате получаем второе число частного – двойка. Наш результат деления будет 62.
Однозначные натуральные числа легко делить в уме. Но как делить многозначные числа? Если в числе уже более двух разрядов, устный счет может занять много времени, да и вероятность ошибки при операциях с многоразрядными числами возростает.
Деление столбиком — удобный метод, часто применяемый для операции деления многозначных натуральных чисел. Именно этому методу и посвящена данная статья. Ниже мы рассмотрим, как выполнять деление столбиком. Сначала рассмотрим агоритм деления в столбик многозначного числа на однозначное, а затем — многозначного на многозначное. Помимо теории в статье приведены практические примеры деления в столбик.
Yandex.RTB R-A-339285-1
Удобнее всего вести записи на бумаге в клетку, так как при расчетах разлиновка не даст вам запутаться в разрядах. Сначала делимое и делитель записываются слева направо в одну строчку, а затем разделяются специальным знаком деления в столбик, который имеет вид:
Пусть нам нужно разделить 6105 на 55 , запишем:
Промежуточные вычисление будем записывать под делимым, а результат запишется под делителем. В общем случае схема деления столбиком выглядит так:
Следует помнить, что для вычислений понадобится свободное место на странице. Причем, чем больше разница в разрядах делимого и делителя, тем больше будет вычислений.
Например, для деления чисел 614 808 и 51 234 понадобится меньше места, чем для деления числа 8 058 на 4. Несмотря на то, что во втором случае числа меньше, разница в числе их разрядов больше, и вычисления будут более громоздкими. Проиллюстрируем это:
Практические навыки удобнее всего отрабатывать на простых примерах. Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Поэтому, разделим числа 8 и 2 в столбик. Конечно, данную операцию легко произвести в уме или по таблице умножения, однако провести подробный разбор будет полезно для наглядности, хоть мы и так знаем, что 8 ÷ 2 = 4 .
Итак, сначала запишем делимое и делитель согласно методу деления в столбик.
Следующим шагом нужно выяснить, сколько делителей содержит делимое. Как это сделать? Последовательно умножаем делитель на 0 , 1 , 2 , 3 . . Делаем это до тех пор, пока в результате не получится число, равное или большее, чем делимое. Если в результате сразу получается число, равное делимому, то под делителем записываем то число, на которое умножали делитель.
Иначе, когда получается число, большее чем делимое, под делителем записываем число, вычисленное на предпоследнем шаге.На место неполного частного записываем то число, на которое умножался делитель на предпоследнем шаге.
Вернемся к примеру.
2 · 0 = 0 ; 2 · 1 = 2 ; 2 · 2 = 4 ; 2 · 3 = 6 ; 2 · 4 = 8
Итак, мы сразу получили число, равное делимому. Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Записываем его под делимым, а число 4 , на которое мы умножали делитель, записываем на место частного.
Теперь осталось вычесть числа под делителем (также по методу столбика). В нашем случае 8 — 8 = 0 .
Данный пример — деление чисел без остатка. Число, получащееся после вычитания — это остаток деления. Если оно равно нулю, значит числа разделились без остатка.
Теперь рассмотрим пример, когда числа делятся с остатком. Разделим натуральное число 7 на натуральное число 3 .
В данном случае, последовательно умножая тройку на 0 , 1 , 2 , 3 . . получаем в результате:
3 · 0 = 0 7
Под делимым записываем число, полученное на предпоследнем шаге. По делителем записываем число 2 — неполное частное, полученное на предпоследнем шаге. Именно на двойку мы умножали делитель, когда получили 6 .
В завершение операции вычитаем 6 из 7 и получаем:
Данный пример — деление чисел с остатком. Неполное частное равно 2 , а остаток равен 1 .
Теперь, после рассмотрения элементарых примеров, перейдем к делению многозначных натуральных чисел на однозначные.
Алгоритм деления столбиком будем рассматривать на примере деления многозначного числа 140288 на число 4 . Сразу скажем, что понять суть метода гораздо легче на практических примерах, и данный пример выбран не случайно, так как иллюстрирует все возможные нюансы деления натуральных чисел столбиком.
1. Запишем числа вместе с символом деления столбиком. Теперь смотрим на первую слева цифру в записи делимого. Возможны два случая: число, определяемое этой цифрой, больше, чем делитель, и наоборот. В первом случае мы работаем с этим числом, во втором — дополнительно берем следующую цифру в записи делимого и работаем с соответствующим двузначным числом. Согласно с этим пунктом, выделим в записе примера число, с которым будем работать первоначально. Это число — 14 , так как первая цифра делимого 1 меньше, чем делитель 4 .
2. Определяем, сколько раз числитель содержится полученном числе. Обозначим это число как x = 14 . Последовательно умножаем делитель 4 на каждый член ряда натуральных чисел ℕ , включая нуль: 0 , 1 , 2 , 3 и так далее. Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
Делаем это, пока не получим в результате x или число, большее чем x . Когда в результате умножения получается число 14 , записываем его под выделенным числом по правилам записи вычитания в столбик. Множитель, на который умножался делитель, записываем под делітелем. Если в результате умножения получается число, большее чем x , то под выделенным числом записываем число, полученное на предпоследнем шаге, а на место неполного частного (под делителем) пишем множитель, на который на предпоследнем шаге проводилось умножение.
В соответствии с алгоритмом имеем:
4 · 0 = 0 14 .
Под выделенным числом записываем число 12 , полученное на предпоследнем шаге. На место частного записываем множитель 3 .
3. Столбиком вычитаем из 14 12 , результат записываем под горизонтальной чертой. По аналогии с первым пунктом сравниваем полученное число с делителем.
4. Число 2 меньше числа 4 , поэтому записываем под горизонтальной чертой после двойки цифру,расположенную в следующем разряде делимого. Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Если же в делимом более нет цифр, то на этом операция деления заканчивается. В нашем примере после полученного в предыдущем пункте числа 2 записываем следубщую цифру делимого — 0 . В итоге отмечаем новое рабочее число — 20 .
Важно!
Пункты 2 — 4 повторяются циклически до окончания операции деления натуральных чисел столбиком.
2. Снова посчитаем, сколько делителей содержится в числе 20 . Умножая 4 на 0 , 1 , 2 , 3 . . получаем:
Так как мы получили в результе число, равное 20 , записываем его под отмеченным числом, а на месте частного, в следубщем разряде, записываем 5 — множитель, на который проводилось умножение.
3. Проводим вычитание столбиком. Так как числа равны, получаем в результате число ноль: 20 — 20 = 0 .
4. Мы не будем записывать число ноль, так как данный этап — еще не окончание деления. Просто запомним место, куда мы могли его записать и запишем рядом число из следующего разряда делимого. В нашем случае — число 2 .
Принимаем это число за рабочее и снова выполняем пункты алгоритма.
2. Умножаем делитель на 0 , 1 , 2 , 3 . . и сравниваем результат с отмеченным числом.
4 · 0 = 0 2
Соответственно, под отмеченным числом записываем число 0 , и под делителем в следующий разряд частного также записываем 0 .
3. Выполняем операцию вычитания и под чертой записываем результат.
4. Справа под чертой добавляем цифру 8 , так как это следующая цифра делимого числа.
Таким образом, получаем новое работчее число — 28 . Снова повторяем пункты алгоритма.
Проделав все по правилам, получаем результат:
Переносим под черту вниз последнюю цифру делимого — 8 . В последний раз повторяем пункты алгоритма 2 — 4 и получаем:
В самой нижней строчке записываем число 0 . Это число записывается только на последнем этапе деления, когда операция завершена.
Таким образом, результатом деления числа 140228 на 4 является число 35072 . Данный пример разобран очень подробно, и при решении практических заданий расписывать все действия столь досканально не нужно.
Приведем другие примеры деления чисел в столбик и примеры записи решений.
Пример 1. Деление натуральных чисел в столбик
Разделим натуральное число 7136 на натуральное число 9 .
После второго, третьего и четвертого шага алгоритма запись примет вид:
Повторим цикл:
Последний проход, и поучаем результат:
Ответ: Неполное неполное частное чисел 7136 и 9 равно 792 , а остаток равен 8 .
При решении практических примеров в иделе вообще не использовать пояснения в виде словесных комментариев.
Пример 2. Деление натуральных чисел в столбик
Разделим число 7042035 на 7 .
Ответ: 1006005
Алгоритм деления многозначных чисел в столбик очень похож на рассмотренный ранее алгорим деления многозначного числа на однозначное. Если быть точнее, изменения касаются только первого пункта, а пункты 2 — 4 остаются неизменными.
Если при делении на однозначное число мы смотрели только на первую цифру делимого, то теперь будем смотреть на столько цифр, сколько есть в делителе. Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Когда число, определяемое этими цифрами, больше делителя, принимам его за рабочее число. Иначе — добавляем еще одну цифру из следующего разряда делимого. Затем следуем пунктам описанного выше алгоритма.
Рассмотрим применение алгоритма деления многозначных чисел на примере.
Пример 3. Деление натуральных чисел в столбик
Разделим 5562 на 206 .
В записи делителя участвуют три знака, поэтому в делимом сразу выделим число 556 .
556 > 206 , поэтому принимаем это число за рабочее и переходим к пункту 2 аглоритма.
Умножаем 206 на 0 , 1 , 2 , 3 . . и получаем:
206 · 0 = 0 556
618 > 556 , поэтому под делителем записываем результат предпоследнего действия, а под делимым — множитель 2
Выполняем вычитание столбиком
В результате вычитания имеем число 144 . Справа от результата под чертой записываем число из соответствующего разряда делимого и получаем новое рабочее число — 1442 .
Повторяем с ним пункты 2 — 4 . Получаем:
206 · 5 = 1030
Под отмеченным рабочим числом записываем 1442 , а в следующий разряд частного записываем цифру 7 — множитель.
Выполняем вычитание в столбик, и понимаем, что на этом операция деления окончена: в делителе более нет цифр, чтобы записать их правее от результата вычитания.
В завершение данной темы приведем еще один пример деления многозначных чисел в столбик, уже без пояснений.
Пример 5. Деление натуральных чисел в столбик
Разделим натуральное число 238079 на 34 .
Ответ: 7002
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Первые годы школьной жизни в младших классах ребенку даются нелегко. Часто после урока математики они не совсем хорошо понимают пройденную тему. Чтобы помочь ребенку в усвоении пройденного материала, потребуется самому объяснить школьнику то, что ему не понятно. На помощь приходят родители, у которых моментально возникает вопрос: «Как объяснить ребенку деление?». Сделать это можно несколькими способами, но изначально стоит убедиться, что ребенок хорошо усвоил такие математические действия, как сложение, вычитание и умножение . (Прочитать про способы обучения детей сложению и умножению можете и ).
(Прочитать про способы обучения детей сложению и умножению можете и ).
Обучение ребенка основам деления
Важно, чтобы ребенок понимал суть такого математического действия, как деление. Для этого необходимо ему объяснить, что деление представляет собой разделение чего-либо на равные доли. Рекомендуется превратить процесс обучения в интересную игру, чтобы ребенок был сконцентрирован.
Деление в игровой форме
СОВЕТ: Таблицу деления так же важно выучить, как и таблицу умножения. Лучше это делать на каникулах!
Помогите ребенку понять, что деление — это обратное действие умножению.
Самым простым способом объяснить деление является проведение наглядной демонстрации разделения предметов на равные доли . В качестве делимых предметов можно использовать все, что угодно, но желательно что-то интересное для ребенка. В качестве примера можно воспользоваться конфетами и игрушками.
Как объяснить ребенку деление при помощи игрушек?
Изначально нужно взять 2 конфеты и попросить ребенка разделить их между 2 плюшевыми игрушками. Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.
Благодаря такому простому примеру ребенок поймет суть математического деления. После этого можно переходить к более сложным примерам деления.
Как происходит деление, подробно и в игровой форме показывается в следующем видео:
Также вы можете взять коробку цветных карандашей, которая будет выступать одним целым, и предложить малышу разделить их между собой и вами поровну. После, попросите ребенка посчитать, сколько карандашей было вначале в коробке и сколько он смог раздать.
По мере понимания ребенка, родитель может увеличивать число предметов и количество участников задачи. Затем нужно рассказать, что не всегда получается разделить что-либо поровну и некоторые предметы иногда остаются «ничейными». К примеру, можно предложить разделить 9 яблок между бабушкой, дедушкой, папой и мамой. Ребенок должен понять, что все получат лишь по 2 яблока, а одно окажется в остатке.
Деление в игровой форме
Таким образом, вы объясните азы деления и подготовите ребенка к более сложным школьным задачам.
СОВЕТ: Старайтесь заниматься со своим ребенком в игровой форме. Тогда ему будет интересно заниматься, а значит, занятия пройдут весело и без особых усилий.
Также вам будет интересно и полезно распечатать таблицу деления в виде картинки.
Делить однозначные числа на однозначные проще всего с использованием . Для этого достаточно объяснить ребенку, что деление является действием обратным к умножению. Сделать это можно на любом правильном примере деления натуральных чисел.
Например: 2 умножить на 3 будет 6. Основываясь на данном примере продемонстрировать ребенку процесс деления. Следует действовать следующим образом: разделить 6 на любой множитель, например, на число 2. В ответе получится 3, то есть множитель неиспользованный при делении.
Таким способом можно делить многозначные (двухзначные) числа на однозначные.
Алгоритм деления в столбик
Прежде, чем начать объяснение деления в столбик, нужно рассказать ребенку о значении делимого, делителя и частного. В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.
В примере 20:4=5, 20 является делимым, 4 делителем, а 5 частным. У каждой отдельной цифры в примере одно наименование.
Многозначные числа (трехзначные и двухзначные) проще всего делить в столбик. Для этого нужно записать многозначные числа уголком.
Например, нужно разделить трехзначное число 369 на однозначное число 3.
В качестве делителя записано трехзначное число 369 , а в качестве делителя однозначное число 3. Первым делом важно объяснить ребенку, что деление в столбик происходит в несколько этапов:
- Определение части делимого подходящего для первичного деления. В данном случае цифра 3. 3:3=1. Цифру 1 нужно записать в графу частное.
- «Спустить» следующее делимое число. В данном случае это цифра 6. 6:3=2 . Полученное число 2 нужно записать в частное.
- Далее необходимо «спустить» следующее делимое число 9. 9 делится без остатка на 3, полученный результат необходимо записать в частное. Результатом деления трехзначного числа 369 на 3 получается 123.

Деление десятичного числа на двухзначное проходит примерно так же. В случае с десятичным числом необходимо объяснить ребенку, что запятую в делителе переносят на столько знаков, на сколько перенесли в делимом. Далее следует обычное деление в столбик.
Необходимо предупредить ребенка о встречающихся случаях деления с остатком. В качестве примера можно поделить двухзначное число 26 на 5 столбиком. В результате остается остаток 1.
Важно после объяснения позволить ребенку самостоятельно решить несколько примеров, чтобы весь изученный материал надолго остался в памяти ребенка.
А еще Вы можете посмотреть видео, где все объясняют понятным языком.
И напоследок, не приучайте себя и ребенка пользоваться онлайн калькулятором, чтоб узнать, как разделить 145 на 9, 34 на 40, 100 на 4, 30 на 80, 416 на 52 и другие примеры. Это не принесет пользы не вам, ни ему.
В 1-ый класс идет не только ребенок – родители вместе с ним начинают и вместе с ним заканчивают образовательное учреждение. Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений. Тогда все у вас получится.
Учитель в школе не всегда успевает объяснить каждому отдельному ученику ту или иную дисциплину. Поэтому у — свои плюсы. Вы можете сами объяснить ребенку, индивидуально и не спеша то, что он не понял. В этот непростой период, главное — это набраться терпения и не ругать школьника из-за неправильных решений. Тогда все у вас получится.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей. Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
- В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5.
 Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8. Запишите в столбик задачу.
- Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3.
 К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным. - При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5. То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления.
Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
правила, методы, примеры как делить квадратные корни
Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.
Единственное, что необходимо все время держать в голове — подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.
Метод 1. Деление подкоренных выражений
Алгоритм действий:
Записать дробь
Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.
Пример 1
144÷36, это выражение следует переписать так: 14436
Использовать один знак корня
В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.
Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.
Пример 2
14436. Это выражение следует записать так: 14436
Это выражение следует записать так: 14436
Разделить подкоренные выражения
Просто разделите одно выражение на другое, а результат запишите под знаком корня.
Пример 3
14436=4, запишем это выражение так: 14436=4
Упростить подкоренное выражение (если необходимо)
Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.
Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.
Пример 4
4 — полный квадрат, потому что 2×2=4. Из этого следует:
4=2×2=2. Поэтому 14436=4=2.
Метод 2. Разложение подкоренного выражения на множители
Алгоритм действий:
Записать дробь
Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.
Пример 5
8÷36, переписываем так 836
Разложить на множители каждое из подкоренных выражений
Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.
Пример 6
Упростить числитель и знаменатель дроби
Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.
Пример 7
2266×62×2×2, из этого следует: 836=226
Рационализировать знаменатель (избавиться от корня)
В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него.
Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.
Пример 8
В выражении 623 необходимо умножить числитель и знаменатель на 3, чтобы избавиться от него в знаменателе:
623×33=62×33×3=669=663
Упростить полученное выражение (если необходимо)
Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.
Пример 9
26 упрощается до 13; таким образом 226упрощается до 123=23
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Метод 3. Деление квадратных корней с множителями
Алгоритм действий:
Упростить множители
Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!
Пример 10
432616. Сначала сокращаем 46: делим на 2 и числитель, и знаменатель: 46=23.
Сначала сокращаем 46: делим на 2 и числитель, и знаменатель: 46=23.
Упростить квадратные корни
Если числитель нацело делится на знаменатель, то делите. Если нет, то упрощайте подкоренные выражения, как и любые другие.
Пример 11
32 делится нацело на 16, поэтому: 3216=2
Умножить упрощенные множители на упрощенные корни
Помним про правило: не оставлять в знаменателе корни. Поэтому просто перемножаем числитель и знаменатель на этот корень.
Пример 12
Рационализировать знаменатель (избавиться от корня в знаменателе)
Пример 13
4327. Следует умножить числитель и знаменатель на 7, чтобы избавиться от корня в знаменателе.
437×77=43×77×7=42149=4217
Метод 4. Деление на двучлен с квадратным корнем
Алгоритм действий:
Определить, находится ли двучлен (бином) в знаменателе
Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.
Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.
Пример 14
15+2— в знаменателе присутствует бином, поскольку есть два одночлена.
Найти выражение, сопряженное биному
Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.
Пример 15
5+2и 5-2 — сопряженные биномы.
Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе
Такая опция поможет избавиться от корня в знаменателе, поскольку произведение сопряженных двучленов равняется разности квадратов каждого члена биномов: (a-b)(a+b)=a2-b2
Пример 16
15+2=1(5-2)(5-2)(5+2)=5-2(52-(2)2=5-225-2=5-223.
Из этого следует: 15+2=5-223.
Советы:
- Если вы работаете с квадратными корнями смешанных чисел, то преобразовывайте их в неправильную дробь.

- Отличие сложения и вычитания от деления — подкоренные выражения в случае деления не рекомендуется упрощать (за счет полных квадратов).
- Никогда (!) не оставляйте корень в знаменателе.
- Никаких десятичных дробей или смешанных перед корнем — необходимо преобразовать их в обыкновенную дробь, а потом упростить.
- В знаменателе сумма или разность двух одночленов? Умножьте такой бином на сопряженный ему двучлен и избавьтесь от корня в знаменателе.
Деление чисел. Делимое, делитель, частное
Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.
Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:
1) 6 — 2 = 4,
2) 4 — 2 = 2,
3) 2 — 2 = 0.
Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:
2 + 2 + 2 = 2 · 3 = 6.
Для записи деления используется знак :
(двоеточие), который ставится между числами. Например:
6 : 2.
Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак =
(равно), после которого записывается полученный результат:
6 : 2 = 3.
Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?
Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.
Решение можно записать так:
9 : 3 = 3.
Ответ: 3 пучка.
Пример. Решить примеры на деление с помощью схем.
Решение:
1) 4 : 2 = 2;
2) 12 : 4 = 3, 12: 3 = 4.
Делимое, делитель и частное
Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:
12 : 3,
12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.
Делитель показывает на сколько равных частей нужно разделить делимое.
Частное — это число, которое получается в результате деления. Например, в записи:
12 : 3 = 4,
4 — это частное. При этом сама запись 12 : 3 тоже называется частным.
Эта запись читается так: частное двенадцати и трёх равняется четырём
или двенадцать разделить на три равно четырём
.
Проверка деления
Рассмотрим выражение:
28 : 4 = 7,
где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:
- Умножить частное на делитель:
7 · 4 = 28,
или умножить делитель на частное:4 · 7 = 28,
если получится делимое, то деление было выполнено верно. - Разделить делимое на частное, если получиться делитель, то деление было выполнено верно:
28 : 4 = 7.
Как объяснить ребенку деление и умножение чисел
Искусство учиться
Как объяснить ребенку деление и умножение чисел
3 апреля 2018 59 068 просмотров
Лиана Хазиахметова
Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.
Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.
Умножение чисел
При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.
Иллюстрация из книги «Как объяснить ребенку математику»
Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.
Некоторые числа легко умножать, зная особые приемы. Вот они.
Таблица из книги «Как объяснить ребенку математику»
В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.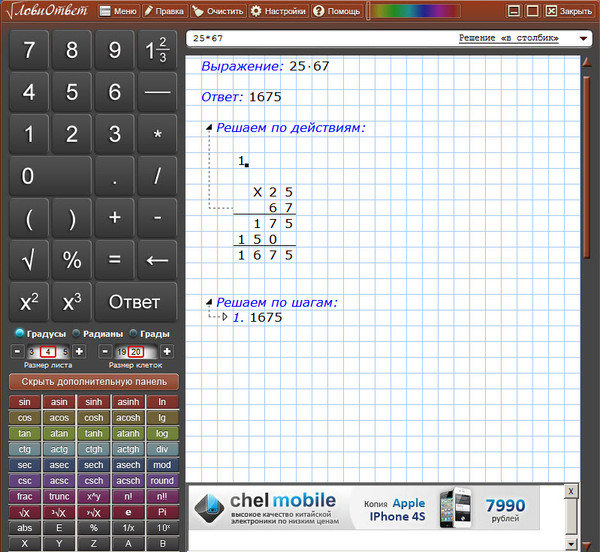
Деление чисел
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.
Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.
Деление как распределение. Из книги «Как объяснить ребенку математику»
Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.
Деление и умножение лучше рассматривать параллельно, чтобы ребенок увидел взаимосвязь. В книге «Как объяснить ребенку математику» есть объяснения более сложных операций, например, деления с остатком, умножения в столбик и так далее. Если визуально показать, как это делается, ребенку легче будет усвоить материал.
Если визуально показать, как это делается, ребенку легче будет усвоить материал.
Рабочие тетради на деление и умножение
Если ваш ребенок освоил азы деления и умножения, то сейчас ему нужна практика. Японская система Kumon предлагает рабочие тетради «Математика. Деление. Уровень 4»
и «Математика. Умножение. Уровень 4». Постепенно, решая все более сложные задачи, ребенок научится работать с большими цифрами. Ниже — пример одного из последних заданий тетради с делениями.
Пример из тетради «Математика. Деление. Уровень 4»
Такие примеры ребенок научится решать легко и быстро, если тренироваться регулярно и по принципу от простого к сложному. Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».
По материалам книги «Как объяснить ребенку математику», рабочих тетрадей «Математика. Деление. Уровень 4» и «Математика. Умножение. Уровень 4».
Обложка поста: pixabay.com
Как решать задачи на деление — математический блог для дифференциации
Как решать задачи разделения
Изучите части проблемы разделения и способы их решения за несколько простых шагов.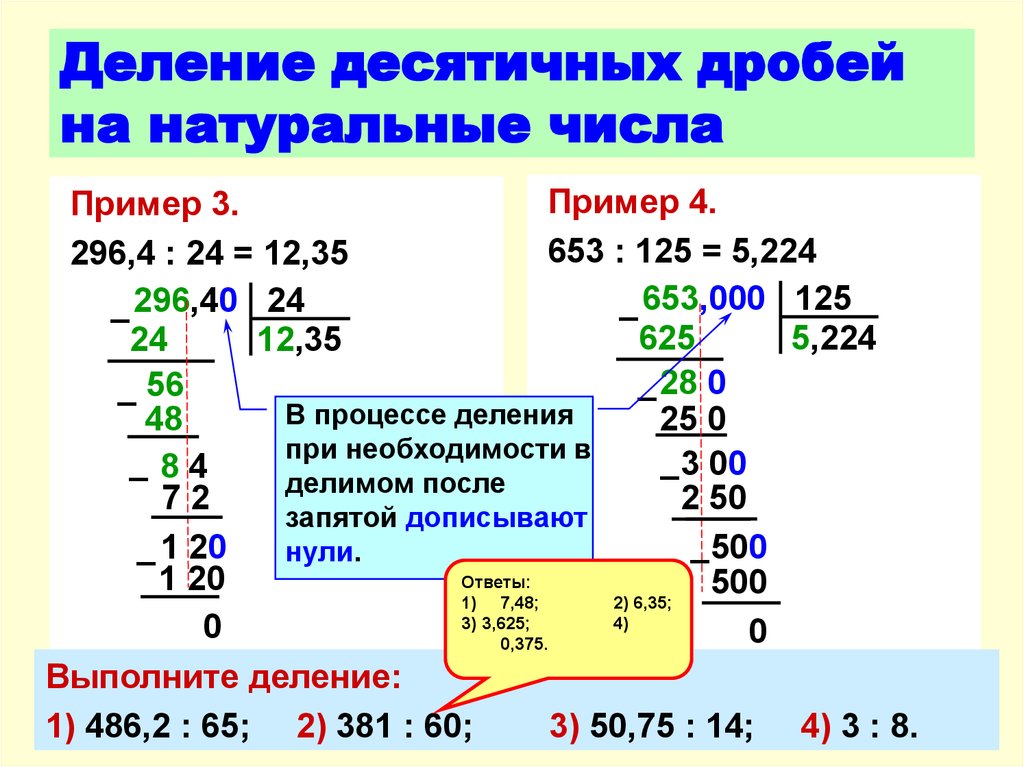
У вас 20 файлов cookie и 10 друзей. Сколько файлов cookie вы должны подарить каждому из своих друзей?
Это основная проблема деления.
Деление — это одна из четырех основных операций: сложение, вычитание и умножение — это три других.
Деление — это простая операция деления числа. Проще всего представить это как количество объектов, разделенных между определенным количеством людей, как в приведенном выше примере. Конечно, чтобы быть честным, вы всегда хотите дать каждому человеку одинаковую сумму! По сути, так и работает деление: вы делите числа на равные группы чисел.
Итак, как можно решить проблему разделения? Во-первых, вы должны знать части проблемы разделения.
Части задачи разделения
Проблема деления состоит из трех основных частей: делимого, делителя и частного.
Дивиденд — это число, которое будет разделено. Делитель — это количество «людей», между которыми делится это число. Частное — это ответ.
Как решать задачи разделения
Решение простых задач деления тесно связано с умножением. Фактически, чтобы проверить свою работу, вам придется умножить частное на делитель, чтобы увидеть, равно ли оно дивиденду. Если нет, значит, вы решили неправильно.
Фактически, чтобы проверить свою работу, вам придется умножить частное на делитель, чтобы увидеть, равно ли оно дивиденду. Если нет, значит, вы решили неправильно.
Давайте попробуем решить одну простую задачу деления.Например:
12 ÷ 2 =
https://happynumbers.com/demo/cards/302938?mode=preview
В этой задаче вы можете увидеть, как «Счастливые числа» помогают детям визуализировать задачу. Всего 12 апельсинов. По 2 штуки в каждую коробку. Сколько там ящиков?
Ответ: 6.
Вы можете проверить ответ, умножив частное 6 на делитель 2 (6 x 2), что дает нам 12. Итак, ответ правильный.
Что такое остаток по математике?
Возможно, вы слышали об остатке и задавались вопросом, что такое остаток в математике?
Остаток в математике используется, когда задача деления не получается равномерной.Например:
11 ÷ 4 =
.
https://happynumbers.com/demo/cards/303658?mode=preview
Как вы можете видеть в приведенном выше примере теннисных мячей, сначала мячи делятся на группы по 4.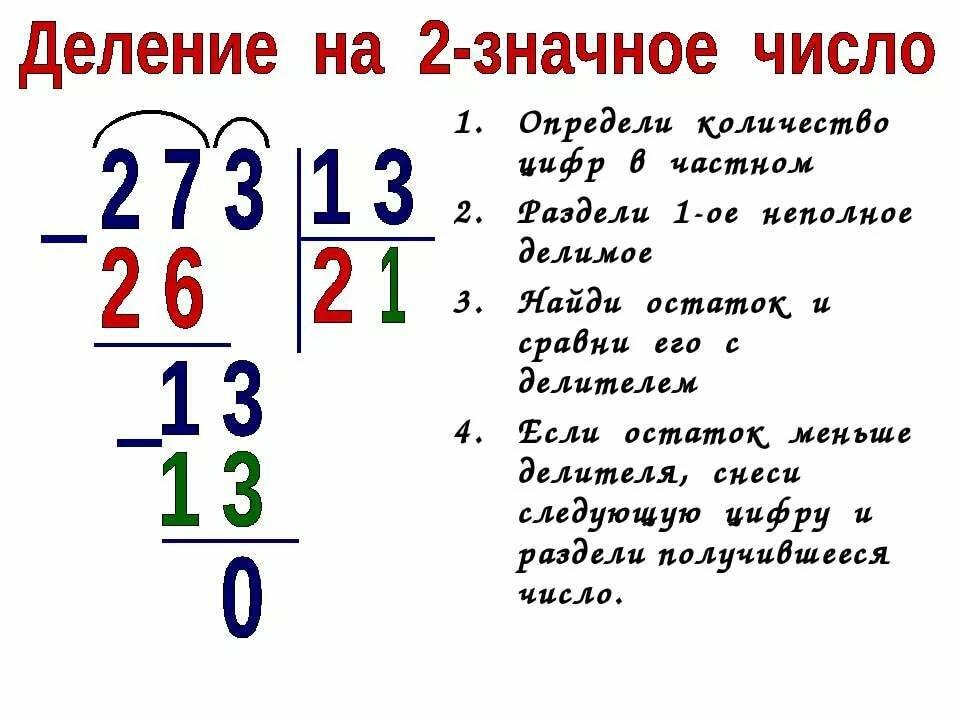 Однако после создания 2 групп мячей остается 3 мяча, которые не могут образовать группу из 4. Это остаток. Таким образом, частное равно 2 (можно составить 2 группы по 4), а остаток равен 3.
Однако после создания 2 групп мячей остается 3 мяча, которые не могут образовать группу из 4. Это остаток. Таким образом, частное равно 2 (можно составить 2 группы по 4), а остаток равен 3.
Чтобы проверить работу, умножьте частное 2 на делитель 4. Ответ: 8. Затем сложите остаток от 3.Ответ — 11, что было первоначальным дивидендом, так что ответ правильный.
Дивизион может становиться все сложнее и сложнее по мере увеличения числа. Затем вы должны использовать такие стратегии, как деление в столбик, оценка и другие, чтобы определить ответы. Однако с помощью этих основных шагов вы можете решить практически любую проблему разделения.
Разделите два числа — WebMath
Быстрый! Мне нужна помощь с: Выберите пункт справки по математике…Calculus, DerivativesCalculus, IntegrationCalculus, Quotient RuleCoins, CountingCombrations, Finding allComplex Numbers, Adding ofComplex Numbers, Calculating withComplex Numbers, MultiplyingComplex Numbers, Powers ofComplex NumberConversion, SubtractingConversion, TemperatureConversion, FindConversion, MassConversion, Mass анализ AverageData, поиск стандартного отклонения, анализ данных, гистограммы, десятичные дроби, преобразование в дробь, электричество, стоимость факторинга, IntegerFactors, Greatest CommonFactors, Least CommonFractions, AddingFractions, ComparingFractions, ConvertingFractions, Convert to a decimalFractions, DividingFractions, MultiplyingFractions, SubplicationFractions are, SubplicationFractions , BoxesGeometry, CirclesGeometry, CylindersGeometry, RectanglesGeometry, Right TrianglesGeometry, SpheresGeometry, SquaresGraphing, LinesGraphing, Любая функцияGraphing, CirclesGraphing, EllipsesGraphing, HyperbolasGraphing, InequalitiesGraphing, Polar PlotGraphing, (x, y) pointInequalities, GraphingInequalities, SolvingInterest, CompoundInterest, SimpleLines, The Equation from point and slopeLines, Equation from slope и y-intLines, The Equation from two pointsLodsottery Практика полиномов Математика, Практика основ , Факторинг разности квадратов многочленов, разложение на множители трехчленов, многочленов, разложение на множители с GCF, многочлены, умножение многочленов, возведение в степень ns, Решить с помощью факторинга Радикалы, Другие корни Радикалы, Отношения квадратного корня, Что они собой представляют, Выведение на пенсию, Экономия на продажной цене, РасчетНаучная нотация, ПреобразованиеНаучной нотации, РазделениеНаучная нотация, Умножение форм, ПрямоугольникиУпрощение, Все, что угодноУпрощение, Образцы, Образцы, Упрощение, Методы Правые треугольники, Ветер, рисунок
Калькулятор длинного деления
— с шагами для решения
Введите делитель и делимое ниже, чтобы вычислить частное и остаток с использованием длинного деления. Результаты и шаги по ее решению показаны ниже.
Результаты и шаги по ее решению показаны ниже.
Результат:
| Полный ответ: | 18 R 3 |
|---|---|
| Частное: | 18 |
| остаток: | 3 |
Решение:
Как сделать длинное деление с остатками
Изучение деления в столбик — важнейшая веха в освоении основных математических навыков и обряд перехода к окончанию начальной школы.Это внушает страх как ученикам начальной школы, так и их родителям.
Недавнее исследование показало, что понимание деления в столбик и дробей в начальной школе напрямую связано со способностью ученика изучать и понимать алгебру позже в школе. [1]
Не бойся!
Выучить деление в столбик может быть легко, и всего за несколько простых шагов вы сможете решить любую задачу деления в столбик. Продолжайте, пока мы разбираем это, но сначала нам нужно охватить анатомию проблемы деления на столбик.
Части задачи о длинном делении
Как показано на изображении выше, проблема длинного деления состоит из нескольких частей.
Делимое — это число справа и под линией деления, которое является делимым числом.
Делитель — это число слева от линии деления и число, на которое делится.
Частное является решением и отображается над делимым над линией деления.Часто при длинном делении частное — это целая числовая часть решения.
Остаток — это оставшаяся часть решения или то, что осталось, что не входит равномерно в частное.
Шаги для решения задачи о длинном делении
Есть несколько основных шагов к решению проблемы длинного деления: деление, умножение, вычитание, уменьшение числа и повторение процесса.
Шаг первый: установите уравнение
Первым шагом в решении задачи деления в столбик является составление уравнения, которое необходимо решить.Если проблема уже связана с длинным разделением, переходите к шагу два.
Если это не так, вот как нарисовать задачу о делении в столбик.
Начните с рисования вертикальной черты для разделения делимого и делимого и верхней черты для разделения делимого и частного.
Разместите дивиденд справа от вертикальной полосы под полосой сверху. Разместите делитель слева от вертикальной черты.
Например, , чтобы разделить 75 на 4, задача длинного деления должна выглядеть так:
Шаг второй: разделите
Решив задачу деления в столбик, начните с деления первой цифры делимого на делитель.
Вы также можете думать об этом как о подсчете того, сколько раз делитель попадет в цифру в делимом.
Отбросьте остаток или десятичную часть результата и запишите целую числовую часть результата в частном над верхней чертой непосредственно над цифрой в делимом.
Например, , делитель «4» переходит в первую цифру делимого «7» два раза, поэтому к частному можно прибавить «1».
Шаг третий: умножить
Следующим шагом будет умножение делителя на цифру, добавленную к частному. Напишите результат под цифрой делимого.
Напишите результат под цифрой делимого.
Этот шаг формирует следующую часть уравнения для следующего шага.
Умножение делителя «4» на «1», которое мы нашли на предыдущем шаге, дает «4». Итак, добавьте «4» под первой цифрой делимого.
Шаг четвертый: вычесть
Теперь добавьте знак минус «-» перед числом, добавленным на предыдущем шаге, и проведите линию под ним, чтобы сформировать уравнение вычитания.
Продолжая приведенный выше пример, добавьте «-» перед «4» и линию вычитания под ним.
Теперь, когда у вас есть задача на вычитание, пора ее решить.
Чтобы решить, вычтите «7» минус «4», что равно «3», поэтому запишите «3» в уравнение.
Если в задаче с делением в столбик делимое состоит из одной цифры, то ура, готово! Оставшееся число, которое является результатом задачи вычитания, является остатком, а число над делимым является решенным частным.
Если в дивиденде осталось больше цифр, переходите к следующему шагу.
Шаг пятый: потяните вниз следующее число
На этом этапе пора работать со следующим числом в дивиденде. Для этого потяните вниз следующую цифру в делимом и поместите ее прямо справа от результата задачи вычитания, описанной выше.
Для этого потяните вниз следующую цифру в делимом и поместите ее прямо справа от результата задачи вычитания, описанной выше.
Следующая цифра делимого — «5». Итак, потяните «5» вниз и запишите его рядом с «3», найденным на предыдущем шаге.
Шаг шестой: повторите
На этом этапе вам может быть интересно, куда идти дальше.Повторяйте шаги со второго по пятый, пока все цифры делимого не будут убраны, разделены, умножены и вычтены.
При делении используйте результат задачи на вычитание в сочетании с опущенной цифрой в качестве делимого и разделите на него делитель.
Продолжая приведенные выше примеры, разделите результат задачи на вычитание и уменьшенную цифру на делитель. Таким образом, следующий шаг — разделить 35 на 4. Результатом будет «8», поэтому прибавьте «8» к частному.
Затем умножьте цифру частного «8» на делитель «4», который равен 32. Добавьте «32» к задаче деления в столбик.
Затем повторите процесс вычитания, вычтя 32 из 35, что равно 3. Добавьте «3» под линией вычитания. Поскольку в дивиденде больше нет оставшихся цифр, это оставшаяся часть решения.
Добавьте «3» под линией вычитания. Поскольку в дивиденде больше нет оставшихся цифр, это оставшаяся часть решения.
По мере того, как вы практикуете эти шаги, используйте калькулятор выше, чтобы подтвердить свой ответ и проверить свои шаги при решении задач с длинным делением.
Как получить частное и остаток в виде десятичной дроби
Если вы зашли так далеко, то у вас должно быть хорошее представление о том, как вычислить задачу деления в столбик, но вы можете застрять, если вам нужно получить частное в виде десятичной дроби, а не целого числа с остатком.
Чтобы вычислить частное в десятичной форме, выполните указанные выше действия, чтобы получить целое число и остаток.
Затем разделите делитель на остаток, чтобы получить остаток в виде десятичной дроби.Наконец, добавьте десятичное число к частному, чтобы получить его в десятичной форме.
Например, , 75 ÷ 4 равно 18 с остатком 3.
Разделите 3 на 4, чтобы получить 0,75 десятичной дроби.
3 ÷ 4 = 0,75
Затем прибавьте 0,75 к 18, чтобы получить частное в виде десятичной дроби.
0,75 + 18 = 18,75
Таким образом, десятичная форма 75 ÷ 4 равна 18,75.
Пошаговое руководство по продольному делению
Что такое продольное деление?
Деление в столбик — это способ решения задач деления с большими числами.По сути, это задачи деления, которые вы не можете решить в уме.
Начало работы
Одна из проблем, с которой учащиеся сталкиваются с задачами деления в столбик, — это запоминание всех шагов. Вот трюк, чтобы научиться делить в столбик. Используйте аббревиатуру DMSB, что означает:
.
D = разделить
M = умножить
S = вычесть
B = сбить
Эта последовательность букв может быть трудно запомнить, поэтому подумайте об аббревиатуре в контексте семьи:
Папа, мама, сестра, брат.
Напишите D M S B в углу листа, чтобы запомнить последовательность, которую вы собираетесь использовать.
Как записать
Во-первых, вы должны записать проблему в формате длинного деления. Типичная задача деления выглядит так:
Дивиденд ÷ Делитель = Частное
Чтобы записать это в формате длинного деления, это выглядит так:
Давайте попробуем довольно простой пример:
65 ÷ 5 =?
Теперь давайте запишем эту проблему в формате длинного деления:
Мы готовы использовать аббревиатуру: D M S B
Шаг 1: D для разделения
Сколько раз 5 перейдет в 65? Это слишком сложно, чтобы обдумать это, поэтому давайте разберемся на более мелкие шаги.
Первая проблема, которую вы решите в этом уравнении, — сколько раз вы можете разделить 5 на 6. Ответ — 1. Итак, вы помещаете 1 в линию частного.
Шаг 2: M для умножения
Вы умножаете свой ответ из шага 1 на ваш делитель: 1 x 5 = 5. Вы пишете 5 под 6.
Шаг 3: S для вычитания
Далее вы вычитаете. В этом случае это будет 6 — 5 = 1.
Шаг 4: B для обрушения
Последним шагом в последовательности является уменьшение следующего числа из делимого, которое в данном случае равно 5. Вы пишете 5 рядом с 1, в результате получается число 15.
Вы пишете 5 рядом с 1, в результате получается число 15.
Теперь вы начинаете все сначала:
Шаг 1: D для разделения
Сколько раз можно разделить 5 на 15. Ответ: 3. Итак, вы помещаете 3 в строку частного.
Шаг 2: M для умножения
Вы умножаете свой ответ из шага 1 на ваш делитель: 3 x 5 = 15. Запишите это под числом 15.
Шаг 3: S для вычитания
Теперь вычтем 15 из 15.15 — 15 = 0.
Нет необходимости в шаге 4. Проблема решена.
Получив ответ, решите задачу в обратном порядке, используя умножение (5 x 13 = 65), чтобы убедиться, что ваш ответ правильный.
В
K5 Learning есть несколько бесплатных рабочих листов с полными делениями для 4-го, 5-го и 6-го классов. Ознакомьтесь с ними в нашем центре рабочих листов по математике.
Узнайте, как решить деление с помощью десятичных чисел
В этом посте мы узнаем, как решить деление с помощью десятичных чисел. Мы увидим различные примеры.
Наконец, мы увидим, как решать задачи деления, пока остаток не станет равен нулю.
Деление десятичного числа на целое
Вы делите как целые числа. Просто поместите десятичную запятую в частное прямо над его позицией в дивиденде.
Рассмотрим пример, разделив 77,5 на 25.
77 разделить на 25 равно 3, а остаток — 2.
Теперь выпадает следующая цифра. Поскольку 5 является первым десятичным числом, мы запишем десятичную точку в частном и разделим 25 на 25, что равно 1.
1 x 25 = 25, таким образом, 25 идет один раз без остатка.
Результатом десятичного деления на целое число является 3,1, а остаток равен нулю.
Деление целого числа на десятичное
Например, мы собираемся разделить 278 на 3.6.
В делителе не может быть десятичных знаков; поэтому удалите десятичную точку из делителя и добавьте к делимому столько нулей, сколько цифр после десятичной точки.
В этом случае нам нужно добавить только один ноль. Итак, теперь нам нужно разделить 2780 на 36.
36 переходит в 278 семь раз с остатком 26.
Теперь опустите 0, чтобы мы могли разделить 260 на 36, что равно 7 с остатком 8.
Решение деления — 77 с остатком 8.
Разделение десятичного числа d на десятичное
Удалите десятичную точку из делителя и переместите десятичную точку делимого вправо на столько цифр, сколько у делителя после десятичной точки. При необходимости добавьте к дивидендам нули.
Теперь разделим 278,1 на 2,52.
Сначала удалите десятичную точку с делителя, и, поскольку делитель имеет два десятичных знака, вам нужно переместить десятичную точку делимого на две позиции.Если в дивиденде всего одна десятичная дробь, добавьте столько нулей, сколько осталось позиций. В этом случае мы добавляем один ноль и делим 27810 на 252
.
252 переходит в 278 один раз с остатком 26.
Мы выпадаем следующее число, которое является 1, поэтому теперь нам нужно разделить 261 на 252, что входит один раз, с остатком 9.
Мы выпадаем следующее число, которое является 0, поэтому теперь нам нужно разделить 90 на 252. Поскольку 90 меньше 252, мы должны записать 0 в частном и опустить следующую цифру.
Мы уже закончили решение деления, потому что цифр больше нет. Решением будет 110 с остатком 90.
Теперь мы увидим , как извлечь десятичные дроби . Если в конце деления у нас остается остаток, мы записываем десятичную точку в частном и добавляем ноль к делимому. Если мы хотим и дальше убирать десятичные дроби, нам придется добавлять нули к дивидендам.
Мы собираемся увидеть пример удаления десятичных знаков, деление 33 на 6.
6 переходит в 33, 5 раз с остатком 3.
Итак, если мы хотим добавить десятичные дроби, мы должны поставить десятичную точку в частном после 5.
Затем мы можем добавить к остатку ноль.
Теперь нам нужно разделить 30 на 6, что равно 5.
И решение 33, разделенное на 6, равно 5,5.
Кроме того, теперь вы можете узнать больше о десятичном разделении!
Подпишитесь на бесплатную пробную версию на Smartick сегодня!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Как решить задачу с однозначным делением
Здравствуйте! Сегодня мы узнаем, как решать задачи с однозначным делением. Готовы ли вы закончить октябрь с проблемой однозначного деления?
Во-первых, нам нужно знать части задачи деления:
- Дивиденд: число, которое вам нужно разделить.
- Делитель: число, на которое делится дивиденд.
- Частное: результат деления.

- Остаток: Остаток после разделения.
Посмотрите, как мы настроили каждую часть подразделения:
Теперь давайте посмотрим, как будет выглядеть задача деления на однозначное число, если мы заменим каждое слово числом:
Мы хотим разделить 243 леденца между 5 друзьями.
Дивиденд будет 243, потому что это число, которое мы хотим разделить. Делитель равен 5, потому что это число, на которое мы собираемся разделить 243 леденца. Частным будет количество конфет, которое получит каждый ребенок. Остаток будет количеством оставшихся конфет.
Итак, как мы решаем частное и остаток в задаче однозначного деления?
- Начнем с первого числа делимого, разделив его на делитель.Если это число меньше делителя, нам нужно будет использовать другое число делимого. В нашем примере первое число делимого — 2, но поскольку оно меньше делителя, равного 5, мы должны использовать другое число: 24. Теперь мы можем начать деление 24/5.

- Следующий шаг нашей проблемы деления — найти число, на которое мы можем умножить делитель, что даст нам то же число, что и делимое. Если такового не существует, нам нужно будет найти ближайшее возможное число, которое все же меньше дивиденда.Ответ, полученный при умножении, вычитается из дивиденда. Следуя нашему примеру: мы должны разделить 24 на 5. Итак, нам нужно найти число, которое дает нам 24 при умножении на 5. Поскольку точного числа не существует, мы должны использовать ближайшее меньшее число: 4 x 5 = 20. В этом случае 20 — это ближайшее к 24 число, которое не превосходит его. Итак, мы записываем 4 в частном и вычитаем 20 из 24, и у нас получается 24-20 = 4 .
- Для решения задачи однозначного деления нам нужно сделать еще один шаг: убрать следующее число делимого и повторить шаг 2.
Приносим следующее число, которое является числом 3, и записываем его рядом с числом 4. Полное число 43.
Теперь мы делим 43 на 5.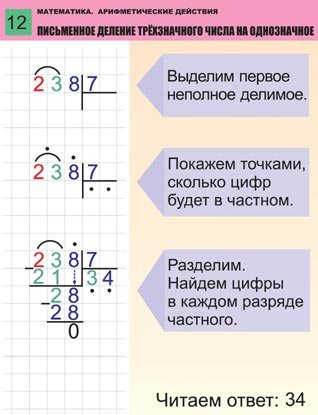 Нам нужно найти число, которое дает нам 43 при умножении на 5. Но, поскольку его не существует, мы должны найти ближайшее число, которое не превосходит 43. В этом случае , это 5 x 8 = 40. Итак, давайте запишем 5 в частном и 40 под 43, чтобы вычесть это: 43 — 40 = 3.
Нам нужно найти число, которое дает нам 43 при умножении на 5. Но, поскольку его не существует, мы должны найти ближайшее число, которое не превосходит 43. В этом случае , это 5 x 8 = 40. Итак, давайте запишем 5 в частном и 40 под 43, чтобы вычесть это: 43 — 40 = 3.
В делимом больше нет чисел, поэтому мы закончили с проблемой деления.
Ответ на нашу задачу однозначного деления: каждый ребенок получит 48 конфет, а 3 конфеты останутся.
Это все у меня до следующей среды. Надеюсь, вы научились решать задачи с однозначным делением.
Удачной недели!
А если вы хотите узнать больше о математике, попробуйте Smartick бесплатно!
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Что такое длинное деление? [Определение, факты и пример]
Игры с длинным разделением
Разделить на 2-значные числа
Разделить 4-значные числа на 2-значные числа, в которых от деления не остается остатка. Вы начнете с оценки частных.
Вы начнете с оценки частных.
охватывает общий базовый учебный план 5.NBT.6Play NowРазделите на 2-значные числа с остатком
Разделите 4-значные числа на 2-значные числа. Начните с оценки частных, которые пригодятся при делении на 2-значные числа.
охватывает Common Core Curriculum 5.NBT.6Играть сейчасСмотреть все игры с разделением >>
Учитесь с помощью полной программы обучения математике K-5
Что такое длинное деление?
В математике деление в столбик — это метод, используемый для деления больших чисел на группы или части.
Деление в столбик помогает разбить проблему деления на последовательность более простых шагов. Как и во всех задачах деления, большое число, являющееся делимым, делится на другое число, которое называется делителем, чтобы получить результат, называемый частным, а иногда и остатком.
Как вы делаете деление в столбик?
Метод деления в столбик включает в себя основные математические операции.
Для деления двух чисел этим методом рисуется таблица. Делитель пишется за пределами правых скобок, а делимое — внутри. Частное пишется над чертой сверху над дивидендом.
деление в столбик состоит из 5 шагов:
| D | Разделить |
| М | Умножить |
| S | Вычесть |
| Б | Сбить |
| R | Повтор или остаток |
Вот пример деления в столбик с четким отображением каждого шага.
Процесс начинается с деления или определения, сколько раз крайняя левая цифра делимого может делиться на делитель.
Затем результат или ответ из шага 1, который становится первой цифрой частного, умножается на делитель и записывается под первой цифрой делимого.
Вычитание производится по первой цифре делимого и записывается остаток.
Следующая цифра делимого уменьшается, а затем процесс повторяется до тех пор, пока все цифры делимого не будут сброшены и не будет найден остаток.
Как разделить десятичные дроби методом длинного деления?
Деление в столбик можно также использовать для разделения десятичных чисел на равные группы. Он выполняет те же шаги, что и при делении в столбик, а именно: деление, умножение, вычитание, уменьшение и повторение или нахождение остатка.
Вот пример деления в столбик с десятичными знаками.
Интересные факты
|
Давайте споем!
Если нужно разделить большие числа,
нарисуйте таблицу для длинного деления сбоку.
Напишите шаги, которые будут вашим руководством,
D, M, S, B и R — Придерживайтесь долгого разделения!
Давайте сделаем это!
Вместо того, чтобы показывать видео для обучения полному делению или раздавать практические задания ученикам четвертого класса, приведите примеры из реальной жизни, когда они могут использовать метод длинного деления для деления.
Допустим, готовя кексы и печенье для продажи в школе, вы можете попросить ребенка подсчитать количество партий, в которых можно приготовить печенье или кексы (исходя из количества форм на подносе), если общее количество печенья и кексы требуются. Вы также можете попросить их подсчитать общее количество необходимых картонных коробок, если в каждую коробку печенья помещается 15 печенья, а в картонную коробку для кексов — 6 кексов.
Деление с остатком онлайн калькулятор в строчку. Умножение и деление в столбик: примеры
Деление – одна из четырех основных математических операций (сложение , вычитание , умножение). Деление, как и остальные операции важно не только в математике, но и в повседневной жизни. Например, вы целым классом (человек 25) сдадите деньги и купите подарок учительнице, а потратите не все, останется сдача. Так вот сдачу вам надо будет поделить на всех. В работу вступает операция деления, которая поможет вам решить эту задачу.
Деление – интересная операция, в чем мы и убедимся с вами в этой статье!
Деление чисел
Итак, немного теории, а затем практика! Что такое деление? Деление – это разбивание на равные части чего-либо. То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
То есть это может быть пакет конфет, который нужно разбить на равные части. Например, в пакетике 9 конфет, а человек которые хотят их получить – три. Тогда нужно разделить эти 9 конфет на трех человек.
Записывается это так: 9:3, ответом будет цифра 3. То есть деление числа 9 на число 3 показывает количество чисел три содержащихся в числе 9. Обратным действием, проверочным, будет умножение . 3*3=9. Верно? Абсолютно.
Итак, рассмотрим пример 12:6. Для начала обозначим имена каждому компоненту примера. 12 – делимое, то есть. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее название «частное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Получается, что число 6 содержится 2 раза в числе 12.
Деление с остатком
Что же такое деление с остатком? Это то же самое деление, только в результате получается не ровное число, как показано выше.
Например, поделим 17 на 5. Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Так как, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17:5=3(2).
Например, 22:7. Точно так же определяемся максимально число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22:7=3(1).
Деление на 3 и 9
Частным случаем деления будет деление на число 3 и число 9. Если вы хотите узнать, делиться ли число на 3 или 9 без остатка, то вам потребуется:
Найти сумму цифр делимого.
Поделить на 3 или 9 (в зависимости от того, что вам нужно).
Если ответ получается без остатка, то и число поделится без остатка.
Например, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18:9=2, 18:3=6. Поделено без остатка.
Например, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63:9=7, а 63:3=21.Такие операции проводятся с любым числом, чтобы узнать делится ли оно с остатком на 3 или 9, или нет.
Умножение и деление
Умножение и деление – это противоположные друг другу операции. Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Умножение можно использовать как проверку деления, а деление – как проверку умножения. Подробнее узнать об умножении и освоить операцию можете в нашей статье про умножение . В которой подробно описано умножение и как правильно выполнять. Там же найдете таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24:4=6, 24:6=4. Решено верно. В этом случае проверка производится путем деления ответа на один из множителей.
Или дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Верно? Да. В данном случае проверка производится путем умножения ответа на делитель.
Деление 3 класс
В третьем классе только начинают проходить деление. Поэтому третьеклассники решают самые простые задачки:
Задача 1 . Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных нужно положить в каждую упаковку, чтобы получилось равно количество в каждой?
Задача 2 . На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
На кануне нового года в школе детям на класс, в котором учится 15 человек, выдали 75 конфет. Сколько конфет должен получить каждый ребенок?
Задача 3 . Рома, Саша и Миша собрали с яблони 27 яблок. Сколько каждый получит яблок, если нужно поделить их одинаково?
Задача 4 . Четыре друга купили 58 штук печенья. Но потом поняли, что им не разделить их поровну. Сколько ребятам нужно докупить печенья, чтобы каждый получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – более серьезное, чем в третьем. Все вычисления проводятся методом деления в столбик, а числа, которые участвуют в делении – не маленькие. Что же такое деление в столбик? Ответ можете найти ниже:
Деление в столбик
Что такое деление в столбик? Это метод позволяющий находить ответ на деление больших чисел. Если простые числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для ребенка не просто. А рассказать о технике решения подобных примеров – наша задача.
Рассмотрим пример, 512:8.
1 шаг . Запишем делимое и делитель следующим образом:
Частное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг . Деление начинаем слева направо. Сначала берем цифру 5:
3 шаг . Цифра 5 меньше цифры 8, а значит поделить не удастся. Поэтому берем еще одну цифру делимого:
Теперь 51 больше 8. Это неполное частное.
4 шаг . Ставим точку под делителем.
5 шаг . После 51 стоит еще цифра 2, а значит в ответе будет еще одно число, то есть. частное – двузначное число. Ставимвторую точку:
6 шаг . Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 вместо первой точки под делителем:
7 шаг . Затем записываем число ровно под числом 51 и ставим знак «-»:
8 шаг . Затем из 51 вычитаем 48 и получаем ответ 3.
* 9 шаг *. Сносим цифру 2 и записываем рядом с цифрой 3:
Сносим цифру 2 и записываем рядом с цифрой 3:
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
Итак, ответ 64, без остатка. Если бы делили число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел выполняется методом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так сложно, как кажется на первый взгляд. Например, (2/3):(1/4). Метод такого деления довольно прост. 2/3 – делимое, 1/4 – делитель. Можно заменить знак деления (:) на умножение (), но для этого нужно поменять местами числитель и знаменатель делителя. То есть получаем: (2/3) (4/1), (2/3)*4, это равно – 8/3 или 2 целые и 2/3.Приведем еще пример, с иллюстрацией для наилучшего понимания. Рассмотрим дроби (4/7):(2/5):
Как и в предыдущем примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Производим сокращение и ответ:10/7, затем выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три цифры: 148 951 784 296. Итак, справа налево: 296 – класс единиц, 784 — класс тысяч, 951 – класс миллионов, 148 – класс миллиардов. В свою очередь, в каждом классе 3 цифры имеют свой разряд. Справа налево: первая цифра – единицы, вторая цифра – десятки, третья – сотни. Например, класс единиц – 296, 6 – единицы, 9 – десятки, 2 – сотни.
Деление натуральных чисел
Деление натуральных чисел – это самое простое деление описанные в данной статье. Оно может быть, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
В каждом уроке новые приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – еще один способ наглядно показать тему деления. Ниже мы найдете ссылку на прекрасную презентацию, в которой хорошо объясняется как делить, что такое деление, что такое делимое, делитель и частное. Время зря не потратите, а свои знания закрепите!
Примеры на деление
Легкий уровень
Средний уровень
Сложный уровень
Игры на развитие устного счета
Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение»
Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Визуальная геометрия»
Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Копилка»
Игра «Копилка» развивает мышление и память. Главная суть игры выбрать, в какой копилке больше денег.В этой игре даны четыре копилки, надо посчитать в какой копилке больше денег и показать с помощью мышки эту копилку. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Игра «Быстрое сложение перезагрузка»
Игра «Быстрое сложение перезагрузка» развивает мышление, память и внимание. Главная суть игры выбрать правильные слагаемые, сумма которых будет равна заданному числу. В этой игре на экране дается три цифры и дается задание, сложите цифру, на экране указывается какую цифру надо сложить. Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Вы выбираете из трех цифр нужные цифры и нажимаете их. Если вы ответили правильно, то вы набираете очки и продолжаете играть дальше.
Развитие феноменального устного счета
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
В курс входит 30 уроков с полезными советами и упражнениями для развития детей. В каждом уроке полезный совет, несколько интересных упражнений, задание к уроку и дополнительный бонус в конце: развивающая мини-игра от нашего партнера. Длительность курса: 30 дней. Курс полезно проходить не только детям, но и их родителям.
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Один из важных этапов в обучении ребёнка математическим действиям – обучение операции деления простых чисел. Как объяснить ребёнку деление, когда можно приступать к освоению этой темы?
Для того чтобы научить ребёнка делению, необходимо, чтобы он к моменту обучения уже освоил такие математические операции, как сложение, вычитание, а также имел чёткое представление о самой сущности действий умножения и деления. То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
То есть, он должен понимать, что деление – это разделение чего-либо на равные части. Также необходимо научить операции умножения и выучить таблицу умножения.
Я уже писала о том, Эта статья может стать для вас полезной.
Осваиваем операцию разделения (деления) на части в игровой форме
На этом этапе необходимо сформировать у ребёнка понимание того, что деление – это разделение чего-либо на равные части. Самый просто способ научить ребёнка этому – предложить ему разделить некоторое количество предметов между ним его друзьями или членами семьи.
Допустим, возьмите 8 одинаковых кубиков и предложите ребёнку разделить на две равные части – для него и другого человека. Варьируйте и усложняйте задание, предложите ребёнку разделить 8 кубиков не на двоих, а на четырёх человек. Проанализируйте вместе с ним результат. Меняйте составляющие, пробуйте с другим количеством предметов и людей, на которые нужно разделить эти предметы.
Важно: Следите, чтобы вначале ребёнок оперировал с чётным количеством предметов, для того, чтобы результатом деления было одинаковое количество частей. Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Это окажется полезным на следующем этапе, когда ребёнку будет нужно понять, что деление – это операция обратная умножению.
Умножаем и делим, используя таблицу умножения
Объясните ребёнку, что, в математике, действие, противоположное умножению, называется «деление». Оперируя таблицей умножения, продемонстрируйте ученику на любом примере взаимосвязь между умножением и делением.
Пример: 4х2=8. Напомните ребёнку, что результатом умножения является произведение двух чисел. После этого объясните, что операция деления, является обратной операции умножения и проиллюстрируйте это наглядно.
Разделите получившееся произведение «8» из примера – на любой из множителей – «2» или «4», и результатом всегда будет другой, не использовавшийся в операции множитель.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Закрепите эти знания, они необходимы для дальнейшего обучения!
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Делим столбиком – приведем пример
Перед началом занятия вспомните вместе с ребёнком, как называются цифры в процессе операции деления. Что является «делителем», «делимым», «частным»? Научите безошибочно и быстро определять эти категории. Это будет очень полезным во время обучения ребёнка делению простых чисел.
Объясняем наглядно
Давайте разделим 938 на 7. В данном примере 938 – это делимое, 7 – делитель. Результатом будет частное, его то и нужно вычислить.
Шаг 1 . Записываем числа, разделив их «уголком».
Шаг 2. Покажите ученику числа делимого и предложите ему, выбрать из них то наименьшее число, которое окажется больше делителя. Из трёх цифр 9, 3 и 8, этим числом будет 9. Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Предложите ребёнку проанализировать, сколько раз число 7 может содержаться в числе 9? Правильно, только один раз. Поэтому первым записанными нами результатом будет 1.
Шаг 3. Переходим к оформлению деления столбиком:
Умножаем делитель 7х1 и получаем 7. Полученный результат записываем под первым числом нашего делимого 938 и вычитаем, как обычно, в столбик. То есть из 9 мы вычитаем 7 и получаем 2.
Записываем результат.
Шаг 4. Число, которое мы видим, меньше делителя, поэтому необходимо его надо увеличить. Для этого объединим его со следующим неиспользованным числом нашего делимого – это будет 3. Приписываем 3 к полученному числу 2.
Шаг 5. Далее действуем по уже известному алгоритму. Анализируем, сколько раз наш делитель 7 содержится в полученном числе 23? Правильно, три раза. Фиксируем число 3 в частном. А результат произведения – 21 (7*3) записываем внизу под числом 23 в столбик.
Шаг.6 Теперь осталось найти последнее число нашего частного. Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Используя уже знакомый алгоритм, продолжаем делать вычисления в столбике. Путём вычитания в столбике (23-21) получаем разницу. Она равняется 2.
Из делимого у нас осталась неиспользованным одно число – 8. Объединяем его с полученным в результате вычитания числом 2, получаем – 28.
Шаг.7 Анализируем, сколько раз наш делитель 7 содержится в полученном числе? Правильно, 4 раза. Записываем полученную цифру в результат. Итак, мы полученное в результате деления столбиком частное= 134.
Как научить ребенка делению – закрепляем навык
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина — автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта.
 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Преподаватель, специалист детского развивающего центра
Дружинина Елена
специально для проекта сайт
Видео сюжет для родителей, как правильно объяснить ребенку деление в столбик:
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.
Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.
Как умножаются в столбик натуральные числа?
Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:
- До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
- Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа.
 Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали. - То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.
Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.
Алгоритм умножения в столбик десятичных дробей
Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.
Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.
Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:
С чего начать обучение делению?
До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.
После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?
После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.
Алгоритм деления чисел в столбик
Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:
- До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
- Записать делимое. Справа от него — делитель.
- Прочертить слева и снизу около последнего уголок.
- Определить неполное делимое, то есть число, которое будет минимальным для деления.
 Обычно оно состоит из одной цифры, максимум из двух.
Обычно оно состоит из одной цифры, максимум из двух. - Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
- Записать результат от умножения этого числа на делитель.
- Написать его под неполным делимом. Выполнить вычитание.
- Снести к остатку первую цифру после той части, которая уже разделена.
- Снова подобрать число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.
Как решать деление в столбик, если в делителе больше одной цифры?
Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.
Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.
Рассмотреть такое деление можно на примере — 12082: 863.
- Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
- После вычитания получается остаток 345.
- К нему нужно снести цифру 2.
- В числе 3452 четыре раза умещается 863.
- Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
- Остаток после вычитания равен нулю. То есть деление закончено.
Ответом в примере будет число 14.
Как быть, если делимое заканчивается на ноль?
Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.
Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если разделить нужно десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.
Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.
Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.
Иногда это нужно для того, чтобы доделить числа до конца.
Деление двух десятичных дробей
Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.
Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.
Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.
В качестве примера: 28,4 делим на 3,2:
- Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра.
 Умножение даст 284 и 32.
Умножение даст 284 и 32. - Их полагается разделить. Причем сразу все число 284 на 32.
- Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
- Деление целой части закончилось, и в ответ полагается поставить запятую.
- Снести к остатку 0.
- Снова взять по 8.
- Остаток: 24. К нему приписать еще один 0.
- Теперь брать нужно 7.
- Результат умножения — 224, остаток — 16.
- Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.
Деление закончено. Результат примера 28,4:3,2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1, или 0,01?
Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.
Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.
Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.
Деление периодических дробей
В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.
Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.
Если в примере разные дроби…
Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.
Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной. Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.
Дети во 2-3 классе осваивают новое математическое действие – деление. Школьнику непросто вникнуть в суть данного математического действия, поэтому ему необходима помощь родителей.
Родителям нужно понимать, как именно преподносить ребенку новую информацию. ТОП-10 примеров расскажут родителям о том, как нужно учить детей делению чисел столбиком.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
1 Организуйте ребенку место для обучения в форме игры. Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10. Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно. Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты. Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
2 Обучать математическому действию можно с помощью цифр. Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
3 Дайте ребенку 6 груш. Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
4 Расскажите ученику о делении с остатком. Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики до 5 класса смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножениz.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5.
 А именно, результатом умножения.
А именно, результатом умножения. - Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление. Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример.
 Число 5 два раза входит в число 10.
Число 5 два раза входит в число 10. - В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66 , а после к 232, 342, 345 , и так далее.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8.
 Запишите в столбик задачу.
Запишите в столбик задачу. - Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Простые примеры для ребенка
На этом же примере можно продолжить:
- При делении 35 на 8 получается остаток 3. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
- При делении 30 на 8 получается 3. Эту цифру нужно записать после запятой.
- Теперь нужно под значением 30 написать 24 (результат умножения 8 на 3). В итоге получится 6. К цифре 6 тоже нужно дописать ноль. Получится 60.
- В число 60 помещается цифра 8 входит 7 раз. То есть, получится 56.
- При вычитании 60 от 56 получается 4. К этой цифре тоже нужно подписать 0. Получается 40. В таблице умножения ребенок может увидеть, что 40 – это результат умножения 8 на 5.
 То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
То есть, в число 40 цифра 8 входит 5 раз. Остатка нет. Ответ выглядит так – 4,375.
Данный пример может показаться ребенку сложным. Поэтому нужно много раз делить значения, у которых будет остаток.
Обучение делению с помощью игр
Родители могут использовать игры на деление для обучения школьника. Можно дать ребенку раскраски, в которых нужно определить цвет карандаша путем деления. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Картинка будет поделена на части, в которых будут результаты деления. А цвета, которые нужно использовать, будут примерами. Например, красный цвет помечен примером: 15 разделить на 3. Получится 5. Нужно найти часть картинки под этим номером и раскрасить ее. Математические раскраски увлекают детей. Поэтому родителям стоит попробовать данный способ обучения.
Обучение делению столбиком наименьшего числа на наибольшее
Деление данным методом предполагает, что частное будет начинаться с 0, а после него будет стоять запятая.
Чтобы ученик корректно усвоил полученную информацию, ему необходимо привести такого плана пример.
Как можно ребенку объяснить деление в столбик. Деление столбиком. Онлайн калькулятор
Как записывать деление в столбик
Деление многозначных чисел легче всего выполнять столбиком. Деление столбиком иначе называют деление уголком .
Перед тем как начать выполнение деления столбиком, рассмотрим подробно саму форму записи деления столбиком. Сначала записываем делимое и справа от него ставим вертикальную черту:
За вертикальной чертой, напротив делимого, пишем делитель и под ним проводим горизонтальную черту:
Под горизонтальной чертой поэтапно будет записываться получающееся в результате вычислений частное:
Под делимым будут записываться промежуточные вычисления:
Полностью форма записи деления столбиком выглядит следующим образом:
Как делить столбиком
Допустим, нам нужно разделить 780 на 12, записываем действие в столбик и приступаем к делению:
Деление столбиком выполняется поэтапно. Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
Первое, что нам требуется сделать, это определить неполное делимое. Смотрим на первую цифру делимого:
это число 7, так как оно меньше делителя, то мы не можем начать деление с него, значит нужно взять ещё одну цифру из делимого, число 78 больше делителя, поэтому мы начинаем деление с него:
В нашем случае число 78 будет неполным делимым , неполным оно называется потому, что является всего лишь частью делимого.
Определив неполное делимое, мы можем узнать сколько цифр будет в частном, для этого нам нужно посчитать, сколько цифр осталось в делимом после неполного делимого, в нашем случае всего одна цифра — 0, это значит, что частное будет состоять из 2 цифр.
Узнав количество цифр, которое должно получиться в частном, на его месте можно поставить точки. Если при завершении деления количество цифр получилось больше или меньше, чем указано точек, значит где-то была допущена ошибка:
Приступаем к делению. Нам нужно определить сколько раз 12 содержится в числе 78. Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Для этого мы последовательно умножаем делитель на натуральные числа 1, 2, 3, …, пока не получится число максимально близкое к неполному делимому или равное ему, но не превышающее его. Таким образом мы получаем число 6, записываем его под делитель, а из 78 (по правилам вычитания столбиком) вычитаем 72 (12 · 6 = 72). После того, как мы вычли 72 из 78, получился остаток 6:
Обратите внимание, что остаток от деления показывает нам, правильно ли мы подобрали число. Если остаток равен делителю или больше него, то мы не правильно подобрали число и нам нужно взять число побольше.
К получившемуся остатку — 6, сносим следующую цифру делимого — 0. В результате, получилось неполное делимое — 60. Определяем, сколько раз 12 содержится в числе 60. Получаем число 5, записываем его в частное после цифры 6, а из 60 вычитаем 60 (12 · 5 = 60). В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит 780 разделилось на 12 нацело. В результате выполнения деления столбиком мы нашли частное — оно записано под делителем:
Рассмотрим пример, когда в частном получаются нули. Допустим нам нужно разделить 9027 на 9.
Допустим нам нужно разделить 9027 на 9.
Определяем неполное делимое — это число 9. Записываем в частное 1 и из 9 вычитаем 9. В остатке получился нуль. Обычно, если в промежуточных вычислениях в остатке получается нуль, его не записывают:
Сносим следующую цифру делимого — 0. Вспоминаем, что при делении нуля на любое число будет нуль. Записываем в частное нуль (0: 9 = 0) и в промежуточных вычислениях из 0 вычитаем 0. Обычно, чтобы не нагромождать промежуточные вычисления, вычисление с нулём не записывают:
Сносим следующую цифру делимого — 2. В промежуточных вычислениях вышло так, что неполное делимое (2) меньше, чем делитель (9). В этом случае в частное записывают нуль и сносят следующую цифру делимого:
Определяем, сколько раз 9 содержится в числе 27. Получаем число 3, записываем его в частное, а из 27 вычитаем 27. В остатке получился нуль:
Так как в делимом больше не осталось цифр, значит число 9027 разделилось на 9 нацело:
Рассмотрим пример, когда делимое оканчивается нулями. Пусть нам требуется разделить 3000 на 6.
Пусть нам требуется разделить 3000 на 6.
Определяем неполное делимое — это число 30. Записываем в частное 5 и из 30 вычитаем 30. В остатке получился нуль. Как уже было сказано, нуль в остатке в промежуточных вычислениях записывать не обязательно:
Сносим следующую цифру делимого — 0. Так как при делении нуля на любое число будет нуль, записываем в частное нуль и в промежуточных вычислениях из 0 вычитаем 0:
Сносим следующую цифру делимого — 0. Записываем в частное ещё один нуль и в промежуточных вычислениях из 0 вычитаем 0. Так как в промежуточных вычислениях, вычисление с нулём обычно не записывают, то запись можно сократить, оставив только остаток — 0. Нуль в остатке в самом конце вычислений обычно записывают для того, чтобы показать, что деление выполнено нацело:
Так как в делимом больше не осталось цифр, значит 3000 разделилось на 6 нацело:
Деление столбиком с остатком
Пусть нам требуется разделить 1340 на 23.
Определяем неполное делимое — это число 134. Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Записываем в частное 5 и из 134 вычитаем 115. В остатке получилось 19:
Сносим следующую цифру делимого — 0. Определяем, сколько раз 23 содержится в числе 190. Получаем число 8, записываем его в частное, а из 190 вычитаем 184. Получаем остаток 6:
Так как в делимом больше не осталось цифр, деление закончилось. В результате получилось неполное частное 58 и остаток 6:
1340: 23 = 58 (остаток 6)
Осталось рассмотреть пример деления с остатком, когда делимое меньше делителя. Пусть нам требуется разделить 3 на 10. Мы видим, что 10 ни разу не содержится в числе 3, поэтому записываем в частное 0 и из 3 вычитаем 0 (10 · 0 = 0). Проводим горизонтальную черту и записываем остаток — 3:
3: 10 = 0 (остаток 3)
Калькулятор деления столбиком
Данный калькулятор поможет вам выполнить деление столбиком. Просто введите делимое и делитель и нажмите кнопку Вычислить.
Алгоритм деления чисел в столбик, обучение ребёнка. Особенности деления многозначных чисел и многочленов.
Школа даёт ребёнку не только дисциплину, развитие талантов и навыков общения, но и знания по фундаментальным наукам. Одна из них — математика.
Хотя программа и нагрузка на учеников часто меняются, но деление в столбик чисел с разным количеством разрядов остаётся неприступной с первого захода вершиной для многих из них. Потому без тренировок дома с родителями часто не обойтись.
Дабы не упустить время и предотвратить образование кома непонятного у ребёнка в математике, освежите в памяти свои знания по делению чисел столбиком. Статья вам в этом поможет.
Как правильно делить числа в столбик: алгоритм деления
Для деления чисел столбиком следуйте по таким шагам:
- правильно запишите действие деления на бумаге. Выбирайте верхний правый угол тетради/листа. Если вы только учитесь выполнять действие деления в столбик, берите бумагу в клетку. Так вы сохраните визуальную последовательность решения,
- разлинейте место между делимым и делителем.

Вам поможет схема ниже.
- планируйте пространство для деления в столбик. Чем длиннее число, которое подлежит делению, и чем корове делитель, тем ниже на станице спуститься решение,
- первое действие деления совершайте с тем количеством цифр делимого, которое равно делителю. Например, если справа от разделительной линии у вас стоит однозначная цифра, то рассматривайте первую у делимого, если двухзначная — то 2 первых,
- перемножьте числа под и над чертой и запишите результат под цифрами делимого, которые вы обозначили для первого действия,
- завершайте действие вычитанием и определением остатка. Нарисуйте горизонтальную линию над ним, чтобы отделить первый шаг решения,
- допишите следующую цифру делимого к остатку и продолжайте решение,
- последний шаг деления — когда вы получите от вычитания 0 либо число, меньше делителя. Во втором случае ваш ответ будет с остатком, например, 17 и 3 в остатке.
Как объяснить ребенку деление и научить делить столбиком?
Во-первых, учтите ряд вводных факторов:
- ребёнок знает таблицу умножения
- хорошо разбирается и умеет применять на практике действия вычитания и сложения
- понимает разницу между целым и его составными элементами
- поиграйте с таблицей умножения.
 Положите её перед ребёнком и на примерах покажите удобство использования при делении,
Положите её перед ребёнком и на примерах покажите удобство использования при делении, - объясните расположение делимого, делителя, частного, остатка. Предложите ребёнку повторить эти категории,
- превратите процесс в игру, придумайте историю про цифры и действие деления,
- подготовьте наглядные предметы для обучения. Подойдут счётные палочки, яблоки, монеты, игрушки, очищенные сведение или апельсин. Предлагайте их распределить между разным количеством людей, например, между мамой, папой и ребенком,
- первым показывайте ребёнку действия с чётными числами, чтобы он видел результат деления, кратный двум.
Сам процесс освоения деления столбиком:
- запишите цифры, разделив их границами. Повторите с ребёнком расположение категорий деления,
- предложите ему проанализировать цифры делимого на предмет «больше-меньше» делителя. Помогайте вопросом — сколько раз одно число помещается во втором. В результате ребёнку следует выделить то число/числа, которые он будет применять для совершения первого действия,
- подскажите алгоритм определения разрядности частного.
 Её удобно изобразить точками, которые потом превратятся в цифры,
Её удобно изобразить точками, которые потом превратятся в цифры, - помогите правильно определить и записать первое число в частное, совершите его умножение на делитель, запишите результат под делимым, выполните вычитание. Объясните, что результат вычитания всегда должен быть меньше делителя. В противном случае действие совершилось с ошибкой и его следует переделать,
- следующий шаг — анализ ситуации с добавлением второго числа от делимого и определения количества раз повторения делителя в нём,
- снова помогите с записью действия,
- продолжайте до момента, когда результат от разницы составит ноль. Это актуально только для деления чисел без остатка,
- закрепите знания у ребёнка еще несколькими примерами. Следите, чтобы он не устал, иначе дайте перерыв.
Как письменно делить в столбик двузначное число на однозначное и двузначное: примеры, объяснение
Приступим к пошаговому разбору примеров на деление в столбик.
Осуществите действие над цифрами 25 и 2:
- запишите их рядом и разделите линиями границы,
- определите нужное количество цифр делимого для первого действия,
- запишите значение под делителем и результат умножения под делимым,
- выполните вычитание,
- допишите вторую цифру делимого и повторите действия на умножение и вычитание.

Частично выполненное задание на деление столбиком двузначного числа на однозначное смотрите ниже:
Учтите, что деление столбиком двухзначного числа на однозначное возможно и в одно действие.
Второй пример. Разделите 87 на 26 в столбик.
Алгоритм аналогичен рассмотренному выше с той лишь разницей, что учитывать нужно сразу 2 числа делителя при определении количества раз повторения в делимом.
Чтобы облегчить задачу ребёнку, который только осваивается азы деления, предложите ему ориентироваться на первые цифры у делимого и делителя. Например, 8:2=4. Пусть ребёнок подставит это число под черту и выполнит умножение. Ему нужно увидеть своими глазами, что 4 много и нужно попробовать с тройкой.
Ниже пример деления столбиком двузначного числа на двузначное с остатком.
Как делить в столбик трехзначное число на однозначное, двузначное и трехзначное: примеры, объяснение
Продолжим разбор действия деления столбиком на примерах с трёхзначным делимым.
Когда делитель одноразрядное число, алгоритм действия аналогичен рассмотренным выше.
Схематически он выглядит так:
В случае деления трёхзначного делимого на двузначный делитель подберите с ребёнком число, соответствующее количеству вмещений второго в первой части первого либо в целом. То есть рассматривайте сначала 2 цифры трехзначного делимого, если они меньше делителя, тогда все три.
Когда ребёнок еще только начал освоение деления столбиком, подскажите ему совершение действий с однозначными числами. То есть с первыми в делимом и делителе. Пусть малыш совершит ошибку, которая приведет к отрицательному значению вычитания и вернётся к подбору числа под чертой, чем запутается с действием сразу для двузначного делителя.
Схема деления трехзначного на двузначное числа такая:
Трехзначные значения в делителе и делимом выглядят громоздкими и пугающими для ребёнка. Успокойте его, объяснив, что принцип действий идентичен, как и при делении простых чисел.
Метод перебора по одной цифре поможет малышу разобраться с каждым числом отдельно. Только количество времени на это действие ему потребуется больше, чем в предыдущих примерах. Для лучшего визуального восприятия объединяйте дугами количество цифр, которые будут участвовать в первом действии.
Схема деления трёхзначного на трёхзначное числа.
Как делить в столбик четырехзначные, многозначные большие числа, многочлены на многочлены: примеры, объяснение
В случае деления четырёхзначного числа на любое, которое содержит до 4 порядков одновременно, обратите внимание ребёнка на нюансы:
- определение правильного количества порядков после действия деления. Например, в примере 6734:56 должно получится двузначное целое число в графе «частное», а в примере 8956:1243 — однозначное целое,
- появление нулей в частном. Когда в ходе решения при переносе следующего числа делимого результат оказывается меньше делителя,
- проверку полученного результата посредством выполнения действия умножения.
 Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Этот нюанс актуален для деления больших чисел без остатка. Если последний присутствует, то советуйте ребёнку проверить себя и ещё раз разделить числа в столбик.
Ниже пример решения.
Для больших многозначных чисел, которые делятся на конкретные значения меньше или равные им по количеству знаков, актуальны все алгоритмы, рассмотренные выше.
Ребёнку следует быть особенно внимательным в таких случаях и правильно определять:
- количество знаков у частного, то есть результата
- цифры у делимого для первого действия
- правильность переноса остальных чисел
Примеры подробного решения ниже.
При совершении действия деления над многочленами обращайте внимание детей на ряд особенностей:
- у действия может быть остаток либо отсутствовать. В первом случае запишите его в числителе, а делитель в знаменателе,
- для совершения действия вычитания дописывайте в многочлен недостающие степени функции, умноженные на ноль,
- совершайте преобразование многочленов путём выделения повторяющихся дву-/многочленов.
 Тогда их сократите и получится результат без остатка.
Тогда их сократите и получится результат без остатка.
Ниже ряд подробных примеров с решениями.
Как делить в столбик с остатком?
Алгоритм деления в столбик с остатком аналогичен классическому. Разница лишь в появлении остатка, который меньше делителя. А значит первый остаётся без изменения.
Запишите его в ответе либо:
- как дробь, где в числителе остаток, а в знаменателе — делитель
- словами, например, 73 целых и 6 в остатке
Как делить столбиком десятичные дроби с запятой?
Существует несколько особенностей при подобном делении. Если вы совершаете действие с:
- десятичной дробью-делимым и целым числом-делителем, то действуйте по обычному алгоритму до тех пора, пока закончатся цифры у делимого перед запятой. Затем поставьте её в частном и продолжайте переносить цифры до окончания деления,
- числом, которое делится на 10, 100, 100 и т.д., то перенесите запятую в делимом влево на количество цифр, равное количеству нулей делителя.
 Например, 749,5:100=7,495,
Например, 749,5:100=7,495, - десятичными дробями одновременно и в делителе, и в делимом, то сначала избавьтесь от запятой у второго элемента. Для этого перенесите её вправо в обоих дробных числах на то количество знаков, которые отделены у делителя. Например, 416,788:5,3 преобразуйте в 4167,88:53 и совершите обычное деление в столбик.
Как делить столбиком меньшее число на большее?
При таком делении у вас частное будет начинаться с 0 и иметь после него запятую.
Чтобы ребёнок лучше усвоил подобное деление и не запутался в количестве нулей, месте постановки запятой в частном, дайте ему такой пример:
- первое действие на вычитание проведите с нулями, записанными по одному под делителем и в графе «частное»,
- поставьте запятую в частном, а остатка после разницы добавьте ноль и продолжайте обычное деление в столбик,
- когда остаток от вычитания опять будет меньше делителя, допишите первому ноль и продолжайте действие. Финальный итог — получение ноля от разницы верхнего и нижнего чисел либо повторения остатка.
 В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
В последнем случае присутствует значение в периоде, то есть бесконечно повторяющееся число/числа.
Ниже пример.
Как делить столбиком числа с нулями?
Последовательность и алгоритм действий аналогичен классическому, рассмотренному в первом разделе.
Из нюансов отметим:
- при наличии нулей в конце делителя и делимого смело сокращайте их. Предложите ребёнку зачеркнуть их карандашом и продолжить деление как обычно. Например, в ситуации 1200:400 ребёнок может убрать оба нуля у обоих чисел, но в ситуации 15600:560 — только по одному крайнему,
- если ноль есть только в делителе, то подбирайте первую цифру для действия, ориентируясь на число перед ним. Например, в примере 6537:70 поставьте 9 в частное первым числом. Для данного примера совершайте умножение на обе цифры делителя и подписывайте их под тремя у делимого.
Когда нулей у делимого много и процесс деления закончился до того, как вы их все использовали, то перенесите их в частное после цифр, которые образовались до этого. Пример, 1000:2=500 — вы перенесли два последних нуля.
Пример, 1000:2=500 — вы перенесли два последних нуля.
Итак, мы рассмотрели основные ситуации деления чисел разного количества разрядности в столбик, определили алгоритм действия и акценты для обучения ребёнка.
Практикуйте полученные знания и помогайте своему чаду осваивать математику.
Поскольку операция деления простых чисел является одним из важных математических действий, многие родители задумываются о том, как научить ребенка делению. Перед тем, как приступить к обучению, вы должны убедиться в том, что малыш уже умеет вычитать, складывать и умножать числа. Лучше всего приступать к изучению деления столбиком, когда ребенок отправляется в третий класс. Очень важно объяснить, что деление представляет собой процесс, по ходу которого целое разбивают на отдельные части. Не забудьте учесть знания таблицы умножения – убедитесь в том, что кроха уверенно знает ее.
Перед тем, как серьезно приступить к обучению, попробуйте освоить эту нехитрую науку в игровой форме. Для того чтобы сформировать у малыша представление о том, что деление – это разбор целого на части, дайте ему несколько предметов и попросите разделить между членами семьи или игрушками. При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.
При этом эффективно использовать нечто целое – фрукт или овощ, например, который можно разрезать на кусочки.
Потренируйтесь на кубиках. Возьмите парное количество этих элементов и предложите ребенку разделить их поровну между собой и вами. Варьируйте задание. Добавьте такое количество кубиков, чтобы их общее количество делилось на три или шесть. Затем можно усложнить задачу и делить на восемь, семь или девять. После выполнения каждого задания тщательно анализируйте результат вместе с малышом. Он должен понимать сам процесс. Если что-то ему непонятно, постарайтесь доходчиво это объяснить. Не зацикливайтесь на определенных предметах. Постоянно меняйте их, чтобы ребенок приспосабливался делить любые объекты.
Важно! Для начала составляйте задания таким образом, чтобы малыш проводил действия с четным количеством объектов. Таким образом, у ребенка получится одинаковое количество предметов. Это пригодится на следующем этапе, чтобы дать понять малышу, что деление – операция обратная умножению.
Вместе с этим ищут и читают:
Видео: Учимся делить по примеру
Методы обучения
Теперь вам необходимо решить, как научить ребенка делить. Если он уже перешел в третий класс, трудностей у вас возникнуть не должно. Для начала объясните малышу зависимость между делением и умножением. Продемонстрируйте ему, как правильно делить столбиком, используя таблицу умножения. Рассмотрим следующий пример: 3*4=12. Расскажите ребенку, что три и четыре – это множители, а двенадцать – произведение. Проиллюстрируйте ему это на наглядном примере. Покажите ему, что если двенадцать разделить столбиком на три, получится четыре.
Объясните ученику, который перешел в третий класс, что категории, описывающие деление, называются «делимое», «делитель», «частное». Продемонстрируйте это наглядно с помощью таблицы. Рассмотрите как можно больше примеров, чтобы малышу было понятнее. Это пригодится в дальнейшем, когда вы будете осваивать деление столбиком. По сути, вам необходимо научить кроху смотреть на таблицу умножения «наоборот».
Перед началом занятий еще раз вспомните категории деления. Теперь попробуем объяснить все наглядно. Например, разделим число девятьсот тридцать восемь на семь. Запишем числа, чтобы делить их столбиком. Если вы только начинаете обучение, то ребенку, который пошел в третий класс, будет проще для начала делить числа без остатка. Теперь показываем ученику числа делимого и предлагаем ему выбрать наименьшее число, которое будет больше, чем делитель. Выбираем число девять. Теперь предложите малышу ответить, сколько чисел семь может содержаться в числе девять? Правильный ответ – одно. Поэтому записываем единичку.
Умножаем семь на один, получаем семь. Этот результат мы записываем под девяткой из числа девятьсот тридцать восемь. Вычитаем от девятки семерку в столбик. В остатке получаем два. Аналогичным образом записываем результат. Полученное число меньше, чем делитель. Таким образом, нам необходимо его увеличить. Объединяем его со следующим неиспользованным числом – тройкой. «Плюсуем» тройку и двойку. Продолжаем процесс деления согласно с алгоритмом. В итоге мы получаем число – сто тридцать четыре.
Продолжаем процесс деления согласно с алгоритмом. В итоге мы получаем число – сто тридцать четыре.
Самое главное в процессе обучения малыша, который перешел в третий класс, чтобы он усвоил простой алгоритм. Развивайте наблюдательность у крохи, проводите аналогии с другими математическими действиями, больше играйте и наблюдайте за природой.
Деление в столбик — это неотъемлемая часть учебного материала младшего школьника. От того, насколько он правильно научится выполнять это действие, будут зависеть дальнейшие успехи в математике.
Как правильно подготовить ребенка к восприятию нового материала?
Деление в столбик — это сложный процесс, который требует от ребенка определенных знаний. Чтобы выполнить деление, необходимо знать и уметь быстро вычитать, складывать, умножать. Немаловажными являются знания разрядов чисел.
Каждое из этих действий следует довести до автоматизма. Ребенок не должен долго думать, а также уметь вычитать складывать не только числа первого десятка, а в пределах сотни за несколько секунд.
Важно формировать правильное понятие деления, как математического действия. Еще при изучении таблиц умножения и деления, ребенок должен четко понимать, что делимое — это число, которое будет делиться на равные части, делитель — указывать, на сколько частей нужно разделить число, частное — это сам ответ.
Как пошагово объяснить алгоритм математического действия?
Каждое математическое действие предполагает четкое соблюдение определенного алгоритма. Примеры на деление в столбик должны выполняться в таком порядке:
- Запись примера в уголок, при этом места делимого и делителя должны быть строго соблюдены. Чтобы помочь на первых этапах ребенку не запутаться, можно сказать, что слева пишем большее число, а справа — меньшее.
- Выделяют часть для первого деления. Оно должно делиться на делимое с остатком.
- При помощи таблицы умножения определяем, сколько раз может поместиться делитель в выделенной части. Важно указать ребенку, что ответ не должен превышать 9.

- Выполнить умножение полученного числа на делитель и записать его в левой части уголка.
- Далее, нужно найти разницу между частью делимого и полученным произведением.
- Полученное число записывают под чертой и сносят следующее разрядное число. Такие действия выполняются до того периода, пока в остатке не останется 0.
Наглядный пример для ученика и родителей
Деление в столбик можно наглядно объяснить на этом примере.
- Записывают в столбик 2 числа: делимое — 536 и делитель — 4.
- Первая часть для деления должна делиться на 4 и частное должно быть менее 9. Для этого подходит цифра 5.
- 4 поместиться в 5 всего 1 раз, поэтому в ответе записываем 1, а под 5 — 4.
- Далее, выполняется вычитание: из 5 отнимается 4 и под чертой записывается 1.
- К единице сносится следующее разрядное число — 3. В тринадцати (13) — 4 поместится 3 раза. 4х3= 12. Двенадцать записывают под 13-ю, а 3 — в частное, как следующее разрядное число.

- Из 13 вычитают 12, в ответе получают 1. Снова сносят следующее разрядное число — 6.
- 16 снова делится на 4. В ответ записывают 4, а в столбик деления — 16, подводят черту и в разнице 0.
Решив примеры на деление в столбик со своим ребенком несколько раз, можно достичь успехов в быстром выполнении задач в средней школе.
Для того чтобы в школе у ребенка не было проблем с уроками, необходимо давать ему базовые знания с самого раннего возраста. Ведь намного проще объяснить ему некоторые вещи в процессе игры, а не во время строгого школьного урока.
Принцип деления для детей
Ребенок часто сталкивается со многими математическими понятиями, даже не догадываясь о них. Ведь все мамы, играя с малышом, рассказывают о том, что у папы супа налито больше, к бабушке идти дольше, чем до магазина и прочие простые примеры. Все это дает малышу начальное представление о математике.
Стоит попробовать предложить ребенку поиграть в игры с делением. Поделите яблоки (груши, вишни, конфеты) между мамой и ребенком, постепенно добавляя и других участников: папу, игрушку, кошку. В начале малыш будет делить, раздавая всем по одному предмету. А вы потом подведите итог. Скажите ему, что было всего 6 яблок, вы разделили их на троих человек, и каждому досталось по два. Объясните, что слово разделить – это значит раздать всем поровну.
Поделите яблоки (груши, вишни, конфеты) между мамой и ребенком, постепенно добавляя и других участников: папу, игрушку, кошку. В начале малыш будет делить, раздавая всем по одному предмету. А вы потом подведите итог. Скажите ему, что было всего 6 яблок, вы разделили их на троих человек, и каждому досталось по два. Объясните, что слово разделить – это значит раздать всем поровну.
Если вам нужно объяснить деление с цифрами, то также можно привести игровой пример. Скажите, что цифры – это те же яблоки. Расскажите, что то число яблок, которое нужно разделить – это делимое. А то число человек, на которых нужно поделить эти яблоки – это делитель. Покажите несколько примеров наглядно. В игровой форме ребенок обязательно все поймет.
Как научить ребенка делению столбиком?
Если вы учите ребенка делить столбиком, то, скорее всего сложение, вычитание и умножение в столбик он уже освоил. Если нет, то обязательно подтяните эти знания, иначе, добавив еще и деление, ребенок вообще запутается.
Итак, делим в столбик. Возьмем не сложный пример: 110 нужно поделить на 5.
- Запишем делимое — 110, а рядом с ним делитель – 5.
- Разделим все это уголком.
- Начинаем объяснять, вот пример диалога:
-Первая цифра 1. 1 на 5 делится?
-Нет.
-Значит, берем следующую самую маленькую возможную цифру, которая делится на 5 – это 11. Сколько раз цифра 5 может поместиться в 11?
-Два раза.
— Записываем цифру 2 в уголке под пятеркой. Проверяем, умножаем 5 на 2.
— Получается 10.
— Записываем это число под 11. Делаем вычитание. 11 минус 10?
— Равно 1.
— Пишем 1 и рядом сносим 0 из делимого (110 которое). Получилось 10. 10 на 5 делится?
— Да, получается 2.
— Записываем 2 под 5.
Для того чтобы облегчить изучение деления, сейчас появились таблицы деления для детей. Принцип действия у них тот же, что и у таблицы умножения. Вот только надо ли учить таблицу деления, если уже выучил умножение? Это будет зависеть от школы и преподавателя.
Вот только надо ли учить таблицу деления, если уже выучил умножение? Это будет зависеть от школы и преподавателя.
просмотров
Как делить в Google Таблицах (Числа, Ячейки или Столбцы)
В настоящее время Google Sheets — это инструмент для работы с электронными таблицами для большинства людей. Это бесплатно, с ним очень легко сотрудничать, и у него есть несколько довольно крутых функций и возможностей.
Даже если вы хотите сделать что-то такое простое, как ведение записей или простые вычисления, такие как умножение или деление, вы можете легко сделать это в Google Sheets.
В этом уроке. Я покажу вам пару способов разделить числа в Google Таблицах.
Вы можете легко делить числа в Google Таблицах, используя встроенную формулу или оператор деления (как мы увидим на примерах).
Итак, приступим!
Оглавление
Разделение двух ячеек в Google Sheets
Если вы хотите разделить два числа в Google Sheets (или две ячейки с числами), то есть несколько способов сделать это в Google Sheets.
Использование функции РАЗДЕЛИТЬ
Выполнение деления в Google Таблицах является настолько обычной задачей, что существует встроенная функция, позволяющая разделить два числа или числа, находящиеся в двух ячейках.
Это функция РАЗДЕЛИТЬ (без знаков для угадывания)!
Предположим, вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Для этого можно использовать приведенную ниже формулу РАЗДЕЛИТЬ:
= ДЕЛИТЬ(A1,B1)
В приведенной выше формуле первым аргументом является делимое (число, которое нужно разделить) и делитель ( число, на которое нужно разделить)
В приведенном выше примере я использовал ссылки на ячейки, но вы также можете жестко закодировать значения в формуле. Например, вы также можете использовать следующую формулу:
=ДЕЛИТЬ(1200,15)
Преимущество использования ссылок на ячейки заключается в том, что результат формулы становится динамическим. Это означает, что если я изменю значение в ячейке A1 или B1, формула автоматически обновится.
Также помните, что делитель не может быть равен 0. Если ваш делитель равен 0, вы получите ошибку деления — #DIV/0!
Использование оператора DIVIDE
Еще один быстрый способ разделить числа в Google Таблицах — использовать оператор деления — косая черта (/)
Предположим, у вас есть данные, как показано ниже, и вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Вы можете использовать приведенное ниже уравнение, чтобы сделать это:
=A1/B1
И если вы хотите быстро разделить числа (вместо ссылок на ячейки), вы также можете сделать это (как показано ниже формула):
= 1200/15
Читайте также: Как умножать в Google Sheets
Порядок приоритета при делении ячеек
При использовании арифметических операций (таких как деление или умножение) в Google Таблицах важно знать порядок приоритета.
Позвольте мне объяснить это на примере.
Предположим, я использую следующую формулу:
= 1200/15+15
Можете ли вы угадать, каков будет результат?
Должно быть 95.
Это происходит из-за того, что в Google Таблицах существует порядок приоритета, когда деление выполняется перед добавлением. Следовательно, сначала он делит 1200 на 15, где результат равен 80. Затем он добавляет 15 к этому результату, давая вам общий результат как 9.5.
Теперь в нашем простом примере это нетрудно понять, но это может привести к проблемам при работе с большими сложными формулами.
В таких случаях лучше не беспокоиться о порядке старшинства, сохраняя вычисления в скобках (скобках).
Например, если вы хотите сначала выполнить сложение, а затем деление, вы можете использовать следующую формулу:
=1200/(15+15)
Это даст вам результат как 40 (=1200/ 30)
Разделение двух столбцов в Google Sheets
В реальных сценариях вы не захотите открывать Google Sheets для простого разделения. Вы можете легко сделать это с помощью калькулятора на своем смартфоне или с помощью простого поиска Google.
Вы можете легко сделать это с помощью калькулятора на своем смартфоне или с помощью простого поиска Google.
Где можно использовать Google Таблицы, так это для быстрого разделения чисел на столбцы и получения результата для сотен ячеек за секунду.
Например, предположим, что у вас есть набор данных, как показано ниже, и вы хотите вычислить деление, когда значение в столбце A делится на соответствующую ячейку в столбце B
Ниже приведена формула, которая это сделает:
=Формуламассива(A1:A20/B1:B20)
Поскольку это формула массива, вам нужно ввести эту формулу только в ячейку C1, и она даст вам результат, как показано выше.
Также нельзя удалять или редактировать часть массива. Однако вы можете удалить весь массив, удалив содержимое ячейки C1.
Разделить без остатка в Google Sheets
Допустим, у вас есть набор данных, как показано ниже, и вы хотите разделить значение в столбце A на значение в столбце B.
Если вы сделаете это, как показано в предыдущем разделе, вы получите целую часть, а также десятичную часть.
Если вам не нужен остаток при делении этих значений (где остаток представляет собой десятичную часть), вы можете использовать следующую формулу:
=ArrayFormula(INT(A1:A20/B1:B20))
В приведенной выше формуле используется та же формула деления, но она заключена в функцию INT, которая возвращает только целую часть результата, а не десятичную часть.
Вот некоторые из способов разделения в Google Таблицах. В зависимости от того, хотите ли вы разделить числа, ячейки или столбцы, вы можете использовать функцию РАЗДЕЛИТЬ или оператор деления.
Я надеюсь, что этот учебник по Google Таблицам был вам полезен!
Другие учебные пособия по Google Sheets, которые могут оказаться полезными:
- Как суммировать столбец в Google Sheets
- Как пронумеровать строки в Google Таблицах (добавить серийные номера)
- Как подсчитать ячейки с определенным текстом в Google Sheets
- Как скрыть нулевые значения в Google Таблицах
- Преобразование формул в значения в Google Sheets
- Как сделать квадрат в Google Таблицах
- Как округлять числа в Google Таблицах
Вычисление значений с использованием данных в ячейках таблицы в Numbers на Mac
Вы можете создавать ячейки формул или функций, которые автоматически выполняют вычисления с использованием данных в любых выбранных вами ячейках. Например, вы можете сравнивать значения в двух ячейках, вычислять сумму или произведение ячеек и так далее. Результат формулы или функции отображается в той ячейке, где вы ее ввели.
Например, вы можете сравнивать значения в двух ячейках, вычислять сумму или произведение ячеек и так далее. Результат формулы или функции отображается в той ячейке, где вы ее ввели.
Вы также можете использовать любые предопределенные математические функции, включенные в Numbers, для создания формул. Существует более 250 функций для приложений, включая статистику, инженерию и финансы, некоторые из которых получают информацию удаленно через Интернет. Подробная информация о каждой функции отображается в интерактивной справке по формулам и функциям и в обозревателе функций, который появляется при вводе знака равенства (=) в ячейке.
Вставка формулы
Вы можете создавать простые или сложные арифметические формулы для выполнения вычислений со значениями в ваших таблицах.
Щелкните ячейку, в которой должен появиться результат, затем введите знак равенства (=).
Открывается редактор формул.
 Перетащите левую часть редактора формул, чтобы переместить его. Вы можете изменить его размер, перетащив его за любой из внешних краев.
Перетащите левую часть редактора формул, чтобы переместить его. Вы можете изменить его размер, перетащив его за любой из внешних краев.Совет: Для выполнения основных вычислений, таких как сумма, среднее значение или произведение, вы также можете выбрать диапазон ячеек, который хотите включить в формулу, щелкнуть на панели инструментов и выбрать формулу. Numbers автоматически вставляет формулу и выбирает ячейку результата на основе вашего выбора.
Щелкните ячейку для использования в формуле или введите значение (например, число, такое как 0 или 5,20).
Введите арифметический оператор (например, +, -, * или /), затем выберите другую ячейку для использования в формуле или введите значение.
По умолчанию Numbers вставляет + между ссылками на ячейки.
Продолжайте добавлять операторы и ссылки на ячейки до тех пор, пока ваша формула не будет завершена, затем нажмите клавишу «Ввод» или щелкните в редакторе формул, когда закончите.

Если щелкнуть , вы выйдете из редактора формул без сохранения изменений.
Если в вашей формуле есть ошибка, в ячейке результатов появляется . Щелкните ее, чтобы увидеть сообщение об ошибке. Если в сообщении указано, что ошибка вызвана другой ячейкой, можно щелкнуть ссылку на ячейку, чтобы выбрать ячейку с ошибкой.
Вставка функции
Щелкните ячейку, в которой должен появиться результат функции, затем введите знак равенства (=).
Вы также можете щелкнуть на панели инструментов и выбрать «Новая формула».
Откроется редактор формул, и в правой части окна появится Браузер функций со списком всех функций. Чтобы получить справку по функции, щелкните ее.
Перетащите левую часть редактора формул, чтобы переместить его. Вы можете изменить его размер, перетащив его за любой из внешних краев.
Введите имя функции (или термины, связанные с функцией, например «адрес») в поле поиска в верхней части Браузера функций или просмотрите доступные функции, затем дважды щелкните имя функции, которую вы хотите хочу.

Функция появляется в редакторе формул со всеми обязательными и необязательными аргументами для функции.
Вы можете получить справку по функции в Браузере функций, выбрать значения для аргументов, временно отобразить формулу в виде текста или преобразовать ее в текст постоянно, щелкая стрелки в редакторе формул (как показано ниже).
Преобразование формулы в текст закрывает редактор формул и оставляет текстовую версию формулы в ячейке.
Когда вы редактируете ячейку, содержащую формулу, представление смарт-ячейки в нижней части окна показывает результат формулы, значения ссылки на ячейку, ошибки и предупреждения.
Выберите аргумент в функции, затем введите значение или выберите ячейки для включения в расчет, выполнив одно из следующих действий:
Выберите ячейку: Щелкните ячейку.
Выберите диапазон ячеек в нескольких строках и столбцах: Перетащите через диапазон ячеек, которые вы хотите включить.

Добавление значений одного столбца или строки: Щелкните полосу в верхней части столбца или слева от строки или выберите все ячейки в столбце или строке.
Когда закончите, нажмите клавишу «Ввод» или щелкните в редакторе формул.
Если щелкнуть , вы выйдете из редактора формул без сохранения изменений.
Если в вашей формуле есть ошибка, в ячейке результатов появляется . Щелкните ее, чтобы увидеть сообщение об ошибке. Если в сообщении указано, что ошибка вызвана другой ячейкой, можно щелкнуть ссылку на ячейку, чтобы выбрать ячейку с ошибкой.
Сравните значения с помощью формулы
Вы можете использовать операторы сравнения, чтобы проверить, равны ли значения в двух ячейках или одно значение больше или меньше другого. Для этого вы должны настроить оператор внутри ячейки, например, A1 > A2, что означает, что значение в ячейке A1 больше, чем значение в ячейке A2. Результат оператора сравнения выражается как «истина» или «ложь».
Результат оператора сравнения выражается как «истина» или «ложь».
Щелкните ячейку, в которой должен появиться результат сравнения, затем введите знак равенства (=).
Открывается редактор формул. Перетащите левую часть редактора формул, чтобы переместить его. Вы можете изменить его размер, перетащив его за любой из внешних краев.
Щелкните ячейку, значение которой вы хотите сравнить, или введите значение для сравнения.
Введите оператор сравнения (>, >=, =, <>, < или <=), затем выберите ячейку, значение которой вы хотите сравнить, или введите статическое значение для сравнения.
Нажмите клавишу «Ввод» или щелкните в редакторе формул, когда закончите.
Если щелкнуть , вы выйдете из редактора формул без сохранения изменений.
Если в вашей формуле есть ошибка, в ячейке результатов появляется . Щелкните ее, чтобы увидеть сообщение об ошибке. Если в сообщении указано, что ошибка вызвана другой ячейкой, можно щелкнуть ссылку на ячейку, чтобы выбрать ячейку с ошибкой.
Ссылки на ячейки в формулах
В формулы можно включать ссылки на ячейки, диапазоны ячеек и целые столбцы или строки данных, включая ячейки в других таблицах и на других листах. Numbers использует значения в указанных ячейках для вычисления результата формулы. Например, если вы включаете «A1» в формулу, это относится к значению в ячейке A1 (ячейке в столбце A и строке 1).
Примечание: Если в вашей таблице используются категории и вы добавляете новую строку в диапазон ячеек-указателей, результаты формулы не будут включать новую строку, пока вы не измените ссылку на ячейку.
В приведенных ниже примерах показано использование ссылок на ячейки в формулах.
Если указанный диапазон состоит из нескольких ячеек, начальная и конечная ячейки разделяются одним двоеточием.
COUNT(A3:D7)
Если ссылка относится к ячейке в другой таблице, ссылка должна содержать имя таблицы (если только имя ячейки не является уникальным во всех таблицах).

Таблица 2::B2
Обратите внимание, что имя таблицы и ссылка на ячейку разделены двойным двоеточием (::). Когда вы выбираете ячейку в другой таблице для формулы, имя таблицы добавляется автоматически.
Если ссылка относится к ячейке таблицы на другом листе, имя листа также должно быть включено (если только имя ячейки не является уникальным на всех листах).
СУММ(Лист 2::Таблица 1::C2:G2)
Имя листа, имя таблицы и ссылка на ячейку разделяются двойным двоеточием. Когда вы щелкаете ячейку на другом листе при построении формулы, имя листа и имя таблицы автоматически включаются в формулу.
Для ссылки на столбец можно использовать букву столбца. Приведенная ниже формула вычисляет общее количество ячеек в третьем столбце:
СУММ(C)
Чтобы сослаться на строку, вы можете использовать номер строки. Приведенная ниже формула вычисляет общее количество ячеек в первой строке:
СУММ(1:1)
Чтобы сослаться на строку или столбец с заголовком, вы можете использовать имя заголовка.
 Формула ниже суммирует все ячейки в строке с заголовком «Доход»:
Формула ниже суммирует все ячейки в строке с заголовком «Доход»:СУММ(Доход)
Приведенная ниже формула относится к столбцу по названию заголовка «Количество гостей» и ячейке B2 в таблице на другом листе.
Сохранить ссылки на строки или столбцы в формулах
Вы можете установить абсолютные ссылки на строки и столбцы в формуле, чтобы вы могли использовать ту же формулу в любом месте электронной таблицы без изменения ссылок на ячейки, как это было бы в противном случае.
Если не сохранить ссылки на строки или столбцы, при перемещении формулы (путем вырезания и вставки или добавления новых строк и столбцов) ссылки корректируются относительно нового местоположения формулы.
Дважды щелкните ячейку результата с формулой, которую вы хотите изменить.
Откроется редактор формул, отображающий функции. Перетащите левую часть редактора формул, чтобы переместить его.

Щелкните треугольник на маркере, представляющем диапазон ячеек, который вы хотите сохранить.
Выберите «Сохранить строку» или «Сохранить столбец» для начального или конечного адреса выбранного диапазона.
Кроме того, вы можете выбрать диапазон в редакторе формул, а затем нажать Command-K, чтобы сохранить строку и столбец диапазона.
Нажмите клавишу «Ввод» или щелкните в редакторе формул, когда закончите.
Если щелкнуть , вы выйдете из редактора формул без сохранения изменений.
Изменение существующей формулы
Существующую формулу можно изменить так, чтобы она ссылалась на другие ячейки.
Дважды щелкните ячейку результата с формулой, которую вы хотите изменить.
Откроется редактор формул, отображающий формулу. Перетащите левую часть редактора формул, чтобы переместить его.
Выполните одно из следующих действий:
Измените ссылки на ячейки: Выберите существующие адреса ячеек, которые вы хотите изменить, затем выберите новые ячейки.

Удалить ссылки на ячейки: В редакторе формул выберите ненужные ссылки на ячейки, затем нажмите Удалить на клавиатуре.
Добавьте дополнительные ссылки на ячейки: Поместите точку вставки в область аргументов формулы, затем щелкните новые ячейки, которые хотите добавить.
Когда закончите, нажмите клавишу «Ввод» или щелкните в редакторе формул.
Если щелкнуть , вы выйдете из редактора формул без сохранения изменений.
Если в вашей формуле есть ошибка, в ячейке результатов появляется . Щелкните ее, чтобы увидеть сообщение об ошибке. Если в сообщении указано, что ошибка вызвана другой ячейкой, можно щелкнуть ссылку на ячейку, чтобы выбрать ячейку с ошибкой.
См. также Форматирование дат, валюты и других данных в Numbers на MacИспользуйте VoiceOver для создания формул и автозаполнения ячеек в Numbers на Mac
Как разделить столбцы в Excel (8 простых способов)
В этой статье я покажу, как разделить столбцы в Excel. Я покажу несколько способов. Выберите тот, который лучше всего подходит для вашей работы.
Я покажу несколько способов. Выберите тот, который лучше всего подходит для вашей работы.
Итак, приступим.
Символ деления в Excel
Как разделить в Excel
Скачать практическую рабочую тетрадь
8 удобных способов разделить столбцы в Excel
1. Деление ячейки на другую ячейку или число в Excel
2. Копирование формулы для разделения столбцов в Excel
3. Применение формулы массива для разделения столбцов
4. Использование формулы для разделения столбцов
4.1.Использование жестко закодированного номера
4.2. Использование динамического метода
5. Использование специальной функции «Вставить» для разделения столбцов
6. Вставка функции QUOTIENT для разделения столбцов
7. Использование процентов для разделения столбцов
8. Применение кода VBA для разделения столбцов
Особые примечания, которые следует помнить
Статьи по Теме
Вывод
Символ деления в Excel В математике для деления двух чисел используется символ обела (÷).
15 ÷ 5 = 3
Но в Excel мы используем косую черту (/) для разделения двух чисел.
15/5 = 3
В Excel мы пишем выражение деления, подобное приведенному выше изображению, где:
- ‘A’ — делимое или числитель — число, которое нужно разделить на другое число ( делитель ).
- ‘B’ — делитель или знаменатель — число, на которое нужно разделить другое число ( делимое ).
Как делить в Excel
Вот несколько примеров деления на в Excel.
Чтобы узнать больше о приоритете операторов и ассоциативности в Excel, прочитайте эту статью: Что такое порядок и приоритет операций в Excel?
Загрузить практическую рабочую тетрадь
Вы можете загрузить следующую рабочую книгу Excel для лучшего понимания и самостоятельной практики.
8 удобных способов разделить столбцы в Excel
В следующих методах здесь мы покажем вам, как разделить столбцы в Excel, используя 8 различных способов, таких как деление ячейки на другую ячейку или число, копирование формулы , применение формулы массива , использование формула с использованием специальной функции пасты , вставив функцию ЧАСТНОЕ, с использованием процентов и применив код VBA . Предположим, у нас есть примерный набор данных.
1. Деление ячейки на другую ячейку или число в Excel
Деление ячейки на другую ячейку или число аналогично делению двух чисел в Excel.
Вместо чисел мы просто используем ссылки на ячейки. Ссылки на ячейки могут быть относительными, абсолютными или смешанными.
Шаг 1:
Вот несколько примеров деления ячеек на другую ячейку или число (изображение ниже).
- Деление клетки на другую.
=B5/C5
- Деление ячейки по значению.
- Разделение ячейки на другую ( ссылка на ячейку является абсолютной ) .
= $B$7/$C$7
Подробнее: Как разделить без использования функции в Excel (с быстрыми шагами)
2. Копирование формулы для разделения столбцов в Excel
Шаг 1:
Мы хотим разделить значения столбца B на значения столбца C .
Шаг 2:
- Сначала выберите ячейку D5 и используйте эту формулу.
=B5/C5
Шаг 3:
- Затем нажмите Введите .
 Формула выводит 10 как 50 , разделенное на 5 , и возвращает 10 . Затем мы выбираем ячейку D5 . И скопируйте формулу в D5 в другие ячейки ниже, удерживая и перетаскивая инструмент ручки автозаполнения Excel. Или вы можете просто дважды щелкнуть инструмент ручки автозаполнения.
Формула выводит 10 как 50 , разделенное на 5 , и возвращает 10 . Затем мы выбираем ячейку D5 . И скопируйте формулу в D5 в другие ячейки ниже, удерживая и перетаскивая инструмент ручки автозаполнения Excel. Или вы можете просто дважды щелкнуть инструмент ручки автозаполнения.
Шаг 4:
- И вот результат. С правой стороны показана формула.
3. Применение формулы массива для разделения столбцов
Разделим столбец на другой, используя формулу массива Excel. Большинство обычных пользователей Excel боятся формулы массива Excel. Если вы один из них, прочитайте эту статью: Базовая формула массива Excel: что такое массив в Excel?
Если вы хотите защитить формулу Excel от изменения или удаления пользователями, вы можете использовать формулу массива.
Позвольте мне показать, как вы могли бы выполнить приведенные выше вычисления, используя формулу массива.
Шаг 1:
- Во-первых, выберите диапазон ячеек от D5 до D14 и введите эту формулу.
=B5:B14/C5:C14
Шаг 2:
- Теперь нажмите CTRL + SHIFT + ENTER (я помню короткую форму CSE ) одновременно. Это способ сделать формулу массива в Excel. Вы видите результаты.
Примечания
- Все ячейки ( D5:D14 ) содержат одну и ту же формулу. Таким образом, вы не можете изменить формулу одной ячейки. Чтобы изменить формулу, вам нужно выделить все ячейки, а затем вы можете отредактировать или удалить формулу. После редактирования или удаления формулы необходимо одновременно нажать CTRL + SHIFT + ENTER еще раз.

4. Использование формулы для разделения столбцов
4.1.Использование жестко закодированного номера
Предположим, вы хотите разделить значения столбца на определенное число 10 (оно может быть любым).
Шаг 1:
- Во-первых, выберите ячейку C 5 и используйте эту формулу.
=B5/10
Шаг 2:
- Итак, нажмите Введите и затем используйте формулу для других ячеек ниже.
- Наконец, здесь вы увидите вывод.
Итак, значения столбца B делятся на определенное число, 10 .
4.2. Использование динамического метода
Возможно, когда-нибудь вы захотите разделить эти числа на другое число, скажем, на 5. Неразумно редактировать формулу для получения результатов.
Мы можем использовать этот метод.
Шаг 1:
- Сначала выберите ячейку D5 и используйте эту формулу
=B5/$C$5
- Поэтому из ячейки C5 в C14 я помещу число, которое будет использоваться для деления значений столбца B .
- Затем обратите внимание на формулу. Вы видите, я сделал из клетки C5 до C14 абсолютная ссылка на ячейку из ячейки C5 до C14 , так как я не хочу, чтобы она менялась, когда я использую формулу для других ячеек в столбце.
Шаг 2:
- Затем нажмите Enter, и используйте формулу для других ячеек в столбце.
- В результате вы увидите результаты здесь, на изображении ниже.

5. Использование специальной функции «Вставить» для разделения столбцов
В этом методе вы можете разделить столбец на определенное число без использования формулы Excel.
Мы будем использовать функцию Excel Специальная вставка .
Шаг 1:
- Во-первых, мы поместим делитель в ячейку. Допустим, в нашем случае делитель стоит в ячейке С3 . Выберите ячейку и скопируйте значение ячейки (сочетание клавиш CTRL + C ) команда.
Шаг 2:
- Точно так же мы выберем числа в столбце B -> Щелкните правой кнопкой мыши моей мыши. Появится меню -> В меню нажмите Специальная вставка.
Примечания
- Сочетание клавиш для открытия диалогового окна «Специальная вставка»: CTRL + ALT + V.

Шаг 3:
- Затем , появится диалоговое окно «Специальная вставка ». В этом диалоговом окне выберите параметр Divide (нижний правый угол диалогового окна). Наконец, нажмите на
Шаг 4:
- Итак, вот окончательный результат.
Все числа заменены новыми значениями (деленными на 50 ). В результате в ячейках не отображаются формулы.
Подробнее: Как разделить всю строку в Excel (6 простых методов)
6. Вставка функции ЧАСТНОЕ для разделения столбцов
Функция QUOTIENT Excel возвращает только целую часть деления.
Шаги:
- Вот синтаксис функции ЧАСТНОЕ.
= ЧАСТНОЕ(числитель, знаменатель)
Проверьте различия между результатами, полученными с помощью общей формулы Excel и использования ЧАСТНОГО функции .
Подробнее: Как делить с десятичной дробью в Excel (5 подходящих примеров)
7. Использование процентов для деления столбцов
Вы знаете 25% = 25/100 = 0,25
Итак, деление столбца на процент на самом деле то же самое, что деление столбца на число.
Шаги:
- Вот несколько примеров деления столбца на проценты.
=B5/25% = 200
=B6/0,25 = 400
=B7/D3 = 600
Подробнее: Как разделить значение, чтобы получить процент в Excel (5 подходящих примеров)
8. Применение кода VBA для разделения столбцов
VBA — это язык программирования, который можно использовать для различных задач, и разные типы пользователей могут использовать его для этих задач. С помощью сочетания клавиш Alt + F11 можно запустить редактор VBA . В последнем разделе мы сгенерируем код VBA , который позволяет очень легко разделить столбцы в Excel .
С помощью сочетания клавиш Alt + F11 можно запустить редактор VBA . В последнем разделе мы сгенерируем код VBA , который позволяет очень легко разделить столбцы в Excel .
Шаг 1:
- Сначала мы откроем вкладку Разработчик .
- Затем мы выберем команду Visual Basic .
Шаг 2:
- Здесь откроется окно Visual Basic .
- После этого из опции Вставить мы выберем новый модуль для записи кода VBA .
Шаг 3:
- Сначала вставьте следующие Код VBA в модуль .
- Затем нажмите кнопку « Run » или нажмите F5 , чтобы запустить программу .

Sub Divide_Columns()
Диапазон("D5:D14").Формула = "=B5/C5"
Конец суб Шаг 4:
- Наконец, как вы видите, столбец D продемонстрирует здесь все результаты.
Особые примечания на память
- Нельзя делить число на ноль. В математике это запрещено.
- При попытке разделить число на ноль Excel показывает #DIV/0! Ошибка .
Таким образом, мы можем обработать эту ошибку двумя способами:
- Использование функции ЕСЛИОШИБКА.
- Использование функции ЕСЛИ.
Обработка #DIV/0! Ошибка при использовании функции ЕСЛИОШИБКА
Вот синтаксис функции ЕСЛИОШИБКА :
=ЕСЛИОШИБКА (значение, значение_если_ошибка)
Здесь вы увидите, как мы применяем функцию ЕСЛИОШИБКА для обработки #DIV/0! Ошибка в Excel.
Затем я буду использовать эту формулу в ячейке D2 .
=ЕСЛИОШИБКА(B5/C5, "Не разрешено")
Обработка #DIV/0! Ошибка при использовании функции ЕСЛИ
Вот синтаксис функции ЕСЛИ :
=ЕСЛИ(логическая_проверка, [значение_если_истина], [значение_если_ложь])
Кроме того, вместо использования функции ЕСЛИОШИБКА вы также можете использовать функцию ЕСЛИ для обработки #ДЕЛ/0! Ошибка (следующее изображение).
Затем в ячейке D2 , я использовал эту формулу.
=ЕСЛИ(C5=0, "Не разрешено", B5/C5)
Затем я скопирую и вставлю эту формулу в другие ячейки столбца.
Подробнее: [Исправлено] Формула деления не работает в Excel (6 возможных решений)
Связанные статьи- Как сложить и разделить в Excel (5 подходящих примеров)
Вывод
В этой статье мы рассмотрели 8 удобных методов для разделения столбцов в Excel. Мы искренне надеемся, что вам понравилась эта статья, и вы узнали много нового. Кроме того, если вы хотите прочитать больше статей об Excel, вы можете посетить наш веб-сайт Exceldemy . Если у вас есть какие-либо вопросы, комментарии или рекомендации, пожалуйста, оставьте их в разделе комментариев ниже.
Разделение меры Power Bi + 9 примеров
В этом руководстве по Power Bi мы обсудим различные примеры Разделить меру двойного деления мощности . А также мы обсудим следующие пункты:
- Двойная мера мощности разделить один столбец на другой
- Двойная мера мощности разделить два столбца
- Двойная мера мощности разделить с фильтром
- Двойная мера мощности разделить на ноль
- Мера двойная мощность разделить на ноль на общую сумму
- Двойная мера мощности разделить по строке за строкой
- Двойная мера мощности разделить два столбца из разных таблиц
- Двойная мера мощности разделить столбец на число
- Вычислить строку в столбце, деленную на сумму этого столбца
Мера деления в степени
В Power bi, чтобы разделить числитель на знаменатель, мы можем использовать функцию DIvide и оператор /
Если вы используете функцию деления, вы должны передать числитель и знаменатель.
Синтаксис функции деления:
Разделить(<числитель>,<знаменатель>, <альтернативный результат>
Читать Power Bi Relationship Functions
Двойная мера мощности разделить один столбец на другой
Здесь мы увидим, как разделить один столбец на другой, используя функцию деления двойного измерения мощности.
Мы будем использовать приведенный ниже пример таблицы, чтобы найти рейтинг кликов (CTR) по формуле Клики/Показы.
двойная мера мощности разделит один столбец на другойСначала мы рассчитаем сумму кликов и сумму показов, а затем рассчитаем сумму кликов/сумму показов, используя показатель Power BI.
- Загрузите данные, используя get data в power bi dektop.
- Щелкните новую меру на ленте, чтобы рассчитать сумму кликов.
- Затем запишите следующую меру:
Всего кликов = СУММА('Таблица'[Клик]) - Далее мы найдем сумму показов, поэтому нажмите на новую меру .

- Затем напишите следующую меру:
Общее количество показов = СУММА('Таблица'[Показ]) - Теперь мы рассчитаем рейтинг кликов (CTR), нажмите на новую меру.
- Затем запишите приведенный ниже показатель:
CTR = DIVIDE([Общее количество кликов],[Общее количество показов])
- Теперь щелкните показатель, чтобы изменить десятичный формат на процентный.
- Затем откроется лента инструмента измерения , в разделе формата измените формат на процент .
- Теперь, чтобы проверить меру, выберите визуализацию карты на панели визуализации.
- В полях перетащите показатель CTR с панели полей.
Прочитать инструкцию переключателя двойного измерения мощности с примерами
мера двойной мощности разделить два столбца
Здесь мы рассмотрим, как разделить два столбца с помощью функции деления меры двоичной мощности.
Мы будем использовать пример таблицы ниже, чтобы найти процент незавершенных задач.
power bi мера разделить два столбцаСначала мы рассчитаем общее количество задач и общее количество выполненных задач, а затем обнаружим, что задача не выполнена. И, наконец, мы найдем процент невыполненных задач, разделив невыполненные задачи на общее количество задач.
- Загрузите данные с помощью команды get data.
- Нажмите на новую меру на ленте, чтобы вычислить сумму задачи.
- Затем запишите следующую меру:
Всего задач = СУММ(Таблица задач[Задачи])
- Теперь мы рассчитаем сумму выполненных задач, щелкните новую меру на ленте.
- Затем запишите следующую меру:
TotalTaskCompleted = SUM(TaskTable[Completed])
- Теперь мы обнаружим, что задача не выполнена, поэтому щелкните новую меру на ленте.
- Затем запишите следующую меру:
Не выполнено = [Всего задач] -[Всего задач завершено]
- Наконец, мы найдем процент невыполненных задач, поэтому щелкните новую меру на ленте.

- Затем запишите новую меру:
Процент невыполненных работ = РАЗДЕЛИТЬ([Не выполнено],[Всего задач],0)
- Теперь, чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
- В поле значения перетащите столбец имени задачи, Задачи, показатель выполненной задачи, показатель незавершенной задачи и процент невыполненной задачи.
Функция чтения счетчика в измерении Power BI
мера двойной мощности разделить с помощью фильтра
Здесь мы увидим, как разделить два столбца и отфильтровать контекст, используя функцию деления и функцию фильтра в измерении.
Мы будем использовать приведенную ниже примерную таблицу для расчета процента совпадений без типа хранилища SIS.
двойное деление мощности с фильтром Сначала мы рассчитаем общий трафик и общую транзакцию продаж. Затем мы найдем процент попаданий, используя функцию деления, и, наконец, мы найдем процент попаданий, отфильтровав тип хранилища.
- Загрузите данные, используя get data в Power Bi Desktop.
- Теперь мы создадим меру, которая будет вычислять общий трафик, поэтому щелкните новую меру на ленте.
- Затем запишите следующую меру:
TotalTraffic = Sum(Sales[Traffic])
- Мы найдем общую транзакцию, поэтому щелкните новую меру на ленте.
- Затем запишите следующую меру:
Общий трафик = Сумма (Продажи [Трафик])
- Мы найдем частоту попаданий, поэтому для этого нажмите на новую меру.
- Затем запишите приведенную ниже меру мощности bi:
Показатель попаданий = РАЗДЕЛИТЬ ([Общее количество транзакций продаж], [Общий трафик], 0)
- Из показателя обращений мы отфильтруем тип магазина SIS, затем мы покажем процент попаданий, поэтому для этого нажмите на новую меру .
- Затем напишите следующую меру:
HitRateFilter =
ВЫЧИСЛИТЬ([Показатель попаданий],
ФИЛЬТР(Продажи, Продажи[Тип магазина] <> "SIS")
) - Щелкните меру фильтра Hit rate на панели полей, на ленте откроются инструменты измерения.

- В разделе форматирования измените формат с общего на в процентах .
- Теперь, чтобы проверить меру, щелкните визуализацию таблицы на панели визуализации в Power Bi.
- В поле значений перетащите столбец с коротким месяцем, столбец типа магазина, столбец трафика, показатель количества попаданий и показатель фильтра числа попаданий
Читать Как создать показатель на основе слайсера в Power BI
Разделение двойного показателя мощности на ноль
Здесь мы увидим, как обрабатывать ошибку деления на ноль с помощью функции деления в показателе .
Мы будем использовать приведенный ниже образец таблицы, где col1 будет числителем, а col2 — знаменателем. И в этих столбцах часть значения либо нулевая, либо нулевая.
деление по степени деления на ноль Используя стандартное деление, мы увидим, какую ошибку мы получим, а затем воспользуемся функцией деления, чтобы решить эту ошибку.
- Загрузите данные с помощью команды get data.
- Нажмите на новую меру на ленте.
- Затем запишите следующую меру:
StandardDivision = СУММ(Таблица2[Столбец1])/СУММ(Таблица2[Столбец2])
- Щелкните меру в области поля, затем в инструментах измерения измените формат меры в процент.
Теперь на скриншоте ниже вы можете видеть, что когда числитель равен нулю, он показывает 0%.
Но когда знаменатель равен нулю или пуст, он показывает бесконечность, а когда числитель пуст, результат отображается как пустой.
мощность bi мера деление на ноль- Теперь мы воспользуемся функцией деления для решения этой ошибки, вместо бесконечности она покажет 0%.
- Нажмите на новую меру на ленте.
- Затем напишите приведенную ниже меру:
Мера = ДЕЛИТЕ (СУММ (Таблица 2 [Столбец 1]), СУММ (Таблица 2 [Столбец 2]), 0)
На приведенном ниже снимке экрана вы можете видеть, что вместо бесконечности мы получаем 0 в качестве вывода, но в последней строке мы все еще получаем пустое значение, где числитель пуст.
Мы можем решить эту проблему, изменив указанную выше меру с помощью функций switch() и IsBlank().
- Нажмите на эту меру, чтобы открыть ее.
- Затем перепишите указанную выше меру:
Мера = ПЕРЕКЛЮЧЕНИЕ(ИСТИНА(),ПУСТО(ДЕЛИТЬ(СУММ(Таблица2[Столбец1]), СУММ(Таблица2[Столбец2]),0)),0,ДЕЛИТЬ(СУММ(Таблица2 [Столбец1]), СУММ(Таблица2[Столбец2]),0))
Теперь на приведенном ниже снимке экрана видно, что ошибки нет, а вывод равен нулю.
двойная мера мощности разделить на нольЧтение показателя Power BI SUM
Разделение показателя Power bi на общую сумму
Здесь мы увидим, как рассчитать общий процент в процентах с помощью функции Division() в мере.
Мы будем использовать данные финансовой выборки для расчета общего процента продаж на основе продукта. Вы можете скачать образцы данных отсюда.
- загрузить данные с помощью get data.
- Щелкните новую меру на ленте, чтобы рассчитать общий процент продаж.

- Затем напишите следующую меру:
% от общей суммы =
РАЗДЕЛЯТЬ (
СУММА (финансы[Продажи]),
ВЫЧИСЛИТЬ (СУММ('финансовые показатели'[Продажи]), ВСЕ('финансовые показатели'[Продукт]))
) - Теперь, чтобы проверить показатель, выберите визуализацию таблицы на панели визуализации.
- В поле значений перетащите столбец продукта, столбец продаж и показатель % от общего итога из области поля.
Чтение двойного измерения мощности по категории
Мера двойного деления деление по строке за строкой
Здесь мы увидим, как разделить строку за строкой, а затем суммируем все строки деления с помощью меры.
Мы будем использовать приведенный ниже образец таблицы, чтобы разделить строку за строкой, а затем просуммируем все деления, используя функцию sumx.
мощность би мера разделить по строке за строкойНапример, сначала мы разделим по строкам общее количество задач и общее количество выполненных задач: 10/5 = 2,0; 11/3 = 3,67, 14/6 = 2,33, 25/25 = 1, 12/9 = 1,33, 18/9 = 2,0, 20/15 = 1,33
Затем просуммируем все деления:
2,0+3,63+2,33+1,0+1,33+2,0+1,33= 13,67
- Загрузите данные с помощью команды получения данных
- Щелкните Новая мера на ленте.

- Затем напишите приведенную ниже меру
Мера 2 = СУММ(TaskTable, [Всего задач]/[TotalTaskCompleted])
- Теперь, чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
- Затем в поле значения перетащите столбец имени задачи, столбец завершено, столбец задач и показатель Measure2 из области полей.
Чтение двойная мера мощности вычесть
мера двойной мощности разделить два столбца из другой таблицы
Здесь мы увидим, как использовать двойную меру мощности разделить два столбца из другой таблицы.
Здесь у нас есть две таблицы, каждая из которых имеет один общий столбец, то есть общий цвет.
Таблица 1
двойная мера мощности разделить два столбца из другой таблицыТаблица 2
мера двойной мощности разделить два столбца из другой таблицы Сначала просуммируем размер в таблице 1 по цветам, затем разделим на количество сотрудников. Например, сумма размера для синего цвета равна 246, а затем делится на 6, что равно 246/6=41
Например, сумма размера для синего цвета равна 246, а затем делится на 6, что равно 246/6=41
- Загрузите данные, используя get data.
- Нажмите на новую меру на ленте.
- Затем запишите следующую меру:
Результат =
var sumbycolor = ВЫЧИСЛИТЬ(СУММ('Таблица 3'[Размер]),ALLEXCEPT('Таблица 3','Таблица 3'[Цвет]))
var staffno = ВЫЧИСЛИТЬ(СУММ('Таблица 4'[Персонал]),ФИЛЬТР('Таблица 3','Таблица 3'[Цвет]=СВЯЗАННЫЕ('Таблица 4'[Цвет])))
Возврат DIVIDE(sumbycolor,staffno) - Теперь, чтобы проверить показатель, выберите визуализацию таблицы на панели визуализации.
- В поле значения перетащите столбец цвета, столбец нотоносца, столбец размера и показатель результата из области поля.
Чтение меры Power BI IF с примерами
мера мощности двойного деления разделить столбец на число
Здесь мы увидим, как разделить столбец на число с помощью меры в степени двоичной.
Мы воспользуемся таблицей ниже, чтобы суммировать баллы по группам, а затем разделим каждый балл на сумму каждой группы.
мощность двойная мера разделить столбец на число- Загрузите данные, используя функцию получения данных.
- Щелкните Новая мера на ленте.
- Затем запишите следующую меру:
Мера 3 =
РАЗДЕЛЯТЬ (
СУММ («Таблица 5» [Оценка]),
ВЫЧИСЛИТЬ ( СУММА («Таблица 5» [Оценка]), ALLSELECTED («Таблица 5» [Категория]))
) - Чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
- Затем в поле значения перетащите столбец группы, столбец категории, столбец оценки и показатель 3 из области поля.
Вычислить строку в столбце, деленную на сумму этого столбца
Здесь мы увидим, как разделить значение строки столбца на сумму этого столбца .
Мы будем использовать приведенный ниже пример для вычисления строки в столбце, деленной на сумму этого столбца.
- Загрузить данные, используя получение данных.
- Затем нажмите Новая мера на ленте.
- Затем запишите следующую меру:
Мера = Var denom= ВЫЧИСЛИТЬ (Сумма («Таблица» [Значения]), ВСЕ («Таблица»))
Возврат SUM('Table'[Values])/denom - Чтобы проверить меру, выберите визуализацию таблицы на панели визуализации.
- Затем перетащите столбец 1, столбец значений и показатель из области полей.
Вам также могут понравиться следующие учебные пособия по Power Bi:
- Microsoft Power BI KPI Visual
- Microsoft Power BI Stacked Column Chart
- Как использовать Microsoft Power BI Точечная диаграмма
- Комбинированная диаграмма Microsoft Power BI
- Отчет Microsoft Power bi и панель мониторинга
- Power BI Измерение умножения с примерами
В этом руководстве по Power bi мы обсудили различные типы примеров в Разделить меру Power Bi . Эти примеры перечислены ниже:
Эти примеры перечислены ниже:
- Двойная мера мощности разделить один столбец на другой
- Двойная мера мощности разделить два столбца
- Двойная мера мощности разделить с фильтром
- Двойная мера мощности разделить на ноль
- Двойная мера мощности разделить на общий итог
- Двойная мера мощности разделить по строкам
- Двойная мера мощности разделить два столбца из разных таблиц
- Двойная мера мощности разделить столбец на число
Бхавана Ратор
Бхавана Ратор — Microsoft MVP (3 раза в области приложений и служб Office) и увлеченный консультант по SharePoint, имеющий около 10 лет опыта работы в сфере ИТ в отрасли, а также в технологиях .Net. Ей нравится делиться своими техническими знаниями на сайтах EnjoySharePoint.com и SPGuides.com
Калькулятор бетона — сколько мне нужно бетона?
Рассчитайте заливку бетонной плиты и фундамента и получите советы по оценке
Используйте эти бесплатные калькуляторы бетона, чтобы оценить, сколько бетона вам потребуется для плит, фундаментов или колонн. Рекомендуется переоценить количество необходимого бетона, чтобы не опоздать на строительной площадке.
Рекомендуется переоценить количество необходимого бетона, чтобы не опоздать на строительной площадке.
ФОРМУЛА ДЛЯ КАЛЬКУЛЯТОРА БЕТОНА
Какое уравнение следует использовать, чтобы узнать, сколько бетона мне нужно?
Как рассчитать бетон:
- Определите желаемую толщину бетона
- Измерьте длину и ширину, которые вы хотите покрыть
- Умножьте длину на ширину, чтобы определить площадь в квадратных футах
- Преобразование толщины из дюймов в футы
- Умножьте толщину в футах на площадь в квадратных футах, чтобы определить кубические футы
- Преобразование кубических футов в кубические ярды путем умножения на 0,037
Вот как выглядят расчеты для бетонного патио размером 10 на 10 футов:
- 10 x 10 = 100 квадратных футов
- 4 ÷ 12 = 0,33
- 100 x 0,33 = 33 кубических фута
- 33 х 0,037 = 1,22 кубических ярда
По сути, вы вычисляете объем, а затем конвертируете его в кубические ярды. Для бетона формула объема выглядит следующим образом: длина х ширина х толщина.
Для бетона формула объема выглядит следующим образом: длина х ширина х толщина.
Чтобы определить, сколько мешков бетона вам понадобится, разделите общее количество необходимых кубических метров на выход.
Используйте следующую производительность для каждого размера мешка:
- Выход 40-фунтового мешка 0,011 кубических ярда
- 60-фунтовый мешок дает 0,017 кубических ярда
- 80-фунтовый мешок дает 0,022 кубических ярда
ГОТОВАЯ СМЕСЬ VS. БЕТОН В МЕШКАХ
Должен ли я заказывать бетон на складе в компании по производству готовых смесей или использовать только мешки?
Более крупные работы, такие как подъездные пути, легче выполнять, если заказывать бетон на складе, а не пытаться смешивать мешок за мешком вручную. Для небольших работ, таких как дорожка, скромный внутренний дворик или фундамент, вам следует вместо этого рассчитать количество бетонных мешков.
Бетон в мешках идеально подходит для:
- Заливки небольших плит для тротуаров или патио
- Установка столбов для заборов или почтовых ящиков
- Ремонт фундаментных стен, дорожек или ступеней
- Заливка небольших бордюров, ступенек или пандусов
- Фундаменты для террас, пергол, стен и др.

Если вы покупаете бетон в мешках, вы можете заказать его доставку, но если это всего несколько мешков, вы будете нести ответственность за его транспортировку самостоятельно. Вам также понадобится дополнительное оборудование для смешивания бетона. Взятый напрокат миксер может быть очень полезен, но тачка подойдет всего для нескольких сумок.
Готовый бетон во дворе подходит для:
- Большие внутренние дворики, подъездные пути, террасы у бассейнов и многое другое
- Фундаментные плиты для дома
- Автостоянки или коммерческие тротуары
Если вы планируете заказать бетон у поставщика готовой смеси, ему необходимо знать, сколько метров бетона необходимо доставить. Многие компании по производству готовых смесей будут иметь минимальный заказ в 1 ярд и будут взимать плату за недостачу при заказе частичных партий. Средний грузовик вмещает от 9и всего 11 ярдов. Если для вашего проекта требуется больше бетона, потребуется несколько грузовиков.
Сколько весит бетон?
Бетон обычно заказывают в кубических метрах, но если вы ищете вес бетона, он зависит от типа используемой смеси. Тем не менее, по оценкам большинства поставщиков готовых смесей, кубический ярд бетона весит около 4000 фунтов. Итак, если вам нужно три ярда, это будет около 12 000 фунтов (3 ярда x 4 000 фунтов). Спросите своего поставщика, если вы хотите знать точный вес.
СОВЕТЫ ПО ОЦЕНКЕ БЕТОНА
Atlanta Brick & Concrete в Атланте, Джорджия
Расчет количества бетона, необходимого для плит (включая нестандартные формы)
Практическое правило: добавьте 1 / 4 » к толщине вашей плиты для вашего бюджета бетона плиты. Это предполагает, что у вас есть работа
Если вы проверяете свой сорт и одна точка имеет размер 4 дюйма, некоторые точки имеют размер от 4,5 до 5 дюймов, лучшим решением как для качества работы, так и для вашего бюджета на бетон является исправить оценку.
Нечетные фигуры: Превратите нечетные фигуры в прямоугольники, а нечетные фигуры неожиданно легко сложить.
Нарисуйте подъездную дорожку 14′ x 20′ и ваша оценка будет хорошей. И вот почему: подъездная дорога 16 футов вверху и 12 футов внизу. Через центр ширина составляет в среднем 14 футов.
Расчет количества бетона, необходимого для фундаментов
Фундаменты редко точно соответствуют чертежу. В каменистой почве фундаменты могут разрушиться при выемке больших камней
Предполагалось, что это будет фундамент размером 12″*12″, но обратите внимание, как обрушилась левая сторона фундамента. Вычислите истинную ширину.
Экскаватор, возможно, копал слишком глубоко, или мог быть дождь, и необходимо было выкопать фундамент глубже, чтобы добраться до твердой почвы. Поэтому важно проверить различные места на вашей ноге и получить средний размер. Затем с помощью калькулятора рассчитайте необходимое количество бетона.
Плиты дома на уровне, которые на 8 дюймов отклоняются от уровня, с плитой на 4 дюйма также имеют часть основания над уровнем грунта.
Этот фундамент размером 12 x 12 дюймов должен быть рассчитан на 12 x 16 дюймов, поэтому предполагается, что фундамент поднимается выше уровня земли, чтобы достичь толщины плиты 4 дюйма. , Если к крыльцу ведут три ступени:
- Используйте калькулятор плит, чтобы рассчитать бетон, необходимый для поверхности крыльца.
- Используйте калькулятор фундамента для расчета сторон крыльца и ступеней
Вот пример:
Это крыльцо имеет площадь 9 кв. футов, поэтому введите в калькулятор плиты толщину 4 дюйма, ширину 3 фута и длину 3 фута. Итого 0,11 кубических ярда.
Крыльцо также имеет 9 погонных футов 6 дюймов. шаг. Поэтому введите в калькулятор фундамента 6 дюймов в глубину и 12 дюймов в ширину (всегда учитывайте ступени шириной 12 дюймов) и 9 футов в длину. Итого получается 0,17 кубических ярда.
Общее количество бетона, необходимое для крыльца 3 на 3 фута будет 0,28 кубических ярда (0,11 + 0,17 кубических ярда = 0,28 кубических ярда)
Повторите это для добавленных слоя шагов.
Крыльцо 3 х 3 фута
Расчет количества заливки основания
Использование запаса прочности: проблемы, вызванные недооценкой количества бетона
Никогда не пытайтесь заказать точное количество необходимого бетона. Включите запас прочности.
Идеально размещенный заказ бетона завершит работу с небольшим остатком. Заказ на 20 кубических ярдов с оставшимся 1 кубическим ярдом является хорошим заказом. Заказ на 20 кубических ярдов, которому не хватает кубических ярдов, не является хорошим заказом.
Дополнительные расходы в связи с нехваткой бетона
- Сверхурочные для бригады
- Короткая загрузка от поставщика готовой смеси
- Может возникнуть холодный стык (где закончилась одна заливка и началась другая)
Три шага к заказу достаточного количества бетона:
- Воспользуйтесь калькулятором бетона
- Измерьте глубину и ширину, как они были построены на месте, а не просто то, что указано в планах.

- Добавить запас прочности
Эмпирическое правило для запаса прочности:
- Если вы заказываете 1-5 кубических ярдов, заказывайте 0,5-1 c.y. дополнительный
- Если вы заказываете 6-10 у.е., заказывайте 1 у.е. дополнительный
- Если вы заказываете 11-20 у.е., заказывайте 1-1,5 у.е. дополнительный
Лишний бетон может расстроить. В конце концов, вы должны заплатить за этот бетон. Однако помните, что вы делаете свою работу услугой, заказывая достаточное количество бетона, а это значит, что у вас останется немного бетона.
Запрос вашего поставщика готовых смесей посетить ваш объект
После того, как вы выбрали поставщика готовых смесей, пригласите представителя на ваш объект, чтобы высказать свое мнение о требуемом количестве. Сравните рисунок с тем, что у вас получилось. Обсудите любые расхождения с поставщиком.
Ваш поставщик готовых смесей имеет неоценимое значение для проверки вашего мнения об условиях работы, проверки вашего запаса прочности, выявления проблем, о которых вы, возможно, не думали, и информирования вас о любых местных условиях, о которых вам необходимо знать.
Последнее обновление: 7 сентября 2022 г.
Калькулятор алиментов
В вашем браузере отключен Javascript. Этот сайт не будет работать корректно без включенного javascript. Добро пожаловать в калькулятор алиментов штата Нью-Гэмпшир.
Кнопка печати/сохранения будет доступна после завершения начальных расчетов. Пожалуйста, будьте
Обязательно просмотрите заполненную форму перед ее сохранением или печатью. Рекомендуется начать с
просмотр и заполнение всех ссылок, связанных с доходами и расходами, прежде чем перейти к текстовым полям и
поле выбора суда, затем закончите, выбрав, хотите ли вы производить платежи еженедельно,
раз в две недели или ежемесячно, выбрав соответствующий переключатель в главной форме. Как только все
после того, как эти шаги были выполнены, рекомендуется просмотреть рабочий лист, чтобы ознакомиться с ним.
с полями вычисляемых значений. Когда вы будете удовлетворены тем, что рабочий лист готов, вы можете нажать кнопку
кнопку печати/сохранения, и будет создана форма в формате PDF, которую вы можете распечатать или сохранить для отправки в суд.
Когда вы будете удовлетворены тем, что рабочий лист готов, вы можете нажать кнопку
кнопку печати/сохранения, и будет создана форма в формате PDF, которую вы можете распечатать или сохранить для отправки в суд.
ШТАТ НЬЮ-ГЭМПШИР
ОТДЕЛ ЗДРАВООХРАНЕНИЯ И СОЦИАЛЬНЫХ СЛУЖБ
ОТДЕЛ СЛУЖБ ПО ПОДДЕРЖКЕ ДЕТЕЙ
Бланк инструкций для печати
Инструкции по заполнению таблицы рекомендаций по алиментам
DCSS 650
15.05
Рабочий лист рекомендаций по алиментам
с использованием сумм, действующих с 1 апреля 2022 г.
Название суда:
Выберите название суда здесь. 1-й округ — Семейный дивизион — Берлин 1-й округ — Семейный дивизион — Колбрук 1-й округ — Семейный дивизион — Ланкастер 2-й округ — Семейный дивизион — Хаверхилл 2-й округ — Семейный дивизион — Ливан 2-й округ — Семейный дивизион — Литтлтон 2-й округ — Семейный дивизион — Плимут 4-й округ — Семейный дивизион — Конвей 3-й округ — Семейное отделение — Оссипи 4-й округ — Семейное отделение — Лакония 5-й округ — Семейное отделение — Клермонт 5-й округ — Семейное отделение — Ньюпорт 6-й округ — Семейное отделение — Конкорд 6-й округ — Семейное отделение — Франклин 6-й округ — Семейное отделение — Хиллсборо 6-й округ — Семейное отделение — Хуксетт 7-й округ — Семейное Дивизион — Dover7th Circuit — Family Division — Rochester8th Circuit — Family Division — Jaffrey8th Circuit — Family Division — Keene9й округ — Семейный дивизион — Гоффстаун 9-й округ — Семейный дивизион — Манчестер 9-й округ — Семейный дивизион — Мерримак 9-й округ — Семейный дивизион — Милфорд 9-й округ — Семейный дивизион — Нашуа 10-й округ — Семейный дивизион — Брентвуд 10-й округ — Семейный дивизион — Кандия 10-й округ — Семейный дивизион — Дерри 10-й округ — Семейный дивизион — 10-й округ Хэмптона — Семейный дивизион — 20-й округ Портсмута — Семейный дивизион — Салем
Номер дела:
Введите номер дела здесь.
Относительно:
Введите здесь имя заявителя.
а также
Введите здесь имя респондента.
Имя ребенка
Дата рождения
Имя ребенка
Дата рождения
Введите здесь имя вашего первого ребенка.
Введите дату рождения вашего первого ребенка здесь.
Введите здесь имя вашего третьего ребенка.
Введите здесь дату рождения вашего третьего ребенка.
Введите здесь имя вашего второго ребенка.
Введите здесь дату рождения вашего второго ребенка.
Введите здесь имя вашего четвертого ребенка.
Введите здесь дату рождения вашего четвертого ребенка.
1. Общее количество детей
Введите здесь общее количество детей, за которых вы отвечаете. 1234 или больше
2. Обязательство должника по разумной медицинской поддержке
(4% ежемесячного валового дохода Должника, округленное до ближайшего доллара)
0,00
3. Обязательство кредитора по разумной медицинской поддержке
(4% от ежемесячного валового дохода кредитора, округленное до ближайшего доллара)
0,00
РАСЧЕТЫ ОПЛАТЫ
ПРИМЕЧАНИЕ. Все доходы и расходы должны быть переведены в месячные суммы
Все доходы и расходы должны быть переведены в месячные суммы
.
(умножьте недельные суммы на 4,33; двухнедельные суммы на 2,17).
ДОЛЖНИК
(Колонка 1)
ОБЯЗАТЕЛЬ
(Колонка 2)
КОМБИНИРОВАННЫЙ
(Колонка 3)
4. Ежемесячный валовой доход
0,00
0,00
5А. суд/админ. заказал поддержку для других детей
0,00
0,00
5Б. 50% фактически уплаченных налогов на самозанятость
0,00
0,00
5С. Обязательный выход на пенсию
Обязательный выход на пенсию
0,00
0,00
5Д. Фактически уплаченные государственные подоходные налоги
0,00
0,00
5Э. Допустимые расходы по уходу за ребенком (должник)
(См. инструкции LINE 5E)
0,00
5эт. Медицинское сопровождение детей (должник)
0,00
5G. Общие вычеты (добавьте строки 5A–5F)
Общая сумма отчислений должника. 0,00
Полные отчисления по обязательствам. 0,00
6. Скорректированный ежемесячный валовой доход
(Вычтите строку 5G из строки 4)
Должник скорректировал ежемесячный валовой доход. 0,00
0,00
Скорректированный ежемесячный валовой доход кредитора. 0,00
Совокупный скорректированный ежемесячный валовой доход. 0,00
7А. Ориентировочная сумма алиментов
(Из таблицы расчетов)
Совокупная рекомендуемая сумма алиментов. 0,00
7Б. Ориентировочный процент
(Из таблицы расчетов)
Комбинированный рекомендуемый процент 0,00
8А. Допустимые расходы по уходу за ребенком (кредитор)
(См. инструкции LINE 8A)
0,00
8Б. Медицинское сопровождение детей (должник)
0,00
8С. Итого допустимые расходы кредитора
Итого допустимые расходы кредитора
(Добавить строки 8А и 8В)
Поле общих допустимых расходов кредитора. 0,00
9. Общий скорректированный ежемесячный валовой доход
Общий ежемесячный валовой доход должника. 0,00
Общий скорректированный ежемесячный валовой доход кредитора. 0,00
Совокупный общий скорректированный ежемесячный валовой доход. 0,00
10. Пропорциональная доля дохода
Должник, пропорциональная доля дохода. 0,00
Обязательная пропорциональная доля дохода. 0,00
11. Обязанность по содержанию родителей
(Строка 10 раз по линии 7А)
Обязанность по содержанию родителей. 0,00
0,00
Обязательное обязательство по содержанию родителей. 0,00
ОПЛАТА РАСЧЕТА
12. Резерв хозрасчета
(Из таблицы расчетов)
Резерв самоокупаемости должника. 0,00
13. Доступный доход для поддержки
(Вычтите строку 12 из строки 9 столбца 1)
Доход должника доступен для поддержки. 0,00
14. Ежемесячная выплата алиментов
(Введите меньшее значение из строки 11, столбца 1 или строки 13, столбца 1. Если строка 13,
столбец 1, меньше 50,00 долларов США, то вводится минимальный заказ в размере 50,00 долларов США. )
)
Неокругленная ежемесячная задолженность по алиментам должника. 0,00
15. Предполагаемое обязательство по алиментам
(Если еженедельно, разделите строку 14 на 4,33; если раз в две недели, разделите строку 14 на 2,17; если
ежемесячно, введите ту же сумму, что и в строке 14.)
** ОКРУГЛИТЕ РЕЗУЛЬТАТ ДО ЦЕЛОГО ДОЛЛАРА **
Предполагаемое обязательство должника по алиментам, округленное в зависимости от выбранной периодичности. 0,00
Частота (выберите один)
| Еженедельно | Раз в две недели | Ежемесячно |
Приготовленный:
Введите здесь имя человека, заполнившего эту форму.




 Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21. К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным.
К остатку нужно дописать 0. При этом после цифры 4 в столбике нужно поставить запятую. Теперь результат будет дробным. Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.
Нужно выбирать раскраски с легкими примерами, чтобы ребенок мог решить примеры в уме.

