Острый угол | это… Что такое Острый угол?
«∠», обозначение угла в математике
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Содержание
|
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон.
Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:
Невыпуклый угол
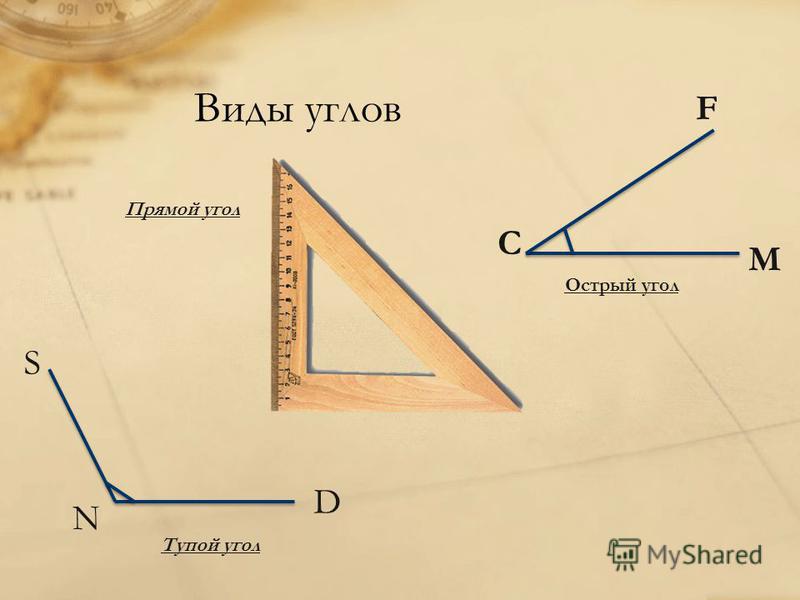
Прямой угол
- Острые (от 0 до 90°)
- Прямые (90°)
- Тупые (от 90° до 180°)
- Развернутые (180°)
- Невыпуклые (от 180° до 360°)
- Полные (360°)
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: ) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на , считаются равными. Следует отметить, что ориентированный угол между прямыми
Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Презентация «Острые и тупые углы»
2 класс
Математика
Тема урока: « Острые и тупые углы»
Внимание!
Презентация к уроку составлена на основе заданий, расположенных в учебнике.
Некоторые задания можно выполнять интерактивно:
1) в режиме редактирования.
Например, продолжить ряд, сравнить или вставить пропущенные числа.
2) во время демонстрации навести курсор на нужную фигуру до появления ладошки. Кликнуть! Нужный предмет переместиться.
3) во время демонстрации использовать инструмент перо или ручка.
МАТЕМАТИКА
Учимся обозначать углы
1
Проведите прямую. Отметьте на ней точку О. Приложите угольник вершиной к точке О. Проведите луч ОС. Отметьте на прямой точки А и В.
С
С
или ВОС
Это – угол СОВ
В
О
В
А
О
Назовите угол, к которому на этом чертеже приложен угол.
Угол обозначают, указывая его вершину и по одной точке на каждой стороне угла. При этом буква, обозначающая вершину, стоит посередине.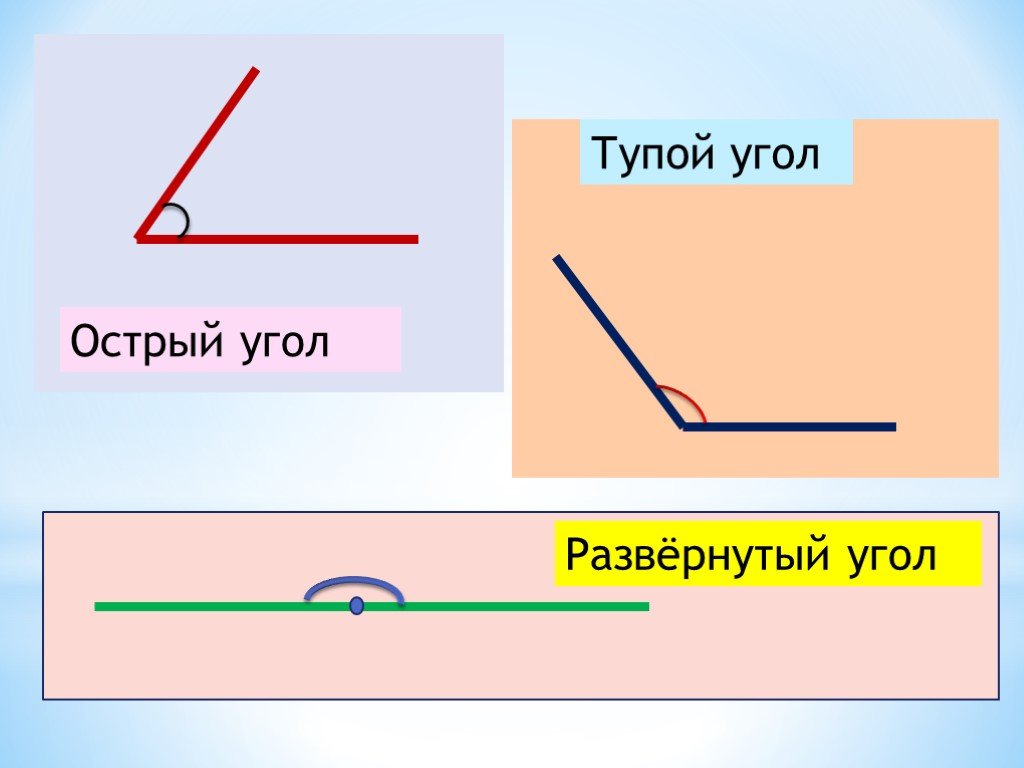
МАТЕМАТИКА
Учимся обозначать углы
Назовите углы на рисунке.
2
B
O
C
D
O
C
O
D
B
Внимание!
Данное задание можно выполнять интерактивно. Во время демонстрации навести курсор на нужную фигуру до появления ладошки. Кликнуть!
BОС
DOВ
BOD
СОВ
DOC
COD
МАТЕМАТИКА
Учимся обозначать углы
2
Назовите углы на рисунке.
B
O
C
D
O
C
O
D
B
COD
DOC
Внимание!
Данное задание можно выполнять интерактивно. Во время демонстрации навести курсор на нужную фигуру до появления ладошки. Кликнуть!
BОС
BOD
DOВ
СОВ
Урок 1.26. Острые и тупые углы
МАТЕМАТИКА
Учимся обозначать углы
Назовите углы на рисунке.
2
B
O
C
D
O
C
O
D
B
BOD
COD
DOC
DOВ
Внимание!
Данное задание можно выполнять интерактивно. Во время демонстрации навести курсор на нужную фигуру до появления ладошки. Кликнуть!
BОС
СОВ
МАТЕМАТИКА
Учимся обозначать углы
2
Назовите углы на рисунке.
B
O
C
D
O
C
O
D
B
BOD
BОС
СОВ
DOC
DOВ
COD
прямой
не прямой
не прямой
Найдите прямой угол.
Урок 1.26. Острые и тупые углы
МАТЕМАТИКА
Учимся различать углы
3
Чем изображённые углы отличаются от прямого?
B
АC
D
E
O
B
O
D
прямой
угол
острый
угол
тупой
угол
Угол, который полностью помещается внутри прямого угла, называется острым .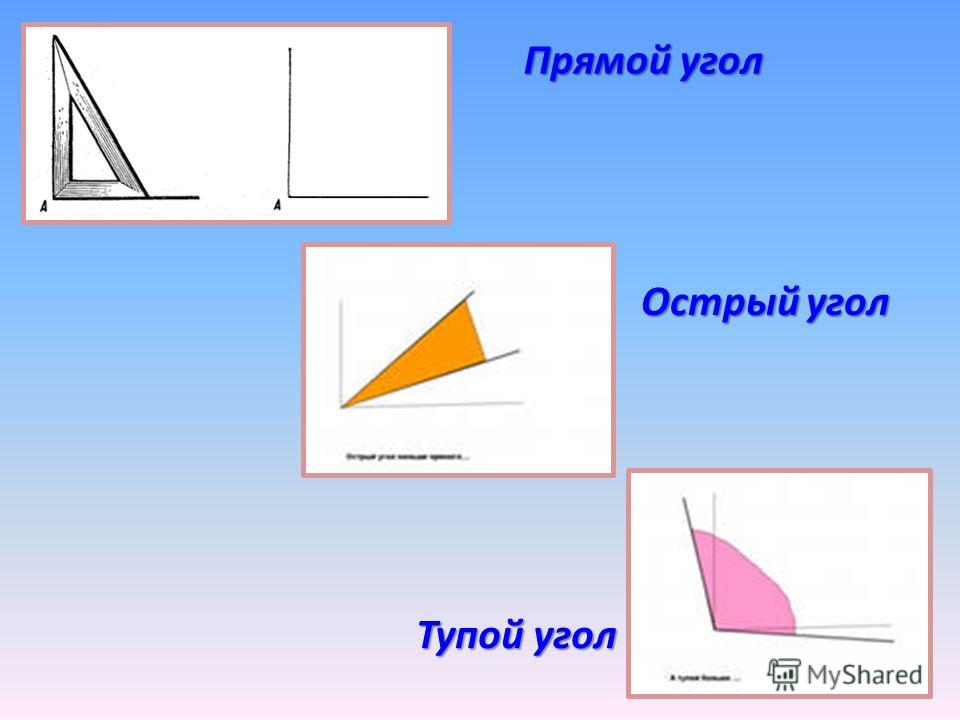
Угол АОВ – острый.
Угол, внутри которого полностью помещается прямой угол, называется тупым . Угол CED – тупой.
МАТЕМАТИКА
Применяем новые знания
4
Назовите острые, прямые, тупые углы.
Угол СОD – острый
В
А
Угол ВОС – острый
С
Угол АОВ – острый
O
D
МАТЕМАТИКА
Применяем новые знания
4
Назовите острые, прямые, тупые углы.
Угол СОD – острый
В
А
Угол ВОС – острый
С
Угол АОВ – острый
O
Угол ВOD – прямой
D
Угол АOС – прямой
Угол AOD – тупой
МАТЕМАТИКА
Применяем новые знания
5
Назовите все фигуры, для которых высказывание «Фигура имеет тупой угол» будет истинным .
Назовите фигуры, для которых это высказывание будет ложным .
Внимание!
Данное задание можно выполнить интерактивно. Для этого презентацию надо перевести в режим редактирования.
МАТЕМАТИКА
Применяем новые знания
5
Назовите все фигуры, для которых высказывание «Фигура имеет тупой угол» будет истинным .
истинное
истинное
истинное
ложное
ложное
ложное
Назовите фигуры, для которых это высказывание будет ложным .
ПРОВЕРЬ!
МАТЕМАТИКА
Выбираем задания и тренируемся
6
Составьте выражение.
9
Найдите его значение, если b = 4, c = 9.
– 4
Т. –
У лебедя b птенцов, а у тетерева с птенцов. На сколько птенцов больше у тетерева, чем у лебедя?
с пт.
Л. –
b пт.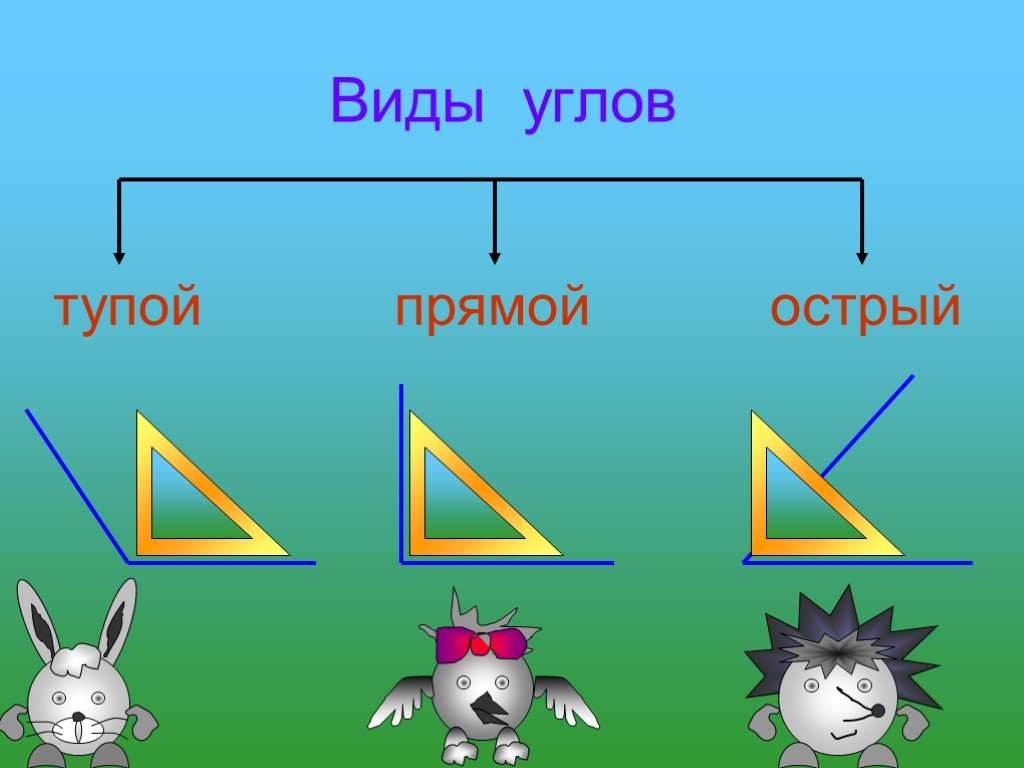
На сколько – ?
c – b
= 5 (пт.)
Ответ: на 5 птенцов больше у тетерева.
МАТЕМАТИКА
7
Рассмотрите треугольник слева. Сравните суммы чисел по сторонам. Подберите числа для второго треугольника так, чтобы суммы чисел по его сторонам были равны 16 .
5
6
3
4
7
2
1
7
4
Внимание!
Данное задание можно выполнить интерактивно. Для этого презентацию надо перевести в режим редактирования.
МАТЕМАТИКА
7
Рассмотрите треугольник слева. Сравните суммы чисел по сторонам. Подберите числа для второго треугольника так, чтобы суммы чисел по его сторонам были равны 16 .
3
5
3
4
9
6
7
2
5
4
7
1
ПРОВЕРЬ!
Что нужно знать об углах для базовых тестов по математике
Обновлено: 25 апреля 2016 г.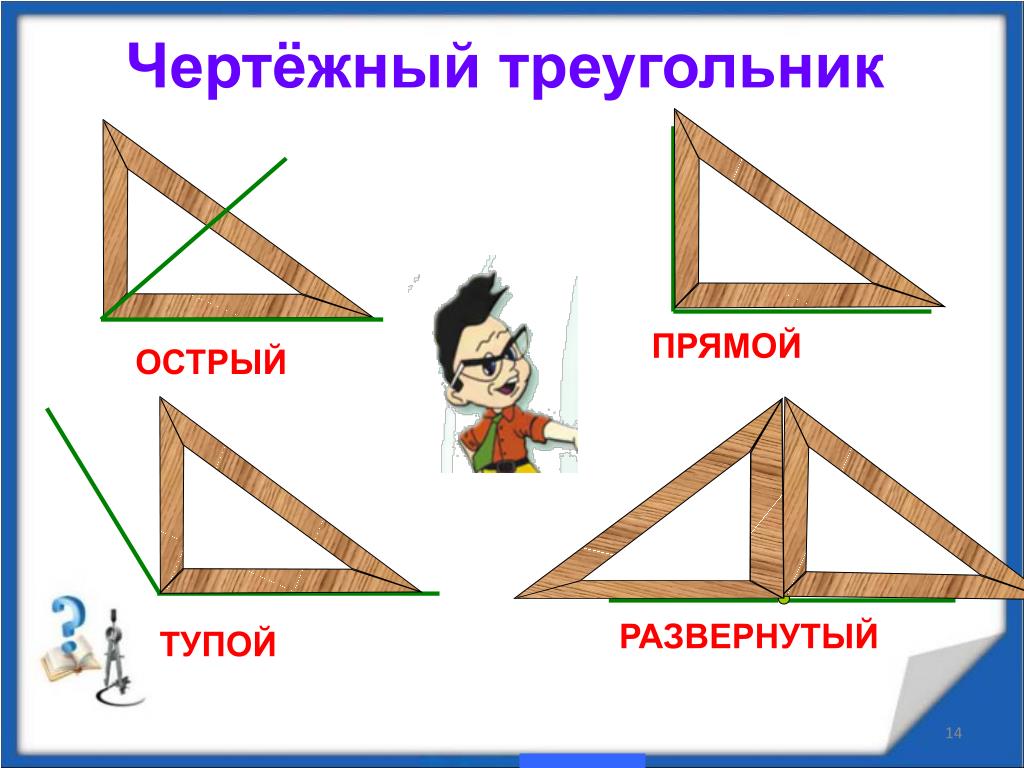
Базовая математика и предварительная алгебра все-в-одном для чайников (+ викторины по главам онлайн)
Исследуйте книгу Купить на Amazon
Угол — это еще одно слово для обозначения угла. Например, вы можете слышать о футболистах, забивающих с острого угла, что означает, что они повернули мяч вокруг острого угла. Слово «угол» также встречается в других словах, таких как «треугольник», что просто означает «три угла». Углы измеряются в градусах. Например, если автомобиль крутится на 360 градусов, он крутится все время, а широта Лондона находится на 53 градусах севернее экватора. Как ни странно, угловые градусы полностью отличаются от температурных градусов — контекст обычно ясно дает понять, с каким типом градусов вам нужно работать (за исключением, возможно, случаев, когда речь идет об остроконечных сосульках!). Оба типа градусов обозначаются маленьким кружком над и после числа, например: 90º.
Углы интересны по многим причинам, но одним из ключевых моментов является то, что их свойства на самом деле не зависят от того, насколько велики линии, ведущие к углу. Например, угол на форзаце одинаков, будь то форзац для крошечных книг или огромных книг — в любом случае угол равен 9.0 градусов.
Определение углов
Когда кто-то говорит, что угол равен определенному числу градусов, он пытается сказать вам, насколько он острый. Небольшой угол означает, что угол очень острый, а угол в 180 градусов вовсе не угол, а прямая линия.Один градус определяется как «одна триста шестая часть окружности», что не очень полезно (но опять же, технические определения метров и килограммов также могут оказаться бесполезными).
Специальные уголки
Вам необходимо знать о следующих специальных углах:360 градусов это полный круг. Если вы повернетесь на 360 градусов, вы вернетесь к тому, с чего начали.
180 градусов это половина круга.
Если вы повернетесь на 180 градусов, вы окажетесь лицом назад.90 градусов — это четверть окружности или прямой угол. Если вы повернетесь на 90 градусов, вы в конечном итоге окажетесь лицом влево или вправо от того места, где вы начали.
Если вы повернетесь на 180 градусов, вы окажетесь лицом назад.Другие типы уголков
Вам необходимо знать следующие слова, связанные с углом:Острый угол — это угол, меньший прямого угла, то есть менее 90 градусов. Подумайте о «симпатичном маленьком щенке», чтобы напомнить себе, что это маленький угол.
Угол рефлекса — это угол, превышающий 180 градусов. Вы знаете, когда ваш врач бьет молотком по внешней стороне колена, чтобы проверить ваши рефлексы? Подумайте об этом, чтобы помнить, что такое рефлекторный угол: внешняя сторона колена всегда больше 180 градусов.
тупой угол находится между ними, то есть больше 90 градусов, но меньше 180.
Измерение углов
Вы измеряете углы транспортиром, одной из тех полукруглых штук, которые были у вас в пенале в школе.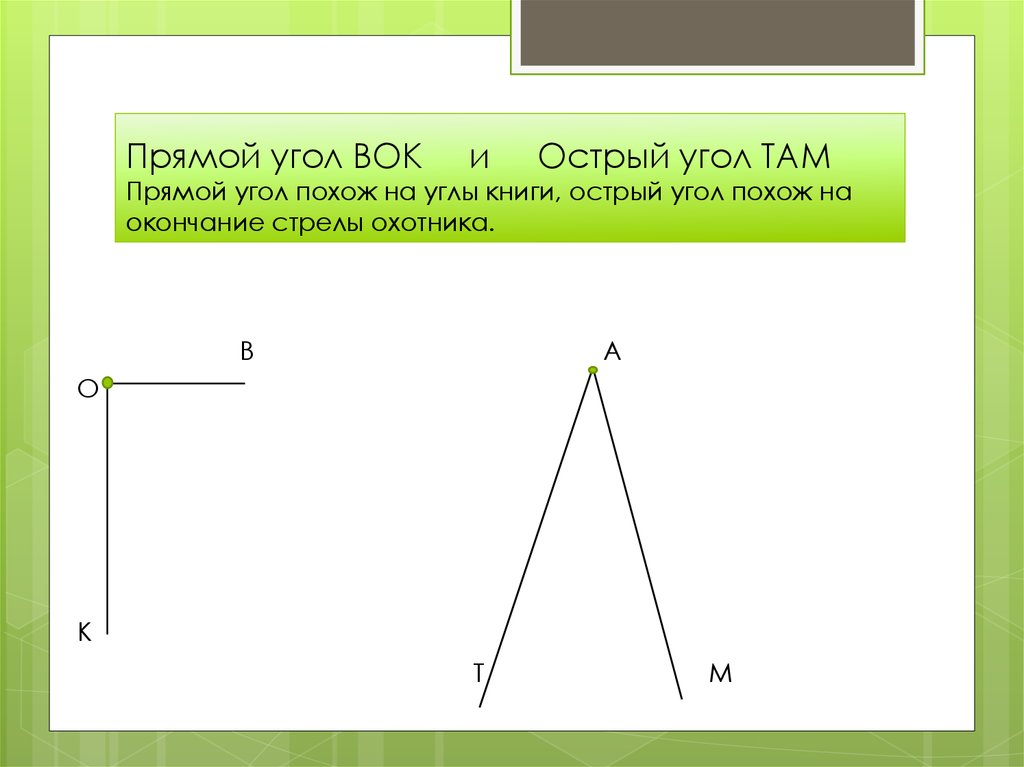
Вот как можно измерить угол с помощью транспортира:
Поместите перекрестие в середину транспортира над углом, где вы хотите измерить угол.
Поверните транспортир так, чтобы одна из линий, идущих в угол, находилась на «нулевой» линии в нижней части транспортира, слева от перекрестия.
Следуйте по другой линии к краю транспортира и прочтите число на шкале — это угол, который вы ищете.
Транспортиры неудобны, потому что они имеют две разные шкалы, идущие по одному и тому же краю, и вы можете легко перепутать, какая из них какая. Всегда используйте внешнюю шкалу, поэтому убедитесь, что ноль, который вы используете, совпадает с нулем на внешней дорожке транспортира.
После того, как вы измерите угол, снова посмотрите на угол и спросите, имеет ли он смысл. Если у вас есть угол, который явно больше 90 градусов (тупой угол), но ваш транспортир говорит, что угол равен 15 градусам, вы знаете, что что-то пошло не так.
Об этой статье
Эту статью можно найти в категории:
- Предалгебра,
На этом уроке геометрии в четвертом классе даются определения линии, луча, угла, острого угла, прямого угла и тупого угла. Мы также изучаем, как размер угла определяется ТОЛЬКО тем, насколько он «раскрылся» по сравнению со всей окружностью. Урок содержит множество разнообразных упражнений для учащихся.
1. Напишите, является ли каждая фигура линией, лучом, отрезком, или угол и назовите его.
2. а. Найдите угол, образованный лучами DE и DF. б. Найдите образовавшийся угол
лучами СА и СЕ. c. Что такое БД? (линия, а
отрезок или луч)?
3. а. Нарисуйте две точки, D и E. Затем нарисуйте линия ДЭ. б. Точка розыгрыша Q вместо на линия. в. Прорисовка лучей DQ и EQ. д. Найдите углы EDQ и DEQ в своем Рисунок.
4.
5. б. Эскиз три разных в. Эскиз прямого угла 6. Обозначьте углы как острые, прямые, тупые или прямые. К
помогите, сделайте эти углы двумя карандашами,
7. У треугольника три угла. В На самом деле, слово «треугольник» означает трехугольную форму.
8.
Этот урок взят из книги Марии Миллер Math Mammoth Geometry 1 и размещен на сайте www. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Мы можем показать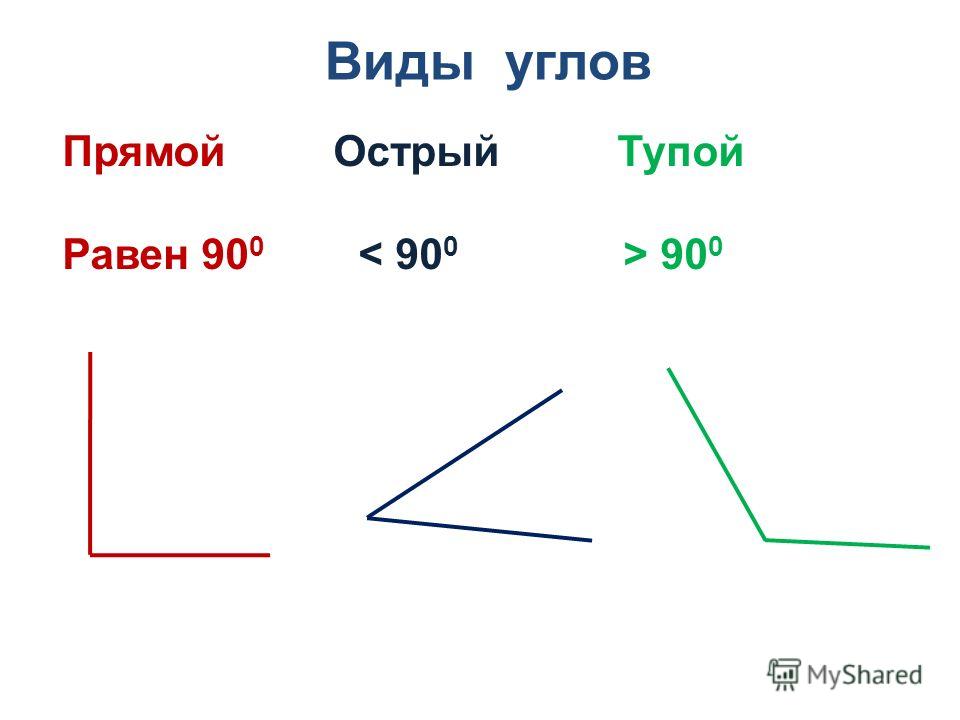 
Мы можем использовать символ ∠ для угла.
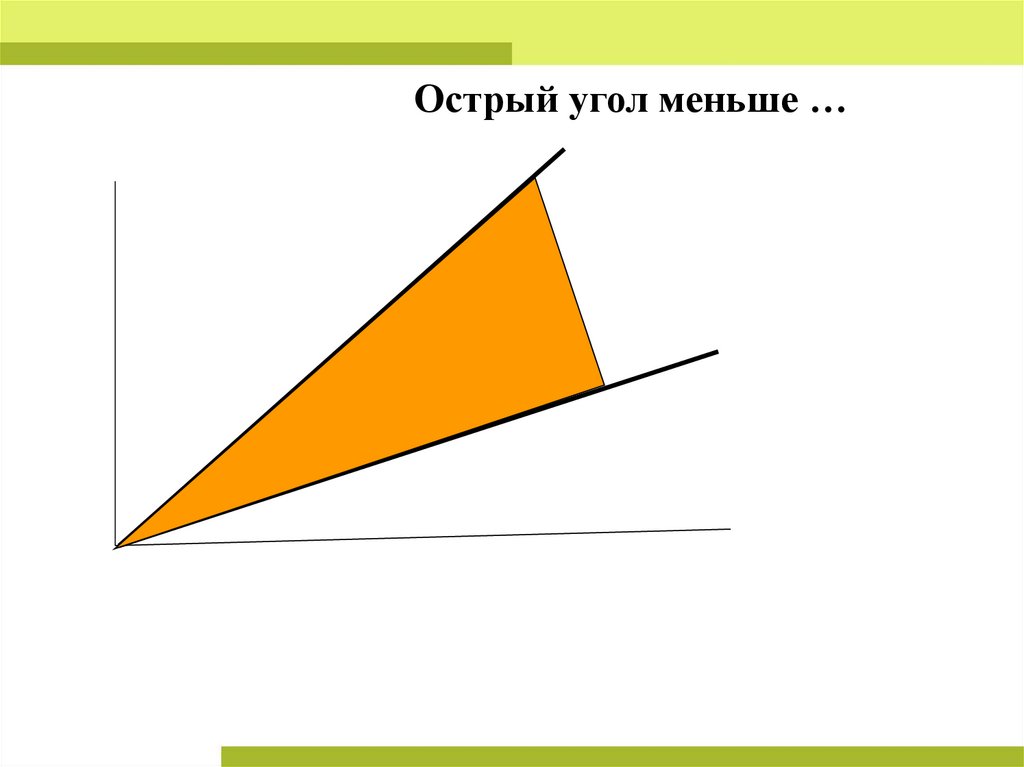
Какой угол больше?
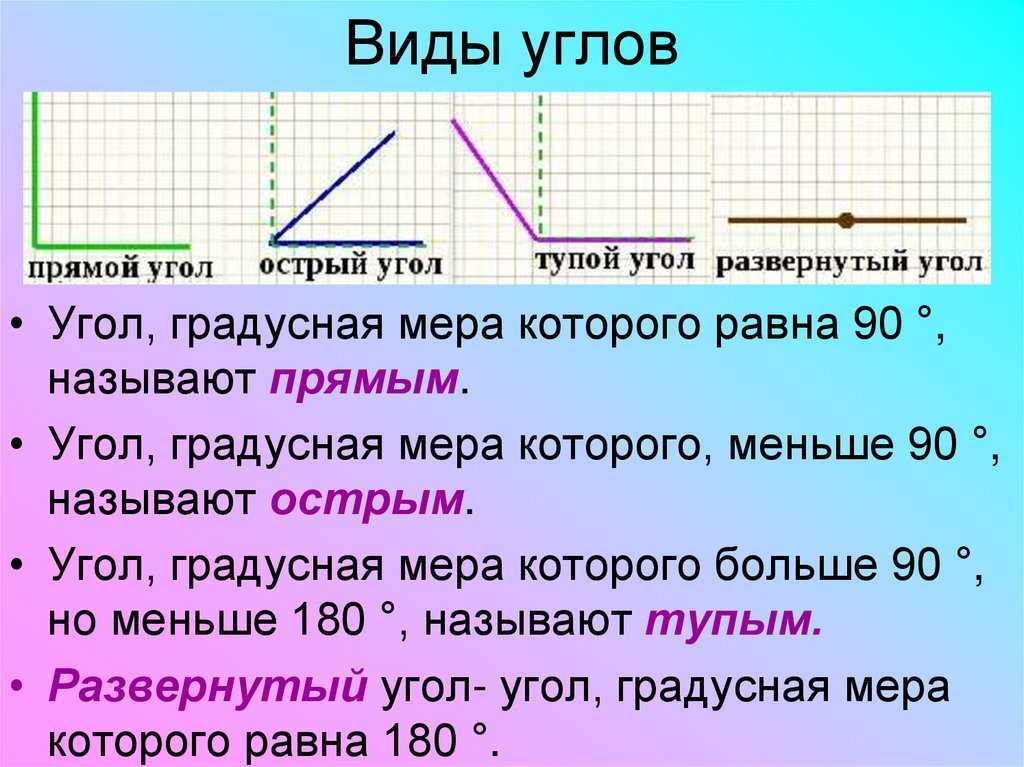а. Эскиз трех разных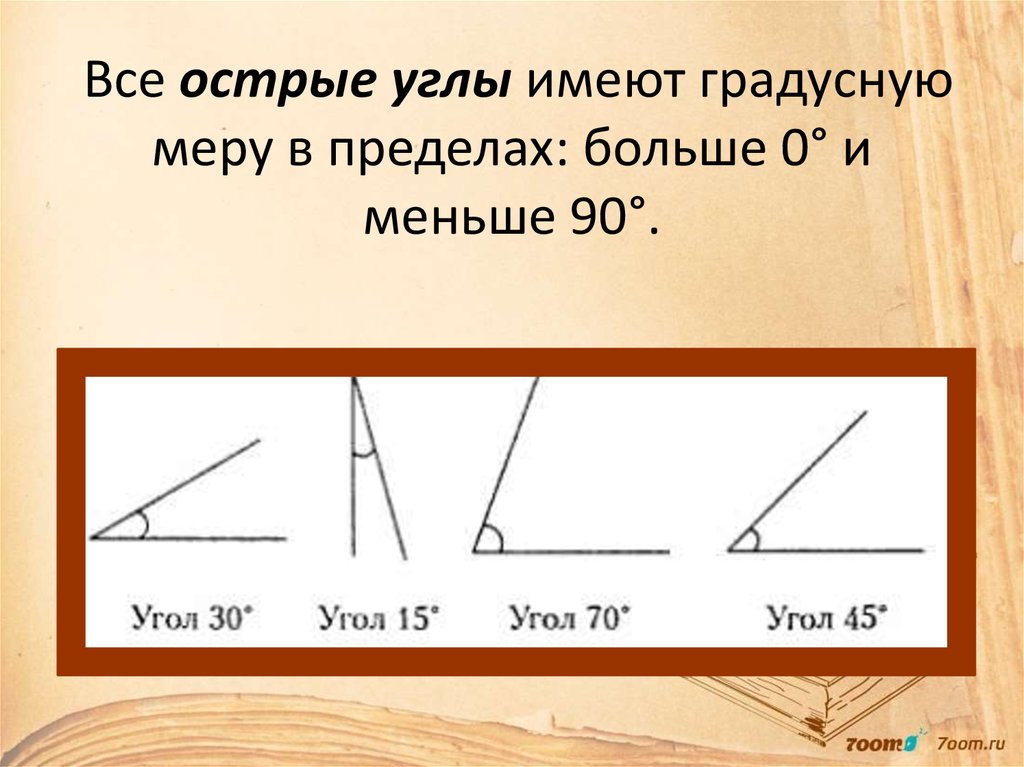 
(Необязательно) Сделайте
Тетрадь по геометрии куда вы записываете каждый новый термин и рисуете картинку
или 