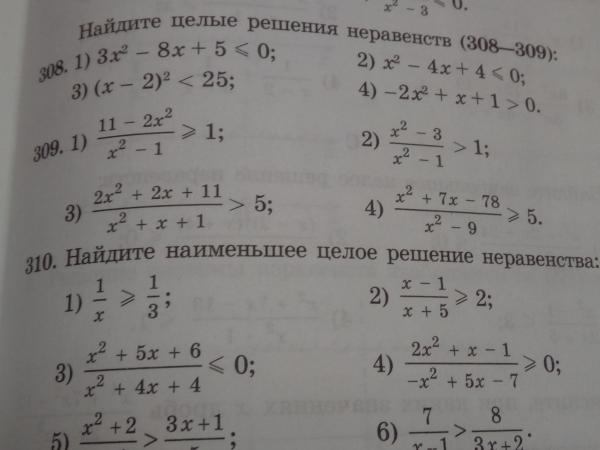Укажите целые решения системы неравенств: Укажите целые решения системы неравенств. 2х-корень из 3 больше 0. 3х-8 меньше 0.

Содержание

Решение систем неравенств с одной переменной

1. Решение систем неравенств с одной переменной

x x
3 4 7,
1 x 0;
6
1
МЕНЮ
2
3
7
5
8
4
6
Задача 1. Если туристы будут проходить в день на 5 км меньше, то они пройдут
за 8 дней расстояние, меньшее 90 км. Если же они будут проходить в день на 5
км больше, то за 6 дней они пройдут расстояние, большее 90 км. Сколько
километров в день проходят туристы?
МЕНЮ

4. Задача 1. Если туристы будут проходить в день на 5 км меньше, то они пройдут за 8 дней расстояние, меньшее 90 км. Если же они

будут проходить в день на 5
км больше, то за 6 дней они пройдут расстояние, большее 90 км. Сколько
километров в день проходят туристы?
МЕНЮ

5. Решение 1

Пусть туристы проходят Х км/д.
Если туристы будут идти (х-5) км/д, то за 8 дней они пройдут 8(х-5) км/д.
По условию задачи 8(х-5)<90.
Если туристы будут идти (х+5) км/д, то за 6 дней они пройдут 6(х+5) км/д.

По условию задачи 6(х+5)>90.
Нужно найти те значения Х, при которых верно как неравенство
8(х-5)<90, так и неравенство 6(х+5)>90, т.е. найти общие решения этих
неравенств. Следовательно, нужно решить систему неравенств:
8( x 5) 90,
6( x 5) 90;
1
8 x 40 90,
x
16
,
4
6 x 30 90;
x 10.
8 x 130,
6 x 60;
МЕНЮ
10
16
1
4
x
Ответ: Более 10 км и менее
1
164
км.

6. 2.Решите систему неравенств и укажите все целые числа, которые являются ее решениями

12 6 x 0,
3x 1 25 x;
МЕНЮ

7. Решение 2

12 6 x 0,
3x 1 25 x;
6 x 12,
4 x 24;
x 2,
x 6.
2
6
[2;6]
Ответ: 2,3,4,5,6.
МЕНЮ
x

8. 3. Найдите целые решения системы неравенств

12a 37 0,
6a 42;
МЕНЮ

9. Решение 3

12a 37 0,
6a 42;
12a 37,
a 7;
1
a
3
,
12
a 7.
3
МЕНЮ
1
12
7
(3 ;7].
x
Ответ: 4,5,6,7.

10. 4. Решите системы неравенств

x x
7,
1. 3 4
1 x 0;
6
y 1
y
1,
2.
2
y 5;
3
3x 1
5. 2 1,
x 1 x;
2
МЕНЮ
3x 1
3. 2 x 2,
2 x x 1;
3
x 1 x 3
2,
6. 2
3
13x 1 0;
2
p 2
2
p
4,
4.
5
p p 6;
2 8
5 y 1 2 y 1
0,
7. 6
2
1 y 4 0;
3

11. Решение 4.1

x x
3 4 7,
1 x 0;
6
*12
*6
4 x 3 x 7,
6 x 0;
7 x 84,
x 6;
x 12,
x 6.
6
Ответ: (- ;6).
МЕНЮ
12
x

12. Решение 4.2

y 1
y
1,
2
y 5;
3
2 y y 1 2,
y 15;
y 1,
y 15.
Ответ: (1;15).

13. Решение 4.3

3x 1
2 x 2,
2 x x 1;
3
3x 1 2 x 4,
6 x x 3;
x 5,
5 x 3;
Ответ: [0,6;5].

14. Решение 4.4

p 2
2
p
4,
5
p p 6;
2 8
10 p p 2 20,
4 p p 48;
9 p 18,
3 p 48;
Ответ: (2;16].

15.

Решение 4.53x 1
2 1,
x 1 x;
2
3x 1 2,
x 2 2 x;
3x 3,
x 2;
Ответ: (-2;-1).

16. Решение 4.6

x 1 x 3
2 3 2,
13x 1 0;
2
3x 3 2 x 6 12,
13x 1 0;
x 3 12,
13 x 1;
x 9,
1
x
.
13
1
; 9).
13
Ответ : (

17. Решение 4.7

5 y 1 2 y 1
6 2 0,
1 y 4 0;
3
5 y 1 6 y 3 0,
3 y 4 0;
y 2,
y 1 .
Ответ: (-1; 2).

18. 5. Решите двойное неравенство:

2 6 2 y 5;
МЕНЮ

19. Решение 5

2 6 2 y 5;
6 2 y 2,
6 2 y 5;
2 y 4,
2 y 1;
y 2,
1
y
.
2
2
1
2
Ответ:1( ; 2).
МЕНЮ
2
х

20. 6. При каких у значения двучлена 3у-5 принадлежат промежутку (-1;1)?

МЕНЮ

21. Решение 6

1 3 y 5 1
3 y 5 1,
3 y 5 1;
3 y 4,
3 y 6;
1
y 1 ,
3
y 2.
1
МЕНЮ
1
3
Ответ:
y
2
(1
1
;
3
2).

22. 7. Решите систему неравенств

x 8,
x 7,
x 4 .

x=t $$

решив уравнение, получим ответ х=2

___-___(2)____+____

Решение неравенства x<2

Найти все целые решения неравенства 2x(в квадрате)+х-6

Решение: Перед нами квадратное неравенство 2х² + х -6 ≤ 0.

Для начала решим квадратное уравнение 2х² + х -6

Решаем квадратное уравнение

x 1 = -2
x 2 = 1.5

Интервалы знакопостоянства
Определяем интервалы, на которых функция не меняет знак — интервалы знакопостоянства.
( -∞, -2) ( -2, 1.5) ( 1.5, +∞)

Определяем, какой знак принимает функция на каждом интервале.
( -∞, -2) плюс
( -2, 1.5) минус
( 1.5, +∞) плюс

Записываем интервалы, удовлетворяющие неравенству.
( -2, 1.5)

Проверяем входят ли концы интервалов в ответ.
[-2, 1.5]
ФИНАЛЬНЫЙ ОТВЕТ:
x принадлежит интервалу [-2, 1.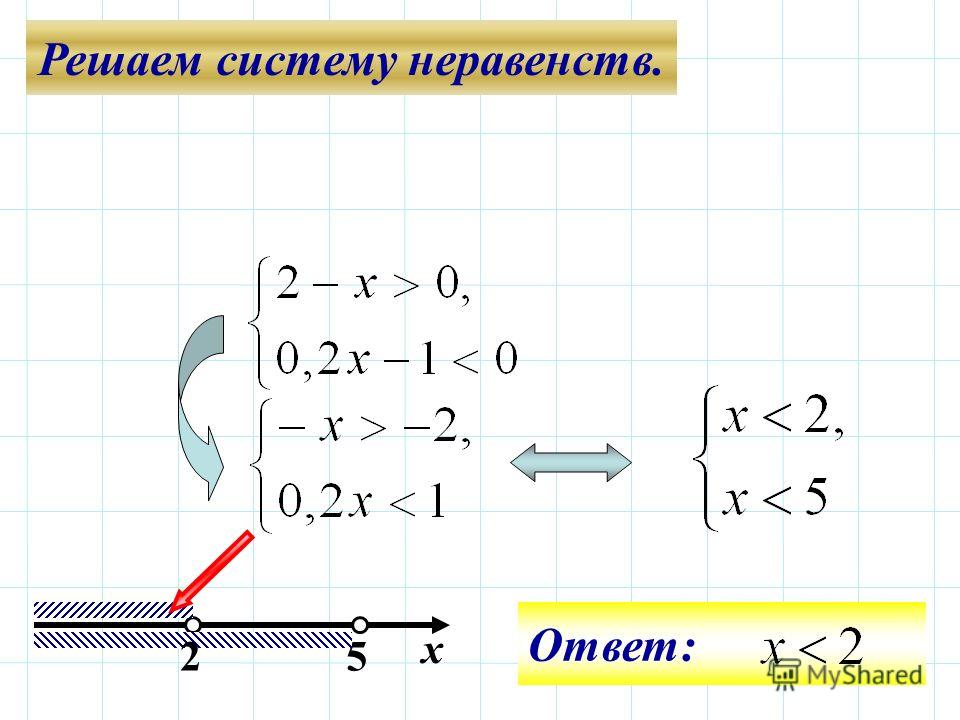 2-4*1*5=36-20=16 \\ \sqrt{D} =4 \\ x_2= \frac{-b+ \sqrt{D} }{2a} = \frac{6+4}{2} =5 \\ x_3= \frac{-b- \sqrt{D} }{2a} = \frac{6-4}{2} =1 $$

3. Знаки на промежутке (смотреть во вложения)

Решение неравенства — [1;∛25) U {5}

Наибольшее целое будет 5

Ответ: 5.

//////////////////////////////////////////////////////////////////////////

Математический обзор систем неравенств

Математический обзор систем неравенств https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g 21 мая 2014 г. 2 декабря 2014 г.

Обзор

Системы неравенств можно решать почти так же, как и линейные уравнения. Если существует решение, в котором системы пересекаются, оно будет в терминах плоской фигуры, а не одной точки.

Обзор неравенств

Предположим, что неравенство имеет форму x + y >2. Набор решений будет состоять из всех значений x и y, которые больше 2; например, значение (3, 2). График для этого набора решений будет включать все точки выше, но не включая линию x + y = 2. Если бы неравенство было x + y ≥ 2, график включал бы линию для x + y = 2. Аналогично, если неравенство если бы x + y <2, набор решений состоял бы из всех значений x и y, меньших 2; например (0, 1). График набора решений будет включать все значения, лежащие ниже линии x + y = 2,9.0007

Системы неравенств

Решение систем неравенств аналогично решению систем уравнений. Предположим, что задача состоит в том, чтобы найти общие решения для y ≥ -3x + 2 и y < x – 2. Она может быть решена любым из методов решения систем уравнений: сложением, заменой или умножением. Оба уравнения проходят через точку (1, -1), так как -1 = -3 + 2 и -1 = 1 – 2. График для набора решений y≥-3x + 2 будет состоять из всех точек выше линия и включает линию, а график для набора решений y < x - 2 будет состоять из всех точек ниже линии y < x - 2. Пересечение этих плоских фигур будет состоять из всех точек, которые включают оба неравенства.

Рисунок 1: Решение представлено точками внутри угла с вершиной (1, -1), где x больше 1, а y меньше -1

Неравенства в виде квадрантов

Другой способ представить системы неравенств — это когда набор решений для неравенства представляет собой весь квадрант или большую часть квадранта на координатной плоскости. Предположим, что x > 0 и y > 0. Если x > 0, то y может быть любым значением, поэтому все точки справа от оси x будут в решении. Однако, если y также больше 0, то будут включены только точки в правом верхнем квадранте (квадрант I). Точно так же, если x больше 0 и y меньше 0, будут включены только точки в нижнем правом квадранте (Квадрант III). Если x меньше 0 и y больше 0, будут включены только точки в верхнем левом квадранте (Квадрант II).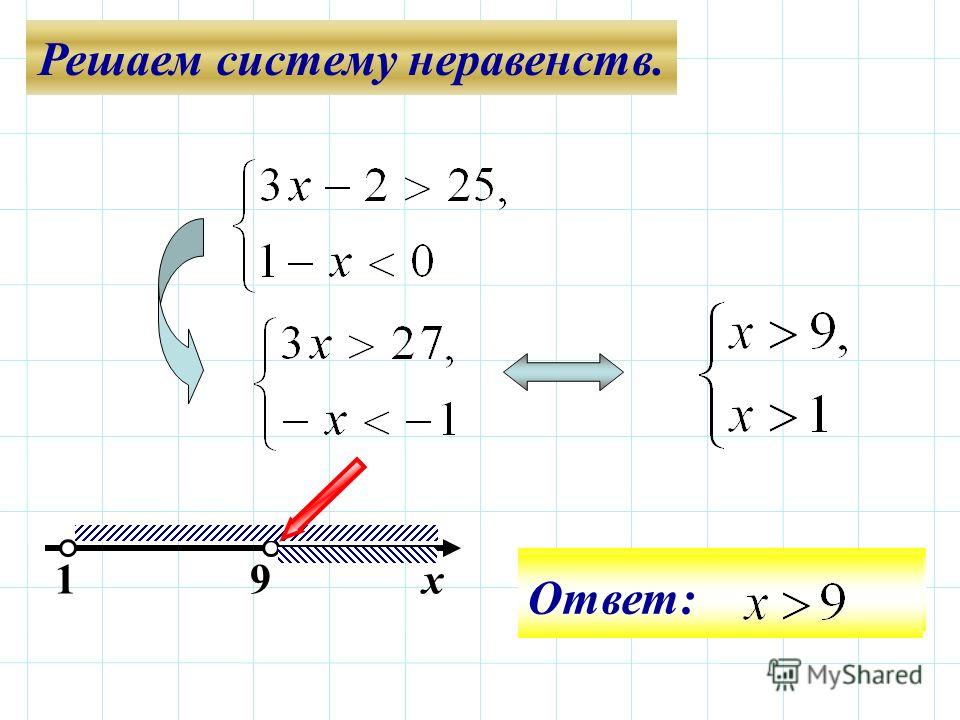 Если x меньше 0 и y также меньше 0, то будут включены точки в нижнем левом квадранте (Квадрант IV).

Рисунок 2: Представление координатной плоскости.

Геометрические представления

Решения систем неравенств можно представить в виде плоских фигур, потому что внутри любой геометрической фигуры содержится бесконечно много точек. Даже если все точки невозможно перечислить, их можно описать. Например, множество решений неравенств y ≥ -3x+2 и y 0, y> 0, x + y <75 и x + y > 50 может быть описан в терминах геометрической фигуры, которую он представляет.

Рис. 3. Геометрическая фигура представляет собой бесконечное множество точек на координатной плоскости.

Заинтересованы в услугах репетитора по алгебре? Узнайте больше о том, как мы помогаем тысячам студентов каждый учебный год.

SchoolTutoring Academy — это ведущая компания, предоставляющая образовательные услуги для учащихся K-12 и колледжей. Мы предлагаем программы репетиторства для учащихся K-12, классов AP и колледжей. Чтобы узнать больше о том, как мы помогаем родителям и учащимся в Грейпвайн, штат Техас, посетите сайт Tutoring in Grapevine, TX 9.0007

Графическая система линейных неравенств

Поиск

Ранее вы узнали, как построить график одного линейного неравенства на плоскости xy. В этом уроке мы будем иметь дело с системой линейных неравенств. Слово «система» подразумевает, что мы будем строить графики двух или более линейных неравенств одновременно. Решением системы будет область или область, где пересекаются графики всех линейных неравенств в системе.

ПРИМЕЧАНИЕ: Для успешного построения графика линейных неравенств вы должны знать, как построить линию на плоскости xy. В противном случае найдите время, чтобы просмотреть материал.

Шаг 1: Отобразите каждое линейное неравенство в системе на одной и той же оси xy . Запомните ключевые шаги при построении графика линейного неравенства:

Изолируйте переменную y слева от неравенства.
Если символы > и \ge , мы заштриховываем область над граничной линией, используя пунктирную и сплошную линии соответственно.
С другой стороны, если символы < и \le , мы заштриховываем область ниже граничной линии, используя пунктирную и сплошную линии соответственно.

Шаг 2: Закрасьте область, где пересекаются или перекрываются все области линейных неравенств. Если области пересечения нет, говорят, что система не имеет решения.

Давайте рассмотрим несколько примеров, чтобы проиллюстрировать процедуру.

Примеры построения графика системы линейных неравенств

Пример 1: Нарисуйте график следующей системы линейных неравенств:

В данной задаче хорошо то, что все переменные y уже находятся в левой части символа неравенства . В этой форме мы можем легко определить, какую область заштриховать относительно линии границы.

Нарисуйте первое неравенство \color{red}y \le x — 1. Поскольку у нас есть символ «меньше или равно», граница будет сплошной, а область под линией мы заштрихуем.

Нарисуйте графически второе неравенство \color{blue}y < - 2x + 1. Символ просто «меньше», поэтому линия границы будет пунктирной или пунктирной, а область под ней мы заштрихуем.

Окончательным решением системы линейных неравенств будет область пересечения двух неравенств, как показано справа.

Мы называем эту область решения «неограниченной», потому что эта область фактически бесконечно расширяется в нисходящем направлении.

В следующем примере вы увидите пример «ограниченной» области.

Пример 2: Нарисуйте следующую систему линейных неравенств:

Система содержит три неравенства, значит, мы собираемся изобразить три из них. Обратите внимание, что все символы неравенства имеют компонент «равно». Это говорит нам о том, что все граничные линии будут сплошными.

Вот график первого неравенства, где граничная линия сплошная, а заштрихованная область находится на ниже от нее.

\color{red}\boxed{y \le {1 \over 2}x + 1}

Второе неравенство будет иметь сплошную граничную линию, а заштрихованная область находится на выше ее.

\color{blue}\boxed{y \ge 2x — 2}

Наконец, третье неравенство также будет иметь сплошную граничную линию, и мы заштрихуем область выше ит.

\color{green}\boxed{y \ge — {1 \over 2}x — 3}

Как видите, заштрихованные области трех линейных неравенств перекрываются прямо в средней части.

Мы называем эту систему «ограниченной», потому что область, в которой лежат все решения, ограничена тремя сторонами, исходящими из граничных линий линейных неравенств.

Пример 3: Нарисуйте следующую систему линейных неравенств:

Когда я смотрю на три неравенства, включенных в систему, мне нужно учитывать три вещи:

Перепишите первое неравенство x + 2y < 2 так, чтобы переменная y была одна в левой части. Если вы правильно разработаете это, чтобы изолировать y, это неравенство будет эквивалентно уравнению y < - {1 \over 2}x + 1.
Неравенство y > — 1 будет иметь горизонтальную граничную линию.
Неравенство x \ge — 3 будет иметь вертикальную граничную линию.

Если вам нужна дополнительная помощь, узнайте, как рисовать вертикальные и горизонтальные линии.

Теперь мы готовы построить график каждого из них.

График первого неравенства будет представлять собой пунктирную граничную линию с заштрихованной областью, расположенной под ней.

\color{red}\boxed{y < - {1 \over 2}x + 1}

График второго неравенства представляет собой пунктирную горизонтальную линию, проходящую через точку пересечения y в точке -1 с заштрихованная область над ним.

\color{blue}\boxed{y > — 1}

График третьего неравенства представляет собой сплошную линию, проходящую через точку пересечения x в точке -3 с заштрихованной областью справа.

\color{green}\boxed{x \ge — 3}

Решением этой системы является общая область, где пересекаются все три неравенства.

Это также «ограниченная система», в которой область решения заключена в два отрезка пунктирной линии и один отрезок сплошной линии.

Пример 4: Нарисуйте графически следующую систему линейных неравенств:

Оба неравенства нужно переписать так, чтобы переменная « y » находится с левой стороны отдельно.

Вот первый. Обязательно меняйте направление символа неравенства всякий раз, когда вы делите неравенство на отрицательное число.

А вот и переписывание второго неравенства. На этот раз мы не делим неравенство на отрицательное число; вот почему ориентация или направление символа неравенства остается прежним.

Давайте нарисуем их на графике.

График {y > — 2x + 1} представляет собой пунктирную или «прерывистую» линию с заштрихованной областью над ней.

No related posts.