Действия с десятичными дробями
Десятичные дроби можно складывать, вычитать, умножать и делить. Также, десятичные дроби можно сравнивать между собой.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Сложение десятичных дробейКак мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой».
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной.
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
3,2 + 5,3 = 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробях
У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок.
Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Смотрим дальше. В разряде сотых располагается четвёрка. Это говорит о том, что в десятичной дроби 0,345 содержится четыре сотых .
Смотрим дальше. В разряде тысячных находится пятёрка. Это говорит о том, что в десятичной дроби 0,345 содержится пять тысячных .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой». Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
1,5 + 3,4 = 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4.
Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти переполнение разряда. В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 5,92.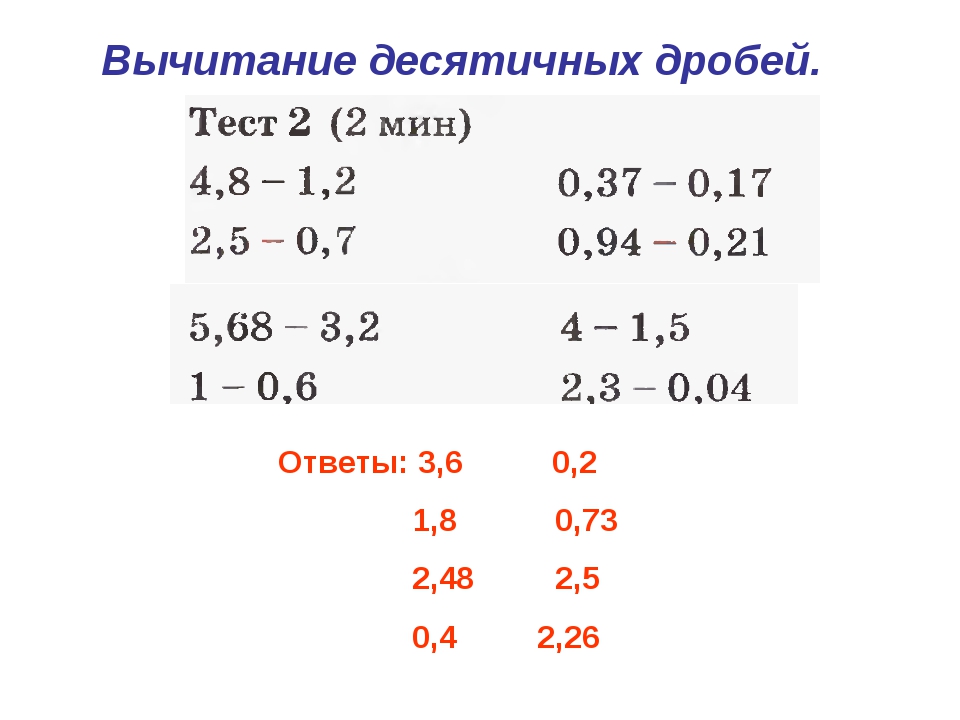
Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5. Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым.
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробей При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.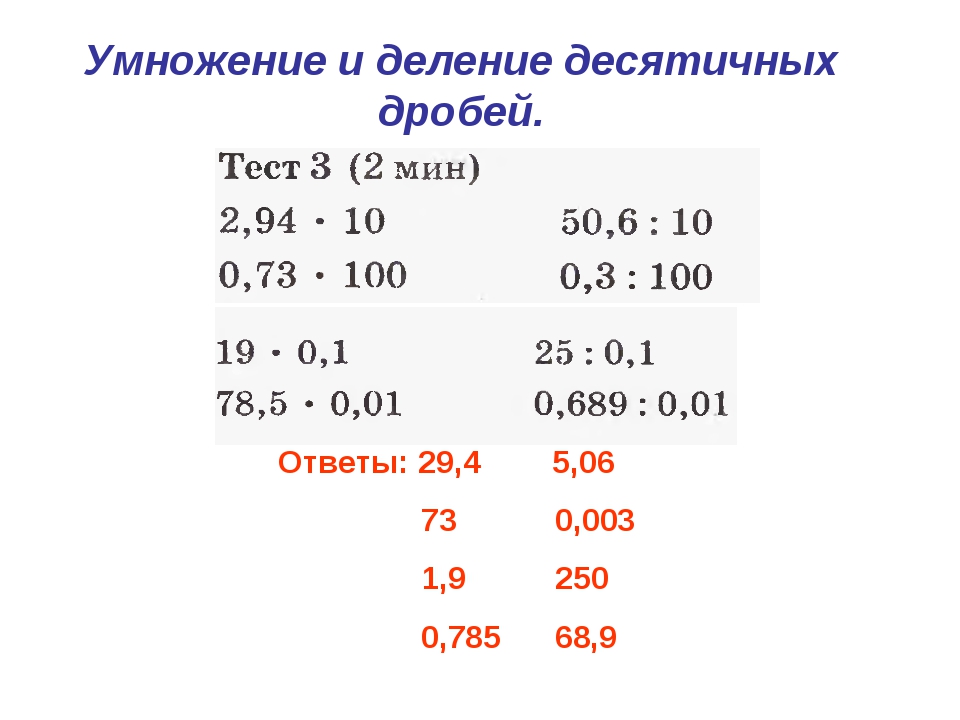
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4. Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь.
Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
3 − 1,2 = 1,8
Умножение десятичных дробей
Умножение десятичных дробей это просто и даже увлекательно.
Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75.
Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное число
Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби.
Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000
Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей.
Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001
Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом.
Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000.
Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Деление меньшего числа на большее. Продвинутый уровень.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь .
Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице», то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части.
Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4 : 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей.
Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4 : 5 равно 0,8
Пример 3. Найти значение выражения 5 : 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 125, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125.
Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5 : 125 равно 0,04
Деление чисел без остатка
В уроке деление мы научились делить числа с остатком. Например, чтобы разделить 9 на 5, мы поступали следующим образом:
и далее говорили, что «девять разделить на пять будет один и четыре в остатке».
Теперь мы получили необходимые знания, чтобы разделить 9 на 5 без остатка. Наша задача раздробить остаток 4 на 5 частей. Другими словами, разделить меньшее число на большее.
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
Что делать дальше мы уже знаем. Вытаскиваем остаток (если есть). Умножаем восьмёрку на делитель 5, и записываем полученный результат под 40:
40−40=0.
Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9 : 5 = 1,8
Пример 2. Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2.
Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8 : 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8 : 2 равно 2,4
Пример 2. Найти значение выражения 8,43 : 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Далее продолжаем вычислять, как в обычном делении. Сносим 4
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0.
Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43 : 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17.
А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9 : 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2) : (3 × 2) = 18 : 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.
На самом деле здесь происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
1,7 × 10 = 17
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и деление десятичной дроби на обычное число. Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру.
Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
2,1 : 10 = 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1 : 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1 : 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и деление десятичной дроби на десятичную дробь. В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
63 : 1 = 63
Значит значение выражения 6,3 : 0,1 равно 63
6,3 : 0,1 = 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
6,3 : 0,1 = 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
6,3 : 0,01 = 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3 : 0,001 = 6300
Задания для самостоятельного решения
Задание 1. Выполните сложение:
0,6 + 0,3
Решение:
Задание 2. Выполните сложение:
1,2 + 5,3
Решение:
Задание 3. Выполните сложение:
1,6 + 0,4
Решение:
Задание 4. Выполните сложение:
0,8 + 0,5
Решение:
Задание 5. Выполните вычитание:
0,9 − 0,4
Решение:
Задание 6. Выполните вычитание:
2 − 0,3
Решение:
Задание 7. Выполните вычитание:
9 − 7,8
Решение:
Задание 8. Выполните вычитание:
4 − 1,8
Решение:
Задание 9. Выполните умножение:
3,2 × 1,8
Решение:
Задание 10. Выполните умножение:
9,3 × 5,8
Решение:
Задание 11. Выполните умножение:
0,23 × 0,07
Решение:
Задание 12. Выполните умножение:
3,14 × 0,25
Решение:
Задание 13. Выполните деление:
9,36 : 6
Решение:
Задание 14. Выполните деление:
0,169 : 13
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Урок 63. деление положительных десятичных дробей. часть 2 — Математика — 6 класс
Математика
6 класс
Урок № 63
Деление положительных десятичных дробей. Часть 2
Перечень рассматриваемых вопросов:
- десятичная запись дробей;
- деление десятичной дроби на натуральное число;
- деление десятичной дроби на десятичную дробь;
- перевод обыкновенной дроби в десятичную.
Тезаурус
Десятичная дробь – это дробь, у которой знаменатель является степенью числа 10.
Десятичные дроби записывают без знаменателей, выделяя целую часть (целая часть правильной дроби считается равной 0) и отделяя её запятой от числителя дробной части.
Чтобы разделить десятичную дробь на натуральное число, нужно делить, не обращая внимания на запятую, а в частном поставить запятую в тот момент, когда закончится деление целой части делимого.
Чтобы разделить десятичную дробь на десятичную, надо:
– перенести в делимом и в делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе;
– выполнить деление на натуральное число.
Чтобы записать обыкновенную дробь в виде десятичной, нужно числитель этой дроби разделить на знаменатель.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Вы уже знаете, как разделить десятичную дробь на натуральное число и на другую десятичную дробь. Применим эти знания к решению вычислительных и текстовых задач.
Как изменится частное, если делимое увеличить в 5 раз?
Очевидно, что при увеличении делимого в 5 раз, частное тоже увеличится в 5 раз.
Как изменится частное, если делитель увеличить в 3 раза?
Как изменится частное, если делимое и делитель увеличить в одинаковое число раз?
Не выполняя вычислений, объясните, почему верно равенство?
35,48 · 2,937 = 0,3548 · 293,7
Вспомним, что, выполняя умножение десятичных дробей, мы не обращаем внимания на запятые. Дроби в правой и левой части состоят из одинаковых цифр, значит, различие лишь в положении запятой. Выполнив умножение правой части, мы отделим запятой в произведении справа 5 цифр. Выполнив умножение левой части, отделим запятой в результате тоже 5 цифр. Таким образом, в правой и левой части получатся одинаковые десятичные дроби. Значит, равенство верно.
Задача. Из одного пункта в противоположных направлениях выехали два велосипедиста. Один ехал со скоростью 12,4 км/ч, другой ехал со скоростью 13,2 км/ ч. Через какое время расстояние между ними станет 133,12 км?
Когда два объекта отправляются из одной точки в разные стороны, речь идёт о скорости удаления. Чтобы найти скорость удаления, нужно сложить скорости обоих велосипедистов.
Скорость удаления равна 25,6 км/ч.
То есть, через 1 час расстояние между ними будет 25,6 км. Найдём, за какое время они удалятся друг от друга на 133,12 км. Разделим расстояние на скорость.
S : v = t
133,12 км : 25,6 км/ч = 5,2 (ч).
Выразим результат в часах и минутах. 0,2 ч это 12 минут.
Ответ: 5 часов 12 минут.
Задача. Из одного посёлка одновременно отправляются в путь пешеход и велосипедист и движутся в одном направлении; пешеход движется со скоростью 4,8 км/ч, а велосипедист движется со скоростью12,4 км/ч. Через какое время расстояние между ними будет 23,94 км?
При одновременном начале движения в одном направлении и разной скорости объектов речь идёт о скорости удаления. Чтобы её найти, нужно из большей скорости вычесть меньшую.
Скорость удаления равна 7,6 км/ч в час, то есть каждый час расстояние между ними будет увеличиваться на 7,6 км.
Найдём, через какое время расстояние между велосипедистами станет 23,94 км. Для этого расстояние разделим на скорость удаления.
S : v = t,
23,94 км : 7,6 км/ч = 3,15 (ч),
Выразим в часах и минутах. 0,15 часа это 9 минут.
Ответ: 3 часа 9 минут.
Разбор заданий тренировочного модуля
Определите закономерность и продолжите ряд чисел.
1; 0,2; 0,04; 0,008; …
Попытаемся найти закономерность. Каждое следующее число в 5 раз меньше предыдущего. Значит, чтобы найти число, стоящее за числом 0,008, нужно 0,008: 5. Получим 0,0016.
Записываем в пропуск 0,0016.
Подстановка элементов в пропуски в тексте
Вставьте в текст нужные слова.
Если делимое увеличить в 7 раз, а делитель уменьшить в 3 раза, то частное … в … раз.
Варианты ответов:
увеличится
уменьшится
21
7
3
Решение
Рассмотрим частное a:b.
Увеличим делимое в 7 раз, а делитель уменьшим в 3 раза. Получим
Ответ: если делимое увеличить в 7 раз, а делитель уменьшить в 3 раза, то частное увеличится в 21 раз.
правила, примеры, решения, как целое число разделить на десятичную дробь
В этой статье мы разберем такое важное действие с десятичными дробями, как деление. Сначала сформулируем общие принципы, затем разберем, как правильно выполнять деление десятичных дробей столбиком как на другие дроби, так и на натуральные числа. Далее мы разберем деление обыкновенных дробей на десятичные и наоборот, а в конце посмотрим, как правильно выполнять деление дробей, заканчивающихся на 0,1, 0,01, 100, 10 и др.
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Пример 1Разделите 1,2 на 0,48.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
1,2=1210=65
0,48=48100=1225.
Таким образом, нам надо разделить 65 на 1225. Считаем:
1,2:0,48=62:1225=65·2512=6·255·12=52
Из получившейся в итоге неправильной дроби можно выделить целую часть и получить смешанное число 212, а можно представить ее в виде десятичной дроби, чтобы она соответствовала исходным цифрам: 52=2,5. О том, как это сделать, мы уже писали ранее.
Ответ: 1,2:0,48=2,5.
Пример 2Посчитайте, сколько будет 0,(504)0,56.
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
0,(504)=0,5041-0,001=0,5040,999=504999=56111
После этого конечную десятичную дробь также переведем в другой вид: 0,56=56100. Теперь у нас есть два числа, с которыми нам будет легко провести необходимые вычисления:
0,(504):1,11=56111:56100=56111·10056=100111
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Ответ: 0,(504):0,56=0,(900).
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Пример 3Найдите, сколько будет 0,779…/1,5602.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
0,779…≈0,78
1,5602≈1,56
Можем продолжить подсчеты и получить примерный результат: 0,779…:1,5602≈0,78:1,56=78100:156100=78100·100156=78156=12=0,5.
Точность результата будет зависеть от степени округления.
Ответ: 0,779…:1,5602≈0,5.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Пример 4Разделите 2,5 на 45.
Решение
Приведем 2,5 к виду обыкновенной дроби: 25510=512. Далее нам надо просто разделить ее на натуральное число. Делать это мы уже умеем:
25,5:45=512:45=512·145=1730
Если перевести результат в десятичную запись, то мы получим 0,5 (6).
Ответ: 25,5:45=0,5(6).
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Определение 1Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Пример 5Вычислите, сколько будет 65,144.
Решение
Используем метод столбика. Для этого допишем к дроби два нуля и получим десятичную дробь 65,1400, которая будет равна исходной. Теперь пишем столбик для деления на 4:
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Ответ: 65,14:4=16,285.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 6Разделите 164,5 на 27.
Решение
Делим сначала дробную часть и получаем:
Отделяем полученную цифру запятой и продолжаем делить:
Мы видим, что остатки стали периодически повторяться, и в частном стали чередоваться цифры девять, два и пять. На этом мы остановимся и запишем ответ в виде периодической дроби 6,0(925).
Ответ: 164,5:27=6,0(925).
Как разделить столбиком одну десятичную дробь на другую
Такое деление можно свести к уже описанному выше процессу нахождения частного десятичной дроби и натурального числа. Для этого нам потребуется умножить делимое и делитель на 10, 100 и др. так, чтобы делитель превратился в натуральное число. Дальше выполняем описанную выше последовательность действий. Такой подход возможен благодаря свойствам деления и умножения. В буквенном виде мы записывали их так:
a:b=(a·10):(b·10), a:b=(a·100):(b·100) и так далее.
Сформулируем правило:
Определение 2Для деления одной конечной десятичной дроби на другую необходимо:
1. Перенести запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, допишем в него нули с правой стороны.
2. После этого делим дробь столбиком на получившееся натуральное число.
Разберем конкретную задачу.
Пример 7Разделите 7,287 на 2,1.
Решение: Чтобы делитель стал натуральным числом, нам надо перенести запятую на один знак вправо. Так мы перешли к делению десятичной дроби 72,87 на 21. Запишем полученные числа столбиком и вычислим
Ответ: 7,287:2,1=3,47
Пример 8Вычислите 16,30,021.
Решение
Нам придется переносить запятую на три знака. В делителе для этого не хватит цифр, значит, нужно воспользоваться дополнительными нулями. Считаем, что получится в итоге:
Видим периодическое повторение остатков 4, 19, 1, 10, 16, 13. В частном повторяются 1, 9, 0, 4, 7 и 5. Тогда наш результат является периодической десятичной дробью 776,(190476).
Ответ: 16,3:0,021=776,(190476)
Описанный нами метод позволяет делать и наоборот, то есть делить натуральное число на конечную десятичную дробь. Посмотрим, как это делается.
Пример 9Подсчитайте, сколько будет 3 5,4.
Решение
Очевидно, что нам придется перенести запятую вправо на один знак. После этого мы можем приступить к делению 30,0 на 54. Запишем данные столбиком и вычислим результат:
Повторение остатка дает нам в итоге число 0,(5), которое является периодической десятичной дробью.
Ответ: 3:5,4=0,(5).
Как разделить десятичные дроби на 1000, 100, 10 и др.
Согласно уже изученным правилам деления обыкновенных дробей, деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и др. Получается, чтобы выполнить деление, в данном случае достаточно просто перенести запятую на нужное количество цифр. Если значений в числе не хватит для переноса, нужно дописать нужное количество нулей.
Пример 10Так, 56,21:10=5,621, а 0,32:100 000=0,0000032.
В случае с бесконечными десятичными дробями мы поступаем таким же образом.
Пример 11Например, 3,(56):1 000=0,003(56) и 593,374…:100=5,93374….
Как разделить десятичные дроби на 0,001, 0,01, 0,1 и др.
Воспользовавшись тем же правилом, мы можем так же разделить дроби на указанные значения. Это действие будет аналогично умножению на 1000, 100, 10 соответственно. Для этого мы переносим запятую на одну, две или три цифры в зависимости от условий задачи и дописываем нули, если цифр в числе окажется недостаточно.
Пример 12К примеру, 5,739:0,1=57,39 и 0,21:0,00001=21 000.
Это правило действует и в случае с бесконечными десятичными дробями. Советуем только быть внимательными с периодом дроби, которая получается в ответе.
Так, 7,5(716):0,01=757,(167), поскольку после того, как мы перенесли запятую в записи десятичной дроби 7,5716716716… на два знака вправо, у нас получилось 757,167167….
Если же у нас в примере непериодические дроби, то все обстоит проще: 394,38283…:0,001=394382,83….
Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот
Это действие мы также сводим к операциям с обыкновенными дробями. Для этого надо заменить десятичные числа соответствующими обыкновенными дробями, а смешанное число записать в виде неправильной дроби.
Если мы делим непериодическую дробь на обыкновенную либо на смешанное число, нужно поступить наоборот, заменив обыкновенную дробь или смешанное число соответствующей им десятичной дробью.
Поиск Поиск-
Школьный помощник
- математика 5 класс
- математика 6 класс
- алгебра 7 класс
- алгебра 8 класс
- геометрия 7 класс
- русский язык 5 класс
- русский язык 6 класс
- русский язык 7 класс
- математика
- алгебра
- геометрия
- русский язык
«»
следующая предыдущая вернуться на предыдущую страницуТакой страницы нет !!!
- Популярные запросы
- Обстоятельство
- Дополнение
- Определение
- Деление дробей
- Алгебра 7 класс
- Русский язык 6 класс
- Алгебра 8 класс
- Русский язык 7 класс
- Математика 6 класс
- Математика 5 класс
- Русский язык 5 класс
- Наименьшее общее кратное
- Наибольший общий делитель. Взаимно простые числа
- Деление и дроби
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
- Окружность и круг
- Квадратный корень из неотрицательного числа
- Доли. Обыкновенные дроби
- Антонимы. Синонимы
- Десятичная запись дробных чисел
- Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)
Умножение и деление десятичных дробей. 6 класс
Урок математики
6 класс
Тема «Умножение и деление десятичных дробей»
Цели:
создать условия для формирования умений умножать и делить десятичные дроби
способствовать формированию умения работать в паре, развитию самооценки учащихся
создать условия для формирования у учащихся бережного отношения к водным ресурсам
Тип урока: урок закрепления знаний и способов действий
Техническое обеспечение: урок проводится в компьютерном классе
Оборудование: карты для самооценки, презентация, записи на доске, капли вырезанные из клейкой бумаги
Технологическая карта урока
Название этапа урока и его продолжи- тельность | Ожидаемый результат | Формы, методы, приемы обучения | Деятельность учителя | Деятельность учащихся | Оборудование и учебные материалы |
1.Организационный момент. Целеполагание, мотивация (1 мин) 2.Повторение правила умножения, устный счет (4мин) 3.Проверка ответов устного счета. Знакомство с числовыми характеристиками водных ресурсов страны. (5 мин) 4. Повторение правила деления. Отработка этого правила (7мин) 5. Мотивация на тему водо-сбережения. Закрепление умений выполнения умножения и деления при решении задач (5мин) 6. Зарядка для глаз (1 мин) 7. Решение задач Самопроверка решений (15 мин) 8. Итоговая оценка за урок. Рефлексия (3мин) 9. Подведение итогов по теме водо-сбережения Домашнее задание (4 мин) | Готовность учащихся к уроку. Определение и принятие цели урока Повторение правила умножения десятичных дробей. Применение этого правила в устных упражнениях Осуществле-ние учащимися проверки заданий устного счета, осознание ценности водных ресурсов страны Повторение правила деления десятичных дробей. Применение этого правила в задании на определение объема капель Готовность учащихся решать задачи, используя умения умножения и деления десятичных дробей Снятие напряжения глаз Умение учащихся решать задачи Оценка учащимися своей работы на уроке, выяснение причин ошибок Формулировка правил водо-сбережения | Словесный индивидуальная и фронтальная форма Словесные методы, индивидуально-фронтальная форма работы Фронтальная и парная форма работы за компьютером Фронтальная работа за компьютером Парная работа за компьютером Индивидуальная работа Фронтальная работа | В ходе беседы сообщает учащимся тему и цель урока Организует повторение правила, работу с устными упражнениями Организует проверку ответов к устным заданиям и выставление соответствующей суммы баллов в оценочную карту. Знакомит учащихся с числовыми характеристиками водных ресурсов страны. В ходе беседы подчеркивает красоту и ценность водных богатств Беларуси Организует повторение учащимися правила деления и выполнения задания на отработку этого правила. Поясняет, как осуществлять проверку ответов, используя игру в презентации «Сложи рисунок» и оценивать свою работу В ходе беседы подводит учащихся к выводу о необходимости беречь водные ресурсы. Разбирает вместе с учащимися задачу. Через её содержание показывает некоторые приемы сбережения воды Называет упражнения Организует работу в парах, поясняет, как использовать «подсказку», в случае затруднений консультирует. Организует проверку решения и самооценки Организует выставление отметки в оценочную карту Предлагает учащимся сформулировать правила водосбережения в домашних условиях. Задает домашнее задание. Предлагает учащимся уходя с урока прикрепить символические капельки возле утверждений, записанных на доске | Участвуют в беседе с учителем, определяют тему и цель урока Рассказывают правило или повторяют его, используя текст слайда, выполняют устные задания Проверяют ответы, полученные в ходе устного счета. Оценивают свою работу. Знакомятся с числовыми характеристиками водных ресурсов страны и некоторыми вида озер Беларуси Рассказывают правило деления. Выполняют задание на определение объема капли. Работают в парах. По ходу решения осуществляют проверку правильности выполнения деления, используя игру в презентации «Сложи рисунок», оценивают свою работу Делают выводы о необходимости сбережения воды. Предлагают план решения задачи. Решают её и записывают. Знакомятся с некоторыми приемами сбережения воды Выполняют упражнения Решают задачи, проверяют их решение, оценивают свою работу. Через содержание задач знакомятся с приемами экономии воды Оценивают свою работу на уроке с помощью оценочной карты. Еще раз просматривают задания, в которых они допустили ошибки. Сдают оценочные карты Формулируют правила водосбережения. Записывают домашнее задание. Прикрепляют капельки возле утверждений, записанных на доске | слайд 1,2 презентации Слайд 3, оценочная карта Слайды 4,6,7, оценочная карта Слайды 5, 8-14, 26, оценочная карта Слайд 14,15,16 Слайды 17-22, оценочная карта Слайд 23, Оценочная карта Слайды 24,25, записи на доске, капли вырезанные из клейкой бумаги |
Ход урока:
Организационный момент. Проверка готовности учащихся к уроку. Мотивация на тему «Умножение и деление десятичных дробей».
Ребята, я думаю, что вы согласитесь, что в жизни каждого пригодится хорошо считать – это именно то, чему мы сейчас учимся, изучая действия с десятичными дробями. На предыдущих уроках мы разобрали правила выполнения умножения и деления десятичных дробей. Цель сегодняшнего урока: уметь применять действия умножения и деления с десятичными дробями при решении примеров и задач. Вспомним, как выполняется умножение и посчитаем устно.
Повторение правил умножения. Устный счет.
Учащиеся считают устно, в тетрадь пишут только ответ:
1)10,4 • 2
2) 9060 • 0,01
3) 0,5 • 20
4) 8 • 0,25
5) 199•0,4
6) 537•0,1
Возникновение кнопки для перехода к слайду с ответами происходит через промежуток времени, который отводится на выполнение заданий устного счета. Рекомендуемое время – 3 минуты. (Для быстрого просмотра презентации установлено время 4с)
Проверка ответов устного счета. Знакомство с числовыми характеристиками водных ресурсов страны.
Ответы показаны на слайде. Учащиеся проверяют и оценивают свою работу по оценочной карте. Затем к ответам появляются комментарии, характеризующие водные ресурсы страны. Их озвучивает учитель: ответы – это не просто числа, а за каждым из них скрывается информация, характеризующая водные богатства Беларуси
1)10,4 • 2 = 20,8 тыс в Беларуси рек и ручьев
2)9060 • 0,01 =90,6тыс км составляет общая длина белорусских рек
3) 0,5 • 20 = 10 тыс озер на территории нашей республики
4) 8 • 0,25 = 2 тыс кв км составляет их общая площадь
5) 199•0,4 =79,6 кв км – площадь наибольшего из озер Беларуси – озера Нарочь
6) 537•0,1 =53,7 м – глубина самого глубокого озера Долгое
Повторение правила деления. Отработка этого правила.
Громадные массы воды, которые характеризуют полученные в ответах числа, складываются из маленьких капель.
Вычислите: Сколько капель в 1л = 1000см³, если объём капли может быть равен
1) 0,01см³
2) 0,02см³
3) 0,005см³
4) 0,25см³
5) 0,016см³
6)Из неисправного крана вода капает со скоростью 1 капля в 10 секунд. За какое время из крана вытечет 6л воды, если объем капли равен 0,5 см³?(1л = 1000 см³)
Правила выполнения какого действия вам нужно вспомнить в этом задании? Повторение правил деления (устно). Ответы:1)100000,2)50 000,3)200000,4)40000 5)62 500, 6) 2000мин≈33ч
Сверка ответов в парах по ходу решения. Используя игру в презентации «Сложи рисунок», проверка полученных ответов (выбор ответов в таблице на слайде, получение рисунка). Самооценка
5. Мотивация на тему водосбережения. Закрепление умений выполнения умножения и деления при решении задач
Ребята, в начале урока мы говорили озерах и реках. А в последнем задании сказано о воде из водопроводного крана. В чем здесь связь? (учащиеся и учитель в короткой беседе выясняют, что воду, которую мы используем, берем из озер, рек и других водоемов, сберегая каждую каплю, мы сохраняем наши водные богатства.) Самый убедительный язык – это язык цифр, поэтому мы вспомнили о бережливости именно на уроке математики. Что же именно нужно делать, чтобы сберечь водные ресурсы страны, подскажут задачи.
Решение с коллективным разбором: учащиеся предлагают способ решения задачи, на слайде постепенно появляется решение, которое учащиеся записывают в тетрадь.
Задача 1
Вася чистит зубы в течение 7 минут каждый день. Он выполняет все правила чистки: около 40 раз медленно и аккуратно обрабатывает поверхность каждого зуба. Но, к сожалению, забывает на это время выключить воду. Сколько воды расходует Вася напрасно за 1 день? За неделю? За год (52 недели)? Скорость вытекания тонкой струи из крана равна 4,5 л/мин. (Сравнение за неделю больше в 1,5 раза, чем полная ванна. За год — это 3 ванных комнаты.)
Зарядка для глаз: 1)Переведите взгляд в окно на Западную Двину (урок проводится в классе с видом на Зап. Двину), воду которой использует наш город ( повторите 2-3 раза)
2) переведите взгляд на классную доску, «напишите» на ней взглядом слово «вода» (2-3 раза)
3) Закройте глаза и представьте красивый пейзаж на берегу водоема
Откройте глаза, продолжаем работу
7. Решение задач Самопроверка решений
Другие способы экономии воды вы узнаете из следующих задач, которые будете решать самостоятельно. В случае затруднений используйте «кнопку» с подсказкой. ( Те кто раньше справится с задачами, получают задание, составить памятку о способах экономии воды в домашних условиях).
Задача2
Традиционно в Беларуси хозяйки моют посуду под струей воды. Энергичная белорусская хозяйка моет посуду после ужина в течении 11 минут. В Великобритании, где давно принято экономить, хозяйка моет посуду после ужина в раковине, дважды наполняя её водой. Объем воды в раковине 8,5л. Скорость вытекания воды из крана 7,5 л/мин. Стоит ли белорусской хозяйке перенять этот опыт? Если она установит в квартире прибор учета воды, сколько денег она сэкономит за месяц, зная, что средняя стоимость одного кубометра тёплой воды равна 2000р? Решение самостоятельное с последующей сверкой решения на слайде.
Экономить воду можно не только, не расходуя её напрасно, но и используя водосберегающие приборы.
Задача 3
Ученик 6 класса Дима решил убедить маму и папу экономить воду, принимая не ванну, а душ с энергосберегающей насадкой. Сколько денег сэкономит семья Димы в месяц, если душ они принимают в течение 20 минут в день при скорости вытекания воды из душа с энергосберегающей насадкой 9,5 литров в минуту (сравните: обычный душ – 26 л/мин), а объем ванны равен 150 л? Средняя стоимость 1м³ воды равна 2000 руб с учетом частичного нагрева и слива.
Проверка решений задач: сравнение с решением на слайде. (Переход к проверке решения задач скрыт на рисунке с изображением душа) Самооценка
Итоговая оценка за урок. Рефлексия.
Карточка самооценки
Фамилия Имя | Умножение (устный счет) | Деление (определение числа капель) | Решение задач №2 и №3 | Итоговая оценка |
6 заданий, без ошибок — 2 с 1-2 ошибками – 1,5 с 3-4 ошибками -1 с 5-6 ошибками – 0,5 | 6 заданий, без ошибок — 2 с 1-2 ошибками – 1,5 с 3-4 ошибками -1 с 5-6 ошибками – 0,5 | За каждую самостоятельно верно решенную задачу – 3 За каждую верно решенную задачу с использованием подсказки – 2 За каждую задачу, решенную с ошибкой – 1 За нерешенную задачу – 0 | Найдите сумму баллов и округлите до единиц | |
9. Итоги по теме водосбережения. Домашнее задание
Итак, ребята, что же каждый из вас может делать для экономии водных ресурсов? (учащиеся рассказывают о способах экономии воды в домашних условиях из составленных ими памяток)
на экране примерная памятка:
Я экономлю воду, если я…
1) Слежу за исправностью кранов
2)Выключаю воду во время чистки зубов
3) Мою посуду в раковине, а не под струёй
4) Использую водосберегающие устройства и приборы учета воды
Выполняй эти правила — и за год сможете сэкономить около 120000 м³, которой хватит на 10 бассейнов.
Домашнее задание: составить и решить задачу на действия с десятичными дробями с водосберегающим содержанием из опыта своей семьи. Повторить правила действий с десятичными дробями
В конце урока учащимся предлагается при выходе из класса прикрепить символическую капельку воды возле одного из утверждений, записанных на доске, которое после проведенного урока кажется им наиболее правильными.
Утверждения:
Экономить воду нужно всем гражданам нашей страны
Беречь воду экономически выгодно каждой семье
Я сегодня сберегу некоторое количество воды
Контрольная работа № 8. Умножение и деление десятичных дробей. Математика 5 класс, с ответами
Вариант 1
1. Вычислите:
1) 6,25 • 3,4; 3) 24,1 : 1 000; 5) 7,31 : 3,4;
2) 32,291 • 100; 4) 7 : 28; 6) 18 : 0,45.
Решение:
1)
х 6,25
3,4
2500
+1875
21,2502) 32,291 * 100 = 3229,1
3) 24,1 : 100 = 0,0241
4)
7,0 |28
— 0 |0,25
70
-56
140
-140
05) 7,31 : 3,4 = 731 : 340 = 2,15
731 |340
-680 |2,15
510
-340
1700
-1700
0
6) 18 : 0,45 = 1800 : 45 = 401800 |45
-180 |40
0
2. Найдите значение выражения: (20- 22,05: 2,1)-6,4+ 9,2.
Решение:
(20 – 22,05 : 2,1) * 6,4 + 9,2 = 70
1)
2205 |210
-210 |10,5
1050
-1050
0
2)
20,0
-10,5
9,5
3)
х 9,5
6,4
380
+570
60,80
4)
60,8
+ 9,2
70,0
3. Решите уравнение: 6,4 (у — 12,8) = 3,2.
Решение:
6,4 (у – 12,8) = 3,2
у – 12,8 = 3,2 : 6,4
у = 0,5 + 12,8
у = 13,3_32 |64
320 |0,5
0
Ответ: у = 13,3.
4. Расстояние между двумя сёлами равно 156,3 км. Из этих сёл одновременно в одном направлении выехали грузовик и велосипедист, причём велосипедист ехал впереди. Через 3 ч после начала движения грузовик догнал велосипедиста. Какой была скорость велосипедиста, если скорость грузовика 64,5 км/ч?
Решение:
1) 3 * 64,5 = 193,5 (км) – проехал грузовик за 3 ч.
2) 193,5 – 156,3 = 37,2 (км) – проехал велосипед за 3 ч.
3) 37,2 : 3 = 12,4 (км/ч) – скорость велосипедиста
Ответ: 12,4 км/ч.
5. Если в некоторой десятичной дроби перенести запятую вправо на одну цифру, то она увеличится на 65,88. Найдите эту дробь.
Решение:
Пусть данная дробь – х. Если мы переносим у дроби запятую на одну цифру вправо, то мы увеличиваем её в 10 раз, тогда:
х * 10 = х + 65,88
10х – х = 65,88
9х = 65,88
х = 65,88 : 9
х = 7,326588 |900
-6300 |7,32
288
-270
180
-180
0
Ответ: эта дробь 7,32.
Вариант 2
1. Вычислите:
1) 8,43 • 5,7; 3) 37,8 : 100; 5) 3,22 : 2,8;
2) 54,29 • 1 000; 4) 8 : 32; 6) 15 : 0,75.
Решение:
1)
х 8,43
5,7
5901
+4215
48,0512) 54,29 * 100 = 54290
3) 37,8 : 100 = 0,378
4)
8,0 |32
-64 |0,25
160
-160
05)
322 |280
— 280 |1,15
420
-280
1400
-1400
06) 15 : 0,75 = 1500 : 75 = 20
1500 |75
-150 |20
0
2. Найдите значение выражения: 50 – (22,95 : 2,7+ 3,4) • 2,8.
Решение:
50 – (22,95 : 2,7 + 3,4) * 2,8 = 16,68
1)
_2295 |270
2160 |8,5
1350
-1350
0
2)
3,4
+ 8,5
11,9
3)
х 11,9
2,8
952
+ 238
33,32
4)
50,00
— 33,32
16,68
3. Решите уравнение: 8,4 (у — 17,9) = 4,2.
Решение:
8,4 (у – 17,9) = 4,2
у – 17,9 = 4,2 : 8,4
у = 0,5 + 17,942,0 |84
— 420 |0,5
0
у = 18,4
Ответ: у = 18,4.
4. С двух станций, расстояние между которыми равно 25,6 км, одновременно в одном направлении вышли два поезда. Первый поезд шёл впереди со скоростью 58,4 км/ч, и через 4 ч после начала движения его догнал второй поезд. Найдите скорость второго поезда.
Решение:
1) 58,4 * 4 = 233,6 (км) – проехал | поезд
2) 233,6 + 25,6 = 259,2 (км) – проехал || поезд
3) 259,2 : 4 = 64,8 (км/ч) – скорость || поезда
Ответ: 64,8 км/ч.
5. Если в некоторой десятичной дроби перенести запятую вправо на одну цифру, то она увеличится на 44,46. Найдите эту дробь.
Решение:
Пусть эта дробь х. Если мы переносим запятую у дроби вправо на одну цифру, значит мы увеличиваем её в 10 раз, т.е.:
10х = х + 44,46
10х – х = 44,46
9х = 44,46
х = 44,46 : 944,46 |9
-36 |4,94
84
-81
36
-36
0
х = 4,94
Значит, данная дробь 4,94.
Ответ: 4,94.
5 класс. Математика. Десятичные дроби — Умножение и деление десятичных дробей
Комментарии преподавателяУпражнение. Как умножить число 25,78 на 10?
Десятичная запись данного числа – это сокращенная запись суммы. Необходимо расписать ее более подробно:
Таким образом, нужно умножить сумму. Для этого можно просто умножить каждое слагаемое:
Выходит, что.
Можно сделать вывод, что умножить десятичную дробь на 10 очень просто: нужно запятую сдвинуть вправо на одну позицию.
Упражнение. Умножить 25,486 на 100.
Умножить на 100 – это то же самое, что и умножить два раза на 10. Иными словами, необходимо сдвинуть запятую вправо два раза:
Деление на 10, 100…
Упражнение. Разделить 25,78 на 10.
Как и в предыдущем случае, необходимо представить число 25,78 в виде суммы:
Так как нужно поделить сумму, то это эквивалентно делению каждого слагаемого:
Итак, .
Выходит, чтобы разделить на 10, нужно запятую сдвинуть влево на одну позицию. Например:
Упражнение. Разделить 124,478 на 100.
Разделить на 100 – это то же самое, что два раза разделить на 10, поэтому запятая сдвигается влево на 2 позиции:
Правило умножения и деления на 10, 100,..
Если десятичную дробь нужно умножить на 10, 100, 1000 и так далее, нужно запятую сдвинуть вправо на столько позиций, сколько нулей у множителя.
И наоборот, если десятичную дробь нужно поделить на 10, 100, 1000 и так далее, нужно запятую сдвинуть влево на столько позиций, сколько нулей у множителя.
Примеры, когда необходимо перенести запятую, а цифр уже не осталось.
Умножить на 100 значит сдвинуть запятую вправо на две позиции.
После сдвига можно обнаружить, что после запятой уже нет цифр, а это значит, что дробная часть отсутствует. Тогда и запятая не нужна, число получилось целое.
Пример 2
Сдвигать нужно на 4 позиции вправо. Но цифр после запятой всего две. Стоит вспомнить, что для дроби 56,14 есть эквивалентная запись.
Теперь умножить на 10 000 не составляет труда:
Если не очень понятно, почему можно дописать два нуля к дроби в предыдущем примере, то дополнительное видео по ссылке сможет помочь в этом.
Эквивалентные десятичные записи
Запись 52 означает следующее:
Если впереди поставить 0, получим запись 052. Эти записи эквивалентны.
Можно ли поставить два нуля впереди? Да, эти записи эквивалентны.
Теперь посмотрим на десятичную дробь:
Если приписать ноль, то получается:
Эти записи эквивалентны. Аналогично можно приписать несколько нулей.
Таким образом, к любому числу можно приписать несколько нулей после дробной части и несколько нулей перед целой частью. Это будут эквивалентные записи одного и того же числа.
Пример 3
Так как происходит деление на 100, то необходимо сдвинуть запятую на 2 позиции влево. Слева от запятой не осталось цифр. Целая часть отсутствует. Такую запись часто используют программисты. В математике же, если целой части нет, то ставят ноль вместо нее.
Пример 4
Сдвигать нужно влево на три позиции, но позиций всего две. Если перед числом написать несколько нулей, то это будет эквивалентная запись.
То есть при сдвиге влево, если цифры кончились, необходимо восполнить их нулями.
Пример 5
В данном случае стоит помнить, что запятая всегда стоит после целой части. Тогда:
Умножение и деление на 0,1, 0,01…
Умножение и деление на числа 10, 100, 1000 – очень простая процедура. Точно так же дело обстоит и с числами 0,1, 0,01, 0,001.
Пример. Умножить 25,34 на 0,1.
Выполним запись десятичной дроби 0,1 в виде обыкновенной. Но умножить на – то же самое, что разделить на 10. Поэтому необходимо сдвинуть запятую на 1 позицию влево:
Аналогично умножить на 0,01 – это разделить на 100:
Пример. 5,235 разделить на 0,1.
Решение данного примера строится аналогичным образом: 0,1 выражается в виде обыкновенной дроби, а делить на – это все равно, что умножить на 10:
То есть чтобы поделить на 0,1, нужно запятую сдвинуть вправо на одну позицию, что равносильно умножению на 10.
Правило умножения и деления на 0,1, 0,01…
Умножить на 10 и разделить на 0,1 – это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию.
Аналогично для 100, 1000 и так далее:
Разделить на 10 и умножить на 0,1 – это одно и то же. Запятую нужно сдвинуть вправо на 1 позицию:
Аналогично для 100, 1000 и так далее:
123,456:0,001 = 123 456Правило деления десятичных дробей на натуральные числа.
Четыре одинаковых игрушки в сумме стоят 921 рубль 20 копеек. Сколько стоит одна игрушка (см. Рис. 1)?
Рис. 1. Иллюстрация к задаче
Решение
Для нахождения стоимости одной игрушки необходимо разделить данную сумму на четыре. Переведём сумму в копейки:
Ответ: стоимость одной игрушки 23030 копеек, то есть 230 рублей 30 копеек, или 230,3 рубля.
Можно решить данную задачу не переводя рубли в копейки, то есть разделить десятичную дробь на натуральное число: .
Чтобы разделить десятичную дробь на натуральное число, нужно делить дробь на это число, как делят натуральные числа, и поставить в частном запятую тогда, когда закончится деление целой части.
Делим в столбик так, как делят натуральные числа. После того как сносим цифру 2 (число десятых – первая цифра после запятой в записи делимого 921,20), в частном ставим запятую и продолжаем деление:
Ответ: 230,3 рубля.
Пример
Делим в столбик так, как делят натуральные числа. После того как сносим цифру 6 (число десятых – цифра после запятой в записи делимого 937,6), в частном ставим запятую и продолжаем деление:
Ответ: .
Пример
Если делимое меньше делителя, то частное будет начинаться с нуля.
1 на 19 не делится, поэтому в частном ставим ноль. Деление целой части окончено, в частном ставим запятую. Сносим 7. 17 на 19 не делится, в частном пишем ноль. Сносим 6 и продолжаем деление:
Ответ: .
Деление десятичной дроби на 10, 100 и т.д.
1)
Делим так, как делят натуральные числа. В частном поставим запятую сразу, как снесем 8 – первую цифру после запятой в делимом 74,8. Продолжаем деление дальше. При вычитании получаем 8, но деление не окончено. Мы знаем, что в конце десятичной дроби можно приписывать нули – от этого значение дроби не изменится. Приписываем ноль и делим 80 на 10. Получаем 8 – деление окончено.
Ответ: .
2)
Ответ: .
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Пример
Чтобы умножить дробь на целое число, нужно умножать, не обращая внимания на запятую, затем в ответе вернуть запятую на место, то есть отделить ею столько же цифр в дробной части, сколько было в исходном числе.
Пример:
Выполняя умножение, не стоит обращать внимания на запятую.
Затем необходимо поставить запятую так, чтобы в дробной части получилось, как и раньше, 3 цифры.
Умножение десятичных дробей
Для умножения двух десятичных дробей принцип абсолютно такой же.
Правило
Чтобы перемножить две десятичные дроби, нужно их перемножить, не обращая внимания на запятые, затем в ответе отделить запятой столько цифр, сколько их было у обоих чисел вместе.
Пример 1
Сначала необходимо переписать каждую дробь в виде целого числа и вспомогательного множителя. Таким образом, каждая дробь будет представлена в виде произведения.
Затем нужно выполнить умножение целых чисел отдельно, вспомогательных множителей отдельно. Полученный результат нужно умножить на 0,001, то есть выполняется отделение запятой дробной части длиной в 3 цифры.
Пример 2
Нужно выполнить умножение, не обращая внимания на запятые. Количество цифр после запятой – 3, поэтому запятая ставится, отделяя 3 цифры. Последний ноль можно убрать из записи.
Пример 3
Выполняется умножение в столбик, при этом не обращая внимания на запятые, но помня, что в конце надо будет также отделить запятой 4 цифры.
Пример 4
В ходе урока мы уже выяснили, что умножать десятичные дроби технически означает просто умножать целые числа. Далее в ответе нужно отделить запятой знаков столько, сколько их было у всех чисел вместе.
Конечно, это правило распространяется и на случай нескольких множителей:
Деление десятичных дробей
Ситуация с делением десятичных дробей такая же: если уметь делить целые числа одно на другое, то тогда получится и десятичную дробь делить на другую десятичную дробь.
Пример
Когда заканчивается целое число, которое надо разделить, то ставится запятая и продолжается выполнение вычислений:
Пример
Здесь ситуация ровно такая же: как только кончается целая часть – ставится запятая:
То есть технически не важно, что делить на целое число – дробь или другое целое число. Алгоритм одинаковый.
Источник видео: https://www.youtube.com/watch?v=97n0NvNRPP0
Источник конспекта: http://interneturok.ru/ru/school/matematika/5-klass/umnozhenie-i-delenie-desyatichnyh-drobey/umnozhenie-i-delenie-desyatichnyh-drobey?konspekt&chapter_id=1898
Источник теста: http://testedu.ru/test/matematika/5-klass/dejstviya-s-desyatichnyimi-drobyami-2.html
Разделение десятичных знаков на десятичные
Это полный урок с видео, инструкциями и упражнениями по делению десятичных знаков на десятичные дроби, предназначенный для 5-го класса. Урок сконцентрирован на идее о том, что можно преобразовать любое деление с десятичным делителем в целочисленное деление, умножив ОБЕ на делимое и делитель на 10, 100, 1000 или другую степень десяти.
Итак, почему мы перемещаем десятичную точку в делимом и делителе на одинаковое количество шагов? Это просто ярлык , и он исходит из идеи выше; фактически делимое и делитель умножаются на одно и то же число.В видео я стремлюсь разобраться в этом «правиле». Фактический урок продолжается под видео.
Здесь вы можете создавать рабочие листы для десятичного деления.
Вы узнали:
| 2,04 ÷ 2 = ________ 0,24 ÷ 6 = ________ 5.2 ÷ 10 = ________ 5.2 ÷ 100 = ________ | |
| Решить. 2,5 ÷ 0,5 = _______ 0,021 ÷ 0,003 = _______ | |
| Но как мы можем решить деления, когда делитель является десятичным , но делитель не влезает четное количество раз в делимое? Например: 4.6 ÷ 0,029 или 0,23 ÷ 0,07 ? | ||
Это основано на следующем принципе:
| ||
1. Решите, думая, сколько раз делитель «умещается» в дивиденде. Что вы можете заметить?
а. 60 ÷ 20 = _______ г. 6 ÷ 2 = _______ с. 0,6 ÷ 0,2 = _______ г. 0,06 ÷ 0,02 = _______ | эл. 350 ÷ 50 = _______ ф. 35 ÷ 5 = _______ г. 3,5 ÷ 0,5 = _______ час. 0,35 ÷ 0,05 = _______ | и. 2,000 ÷ 10 = _______ Дж. 200 ÷ 1 = _______ к. 20 ÷ 0,1 = _______ л. 2 ÷ 0,01 = _______ |
| Что вы заметили? Это неудивительно: 0,02 подходит
в 0,06, столько раз, сколько 2 умещается в 6, столько же |
2. Решите более простую из двух задач в каждой. коробка. Ответы на оба вопроса одинаковы.
а. 5 ÷ 0,2 = _______ 50 ÷ 2 = ________ | г. 7 ÷ 0,35 = ________ 700 ÷ 35 = ________ | г. 36,9 ÷ 3 = __________ 0.369 ÷ 0,03 = _______ |
Способ преобразить больше сложную задачу с десятичным делением, например 3.439 ÷ 5.6, в задачу с тем же ответом , но с делителем целого числа это:
| ||||||||||||||||||||||||||||||
Последняя задача, 60 ÷ 3, легко решить.Ответ 20. Итак, ответ на 0,6 ÷ 0,03 также 20 . Проверить умножением: 20 × 0,03 это 20 раз 3 сотых = 60 сотых = 0,60 = 0,6. Это проверяет. | ||||||||||||||||||||||||||||||
|
3.Умножайте и делимое, и делитель на 10 несколько раз, пока не получите
получить делитель целого числа .
Затем разделите в столбик. Первый частично сделан за вас.
а. 0,445 ÷ 0,05 4,45 ÷ 0,5 44,5 ÷ 5 | г. 2,394 ÷ 0,7 |
4. Умножайте делимое и делитель на 10 несколько раз, пока не получите
получить целочисленный делитель .
Затем разделите в столбик.
а. 0,832 ÷ 0,4 | г. 0,477 ÷ 0,09 |
г. 9,735 ÷ 0,003 | г. 1,764 ÷ 0,006 |
эл. 2,805 ÷ 0,11 | ф. 546,6 ÷ 1,2 |
Здесь вы можете создавать рабочие листы для десятичного деления.
Этот урок взят из книги Марии Миллер Math Mammoth Decimals 2, размещенной на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Математика Мамонт Десятичные 2
Самообучающийся рабочий текст для 5-6 классов, охватывающий четыре операции с десятичными знаками до трех десятичных знаков, с упором на десятичное умножение и деление. В книге также рассматриваются разряды, сравнение, округление, сложение и вычитание десятичных знаков. Есть много проблем с умственной математикой.
Скачать (6 $.25) . Также имеется в виде печатной копии.
=> Узнайте больше и посмотрите бесплатные образцы!
Математика для 6-х классов — Блок 3: многозначное и дробное вычисление
Сводка по установке
В Модуле 3 ученики шестого класса сосредотачиваются на системе счисления, расширяя свое понимание умножения и деления до дробного деления и развивая беглость с целыми числами и десятичными операциями. На протяжении всего модуля студенты работают над разработкой и пониманием эффективных алгоритмов.Изучая структуру конкретных моделей и паттернов, которые возникают из этих структур, учащиеся понимают такие концепции, как умножение на обратную дробь при делении или использование длинного деления в качестве сокращения частичных частных (МР.8). С помощью этих эффективных вычислительных алгоритмов студенты решают и интерпретируют реальные проблемы, в том числе оценивают приложения из Модуля 2. На протяжении этого модуля студенты будут развивать, практиковать и демонстрировать свободное владение десятичными операциями; тем не менее, возможности практики и демонстрации должны продолжаться в течение года с целью свободного владения языком к концу года.Некоторые возможности уже встроены в будущие модули, такие как модуль по выражениям и модуль по уравнениям, но необходимо запланировать и включить дополнительные возможности. Дополнительную информацию, а также предложения по стратегии и действиям см. В нашем Руководстве по методическим навыкам и беглому владению языком.
В начальных классах учащиеся развивали свое понимание системы десятичных оснований. Они находили суммы, продукты и частные, используя конкретные модели, числовую стоимость, свойства операций и отношения между операциями.Умышленно студенты не изучали стандартный алгоритм, пока у них не было концептуального понимания, подтверждающего его. Некоторые из этих стратегий пересматриваются в этом разделе, чтобы убедиться, что студенты твердо понимают аргументы, лежащие в основе алгоритма, вместо того, чтобы использовать его без понимания.
Когда учащиеся освоят положительную систему счисления дробей, десятичных и целых чисел, ученики шестого класса будут исследовать числа слева от 0 на числовой прямой или отрицательные рациональные числа в Блоке 4.В седьмом классе ученики узнают, как вычислять со всеми рациональными числами, включая отрицательные, а в восьмом классе и в старшей школе ученики узнают об иррациональных числах, завершая свое изучение действительной системы счисления.
Обратите внимание, что в Массачусетской структуре математики стандарт 6.NS.4 незначительно отличается от CCSSM; он определяет использование разложения на простые множители для нахождения наибольшего общего делителя и наименьшего общего кратного пар чисел. Уроки этого раздела включают эту стратегию, среди прочего, как один из способов решения таких проблем.
Темп: 20 учебных дней (17 уроков, 2 гибких дня, 1 оценочный день)
Чтобы узнать, как изменить темп на 2020-2021 учебный год в связи с закрытием школ, см. Наши рекомендуемые корректировки объема и очередности занятий для 6-го класса.
Рабочие листы по умножению и делению десятичных знаков для 6-го класса PDF
Важные факты об умножении и делении десятичных знаков в рабочих листах для 6-го класса
Умножение и деление десятичных знаков — наиболее часто используемые операции в нашей повседневной жизни, особенно при работе с деньгами, измерениями.В связи с этим наши интересные задачи со словами — рабочие листы умножения и деления десятичных знаков 6 -й класс pdf помогут вашим детям похвастаться беглостью в десятичных вычислениях и при этом понимать ситуации реального мира.
Особым образом смоделированные в явном виде стратегии из наших упражнений 6 th умножить и разделить десятичные дроби с ответами пробудят мозг ребенка, чтобы он стал экспертом во всех формах десятичного умножения и деления.Некоторые интересные темы, которые вы найдете здесь, включают умножение десятичных знаков , деление десятичных знаков на целые числа, деление десятичных дробей, неравенство десятичных знаков при умножении целых чисел, задачу деления десятичных знаков на целые числа и т. Д.
Простые и забавные принципы умножения и деления десятичных знаков
Веселые и простые принципы умножения и деления десятичных дробей — это простые короткие приемы, важные для оттачивания навыков детского умножения десятичных чисел и деления.
1. Умножение десятичных знаков упражнения с ответами
Упражнения по умножению десятичных знаков смоделировали самый простой и кратчайший способ прийти к правильным ответам. Обычно первое, что нужно сделать;
- Подсчитайте и запишите общее количество десятичных знаков (цифр) в множителях.
Например: - Не обращайте внимания на десятичные знаки и умножайте множители, как если бы они были целыми числами.
- Разместите десятичную точку в продукте, убедившись, что количество десятичных знаков в продукте должно равняться общему количеству десятичных знаков в множителях.
Теперь мы можем добавить наши три (3) десятичных знака к ответу ( 315 ).Получаем 0,315
0,35 x 0,9 = 0,315
2. Упражнения на деление десятичных знаков с ответами
Десятичное деление имеет свою собственную короткую стратегию вычисления, отличную от умножения.Здесь
В случае, если делитель целого числа, (6,496 ÷ 5)
- Продолжить обычный процесс разделения. Поместите десятичную запятую в частное прямо над его позицией в делимом.
В случае, если делителем является десятичное число (250 ÷ 0,8), мы будем использовать ; - Прежде всего избавьтесь от десятичной точки в делителе, умножив ее на 10 или 100, в зависимости от количества десятичных знаков, т.е.е. если в делителе всего один десятичный знак, мы умножаем его на 10; два десятичных знака умножаем на 100 и т.д.
- Во-вторых, поскольку мы умножили делитель, мы обязаны умножить дивиденд, чтобы создать равновесие. Если мы умножим делитель на 10 или 100, мы также умножим делимое на 10 или 100 соответственно.
- Когда продукты получены, мы можем выполнить наш обычный пошаговый процесс разделения.
- Обратите внимание: если ваш ответ выражен в виде дроби или имеет остаток, поставьте десятичную точку и добавьте ноль к остатку, а затем продолжите деление.
Таким образом, ваш ответ будет в десятичной, а не дробной форме.
Решение большего количества задач с десятичными словами
Пример 1. Школьные обеды стоят 14,50 долларов в неделю. Примерно сколько будет стоить 15,5 недель обедов?
Анализ: Нам нужно оценить произведение 14,50 долларов и 15,5. Для этого мы округлим на один множитель в большую и на меньшую сторону.
Оценка недвижимости:
Ответ: Стоимость 15.5 недель школьных обедов обойдутся примерно в 200 долларов.
Пример 2: Студент зарабатывает 11,75 долларов в час за садоводство. Если в этом месяце она проработала 21 час, то сколько она заработала?
Анализ: Чтобы решить эту проблему, умножим 11,75 доллара на 21.
Умножить:
Ответ: В этом месяце студент заработает на садоводстве 246,75 долларов.
Пример 3: автомобиль Рика проезжает по шоссе 29,7 миль на галлон. Если его топливный бак вмещает 10,45 галлона, то как далеко он сможет проехать на одном полном баке бензина?
Анализ: Чтобы решить эту задачу, умножим 29.7 по 10,45
Умножить:
Ответ: Рик может проехать 310,365 миль с одним полным баком бензина.
Пример 4: Член школьной команды по легкой атлетике пробежал в общей сложности 179,3 мили на тренировке за 61,5 дня. Примерно сколько миль он в среднем пробегал в день?
Анализ: Нам нужно оценить частное 179,3 и 61,5.
Оценка недвижимости:
Ответ: В среднем он проезжал около 3 миль в день.
Пример 5: У владельца магазина 7.11 фунтов. конфет. Если она разложит конфеты по 9 банкам, сколько конфет будет в каждой банке?
Анализ: Мы разделим 7,11 фунта. на 9, чтобы решить эту проблему.
Разделить:
Ответ: Каждая банка будет содержать 0,79 фунта. конфет.
Пример 6: Пол будет платить за свою новую машину 36 ежемесячных платежей. Если его автокредит составляет 19 061 доллар, то сколько Пол будет платить каждый месяц? Округлите ответ до ближайшего цента.
Анализ: Чтобы решить эту проблему, мы разделим 19 061 доллар.00 на 36, затем округлите частное до ближайшего цента (сотых).
Разделить:
Ответ: Пол будет производить 36 ежемесячных выплат по 529,47 долларов каждый.
Пример 7: Какова средняя скорость в милях в час автомобиля, который преодолевает 956,4 мили за 15,9 часа? Округлите ответ до ближайшей десятой.
Анализ: мы разделим 956,4 на 15,9, а затем округлим частное до ближайшей десятой.
Шаг 1:
Шаг 2:
Ответ: Округляя до десятых, средняя скорость автомобиля составляет 60.2 мили в час.
Резюме: В этом уроке мы узнали, как решать текстовые задачи с использованием десятичных знаков. Для решения этих задач мы использовали следующие навыки:
- Вычисление десятичных произведений
- Умножение десятичных знаков на целые числа
- Умножение десятичных знаков на десятичные
- Расчет десятичных частных
- Десятичные дроби на целые числа
- Округление десятичных частных
- Разделение десятичных знаков на десятичные
Упражнения
Указания: прочтите каждый вопрос ниже.Вы можете использовать бумагу и карандаш, чтобы решить эти проблемы. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
| 1. | Оцените сумму денег, которую вам нужно заплатить за баллон с бензином, если один галлон стоит 3,04 доллара, а в баллоне — 11,9 галлона. |
| 2. | На наклейке на новую машину Дина указано, что скорость автомобиля в среднем составляет 32,6 мили на галлон. Если топливный бак вмещает 12,3 галлона, то как далеко Дин сможет проехать на одном полном баке бензина? |
| 3. | Ларри проработал 15 дней, в общей сложности 116,25 часа. Сколько часов он в среднем проводил в день? |
| 4. | Шесть коробок с бумагами стоят 159 долларов.98. Сколько стоит одно дело? Округлите ответ до ближайшего цента. |
| 5. | В одном дюйме 2,54 сантиметра. Сколько дюймов в 51,78 сантиметре? Округлите ответ до ближайшей тысячной. |
Учебный план 6-го класса
Ниже приведены необходимые навыки и ссылки на ресурсы, которые помогут в освоении этого навыка. Мы также поощряем множество упражнений и работу с книгами.Curriculum Home
Важно: это только руководство.
Обратитесь в местный орган управления образованием, чтобы узнать их требования.
6 класс | Вычитание
☐ Поймите, что подразумевается под дополнением десятков, дополнением до одной сотни и т. Д. Целого числа; и воспользуйтесь методом вычитания путем сложения.
6 класс | Умножение
☐ Определите нулевое свойство умножения
6 класс | Числа
☐ Чтение и запись целых чисел в триллионы
☐ Определите абсолютное значение и определите абсолютное значение рациональных чисел (включая положительные и отрицательные)
☐ Найдите рациональные числа на числовой прямой (включая положительные и отрицательные)
☐ Порядок рациональных чисел (включая положительные и отрицательные)
☐ Определение и определение коммутативных и ассоциативных свойств сложения и умножения
☐ Вычислять числовые выражения, используя порядок операций (может включать показатели степени два и три)
☐ Определить и определить свойство распределения умножения над сложением
☐ Определение и идентификация идентичности и обратных свойств сложения и умножения
6 класс | Десятичные знаки
☐ Представляют дроби как завершающие или повторяющиеся десятичные знаки
☐ Используйте различные стратегии для сложения, вычитания, умножения и деления десятичных дробей до миллионных долей
6 класс | Дроби
☐ Сложить и вычесть дроби с разными знаменателями
☐ Умножайте и делите дроби с разными знаменателями.
☐ Умножайте и делите смешанные дроби с разными знаменателями
☐ Определите мультипликативное обратное (обратное) число
☐ Найдите несколько представлений рациональных чисел (дроби, десятичные дроби и проценты от 0 до 100)
6 класс | Проценты
☐ Чтение, запись и определение процентов от целого (от 0% до 100%)
☐ Решение проблем с процентами, связанными с процентами, ставкой и базой
6 класс | Соотношения
☐ Решение простых пропорций в контексте
☐ Проверить пропорциональность, используя произведение средних, равное произведению крайних значений
☐ Понять концепцию соотношения
☐ Эквивалентные коэффициенты в виде доли
☐ Отличить разницу между ставкой и соотношением
☐ Решите пропорции, используя эквивалентные дроби
6 класс | Измерение
☐ Измерение емкости и вычисление объема прямоугольной призмы
☐ Определите метрические единицы объема (миллилитры, литры)
☐ Укажите эквивалентные метрические единицы вместимости (миллилитры в литры и литры в миллилитры; или наоборот)
☐ Определите инструменты и методы, необходимые для измерения с соответствующим уровнем точности: емкость (метрические единицы)
☐ Определите личные рекомендации для емкости (метрические единицы)
☐ Понять преобразование измерений
☐ Преобразование из градусов Цельсия в градусы Фаренгейта и наоборот
☐ Определите стандартные единицы вместимости США (жидкие унции, чашки, пинты, кварты и галлоны)
☐ Определите эквивалентные стандартные единицы вместимости США (жидкие унции в чашки, чашки в пинты, пинты в кварты и кварты в галлоны; или наоборот)
☐ Определите инструменты и методы, необходимые для измерения с надлежащим уровнем точности: пропускная способность (стандартные единицы США)
☐ Определите личные рекомендации по мощности (стандартные единицы США)
6 класс | Время
☐ Високосные годы
☐ Понимание AD и BC
☐ Знайте, что такое двадцать четыре часа в сутки, и как переводить между двадцатью четырьмя часами и временем до и после полудня.
6 класс | Геометрия (плоскость)
☐ Вычислите длину соответствующих сторон подобных треугольников (или других простых аналогичных форм), используя принцип пропорциональности
☐ Вычислить площадь основных многоугольников, нарисованных на координатной плоскости (прямоугольники и фигуры, состоящие из прямоугольников, имеющих стороны с целой длиной)
☐ Определите площади треугольников и четырехугольников (квадратов, прямоугольников, параллелограммов, ромбов и трапеций) и разработайте формулы
☐ Используйте различные стратегии, чтобы найти площадь правильных и неправильных многоугольников
☐ Определить радиус, диаметр, хорды и центральные углы окружности
☐ Понимать взаимосвязь между диаметром и радиусом окружности
☐ Определите площадь и длину окружности круга по соответствующей формуле
☐ Вычислить площадь сектора круга с учетом меры центрального угла и радиуса круга
☐ Понимать взаимосвязь между длиной окружности и диаметром окружности
☐ Определите площадь эллипса по соответствующей формуле
6 класс | Геометрия (сплошная)
☐ Определите объем прямоугольных призм (кубоидов) путем подсчета кубиков и разработайте формулу
6 класс | Алгебра
☐ Используйте подстановку для вычисления алгебраических выражений (может включать в себя показатели степени один, два и три)
☐ Решите и объясните двухэтапные уравнения с целыми числами с помощью обратных операций
☐ Вычислить формулы для заданных входных значений (окружность, площадь, объем, расстояние, температура, процент и т. Д.)
6 класс | Экспоненты
☐ Представляют многократное умножение в экспоненциальной форме
☐ Представьте экспоненциальную форму как повторное умножение
☐ Вычислять выражения с показателями степени, где степень является показателем единицы, двух или трех
6 класс | Координаты
☐ Определите и нанесите точки во всех четырех квадрантах
6 класс | Линейные уравнения
☐ Перевести двухэтапные словесные выражения в алгебраические
☐ Перевести двухступенчатые словесные предложения в алгебраические уравнения
6 класс | Данные
☐ Разработайте концепцию выборки при сборе данных от совокупности и определите лучший метод сбора данных для конкретного вопроса
☐ Записать данные в таблицу частот
☐ Построение диаграмм Венна для сортировки данных
☐ Определите и выровняйте наиболее подходящий график для отображения заданного набора данных (пиктограмма, гистограмма, линейная диаграмма, гистограмма или круговая диаграмма)
☐ Определение среднего значения, режима и медианы для заданного набора данных
☐ Определить диапазон для заданного набора данных
☐ Чтение и интерпретация графиков
☐ Обоснование прогнозов, сделанных на основе данных
☐ Запишите и интерпретируйте данные, используя график стебля и листа.
☐ Рассчитайте относительные частоты по таблице частот.
☐ Чтение и интерпретация частотных таблиц
6 класс | Оценка
☐ Оценка объема, площади и окружности
☐ Обосновать обоснованность сметы
☐ Оценить процент количества (от 0% до 100%)
☐ Обоснуйте обоснованность ответов с помощью оценки (с округлением)
6 класс | Вероятность
☐ Определить вероятность зависимых событий
☐ Определите количество возможных исходов для сложного события, используя фундаментальный принцип подсчета, и используйте его для определения вероятностей событий, когда исходы имеют равную вероятность
☐ Перечислить возможные исходы сложных событий
6 класс по математике
Обзор курса В курсе математики Acellus для 6 класса учащиеся изучают математические концепции, которые помогут им при переходе в среднюю школу и подготовке к предалгебре.Г-н Роджерс воплощает математику в жизнь, предлагая привлекательные и увлекательные приложения из реального мира.
Темы курса включают:
- Соотношения, нормы и пропорции
- Дроби, десятичные дроби и проценты
- Сложение и вычитание десятичных знаков
- Умножение и деление десятичных знаков
- Умножение и деление на дроби и смешанные числа
- Общие и необычные знаменатели
- Целые и рациональные числа
- Выражения, экспоненты и переменные
- Математические свойства и выражения
- Одношаговые уравнения
- Решение одношаговых уравнений с десятичными знаками, дробями и перекрестными произведениями
- Функции и неравенства
- Двух- и трехмерные фигуры
- Статистика
Пример урока — Ситуации из реального мира
;Этот курс разработан Международной академией наук. Учить больше
Объем и последовательность
Блок 1 — Передаточные числа Учащиеся начинают курс математики 6-го класса с изучения соотношений — определения и записи соотношений соотношений, а также использования умножения для сравнения чисел. Они исследуют правила делимости, факторы, наибольшие общие факторы и коэффициенты упрощения, а также практикуются на реальных примерах. Блок 2 — Нормы и пропорции В этом модуле учащиеся узнают, что подразумевается под расценками. Они практикуются в их поиске, а затем исследуют, как эта концепция используется в реальном мире. Затем они определяют пропорции и упражняются в их написании. Они решают проблемы, используя пропорциональные отношения, и исследуют реальные ситуации, в которых могут использоваться пропорции. Блок 3 — Дроби, десятичные дроби и проценты Студенты изучают основы дробей и десятичных знаков. Они изучают преобразование между этими двумя формами и практикуют преобразование дробей в десятичные и десятичные в дроби. Блок 4 — Проценты Затем студенты изучают проценты. Они учатся записывать проценты как дроби и десятичные дроби, а десятичные и дробные числа — как проценты. Они проверяют проценты больше 100% и меньше 1%. Они учатся использовать гистограмму для вычисления процентов и считают, как дроби, десятичные дроби и проценты связаны друг с другом. Блок 5 — Сложение и вычитание с десятичными знаками Этот блок начинается с принципов, необходимых для добавления десятичных знаков. Студенты учатся складывать целые числа с десятичными и добавлять десятичные к десятичным.Они рассматривают, как эти навыки можно использовать в реальном мире. Они продолжают изучать принципы, используемые для вычитания десятичных знаков, а затем практикуют вычитание десятичных знаков из целых чисел, а также вычитание десятичных знаков из десятичных. Они исследуют, как эти навыки можно применить для решения реальных проблем. Блок 6 — Умножение и деление с десятичными знаками Затем ученики повторяют умножение целых чисел, а затем расширяют свое понимание десятичных дробей, умножая десятичные дроби и целые числа.Они изучают умножение десятичных дробей на десятичные дроби, умножение и деление десятичных дробей на степени десяти. Блок 7 — Больше делений с десятичными знаками Студенты изучают стандартный алгоритм деления целых чисел, затем рассматривают деление десятичных дробей на целые числа и исследуют практическое применение этого навыка. Далее они углубляются в деление десятичных знаков на десятичные дроби, а затем сравнивают и сравнивают четыре операции с десятичными знаками. Блок 8 — Умножение дробей и смешанных чисел Уделяя особое внимание умножению дробей, учащиеся изучают умножение дробей на целые числа.Они учатся находить процент от числа, умножать дроби на дроби и упрощать перед умножением дробей. Они рассматривают практическое применение этих навыков, а затем обсуждают разницу между смешанными числами и неправильными дробями, а также способы преобразования одного числа в другое и обратно. Они также исследуют, как умножать смешанные числа. Раздел 9 — Деление на дроби В этом разделе учащиеся начинают с деления целых чисел на дроби и исследуют практическое применение этого навыка.Они продолжают деление дробей на дроби, деление смешанных чисел и деление смешанных чисел и дробей. Они используют умножение, чтобы убедиться, что десятичные дроби и дроби — это два способа записать одно и то же число. Раздел 10 — Общие и необычные знаменатели Начиная с обзора сложения и вычитания дробей, имеющих общие знаменатели, студенты затем повторяют, как найти наименьшее общее кратное. Затем они исследуют сложение и вычитание дробей с необычными знаменателями.Они сравнивают и противопоставляют четыре операции, выполняя их все с одной и той же парой дробей. Раздел 11 — Целые и рациональные числа Учащиеся изучают практическое использование целых чисел, а затем изучают графики, абсолютные значения, а также сравнение и упорядочение целых чисел. Затем они определяют рациональные числа и учатся их сравнивать и упорядочивать. Они учатся находить и графически отображать упорядоченные пары, а также исследуют рациональные числа на координатной плоскости. После этого модуля студентам предоставляется промежуточный обзор и экзамен. Блок 12 — Выражения, экспоненты и переменные В этом модуле студенты исследуют переменные. Они обсуждают части выражения и определяют, как записывать словесные фразы как выражения. Они исследуют использование показателей степени и изучают порядок операций. Они обсуждают замену значений переменных и использование подстановки в алгебраических выражениях. Раздел 13 — Математические свойства и выражения Учащиеся обсуждают семь свойств математики и учатся использовать свойство распределения для умножения в уме.Они изучают эквивалентные выражения и используют свойство распределения для перезаписи и факторизации выражений. Они исследуют упрощение, комбинируя похожие термины, и углубляются в эквивалентные выражения. Глава 14 — Одношаговые уравнения Изучив уравнения, учащиеся исследуют их решение с заменой. Они учатся решать и писать уравнения сложения, вычитания, умножения и деления за один шаг, а также практикуются в решении уравнений за один шаг. Раздел 15 — Решение десятичных уравнений Продолжая изучение решения уравнений, студенты рассматривают возможность использования десятичных знаков в этой операции.Они учатся использовать десятичные дроби для решения уравнений сложения, вычитания, умножения и деления. Затем они получают дополнительную практику решения уравнений с десятичными знаками. Раздел 16 — Решение уравнений с дробями и кросс-произведениями Дроби — это следующий тип чисел, который студенты изучают в связи с уравнениями. Они исследуют и практикуют решение уравнений сложения, вычитания, умножения и деления с дробями. Они также учатся решать процентные задачи и решать уравнения с перекрестными произведениями. Раздел 17 — Функции и неравенства Учащиеся открывают для себя функции и узнают о таблицах функций. Они исследуют геометрические и арифметические последовательности и правила функций, а также пишут уравнения, представляющие функции. Они исследуют функции на координатной плоскости, графические линейные функции и изучают функции реального мира в виде таблиц и графиков. Затем они рассматривают неравенство и учатся писать и изобразить их. Блок 18 — Двумерные фигуры Начиная с обзора многоугольников, студенты изучают двумерные фигуры.Они учатся находить площадь и применять этот навык к параллелограммам. Они исследуют поиск недостающих длин параллелограммов и определение площади треугольников и трапеций. Они исследуют многоугольники на координатной плоскости и определяют их площадь и периметр. Они также узнают, как найти площадь составных фигур. Блок 19 — Трехмерные фигуры В этом модуле учащиеся анализируют трехмерные фигуры. Они учатся находить объемные прямоугольные и треугольные призмы и применять эти навыки в реальном мире.Также они умеют находить дробные длины сторон. Блок 20 — Больше трехмерных фигур Студенты узнают, что такое площадь поверхности и как ее измерить. Затем их учат, что такое сети и как их использовать для определения площади поверхности. Они применяют эти новые навыки с прямоугольными призмами, треугольными призмами и пирамидами. Раздел 21 — Статистика В этом последнем разделе студенты практикуют понимание и определение статистических вопросов. Затем они исследуют точечные графики, за которыми следуют меры среднего значения, моды и медианы, а также меры вариации диапазона.Они исследуют среднее абсолютное отклонение и выбирают соответствующие меры, а также анализируют линейные графики, гистограммы, прямоугольные диаграммы и форму данных. За этим блоком следует Заключительный обзор и экзамен. В этом курсе нет разделов.Задания по математике для 6-х классов
Задания для сложения
Это главная страница для дополнительных заданий. Следуйте ссылкам на рабочие листы Spaceship Math Addition, рабочие листы для сложения с несколькими цифрами, рабочие листы без добавления и другие темы для добавления.Эти дополнительные рабочие листы бесплатны для личного использования или использования в классе.
Дополнительные рабочие листыРабочие листы вычитания
Это главная страница рабочих листов вычитания. Перейдите по ссылкам на рабочие листы космического корабля по математическому вычитанию, тесты на вычитание по времени, рабочие листы для многозначного вычитания, простые рабочие листы заимствования и перегруппировки, а также математические рабочие листы со смешанными задачами сложения и вычитания
Рабочие листы вычитанияРабочие листы умножения
Это главная страница рабочих листов умножения.Уберите пальцы, потому что это первая математическая операция, требующая запоминания фактов. Вы найдете рабочие листы умножения для восьми простых правил папы для освоения таблицы умножения, умножения RocketMath, многозначного умножения, квадратов и других тем рабочего листа умножения. Все эти рабочие листы умножения включают ключи ответов, их можно сразу распечатать и использовать в классе или дома.
Рабочие листы умноженияРабочие листы деления
Это главная страница рабочих листов деления.Сюда входят рабочие листы космического корабля Math Division, рабочие листы с многозначным делением, рабочие листы квадратного корня, кубические корни, рабочие листы смешанного умножения и деления. Эти рабочие листы деления бесплатны для личного использования или использования в классе.
Рабочие листы деленияТаблица умножения
Пытаетесь запомнить факты умножения? Эта страница содержит таблицы умножения для печати, которые идеально подходят для справки. Существуют различные варианты каждой таблицы умножения с фактами от 1-9 (продукты 1-81), 1-10 (продукты 1-100), 1-12 (продукты 1-144) и 1-15 (продукты 1-255). .Каждая из этих таблиц умножения представляет собой SVG с высоким разрешением, поэтому факты умножения печатаются красиво!
Таблица умноженияТаблица умножения
Вы ищете печатную таблицу умножения, в которой есть больше, чем просто факты? Один с некоторыми дополнительными математическими фактами о множителях? Или уникальный дизайн? В цвете? Все таблицы умножения на этой странице представляют собой SVG-файлы с высоким разрешением, которые прекрасно печатаются на вашем принтере и являются отличным ресурсом для изучения таблиц умножения в классе начальной школы или дома!
Таблица умноженияРабочие листы семейства фактов
Рабочие листы семейства фактов сосредоточены на наборах связанных математических фактов, а не на конкретных операциях.Обучайте своих детей сложению и вычитанию одновременно и укрепляйте отношения в семье фактов! На каждом уровне представлены две группы фактов, которые позволяют постепенно практиковаться, или просто используйте рабочие листы в конце для всестороннего обзора семейства фактов.
Рабочие листы «Факты о семье»Рабочие листы с длинным делением
Вводные рабочие листы с длинным делением, рабочие листы с длинным делением с остатками и без остатков, с длинным делением с десятичными знаками. Все эти листы с длинным делением содержат подробные, развернутые ответы.
Рабочие листы с длинным делениемУменьшение фракций
Рабочие листы для уменьшения фракций. Таблицы различных дробей в этом разделе предназначены для сокращения простых дробей, неправильных дробей и смешанных дробей.
Уменьшение дробейСравнение дробей
Практические рабочие листы для сравнения дробей. Задачи о дробях на этих листах требуют, чтобы дети сравнивали одинаковые и непохожие знаменатели, неправильные дроби и смешанные дроби.
Сравнение дробейСложение дробей
Рабочие листы для сложения дробей с общими знаменателями, с разными знаменателями, как простые дроби и как смешанные дроби. Полная работа с шагами показана для каждой проблемы в клавишах ответов.
Сложение дробиВычитание дробей
Рабочие листы для вычитания дробей с общими знаменателями, с разными знаменателями, как простые дроби и как смешанные дроби. Ключи полного ответа, которые показывают работу!
Вычитание дробиУмножение дробей
Эти рабочие листы по математике предоставляют практические навыки умножения дробей.Включает проблемы с целыми и без целых, а также с перекрестной отменой и без нее. Каждый рабочий лист PDF-файлов здесь имеет подробный ключ ответа, который показывает работу, необходимую для решения проблемы, а не только окончательный ответ!
Умножение на дробьРазделение на фракции
Таблицы деления на фракции с разделением на две части. Включает простые дроби, смешанные дроби и неправильные дроби, а также задачи, для решения которых используется шаг перекрестного умножения.
Дробное делениеДроби как десятичные числа
Рабочие листы для преобразования дробей в десятичные числа, в том числе с использованием деления в столбик.
Дроби как десятичныеЗадачи со словами до алгебры
Задачи со сложением, вычитанием, умножением и делением до алгебры, связанные с отношениями между числами в простых уравнениях … Отличный первый шаг для облегчения изучения алгебры!
Задачи со словами до алгебрыИнвестирование
Рабочие листы, которые обучают основным математическим концепциям инвестирования, включая рыночную капитализацию, соотношение цены и прибыли, дивиденды.
ИнвестированиеОтрицательные числа
Эти рабочие листы с отрицательными числами объединяют отрицательные числа с другими целыми числами (как положительными, так и отрицательными) с помощью основных математических операций, умножения отрицательных чисел с многозначными числами и деления в столбик с отрицательными числами.
Отрицательные числаПроценты
Рабочие листы для практики использования и вычисления процентов от других чисел, включая преобразование между дробями и процентами.
ПроцентыШаблоны чисел
Эти рабочие листы шаблонов чисел помогают учащимся развить необходимые навыки для определения шаблонов и взаимосвязей между числами.
Числовые узорыСреднее, Медиана, Диапазон
Рабочие листы для определения среднего, медианы, режима и диапазона для наборов чисел.Проблемы включают в себя наборы всех положительных целых чисел, всех отрицательных целых чисел и наборы смешанных знаков, а также практику использования калькулятора.
Среднее, Медиана, ДиапазонСудоку
Судоку для детей и взрослых, включая легкие и сложные трудности, злые судоку, самурайские судоку и многое другое!
СудокуMagic Square
Головоломки Magic Square — отличное введение в логику и решение задач … Попробуйте эти 3×3, 4×4 и 5×5, чтобы повысить свои математические навыки!
Магический квадратФакторизация, GCD, LCM
В распечатываемых на этой странице листах факторизации простых чисел учащиеся должны разложить на множители все большие целые числа.Это первый шаг для определения наибольших общих делителей двух чисел или определения наименьшего общего кратного двух чисел, но, кроме того, факторизация простых чисел вводит понятия простых чисел и составных чисел.
Факторизация, НОД, НОКПредварительная алгебра
Навыки предварительной алгебры, включая решение недостающих значений.
ПредалгебраРабочие листы экспонентов
Вводит квадраты, кубы и экспоненты, смешанные с другими основными операциями.Включает в себя практику, которая построит сайт-память общих экспоненциальных членов
Рабочие листы экспонентовРабочие листы для порядка операций
Миллиметровая бумага
Миллиметровая бумага, сеточная и точечная бумага для печати бесплатно для математических задач, поделок, зентанглинга, ландшафтного дизайна, архитектуры или просто рисования. Все стили миллиметровой бумаги включают дюймовые и сантиметровые вариации. Все эти PDF-файлы предназначены для печати на бумаге размером 8,5 x 11 дюймов.
Миллиметровая бумагаКоординатная плоскость
Пустые координатные плоскости на этой странице включают варианты с метками на оси или на краю сетки, а также версии с метками квадрантов.Вы можете найти полные 4-х квадрантные координатные плоскости, а также просто пустые 1-квадрантные координатные плоскости в настройках макетов для решения нескольких домашних задач на одной странице.
Координатная плоскостьдюймов Измерение
Эти рабочие листы измерения дюймов (обычные единицы) помогут развить навыки выполнения линейных измерений либо одной точки, либо измерения длины объекта. Существуют различные измерительные рабочие листы с задачами, подходящие для учеников детского сада, первого, второго или третьего класса математики.
Дюймы измеренияМетрические измерения
Таблицы метрических измерений для определения измеренных положений и измерения объектов в сантиметрах и миллиметрах на линейке. Эти рабочие листы являются отличной практикой для учеников первого, второго, третьего и четвертого классов, а также могут предоставить практическую практику вычитания при измерении длины предметов на линейке.
Метрические измеренияПреобразование единиц измерения в метрической системе СИ
В этих таблицах используются дроби единиц для преобразования значений единиц измерения из одного измерения в другое.Этот подход более распространен на уроках химии, физики или других естественных наук и требует от студентов сосредоточиться на отмене единиц, чтобы достичь решения с правильным значением и правильными единицами.
Преобразование единиц измерения в системе СИПреобразование обычных единиц
Практика преобразования обычных единиц измерения расстояния (дюймы в футы), объема (унции в галлоны) и массы (унции в фунты). Эти рабочие листы также используют единичные дроби для преобразования единиц измерения из одного измерения в другое.Этот подход более распространен на уроках химии, физики или других естественных наук и требует от студентов сосредоточиться на отмене единиц, чтобы достичь решения с правильным значением и правильными единицами.
Преобразование обычных единицОбычная и метрическая
В этих таблицах используются единичные дроби для преобразования значений между единицами СИ (метрическая) и обычными единицами. В этом разделе рассматривается практика преобразования дюймов в метры, литров в галлоны и граммов в фунты.
Обычные и метрические Диаграмма квадратного корняЕсли вы ищете список точных квадратных корней или полную таблицу квадратных корней от 1 до 100, таблица квадратного корня с этой страницы поможет вам найти радикалы! Существуют как цветные, так и черно-белые версии диаграмм в формате PDF для печати.
Диаграмма квадратного корняДиаграмма дробей
В этом уникальном отображении эквивалентных дробей значения дробей объединены в числовой прямой для создания элегантной симметрии.Он не только выделяет дроби в их наименьшей, наиболее сокращенной форме, но и предоставляет удобный десятичный эквивалент для наиболее часто используемых дробей. Это действительно одна из лучших справочных таблиц, которые я создал за 10 лет создания математических ресурсов!
График фракцийГоловоломки для поиска слов
Используйте эти математические головоломки для поиска слов, чтобы познакомить школьников со словарем и терминами с новыми математическими концепциями! Эти головоломки для поиска слов включают наборы для различных уровней обучения Common Core, а также конкретные темы по геометрии, алгебре и многому другому!
Пазлы с поиском словТаблица вероятностей
Таблица привязки вероятностей для справки о проблеме! На этой иллюстрированной таблице описаны сценарии с монетами, игральными костями и игральными картами.Он включает в себя шансы на наиболее вероятный и наименее вероятный исход.
Диаграмма вероятности Таблица измеренийЭта таблица измерений является хорошим справочным пособием для решения проблем со словами, связанных с преобразованием единиц объема, длины или температуры из одной системы в другую. Значения отображаются на одной шкале как в обычной, так и в метрической системе. Отлично подходит для измерения на кухне и приготовления пищи!
Таблица измеренийLinear Equations
Рабочие листы с линейными уравнениями, включая вычисление наклона по двум точкам, вычисление пересечений по оси Y, графическое отображение уравнений в форме пересечения уклона, построение графиков уравнений в форме точечного уклона, отображение систем уравнений, построение графиков линейных уравнений, построение графиков линейных неравенств и многое другое!
Линейные уравненияЧисловая строка
Числовая строка может быть мощным инструментом для изучения отрицательных чисел, соотношений или просто вводных операций сложения и вычитания.PDF-файлы числовых линий на этой странице включают различные диапазоны (10, 12, 15, 20, 15 и 100) как начиная с нуля, так и с отрицательными диапазонами. Полный набор линий дробных чисел, отмеченных общими знаменателями, входит в диапазоны от -5 до 5. Существуют также числовые строки для конкретных приложений для прошедшего времени, температуры и денег, а также пустые числовые строки для обычных диапазонов и дробей.
Числовая строкаЗадания по математике для шестого класса
Шестой класс! Почти готов к средней школе! Но это не значит, что это конец математической практики, нет.Эти рабочие листы по математике для шестого класса охватывают большинство основных математических тем предыдущих классов, в том числе рабочие листы преобразования, рабочие листы измерений, рабочие листы среднего, среднего и диапазона, числовые шаблоны, экспоненты и различные темы, выраженные в виде задач со словами. Учащиеся 6-х классов должны отлично владеть математическими фактами и уметь быстро и почти с идеальной точностью выполнять тесты на сложение, вычитание, умножение и деление по времени. Учащиеся 6-го класса также должны хорошо разбираться в дробях, и темы, обсуждаемые в таблицах дробей на этой странице, должны быть знакомы.Уверенные в этих математических темах, учащиеся 6-х классов должны быть готовы к предалгебре, поскольку они переходят к следующей части своего открытия в области математики.