Определители четвертого порядка — Мегаобучалка
Методы их вычисления
Определение. Выражение
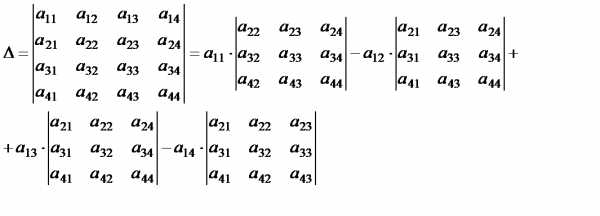
называется определителем четвертого порядка. Этот определитель можно записать в виде:
, (6)
где — минор элемента, стоящего на пересечении i-ой строки и j-го столбца, -алгебраическое дополнение этого элемента.
Формулу (6) можно записать с помощью значка суммирования :
, (7)
где i=1,2,3,4.
Формула (7) называется разложением определителя по элементам
i-ой строки. Можно записать и разложение определителя по элементам j-го столбца:
(8)
где j=1,2,3,4.
Метод понижения порядка определителя основан на обращении всех, кроме одного, элементов строки или столбца определителя в нуль с помощью свойств определителей.
Пример 11.Вычислить определитель
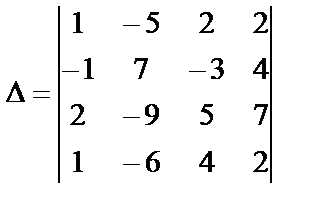
Решение. Прибавим элементы первой строки к элементам второй строки:
 .
.
Элементы первой строки умножим на (-2) и прибавим к элементам третьей строки:
 .
.
Элементы первой строки умножим на (-1) и прибавим к элементам четвертой строки:
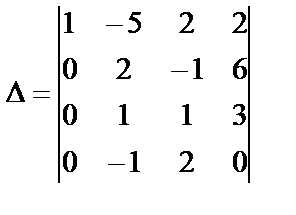 .
.
Разложим полученный определитель по элементам первого столбца
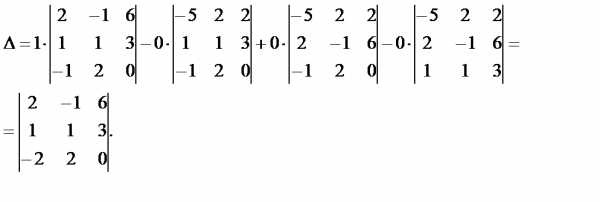
Переставим первые две строки, при этом знак определителя изменится на противоположный, одновременно вынесем общий множитель 3 элементов третьего столбца за знак определителя:
.
Умножим элементы первой строки на (-2) и прибавим к элементам второй строки:
.Полученный определитель разложим по элементам второй строки
Пример 12. Вычислить определитель 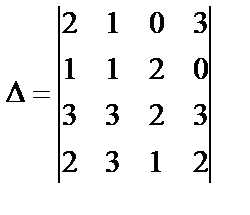 .
.
Решение. Поменяем местами первую и вторую строки, при этом по свойству 2 знак определителя изменится на противоположный:
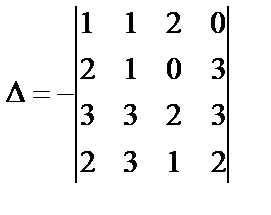 .
.
Сначала элементы первой строки умножим на (-2) и прибавим к элементам второй и четвертой строк, а затем элементы первой строки умножим на (-3) и прибавим к элементам третьей строки, получим:
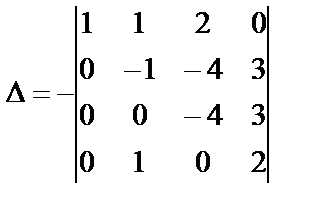 .
.
Элементы второй строки прибавим к элементам четвертой строки:
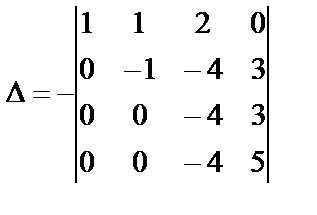 .
.
Элементы третьей строки умножим на (-1) и прибавим к элементам четвертой строки:
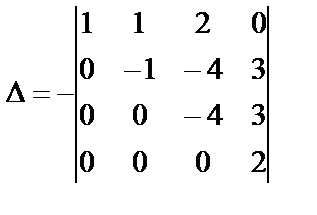
Получим определитель треугольного вида, значение которого равно произведению элементов главной диагонали .
Пример 13. Вычислить определитель
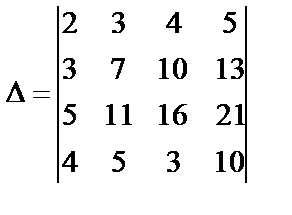 .
.
Решение.Разложим определитель по элементам третьей строки
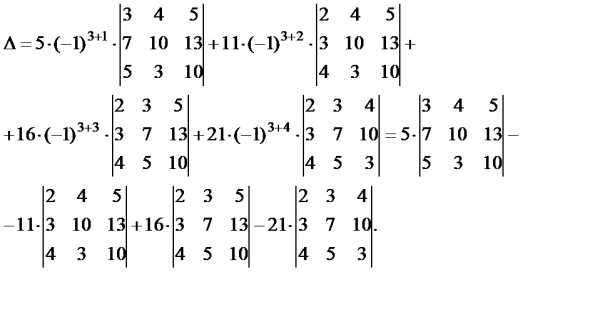
Полученные определители третьего порядка вычислим по правилу треугольника

Задания для самостоятельного решения.
1.Вычислить определители:
2. Решить уравнения:
3. Решить неравенства:
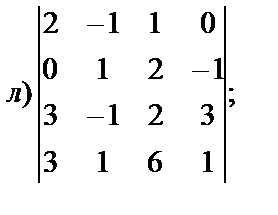
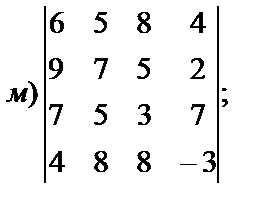
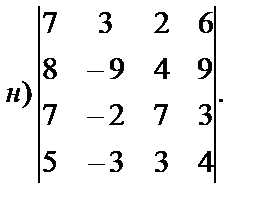
4. Вычислить определители:
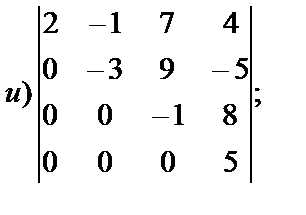
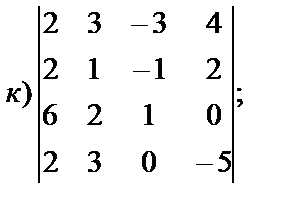
Ответы: 1. а)7; б)26; в)0; г)0; д)30. 2. а)5; б)2; в)2;
г) 3. а) б) в) г)[-1;7]. 4. а)-24; б)-40; в)-9; г)57; д)-5; е)1; ж)1; з)55; и)30; к)48; л)0; м)-1004; н)150.
Матрицы
Основные понятия
Определение. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины и n столбцов одинаковой длины, которая записывается в виде
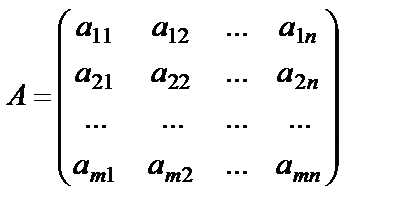 (9)
(9)
или, сокращенно, , где , (т.е. ) – номер строки, (т.е. ) – номер столбца, числа называются элементами матрицы. Матрицу называют матрицей размера и пишут . Например. , .
Определение. Две матрицы и равны между собой, если их размеры совпадают, а их соответствующие элементы равны, т.е. , если , где .
Например. Так как размеры матриц совпадают и соответствующие элементы равны, поэтому матрицы и равны, т.е.
Определение. Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера называют матрицей n-го порядка.
Например. т.е. дана матрица второго порядка.
Определение. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называются диагональной.
Матрица — диагональная.
Определение. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой .
или 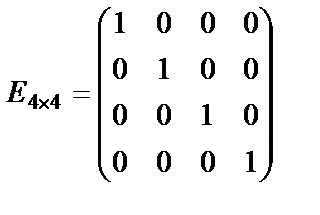
Определение. Квадратная матрица называется треугольной, если все элементы, расположенные над главной диагональю (или под главной диагональю), равны нулю.
или — треугольные матрицы.
Важной характеристикой квадратной матрицы порядка n является ее определитель (или детерминант), который обозначается или . .
Определение. Квадратная матрица, у которой определитель отличен от нуля, т.е. , называется невырожденной. В противном случае матрица называется вырожденной.
Например,
Матрица А – вырожденная.
Матрица В – невырожденная.
Определение. Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О.
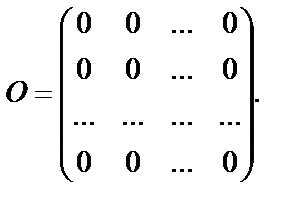
В матричном исчисление матрицы О и Е играют роль чисел 0 и 1 в арифметике.
Определение. Матрица, содержащая одну строку, называется матрицей-строкой
Матрица, содержащая один столбец, называется матрицей-столбцом
Матрица размера , состоящая из одного числа, отождествляется с этим числом, т.е. есть 3.
Определение. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается .
Если , то , если , то .
Транспонированная матрица обладает следующим свойством: .
megaobuchalka.ru
1.2.4. Примеры решения задач по теме «Определители»
Задача 1.
Вычислить определитель
.
Указание
Воспользуйтесь либо правилом треугольников, либо разложением определителя по 2-й строке или 2-му столбцу, содержащим нулевой элемент.
Решение
1-й способ (правило треугольников).
Вычислим определитель 3-го порядка, используя его определение:
Δ = 2·0·(-1) + (-3)·(-4)·2 + 5·1·1 — 2·0·5 -1·(-4)·2 – (-1)·1·(-3) =
= 0 + 24 + 5 – 0 + 8 – 3 = 34.
2-й способ (разложение по строке).
Применим свойство определителя:
.
Для удобства вычисления выберем 2-ю строку, содержащую нулевой элемент (А22 = 0), поскольку при этом нет необходимости находить А22, так как произведение А22 А22 = 0. Итак,
(напомним, что определитель второго порядка, входящий в алгебраическое дополнение Aij, получается вычеркиванием из исходного определителя I-й строки и J-го столбца).
Тогда Δ = А21 А21 + А23 А23 = 1·2 + (-4)(-8) = 34.
Ответ: Δ = 34.
Задача 2.
Используя свойства определителя, вычислить определитель
.
Указание
Вычитая из 2-й и 3-й строк определителя соответствующие элементы 1-й строки, добьемся того, что в 1-м столбце останется только один ненулевой элемент. Далее можно разложить определитель по 1-му столбцу.
Решение
Поскольку все элементы первого столбца равны 1, вычтем из 2-й и 3-й строк определителя соответствующие элементы 1-й строки (при этом величина определителя не изменится – свойство 6):
.
Заметим, что теперь все элементы 2-й строки кратны двум, а элементы 3-й строки кратны трем. По следствию 2.2 соответствующие множители можно вынести за знак определителя:
.
Вычтем из элементов 3-й строки полученного определителя соответствующие элементы 2-й строки:
И разложим определитель по 1-му столбцу:
Ответ: Δ = 6.
Разумеется, можно было вычислять этот определитель непосредственно (например, по правилу треугольников), но использование свойств определителей позволило существенно сократить и упростить численные расчеты. |
Задача 3.
Используя свойства определителей, вычислить определитель
.
Указание
Прибавьте к элементам 2-й строки соответствующие элементы 1-й строки, а из элементов 3-й строки вычтите удвоенные элементы 1-й строки. Затем вынесите за знак определителя все общие множители элементов какой-либо строки или столбца.
Решение
Прибавим к элементам 2-й строки соответствующие элементы 1-й строки, а из элементов 3-й строки вычтем удвоенные элементы 1-й строки:
Вынесем за знак определителя множитель -1 из 2-й строки и 3 – из 3-й:
Теперь из 3-го столбца вынесем множитель -2:
Вычтем из элементов 2-го столбца элементы 3-го столбца и разложим полученный определитель по 3-й строке:
Ответ: Δ = 306.
Задача 4.
Решить уравнение
Указание
Разложив определитель, стоящий в левой части равенства, по первой строке, и приравняв его 40, вы получите квадратное уравнение для Х.
Решение
Разложим определитель, стоящий в левой части равенства, по первой строке. Предварительно найдем соответствующие алгебраические дополнения:
Тогда
И требуется решить квадратное уравнение
.
Ответ:
Задача 5.
Решить неравенство
Указание
Раскройте определитель, стоящий в левой части неравенства, по 1-й строке.
Решение
Раскроем определитель, стоящий в левой части неравенства, по 1-й строке:
3(10 — 12) – X(2X – 9) + 4X – 15 > — 3;
-2X2 + 13X – 18 > 0;
2X2 – 13X + 18 < 0;
2 < X < 4,5.
Ответ: (2; 4,5).
Задача 6.
Используя свойства определителей (не раскрывая определитель), вычислить определитель
Указание
Используйте тригонометрическую формулу cos 2A = cos2A — sin2A и свойство определителя с двумя равными столбцами.
Решение
Из тригонометрии известно, что cos 2A = cos2A — sin2A. Вычтем из элементов
2-го столбца определителя соответствующие элементы 1-го столбца:

У полученного определителя, равного исходному (свойство 6), два столбца одинаковы, поэтому он равен нулю (следствие 2.1).
Ответ: 0.
Задача 7.
Вычислить определитель 4-го порядка
.
Указание
Преобразуйте определитель так, чтобы три из четырех элементов какой-либо строки или столбца стали равными нулю. Для этого воспользуйтесь свойством 6.
Решение
Преобразуем определитель так, чтобы три из четырех элементов какой-либо строки или столбца стали равными нулю. Для этого воспользуемся свойством 6. Его особенно удобно применять, если в определителе существует элемент, равный +1. Выберем в качестве такого элемента А13 = 1 и с его помощью обратим все остальные элементы 3-го столбца в нуль. С этой целью:
А) к элементам 2-й строки прибавим соответствующие элементы 1-й строки;
Б) из элементов 3-й строки вычтем элементы 1-й строки, умноженные на 2;
В) из элементов 4-й строки вычтем элементы 1-й строки
(напомним, что при этом величина определителя не изменится). Тогда
Разложим полученный определитель по 3-му столбцу:
Вычтем из элементов 1-й строки нового определителя удвоенные элементы 2-й строки:
И разложим этот определитель по 1-й строке:
Ответ: Δ = -9.
Задача 8.
Вычислить определитель 4-го порядка
Указание
Разложите определитель по 1-й строке, а затем полученный определитель 3-го порядка вновь разложите по 1-й строке.
Решение
Разложим определитель по 1-й строке:
Полученный определитель 3-го порядка вновь разложим по 1-й строке:
Ответ: Δ = 24.
Обратите внимание: если в определителе все элементы, стоящие по одну сторону от главной диагонали, равны нулю, то определитель равен произведению элементов, Стоящих на главной диагонали. |
Ответ: Δ = 24.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Вычисление определителей 2 — 4-го порядка
Научиться вычислять определители, обратные матрицы и т.д. — одно из основных заданий для первокурсников, которые получают образование на факультетах с математическим уклоном в обучении. Многие сервисы в интернете предлагают онлайн нахождения определителей и всего что касается матриц, однако мало программ — математических калькуляторов которые показывают ход решения. В конце статьи Вашему вниманию предлагается такой калькулятор, но об этом позже, а сейчас давайте рассмотрим несколько примеров нахождение определителя матрицы.
За справочник возьмем сборник задач Дубовика В.П., Юрика И.И. «Высшая математика». Позже будут добавлены примеры вычисления определителя матрицы из других источников.
———————————————
Примеры.
1) (1.4)
Применим правило вычисления определителя для матрицы второго порядка.
2) (1.6)
Выполним вычисления согласно правилу
3) (1.8)
Данный пример выглядит сложным но со знанием следующих правил логарифма
решается на удивление быстро.
4) (1.14)
Вычислим данный определитель двумя способами: по правилу треугольников и через алгебраические дополнения.
А сейчас разложим по элементам первого рядка, поскольку в нем больше нулей
В этом примере специально выписаны дополнение у нулевых множителей, так как не все понимают откуда берутся дополнения. По правилу они равны определителю, который образуется вычеркиванием строки и столбца того элемента для которого ищутся, умноженному на минус единицу в степени
.
Схематически на примере матрицы четвертого порядка это выглядит так:
Внимательно посмотрите, какие элементы в определителе выписаны для дополнений и Вам все станет понятно.
Суть метода алгебраических дополнений заключается в том, что когда мы матрицу с нулевыми элементами может разложив ее по по строке или столбцу в котором больше нулей нам остается вычислить столько определителей на порядок меньших основной матрицы, сколько ненулевых элементов. Это значительно упрощает вычисления.
6) (1.19)
Если вычисления проводить по правилу треугольников, то получим много нулевых произведений. В такого рода примерах целесообразно использовать алгебраические дополнения.
7) (1.21)
Вычислим определитель через алгебраические дополнения третьей строки
Как можно убедиться, решение с помощью алгебраических дополнений в случаях разреженных матриц можно получить быстро и без большого количества вычислений.
8) (1.58)
Выполним элементарные преобразования. От другого рядка вычтем первый, а от четвертого — третий. Получим разреженную матрицу
Определитель найдем через алгебраические дополнения к четвертой строке
Вычислим каждый из слагаемых
Подставляем в определитель
9) (1.72)
Найдем определитель через расписание по строкам и столбцам, содержащие нули (выделены черным).
Таким методом нахождения определителя пятого порядка свелось к простым вычислениям. Практикуйте и изучайте правила и через некоторое время у Вас будет выходить не хуже. До встречи в следующих уроках!
———————————————-
yukhym.com
4.1.2 Вычисление определителя — го порядка
Определение. Если в определителе -го порядка вычеркнуть строку и столбец, то оставшийся определитель -го порядка называется минором данного элемента и обозначается .
Определение. Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком .
Алгебраическое дополнение элемента обозначается через . Следовательно, .
Пример 3. Дан определитель . Найти минор и алгебраическое дополнение элемента (выделен пунктиром).
Решение. Вычеркивая в определителе первую строку и второй столбец, на пересечении которых находится элемент , получим . Тогда .
Теорема 1. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т. е.
, (*)
Где – фиксировано.
Выражение (*) называют разложением определителя по элементам строки с номером .
Вычисление определителя -го порядка сводится к вычислению одного определителя -го порядка, для чего в какой–либо строке (или столбце) получают нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).
Пример 4. Вычислить определитель
Решение.
Наша задача состоит в том, чтобы, пользуясь свойствами определителя, получить максимальное число нулей в какой-нибудь строке или столбце, а затем применить теорему 1. Во второй строке уже имеются два нуля, получим еще нули в этой строке. Для этого прибавим к элементам второго столбца соответствующие элементы четвертого столбца, умноженные на 2, а к элементам третьего столбца прибавим соответствующие элементы четвертого, умноженные на . Получим определитель, равный исходному
Применим теорему 1 ко второй строке, т. е. разложим определитель по элементам второй строки. Получим определитель 4-го порядка.
Теперь получим нули во втором столбце. Для этого к элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на , а к элементам четвертой – элементы первой, умноженные на .
Получим .
Разлагая его по элементам второго столбца, получим
.
Теперь можно разложить полученный определитель, например, по первому столбцу:
.
Легко вычисляются определители квадратных матриц треугольного или диагонального видов. В этом случае определитель равен произведению элементов, расположенных на диагонали.
Квадратная матрица вида называется диагональной, а квадратные матрицы и называются матрицами треугольного вида.
Пример 5. Вычислить определитель
Решение.
Будем получать нули под главной диагональю.
1-й этап. Берем первую строку и с ее помощью получим нули в первом столбце. Первую строку умножим на и прибавим ко второй, затем первую строку умножим на 2 и прибавим к четвертой. Получим
2-й этап. Работаем со второй строкой и получаем нули во втором столбце. Вторую строку умножаем на и прибавляем к третьей; вторую строку умножаем на 2 и прибавляем к четвертой:
3-й этап. Из четвертой строки вынесем и переставим третью и четвертую строки:
И последний этап.
Третью строку умножим на и прибавим к четвертой:
.
Разлагаем определитель по элементам первого столбца
.
Снова разлагаем определитель D по элементам первого столбца:
.
Действительно, определитель равен произведению элементов, стоящих на диагонали.
Для самостоятельного решения.
1. Вычислить определители
А) . Ответ: .
Б) . Ответ 10.
Указание: Чтобы уменьшить числа, вычтите какую-нибудь строку из остальных. Эту операцию можно проделать несколько раз. Цель: сделать на каком-нибудь месте единицу.
2. Вычислить определитель, приведя его к треугольному виду.
. Ответ: 52.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
