Степень корня указывается над знаком корня слева. \[\sqrt[x]{a}\], в данном примере х — степень. Если запись не имеет такого обозначения, значит перед нами корень квадратный.
Умножение корней
Существует несколько вариантов умножения корней, это умножение с множителем, без множителя и с разными показателями.
Умножение без множителей
Первым делом рассмотри, как умножаются корни без множителя.
Убедившись, что корни, с которыми необходимо произвести действие имеют одинаковые степени. Например квадратный корень из числа а, можно умножать на квадратный корень из d.
Рассмотрим правило на двух примерах произведения двух квадратных и двух кубических корней.
Примеры:
\[\sqrt{2} * \sqrt{6}=\] первый пример умножение квадратных корней.
\[\sqrt[3]{3} * \sqrt[3]{18}=\] второй пример умножение кубических корне.
Решение:
Для того чтобы решить данные примеры необходимо произвести умножение под корнем.
{2} * 3}=2 \sqrt{3}\], в данном примере число 12 можно разложить на произведение чисел 4 и 3, где 4 равно двум в квадрате. Поэтому 2 выносим за приделы корня и упрощаем выражение.
\[\sqrt[3]{54}=\sqrt[3]{27 * 2}=\sqrt[3]{(3 * 3 * 3) * 2}=3 \sqrt[3]{2}\] в данном случае получившееся подкоренное число 54 можно разложить на произведение двух чисел 27 и 2 , где 27 = 33, тройку выносим за корень кубический, тем самым мы упростили выражение.
Точно также производится умножение корней других степеней, при этом не важно количество умножаемых корней, правило не изменится.
Умножение корней с множителями
В данном случае мы так же рассматриваем примеры умножения корней с одинаковыми степенями. Множителем является число, стоящее перед корнем. Если при написании множитель отсутствует, то он равен единице. Умножить корень на число значит умножить число на множитель перед корнем. Для того чтобы произвести умножение с такими корнями, необходимо перемножить множители.
Пример умножения корней:
\[2 \sqrt{6} * \sqrt{6}=2 \sqrt{6 * 6}=2 \sqrt{36}=2 * 6=12\] в данном примере мы сначала произвели умножение множителей 1 и 2 , затем воспользовавшись первым правилом умножения корней, произвели умножение под знаком корня чисел 6 и 6.
Следующим шагом упрощаем выражение, корень из 36, равен целому числу 6. последним действием умножаем его на полученный множитель 2. и получаем ответ 12.
Пример 2.
\[2 \sqrt{6} * 3 \sqrt{3}=2 * 3 \sqrt{6 * 3}=6 \sqrt{18}=6 \sqrt{9 * 2}=6 * 3 \sqrt{2}=18 \sqrt{2}\]
В приведённом примере, мы также в начале производим умножение множителей 2 и 3, затем производим умножение подкоренных чисел 6 и 3, в результате получаем 6 корней из 18.
После производим упрощение выражения под знаком корня, для этого разложили его на множители, таким образом чтобы одно из чисел можно было вынести за пределы знака корень такими числами стали 9 и 2, в результате получилось, что вынесенное число равно трём, так как 9 = \[3^{2}\] .
Теперь умножим получившийся ранее множитель 6 на вынесенное из под корня число 3, и получим ответ 18 корней из двух.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Умножение корней с разными показателями
Теперь разберём, как умножить корни если их показатели степени разные. Для этого необходимо найти наименьшее общее кратное число для этих показателей. Таким числом является наименьшее число, которое можно разделить на оба эти показателя. Для того чтобы разобраться лучше в данном методе, приведём пример.
Пример:
\[\sqrt[2]{2} * \sqrt[3]{5}=\]
Сначала необходимо найти наименьшее общее кратное, наименьшим в данном случае является произведение 2*3 = 6. Значит для того чтобы произвести умножение корней необходимо привести их к показателю шестой степени.
Записываем новое полученное выражение \[\sqrt[6]{2} * \sqrt[6]{5}=\]
Теперь находим числа на которые нужно умножить показатели, чтобы найти наименьшее общее кратное
Для первого корня это деление 6\2 = 3, для второго 6\3 =2
Следующим шагом нужно возвести подкоренное число в степень, которая ровна числам найденным ранее, при нахождении НОК, то есть \[\sqrt[6]{2^{3}} * \sqrt[6]{5^{2}}=\]
Далее имея одинаковые показатели производим действия по умножению корней, так как делали это в предыдущих правилах.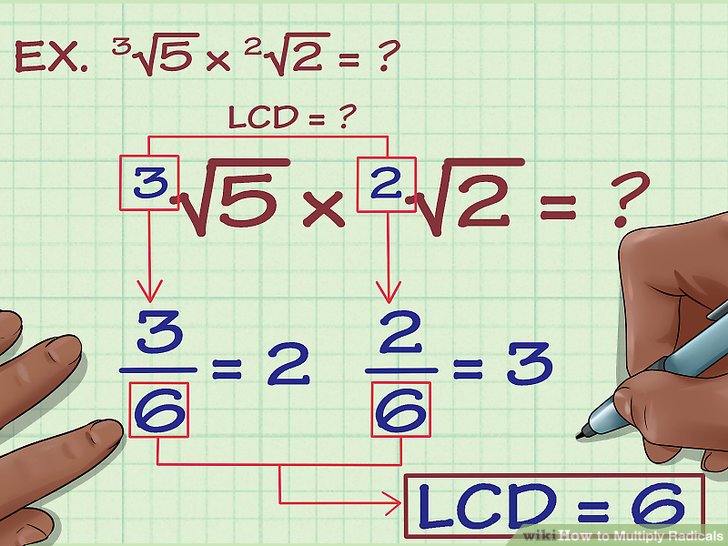
{2}}=\sqrt[6]{8 * 25}=\sqrt[6]{200}\]
Если полученное выражение можно упростить, то упрощаем его. В данном случае это невозможно.
Как мы видим произвести умножение корней не так и сложно, главное запомнить основные правила и формулы умножения корней и пользоваться ними.
§ Квадратный корень из дроби
Квадратный корень Квадратный корень из произведения Квадратный корень из дроби Как избавиться от иррациональности Как вынести из-под корня Как внести под знак корня
В примерах по извлечению квадратного корня из дроби требуется работать с обыкновенными дробями.
Поэтому рекомендуем перед решением примеров освежить знания по действиям с
обыкновенными дробями:
- правильные и неправильные дроби;
- сложение дробей;
- вычитание дробей;
- умножение дробей;
- деление дробей.
Свойство квадратного корня из дроби
Запомните!
Квадратный корень из дроби равен корню из числителя, деленному на корень из знаменателя.
=
, если a ≥ 0 и b > 0.
Как найти квадратный корень из дроби
По традиции от теории переходим к практике. Разберем пример вычисления квадратного корня из дроби.
Разбор примера
Вычислить:
1)
= …
Используем правило квадратного корня из дроби. Извлечем квадратный корень отдельно из числителя и знаменателя.
=
| √9 |
| √100 |
=
Запомните!
Правило извлечения квадратного корня из дроби действует и в обратную сторону.
Квадратный корень из числителя, деленный на квадратный корень из знаменателя, равен квадратному корню из всей дроби.
=
, если a ≥ 0 и b > 0.
Разбор примера
Вычислить:
1)
=
= √9 = 3
Как извлечь квадратный корень из смешанного числа
Запомните!
Чтобы извлечь квадратный корень из смешанного числа надо:
- избавиться от целой части, т.е. привести дробь к неправильному виду;
- использовать свойство квадратного корня из дроби.
Разбор примера
Вычислить:
4)
| 5 |
= …
Избавимся от целой части дроби и превратим ее в неправильную.
| 5 |
=
|
=
|
=
=
= …
Используем свойство квадратного корня из дроби.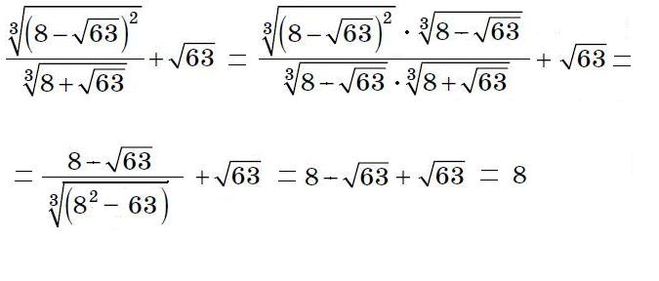
| 5 |
=
|
=
|
=
=
=
= …
Для завершения примера не забудем выделить целую часть.
| 5 |
=
|
=
|
=
=
=
=
= 2
Запомните!
Нельзя складывать или вычитать подкоренные дроби между собой, объединяя их общим знаком квадратного корня.
+
≠
| + |
Разбор примера
Вычислить:
4)
+
= …
Перед тем как работать с дробями требуется выполнить действие извлечения квадратного корня из дробей.
+
=
+
= …
Вспомним, что квадратный корень из единицы равен единице ( √1 = 1 ) и используем правило сложения дробей.
+
=
+
=
+
=
=
= 1
Примеры извлечения квадратного корня из дробиРазбор примера
2) 5
− 3
= …
Вспомним, что в краткой записи между квадратным корнем и числом знак умножения «·» не пишут.
Для наглядности поставим его в пример и вычислим пример по правилу
умножения числа на дробь.
5
− 3
=
=
5
·
− 3 ·
=
=
5
·
− 3 ·
=
=
5
·
− 3 ·
= …
Вспомним правило умножения дроби на число.
5
− 3
=
=
5
·
− 3 ·
=
=
5
·
− 3 ·
=
=
5
·
− 3 ·
=
| 5 · 1 |
| 5 |
−
| 3 · 1 |
| 3 |
=
=
1 − 1 = 0
Разбор примера
Вычислить:
4)
| 20 · √18 |
| 5 · √2 |
= …
Чтобы вычислить квадратный корень, используем правило умножения дробей
и правило квадратного корня из дроби.
| 20 · √18 |
| 5 · √2 |
=
·
= 4 ·
=
=
4 · √9 =
4 · 3 = 12
Разбор примера
Вычислить:
2)
| 5 · 11 |
= …
Избавимся от целой части в смешанных числах, чтобы можно было использовать свойство квадратного корня из дроби.
| 5 · 11 |
=
=
|
=
=
| · |
=
·
=
=
·
| √289 |
| √25 |
= …
Вспомним таблицу квадратов, чтобы вычислить
√289.
| 5 · 11 |
=
=
|
=
=
| · |
=
·
=
=
·
| √289 |
| √25 |
=
·
=
| 7 · 17 |
| 3 · 5 |
=
=
= …
Выделим целую часть смешанного числа для того, чтобы дать окончательный ответ.
| 5 · 11 |
=
=
|
=
=
| · |
=
·
=
=
·
| √289 |
| √25 |
=
·
=
| 7 · 17 |
| 3 · 5 |
=
=
= 7
Квадратный корень Квадратный корень из произведения Квадратный корень из дроби Как избавиться от иррациональности Как вынести из-под корня Как внести под знак корня
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
Как умножать радикалы вместе — Криста Кинг Математика
Умножение радикалов с одинаковым корнем
При умножении двух радикалов с одинаковым корнем (оба квадратных корня, оба кубических корня и т. д.) мы просто умножаем подкоренные (выражения под знаками радикалов) и ставим произведение под знаком корня.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Как умножать радикалы
Пройти курс
Хотите узнать больше о Pre-Algebra? У меня есть пошаговый курс для этого.
🙂Узнать больше
Нахождение произведения корней
Пример
Нахождение произведения.
???\sqrt3\sqrt2???
Когда мы видим два радикала рядом друг с другом вот так, это означает, что мы должны их перемножить.
Чтобы умножить два квадратных корня, мы просто умножаем подкоренные и ставим произведение под знаком радикала. То есть произведение двух квадратных корней равно квадратному корню из произведения подкоренных.
???\sqrt{3\cdot2}???
???\sqrt{6}???
Полезно помнить, что мы можем использовать это правило для умножения радикалов и в обратном направлении. Другими словами, если нам дано ???\sqrt{6}???, мы можем разложить ???6??? как ???3\cdot2???, затем переписать ???\sqrt6??? как ???\sqrt{3\cdot2}???, и, наконец, перепишите квадратный корень из произведения (из ???3??? и ???2???) как произведение их квадратных корней.
???\sqrt{6}???
???\sqrt{3\cdot2}???
???\sqrt3\sqrt2???
Иногда переписывание радикала как произведения радикалов может помочь нам решить проблему, над которой мы работаем, поэтому полезно помнить, что с этим правилом умножения радикалов можно действовать в обоих направлениях.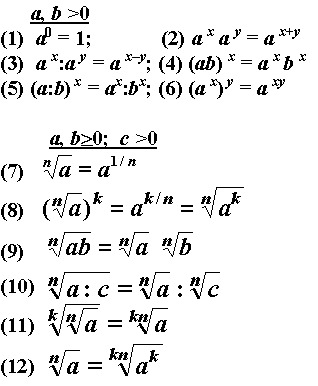
Теорема о квадратных корнях говорит нам, что если ???m??? и/или ???н??? неотрицательные действительные числа, то
???\sqrt{m}\sqrt{n}=\sqrt{mn}??? и ???\sqrt{mn}=\sqrt{m}\sqrt{n}???
Давайте сделаем еще один пример, где мы умножаем два квадратных корня.
Чтобы умножить два квадратных корня, мы просто умножаем подкоренные и ставим произведение под знаком радикала.
Пример
Найдите продукт.
???\sqrt5\sqrt5???
Давайте повторим те же шаги, что и раньше, где мы перепишем произведение квадратных корней как квадратный корень из произведения подкоренных.
???\sqrt{5\cdot5}???
???\sqrt{25}???
Но теперь нам нужно понять, что ???\sqrt{25}??? просто ???5???, так как ???5??? умноженное само на себя равно ???25???. Итак, мы можем написать ???\sqrt{25}??? как раз ???5???.
Что приводит нас к тому, что при умножении двух одинаковых квадратных корней результат будет таким же, как подкоренное в каждом из квадратных корней.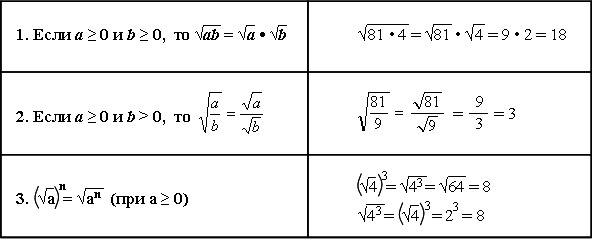
Итак,
Точно так же, когда у нас есть произведение трех одинаковых кубических корней, мы получаем число, равное подкоренному в каждом из них. Например,
???\sqrt[3]{-21}\sqrt[3]{-21}\sqrt[3]{-21}=-21???
Также, когда у нас есть четыре одинаковых корня четвертой степени, мы получаем число, равное подкоренному в каждом из них. Например,
???\sqrt[4]{13}\sqrt[4]{13}\sqrt[4]{13}\sqrt[4]{13}=13???
И так далее для корней с более высокими номерами.
Давайте сделаем еще один пример умножения квадратных корней — на этот раз, когда один из них имеет коэффициент, отличный от ???1???.
Пример
Найдите продукт.
???(4\sqrt2)\cdot\sqrt3???
То, что у нас есть коэффициент, отличный от ???1??? ничего не меняет. Мы можем оставить коэффициент впереди и умножить только квадратные корни.
???(4\sqrt2)\cdot\sqrt3???
???4(\sqrt2\cdot\sqrt3)???
???4\sqrt{2\cdot3}???
???4\sqrt{6}???
Получить доступ к полному курсу Pre-Algebra
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, преалгебра, предварительная алгебра, радикалы, корни, сурды, умножение радикалов, умножение корней, умножение сурдов
0 лайковКвадраты и квадратные корни
Сначала узнайте о квадратах, затем получите квадратные корни.
Как возвести число в квадрат
Чтобы возвести число в квадрат: умножьте его само на себя .
Пример: Сколько будет 3 в квадрате?
| 3 В квадрате | = | = 3 × 3 = 9 |
«Квадрат» часто пишется как маленькая двойка, например:
.
Здесь написано «4 в квадрате равно 16»
(маленькая двойка говорит
число появляется дважды при умножении)
Квадраты От 0
2 до 6 2| 0 Квадрат | = | 0 2 | = | 0 × 0 | = | 0 |
| 1 Квадрат | = | 1 2 | = | 1 × 1 | = | 1 |
| 2 Квадрат | = | 2 2 | = | 2 × 2 | = | 4 |
| 3 В квадрате | = | 3 2 | = | 3 × 3 | = | 9 |
| 4 В квадрате | = | 4 2 | = | 4 × 4 | = | 16 |
| 5 Квадрат | = | 5 2 | = | 5 × 5 | = | 25 |
| 6 Квадрат | = | 6 2 | = | 6 × 6 | = | 36 |
| Квадратов тоже в таблице умножения: |
Отрицательные числа
Мы также можем возвести в квадрат отрицательных числа .
Пример: Что произойдет, если возвести в квадрат (−5) ?
Ответ:
(−5) × (−5) = 25
(поскольку отрицательное, умноженное на отрицательное, дает положительное)
Было интересно!
Когда мы возводим в квадрат отрицательное число , мы получаем положительный результат.
Точно так же, как возведение в квадрат положительного числа:
.(Подробнее читайте Квадраты и квадратные корни в алгебре)
Квадратные корни
квадратный корень из идет в другую сторону:
3 в квадрате равно 9, поэтому квадратный корень из из 9 это 3
Квадратный корень из числа равен …
… значение, которое может быть , умноженное само на себя , чтобы указать исходный номер.
Квадратный корень из 9 равен …
… 3 , потому что при умножении 3 на само получается 9 .
Это все равно, что спросить:
Что мы можем умножить само на себя, чтобы получить это?
Чтобы помочь вам вспомнить , подумайте о корне дерева: «Я знаю дерево , но какой корень его создал? « В данном случае дерево «9», а корень «3». |
Вот еще несколько квадратов и квадратных корней:
| 4 | 16 | |
| 5 | 25 | |
6 | 36 | |
7 | 49 | |
Десятичные числа
Это также работает для десятичных чисел.
Попробуйте ползунки ниже (примечание: «…» означает, что десятичные дроби продолжаются бесконечно):
Использование ползунков:
- Чему равен квадратный корень из 8 ?
- Чему равен квадратный корень из 9 ?
- Чему равен квадратный корень из 10 ?
- Что такое 1 в квадрате?
- Что такое 1,1 в квадрате?
- Что такое 2,6 в квадрате?
Негативы
Ранее мы обнаружили, что можем возводить в квадрат отрицательные числа:
Пример: (−3) в квадрате
(−3) × (−3) = 9
И, конечно же, 3 × 3 = 9 .
Таким образом, квадратный корень из 9 может быть равен −3 или +3
.Пример: Чему равен квадратный корень из 25?
(−5) × (−5) = 25
5 × 5 = 25
Таким образом, квадратные корни из 25 равны −5 и +5
.Символ квадратного корня
| Это специальный символ, означающий «квадратный корень». это вроде как галочка, и на самом деле началась сотни лет назад в виде точки с движением вверх. Он называется радикалом и всегда делает математику важной! |
Мы используем его так:
и мы говорим «квадратный корень из 9 равен 3»
Пример: Что такое √25?
25 = 5 × 5, другими словами, когда мы умножаем 5 отдельно (5 × 5) получаем 25
Итак, ответ:
√25 = 5
Но подождите! Разве квадратный корень из не может также равняться −5 ? Потому что (−5) × (−5) = 25 тоже.
- Ну, квадратный корень из 25 может быть -5 или +5.
- Но когда мы используем радикальный символ √ , мы даем только положительный (или нулевой) результат .
Пример: Что такое √36 ?
Ответ: 6 × 6 = 36, поэтому √36 = 6
Идеальные квадраты
Совершенные квадраты (также называемые «квадратными числами») — это квадраты целых чисел:
| Идеальный Квадраты | |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
| 11 | 121 |
| 12 | 144 |
| 13 | 169 |
| 14 | 196 |
| 15 | 225 |
и т. д… |
Постарайтесь запомнить их до 12.
Вычисление квадратных корней
Легко извлечь квадратный корень из полного квадрата, но действительно сложно из вычислить другие квадратные корни.
Пример: что такое √10?
Итак, 3 × 3 = 9 и 4 × 4 = 16, поэтому мы можем предположить, что ответ находится между 3 и 4.
- Попробуем 3,5: 3,5 × 3,5 = 12,25
- Попробуем 3,2: 3,2 × 3,2 = 10,24
- Попробуем 3,1: 3,1 × 3,1 = 9,61
- …
Приближаемся к 10, но для получения хорошего ответа потребуется много времени!
В этот момент я достаю свой калькулятор, и он говорит: .3,1622776601683793319988935444327 Но цифры продолжаются и продолжаются без какой-либо закономерности. Так даже ответ калькулятора только приближение ! |
Примечание: такие числа называются иррациональными числами, если вы хотите узнать больше.
Самый простой способ вычисления квадратного корня
| Используйте кнопку квадратного корня вашего калькулятора! |
А также используйте свой здравый смысл, чтобы убедиться, что у вас есть правильный ответ.
Увлекательный способ вычисления квадратного корня
Существует забавный метод вычисления квадратного корня, который с каждым разом становится все более и более точным:
| а) начните с предположения (допустим, 4 — это квадратный корень из 10) | |
| б) разделить на предположение (10/4 = 2,5) в) добавить это к предположению (4 + 2,5 = 6,5) d) затем разделите этого результата на 2, другими словами, разделите его пополам. (6,5/2 = 3,25) e) теперь установите это как новое предположение и снова начните с b) |
- Наша первая попытка увеличила число с 4 до 3,25
- Повторный переход (от b до e ) дает нам: 3,163
- Повторный переход (от b до e ) дает нам: 3,1623
Таким образом, после 3-х раз ответ равен 3,1623, что очень хорошо, потому что:
3,1623 х 3,1623 = 10,00014
Теперь.