Умножение матриц
Расчет умножения матриц онлайн. Умножьте матрицы порядка 2×3, 1×3, 3×3, 2×2 с 3×2, 3×1, 3×3, 2×2. Динамические расчеты, нахождения произведения матриц.
Умножение матриц возможно когда число столбцов первой матрицы равно числу строк второй матрицы.
Матрица 1
X
Матрица 2
3x33x22x33x11x32x2
X
3x33x22x33x11x32x2
В первой части мы рассмотрим умножение квадратных матриц. В следующей части Вы узнаете, как умножить разные матрицы (например, 2х3 до 3х3).
Здесь мы будем умножать матрицу 3х3 (3 ряда, 3 колонки) на другую матрицу 3х3 (3 ряда, 3 колонки).
| Матрица A | Матрица B | |||||||||||||||||||
| x |
|
В результате мы получим матрицу 3х3.
Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.
Шаг 1:Рассчитаем x11
Для того, чтобы вычислить результат x11 мы будем использовать первую строку матрицы А и первый столбец матрицы В.
| Результат X | Матрица A | Матрица B | |||||||||||||||||||||||||||||
| = |
| x |
|
Мы можем представить результат x11 = a11 x b11 + a12 x b21 + a13 x b31
Шаг 2: Рассчитаем x12
Для того, чтобы вычислить результат x12 мы будем использовать первую строку матрицы А и втором столбце матрицы В.
| Матрица A | Матрица B | ||||||||||||||||||||||||||||||
| = |
| x |
|
Мы можем представить резальтат x12 = a11 x b12 + a12 x b22 + a13 x b32
По той же методике мы вычислим значения для всех ячеек.
| Результат Матрица | |||||||||
|
людей нашли эту статью полезной. А Вы?
Решение высшей математики онлайн
‹— Назад
Определение 14.4 Произведением матрицы размеров на матрицу размеров называется матрица размеров , элементы которой вычисляются по формуле
(14. 5) |
где , .
Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой — второй.
Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.
В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.
Правило вычисления элементов произведения можно сформулировать следующим образом.
Для того, чтобы вычислить элемент произведения, стоящий в -ой строке и -ом столбце, нужно взять -ую строку первого сомножителя и -ый столбец второго сомножителя, попарно перемножить их элементы, стоящие на одинаковых местах, и результаты сложить.
(Точно так же мы поступаем, когда находим скалярное произведение двух векторов по их координатам, см. формулу (14.2).)
Пример 14.3 Даны матрицы , . Найдите произведения и .
Решение. Рассмотрим произведение . Число столбцов в первом сомножителе равно 3, число строк во втором сомножителе тоже равно 3. Числа совпали, следовательно, произведение определено.
Результатом умножения будет матрица , , у которой строк столько, сколько их в первом сомножителе, то есть 3, а столбцов столько, сколько их во втором сомножителе, то есть 2. Итак, матрица имеет размеры .
Находим элемент . В его вычислении участвует первая строка первого сомножителя и первый столбец второго сомножителя :
Находим элемент . В его вычислении участвует первая строка первого сомножителя и второй столбец второго сомножителя :
Все элементы первой строки матрицы вычислены.
Находим элемент . В его вычислении участвует вторая строка первого сомножителя и первый столбец второго сомножителя :
Находим элемент . В его вычислении участвует вторая строка первого сомножителя и второй столбец второго сомножителя :
Вычислены все элементы второй строки матрицы . Аналогично находим элементы третьей строки:
Итак, .
Рассмотрим произведение . Число столбцов в первом сомножителе равно 2, число строк во втором сомножителе равно 3. Числа не совпали, следовательно, произведение не определено.
Ответ: , произведение не определено.
Замечание 14.3 Легко проверить, что произведение квадратных матриц одного порядка всегда существует (определено).
У читателя может возникнуть законный вопрос: «Зачем так сложно определять произведение матриц? Нельзя ли его определить попроще, например, как произведение элементов матриц-сомножителей, стоящих на одинаковых местах?» Ответ на этот вопрос мы увидим позже, когда будем рассматривать системы линейных уравнений, правило изменения координат векторов при изменении базиса и такие неизвестные пока читателю объекты как линейные преобразования и квадратичные формы.
Тогда мы увидим, что введенное определение умножения матриц используется очень эффективно, что оно «похоже» на умножение чисел. Если же произведение матриц определить по-другому, то его не удается разумно использовать ни в математике, ни в прикладных науках.
Рассмотрим, какими свойствами обладает операция умножения матриц.
Прежде всего отметим, что умножение матриц — некоммутативная операция. Это означает, что существуют такие матрицы и , что
Для прямоугольных матриц мы убедились в этом в примере 14.3. В нем произведение существует, а произведение — нет. Для квадратных матриц это видно из следующего примера. Пусть , . Тогда
то есть .
Предложение 14.4 Умножение матриц обладает следующими свойствами: — ассоциативность умножения; , где — число; , — дистрибутивность умножения; , , где — единичная матрица соответствующего порядка.
Предполагается, что все указанные произведения имеют смысл.
Доказательство. На протяжении всего доказательства предполагается, что — матрица размеров .
Докажем свойство ассоциативности. Чтобы произведение было определено, матрица должна иметь размеры . Произведение обозначим буквой . Тогда матрица имеет размеры . Чтобы произведение было определено, матрица должна иметь размеры . Матрицу обозначим , матрицу обозначим , матрицу обозначим . Покажем, что элементы, стоящие в -ой строке и -ом столбце матриц и , равны друг другу, то есть что .
По определению
Подставив из второго равенства в первое, получим
В силу предложения 14.1
В силу предложения 14.3
(14. 6) |
С другой стороны
откуда
Применим предложение 14.1
Сравнивая этот результат с (14.6), заключаем, что . Ассоциативность умножения доказана.
Свойство 2 предоставляем читателю доказать самостоятельно.
Докажем дистрибутивность умножения. Чтобы произведение было определено, матрицы и должны иметь размеры . Положим , , , , . Для доказательства равенства , нужно доказать, что , , .
Так как , то
По определению суммы матриц, . Следовательно,
| (14.7) |
С другой стороны,
Тогда
Сравнивая полученный результат с (14.
7), получаем . Первое равенство в свойстве дистрибутивности доказано. Второе равенство доказывается аналогично.
Докажем первое равенство в свойстве 4. Чтобы произведение было определено, матрица должна иметь порядок . Пусть . Тогда
где — символ Кронекера . Сумма справа имеет вид
Таким образом , первое равенство в свойстве 4 доказано. Второе равенство доказывается аналогично.
Замечание 14.4 Из ассоциативности умножения матриц следует, что если произведение содержит три и более сомножителей, то его можно записывать без использования скобок. Например, или . Эта кажущаяся очевидной запись произведения верна не для всяких математических объектов. Действительно, в силу предложения 10.23, для векторного произведения векторов запись неприемлема, так как результат вычисления этого произведения зависит от расстановки скобок.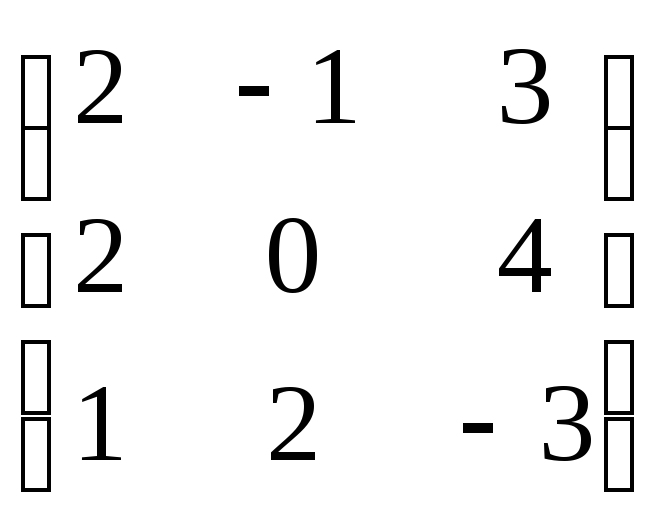
Замечание 14.5 Свойство дистрибутивности позволяет раскрывать скобки в матричных выражениях. Но нужно обратить внимание, что, раскрывая скобки, нельзя менять порядок сомножителей.
Замечание 14.6 Свойство 4 объясняет происхождение названия «единичная» матрица. В умножении матриц единичная матрица ведет себя так же, как число 1 при умножении чисел.
Упражнение14.4.6. Докажите, что произведение двух верхних треугольных матриц одного порядка является верхней треугольной матрицей того же порядка. Докажите аналогичное утверждение для нижних треугольных матриц.
Упражнение14.4.7. По определению считается, что . Покажите, что для матриц формула не верна. Объясните почему.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Умножение матриц с помощью калькулятора TI83 или TI84
Графические калькуляторы, такие как TI83 и TI84, могут выполнять множество различных операций с матрицами, включая умножение.
Содержание
- Пошаговый процесс на примере
- Распространенные ошибки
- Дополнительное чтение
реклама 9{-1}\справа]\).
(Примечание: некоторые старые модели калькуляторов TI83 имеют кнопку MATRIX)
Используйте клавишу со стрелкой вправо, чтобы перейти в меню EDIT.
Нажмите Enter, чтобы выбрать матрицу A.
Введите размер матрицы и значения, вводя каждое число и нажимая [ENTER]. Обратите внимание, что первая матрица представляет собой матрицу 2 x 3 (строки по столбцам).
\(A=\left[\begin{array}{ccc}-1 & 5 & -2\\ 3 & 7 & 7\\\end{array}\right]\) 9{-1}\справа]\).
Нажмите клавишу со стрелкой вправо, чтобы перейти в меню EDIT.
Нажмите [2] или выделите 2. [B] и нажмите [ENTER].
Введите размер матрицы и значения, вводя каждое число и нажимая [ENTER].
Обратите внимание, что вторая матрица из нашего примера представляет собой матрицу 3 x 2 (строки по столбцам).
\(\left[\begin{array}{cc}4 и 0\\ 1 & 1\\ 3 & 9\end{массив}\right]\)
Шаг 3: Нажмите [2ND] и [MODE], чтобы выйти из матричного экрана 9{-1}\справа]\).
Нажмите [2] или выделите 2. [B] и нажмите [ENTER].
Нажмите [ENTER], чтобы умножить матрицы.
Отсюда вы получите окончательный ответ. Теперь мы можем написать:
\(\begin{align} AB &=\left[\begin{array}{ccc}-1 & 5 & -2\\ 3 & 7 & 7\\\end{array}\right]\left[\begin {массив} {cc} 4 & 0 \\ 1 & 1 \\ 3 & 9 \ end {массив} \ right]
\\ & = \ boxed {\ left [\ begin {array} {cc} -5 & — 13\\ 40 и 70\\\конец{массив}\справа]}\конец{выравнивание}\)
Распространенная ошибка: НЕСООТВЕТСТВИЕ DIM
Предположим, что вы выполнили эти шаги и получили следующий экран.
В этом случае вы должны проверить две вещи:
- Вы ввели правильную информацию о матрице и выбрали ли вы правильные матрицы для умножения?
- Определен ли продукт?
Если вы правильно ввели матрицы, то эта ошибка означает, что продукт не определен.
В частности, если вы записываете размеры матриц, внутренние числа должны совпадать. В приведенном выше примере у нас были 2 x 3 и 3 x 2. Обратите внимание, что числа внутри совпадают, поэтому продукт был определен, и мы смогли найти ответ.
Однако произведение 2 x 2 и 3 x 2 будет неопределенным, поскольку внутренние числа не совпадают. Вы бы просто написали «Не определено» в качестве ответа, если бы решали подобную задачу на экзамене или викторине.
Чтобы узнать больше о том, когда умножение матриц определено или нет, см. следующую ссылку.
Когда определено умножение матриц?
реклама
Продолжить изучение матриц и калькулятора TI83/84
В следующих статьях содержится дополнительная информация об использовании калькулятора с матрицами:
- Поиск обратной матрицы с помощью калькулятора
- Сокращение строки на калькуляторе
Подпишитесь на нашу рассылку!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и наборы задач.
Подпишитесь, чтобы время от времени получать электронные письма (раз в пару или три недели), сообщающие о новинках!
Калькулятор умножения матриц с шагами
Калькулятор умножения матриц с шагами — онлайн и бесплатно!Share Algebra Calculator
Add to Bookmarks
Add Algebra Calculator to Your Browser Bookmarks
1. For Windows or Linux — Press Ctrl+D
2. For MacOS — Press Ctrl+D
3. Для iPhone (Safari) — Коснитесь и удерживайте , затем коснитесь Добавить закладку
4. Для Google Chrome — нажмите 3 точки значок 9 в правом верхнем углу, затем нажмите 5 звездочку вверху справа
Как использовать?
Как пользоваться калькулятором умножения матриц
1
Шаг 1
Введите задачу на умножение матриц в поле ввода.
2
Шаг 2
Нажмите Enter на клавиатуре или на стрелку справа от поля ввода.
3
Шаг 3
Во всплывающем окне выберите нужную операцию. Вы также можете воспользоваться поиском.
Что такое умножение матриц
Данное методическое пособие поможет вам научиться выполнять операции с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, поэтому даже неподготовленный человек может научиться выполнять действия с матрицами.
Мы рассмотрели действия сложения, вычитания и умножения матриц на число. Другое действие над ними — умножение. Его сложнее выполнить, да и само правило может показаться немного странным. При этом важно уметь определять размеры матриц.
Умножение матриц — одна из самых распространенных операций над матрицами. Матрица, которая получается после умножения, называется произведением матриц.
Процесс умножения матриц возможен только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы. Матрица P может быть умножена на матрицу K только в том случае, если количество столбцов матрицы P равно количеству строк матрицы K. Матрицы, для которых это условие не выполняется, не могут быть умножены. Довольно часто можно встретить задания с подвохом, когда ученику предлагается перемножить матрицы, умножение которых заведомо невозможно.
Умножение матриц выполняется путем умножения строки на столбец. Находит произведения первого элемента строки и первого элемента столбца, второго элемента строки и второго элемента столбца и т. д. Затем полученные произведения суммируются. В нашем калькуляторе можно найти произведение матриц онлайн бесплатно с подробным решением и даже с комплексными числами.