Умножение перестановок: Помогите решить / разобраться (М)

Помогите решить / разобраться (М)

Сообщения без ответов | Активные темы | Избранное

Правила форума

Посмотреть правила форума

Aster1sk	Умножение перестановок 22.05.2019, 16:15
22/05/19 2	Добрый день! Параллельно ковыряю несколько учебников по высшей алгебре, в частности Курош и Кострикин. Разбираю перестановки и решаю задачи по теме. И я обнаружил, что у Кострикина и у Куроша умножение отличается! Если умножаются 2 перестановки, например и , то у Куроша первый столбец выглядит как , а у Кострикина то есть с моей точки зрения (которая сформировалась после прочтения Куроша) Кострикин перемножает их в обратном порядке. Помогите разобраться, я не понимаю, как правильно.

Someone	Re: Умножение перестановок 22.05.2019, 17:12
Заслуженный участник 23/07/05 17973 Москва	Aster1sk в сообщении #1394583 писал(а): Помогите разобраться, я не понимаю, как правильно. Как определите, так и правильно. Курош определил так, Кострикин эдак… Только позаботьтесь, чтобы ваши читатели знали, как именно Вы определили. — Ср май 22, 2019 17:14:04 — Да, и не забывайте, что при разных определениях умножения формулы будут выглядеть, вообще говоря, по-разному.

Munin	Re: Умножение перестановок 22.05.2019, 17:46
Заслуженный участник 30/01/06 72407	Всё очень просто. Да, есть два способа перемножать перестановки. А именно, если у вас записано то её можно воспринимать: — слева направо: сначала вычисляется перестановка а потом к её результату применяется перестановка ; — справа налево: сначала вычисляется перестановка а потом к её результату применяется перестановка Оба варианта «законны»: первый естественный для «наивного» читателя, и если перестановки воспринимать просто «как объект в себе», а второй — естественный, если воспринимать перестановки как (биективные) функции, а умножение — как композицию: Так что вся проблема сводится к тому, что где-то в начале раздела про перестановки в книге просто указывается, в каком именно смысле здесь понимается порядок умножения. Надо это место внимательно прочитать, и запомнить. Выкладки одного типа переводятся в выкладки другого типа автоматически: просто записываются задом наперёд. Соответственно, и сопоставить две книги не проблема.

Connector	Re: Умножение перестановок 22. 05.2019, 18:57
02/05/19 396	Все дело в удобстве обозначений: это чисто языковой вопрос. Здесь также важно, какую символику автор выбирает для значения функции в точке : или ; в зависимости от этого оба варианта могут оказаться «естественными», как пишет Munin , даже если воспринимать перестановки как биективные функции.

Aster1sk	Re: Умножение перестановок 23. 05.2019, 07:10
22/05/19 2	Действительно, у Кострикина есть прямое указание на связь темы перестановок с темой множеств и отображений, и в этом смысле его вариант, конечно, более логичный. у Куроша же умножение даётся между прочим, а сама тема перестановок привязана к определителям (что в момент прочтения казалось весьма уместным). Возможно, где-то дальше в соответствующей теме есть пояснение, что, когда дело касается множеств, правила умножения будут немного противоположными. До этого я ещё не дошёл. В любом случае, всем спасибо.

Munin	Re: Умножение перестановок 23. 05.2019, 11:27
Заслуженный участник 30/01/06 72407	Aster1sk в сообщении #1394691 писал(а): У Куроша же умножение даётся между прочим, а сама тема перестановок привязана к определителям (что в момент прочтения казалось весьма уместным). Довольно часто это так и делается, то есть перестановки — мелкий вспомогательный аппарат, чтобы определять знакочередование при антисимметризации. Не только определители: это встречается в антисимметричных тензорах (частным случаем которых и является определитель), в диаграммах Юнга и основанных на них понятиях. .. Но всегда как мелкая служебная деталь. В линейной алгебре. А группа перестановок сама по себе — это сильно другая ветвь алгебры, это теория групп (её конечная часть). Aster1sk в сообщении #1394691 писал(а): Возможно, где-то дальше в соответствующей теме есть пояснение, что, когда дело касается множеств, правила умножения будут немного противоположными. Вряд ли. Скорее, в пределах одной книги правила будут везде одинаковыми, чтобы не путать читателя. Ну а в разных книгах может быть по-разному. Но всегда явно оговорено (если автор хороший, а названные вами — хорошие).

Padawan	Re: Умножение перестановок 23. 05.2019, 12:38
Заслуженный участник 13/12/05 4392	Aster1sk в сообщении #1394691 писал(а): Действительно, у Кострикина есть прямое указание на связь темы перестановок с темой множеств и отображений, и в этом смысле его вариант, конечно, более логичный. Если мне не изменяет память, умножение линейных операторов у Куроша тоже идет слева направо, т.е. (еще так в учебнике Мальцева по линейной алгебре). Поэтому у Куроша тоже все логично

bot	Re: Умножение перестановок 23. 05.2019, 14:14
Заслуженный участник 21/12/05 5842 Новосибирск	Padawan в сообщении #1394741 писал(а): Поэтому у Куроша тоже все логично Всё сводится к тому, с какой стороны писать символ оператора — слева от аргумента (со скобками или без) или справа от него, тут уж без выбора — скобок не будет. Так что у Куроша и Мальцева кроме логичности ещё и экономия.

Munin	Re: Умножение перестановок 23. 05.2019, 14:46
Заслуженный участник 30/01/06 72407	Я аж заинтересовался. Да, действительно, Курош использует именно такой порядок. Тогда стоит рекомендовать Aster1sk не читать учебник Куроша , поскольку иначе можно подхватить привычку, которая помешает дальше читать все остальные книги и общаться с окружающими. Сегодня общепринято работать с вектор-столбцами, и соответственно операторы на них умножаются слева (умножение на оператор тождественно умножению на матрицу). — 23.05.2019 14:48:04 — (Разумеется, легко можно получить и обратный порядок, просто транспонировав все формулы, но это требует всё-таки отдельных умственных усилий, а поначалу надо запоминать все формулы в одном стандартном порядке.)

Padawan	Re: Умножение перестановок 23.05.2019, 17:46
Заслуженный участник 13/12/05 4392	(Оффтоп) Munin в сообщении #1394770 писал(а): Тогда стоит рекомендовать Aster1sk не читать учебник Куроша Ну Вы даете! Вот Мальцев тоже такие обозначения использует, но, на мой взгляд, это один из лучших учебников по линейной алгебре (сам по нему учился на первом курсе). И небольшое расхождение в обозначениях — это мелочь на фоне остальных достоинств (не помню каких, помню, что очень понравился учебник). Про Куроша в части линейной алгебре ничего плохого не скажу, но и хорошего тоже нет. Учебник как учебник.

Munin	Re: Умножение перестановок 23.05.2019, 18:06
Заслуженный участник 30/01/06 72407	Есть Мальцев А. И. Основы линейной алгебры, а есть Мальцев И.А. Линейная алгебра.

Padawan	Re: Умножение перестановок 23.05.2019, 18:23
Заслуженный участник 13/12/05 4392	Munin в сообщении #1394821 писал(а): Мальцев А. И. Основы линейной алгебры

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 12 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения

Найти:

Умножение — перестановка — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Умножение перестановок определяется так же, как и для любых преобразований.  [1]

Операция умножения перестановок ассоциативна.  [2]

Действие умножения перестановок ассоциативно.  [3]

Алгоритм А производит умножение перестановок почти так же, как это обычно делает человек. Зачастую мы обнаруживаем, что задачи, которые необходимо решить с помощью компьютера, очень похожи на задачи, многие годы стоявшие перед людьми; поэтому освященные веками методы решения, предназначенные для использования такими же простыми смертными, как мы, также пригодны для реализации на машине.  [4]

При таком способе записи умножение перестановок несколько усложняется. В этом случае перестановку, записанную справа, тоже выполняют первой. Начинают с того, что в правой перестановке выбирают какой-нибудь исходный индекс. Его записывают как первый индекс в произведении. Затем отыскивают индекс, в который переходит исходный индекс в правой перестановке, среди индексов левой перестановки, а в произведении перестановок указывают на втором месте тот индекс, в который переходит найденный индекс левой перестановки после ее выполнения. Далее начинают с того индекса, который только что записан в произведении, и повторяют для него все указанные выше операции, пока в произведении не образуется цикл. При необходимости процесс повторяют со следующим исходным индексом до тех пор, пока произведение не включит всех индексов.  [5]

Согласно результатам § 5 умножение перестановок подчиняется следующим правилам.  [6]

Доказать, что при умножении перестановки на транспозицию четность числа инверсий ее второго ряда изменяется.  [7]

Согласно результатам § 5, умножение перестановок подчиняется следующим правилам.  [8]

Используя найденное соответствие, определим операцию умножения перестановок.  [9]

Множество / С образует группу относительно операции умножения перестановок. Она называется четверной группой Клейна.  [10]

Видно, что умножение матриц, как н умножение перестановок, или умножение элементов групп вращения, или точечных групп, не обязательно коммутативно. Однако умножение матриц ассоциативно.  [11]

Конечное множество А перестановок является группой относительно операции умножения перестановок, если произведение любой пары элементов из А принадлежит А.  [12]

Согласно определению, произвольная подгруппа Т группы Sn замкнута относительно операции умножения перестановок и относительно перехода к обратной перестановке. Тем самым, условие теоремы является необходимым. Покажем, что оно и достаточно. Условие I) означает, что для множества Т выполнено первое требование определения группы. Операция умножения перестановок из Т ассоциативна, поскольку умножение произвольных перестановок, а следовательно, и тех, которые принадлежат Т, подчиняется ассоциативному закону. Итак, для множества Т и операции умножения перестановок выполнено второе требование определения группы.  [13]

Некоторые множества перестановок из симметрической группы Sn сами могут образовывать группу относительно умножения перестановок.  [14]

Подмножество Т множества Sn называется подгруппой группы 5Л, если оно образует группу относительно операции умножения перестановок.  [15]

Страницы:      1    2

перестановок | Колледж Алгебра

Результаты обучения

• Используйте принцип сложения, чтобы определить общее количество вариантов для данного сценария.
• Используйте принцип умножения, чтобы найти количество перестановок n различных объектов.
• Найдите количество перестановок n различных объектов по формуле.
• Найдите количество перестановок n неразличимых объектов.

Использование принципа сложения

Компания, занимающаяся продажей индивидуальных чехлов, предлагает чехлы для планшетов и смартфонов. Есть 3 поддерживаемые модели планшетов и 5 поддерживаемых моделей смартфонов. Принцип сложения говорит нам, что мы можем добавить количество опций планшета к количеству опций смартфона, чтобы найти общее количество опций. По принципу сложения всего 8 вариантов.

Общее примечание: принцип сложения

В соответствии с принципом сложения , если одно событие может произойти [latex]m[/latex] способами, а второе событие без общих исходов может произойти [latex]n[ /latex] способами, то первое или второе событие может произойти [latex]m+n[/latex] способами.

Пример: использование принципа сложения

В меню ужина есть 2 варианта вегетарианских блюд и 5 вариантов мясных блюд. Каково общее количество вариантов входа?

Показать решение

Попробуйте

Студент покупает новый компьютер. Он выбирает между 3 настольными компьютерами и 4 портативными компьютерами. Каково общее количество опций компьютера?

Показать раствор

Использование принципа умножения

Принцип умножения применяется, когда мы делаем более одного выбора. Предположим, мы выбираем закуску, основное блюдо и десерт. Если в меню ужина с фиксированной ценой есть 2 варианта закусок, 3 варианта основных блюд и 2 варианта десерта, всего имеется 12 возможных вариантов по одному, как показано на древовидной диаграмме.

Возможные варианты:

1. суп, курица, торт
2. суп, курица, пудинг
3. суп, рыба, пирог
4. суп, рыба, пудинг
5. суп, бифштекс, торт
6. суп, стейк, пудинг
7. салат, курица, торт
8. салат, курица, пудинг
9. салат, рыба, торт
10. салат, рыба, пудинг
11. салат, стейк, торт
12. салат, стейк, пудинг

Мы также можем найти общее количество возможных обедов путем умножения.

Мы также можем заключить, что существует 12 возможных вариантов ужина, просто применив принцип умножения.

Общее примечание: принцип умножения

В соответствии с принципом умножения , если одно событие может произойти [latex]m[/latex] способами, а второе событие может произойти [latex]n[/latex] способами после того, как произошло первое событие, то два события могут произойти [latex]m\times n[/latex] способами. Это также известно как Фундаментальный Принцип Подсчета .

Пример: использование принципа умножения

Диана упаковала 2 юбки, 4 блузки и свитер для своей деловой поездки. Ей нужно будет выбрать юбку и блузку для каждого наряда и решить, надевать ли свитер. Используйте принцип умножения, чтобы найти общее количество возможных нарядов.

Показать решение

Попробуйте

Ресторан предлагает специальное предложение на завтрак, которое включает бутерброд, гарнир и напиток. Есть 3 вида сэндвичей на завтрак, 4 варианта гарнира и 5 вариантов напитков. Найдите общее количество возможных специальных завтраков.

Показать раствор

Принцип умножения можно использовать для решения различных типов задач. Один тип задач связан с размещением объектов по порядку. Мы собираем буквы в слова и цифры в числа, выстраиваемся в очередь для фотографий, украшаем комнаты и многое другое. Порядок объектов называется перестановка .

Нахождение количества перестановок

n различных объектов с использованием принципа умножения

Для решения задач перестановки часто полезно рисовать отрезки для каждого варианта. Это позволяет нам определить количество каждого варианта, чтобы мы могли умножить. Например, предположим, что у нас есть четыре картины, и мы хотим найти количество способов, которыми мы можем повесить три картины на стену по порядку. Мы можем нарисовать три линии, чтобы обозначить три места на стене.

Есть четыре варианта первого места, поэтому пишем 4 в первой строке.

После того, как первое место было занято, есть три варианта для второго места, поэтому мы пишем 3 во второй строке.

После того, как второе место занято, есть два варианта для третьего места, поэтому мы пишем 2 в третьей строке. Наконец, мы находим продукт.

Есть 24 возможных перестановки картин.

Как: Имея [latex]n[/latex] различные варианты, определите, сколько существует перестановок.

1. Определите, сколько вариантов есть для первой ситуации.
2. Определите, сколько вариантов осталось для второй ситуации.
3. Продолжайте, пока все ячейки не будут заполнены.
4. Перемножьте числа вместе.

Пример: определение количества перестановок с использованием принципа умножения

На соревнованиях по плаванию девять пловцов соревнуются в гонке.

1. Сколькими способами они могут поставить первое, второе и третье места?
2. Сколькими способами они могут занять первое, второе и третье места, если пловец по имени Ариэль выиграет первое место? (Предположим, что есть только один участник по имени Ариэль.)
3. Сколькими способами все девять пловцов могут выстроиться в очередь для фото?

Показать раствор

Попробуйте

Семья из пяти человек снимает портреты. Используя принцип умножения, найдите следующее.
Сколькими способами семья может выстроиться для портрета?

Показать раствор

Сколькими способами фотограф может выстроить в ряд 3 членов семьи?

Показать решение

Сколькими способами семья может выстроиться для портрета, если родители должны стоять на каждом конце?

Показать раствор

Нахождение количества перестановок

n различных объектов с помощью формулы

Для некоторых задач перестановки неудобно использовать принцип умножения, потому что нужно умножать очень много чисел. К счастью, мы можем решить эти проблемы с помощью формулы. Прежде чем мы изучим формулу, давайте рассмотрим два общепринятых обозначения перестановок. Если у нас есть набор объектов [latex]n[/latex] и мы хотим выбрать объекты [latex]r[/latex] из набора по порядку, мы пишем [latex]P\left(n,r\right) [/латекс]. Другой способ записать это — [латекс]{}_{n}{P}_{r}[/латекс], нотация, обычно встречающаяся на компьютерах и калькуляторах. Чтобы вычислить [латекс]P\влево(n,r\вправо)[/латекс], мы начнем с нахождения [латекс]n![/латекс], количества способов выстроить в линию все [латекс]n[/латекс] объекты. Затем мы делим на [латекс]\левый(n-r\правый)![/латекс], чтобы исключить элементы [латекс]\левый(n-r\правый)[/латекс], которые мы не хотим выстраивать в ряд.

Давайте посмотрим, как это работает, на простом примере. Представьте себе клуб из шести человек. Им нужно избрать президента, вице-президента и казначея. Шесть человек могут быть избраны президентом, любой из пяти оставшихся человек может быть избран вице-президентом, а любой из оставшихся четырех человек может быть избран казначеем. Это можно сделать несколькими способами: [латекс]6\умножить на 5\умножить на 4=120[/латекс]. Используя факториалы, мы получаем тот же результат.

[латекс]\dfrac{6!}{3!}=\dfrac{6\cdot 5\cdot 4\cdot 3!}{3!}=6\cdot 5\cdot 4=120[/latex]

Есть 120 способов выбрать 3 офицеров по порядку из клуба с 6 членами. Мы называем это перестановкой 6, взятых по 3 за раз. Общая формула выглядит следующим образом.

[латекс]P\left(n,r\right)=\dfrac{n!}{\left(n-r\right)!}[/latex]

Обратите внимание, что формула по-прежнему работает, если мы выбираем все [latex]n[/latex] объектов и расставить их по порядку. В этом случае мы будем делить на [латекс]\левый(n-n\правый)![/латекс] или [латекс]0![/латекс], который, как мы сказали ранее, равен 1. Таким образом, количество перестановок [ latex]n[/latex] объекты, взятые [latex]n[/latex] за раз, равны [latex]\frac{n!}{1}[/latex] или просто [latex]n!\text{.}[ /латекс]

A Общее примечание: формула для перестановок

n различных объектов

При заданных [latex]n[/latex] различных объектах количество способов выбрать [latex]r[/latex] объекты из набора по порядку равно

[латекс]P\left(n,r\right)=\dfrac{n!}{\left(n-r\right)!}[/latex]

Как: Учитывая задачу со словами, оценить возможные перестановки .

1. Определить [латекс]n[/латекс] по предоставленной информации.
2. Определить [латекс]r[/латекс] по предоставленной информации.
3. Замените в формуле [latex]n[/latex] и [latex]r[/latex] указанными значениями.
4. Оценить.

Пример: определение числа перестановок с помощью формулы

Профессор создает экзамен из 9 вопросов из банка тестов из 12 вопросов. Сколько способов она может выбрать и расположить вопросы?

Показать раствор

Вопросы и ответы

Могли бы мы решить  используя принцип умножения?

Да. Мы могли бы умножить [latex]15\cdot 14\cdot 13\cdot 12\cdot 11\cdot 10\cdot 9\cdot 8\cdot 7\cdot 6\cdot 5\cdot 4[/latex] , чтобы найти тот же ответ .

Попробуйте

В спектакле участвуют 7 актеров, готовящихся выйти на сцену. Используя формулу перестановки, найдите следующее.

Сколькими способами могут выстроиться 7 актеров?

Показать раствор

Сколькими способами можно выбрать 5 из 7 актеров, чтобы выстроиться в очередь?

Показать раствор

Нахождение числа перестановок n неразличимых объектов

Мы изучали перестановки, в которых все задействованные объекты были различными. Что произойдет, если некоторые из объектов неразличимы? Например, предположим, что есть лист из 12 наклеек. Если бы все наклейки были разными, было бы [латекс]12![/латекс] способов заказать наклейки. Однако 4 наклейки — это одинаковые звезды, а 3 — одинаковые луны. Поскольку все объекты не различны, многие из подсчитанных нами перестановок [latex]12![/latex] являются дубликатами. Общая формула для этой ситуации выглядит следующим образом.

[латекс]\dfrac{n!}{{r}_{1}!{r}_{2}!\dots {r}_{k}!}[/latex]

В этом примере мы нужно разделить на количество способов заказать 4 звезды и количество способов заказать 3 луны, чтобы найти количество уникальных перестановок наклеек. Есть [латекс]4![/латекс] способов упорядочить звезды и [латекс]3![/латекс] способы упорядочить луну.

[латекс]\dfrac{12!}{4!3!}=3\text{,}326\text{,}400[/latex]

Существует 3 326 400 способов заказать лист наклеек.

Общее примечание: формула для нахождения количества перестановок

n Неразличимые объекты

Если в наборе есть [latex]n[/latex] элементы и [latex]{r}_{1}[/latex] одинаковы, [latex]{r}_{ 2}[/latex] одинаковы, [latex]{r}_{3}[/latex] одинаковы и так далее до [latex]{r}_{k}[/latex], количество перестановок может можно найти по

[латекс]\dfrac{n!}{{r}_{1}!{r}_{2}!\dots {r}_{k}!}[/latex]

Пример: Нахождение количества перестановок

n неразличимых объектов

Найдите количество перестановок букв в слове DISTINCT.

Показать решение

Попробуйте

Найдите количество перестановок букв в слове ПЕРЕВОЗЧИК.

Показать раствор

Поддержите!

У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.

Улучшить эту страницуПодробнее

GMAT Перестановка и комбинация | Когда складывать и умножать

10 минут чтения

Вы всегда путаетесь, нужно ли добавлять или умножать случаи при решении вопросов GMAT о перестановке и комбинации? Часто ли вы получаете неправильные вопросы просто потому, что вы добавили объекты вместо их умножения? Если ответ на какой-либо из приведенных выше вопросов положительный, читайте дальше и узнайте, как избавиться от путаницы, используя «И» и «ИЛИ» в вопросах GMAT о перестановке и комбинации.

Прочитайте наши предыдущие 2 статьи из этой серии о перестановках и комбинациях GMAT:

• Разница между перестановкой и комбинацией | GMAT квант
• Перестановки и комбинации | Избегайте этих 3 ошибок | GMAT квант

В этой статье мы обсудим следующее –

• Когда добавлять – Использование ключевого слова «ИЛИ»
• Когда умножать – Использование ключевого слова «И»
• Что делать, когда «И» или Ключевое слово «ИЛИ» отсутствует
• Иллюстративные вопросы — перестановки и комбинации
• Выводы — решение вопросов GMAT о перестановках и комбинациях
• Вопросы перестановок и комбинаций для практики

Для любых стратегических советов для поступления на GMAT или MBA s, напишите нам по адресу acethegmat@e- gmat. com. Подпишитесь на бесплатную пробную версию  и получите неограниченный доступ к файлам концепций, сеансам в реальном времени и практическим вопросам.

Когда добавлять – использование ключевого слова «ИЛИ» (Концепция перестановки и комбинирования GMAT 1)

При решении любого вопроса о перестановке и комбинации в GMAT ученики чаще всего путаются: «Мне нужно сложить все падежи или мне нужно умножить все падежи?» Давайте поймем, что я пытаюсь сказать с помощью двух вопросов.

• У Эми 3 разных вида обуви и 2 разных вида сандалий. Всякий раз, когда она выходит на улицу, она любит надевать туфли или сандалии. Сколькими способами она может решить, что надеть?
• У Джо есть 3 вида рубашек и 2 вида брюк. Всякий раз, когда он выходит из дома, он любит надевать рубашку и брюки. Сколькими способами он может решить, что надеть?

Посмотрите на эти две ситуации. В обоих случаях цифры совпадают. Единственная разница в том, что Эми выберет либо туфли, либо сандалии, а во втором случае Джо выберет и рубашку, и брюки.

Давайте сначала сосредоточимся на ситуации с Эми, а затем перейдем к Джо.

Решение:

Предполагая, что у нее есть красные, зеленые и черные туфли, а также коричневые и синие сандалии, давайте перечислим все возможные варианты, которые у нее есть.

1. Она может носить красные туфли ИЛИ
2. Она может носить зеленые туфли ИЛИ
3. Она может носить черные туфли ИЛИ
4. Она может носить коричневые сандалии ИЛИ
5. Она может носить синие сандалии

Обратите внимание, что у нас есть использовал слово ИЛИ после каждого случая. Операция здесь подчеркивает тот факт, что у Эми нет возможности носить две разные вещи одновременно! Ей нужно выбрать только 1 из них.

Таким образом, ответ в данном случае будет 5.

Теперь давайте воспользуемся методом ключевого слова (ИЛИ), чтобы легко решить этот вопрос!

Подход ключевых слов e-GMAT к решению вопросов GMAT о перестановке и комбинации

Посмотрите на вопрос еще раз:

• У Эми есть 3 разных типа обуви и 2 разных типа сандалий. Всякий раз, когда она выходит на улицу, она любит надевать либо туфли, либо сандалии. Сколькими способами она может решить, что надеть?
• Обратите внимание на ИЛИ, которое я выделил в этом вопросе
• Всякий раз, когда вы читаете вопрос, ищите ключевое слово «ИЛИ» или «И». Ища ключевое слово, сосредоточьтесь на том, что нам нужно выяснить.
• В этом случае нам нужно найти количество способов, которыми она может носить туфли ИЛИ сандалии.
• Поскольку здесь используется слово ИЛИ, мы можем заключить, что оба события не могут произойти одновременно.

Под событием я подразумеваю, что Эми не может носить туфли и сандалии вместе.

Всякий раз, когда у нас есть ситуация, в которой два события не могут произойти одновременно, мы просто добавляем все случаи. Таким образом, в этом случае мы скажем:

Всего возможных случаев для Эми = Она будет носить туфли ИЛИ она будет носить сандалии

Количество способов, которыми она может носить обувь = 3

Количество способов, которыми она может носить сандалии = 2

Следовательно, всего возможных случаев = 3 ИЛИ 2 = 3 + 2 = 5

Вывод

• Всякий раз, когда мы сталкиваемся с ситуацией, включающей 2 или более событий, и появление одного события не влияет на появление другого события, т. е. оба события не могут произойти одновременно, то в этом случае мы просто сложим все события.
• Ищите слово ИЛИ в вопросе, выясняя, что вам нужно выяснить, и если ИЛИ присутствует, то это означает, что вам нужно сложить события

Гильермо набрал Q50 и получил признание от Уортонская школа. В своей удивительной истории успеха он рассказывает о том, как он управлял своей работой и подготовкой с помощью надежного учебного плана.

Дьявол кроется в деталях! Планирование мельчайших деталей вашего учебного расписания сделает вас на один шаг ближе к вашему целевому результату GMAT. Узнайте о других преимуществах четко определенный план обучения в этой статье.

Сэкономьте более 60 часов подготовки к GMAT, составив четкий план обучения всего за 3 шага:

Когда умножать — использование ключевого слова «И» (Концепция перестановки и комбинирования GMAT 2)

Теперь позвольте мы посмотрим на дело Джо.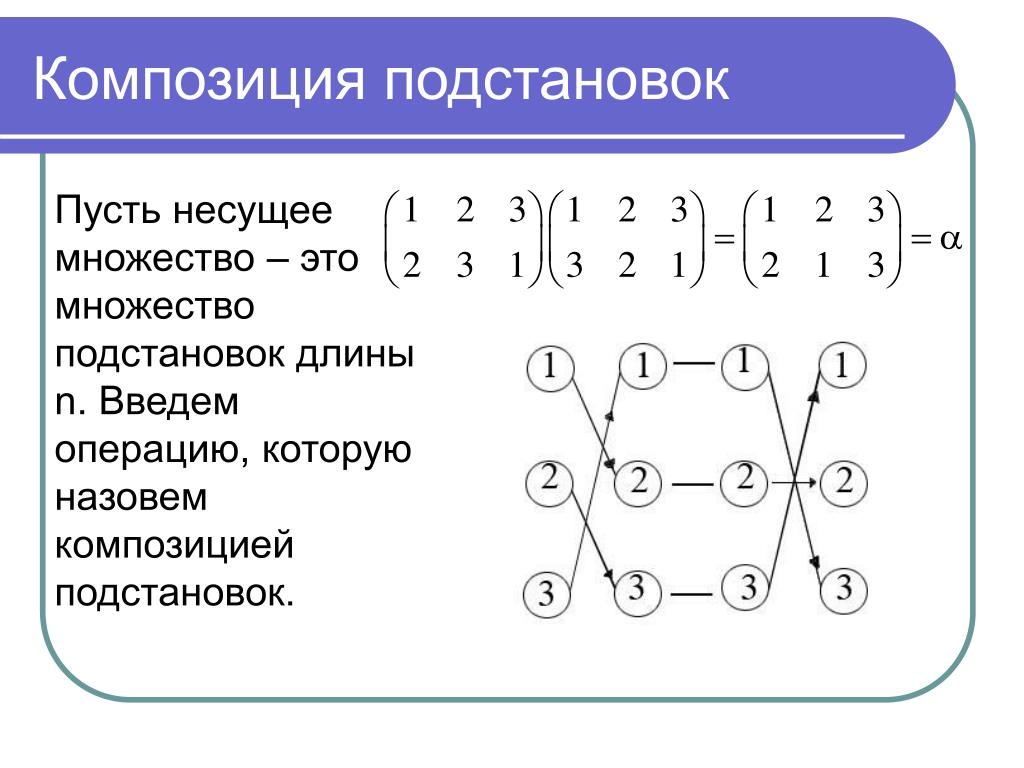

Предполагая, что у него есть красная, зеленая и черная рубашка, а также коричневые и синие брюки, перечислим все возможные варианты, которые у него есть.

1. Он может носить красную рубашку И коричневые брюки
2. Он может носить красную рубашку И синие брюки
3. Он может носить зеленую рубашку И коричневые брюки
4. Он может носить зеленую рубашку И синие брюки
5. Он может носить Черная рубашка И коричневые брюки
6. Он может носить черную рубашку И синие брюки

Обратите внимание, как я использовал слово И после каждого случая. И здесь подчеркивает тот факт, что Джо должен носить и рубашку, и брюки одновременно!

Мы не можем представить сценарий, в котором он носит только рубашку ИЛИ одни брюки.

Из приведенных выше случаев мы видим, что у него есть 6 различных вариантов ношения рубашки и брюк.

Теперь давайте воспользуемся подходом с ключевыми словами (И), чтобы легко решить этот вопрос!

Посмотрите еще раз на вопрос:

• У Джо есть 3 разных типа рубашек и 2 разных типа брюк. Всякий раз, когда он выходит, он любит носить рубашку И брюки. Сколькими способами он может решить, что надеть?
  • Обратите внимание на И, которое я выделил в этом вопросе.
• В этом случае также сосредоточьтесь на том, что нам нужно выяснить.
  • В этом случае нам нужно найти количество способов, которыми он может носить рубашку И брюки.
  • Поскольку здесь используется слово И, мы можем сделать вывод, что оба события должны произойти вместе.
• Это означает, что ему нужно носить рубашку и брюки вместе.

Всякий раз, когда у нас есть ситуация, в которой два события могут произойти одновременно, мы просто «перемножаем» все случаи.

Таким образом, в этом случае мы можем сказать:

Всего возможных случаев для Джо = Он будет носить рубашку И он будет носить брюки

Количество способов, которыми он может носить рубашку = 3 (красный ИЛИ зеленый ИЛИ черный)[ Ключевое слово ИЛИ: отсюда добавление]

Количество способов, которыми он может носить брюки = 2 (Синий ИЛИ Коричневый)

Таким образом, общее количество возможных случаев = 3 И 2 = 3 x 2 = 6

Вынос

• Помните всякий раз, когда мы сталкиваемся с ситуацией, включающей 2 или более событий и каждое событие может произойти одновременно , т. е. событие 1, событие 2, событие 3 и т. д., все может произойти одновременно.
  • Тогда, в таком случае, мы просто УМНОЖИМ все события!
• Ищите слово И в вопросе при выяснении того, что вам нужно узнать, а если И присутствует, то значит нужно умножить события.

Что делать, если ключевое слово «И» или «ИЛИ» отсутствует?

Теперь может возникнуть ситуация, когда в вопросе явно не упоминается слово «И» или «ИЛИ».

Что нам тогда делать? Давайте разберемся в этом с помощью 3 вопросов из перестановки и комбинации GMAT:

Пример 1

Сколькими способами на приведенной выше диаграмме можно добраться из пункта A в пункт D?

Решение

В вопросе и на диаграмме вы видите, что нет упоминания слов И или ИЛИ, так что же нам делать?

• Что ж, мы просто посмотрим на каждую конечную точку и выясним, что именно мы делаем.
• Итак, подумайте, сколькими способами мы можем добраться из точки А в точку Б?
  • Мы можем пойти в одну сторону, верно?
  • Итак, давайте просто напишем A => B: 1 способ
• Теперь, когда мы хотим перейти из B в C, мы можем пойти через X ИЛИ Y.
  • Обратите внимание, как мы используем здесь слово ИЛИ.
  • Мы знаем, что не можем одновременно пройти по обоим маршрутам. И, таким образом, нам нужно использовать слово ИЛИ здесь.

• Таким образом, общее количество способов добраться из B в C = 2
• B -> X -> C ИЛИ B-> Y-> C = 2 пути

• Наконец, мы хотим добраться до пункта назначения D; мы можем пойти через P OR Q
  • В этом случае мы также используем слово ИЛИ.
  • Следовательно, мы просто добавим все случаи и получим C->D = 2 способа.
• Итак, теперь мы знаем, что можем добраться из A в B одним способом, затем из B в C двумя способами и из C в D двумя способами.
  • Теперь спросите себя, должны ли мы складывать эти случаи или умножать?
  • Можем ли мы добраться из A в D, пройдя через A в B или B в C или C в D?
    • Нет, мы не можем, верно?
    • Нам нужно пройти из A в B, а затем из B в C и, наконец, из C в D, чтобы добраться до пункта назначения.

Таким образом, всего возможных случаев = 1 x 2 x 2 = 4 способа

Пример 2

Давайте немного усложним задачу и подумаем, как решить следующий вопрос.

Сколько трехзначных четных чисел можно составить, используя цифры 1,2,3, 4 и 5 без повторения цифр?

Решение

В этом вопросе не упоминаются ключевые слова «И» или «ИЛИ». Следовательно, мы попытаемся выяснить, о чем идет речь.

Любое трехзначное число может быть представлено как:

Нам нужно составить трехзначное число.

• А теперь подумайте, можем ли мы составить трехзначное число, просто заполнив разряд единиц ИЛИ разряд десятков ИЛИ разряд сотен?
  • Нет, мы не можем, верно?
• Таким образом, мы должны заполнить разряд единиц И разряд десятков И разряд сотен, чтобы получить трехзначное число.
• Обратите внимание, здесь мы использовали ключевое слово AND. Следовательно, мы перемножим все случаи

. Нам нужно составить трехзначное четное число.

• Следовательно, разряд единиц числа должен быть четным.
• Среди данных цифр: 1, 2, 3, 4 и 5 единицы могут быть заполнены 2 цифрами.
  • 2 ИЛИ 4.
  • Вы видите здесь использование ключевого слова ИЛИ?
• Следовательно, количество способов заполнить разряд единиц = 2

Теперь мы заполнили цифру единиц, чтобы позаботиться о четном характере числа.

• Осталось 4 цифры – 1 четная и 3 нечетные.
• Разряд десятков может быть заполнен 1 ИЛИ 3 ИЛИ 5 ИЛИ оставшимся числом между (2/4).
• Таким образом, всего способов заполнить разряд десятков = 4 способа.

Теперь нам нужно заполнить только последнюю цифру, а у нас осталось 3 цифры.

• Теперь вы можете представить себе, что мы будем использовать ИЛИ для выбора 1 из 3 цифр?
  • Мы можем выбрать 1-ю оставшуюся цифру ИЛИ 2-ю оставшуюся цифру ИЛИ 3-ю оставшуюся цифру
  • Здесь мы использовали ключевое слово ИЛИ. Следовательно, мы добавим случаи.

Таким образом, всего способов заполнить разряд десятков = 3 способа.

Как уже говорилось, нам нужно перемножить все эти 3 отдельных случая, чтобы получить общее количество способов, которыми можно составить число.

Отсюда общее количество путей = 3*4*2=24 пути

Пример 3

Давайте подойдем к последнему вопросу этой статьи.

Комитет из 2 членов должен быть сформирован из группы из 4 мужчин и 3 женщин членов клуба. Сколькими способами можно сформировать комитет?

Мы можем выбрать либо 2 мужчин, либо 2 женщин, либо 1 мужчину и 1 женщину для формирования комитета.

Найдите ключевые слова- AND и OR в приведенном выше утверждении.

Теперь это легко, мы знаем, что мы складываем количество случаев, когда у нас есть ИЛИ, и мы умножаем случаи, когда у нас есть И.

Всего способов= (способов выбрать 2 самцов) + (способов выбрать 2 самок) + (способов выбрать 1 самца) x (способов выбрать 1 самку)

Найдем, из скольких мы можем выбрать 2 самцов, 2 самки и 1 самец и 1 самка.

У нас есть 4 самца:

• Мы можем выбрать 2 самца из 4 самцов способами 4c2 и,
• Мы можем выбрать 1 самца из 4 самцов 4c1 способами.

У нас есть 3 самки:

• Мы можем выбрать 2 самок 3c2 способами и,
• Мы можем выбрать 1 самку 3c1 способами.

Таким образом, всего способов = 4c2+ 3c2+ 4c1*3c1    = 6+3+4*3=21

Таким образом, комитет может быть сформирован 21 способом .

Выводы – Как решать вопросы GMAT о перестановке и комбинации

1. Определенные ключевые слова могут быть X-фактором при решении вопросов PNC. Вы можете доверять им, но в то же время применять здравый смысл, чтобы убедиться, что вы на правильном пути.
2. Всегда пытайтесь выяснить после прочтения вопроса , являются ли события зависимыми или независимыми . Этот вывод поможет вам решить вопрос более эффективно.
3. В ситуации, когда задействовано ИЛИ , пожалуйста, Сложите все события .
4. В ситуации, когда задействованы И , УМНОЖИТЕ все события.
5. Всякий раз, когда ключевое слово недоступно , всегда старайтесь сначала записать все события , а затем решить, нужны ли они вам вместе или по отдельности.

Если вы планируете сдавать GMAT, мы можем помочь вам составить индивидуальный план обучения и предоставить доступ к качественному онлайн-контенту для подготовки.   Напишите нам по адресу [email protected]. Мы являемся самой популярной компанией по подготовке к GMAT на gmatclub – более 2400 отзывов  и являются единственной подготовительной компанией, набравшей более 700 баллов, чем любой другой клуб-партнер GMAT .   Почему бы вам не воспользоваться бесплатной пробной версией и не судить самостоятельно?

Принципы и вопросы GMAT по практике перестановки и комбинирования

Теперь давайте применим приведенные выше выводы к нескольким вопросам в стиле GMAT.