Интерактивировать: целочисленное умножение
Ученик: Итак, теперь, когда я понимаю сложение и вычитание, есть ли еще операции?
Наставник: Да, есть. Следующая операция называется умножение. Мы записываем задачи на умножение в виде a x b или a, умноженное на b. Для примера будем рассмотрим 5 x 3. Это означает, что 5 прибавляется к себе 3 раза (5 + 5 + 5), но лучше думать о том, что это означает 5 групп по 3 единицы в каждой. Следовательно, чтобы решить 5 х 3 вы бы подсчитали количество единиц в каждой группе.
Студент: Я чувствую себя немного смущенным.
Наставник: Хорошо, мы будем использовать пример, который вы можете визуализировать. Представьте 5 отдельных тарелок, в каждой по 3 кварталы на них. Сколько кварталов всего вместе?
Ученик: Ну, если на каждой из 5 тарелок по 3 четвертинки, то всего 15 четвертинок. все вместе. Итак, 5 х 3 = 15.
Ментор: Точно.
Ученик: Тогда на каждой из трех тарелок было бы 5 четвертей, то есть всего 15 четвертей. Так 3 x 5 = 15. Значит ли это, что умножение так же коммутативно, как и сложение?
Наставник: Да, умножение коммутативно. Для любых a и b а x b = b x a. Тоже ассоциативный. Если вы умножаете три числа, то (a x b) x c = a x (b x c). Теперь, что вы думаете произойдет в случае, если число было умножено на 0 или 1? Если у вас возникли проблемы, просто попробуйте визуализировать, что это значит.
Ученик: Хм, если бы у вас было любое количество тарелок p, на каждой из которых было бы 0 четвертаков, у вас было бы 0 четвертинок. вообще. Таким образом, любое число, умноженное на 0, равно 0. Теперь, если у вас есть 1 тарелка с q четвертями, то всего будет q кварталов. Таким образом, любое число, умноженное на 1, — это просто само число.
Наставник: Совершенно верно.
Вы очень хорошо это продумали.
Ученик: Это не так сложно, но как насчет отрицательных чисел? Я знаю, как их добавить, но как вы умножать отрицательные числа?
Наставник: Ну, сначала я должен немного подробнее объяснить, что такое отрицательное число. Несмотря на то, отрицательные числа меньше нуля, это не значит, что они меньше нуля. А отрицательное число есть просто отрицание положительного числа. Например, что будет, если вы проехали одну милю на восток, а затем вернулись на одну милю на запад?
Ученик: Вы окажетесь там, где начали.
Наставник: Именно так, одна миля, которую вы прошли на запад, свела на нет милю, которую вы прошли на восток. Другой способ
выразить свое движение на запад означало бы сказать, что вы путешествовали -(одна миля на восток), или минус одна миля
восток. Таким образом, мы можем думать о знаке минус как об операторе, как и знак умножения.
оператор.
Ученик: Куда именно все это нас ведет?
Наставник: Именно там, где мы хотим быть. Помните, что положительная единица плюс отрицательная единица всегда равен нулю, таким образом, положительное и отрицательное число находятся в обратной зависимости. Этот означает, что отрицание положительного есть отрицательное, а отрицательное отрицательного есть положительный. Зная это, теперь мы можем перейти к умножению на отрицательные числа.
Основываясь на определении, которое я дал вам ранее, как вы думаете, чему равно 2 x (-3)?
Ученик: Ну, 2 x (-3) будет 2 группами, каждая по (-3) юнитов, так что будет (-6) юнитов.
Наставник: Хорошо, это было сложно, но в основном просто. Как насчет этого: сколько будет (-2) x 3?
Ученик: Это будет (-2) группы по 3 юнита в каждой. Но как считать отрицательные группы?
Наставник: Во-первых, позвольте мне перефразировать это как минус 2 группы, по 3 единицы в каждой.
Теперь отрицательная группа
просто группа, которая отрицала бы положительную группу. Какая группа будет отрицать группу
3 единицы?
Ученик: Группа из 3 юнитов будет сведена на нет группой из (-3) юнитов, верно?
Наставник: Да, поэтому (-2) х 3 = 2 х (-3), что, как мы уже знаем, равно (-6) единицам. Что теперь делать вы думаете, что (-2) x (-3) равно?
Ученик: Ну, это будут отрицательные 2 группы, по 3 отрицательных единицы в каждой. Так что мне нужно знать, что вид группы будет отрицать группу из 3 отрицательных единиц. . . группа из 3 положительных единиц! Так (-2) х (-3) = 2 х 3 = 6. Думаю, это правильно.
Наставник: Совершенно верно. Из этих нескольких примеров вы можете видеть, что отрицательное число умножение положительного числа даст вам отрицательное число, а умножение отрицательного числа на отрицательное число даст вам положительное число.
Десятичные и целые числа.
Свойства целых чиселТе же знакомые свойства целых чисел применимы и к целым числам. Если вы как и многие студенты, всякий раз, когда вы видите одно из этих «свойств», вы стонете внутри и думаете: «Зачем мне учиться всему этому?» Хотите верьте, хотите нет, но свойства чисел придумали не злые математики пытать студентов-математиков! Это основные правила нашей системы математики, и вы будете использовать их всю оставшуюся жизнь. Очень важно, чтобы ты понять, как применять каждый из них, когда вы решаете математические задачи. Когда ты доберитесь до алгебры, вы будете использовать эти свойства снова и снова! Давайте рассмотрим каждый из них подробно и простым языком.
| Коммутативное свойство дополнения | |
| Переместительное свойство умножения | |
| Ассоциативное свойство дополнения | |
| Ассоциативное свойство умножения | |
| Распределительное имущество |
Переместительное свойство сложения
Переместительное свойство
свойство сложения говорит о том, что мы можем складывать числа в любом порядке.
-2 + 4 = 4 + (-2)
Коммутативный
свойство умножения
Переместительное свойство умножения очень похоже. Он говорит, что мы
может умножать числа в любом порядке без изменения результата.
пример показывает нам, что «отрицательное два раза положительное четыре» является
то же, что «положительное четыре раза отрицательное два».
-2(4) = 4(-2)
Ассоциативный
имущество дополнения
Ассоциативное свойство сложения говорит нам, что мы можем группировать числа в
сумму любым способом, который мы хотим, и все равно получим тот же ответ. Вы можете вспомнить
ассоциативное свойство, думая о двух числах, связанных друг с другом,
а затем один уходит, чтобы ассоциироваться с другим номером.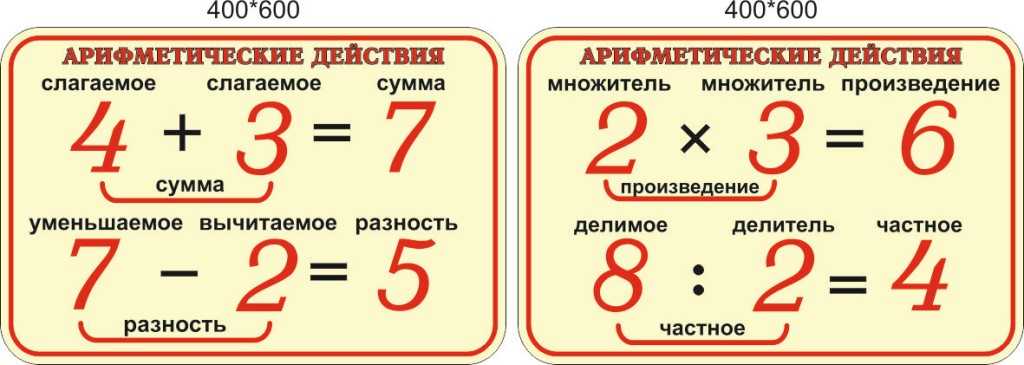
Пример показывает нам, что мы можем добавить «отрицательные два и положительные четыре» вместе, а затем добавьте эту сумму к положительным трем, чтобы получить окончательный ответ, или мы можем сначала сложить вместе «положительные четыре и положительные три» а затем добавьте эту сумму к отрицательным двум, чтобы получить окончательный ответ. Ответ будет одинаковым независимо от того, как мы это делаем.
(-2 + 4) + 3 = -2 + (4 + 3)
Ассоциативный
свойство умножения
Ассоциативное свойство умножения говорит нам, что мы можем группировать
номера в продукте любым способом, который мы хотим, и все равно получим тот же ответ.
Пример
показывает нам, что мы можем либо умножать «отрицательные два и положительные четыре»
вместе, а затем умножьте это произведение на положительное три, чтобы получить окончательный результат.
ответ, или мы можем перемножить «положительные четыре и положительные три» вместе
сначала, а затем умножьте это произведение на минус два, чтобы получить окончательный ответ.
-2(4) x 3 = -2(4 x 3)
Распределительный
имущество
Распределительное свойство вступает в игру, когда выражение, включающее сложение
затем умножается на что-то. Это говорит нам, что мы можем сначала добавить, а затем
умножить или сначала умножить, а потом добавить. В любом случае умножение
«распределено» по всем терминам в круглых скобках.
В примере мы можем сначала добавить числа в скобках — 4+3 — а затем умножьте результат на -2 ; или мы можем умножить -2 и каждый термин отдельно, а затем добавить два продукта вместе. Ответ одинаково в обоих случаях.
-2(4 + 3) = (-2 х 4) + (-2 х 3)
Смотреть вне!
Вычитание не является ни коммутативным, ни ассоциативным.
Подразделение
ни коммутативный, ни ассоциативный.