Значение синуса косинуса и тангенса для углов: Найдите значения синуса. Косинуса и тангенса угла, равного 135 градусов

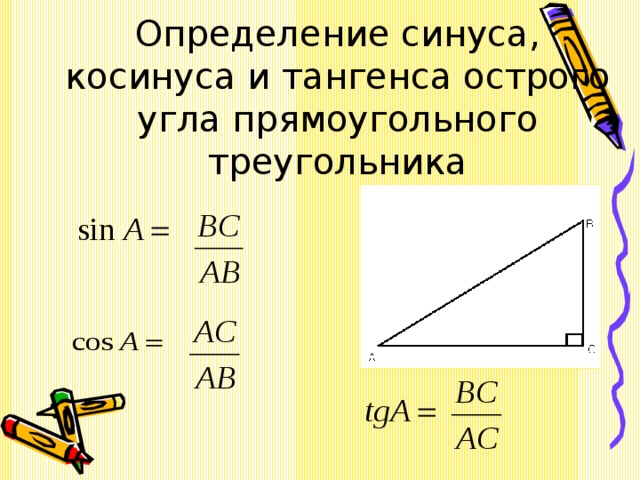
Конспект урока геометрии в 8 классе Значение синуса, косинуса, тангенса для углов 30, 45 и 60 градусов.

Урок по геометрии в 8 классе по теме

«Значения синуса, косинуса и тангенсадля углов 30

Комбинированный урок.

Продолжительность: 1 урок, 45 минут.

Цель урока:

Вывести значения синуса, косинуса и тангенса для углов 30⁰, 45⁰ и 60⁰. Формировать навыки решения прямоугольных треугольников, используя синус, косинус и тангенс острого угла, в ходе решения задач.

Задачи урока:

повторить понятия синуса, косинуса, тангенса острого угла прямоугольного треугольника;

повторить теорему Пифагора;

вычислить значения синуса, косинуса и тангенса для углов 30⁰, 45⁰ и 60⁰ в ходе решения задач;

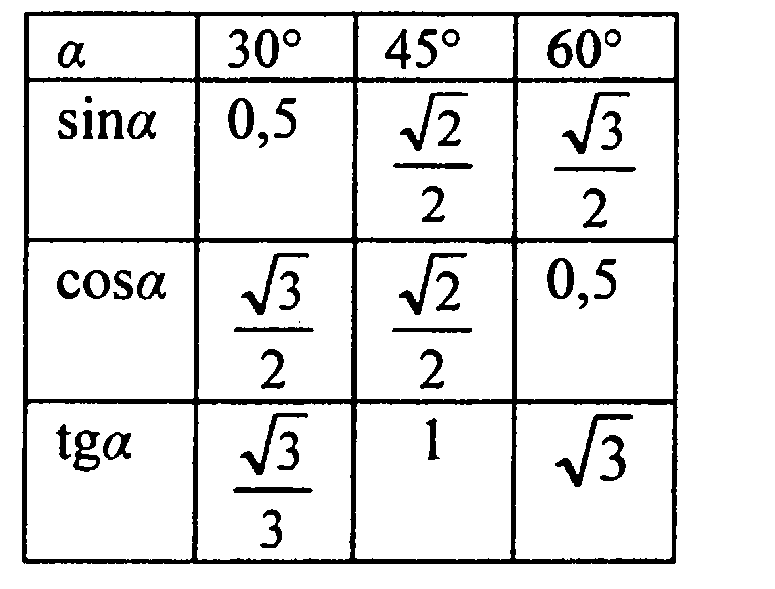
составить таблицу значений синуса, косинуса и тангенса для углов 30⁰, 45⁰ и 60⁰;

решать задачи на прямоугольный треугольник, используя понятия синус, косинус и тангенс острого угла;

развивать логическое мышление, взаимооценку, самооценку и самоконтроль учащихся.

Оборудование: компьютер.

Демонстрации: презентация MicrosoftPowerPoint 2010.

Ход урока:

I. Организационный момент.

Учащиеся готовы к уроку. Начинаем наш урок с проверки домашнего задания.

II. Проверка домашнего задания.

Учащимся задано на дом следующее задание: № 591 (в), тест, выучить определения синуса, косинуса и тангенса острого угла прямоугольного треугольника.

Учащиеся обмениваются своими тетрадями с соседями по парте и проверяют с помощью компьютера домашнее задание (слайды презентации № 4, 5), оценивают работу соседа, ставят оценку за работу.

III. Устная работа.

Учитель актуализирует знания учащихся в ходе устной работы по домашнему заданию (слайд презентации № 6).

Учащиеся отвечают на предложенные вопросы и решают задачи на готовых чертежах (слайды презентации № 7, 9). Если возникают трудности с решением предложенных заданий, то учащиеся устно разбирают решение задач с помощью компьютера (слайды презентации № 8, 10).

IV. Сообщение темы и целей урока.

Учитель сообщает тему урока, ученики записывают ее в тетрадь. Учитель сообщает цели урока.

V. Введение нового материала.

Учитель: «Сегодня на уроке мы вычислим значение синуса, косинуса и тангенса для углов 30⁰, 45⁰ и 60⁰ в процессе решения задач».

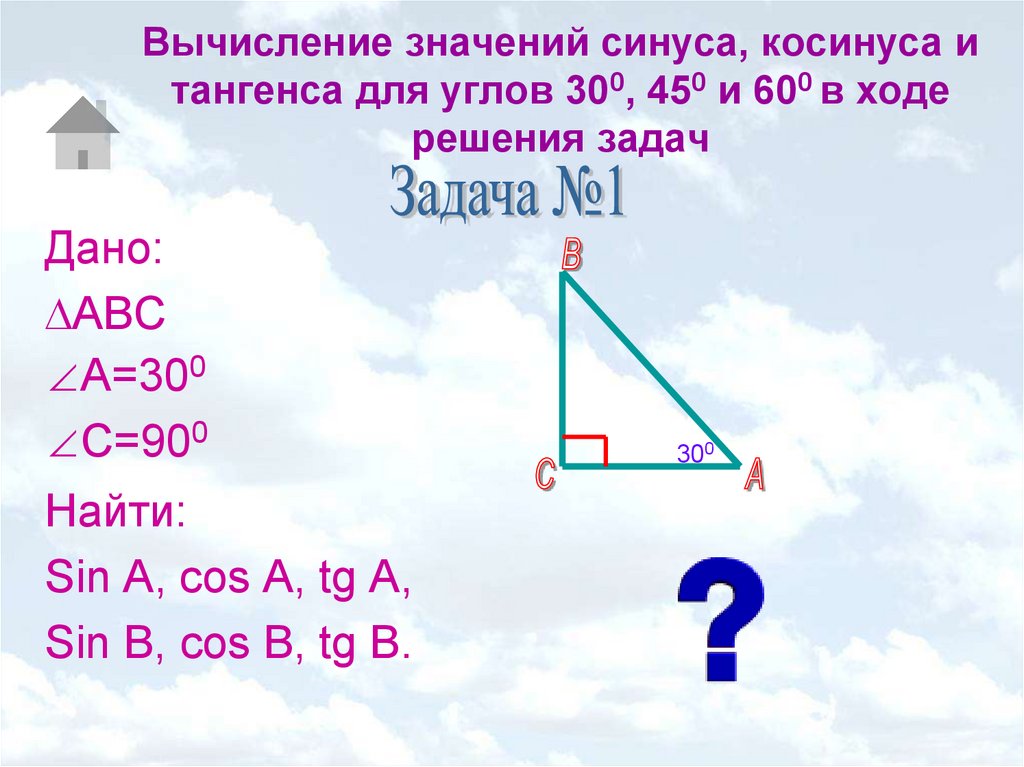
Учитель предлагает учащимся решить первую задачу (слайд презентации № 11).

Ученики делают чертеж в тетради, следуя за рекомендацией учителя принимают сторону ВС за х, решают задачу.

Учащиеся сверяют своё решение с решением задачи № 1 (слайд презентации № 12).

Если учащиеся допустили ошибки, то исправляют их.

Учитель предлагает учащимся решить вторую задачу самостоятельно (слайд презентации № 13). Учащиеся решают задачу, сверяют своё решение с образцом (слайд презентации № 14).

Учащиеся заполняют таблицу значений синуса, косинуса и тангенса для углов 30⁰, 45⁰ и 60⁰.

Выполнение учащимися физкультминутки для улучшения мозгового кровообращения:

Исходное положение (далее — и.п.) — сидя на стуле. 1 — 2 — отвести голову назад и плавно наклонить назад, 3 — 4 — голову наклонить вперед, плечи не поднимать. Повторить 4 — 6 раз. Темп медленный.

И физкультминутки для глаз: Крепко зажмурить глаза (считать до 3, открыть их и посмотреть вдаль (считать до 5). Повторять 4 — 5 раз.

VI. Решение упражнений.

Учащиеся самостоятельно решают задачи 3 и 4. Решение и ответы к заданиям сверяют с образцом с помощью компьютера.

Задача № 3.

Впрямоугольной трапеции основания равны 6 и 11, меньшая боковая сторона равна 4. Найдите синус, косинус и тангенс острого угла трапеции.

Задача № 4.

Впрямоугольном треугольнике гипотенуза равна с, а один из острых углов равен a. Выразите второй острый угол и катеты через с и a и найдите их значения, если с=24, а a=60⁰.

VII. Итоги урока.

Учитель в ходе устного опроса подводит итоги урока (слайды презентации № 20, 21).

Учащиеся устно отвечают на вопросы.

Учитель задает учащимся следующие вопросы:

— С каким настроением Вы работали на уроке?

— Устали ли Вы?

— Какую бы отметку Вы бы поставили себе за этот урок?

VIII. Выставление оценок за урок с комментарием учителя.

IХ. Домашнее задание:

Выучить значения синуса, косинуса и тангенса для углов 30⁰, 45⁰ и 60⁰;

№ 595; № 597; № 598(б) (слайд презентации № 22).

Литература:

Атанасян Л. С., Бутузов В. Ф. и др. Геометрия: учебник для 7-9 кл. общеобразовательных учреждений.- М.: Просвещение, 2014.

Гаврилова Н. Ф. Поурочные разработки по геометрии: 8 класс. – М., ВАКО, 2013.

4

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/302389-konspekt-uroka-geometrii-v-8-klasse-znachenie

8 класс.

Синус, ко­си­нус и тан­генс остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка

На этом уроке мы по­зна­ко­мим­ся с си­ну­сом, ко­си­ну­сом и тан­ген­сом – три­го­но­мет­ри­че­ски­ми функ­ци­я­ми, свя­зы­ва­ю­щи­ми ост­рый угол пря­мо­уголь­но­го тре­уголь­ни­ка с ка­те­та­ми и ги­по­те­ну­зой этого тре­уголь­ни­ка. Это очень важ­ные по­ня­тия, ко­то­рые будут встре­чать­ся не толь­ко в гео­мет­рии, но и в ал­геб­ре, фи­зи­ке и во мно­гих дру­гих на­у­ках.

На­пом­ним ос­нов­ные све­де­ния о пря­мо­уголь­ном тре­уголь­ни­ке (см. Рис. 1).

Рис. 1

;

 – ка­те­ты;  – ги­по­те­ну­за.

Также в пря­мо­уголь­ном тре­уголь­ни­ке сумма ост­рых углов равна : .

Для пря­мо­уголь­но­го тре­уголь­ни­ка также верна тео­ре­ма Пи­фа­го­ра: .

Вве­дём те­перь по­ня­тие си­ну­са, ко­си­ну­са и тан­ген­са остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка.

Опре­де­ле­ние

Си­ну­сом остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка на­зы­ва­ет­ся от­но­ше­ние про­ти­во­ле­жа­ще­го этому углу ка­те­та к ги­по­те­ну­зе.

, .

Опре­де­ле­ние

Ко­си­ну­сом остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка на­зы­ва­ет­ся от­но­ше­ние при­ле­жа­ще­го к этому углу ка­те­та к ги­по­те­ну­зе.

, .

Опре­де­ле­ние

Тан­ген­сом остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка на­зы­ва­ет­ся от­но­ше­ние про­ти­во­ле­жа­ще­го этому углу ка­те­та к при­ле­жа­ще­му ка­те­ту.

, .

С по­мо­щью вве­дён­ных по­ня­тий можно на­хо­дить ка­те­ты или ги­по­те­ну­зу.

На­при­мер, из фор­му­лы: . Ана­ло­гич­но: .

Также можно по­лу­чить фор­му­лу для связи длин двух ка­те­тов: .

При ре­ше­нии задач очень важно знать со­от­но­ше­ния между си­ну­сом, ко­си­ну­сом и тан­ген­сом остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка.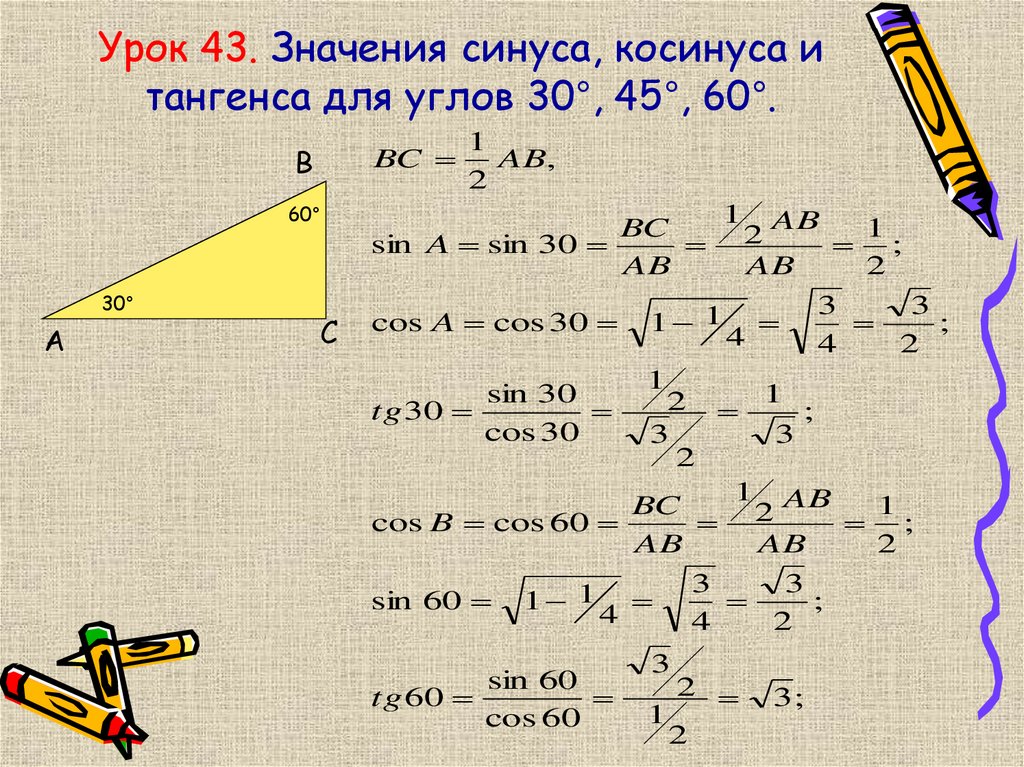

Рас­смот­рим сле­ду­ю­щие две фор­му­лы: . Так как сумма ост­рых углов пря­мо­уголь­но­го тре­уголь­ни­ка равна , то фор­му­ла при­об­ре­та­ет сле­ду­ю­щий вид:

Ана­ло­гич­но по­лу­ча­ем: . Так как сумма ост­рых углов пря­мо­уголь­но­го тре­уголь­ни­ка равна , то фор­му­ла при­об­ре­та­ет сле­ду­ю­щий вид:

До­ка­жем те­перь важ­ную фор­му­лу, свя­зы­ва­ю­щую тан­генс с си­ну­сом и ко­си­ну­сом:

До­ка­за­тель­ство

За­пи­шем опре­де­ле­ние си­ну­са и ко­си­ну­са остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка: , . Тогда: . До­ка­за­но.

Ана­ло­гич­но: .

Рас­смот­рим сле­ду­ю­щую важ­ную за­да­чу.

За­да­ча

Даны пря­мо­уголь­ные тре­уголь­ни­ки . Кроме того, .

До­ка­зать:.

До­ка­за­тель­ство

 (так как оба тре­уголь­ни­ка пря­мо­уголь­ные с рав­ны­ми ост­ры­ми уг­ла­ми). Зна­чит, вы­пол­ня­ет­ся сле­ду­ю­щее со­от­но­ше­ние: .

От­сю­да по­лу­ча­ем: .

.

.

До­ка­за­но.

Вывод: синус, ко­си­нус и тан­генс не за­ви­сят от тре­уголь­ни­ка, а за­ви­сят толь­ко от угла.

Сфор­му­ли­ру­ем и до­ка­жем одну из важ­ней­ших тео­рем, свя­зы­ва­ю­щих синус и ко­си­нус остро­го угла пря­мо­уголь­но­го тре­уголь­ни­ка, – ос­нов­ное три­го­но­мет­ри­че­ское тож­де­ство.

Ос­нов­ное три­го­но­мет­ри­че­ское тож­де­ство: .

При­ме­ча­ние: 

До­ка­за­тель­ство

, тогда:  (при до­ка­за­тель­стве мы поль­зо­ва­лись тео­ре­мой Пи­фа­го­ра: ).

До­ка­за­но.

Рас­смот­рим при­мер, ил­лю­стри­ру­ю­щий связь три­го­но­мет­ри­че­ских функ­ций.

Дано:  – пря­мо­уголь­ный (), .

Найти: 

Ре­ше­ние

Вос­поль­зу­ем­ся ос­нов­ным три­го­но­мет­ри­че­ским тож­де­ством: . Под­ста­вим в него из­вест­ное нам зна­че­ние си­ну­са: . От­сю­да: . Так как ко­си­нус, по опре­де­ле­нию, – это от­но­ше­ние ка­те­та к ги­по­те­ну­зе, то он может быть толь­ко по­ло­жи­тель­ным, по­это­му: .

Най­дём те­перь тан­генс угла, поль­зу­ясь фор­му­лой: .

Ответ: .

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/8-klass/podobnye-treugolniki/sinus-kosinus-i-tangens-ostrogo-ugla-pryamougolnogo-treugolnika

http://www.youtube.com/watch?v=CvQYL11ce4c

http://www.funlib.ru/cimg/2014/102107/3325015

http://edu.convdocs.org/tw_files2/urls_25/7/d-6526/img4.jpg

http://player.myshared.ru/771881/data/images/img6.jpg

Нахождение точного значения синуса, косинуса и тангенса углов

1. Математика
2. Геометрия и топология
3. Аналитическая геометрия
4. Тригонометрия
5. 68277

Не то, что вы ищете? Найдите наши решения ИЛИ задайте свой собственный вопрос.

Этот контент был скопирован с сайта BrainMass.com. Просмотрите оригинал и получите готовое решение здесь!

1. Найдите точное значение синуса, косинуса и тангенса угла. 11 пирог/12

2. Найдите все решения уравнения в интервале [0, 2pie).
Sin(x-5pie/6)-sin(x+ 5pie/6) =1

3. Найдите точное значение sin2x, используя формулу двойного угла. Пожалуйста, помогите объяснить использование формулы двойного угла.
Sin x=1/7, 0

4. Учитывая cos theta = 4/9, где 3pie/2 <или равно theta <или равно 2pie.

5. Выразите 2sin3xcos6x в виде суммы, содержащей только синусы или косинусы.

6. Выразите cos7x-cos5x как произведение, содержащее только синусы и/или косинусы. 92 х-18 = 0

10. Большой столб высотой 175 футов. В определенный день в полдень он отбрасывает 198-футовую тень. Каков угол возвышения солнца?

Вложения

• Trig help.doc

Предварительный просмотр решения

Ниже приведена текстовая часть решения. Полное решение смотрите в прикрепленном файле. Уравнения, диаграммы, графики и специальные символы будут отображаться здесь некорректно. Спасибо.
=========================================

Вам необходимо обновить все ваши идентификаторы триггеров. Есть много веб-сайтов, которые говорят об этом. Я выделил триггерные тождества, которые использовал в каждой задаче.

1. Найдите точное значение синуса, косинуса и тангенса угла. 11шт/12

Использование: sin x = sin (p-x)

Грех (11p/12) = sin(p-11p/12) = sin(p/12)

Поскольку мы знаем, что такое sin pi/6, использование следующего тождества имеет смысл.

Использование: cos 2x = 1 — 2sin2 x è sinx = sqrt {½ (1-cos2x)}

Sin (11p/12) = sin(p-11p/12) = sin(p/12) = sqrt {½ (1-cos(p/6)}= Ö (1/2 (1-Ö3/2) )
Sin (11p/12 = Ö(2-Ö3)/2 Это точное значение.

Вычисляем Sin (11p/12) = 0,258819

2. Найдите все решения уравнения в интервале [0, 2pie).
Sin(x-5pie/6)-sin(x+ 5pie/6) =1

Использовать тождество триггера: sin C — sin D = 2 cos (C+D)/2 * sin (C-D)/2

Sin(x-5pie/6)-sin(x+ 5pie/6) = 2 cos x * sin -(5pi/6) = 1

2 cos x * sin -(5pi/6) = 1 è cos x * sin 5pi/6 = — 1/2,
мы знаем sin 5pi/6 = sin pi — 5pi/6 = sin pi/6 = ½

cos x * 1/2 = -1/2, è cos x = -1

Между 0 и 2pi у нас есть только один . ..

Резюме решения

Я предоставил пошаговые решения на все вопросы. Каждое используемое тригонометрическое тождество было напечатано. Это очень хороший вопрос и ответ на решение триггерных тождеств. Также отличные практические вопросы.

РЕКЛАМА

Cos(), Sin(), Tan(), ACos(), ASin(), ATan(), ATn2(), DToR(), RToD(), Pi()

Cos(), Sin(), Tan(), ACos(), ASin(), ATan(), ATn2(), DToR(), RToD(), Pi()

Синус, синус,
везде есть синус,
ломаю пейзаж,
сношу мне мозг
— с извинениями перед Five Man Electric Band

nRetValue = COS(nAngle)
nRetValue = SIN(nAngle)
nRetValue = TAN(nAngle)
 

  Пример 
 

? COS(PI()/3) && возвращает 0,50
? SIN(PI()/3) && возвращает 0,87
? TAN(PI()/3) && возвращает 1,73
 

  Использование 
 

nRetValue = ACOS(nTrigValue)
nRetValue = ASIN (nTrigValue)
nRetValue = ATAN (nTrigValue)
nRetValue = ATN2(nXValue, nYValue)
 

? ACOS(.5) && возвращает 1,047 или PI/3
 

nAngleInRadians = DTOR( nAngleInDegrees)
nAngleInDegrees = RTOD ( nAngleInRadians )