Математика — страница 2
Сейчас читают:
- Как оформлять реферат правильно — образец
- Оформление курсовой работы по ГОСТу: образец
- Как оформить титульный лист реферата?
- Оформление рисунков в дипломе (примеры)
- Правила оформления приложений в курсовой работе
- Оформление списка литературы по ГОСТу 2020, 2021 образец
- Оформление диплома в 2022 году
- Оформление курсовой работы по госту 2020, 2021
Не успеваете написать работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Подтверждение
Ваша заявка принята.
Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.
Ошибка оформления заказа
Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.
Математика
12.11.21
6 мин.
Обыкновенные правильные дроби, определение и их примеры
При изучении обыкновенных дробных выражений ученики сталкиваются с проблемой идентификации неправильной и правильной дробей в примерах при решении задач. Но это не особо влияет на результат вычислений, однако особенности этих двух числовых тождеств должен знать каждый.
Читать полностью
Математика
12.11.21
6 мин.
Правило и примеры признака делимости на 11
В школе в 5 классе изучается подробно признак делимости на 11. Правила и примеры основаны на определенной методике, разработанной специалистами и позволяющей за короткое время освоить эту тему. Обучение начинается с изучения делителей, находящихся в диапазоне от двух до десяти включительно. Математики рекомендуют на начальном этапе разобраться в теоретических основах, а затем переходить к практике. Общие сведения Любая арифметическая операция…
Читать полностью
Математика
12.11.21
6 мин.
Основные правила и свойства вычитания для 5 класса
Учащиеся средних образовательных школ изучают в 5 классе свойства вычитания и сложения.
Они применяются для решения примеров, ускорения вычислений в устной форме и т. д. В высших учебных заведениях правила используются для упрощения выражений, нахождения корней дифференциальных уравнений и пределов, а также для выполнения других операций.
Общая информация
Вычитание — операция уменьшения числа на…
Читать полностью
Математика
12.11.21
6 мин.
Взаимно обратные числа и их объяснение в математике 6 класса
При сокращении выражений дробного типа ученики иногда сталкиваются с понятием «взаимно обратных чисел». В математике 6 класса эта тема рассматривается подробнее, поскольку количество задач на упрощение тождеств увеличивается по следующим причинам, а именно: доказательства теорем и различных соотношений, выведение формул и выполнение операций вычисления. Специалисты сначала рекомендуют изучить теорию, а затем переходить к практике. Общие сведения Одним из…
Читать полностью
Математика
12.
11.21
12 мин.
Понятие дроби в математике 5 класса и основные ее свойства
Не всегда числа выражаются целыми величинами. Понятие дроби в математике 5 класса рассматривается более подробно, поскольку каждый ученик должен понимать основные принципы работы с числами любого формата. Это позволит грамотно выполнять вычисления, используя свойства дробных выражений. Специалисты рекомендуют изучить теорию, а затем перейти к ее практическому применению. Общие сведения Числа делятся на целые и дробные.…
Читать полностью
Математика
12.11.21
12 мин.
Способ перевести десятичную дробь в обыкновенную: правила
При изучении математики важно не только знать, как перевести десятичную дробь в обыкновенную, но и уметь применять полученные знания на практике. Обучают этой науке в четвертом классе средней школы. Преобразование выражений позволяет упрощать различные задачи, делая решение простым и понятным.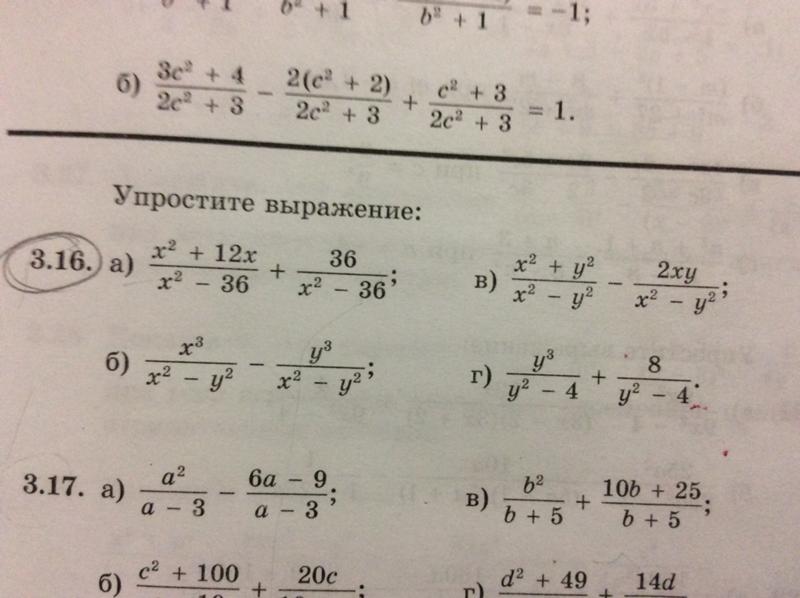
Сама операция несложная, но требует понимания смысла использования дробных чисел. Лишь в этом случае действие можно будет довести до автоматизма и выполнять устно.
Читать полностью
Математика
12.11.21
13 мин.
Примеры смешанных дробей в математике для 5 класса
Ученики изучают на уроках математики в 5 классе смешанные дроби и примеры работы с ними. Однако не всегда усваивают теоретический материал, а на практике не могут решать задачи с обыкновенными дробными величинами. Специалисты нашли выход с этой ситуации, предложив специальные алгоритмы для оптимизации вычислений без ошибок. Для их изучения необходимы определенные базовые знания. Общие сведения…
Читать полностью
Математика
12.11.21
12 мин.
Примеры умножения обыкновенных дробей (математика, 6 класс)
Расчеты выполняются не только с натуральными целыми числами, но и с дробными.
Читать полностью
Математика
12.11.21
13 мин.
Деление с остатком для примеров в математике 5 класса
Изучение арифметических операций подробно начинается на уроках математики в 5 классе на примерах, а деление с остатком не является исключением. Некоторые ученики не представляют, какой важной для дальнейшего изучения дисциплин с физико-математическим уклоном считается эта тема. Однако сначала требуется рассмотреть теорию, а затем переходить к практическому применению знаний, полученных в процессе обучения.
Читать полностью
Математика
12.11.21
13 мин.
Правила по сложению и вычитанию дробей (математика, 5 класс)
После рассмотрения натуральных чисел и действий над ними переходят к изучению правил сложения и вычитания дробей. На математике в 5 классе этой теме уделяется несколько уроков. Преподаватель не только даёт алгоритм вычислений, но и учит школьников применять знания на практике. Научиться правильно и быстро выполнять эти алгебраические действия важно, так как в дальнейшем это умение приходиться использовать практически при изучении любой науки.
Читать полностью
Математика
12.11.21
13 мин.
Правила сравнения обыкновенных дробей и пример решения задач
В пятом классе изучаются правила сравнения обыкновенных дробей. Однако некоторые ученики не могут понять эту тему, хотя она, на первый взгляд, кажется очень простой.
Не всегда получается сравнить оба дробных выражения, так как школьная методика преподносится не совсем верно. Чтобы исправить этот недочет, специалисты разработали универсальный алгоритм, который будет понятен каждому.
Общие сведения
Для применения правил сравнения дробей…
Читать полностью
Математика
12.11.21
14 мин.
Нахождение простых и составных чисел (математика, 6 класс)
Выявление принадлежности величины в математике (6 класс) к простому или составному числу — задача непростая, когда под рукой нет специальных таблиц или средств вычислительной техники (компьютеров, планшетов, смартфонов) с предустановленным специализированным программным обеспечением. Однако специалисты предлагают уникальную методику, позволяющую решить поставленную задачу.
Общие сведения
Для использования алгоритма идентификации чисел нужны определенные знания. Начинать следует с расшифровки терминов.
Читать полностью
Математика
12.11.21
12 мин.
Формулы для решения линейных уравнений (математика, 5 класс)
Очень часто необходимо находить корни равенств с неизвестными на уроках математики в 5 классе. Формулы уравнений линейного типа применяются как раз для этих целей. Для их решения нужно следовать некоторой методике, которая называется алгоритмом. Однако для этого нужен определенный «багаж» знаний, включающий приведение подобных компонентов и упрощение выражения. Общие сведения Большая часть учебников по математике для…
Читать полностью
Математика
12.11.21
13 мин.
Методика перевода числа в восьмеричную систему счисления
Перевод чисел на язык, который понятен любой электронно-вычислительной машине, осуществляется по определенному алгоритму в некоторое представление.
Наиболее востребованными являются двоичная, шестнадцатеричная, а также восьмеричная системы счисления. Однако перед переходом к практике специалисты рекомендуют рассмотреть теорию конвертации первой и последней формы информации (2 и 8).
Общие сведения
Для работы с системами счисления (СС) необходимо разобрать их…
Читать полностью
Математика
12.11.21
11 мин.
Как найти наибольший общий делитель для двух чисел
При решении задач по математике в начальных классах иногда требуется найти наибольший общий делитель, или сокращенно — НОД. Однако не все учащиеся знают правильный алгоритм этой операции, а также путают ее с НОК (наименьшим общим кратным). Чтобы не совершать таких ошибок, специалисты-математики разработали универсальные алгоритмы отличия и нахождения искомых значений. Общие сведения Специалисты…
Читать полностью
Математика
12.
11.21
12 мин.
Алгоритм приведения дробей к общему знаменателю в 5 классе
Операция приведения дробей к общему знаменателю в 5 классе используется при выполнении сложения и вычитания, а также для упрощения выражений. Делать это позволяет определенная методика, которой следует придерживаться. Она также оптимизирует вычислительный процесс, экономя драгоценное время и уменьшая число ошибок на начальной стадии обучения. Перед ее изучением математики рекомендуют получить базовые знания. Базовая информация Обыкновенная дробь…
Читать полностью
Математика
12.11.21
9 мин.
Правила умножения и деления натуральных чисел для 5 класса
Одними из базовых математических операций являются умножение и деление натуральных чисел. В 5 классе они изучаются более подробно с учетом всех «тонкостей». Специалисты разработали специальные алгоритмы, позволяющие произвести расчеты без ошибок.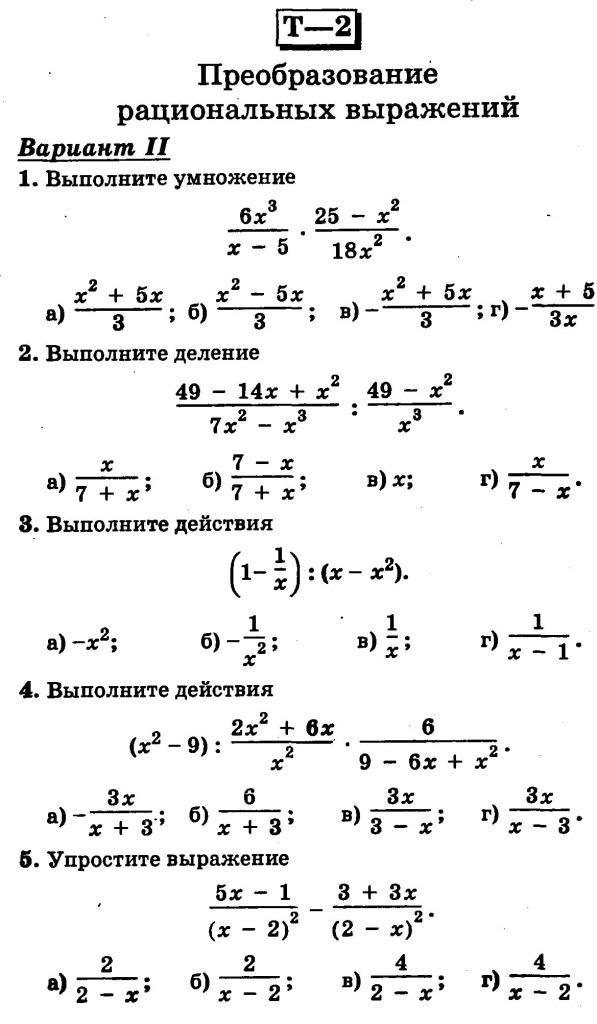
Однако перед обучением нужно разобрать основные определения и понятия, а затем приступать к практике.
Общие сведения
Умножением двух или нескольких чисел называется математическая операция, состоящая…
Читать полностью
Математика
12.11.21
14 мин.
Правила вычитания дробей с разными знаменателями
Пожалуй, одной из самых популярных арифметических операций в алгебре является вычитание дробей с разными знаменателями. Алгоритм выполнения этого действия несложен и ничем не отличается, по сути, от сложения. Базируется он на основном свойстве отношений, позволяющем домножить числитель и знаменатель на одно и то же число. Следует отметить, что знание операции позволяет в…
Читать полностью
Математика
12.11.21
14 мин.
Примеры и способы решений неполных квадратных уравнений
Неполные квадратные уравнения чаще всего встречаются в различных математических задачах школьной программы.
Главное их отличие от обычных в том, что они содержат меньше членов, поэтому и решать их довольно легко. Минимум существует 3 способа. Зная их, можно будет решить пример любой сложности, в некоторых случаях даже устно, причём даже за считаные секунды.
Понятие и термины
Под…
Читать полностью
Математика
12.11.21
9 мин.
Сочетательное свойство и законы умножения для 5 класса
Арифметические операции произведения, сложения, вычитания и деления применяются в различных дисциплинах с физико-математическим уклоном. У каждой из них существуют определенные законы, позволяющие оптимизировать процессы вычисления. Для сложения и произведения следует применять распределительное, переместительное и сочетательное свойства умножения или сложения. Общие сведения Для удобства описания арифметических операций следует ввести буквенные обозначения. Пусть первый коэффициент эквивалентен переменной «о»,…
Читать полностью
Математика
12.
11.21
13 мин.
Правила вычитания десятичных дробей и примеры решений
Арифметические действия относятся к элементарным операциям алгебры. Одним из важных умений является вычитание десятичных дробей. Этот навык используется не только в классических вычислениях, но и при изучении высшей математики. Понимая суть и зная алгоритм, можно громоздкое, сложное к восприятию выражение преобразовать к простому виду, что поможет правильно и быстро найти ответ. Общие сведения Под дробью в математике понимают…
Читать полностью
Математика
12.11.21
13 мин.
Как находить в 6 классе взаимно простые числа и что это такое
Одним из основных понятий в арифметике является деление. Каждая величина характеризуется делимостью. В зависимости от неё определяют и взаимно простые числа. Что это такое и какую пользу несёт знание правила их нахождения, изучают в шестом классе средней школы.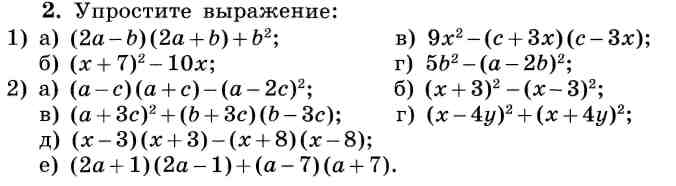
Это базисное понятие, которое позволяет в дальнейшем выполнять различные математические упрощения и преобразования как при решении элементарных задач, так и сложного уровня на уроках высшей математики.
Читать полностью
Математика
12.11.21
8 мин.
Правило деления обыкновенных дробей для 5 класса
В различных дисциплинах с физико-математическим уклоном встречается операция упрощения выражений. Иногда последние представлены в виде обыкновенных дробей. Правила деления и умножения дробных тождеств нужно знать, чтобы не совершать ошибок при вычислениях. Специалисты рекомендуют изучить теорию, а потом перейти к ее практическому применению. Общие сведения Многие начинающие математики путают правила работы с обыкновенными выражениями, поскольку при делении…
Читать полностью
Математика
12.11.21
7 мин.
Деление с остатком в столбик для 5 класса с примерами
Деление с остатком в столбик является распространенной операцией, которая применяется не только в физике и математике, но и в программировании.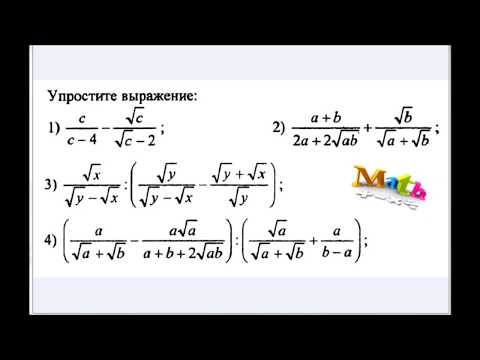
Это следует знать, поскольку не всегда под рукой оказываются средства для выполнения вычислений (онлайн-калькулятор и компьютер). Математики рекомендуют изучить сначала теорию, а затем перейти к практике.
Общие сведения
Практически любую арифметическую операцию возможно выполнить в столбик.…
Читать полностью
3.3. Преобразование алгебраических выражений
Определение 3.8. Алгебраическим выражением называется выражение, составленное из чисел и переменных, знаков действия над ними (сложения, вычитания, умножения, деления, возведения в степень с рациональным показателем, извлечения арифметического корня) и скобок.
Два выражения
называют тождественно
равными,
если при всех допустимых для них значениях
переменных соответственные значения
этих выражений равны. Замену одного
выражения другим, тождественно равным
ему выражением, называют тождественным
преобразованием выражения.
Различают целые рациональные, дробные рациональные и иррациональные выражения. К целым рациональным выражениям относят одночлены и многочлены. Способы их преобразования были рассмотрены в пункте 3.2.
При тождественных преобразованиях дробных рациональных выражений (то есть содержащих деление на выражение с переменной) используются следующие основные приемы.
1. Сокращение дробей, основанное на свойстве дроби: . Например,
, ().
2. Приведение к общему знаменателю – для этого необходимо:
1) разложить знаменатель каждой дроби на множители;
2) составить наименьший общий знаменатель;
3) домножив числитель и знаменатель каждой дроби на дополнительные множители, привести их к общему знаменателю.
Напомним, что действия над алгебраическими дробями осуществляются следующим образом
,
,.
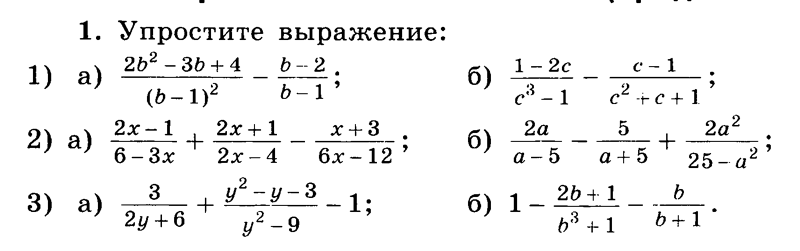
Пример 3.12. Упростить выражение
.
Решение.
, ().
Ответ: , ().
Пример 3.13. Упростить выражение
.
Решение.
, (,).
Ответ: , (,).
Рассмотрим далее преобразование иррациональных выражений. Выражение называется иррациональным, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень. Как правило, тождественные преобразования выполняются на множестве неотрицательных чисел. При решении примеров мы будем это подразумевать и специально не оговаривать.
Пример 3.14. Упростить выражение .
Решение.
.
Ответ: .
Пример 3.15. Упростить выражение .
Решение.
.
Избавимся от иррациональности в знаменателе. Для этого домножим числитель и знаменатель на выражение, сопряженной к знаменателю, то есть на сумму . Получим
.
Ответ: .
Пример 3.16. Упростить выражение
.
Решение. Избавимся от иррациональности в знаменателе каждой из дробей в первой скобке:
,
.
Подстановка полученных выражений дает
.
Ответ: .
Пример 3.
17. Упростить
выражение
.
Решение. Сделаем замену переменной . Тогда исходное выражение примет вид
.
Рассмотрим далее пример, содержащий произведение корней с различными показателями.
Ответ: .
Пример 3.18. Упростить выражение .
Решение.
.
Ответ: .
Пример 3.19. Вычислить .
Решение. Заметим, что
, тогда
=.
Ответ: 6.
Пример 3.20. Вычислить .
Решение. Так как , то
=.
Ответ: 6.
Пример 3.21. Вычислить .
Решение.
.
Ответ: .
Пример 3.22. Найти значение выражения при .
Решение. Упростим предварительно заданное выражение
,
тогда при получим .
Ответ: 9.
Пример 3.22. Найти значение выражения a) ,
б) , в) .
Решение. а) Представим оба подкоренных выражения в виде полных квадратов: и , тогда
.
б) Действуя аналогично пункту а), получаем
=
.
в) .
Ответ: a) ; б) 4; в) 3.
Пример 3.23. Упростить выражение
Решение. Проведем преобразования в ОДЗ
().
Ответ:
Пример 3.24. Упростить выражение
Решение. Проведем преобразования в ОДЗ ().
.
Ответ: , .
Пример 3.25. Упростить выражение
.
Решение. Воспользуемся равенством:
.
Тогда
.
Раскрывая скобки и приведя подобные, получаем
.
Ответ: .
открытых учебников | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula.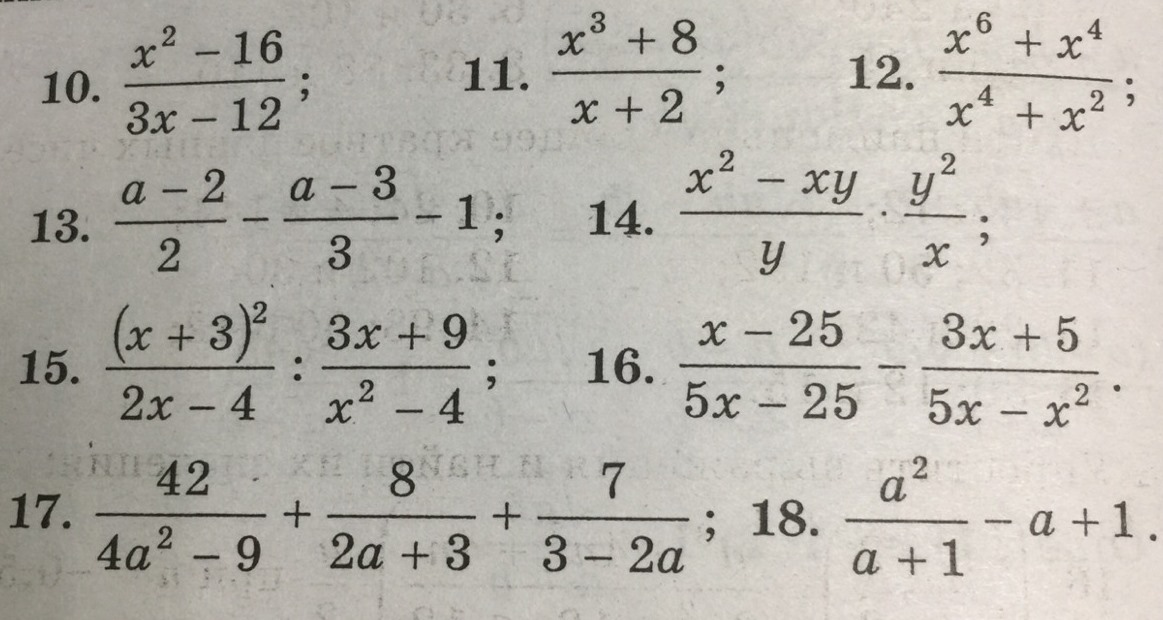
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Рациональное выражение. Как упростить рациональные выражения.
Рабочий лист и ключ ответа на упрощение рациональных выражений
Упрощение рациональных выражений требует хороших навыков факторизации. Суть в том, что вы ищете факторы, которые являются общими как для числителя, так и для знаменателя рационального выражения.
Примеры
Действия по упрощению рациональных выражений
1) Найдите множители, общие для числителя и знаменателя.
2) 3x — это общий множитель числителя и знаменателя. Заметим, что ясно, что x ≠0.
3) Отменить общий множитель.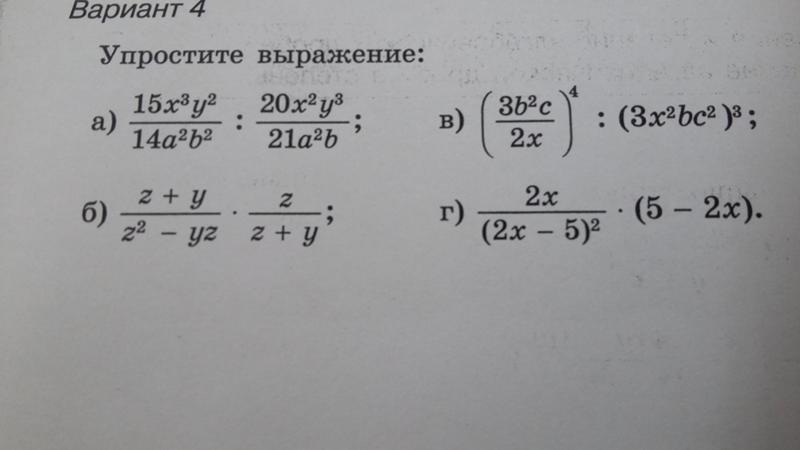
4) Если возможно, поищите другие множители, общие для числителя и знаменателя. В нашем примере мы можем использовать фольгу в обратном порядке, чтобы разложить (x — 1) в знаменателе и дополнительно исключить этот бином как из числителя, так и из знаменателя.
5) После отмены остается 1/(x-1).
6) Окончательное упрощенное рациональное выражение справедливо для всех значений x, кроме 0 и 1.
Как упростить рациональные выражения Пример
Рабочий лист и ключ ответа на упрощение рациональных выражений 92 — 4х — 21} = \frac{x(x + 3)}{(x — 7)(x + 3)} \end{align*} $$
С учетом знаменателя мы знаем, что наш окончательный ответ должен будет ограничить значения $$x$$ так, чтобы $$x \neq -3$$ и $$x \neq 7$$.
Шаг 2
Разделите общие множители.
$$ \начать{выравнивать*} \ гидроразрыв {х (х + 3)} {(х — 7) (х + 3)} & = \frac{x\cancelred{(x + 3)}}{(x — 7)\cancelred{(x + 3)}}\\[6pt] & = \frac{x}{x — 7};\quad x \neq -3 \конец{выравнивание*} $$
Обратите внимание, что другое ограничение (что $$x \neq 7$$) по-прежнему явно указано в конечном выражении.
2 — 4x — 21} = \frac{x}{x — 7};\quad x \neq -3
\конец{выравнивание*}
$$
92 — 4}
знак равно
\ гидроразрыва {(х+2)(х+2)}{(х+2)(х-2)}
\конец{выравнивание*}
$$
Мы видим, что, исходя из факторизованного знаменателя, наш ответ должен ограничивать значения $$x$$ так, чтобы $$x \neq -2$$ и $$x \neq 2$$.
Шаг 2
Разделите общий множитель.
$$ \начать{выравнивать*} \ гидроразрыва {(х+2)(х+2)}{(х+2)(х-2)} & = \frac{\cancelred{(x+2)}(x+2)}{\cancelred{(x+2)}(x-2)}\\[6pt] & = \frac{x+2}{x-2};\quad x \neq 2 \конец{выравнивание*} $$
Обратите внимание, что другое ограничение (что $$x \neq -2$$) по-прежнему явно указано в конечном выражении.
2 — 4} = \frac{x+2}{x-2};\quad x \neq 2
\конец{выравнивание*}
$$
92 -17х — 12)}{х(х-4)}\\[6pt]
& = \ гидроразрыв {х (х — 4) (5х + 3)} {х (х-4)}
\конец{выравнивание*}
$$
Из факторизованного знаменателя мы видим, что наш окончательный ответ должен будет ограничить $$x$$ так, чтобы $$x \neq 0$$ и $$x \neq 4$$.
Шаг 2
Разделите общие множители.
$$ \начать{выравнивать*} \ гидроразрыва {х (х — 4) (5х + 3)} {х (х-4)} & знак равно \ гидроразрыва {\ отменено {х (х — 4)} (5x + 3)} {\ отменено {х (х-4)}} \\ [6pt] & = \frac{5x + 3}{1}\\[6pt] & = 5х + 3; \quad x \neq 0, 4 \конец{выравнивание*} $$ 92 + 6x — 7)}\\[6pt] = \ гидроразрыва {2 (х + 6) (х + 7)} {2 (х + 7) (х — 1)} \конец{выравнивание*} $$
Из факторизованного знаменателя видно, что наш окончательный ответ должен будет ограничить значения $$x$$ так, чтобы $$x \neq -7$$ и $$x \neq 1$$.
Шаг 2
Разделите общие множители.
$$ \начать{выравнивать*} \ гидроразрыва {2 (х + 7) (х + 6)} {2 (х + 7) (х — 1)} & знак равно \ гидроразрыва {\ отменено {2 (х + 7)} (х + 6)} {\ отменено {2 (х + 7)} (х — 1)} \\ [6pt] & = \frac{x + 6}{x — 1};\quad x \neq -7 \конец{выравнивание*} $$
Обратите внимание, что другое ограничение по-прежнему явным образом является частью конечного выражения.
2 + 12x — 14} = \frac{x + 6}{x — 1};\quad x \neq -7
\конец{выравнивание*}
$$
92 + 17x + 8)}\\[6pt]
& = \ гидроразрыва {3x(x+8)(2x+3)}{5x(x+8)(2x+1)}
\конец{выравнивание*}
$$
Из факторизованного знаменателя мы видим, что наш окончательный ответ должен будет ограничить $$x$$ так, чтобы $$x \neq -8$$, $$x \neq — \frac 1 2$$ и $$x \ 0$$.
Шаг 2
Разделите общие множители.
$$ \начать{выравнивать*} \ гидроразрыва {3x(x+8)(2x+3)}{5x(2x+1)(x+8)} & = \frac{3\cancelred{x(x+8)}(2x+3)}{5\cancelred{x(x+8)}(2x+1)}\\[6pt] & = \frac{3(2x+3)}{5(2x+1)}; \quad x \neq -8, 0 \конец{выравнивание*} $$
Другое ограничение (то, что $$x \neq — \frac 1 2$$) остается явным в окончательном выражении.
2 + 40x}
= \ гидроразрыва {3 (2x + 3)} {5 (2x + 1)}; \quad x \neq -8, 0
\конец{выравнивание*}
$$
93}
& = \frac{-x(x — 5)(x — 4)}{x(x — 6)(x -4)}
\конец{выравнивание*}
$$
Шаг 2
Разделите общие множители.
$$
\начать{выравнивать*}
\frac{-x(x — 5)(x — 4)}{x(x — 6)(x -4)}
& = \frac{-\cancelred{x}(x — 5)\cancelred{(x — 4)}}{\cancelred{x}(x — 6)\cancelred{(x — 4)}}\\[ 6pt]
& = \frac{-(x — 5)}{(x — 6)}\\[6pt]
& = -\фракция {х — 5} {х — 6}
\конец{выравнивание*}
$$
92 — 3x — 12}$$.