Карточки. Сложные уравнения 4 класс | Тренажёр по математике (4 класс) на тему:
Опубликовано 05.06.2016 — 16:09 — Кондакова Галина Власьевна
Составлены карточки со сложными уравнениями.
Скачать:
Предварительный просмотр:
х-80=280+2 | 64-х=91:7 | Х+49=4528*4 | 55+Х=4352-2398 |
Х-85=350+150 | 600-х=802:2 | Х+57=7146*6 | 789+Х=6342-699 |
Х-120=912:3 | 4980-Х=201*10 | Х+85=350+150 | 775+Х=5741-85 |
х – 12 = 75 : 3. | 45-х=11+7 | Х+39=786*4 | 89+Х=678956-87 |
х – 27 = 78 + 14 | 600-х=81:9 | Х+29=56744*2 | 899+Х=4532-631 |
х – 16 = 96 – 28 | 76854-Х=30*100 | Х+3716=4650+1856 | 67+Х=228:4 |
Х-54=506-102 | 14000-Х=68*9 | Х+642=805+228 | 473+Х=180:6 |
Х-55=607-428 | 604-Х=70*3 | Х+286=900+638 | 372+Х=5000:10 |
Х-120=45-38 | 703-Х=135*5 | Х+76=978+359 | 199+Х=605:5 |
Х-572=350-156 | 879-Х=87*8 | Х+78=1800+350 | 940+Х=843:3 |
По теме: методические разработки, презентации и конспекты
Презентация к уроку математики 3 класс «Сложные уравнения»
Представляю свою разработку урока и презентацию к уроку математики 3 класс «Сложные уравнения».
Тема дается детям не всегда легко. Я попыпалась в презентации как можно доступнее преподнести оформ…
Решение сложных уравнений 3 класс 1 часть
Учебный материал, который помогает детям научиться решать уравнения в которых один из компонентов уравнения представлен в виде математического выражения. В презентации даются тесты для повторени…
Решение сложных уравнений 3 класс 2 часть
Обучающий тест для учащихся 3 класса для обучения решению сложных уравнений, в которых компоненты — сложные математические выражения. Дети должны увидеть последнее действие в у…
Урок математики в 4 классе.Тема «Решение сложных уравнений».( Система Д.Б. Эльконина — В.В. Давыдова).
Данный урок направлен на выявление правила решения сложных уравнений и формирование умения пользоваться им при решении сложных уравнений и задач. В процессе урока дети решают проблемные за…
Урок математики в 4 классе «Решение сложных уравнений»
для проведения урока класс был разделён на группы.
Урок посвящён зимним Олимпийским играм в Сочи….
Математика. Тема: Решение сложных уравнений. 4 класс
Проблемный урокЦель урока — познакомить с алгоритмом решения сложных уравнений…
Методическая разработка технологической карты урока математики в 4 классе (по УМС «Начальная школа 21 века) «Решение простых и сложных уравнений» (из опыта работы учителя).
Методическая разработка технологической карты урока математики в 4 классе (по УМС «Начальная школа 21 века). Урок «открытия новых знаний»….
Поделиться:
Урок математики по теме «Решение уравнений» (4-й класс)
- Золотова Юлия Михайловна
Разделы: Начальная школа
Класс: 4
Цель: Рассмотреть практические способы решения уравнений, требующих выполнения более одного арифметического действия.
Оборудование урока: компьютерная презентация устного счета, карточки с уравнениями, карточки трех ступеней для самостоятельной работы над задачами, кубик обратной связи
Ход урока
1. Оргмомент
Проверка готовности к уроку. В тетрадях записывается число, классная работа.
2. Устный счет (компьютерная презентация, слайд №1)
Игра «Соревнование улиток»
Ваш любимый пес Алик на соревновании улиток. Две улитки должны подняться до вершины горы. Кто же из них окажется первой? Наша с вами улитка под №1 слева. Улитка делает шаг, только если мы правильно найдем значение выражения.
Вы готовы?
Сигнал к старту уже прозвучал. Повторяем порядок действий и называем правильные значения выражений.
(122 + 18) : 70 = 2
(64 : 8 + 20) : 7 = 4
20 · (26 + 14) : 100 = 8
1 · (30 + 2) – 4 · 4 = 16
5 · 4 + 12 = 32
(400 – 300) – 36 = 64
У нас получился ряд чисел.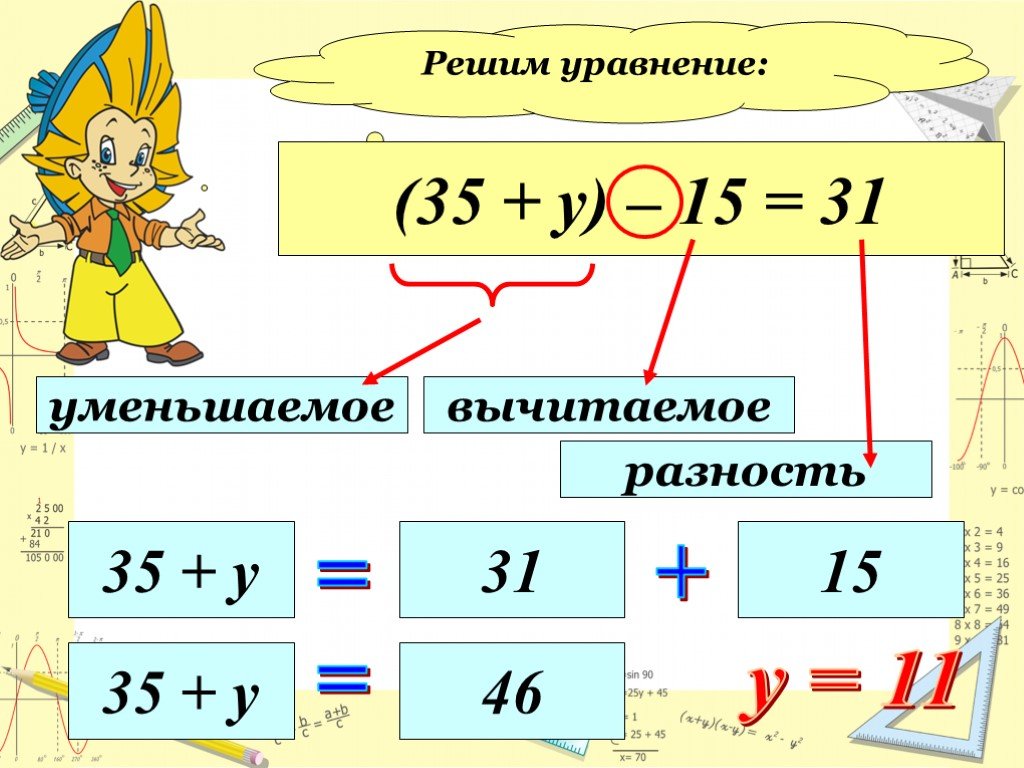
2, 4, 8, 16, 32, 64
Какую закономерность в составлении этого ряда заметили? (каждое следующее число увеличено в два раза)
Продолжите этот ряд чисел и назовите не менее трех следующих чисел. (128, 256, 512…)
Молодцы! Мы решали все правильно, поэтому наша улитка на вершине горы.
За каждым числом зашифрована буква. Перевернем их и прочитаем тему сегодняшнего урока.
2 4 8 16 32 64 128 256 512
У Р А В Н Е Н И Е
Что называется уравнением?
Что называется корнем уравнения?
Что значит решить уравнение?
Мы уже умеем решать простые уравнения, а сегодня мы познакомимся с решением сложных уравнений, где надо выполнить несколько арифметических действий.
На магнитной доске в произвольном порядке карточки с уравнениями.
На какие группы можно разделить все эти уравнения? (уравнения распределяются в 3 столбика)
1) 7000 – х = 2489
7000 – х = 3489
7000 – х = 1689
Почему мы выделили эти уравнения в первую группу? (простые уравнения с одинаковым уменьшаемым) Можем мы их решить ?
Найдите среди них уравнение с наибольшим корнем и решите его (один ученик у доски)
2) 71 : х = 20 + 7
х : 3 = 16 + 11 ( это уравнения, в правой части которых выражение)
Можем ли мы решить уравнения второго столбика?
Решите любое из уравнений, но замените в правой части сумму на разность. Корень уравнения при этом должен остаться прежним. (два ученика у доски)
3) ( 490 – х ) – 250 = 70
Посмотрите на оставшееся уравнение. Легко ли нам его решить? Почему?
4. Работа над новым материалом. (фронтальная беседа с классом, в ходе которой рассматривается решение уравнения)
( 490 – х ) – 250 = 70
490 – х = 70 + 250
490 – х = 320
х = 490 – 320
х = 170
( 490 – 170 ) – 250 = 70
70 = 70
Ответ: 70
5.
Закрепление.
1) Решение уравнения (один из сильных учеников у доски)
5 · а + 500 = 4500 : 5
5 · а + 500 = 900
5 · а = 900 – 500
5 · а = 400
а = 400 : 5
а = 80
5 · 80 + 500 = 900
900 = 900
Ответ: 80
2) № 399
Решите уравнения.
а + 156 = 17 ∙ 20 (1604 – у) – 108 = 800
252 : 36 ∙ х = 560 103300 : (х + 297) = 25 ∙2
Мы решили два новых сложных уравнения. Посмотрите на уравнения, которые перед вами. Все ли они сложные? Какое уравнение лишнее? Почему? Остальные – в левой части выражение в несколько действий. Найдите среди них с таким порядком действий, которое уже встречалось сегодня.
(1604 – у) – 108 = 800
1604 – у = 800 + 108
1604 – у = 908
у = 1604 – 908
у = 696
(1604 – 696) – 108 = 800
800 = 800
Ответ: 696
Уравнение решают в парах.
Один ученик на развороте доски для последующей проверки.
6. Решение задачи
Самостоятельная работа по карточкам 3 ступеней. Выполнив задание первой ступени, ученик переходит к выполнению задания второй ступени, затем третьей.( различные способы дифференцированной работы)
| 1 ступень | 2 ступень | 3 ступень |
| Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили часть саженцев, им осталось посадить еще12350 деревьев. Сколько деревьев они уже высадили? Реши задачу, составив уравнение |
Измени задачу так, чтобы она решалась уравнением, в правой части которого было бы выражение. Запиши это уравнение и реши его. |
Школьники должны были высадить 25700 саженцев деревьев. После того, как они высадили несколько саженцев липы и 8580 кленов, им осталось высадить 12350саженцев. Сколько лип они уже посадили? |
Проверка фронтальная
1) 25700 – х = 12350
х = 25700 – 12350
х = 13350
25700 – 13350 = 12350
12350 = 12350
Ответ: 13350 саженцев.
2) 25700 – х = 12000 + 350
3) 25700 – (х + 8580) = 12350
х + 8580 = 25700 – 12350
х + 8580 = 13350
х = 13350 – 8580
х = 4770
25700 – (4770 + 8580) =12350
12350 = 12350
Ответ: 4770 лип.
4) А какое еще уравнение можно было составить?
(25700 – х) – 8580 = 12350
Мы решили три задачи, составив три уравнения. Какое уравнение отнесем к сложным? Почему?
7. Домашнее задание.
Рассмотреть, как решались уравнения в учебнике на стр. 106 и решить уравнение в тетради на печатной основе № 44 (а).
Решить задачу № 47. Дополнительное задание: какие еще вопросы можно поставить к этой задаче?
8. Итог урока.
Какие уравнения учились решать на уроке?
Трудно было?
Кому было легко?
Математическая задача: добавить символы — вопрос № 3439, алгебра, уравнение
Добавить знаки (+, -, *, /, скобки) для заполнения уравнений
1 3 6 5 = 10
Эта математическая задача для 4-го класса класс начальной школы — пока без отрицательных чисел.
Правильный ответ:
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Спасибо!
Советы для связанных онлайн-калькуляторов
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- arithmetic
- multiplication
- division
- addition
- subtraction
- basic functions
- причина
Уровень задачи:
- практика для 10-летних
- практика для 11-летних
- практика для 9-летних
- Параллельность и ортогональность
Мне нужна помощь по математике в этой задаче: a=(-5, 5 3) b=(-2,-4,-5) (это векторы) Разложите вектор b в b=v+w, где v параллелен a, а w ортогонален a, найти v и w - Скобки 2
Добавить круглую скобку, чтобы получить истину: 5-2×6-4+2=5 - Вычислить со скобками
Найди ошибку — скажи, в чем ошибка 6[(4 + 9) — 32] ÷ 2 6[13-32]÷2 6[13-9]÷2 6[9]÷2 6[4.
5] 27 - Найти ошибку в расчете
Расчеты Салли следующие: 39-9×4+12 =30×16 =480 Какие ошибки в этом расчете? - Скобки: 5545
Добавление знака плюс минус, разделенного двумя скобками: 5 5 5 5 = 15 - Сложение смешанных чисел
Сложение двух смешанных дробей: 2 4/6 + 1 3/6 - Сложение смешанных чисел
Сложите эти два смешанных числа: 1 5/6 + 2 2/11 = - Выражение 2892
Добавьте к выражению 1 + 2×3 — 4×5:6 a / одну пару скобок, чтобы результат был как можно больше b / одну пару скобок так, чтобы результат был как можно меньше - Вычислить выражение 6
Тренировка 5×4-12/2+5 Порядок операций — это порядок, в котором вы работаете с математическими выражениями: круглые скобки, показатели степени, умножение, деление, сложение и вычитание. - Уравнения 5070
Решите в RxRxR систему из 3 линейных уравнений с тремя неизвестными: 1/2 x + 3/4 y = 6z 2x-z = 10 1/2 2z + x = 2y + 7 Примечание: / — дробь строка - Уравнение с дробями
Как еще можно записать уравнение 7/8 x + три четверти = минус 6? - Со скобкой
Вычислить (оценить) простое математическое выражение с отрицательными числами и скобкой: 13+15*5-2*(-6) - Уравнения: 43501
Решить два уравнения: 7 * (x + 1) — (3x + 1) = 21/2 а / 3-а + 6/12 = 2а-4 - Многочлен: 29981
Вычислить значение многочлена: 14 * 32 — 27:3 + 11 * 4:2 = - Сложите две дроби
Сколько будет 1/4 + 10/16? - Уравнение
Решите уравнение и проверьте результат: 1,4x — 3/2 + x — 9,8 = x + 0,4/3 — 7 + 1,6/6 - Уравнение окружности
Найти уравнение окружности, вписанной в ромб ABCD где A[1, -2], B[8, — 3] и C[9, 4].
5] 27
Что такое скобки в математике? Определение, типы, примеры и использование
Что такое скобки?
Вы наверняка видели в учебниках по математике различные символы, подобные этим: (, ), [ ], { и }. Эти символы называются скобками. Скобки в математике служат очень важной цели; эти символы помогают нам сгруппировать различные выражения или числа вместе. Скобки подразумевают, что вещь или выражение, заключенное в них, должно иметь более высокий приоритет по сравнению с другими вещами.
Различные виды скобок
Обычно в математике используются три вида скобок,
- Скобки или круглые скобки, ( )
- Фигурные скобки или фигурные скобки { }
- Квадратные или коробчатые скобы [ ]
Скобки Скобки
Они также известны как круглые скобки и записываются как ( ). Это самые распространенные виды брекетов. Они используются для группировки различных значений и уравнений вместе.
При использовании просто вокруг чисел круглые скобки обозначают умножение.
9{-3}$
Примеры: (2 + 4), 5(111), 25 – (12 + 8) и т. д.
Фигурные скобки
Как и скобки, фигурные скобки также используются для группировки различных математических компонентов; однако фигурные скобки также используются для обозначения множеств или для написания вложенных выражений. Примеры:
[4 + [3 $\times$ (- 2)] – [{(4 $\times$ 6) + (14 $\div$ 7)} – (- 3)],
[{ 12 − (12 − 2) } + (5 − 7)] + 9 и т. д.
Квадратные скобки
Квадратные скобки обычно используются для различения подвыражений сложного математического выражения.
Примеры: [100 – (3 – 1) + (7 x 8)], 10 x [(4 – 2) x ( 4 x 2)] и т. д.
Порядок операций скобок
При оценке математическое выражение, состоящее из разных скобок, мы должны следовать определенным правилам. Это называется правилами работы или порядком работы скобок.
- Общий порядок работы скобки можно проиллюстрировать как [ { ( ) } ]; это означает, что в данной задаче вам придется сначала упростить значения в самой внутренней скобке.
- Вторым шагом в решении этих задач является поиск показателя степени; если есть, решите сначала.
- На третьем шаге ищем выражения с операторами умножения или деления. Если оба оператора присутствуют, мы проверяем выражение слева направо. Какой бы оператор ни пришел первым, мы сначала решим этот оператор.
Например, в выражении 10 6 ÷ 5 мы проверяем слева направо, поскольку сначала идет умножение, поэтому мы сначала решаем умножение, а затем деление.
10 $\times$ 6 ÷ 5
= 60 ÷ 5
= 12
- На четвертом и последнем шаге мы ищем числа, которые нужно сложить или вычесть. Мы следуем той же инструкции, если присутствуют оба оператора, мы смотрим слева направо в выражении, и какой бы оператор ни был первым, мы решаем это выражение первым. Но если операции в скобках, мы всегда сначала решаем скобки, так как скобки имеют наивысший приоритет.
Чтобы запомнить упомянутые выше шаги, мы можем использовать аббревиатуру PEMDAS,
P – Скобки,
E – Экспоненты
M – Умножение
D – Деление
A – Сложение
S – Вычитание.
давайте воспользуемся pemdas для вычисления выражения Следуйте порядку решения круглых скобок ( ), затем фигурных скобок { }, а затем квадратных скобок [ ].
= 100 − [(2) + (56)]
= 100 − 58
Шаг 2: В данном выражении нет показателя степени.
Шаг 3: В данном выражении нет ни умножения, ни деления.
Шаг 4: Решите вычитание.
= 100 − 58
= 42
Решаемые примеры
Вопрос 1: Найдите значение выражения: (5 + 4) − (3 − 2).
Ответ: Данное выражение:
(5 + 4) − (3 − 2),
Шаг 1: Решение значений в скобках,
−(9) (1),
Таким образом, ответ равен (9) − (1) = 8.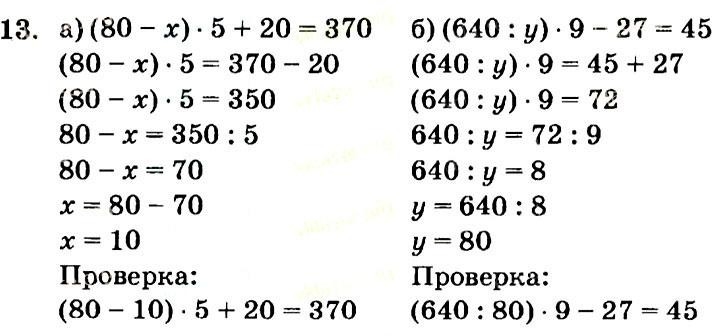
Вопрос 2: Найдите значение выражения: {(7 − 2) × 3} ÷ 5
Ответ : Данное уравнение имеет вид
Решение фигурной скобки
= {15} ÷ 5
= 15 ÷ 5
= 3
Вопрос 3: Найдите значение выражения: (12 ÷ 6) × (4 − 2)
Решение:
Уравнение:
(12 ÷ 6) × (4 − 2) 2) x (2)
Таким образом, ответ: (2) x (2) = 4
Вопрос 4: Найдите значение выражения: [120 + { (3 x 4) + (4 − 2) − 1 } + 20]
Ответ: Следуя правилу PEMDAS, сначала
Шаг 1: Найдем значения в скобках ( ),
[120 + { (3 x 4) + (4 − 2 ) — 1 } + 20 ]
= [ 120 + { (12 ) + ( 2 ) — 1 } + 20 ],
Теперь вычисляем значения в скобках { } ,
= [ 120 + { 13 } + 20 ],
Наконец, сложите все значения в скобках [ ],
Ответ: 153.
Практические задачи
1
Решите: [{(22 + 33) × 42} −(20 ÷ 5)]
490
492
494
500
Правильный ответ: 492
Шаг 1: Решите все скобки, учитывая приоритет.
2$ 9{2} = 4,096 $
4
Решите это выражение, 12 + (5 + 3),
18
20
16
8
Правильный ответ: 20
Правильный ответ — 20.
Часто задаваемые вопросы
Почему скобки важны в математике?
Скобки — очень важная часть математического уравнения; они отделяют разные математические выражения друг от друга и помогают установить приоритет для выражений, которые необходимо решить в первую очередь.
Является ли PEMDAS единственным методом решения проблем со скобами?
BODMAS — это другой аббревиатур от PEMDAS, где B означает скобки, O — числа или экспоненты, D — деление, M — умножение, A — сложение и S — вычитание. Любое выражение считается правильно решенным, если оно соответствует правилу PEMDAS или BODMAS.
Есть ли еще виды кронштейнов?
Угловые скобки также используются в различных математических выражениях; они представлены с〈 〉.