Внеклассный урок — Целые и дробные рациональные уравнения
Целые и дробные рациональные уравненияРациональные уравнения – это уравнения, в которых и левая, и правая части являются рациональными выражениями.
(Напомним: рациональными выражениями называют целые и дробные выражения без радикалов, включающие действия сложения, вычитания, умножения или деления — например: 6x; (m – n)2; x/3y и т.п.)
Рациональное уравнение называется целым, или алгебраическим, если в нем нет деления на выражение, содержащее переменную.
Примеры целого рационального уравнения:
5x – 10 = 3(10 – x)
3x
— = 2x – 10
4
Если в рациональном уравнении есть деление на выражение, содержащее переменную (x), то уравнение называется дробно-рациональным.
Пример дробного рационального уравнения:
15
x + — = 5x – 17
x
Дробные рациональные уравнения обычно решаются следующим образом:
1) находят общий знаменатель дробей и умножают на него обе части уравнения; 2) решают получившееся целое уравнение; 3) исключают из его корней те, которые обращают в ноль общий знаменатель дробей.
|
Примеры решения целых и дробных рациональных уравнений.
Пример 1. Решим целое уравнение
x – 1 2x 5x
—— + —— = ——.
2 3 6
Решение:
Находим наименьший общий знаменатель. Это 6. Делим 6 на знаменатель и полученный результат умножаем на числитель каждой дроби. Получим уравнение, равносильное данному:
3(x – 1) + 4x 5х
—————— = ——
6 6
Поскольку в левой и правой частях одинаковый знаменатель, его можно опустить. Тогда у нас получится более простое уравнение:
3(x – 1) + 4x = 5х.
Решаем его, раскрыв скобки и сведя подобные члены:
3х – 3 + 4х = 5х
3х + 4х – 5х = 3
2х = 3
х = 3:2
x = 1,5.
Пример решен.
Пример 2. Решим дробное рациональное уравнение
x – 3 1 x + 5
—— + — = ———.
x – 5 x x(x – 5)
Решение:
Находим общий знаменатель. Это x(x – 5). Итак:
Это x(x – 5). Итак:
x2 – 3х x – 5 x + 5
——— + ——— = ———
x(x – 5) x(x – 5) x(x – 5)
Теперь снова освобождаемся от знаменателя, поскольку он одинаковый для всех выражений. Сводим подобные члены, приравниваем уравнение к нулю и получаем квадратное уравнение:
x2 – 3x + x – 5 = x + 5
x2 – 3x + x – 5 – x – 5 = 0
x2 – 3x – 10 = 0.
Решив квадратное уравнение, найдем его корни: –2 и 5.
Проверим, являются ли эти числа корнями исходного уравнения.
При x = –2 общий знаменатель x(x – 5) не обращается в нуль. Значит, –2 является корнем исходного уравнения.
При x = 5 общий знаменатель обращается в нуль, и два выражения из трех теряют смысл. Значит, число 5 не является корнем исходного уравнения.
Ответ: x = –2
Дробные рациональные уравнения 8 класс онлайн-подготовка на Ростелеком Лицей
Тема 7: Квадратные уравнения
- Видео
- Тренажер
- Теория
Заметили ошибку?
Дробно-рациональные уравнения
Дробно-рациональные уравнения (дробные рациональные уравнения или просто дробные уравнения) — это уравнения c одной переменной вида
fx=g(x),
где f(x) и g(x) — рациональные выражения, хотя бы одно из которых содержит алгебраическую дробь с переменной в знаменателе.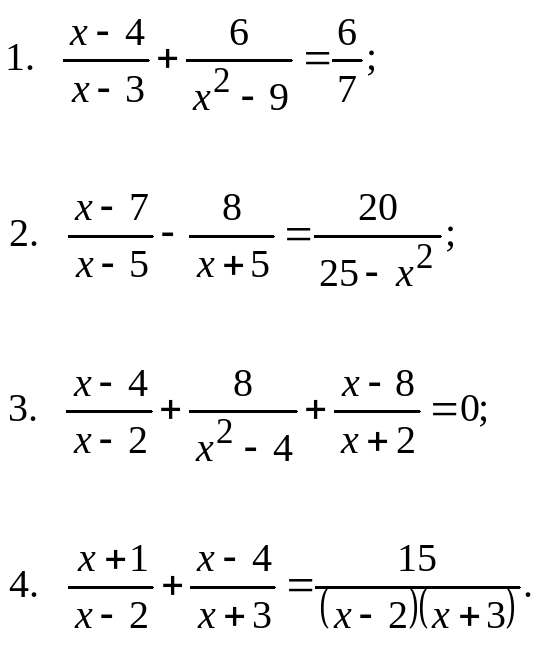
В общем виде дробно-рациональные уравнения решают по следующей схеме:
-
Все слагаемые переносим в одну сторону.
-
Дроби приводим к НОЗ (наименьшему общему знаменателю).
-
После упрощения решаем уравнение типа «дробь равна нулю».
В частных случаях дробно-рациональные уравнения могут быть решены с помощью замены переменной либо разложением на множители.
Начнем с рассмотрения примеров общего случая.
Решить дробно-рациональные уравнения:
-
4x-2-3x+4=1
Переносим все слагаемые в левую часть уравнения и приводим дроби к наименьшему общему знаменателю:
4\(x+4)x-2-3\(x-2)x+4-1\(x-2)(x+4)=0
4x+4-3x-2-(x-2)(x+4)(x-2)(x+4)=0
4x+16-3x+6-(x2+4x-2x-8)(x-2)(x+4)=0
x+22-x2-4x+2x+8(x-2)(x+4)=0
Пришли к уравнению типа «дробь равна нулю».
 Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:-x2-x+30(x-2)(x+4)=0 ⇔ -x2-x+30=0(x-2)(x+4)≠0
Находим значения переменной, при которых знаменатель обращается в нуль, и исключаем их из области допустимых значений:
(x-2)(x+4)≠0
x-2≠0; x+4≠0
x≠2; x≠-4
Теперь находим значения переменных, при которых числитель обращается в нуль:
-x2-x+30=0 |∙(-1)
x2+x-30=0
Это — квадратное уравнение. Его корни x1=5; x2=-6.
Оба корня удовлетворяют условиям x≠2; x≠-4.
Ответ: 5; -6.
-
x+2×2-2x-xx-2=3x
Замечаем, что знаменатель первой дроби раскладывается на удобные множители: x2-2x=x(x-2).
Переносим все слагаемые в одну сторону и приводим дроби к наименьшему общему знаменателю:
x+2\1x(x-2)-x\xx-2-3\(x-2)x=0
x+2-x2-3(x-2)x(x-2)=0
x+2-x2-3x+6x(x-2)=0
-x2-2x+8x(x-2)=0 ⇔ -x2-2x+8=0x(x-2)≠0
x(x-2)≠0
x≠0; x≠2 — при этих значениях переменной знаменатель обращается в нуль, поэтому их исключаем из ОДЗ.

-x2-2x+8=0 |∙(-1)
Из двух корней квадратного уравнения
x2+2x-8=0
x1=-4; x2=2 — второй не входит в ОДЗ. Поэтому в ответ включаем лишь первый корень.
Ответ: -4.
-
x2-x-6x-3=x+2
Переносим все слагаемые в одну сторону и приводим дроби к НОЗ:
x2-x-6\1x-3-x\(x-3)-2\(x-3)=0
x2-x-6-xx-3-2(x-3)x-3=0
x2-x-6-x2+3x-2x-6x-3=0
0xx-3=0 ⇔ 0x=0x-3≠0
Значение переменной, при котором знаменатель обращается в нуль, исключаем из ОДЗ: x≠3.
Уравнение 0x=0 — частный случай линейного уравнения. Оно имеет бесконечное множество решений: какое бы число мы не подставили вместо x, получим верное числовое равенство. Единственное значение x, которое не входит в множество решений данного уравнения — 3.Ответ: x — любое число, кроме 3.

-
5x-2-3x+2=20×2-4
Замечаем в знаменателе третьей дроби формулу сокращённого умножения и пользуемся ей для разложения на множители. Переносим все слагаемые в левую часть и приводим дроби к наименьшему общему знаменателю:
5\(x+2)x-2-3\(x-2)x+2-20\1x-2x+2=0
5x+2-3x-2-20(x-2)(x+2)=0
5x+10-3x+6-20(x-2)(x+2)=0
2x-4(x-2)(x+2)=0 ⇔ 2x-4=0(x-2)(x+2)≠0
(x-2)(x+2)≠0
x≠2; x≠-2 — при этих значениях переменной дробь не имеет смысла, поскольку знаменатель обращается в нуль.
2x-4=0
x=2
Так как 2 не входит в ОДЗ, данное уравнение не имеет корней.
Ответ: корней нет.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.1.5 Решение уравнений, содержащих дроби
РАЗДЕЛ 1.5 Цели обучения
1.5: Решение уравнений, содержащих дроби
- Использование свойств равенства для решения одношаговых уравнений, содержащих дроби
- Очистить дроби в уравнении, а затем решить уравнение
- Решение многошаговых уравнений, содержащих дроби
- Решите основное рациональное уравнение
ПОДУМАЙТЕ ОБ ЭТОМ
Можете ли вы определить что бы вы сделали по-другому, если бы вас попросили решить подобные уравнения?
Решите [латекс]\фракция{1}{4} + у = 3[/латекс]. Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы решили это уравнение с дробью.
Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы решили это уравнение с дробью.
Показать решение
Использовать свойства равенства для решения одношаговых уравнений, содержащих дроби
Вспомнить свойство сложения равенства из предыдущего раздела
Аддитивное свойство равенства
Для всех действительных чисел a , b и c : Если [латекс]а=b[/латекс], то [латекс]а+с=b+с[/ латекс].
Если два выражения равны друг другу, и вы добавляете одно и то же значение к обеим частям уравнения, уравнение останется равным.
В следующем видео показано, как использовать свойство сложения равенства для решения уравнений с дробями.
Выполняя шаги по решению уравнения, вы пытаетесь изолировать переменную. Переменная — это величина, которую мы еще не знаем. У вас есть решение, когда вы получаете уравнение x = некоторое значение.
Переменная — это величина, которую мы еще не знаем. У вас есть решение, когда вы получаете уравнение x = некоторое значение.
Вызов свойства равенства умножения из предыдущего раздела
Свойство равенства умножения
Для всех действительных чисел a , b и c : Если a = b , a\cdot{c}=b\cdot{c}[/latex] (или ab = ac ).
Если два выражения равны друг другу и вы умножаете обе части на одно и то же число, полученные выражения также будут эквивалентны.
В следующем примере нас просят решить [латекс]-\frac{7}{2}=\frac{k}{10}[/latex] для k . Мы решим это одношаговое уравнение, используя свойство равенства умножения. Вы увидите, что переменная является частью дроби в данном уравнении, и использование свойства равенства умножения позволяет нам удалить переменную из дроби. Помните, что дроби подразумевают деление, поэтому вы можете думать о [latex]\frac{k}{10}[/latex] как о переменной k делится на 10. Чтобы «отменить» деление, вы можете использовать умножение, чтобы изолировать k . Наконец, обратите внимание, что в уравнении есть отрицательный член, поэтому будет важно подумать о знаке каждого члена, когда вы будете решать задачу. Останавливайтесь после каждого шага, чтобы убедиться, что все термины имеют правильный знак.
Помните, что дроби подразумевают деление, поэтому вы можете думать о [latex]\frac{k}{10}[/latex] как о переменной k делится на 10. Чтобы «отменить» деление, вы можете использовать умножение, чтобы изолировать k . Наконец, обратите внимание, что в уравнении есть отрицательный член, поэтому будет важно подумать о знаке каждого члена, когда вы будете решать задачу. Останавливайтесь после каждого шага, чтобы убедиться, что все термины имеют правильный знак.
Очистить дроби в уравнении, а затем решить уравнение
Иногда вы столкнетесь с многошаговым уравнением с дробями. Если вы предпочитаете не работать с дробями, вы можете использовать свойство равенства умножения, чтобы умножить обе части уравнения на общий знаменатель всех дробей в уравнении. Это удалит все дроби из уравнения.
Это удалит все дроби из уравнения.
Чтобы найти наименьший общий знаменатель , нужно найти «наименьшее общее кратное» (НОК). Если вам нужен обзор того, как найти LCM, посмотрите видео ниже:
Теперь давайте посмотрим на пример ниже и посмотрим, как мы используем общий знаменатель для очистки дробей перед решением уравнения.
Конечно, если вам нравится работать с дробями, вы можете просто применить свои знания операций с дробями и решить.
Решение многошаговых уравнений, содержащих дроби
В следующем видео мы покажем, как решить многошаговое уравнение с дробями.
Если уравнение содержит скобки, сначала распределите коэффициент перед скобками, а затем очистите дроби. В следующем видео мы покажем пример.
В следующем видео мы покажем пример.
Пример 3
Решите уравнение [латекс]\frac{3}{2}(\frac{5}{9}x + \frac{4}{27})=\frac{32}{9 }[/latex]
Показать ответ
Вот несколько шагов, которые необходимо выполнить при решении многошаговых уравнений.
Этапы решения многошаговых уравнений
1. Упростите каждую часть, удалив круглые скобки и объединив одинаковые члены.
2. (Необязательно) Умножьте, чтобы очистить все дроби или десятичные числа.
3. Добавьте или вычтите, чтобы изолировать переменный термин — возможно, вам придется переместить термин вместе с переменной.
4. Умножьте или разделите, чтобы изолировать переменную.
5. Проверьте решение.
Решение основного рационального уравнения
Рациональные уравнения
Уравнения, содержащие дробные выражения, иногда называются рациональные уравнения . Например, [латекс] \frac{2x+1}{4}=\frac{x}{3}[/latex] является рациональным уравнением. Рациональные уравнения могут быть полезны для представления ситуаций из реальной жизни и для поиска ответов на реальные проблемы. В частности, они неплохо подходят для описания различных пропорциональных отношений.
Например, [латекс] \frac{2x+1}{4}=\frac{x}{3}[/latex] является рациональным уравнением. Рациональные уравнения могут быть полезны для представления ситуаций из реальной жизни и для поиска ответов на реальные проблемы. В частности, они неплохо подходят для описания различных пропорциональных отношений.
Разница между линейным уравнением и рациональным уравнением заключается в том, что рациональные уравнения могут иметь многочлены в числителе и знаменателе дробей. В следующих примерах мы очистим знаменатели рационального уравнения от члена, имеющего полином в числителе. Примечание. Мы обсудим многочлены более подробно в следующем модуле. В следующем примере [латекс]{х+5}[/латекс] — полином, о котором идет речь.
В следующем примере мы покажем, как решить рациональное уравнение с переменными в обеих частях уравнения.
Урок 13: Уравнения дробей — Алгебра II 2011-2012
|


 Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе:
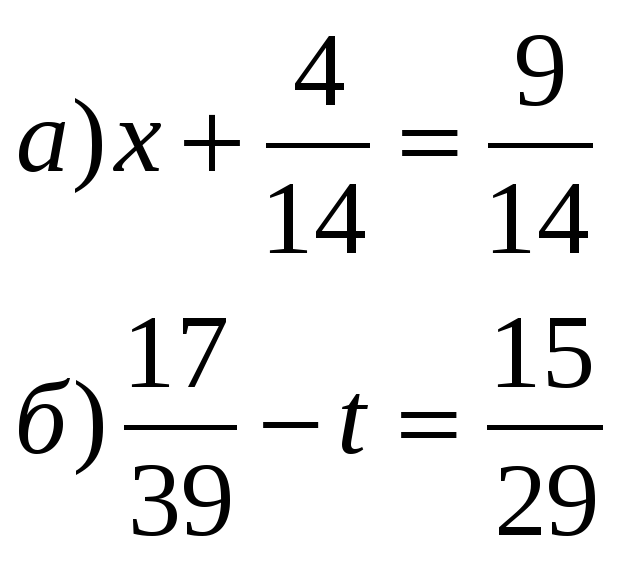

 ЖКИ 12,
значит умножаем все уравнение на 12:
ЖКИ 12,
значит умножаем все уравнение на 12:

 (Примечание: 20%
спиртовой раствор означает, что раствор содержит 20 % спирта и 80 % воды).
(Примечание: 20%
спиртовой раствор означает, что раствор содержит 20 % спирта и 80 % воды). Если общий путь составил 150 км и
2 часа 40 минут, какое расстояние он проехал на каждой скорости?
Если общий путь составил 150 км и
2 часа 40 минут, какое расстояние он проехал на каждой скорости?
 ток и обратно через 5 часов. Какова скорость лодки в неподвижном состоянии
вода?
ток и обратно через 5 часов. Какова скорость лодки в неподвижном состоянии
вода?
 0036 б тогда и только тогда, когда б — а положительный.
Это записывается в следующем виде.
0036 б тогда и только тогда, когда б — а положительный.
Это записывается в следующем виде.