Уравнения с дискриминантом как решать: Квадратные уравнения — урок. Алгебра, 8 класс.

Содержание

Как решать квадратные уравнения в Python

Если квадратные уравнения являются классической задачей в математике, то они также являются классической задачей в программировании. Их решение – идеальное упражнение для тех, кто только начинает программировать, поскольку оно включает ввод с клавиатуры, вывод на экран, арифметические и условные вычисления. Вы хотите узнать, как решать уравнения второй степени в Python?

Об этом я подробно расскажу в этой статье.

Итак, представьте уравнение ax² + bx + c = 0:

Вычисляем дискриминант: disc = b * b – 4 * a * c
Если он отрицательный, то уравнение не имеет решения.
Если disc больше нуля, вычисляем его корень: root = srqt(disc).
Вычислим решения: x_1 = (-b + root) / (2 * a) и x_2 = (-b – root) / (2 * a).

Далее я шаг за шагом рассказываю вам, как решать квадратные уравнения, останавливаясь на каждой детали, чтобы вы могли понять все досконально.

Содержание

1 Получение значений коэффициентов
2 Вычисление дискриминанта
3 Уравнения второй степени не имеющие решения
4 Вычисление решений (или решения)
5 Полный код
6 Создание функции для решения квадратных уравнений
7 Проверка решений

Получение значений коэффициентов

Первым шагом является получение значений коэффициентов. Хотя верно, что в реальном приложении, где вам нужно решить уравнения второй степени, эти коэффициенты будут поступать из файлов, баз данных или других вычислительных блоков, в данном примере мы будем получать их непосредственно от пользователя, через клавиатуру.

Для получения значения, предоставленного пользователем, можно использовать функцию ввода, которая ждет, пока пользователь введет значение и нажмет клавишу Enter. Значение, предоставленное пользователем, возвращается функцией в виде текстовой строки, которую нам нужно преобразовать в десятичное число с помощью функции float.

В этом случае мы должны запросить у пользователя три значения, так как три – это коэффициенты, которые обрабатываются в уравнении второй степени, которое, как вы помните, имеет следующий вид: ax² + bx + c = 0, где x – неизвестное, которое нужно вычислить, а a, b и c – коэффициенты.

Обратите внимание, что уравнение второй степени не определено, если коэффициент a равен 0, поэтому можно предположить, что значение этого коэффициента всегда будет отлично от 0.

Также возможно, что пользователь вводит не числовые значения при запросе. Это нужно проверить в нашей программе, чтобы избежать нарушения выполнения программы. Я не буду рассказывать об этом здесь, чтобы не делать эту статью слишком длинной, но я объясню в другой статье, как запрашивать у пользователя значение до тех пор, пока оно не станет правильным. Следуя указаниям в этой статье, вы можете проверить, что коэффициент a отличен от 0 и что введенные значения являются числовыми.

Таким образом, для данной программы мы будем считать, что пользователь всегда вводит правильные значения для коэффициентов a, b и c. Запросить их можно следующим образом:

a = float(input('Введите значение коэффициента a: '))
b = float(input('Введите значение коэффициента b: '))
c = float(input('Введите значение коэффициента c: '))
Code language: JavaScript (javascript)

Этот код выводит сообщение, переданное в качестве параметра функции ввода, и ждет, пока пользователь введет значение. После получения значения input возвращает его, затем оно преобразуется в тип float с помощью одноименной функции и присваивается переменной.

Если вы заметили, этот код немного повторяется, так что мы будем использовать специальные возможности Python, чтобы избежать повторений. Эта часть необязательна, поэтому, если вы хотите, вы можете продолжить в следующем разделе, где мы начнем выполнять вычисления, но имейте в виду, что позже, когда я представлю полный код, я буду использовать эти оптимизации.

Чтобы улучшить этот код, я собираюсь использовать функции сжатия и распаковки списков.

Сжатие списка позволяет нам создать список значений, которые в нашем случае будут тремя коэффициентами, с помощью цикла очень простым способом в одной строке. С другой стороны, распаковка позволяет нам извлекать значения из сформированного списка и хранить их непосредственно в трех переменных.

Итак, я могу создать список с тремя значениями (три коэффициента), используя следующий код:

[float(input(f'Введите значение коэффициента {koef}: ')) for koef in ('a', 'b', 'c')]
Code language: CSS (css)

В предыдущем коде я прохожу по кортежу (‘a’, ‘b’, ‘c’), делая вызов input (и соответствующего вызова float) для каждого из его значений.

В итоге полученные значения сохраняются в списке.

Теперь настала очередь распаковки.

Так, если, например, я сделаю следующее a, b, c = [1, 2, 3], то легко увидеть, что значения 1, 2 и 3 будут соответствовать переменным a, b и c и именно в таком порядке.

Комбинируя теперь две предыдущие инструкции, мы можем получить от пользователя три коэффициента для нашего уравнения без повторения кода и в одной строке (предполагая, как и раньше, что значения, введенные пользователем, будут действительными):

a, b, c = [float(input(f'Введите значение коэффициента {koef}koef: ')) for koef in ('a', 'b', 'c')]
Code language: JavaScript (javascript)

Мы могли бы просто сохранить список и продолжать работать со значениями, хранящимися в нем, но код будет сложнее для чтения и менее понятным.

Вычисление дискриминанта

Получив значения, мы можем приступить к расчетам. Универсальным способом решения уравнений второй степени является применение так называемой формулы Бхаскары, которая выглядит следующим образом:

Если вы остановитесь и проанализируете ее, то увидите, что вам нужно вычислить квадратный корень из выражения b² – 4ac.

Квадратный корень не определен для отрицательных чисел. По этой причине, если это выражение, которое мы будем называть дискриминантом, имеет отрицательное значение, корень не может быть вычислен, и квадратное уравнение не имеет реального решения (хотя оно имеет одно решение в области комплексных чисел, что выходит за рамки данной статьи).

Это ситуация, с которой мы должны справиться, поэтому первое, что мы должны сделать, это вычислить значение дискриминанта, что мы сделаем очень простым способом:

disc =  b * b - 4 * a * c

Вычислить квадрат величины очень легко, умножив эту величину на саму себя. Поэтому, если мы хотим получить значение b в квадрате, то есть b², мы можем сделать b * b, как показано в коде выше.

В Python также есть оператор для вычисления степени, который представляет собой двойную звездочку **, поэтому вы также можете вычислить квадрат b следующим образом: b ** 2.

Уравнения второй степени не имеющие решения

Как я вам только что рассказал, существуют уравнения второй степени, которые не имеют решения, что происходит, когда дискриминант отрицателен.

Необходимо выполнить эту проверку, которая заставит нас показать пользователю сообщение об ошибке, указывающее на то, что представленное уравнение не имеет решения.

Это делается очень простым способом с помощью условия:

disc =  b * b - 4 * a * c
if disc < 0:
    print('Уравнение не имеет решения.')
Code language: PHP (php)

Если дискриминант больше или равен нулю, то мы имеем решение, и остается только вычислить его.

Вычисление решений (или решения)

Бывает, что квадратное уравнение имеет два разных решения. Это возможно потому, что квадрат любого числа всегда является положительным числом, поскольку отрицательное число, умноженное на другое отрицательное число, дает положительное число. То есть существуют различные числа, которые при возведении в квадрат дают одно и то же число.

Другими словами, результат квадратного корня на самом деле всегда равен двум, что является величиной, полученной в результате операции с положительным знаком и с отрицательным знаком.

Чтобы было понятно, если сделать квадратный корень из 4, то получится 2. Но результат корня не только 2, но и -2, так как 2² = 4 и (-2)² = 4.

Мы также должны учесть это при вычислении решения уравнения, так что нам придется получить два разных значения: одно с учетом положительного результата корня, а другое – с учетом отрицательного.

Для этого, всегда предполагая, что дискриминант является неотрицательным числом, мы можем вычислить два различных решения уравнения следующим образом:

root = sqrt(disc)
x_1 = (-b + root) / (2 * a)
x_2 = (-b - root) / (2 * a)

Обратите внимание, что сначала я вычисляю положительное значение корня с помощью функции sqrt, которая находится в модуле math. Не забудьте выполнить from math import sqrt, чтобы иметь возможность использовать его. Причина вычисления его заранее, поскольку я также ранее сохранил значение дискриминанта в переменной, заключается в том, чтобы избежать повторения кода при вычислении двух решений x_1 и x_2. Это также делает код более четким, легко читаемым и менее склонным к ошибкам.

Однако может случиться так, что x_1 и x_2 имеют одинаковое значение. То есть уравнение имеет только одно решение (иногда его называют двойным решением). Это происходит, когда дискриминант равен 0, потому что результат корня также будет равен 0, и между выражениями для вычисления x_1 и x_2 не будет разницы, то есть они будут одинаковыми.

Интересно также выделить такую ситуацию. Для этого достаточно проверить, что дискриминант равен 0, и таким образом вычислить единственное решение в этом случае. Это можно сделать следующим образом:

root = sqrt(disc)
x_1 = (-b + root) / (2 * a)      # вычисляем первое решение
if disc != 0:                    # проверяем, существует ли другое решение
    x_2 = (-b - root) / (2 * a)  # вычисляем второе решение
Code language: PHP (php)

Теперь остается только вывести решения на экран. Вы увидите это ниже, когда мы соберем воедино весь код, который уже видели.

Полный код

Давайте посмотрим, как все это выглядит, собрав вместе различные фрагменты кода, которые мы рассмотрели, и выведя несколько сообщений пользователю. Я добавляю комментарии к коду, чтобы было понятно, что делается в каждой строке:

from math import sqrt
# выводим приветственное сообщение
print('Привет! Давайте решим квадратное уравнение:')
print('    ax² + bx + c = 0\n')
# запросим у пользователя коэффициенты
a, b, c = [float(input(f'Введите значение коэффициента {koef}: ')) for koef in ('a', 'b', 'c')]
# вычисляем дискриминант
disc =  b * b - 4 * a * c
if disc < 0: # проверяем, существуют ли реальные решения
    print(f'Уравнение не имеет реальных решений.')
else:
    root = sqrt(disc)      # вычисляем корень
    x_1 = (-b + root) / (2 * a)     # вычисляем первое решение
    if disc != 0:          # проверяем, существует ли другое решение
        x_2 = (-b - root) / (2 * a) # вычисляем второе решение
        print(f'Решения {x_1} и {x_2}.
  ') # покажем два решения
    else:
        print(f'Единственным решением является x = {x_1}') # покажем единственное решение
Code language: PHP (php)

Вы видите, что после предыдущих объяснений полный код получился простым и лаконичным. Давайте посмотрим результаты выполнения некоторых операций, чтобы вы могли увидеть, как это работает. Первый – это прогон, в котором решаемое уравнение второй степени имеет два различных решения (т.е. дискриминант больше 0):

Привет! Давайте решим квадратное уравнение: ax² + bx + c = 0 Введите значение коэффициента a: 2.25 Введите значение коэффициента b: 1.5 Введите значение коэффициента c: -2 Решения 0.6666666666666666 и -1.3333333333333333.

Теперь рассмотрим случай, когда существует только одно решение (или двойное решение, когда дискриминант равен 0):

Привет! Давайте решим квадратное уравнение: ax² + bx + c = 0 Введите значение коэффициента a: -2 Введите значение коэффициента b: 4 Введите значение коэффициента c: -2 Единственным решением является x = 1. 0

И, наконец, вариант, в котором не существует реального решения, потому что дискриминант отрицательный:

Привет! Давайте решим квадратное уравнение: ax² + bx + c = 0 Введите значение коэффициента a: 1 Введите значение коэффициента b: 2 Введите значение коэффициента c: 3 Уравнение не имеет реальных решений.

Создание функции для решения квадратных уравнений

Теперь мы поместим наш код в функцию, которая получает коэффициенты a, b и c и возвращает решение или решения уравнения. Это удобно, если нам нужно решить несколько уравнений в нашей программе.

Мы будем думать о функции так, чтобы она возвращала список значений, поскольку, как мы видели, реально возможные решения могут быть 0, 1 или 2. Таким образом, достаточно проверить длину списка, возвращаемого нашей функцией, чтобы узнать количество решений уравнения.

Теперь функция не должна ничего выводить на экран, мы позаботимся об этом после вызова нашей функции, поэтому мы уберем вызовы функции print и заменим их в конце инструкциями по добавлению вычисленных решений в список решений.

Кроме того, поскольку наша функция уже получает значения коэффициентов в качестве параметров, нам не нужно делать вызовы input внутри нее. Давайте посмотрим на код:

from math import sqrt
def solve_square_equation(a, b, c):
    solutions = [] #  создаем пустой список для решений
    disc = b * b - 4 * a * c
    if disc >= 0:  # проверяем, существуют ли реальные решения
        root = sqrt(disc)
        solutions.append((-b + root) / (2 * a))    # вычисляем первое решение
        if disc != 0:
           solutions.append((-b - root) / (2 * a)) # вычисляем второе решение, если оно существует
    return solutions
Code language: PHP (php)

Обратите внимание, что, хотя мы могли бы запросить у пользователя значения коэффициентов, как мы делали это ранее, в данном случае мы собираемся предоставить их напрямую:

solutions = solve_square_equation(1. 17, -4.48, -0.5)
print(solutions)
solutions = solve_square_equation(4, -3, 1)
print(solutions)
soluciones = solve_square_equation(5, 1, 0)
print(solutions)
Code language: PHP (php)

Если мы непосредственно выведем содержимое списка решений, предоставленного нашей функцией, то получим следующее, где видно, что для первого случая у нас есть два решения, для второго нет решения, а для третьего два решения:

[3.9375907690225196, -0.10853093996269035]
[]
[0.0, -0.2]
Code language: JSON / JSON with Comments (json)

Проверка решений

В качестве дополнения, давайте теперь создадим еще одну функцию для проверки того, является ли число действительным решением, то есть действительным x, для заданного квадратного уравнения.

Для этого нам нужно определить функцию, которая принимает четыре различных параметра, где три из них будут коэффициентами a, b и c, а другой – значением проверяемого x.

Эта функция должна будет подставить эти четыре значения в общее выражение квадратного уравнения ax² + bx + c = 0 и проверить, что равенство выполняется.

Обратите внимание, что мы должны провести сравнение вещественных чисел. Всякий раз, когда нам приходится это делать, мы должны определить небольшой предел допустимой погрешности, в пределах которого мы можем считать два действительных числа равными. Это связано с тем, что, например, два числа 1.000000 и 1.000001 различны, если сравнивать их с помощью компаратора равенства ==, но в нашем случае мы можем захотеть считать их равными числами.

Таким образом, определив переменную margin как небольшую погрешность, например, 0,0001 (одна десятитысячная), наш код должен будет считать, что два числа, вычитание которых по абсолютной величине (для устранения отрицательного знака результата) меньше этой погрешности, равны. Таким образом, если взять числа d и e, то наше сравнение будет уже не d == e, а abs(d – e) <= margin.

Код нашей функции для проверки правильности решения будет выглядеть следующим образом:

def valid_solution(x, a, b, c, margin=0. 0001):
    return abs(a * x * x + b * x + c) < margin
Code language: JavaScript (javascript)

Обратите внимание, что я даю значение по умолчанию параметру margin, чтобы не указывать его в каждом вызове функции valid_solution.

Давайте протестируем нашу функцию на нескольких примерах, чтобы увидеть, как она работает:

print(valid_solution(3.9375, 1.17, -4.48, -0.5, margin=0.001))
print(valid_solution(0, 5, 1, 0))
print(valid_solution(2, 5, 1, 0))
print(valid_solution(0, 4, -3, 1))
Code language: PHP (php)

Как вы можете видеть, в первом случае я варьирую margin по своему усмотрению. В остальных случаях я оставляю значение маржи по умолчанию. Результатом выполнения этого кода является:

True
True
False
False
Code language: PHP (php)

И это все. Надеюсь, я пролил свет на этот классический пример для изучения программирования.

Решение квадратных уравнений

Квадратным уравнением называется уравнение вида , где .

— коэффициент при , или старший коэффициент.

— коэффициент при х, или второй коэффициент.

— свободный член.

Например, в уравнении , , .

B уравнении , ,

Если в квадратном уравнении или , то такое квадратное уравнение называется НЕПОЛНЫМ.

Неполное квадратное уравнение решается с помощью разложения на множители.

1. Если , то нужно вынести за скобки общий множитель.

Например,

Приравняем каждый множитель к нулю:

или

Ответ: {0, }

2. Если , то нужно разложить на множители по формуле разности квадратов:

Например:

Приравниваем каждый множитель к нулю, получаем:

или

Коротко это уравнение решается так:

В этом месте важно не забыть знак перед корнем!

Ответ: {}

Если в квадратном уравнении и , то такое квадратное уравнение называется ПОЛНЫМ.

Полное квадратное уравнение решается с помощью нахождения ДИСКРИМИНТА.

Дискриминант квадратного уравнения вычисляется по формуле:

Формулы для вычисления корней квадратного уравнения выглядят так:

В этих формулах дискриминант присутствует под знаком квадратного корня, поэтому

Eсли , то квадратное уравнение не имеет действительных корней.

Если , то квадратное уравнение имеет два различных действительных корня, которые можно найти по приведенным выше формулам.

Если , то квадратное уравнение имеет два совпадающих корня:

Иногда говорят, что в этом случае квадратное уравнение имеет один корень.

Итак, при решении квадратного уравнения удобно пользоваться таким алгоритмом:

1. Определяем, является ли квадратное уравнение полным, или неполным.

2. Если уравнение неполное, раскладываем левую часть на множители и приравниваем каждый множитель к нулю.

3. Если уравнение полное, то

находим дискриминант квадратного уравнения по формуле
если дискриминант меньше нуля, то записываем, что квадратное уравнение не имеет действительных корней
если дискриминант равен нулю, то находим корни квадратного уравнения по формуле
если дискриминант больше нуля, то находим корни квадратого уравнения по формулам:,

Если коэффициент квадратного уравнения — четное число, то есть его можно записать как , или то для нахождения корней квадратного уравнения удобно пользоваться формулами для четного второго коэффициента:

Два полезных замечания:

1. Если для коэффициентов квадратного уравнения выполняется равенство , то ,

2. Если для коэффициентов квадратного уравнения выполняется равенство , то ,

Эти свойства помогают устно решать некоторые громоздкие квадратные уравнения. Например, в квадратном уравнении сумма коэффициентов равна 0, поэтому , .

В уравнении выполняется равенство , поэтому ,

Рассмотрим несколько примеров.

Решим квадратные уравнения:

а) найдем дискриминант этого уравнения:

Дискриминант больше нуля, значит уравнение имеет два различных корня.

б) Тогда: ,

Ответ: {1; 1/2}

а) Найдем дискриминант этого уравнения:

. Очевидно, что , и даже нет необходимости вычислять его точное значение.

Ответ: уравнение не имеет действительных корней.

а) Найдем дискриминант этого уравнения:

б) Так как , уравнение имеет два совпадающих корня,

Если внимательно посмотреть на квадратный трехчлен, стоящий в левой части уравнения, то становится очевидно, то что его можно преобразовать по формуле квадрата разности к выражению

, отсюда

Ответ: 1/4.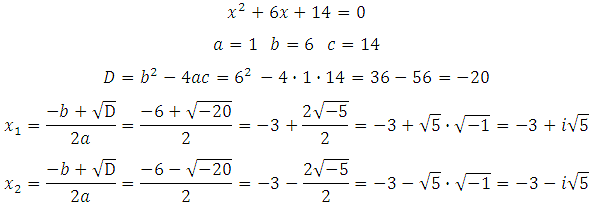

А теперь я предлагаю вам посмотреть видеоурок с решением квадратного уравнения:

И.В. Фельдман, репетитор по математике.

2 — 4 ac , называется дискриминантом и может использоваться для определения количества и типа решений квадратного уравнения, не выполняя всю работу по поиску фактических решений.

Кроме того, если дискриминант отрицателен, мы получим два невещественных решения (комплексные решения). Если дискриминант представляет собой полный квадрат, то уравнение будет иметь рациональные решения.

Используйте Дискриминант, чтобы определить число и введите решения .

Если дискриминант представляет собой полный квадрат, то квадратичный фактор можно разложить на множители. В этом случае обычно более эффективно решать с помощью факторинга, и это следует делать именно так, если не указано иное. Однако обратите внимание, что какой бы метод вы ни выбрали, вы должны получить одинаковые ответы.

Решить .

Слова «проблемы» в этой главе должны показаться вам знакомыми. Настройки аналогичны, но обычно приводят к квадратным уравнениям. Вы можете использовать квадратичную формулу или любой другой метод, изученный до сих пор, чтобы решить их.

Геометрическая задача : Площадь квадрата 32 квадратных фута. Найдите длину каждой стороны квадрата.

Геометрическая задача м: Площадь круга равна квадратным сантиметрам. Найдите длину диаметра.

Геометрическая задача : Длина прямоугольника в 2 раза меньше его ширины, чем в 3 раза. Найдите площадь прямоугольника, если его площадь равна 65 квадратных метров.

Ти p: Не забудьте указать в ответе правильные единицы измерения. Большинство инструкторов снимут несколько баллов, если вы пренебрежете единицами измерения.

Геометрическая задача : Основание треугольника в два раза больше его высоты. Найдите длину основания и высоту, если площадь треугольника 25 квадратных дюймов.

Для любого прямоугольного треугольника сумма квадратов катетов будет равна квадрату гипотенузы. Используйте это соотношение, чтобы найти любую недостающую часть треугольника при любых двух других сторонах.

Теорема Пифагора Задача : Длины катетов прямоугольного треугольника равны 6 дюймам и 8 дюймам. Найдите длину гипотенузы.

Теорема Пифагора Задача : Основание 10-футовой лестницы расположено в 4 футах от стены и прислонено к ней. Определите высоту лестницы.

Теорема Пифагора Задача : Экран компьютера имеет размеры 14,5 дюймов на 11 дюймов. Найдите длину диагонали.

Теорема Пифагора Задача : Если Джо проехал 100 миль на юг и 50 миль на запад до пляжа, то как далеко он находится от дома?

Если объект запускается с высоты s футов с начальной скоростью футов в секунду, его высота определяется следующей формулой.

Проблема со снарядом : Объект брошен с земли с начальной скоростью 32 фута в секунду. Через какое время объект вернется на землю?

Проблема со снарядом : Объект запускается с вершины 32-футового здания с начальной скоростью 128 футов в секунду. Сколько времени потребуется, чтобы достичь земли?

Проблема со снарядом : Объект запускается с уровня земли со скоростью 128 футов в секунду. Сколько времени потребуется, чтобы достичь высоты 256 футов?

Вспомните формулы для расчета рабочей силы из главы 7.

Проблема с нормой рабочей силы . Обычно сыну Джо требуется на 2 часа больше времени, когда он работает в одиночку, чтобы выполнить еженедельную работу во дворе. Если Джо и его сын делают работу вместе, это занимает 1 1/2 часа. Сколько времени потребуется Джо, чтобы работать во дворе в одиночку?

Примеры видео на YouTube :

Комплексные номера

PDF

КОМПЛЕКСНЫЕ ЧИСЛА

Обзор устройства
В этом блоке вводятся мнимые и комплексные числа. Комплексные числа расширены за счет включения воображаемых решений квадратных уравнений. Рассматриваются операции с комплексными числами, в том числе рационализация знаменателя дробей, имеющих в знаменателе радикалы Дискриминант
Дискриминант квадратного уравнения дает представление о количестве корней и природе корней уравнения. Если ах ² + бх + с = 0 является уравнением, тогда дискриминант уравнения равен b ² − 4 ac .

Дискриминант можно увидеть в квадратичной формуле. Дискриминант — это выражение под радикалом, б ² − 4 ак .

Типы решений

*Мнимые решения — это числа, содержащие квадратный корень из отрицательного числа. Квадратный корень из отрицательного числа равен undefined в «действительной» системе счисления. В следующем разделе мы расширим систему счисления, включив в нее комплексные числа, имеющие мнимые части.

Пример #1 : Найдите дискриминант и определите количество решений для каждого из приведенных ниже квадратичных уравнений.

1.) 3 x ² − 6 x + 4 = 0	2.) 4 х ² − 20 х + 25 = 0	*3. ) 9 x ² + 12 x = −2
б ² − 4 ак	б ² − 4 ак	б ² − 4 ак
(−6) ² − 4(3)(4)	(−20) ² − 4(4)(25)	(12) ² − 4(9)(2)
36 − 48 = −12	400 − 400 = 0	144 − 72 = 72
2 воображаемых решения	1 реальное решение	2 реальных решения

*Примечание. В третьем квадратном уравнении представьте квадратное уравнение в стандартной форме:
. 9 х ² + 12 х = 0, чтобы определить a = 9, b = 12 и c = 2.

Квадратичная формула (06:38) Стоп! Перейдите к вопросам 1–3 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу.

Воображаемые числа

При работе с квадратичной формулой дискриминант иногда бывает отрицательным. В этом случае мы можем еще больше упростить формулу, если будем знать о мнимых и комплексных числах.

Мнимое число — это число в форме ai , где a — любое действительное число, а i ² = −1; таким образом i = .

При нахождении квадратного корня из отрицательного числа первое, что нужно сделать, это вынести за скобки (–1), что равно i.
Пример №1 : Упрощение:

Мнимые и комплексные числа — Электричество (04:35)
Пример №2 : Упростить:

Пример №3 : Упрощение:
Циклические степени числа i

Силы и являются циклическими и повторяются по схеме из 4 цифр. Таким образом, силы чисел и имеют четыре возможных исхода.

Если мы продолжим рисунок, мы имеем следующее:
I ⁵ = I ⁴ ⋅ I = (1) I ⋅ I = (1) I = I = (1) I = I = (1) I = I = = = I = = I = = I = = I = .

я ⁶ = я ⁴ ⋅ i ² = (1)(−1) = −1

i ⁷ = i ⁴ ⋅ i ³ = (1)(− i ) 3 0

i ⁸ = i ⁴ ⋅ i ⁴ = (1)(1) = 1

Таблица ниже расширена, чтобы показать циклический шаблон.

Давайте подробнее рассмотрим этот шаблон.
Каковы значения i ⁹ , i ¹⁰ , i ¹¹ и i ^{3 13} ?
и , 1, и , и 1
«Нажмите здесь», чтобы проверить ответ.
Когда степени i равны единице ( i ⁴ = 1, i ⁸ = 1, i ¹² = 1 и так далее),
), степени i кратны какому числу?
Четыре
«Нажмите здесь», чтобы проверить ответ.
Сколько стоит я ⁹⁹ ?
i ⁹⁹ = i ⁹⁶ * i ³ = 1 * i = i
3
«Нажмите здесь», чтобы проверить ответ.
Пример #4 : i ²⁶ = ?
я ²⁶ = я ²⁴ ⋅ и ² Запишите показатели как произведение показателей.
      = 1 ⋅ i ² i ²⁴ = 1 (Циклическая модель показывает, что показатели степени i , кратные 4, равны 1.)
      = 1 ⋅ (−1)
      = −1
i ² = −1

i ²⁶ = −1

Стоп! Перейдите к вопросам 4–9 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу.
Комплексные номера

*Два комплексных числа равны, если равны действительные части и равны мнимые части.
Пример №1 : Решите для « x » и « y »: −3 x + 4 iy = 21 − 16 i
настоящие детали
воображаемые части
−3 х = 21
4 iy = −16 i
     x = −7
у = -4

Таким образом, x = –7 и y = –4

Комплексные числа — Электричество (03:15)
Теперь давайте посмотрим, как мнимые числа используются для нахождения решений некоторых квадратных уравнений, решения которых представлены в виде комплексных чисел.
Пример #2 : Найдите решение следующего квадратного уравнения:   x ² − 4 x + 13 = 0,6 6

Пример #3 : Найдите решение следующего квадратного уравнения: 6 x ² − 3 x + 1 = 0,

Стоп! Перейдите к вопросам № 10–13 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу.
Вычисления с комплексными числами
Сложение и вычитание комплексных чисел

Чтобы сложить или вычесть комплексные числа:
— объединить действительные части
-соединить мнимые части

Пример #1 : Найдите сумму: (−10 − 6 i ) + (8 − i )
(−10 − 6 i ) + (8 − i )
−10 – 6 i + (8 – i ) Пишите без скобок.
(−10 + 8) + (− 6 i − i ) Переставить действительную и мнимую части.
−2 + −7 i Объединить действительную и мнимую части.
−2 −7 я Упростить

Пример #2 : Найдите разницу: (−9 + 2 i ) − (3 − 4 i )
(−9 + 2 i ) − (3 − 4 i )
−9 + 2 i −3 + 4 i Пишите без скобок. (Примечание – −4 90 130 i = +4 i )
−9 − 3 + 2 и + 4 и Переставить действительную и мнимую части.
−12 + 6 i Объединить действительную и мнимую части.
Умножение комплексных чисел

Умножение двух комплексных чисел выполняется аналогично умножению двух двучленов. Вы можете использовать процесс умножения FOIL.
Чтобы умножить комплексные числа в форме двучлена на двучлен:
-умножение ФОЛЬГОЙ
-комбинировать подобные термины
-изменить i ² на (−1)

Пример #3 : Найдите произведение: (2 − i )(−3 − 4 i )
(2 − i )(−3 − 4 i )
−6 − 8 i + 3 i + 4 i ² ФОЛЬГА
−6 − 8 i + 3 i + 4(−1) Экспресс я ² = −1
−6 − 5 i − 4 Упростить
−10 − 5 i Соедините настоящие части.

Пример № 4 : Найдите произведение:0131 )(−4 + 5 i )
−32 + 40 i + 12 i − 15 i ² ФОЛЬГА
−32 + 40 i + 12 i − 15(−1) Экспресс i ² = −1
−32 + 52 i + 15 Упростить
−17 + 52 i Соедините настоящие части.

В следующем примере мнимое число умножается на комплексное число с применением распределительного свойства. Пример #5 : Найдите продукт:0131 ) 5 i (−7) −5 i (2 i ) Распространение −35 i − 10 i ² Упростить −35 i − 10(−1) Экспресс i ² = −1 −35 i + 10 Упростить 10 − 35 i Примените свойство коммутативности, чтобы выразить комплексное число в правильной форме.

Стоп! Перейдите к вопросам 14–21 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу.

Конъюгат комплексного числа

Чтобы упростить дробь, содержащую комплексные числа, часто нужно использовать сопряжение комплексного числа . Например, сопряжение 3 + 5 i равно 3 − 5 i , а сопряжение 4 − 9 i равно 4 + 9 i.

Чтобы упростить частное с мнимым числом в знаменателе, умножьте на дробь, равную 1, используя сопряжение знаменателя. это называется рационализация знаменателя .

Пример №1 : Рационализировать знаменатель для данного комплексного числа.

Пример № 2 : рационализируйте знаменатель для данного комплексного числа.