Уравнения с модулями 7 класс объяснение: Решение уравнений с модулем в курсе математики 7-8 класса

Алгебраическое и графическое решение уравнений, содержащих модули реферат по математике | Сочинения Математика

Скачай Алгебраическое и графическое решение уравнений, содержащих модули реферат по математике и еще Сочинения в формате PDF Математика только на Docsity! Алгебраическое и графическое решение уравнений, содержащих модули Цель работы: хотя уравнения с модулями ученики начинают изучать уже с 6-го – 7-го класса, где они проходят самые азы уравнений с модулями. Я выбрал именно эту тему, потому что считаю, что она требует более глубокого и досканального исследования. Я хочу получить более широкие знания о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины. 1. Введение: Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово(омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, програмировании и других точных науках. В архитектуре-это исходная еденица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике-это термин, применяемый в различных облостях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению. 2. Понятия и определения Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы: Уравнение-это равенство, сродержащее переменные. Уравнение с модулем-это уравнение, содержащие переменную под знаком абсолютной величины(под знаком модуля).Например: |x|=1 Решить уравнение-это значит найти все его корни, или доказать, что корней нет. В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно: Модуль-абсолютная величина числа, равная расстоянию от начала отсчета до точки на числовой прямой. 3. Доказательство теорем Определение. Модуль числа a или абсолютная величина числа a равна a, если a больше или равно нулю и равна -a, если a меньше нуля: Из определения следует, что для любого действительного числа a, Теорема 1. Абсолютная величина действительного числа равна большему из двух чисел a или -a. Доказательство 1. Если число a положительно, то -a отрицательно, т. е. -a < 0 < a. Отсюда следует, что — a < a. Например, число 5 положительно, тогда -5 — отрицательно и -5 < 0 < 5, отсюда -5 < 5. В этом случае |a| = a, т. е. |a| совпадает с большим из двух чисел a и — a. 2. Если a отрицательно, тогда -a положительно и a < — a, т. е. большим числом является — a. По определению, в этом случае, |a| = -a — снова, равно большему из двух чисел -a и a. Следствие 1. Из теоремы следует, что |-a| = |a|. В самом деле, как , так и равны большему из чисел -a и a, а значит равны между собой. Следствие 2. Для любого действительного числа a справедливы неравенства Умножая второе равенство на -1 (при этом знак неравенства изменится на противоположный), мы получим следующие неравенства: справедливые для любого действительного числа a. Объединяя последние два неравенства в одно, получаем: Теорема 2. Абсолютная величина любого действительного числа a равна арифметическому квадратному корню из В самом деле, если то, по определению модуля числа, будем иметь С другой стороны, при значит |a| = Если a < 0, тогда |a| = -a и и в этом случае |a| = Эта теорема дает возможность при решении некоторых задач заменять |a| на Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчета. Если то на координатной прямой существует две точки a и -a, равноудаленной от нуля, модули которых равны. Если a = 0, то на координатной прямой |a| изображается точкой 0 (см. рис.) Рис 4.Способы решения уравнений, содержащих модуль. Для решения уравнений, содержащих знак абсолютной величины, мы будем основыватся на определении модуля числа и свойствах абсолютной величины числа. Мы решим несколько примеров одним и тем же способом и посмотрим, какой из способов окажется проще для решения уравнений, содержащих модуль. Пример 1. Решитм аналитически и графически уравнение |x — 2| = 3. Решение Аналитическое решение 1-й способ Рассуждать будем, исходя из определения модуля. Если выражение, находящееся под модулем неотрицательно, т. е. x — 2 0, тогда оно «выйдет» из под знака модуля со знаком «плюс» и уравнение примет вид: x — 2 = 3. Если значения выражения под знаком модуля отрицательно, тогда, по определению, оно будет равно: или x — 2=-3 Таким образом, получаем, либо x — 2 = 3, либо x — 2 = -3. Решая полученные уравнения, находим: Рис. 11 Графики не пересекаются, значит уравнение не имеет решений (см. рис. 11). Ответ: нет решений. Пример 3. Решите аналитически и графически уравнение |-x + 2| = 2x + 1. Решение: Аналитическое решение 1-й способ Прежде следует установить область допустимых значений переменной. Возникает естественный вопрос, почему в предыдущих примерах не было необходимости делать этого, а сейчас она возникла. Дело в том, что в этом примере в левой части уравнения модуль некоторого выражения, а в правой части не число, а выражение с переменной, — именно это важное обстоятельство отличает данный пример от предыдущих. Поскольку в левой части — модуль, а в правой части, выражение, содержащее переменную, необходимо потребовать, чтобы это выражение было неотрицательным, т. е. Таким образом, область допустимых значений модуля Теперь можно рассуждать также, как и в примере 1, когда в правой части равенства находилось положительной число. Получим две смешанных системы: (1) и (2) Решим каждую систему: (1) входит в промежуток и является корнем уравнения. (2) x = -3 не входит в промежуток и не является корнем уравнения. Ответ: 2-й способ Установим, при каких значениях x модуль в левой части уравнения обращается в нуль: Получим два промежутка, на каждом из которых решим данное уравнение (см. рис. 12): Рис. 12 В результате будем иметь совокупность смешанных систем: Решая полученные системы, находим: (1) входит в промежуток и является корнем уравнения. (2) не входит в промежуток и x=-3 не является корнем уравнения Ответ: 4.1.Решение при помощи зависимостей между числами a и b, их модулями и квадратами этих чисел. Помимо приведенных мною выше способов существует определенная равносильность, между числами и модулями данных чисел, а также между квадратами и модулями данных чисел: |a|=|b| F 0D B a=b или a=-b a2=b2 F 0D B a=b или a=-b (1) Отсюда в свою очередь получим, что F 0 D B|a|=|b| a2=b2 (2) Пример 4. Решим уравнение |x + 1|=|2x – 5| двумя различными способами. 1.Учитывая соотношение (1), получим: x + 1=2x – 5 или x + 1=-2x + 5 x – 2x=-5 – 1 x + 2x=5 – 1 -x=-6|(:1) 3x=4 x=6 x=11/3 Корень первого уравнения x=6, корень второго уравнения x=11/3 Таким образом корни исходного уравнения x1=6, x2=11/3 2. В силу соотношения (2), получим (x + 1)2=(2x – 5)2, или x2 + 2x + 1=4×2 – 20x + 25 x2 – 4×2 +2x+1 + 20x – 25=0 -3×2 + 22x – 24=0|(:-1) 3×2 – 22x + 24=0 F 0 B 4 F 0 D ED/4=121-3 24=121 – 72=49>0 уравнение имеет 2 различных корня. x1=(11 – 7 )/3=11/3 x2=(11 + 7 )/3=6 Как показывает решение, корнями данного уравнения также являются числа 11/3 и 6 Ответ: x1=6, x2=11/3 Пример 5. Решим уравнение (2x + 3)2=(x – 1)2. Учитывая соотношение (2), получим, что |2x + 3|=|x – 1|, откуда по образцу предыдущего примера(и по соотношению (1)): 2х + 3=х – 1 или 2х + 3=-х + 1 2х – х=-1 – 3 2х+ х=1 – 3 х=-4 х=-0,(6) Таким образом корнями уравнения являются х1=-4, и х2=-0,(6) Ответ: х1=-4, х2=0,(6) Пример 6. Решим уравнение |x – 6|=|x2 – 5x + 9| Пользуясь соотношением (1), получим: х – 6=х2 – 5х + 9 или х – 6 = -(х2 – 5х + 9) -х2 + 5х + х – 6 – 9=0 |(-1) x – 6=-x2 + 5x — 9 x2 — 6x + 15=0 x2 – 4x + 3=0 F 0 2 A F 0 D E F 0 2 A F 0 D ED=36 – 4 15=36 – 60= -24 <0 D=16 – 4 3=4 >0 2 р.к. F 0 D E корней нет. x1=(4- 2 ) /2=1 x2=(4 + 2 ) /2=3 F 0 2 A F 0 2 AПроверка: |1 – 6|=|12 – 5 1 + 9| |3 – 6|=|32 – 5 3 + 9| 5 = 5(И) 3 = |9 – 15 + 9| 3 = 3(И) Ответ: x1=1; x2=3 4.2.Использование геометрической интерпритации модуля для решения уравнений. Геометрический смысл модуля разности величин-это расстояние между ними. Например, геометрический смысл выражения |x – a | -длина отрезка координатной оси, соединяющей точки с абсцисами а и х . Перевод алгеб-раической задачи на геометрический язык часто позволяет избежать громоздких решений. Пример7. Решим уравнение |x – 1| + |x – 2|=1 с использованием геометрической интерпритации модуля. Будем рассуждать следующим образом: исходя из геометрической интерпри-тации модуля, левая часть уравнения представляет собой сумму расстояний от некторой точки абсцисс х до двух фиксированных точек с абсциссами 1 и 2. Тогда очевидно, что все точки с абсциссами из отрезка [1; 2] обладают требуемым свойством, а точки, расположенные вне этого отрезка- нет. Отсюда ответ: множеством решений уравнения является отрезок [1; 2]. F 0 C EОтвет: х [1; 2] Пример8. Решим уравнение |x – 1| — |x – 2|=1 1 с использованием геометрической интерпритации модуля. Будем рассуждать аналогично предыдущему примеру, при этом получим, что разность расстояний до точек с абсциссами 1 и 2 равна единице только для точек, расположенных на координатной оси правее числа 2. Следовательно решением данного уравнения будет являтся не отрезок, заключенный между точками 1 и 2, а луч, выходящий из точки 2, и направленный в положительном направлении оси ОХ. F 0 C E F 0 A 5Ответ: х [2; + ) Обобщением вышеприведенных уравнений являются следующие равносильные переходы: |x – a| + |x – b|=b – a, где b F 0B 3 a F 0 D B a F 0 A 3 x F 0 A 3 b |x – a| — |x – b|=b – a, где b F 0B 3 a F 0 D B x F 0 B 3 b 4.3. Графики простейших функций, содержащих знак абсолютной величины Под простейшими функциями понимают алгебраическую сумму модулей линейных выражений. Сформулируем утверждение, позволяющее строить графики таких функций, не раскрывая модули ( что особенно важно, когда модулей достаточно много ): «Алгебраическая сумма модулей n линейных выражений представляет собой кусочно- линейную функцию, график которой состоит из n +1 прямолинейного отрезка. Тогда график может быть построен по n +2 точкам, n из которых представляют собой корни внутримодульных выражений, ещё одна — произвольная точка с абсциссой, меньшей меньшего из этих корней и последняя — с абсциссой, большей большего из корней. Например: 1)f(x)=|x — 1| Вычисляя функции в точках 1, 0 и 2, получаем график, состоящий из двух отрезков(рис.1) Уравнение равносильно системе Ответ: Пример12.Решить уравнение х2 — 4х +|x — 3| +3=0 Для освобождения от знака абсолютной величины разобьем числовую прямую на две области и будем искать решения исходного уравнения в каждой из этих областей отдельно: F 0 B 3__________x 3__________________|____________x<3_________________ |x – 3|=x – 3 |x – 3|=-x + 3 x2 — 4x + x – 3 + 3=0 x2 – 4x – x + 3 + 3=0 x2 – 3x=0 x2 – 5x + 6=0 x(x – 3) x1=0 или F 02 A F 0 D Ex2=3 D=25 – 4 6=1> 0 два различ. корня x=0 –посторонний корень, так как x1= (5- 1 )/2 =2 не удовлетворяет промежутку. x2=(5 + 1)/2=3 x=3 — посторонний корень, так как не удовлетворяет промежутку. Значит, исходное уравнение имеет два решения х1=2 и х2=3 Ответ: х1=2, х2=3 Пример13. Решить уравнение | 2x + 8 | – | x – 5 | = 12. Решение. Раскрытие пары модулей приводит к трем случаям (без F 0A 3 F 0 2 0 F 0 B 3x + 4 0, x – 5 0). Ответ: {– 25; 3}. Пример 14. Решить уравнение . Решение: Напишем равносильную смешанную систему: Ответ: х=-4 Пример 15 Решить графически уравнение |1 – x| — |2x + 3| + x + 4=0 Решение: Представим уравнение в виде |1 – x| — |2x + 3| =-х – 4 Построим два графика у=|1 – x| — |2x + 3| и у=-х – 4 1) у=|1 – x| — |2x + 3| Критические точки: х=1, х=-1.5 (1 – х) ________+________|______ +____________|_____-______ > (2х +3) — -1.5 + 1 + а) х< -1.5, (1– x)>0 и (2х + 3)<0, т.е функция примет вид у=1 – х + 2х + 3, у=х + 4 –графиком является прямая, проходящая через две точки (0; 4), (-4; 0) F 0 2 0 F 0 A 3б)При -1.5 x <1, (1 – х)>0 и (2x +3 F 0 B 3) 0, т.е функция примет вид у=1 – х – 2х -3, у=-3х – 2 –графиком является прямая, проходящая через две точки (0; -2), (-1; 1). F 0 2 0 F 0 B 3 F 0 2 0 F 0 A 3в)При х 1, (1 – х) 0 и (2х + 3)>0, т.е. функция примет вид у= -1 + х – 2х – 3, у= -х – 4 –графиком является прямая, проходящая через две точки (0; -4), (-4; 0). График функции у= — х – 4 совпадает с графиком у=|1 – x| — |2x + 3|, F 02 0 F 0 B 3при х 1, F 0 2 0 F 0 B 3Поэтому решением являются все х 1 и х= -4 F 0 2 0 F 0 B 3Ответ: х 1,х= -4 Аналитическое решение. y=|1 – x| — |2x + 3| y=-x – 4 Построим числовую прямую так, чтобы по определению модуля знак абсолютной величины числа можно будет снять. Для этого найдем критические точки: 1- х=0 и 2х – 3 =0, х=1 х=-1,5 F 0 A 3___________х<-1,5_____|_______-1,5 F 0 B 3x <1_____|_________x 1__________ |1 – x|=1 – x |1 – x|=1 – x |1 – x|=-1 + x |2x + 3|=-2x – 3 |2x + 3|=2x + 3 |2x + 3|=2x + 3 1 – x + 2x + 3 + x + 4=0 1 – x – 2x – 3 + x +4=0 -1 + x – 2x – 3 + x + 4=0 2x=-8 -2x=-2 0x=0 F 0 D Ex=-4 x=1 x – любое число. F 0 D EУдовлетворяет данному Не удовлетворяет F 0 C E F 0 A 5x [1; + ) F 0 D E F 0 D Eпромежутку является данному промежут- F 0 B 3x 1 корень уравнения F 0 D Eкорнем уравнения. ку не является кор- нем уравнения. Объеденив данные промежутки, получим, что решением данного уравнения являются: x=-4 и F 0B 3x 1 Ответ: F 0B 3x=-4, x 1

Решение уравнений с параметрами содержащие модуль решением. Решение уравнений с модулем и параметром план-конспект занятия по алгебре (10 класс) на тему

06.11.2019

К задачам с параметром можно отнести, например, поиск решения линейных и квадратных уравнений в общем виде, исследование уравнения на количество имеющихся корней в зависимости от значения параметра.

Не приводя подробных определений, в качестве примеров рассмотрим следующие уравнения:

у = kx, где x, y – переменные, k – параметр;

у = kx + b, где x, y – переменные, k и b – параметр;

аx 2 + bх + с = 0, где x – переменные, а, b и с – параметр.

Решить уравнение (неравенство, систему) с параметром это значит, как правило, решить бесконечное множество уравнений (неравенств, систем).

Задачи с параметром можно условно разделить на два типа:

а) в условии сказано: решить уравнение (неравенство, систему) – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя.

б) требуется указать возможные значения параметра, при которых уравнение (неравенство, система) обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.

Параметр, являясь неизвестным фиксированным числом, имеет как бы особую двойственность. В первую очередь, необходимо учитывать, что предполагаемая известность говорит о том, что параметр необходимо воспринимать как число. Во вторую очередь, свобода обращения с параметром ограничивается его неизвестностью. Так, например, операции деления на выражение, в котором присутствует параметр или извлечения корня четной степени из подобного выражения требуют предварительных исследований.

Поэтому необходима аккуратность в обращении с параметром.

Например, чтобы сравнить два числа -6а и 3а, необходимо рассмотреть три случая:

1) -6a будет больше 3a, если а отрицательное число;

2) -6а = 3а в случае, когда а = 0;

3) -6а будет меньше, чем 3а, если а – число положительное 0.

Решение и будет являться ответом.

Пусть дано уравнение kx = b. Это уравнение – краткая запись бесконечного множества уравнений с одной переменной.

При решении таких уравнений могут быть случаи:

1. Пусть k – любое действительное число не равное нулю и b – любое число изR, тогда x = b/k.

2. Пусть k = 0 и b ≠ 0, исходное уравнение примет вид 0 · x = b. Очевидно, что у такого уравнения решений нет.

3. Пусть k и b числа, равные нулю, тогда имеем равенство 0 · x = 0. Его решение – любое действительное число.

Алгоритм решения такого типа уравнений:

1. Определить «контрольные» значения параметра.

2. Решить исходное уравнение относительно х при тех значениях параметра, которые были определены в первом пункте.

3. Решить исходное уравнение относительно х при значениях параметра, отличающихся от выбранных в первом пункте.

4. Записать ответ можно в следующем виде:

1) при … (значения параметра), уравнение имеет корни …;

2) при … (значения параметра), в уравнении корней нет.

Пример 1.

Решить уравнение с параметром |6 – x| = a.

Решение.

Легко видеть, что здесь a ≥ 0.

По правилу модуля 6 – x = ±a, выразим х:

Ответ: х = 6 ± a, где a ≥ 0.

Пример 2.

Решить уравнение a(х – 1) + 2(х – 1) = 0 относительно переменной х.

Решение.

Раскроем скобки: aх – а + 2х – 2 = 0

Запишем уравнение в стандартном виде: х(а + 2) = а + 2.

В случае, если выражение а + 2 не нуль, т. е. если а ≠ -2, имеем решение х = (а + 2) / (а + 2), т.е. х = 1.

В случае, если а + 2 равно нулю, т.е. а = -2, то имеем верное равенство 0 · x = 0, поэтому х – любое действительное число.

Ответ: х = 1 при а ≠ -2 и х € R при а = -2.

Пример 3.

Решить уравнение x/a + 1 = а + х относительно переменной х.

Решение.

Если а = 0, то преобразуем уравнение к виду а + х = а 2 + ах или (а – 1)х = -а(а – 1). Последнее уравнение при а = 1 имеет вид 0 · x = 0, следовательно, х – любое число.

Если а ≠ 1, то последнее уравнение примет вид х = -а.

Данное решение можно проиллюстрировать на координатной прямой (рис. 1)

Ответ: нет решений при а = 0; х – любое число при а = 1; х = -а при а ≠ 0 и а ≠ 1.

Графический метод

Рассмотрим еще один способ решения уравнений с параметром – графический. Этот метод применяется достаточно часто.

Пример 4.

Сколько корней в зависимости от параметра a имеет уравнение ||x| – 2| = a?

Решение.

Для решения графическим методом строим графики функций y = ||x| – 2| и y = a (рис. 2) .

На чертеже наглядно видны возможные случаи расположения прямой y = a и количество корней в каждом из них.

Ответ: корней у уравнения не будет, если а 2 и а = 0; три корня уравнение будет иметь в случае а = 2; четыре корня – при 0

Пример 5.

При каком а уравнение 2|x| + |x – 1| = a имеет единственный корень?

Решение.

Изобразим графики функций y = 2|x| + |x – 1| и y = a. Для y = 2|x| + |x – 1|, раскрыв модули методом промежутков, получим:

{-3x + 1, при x

y = {x + 1, при 0 ≤ x ≤ 1,

{3x – 1, при x > 1.

На рисунке 3 хорошо видно, что единственный корень уравнение будет иметь только при а = 1.

Ответ: а = 1.

Пример 6.

Определить число решений уравнения |x + 1| + |x + 2| = a в зависимости от параметра а?

Решение.

График функции y = |x + 1| + |x + 2| будет представлять собой ломаную. Ее вершины будут располагаться в точках (-2; 1) и (-1; 1) (рисунок 4) .

Ответ: если параметр a будет меньше единицы, то корней у уравнения не будет; если а = 1, то решение уравнения является бесконечное множество чисел из отрезка [-2; -1]; если значения параметра а будут больше одного, то уравнение будет иметь два корня.

Остались вопросы? Не знаете, как решать уравнения с параметром?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Занятие «Решение линейных уравнений с параметром, содержащих модуль».

Цель: сформировать умение решать линейные уравнения с параметром, содержащие модуль; развивать логическое мышление и навыки самостоятельной работы.

Оборудование: презентация.

Ход урока.

1.Для актуализации знаний учащихся необходимо повторить понятие модуля и решить несколько уравнений с модулем: |х|=3; |х|= — 5; |х|=0.

Затем предложить учащимся ответить на вопрос: Сколько корней может иметь уравнение с модулем и от чего это зависит?

Вывод содержится на 2 слайде. Его записывают в тетради.

Разбор решения уравнения |х — 2 |= 3

Фронтальная работа с классом: решение уравнения 1. |х + 4 |= 0.

Самостоятельное решение уравнений:

2. |х — 3 |= 5; 3. |4 — х |= 7; 4. |5 — х |= — 9. Проверка.

Разбор решения задание 1 :

Определите число корней уравнения

||х| +5 — а |= 2. (слайд 3)

Комментарии учителя: это уравнение с параметром, т.е. с переменной а. В зависимости от значения этой переменной будет изменяться вид уравнения. А значит, и число корней уравнения зависит от а.

Предложить учащимся ответить на вопрос задания «Найдите все значения а, при каждом из которых уравнение ||х| +5 — а |= 2 имеет ровно 3 корня. (Если значений а более одного, то в бланке ответов запишите их сумму). Ответ: 7. (слайд 4)

Решить у доски задание 2: Найдите все значения а, при каждом из которых уравнение ||х| — 3 + а |= 4 имеет ровно 3 корня. Ответ: — 1.

Самостоятельная работа. Задание 3 .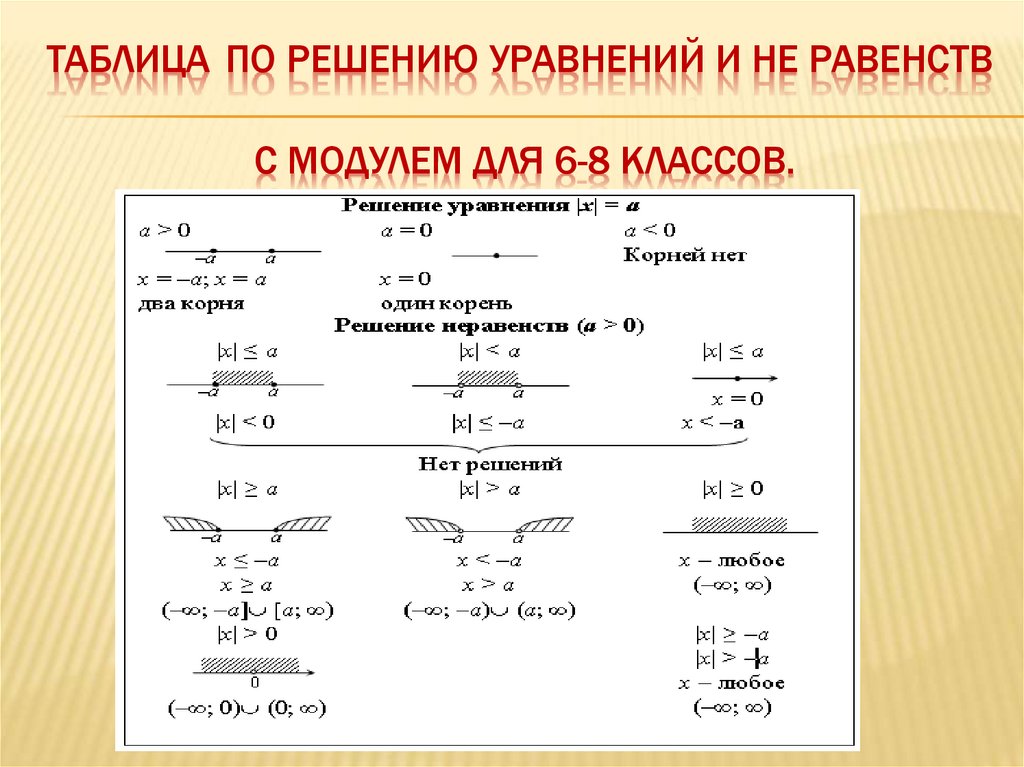

Найдите все значения а, при каждом из которых уравнение ||х| -4+ а |= 3 имеет ровно 1 корень. Ответ: 7.

Задание 4 . При каких значениях а уравнение

|а — 5 — |х||= 3 имеет нечетное число корней (если значений а более одного, то в бланке ответов запишите их сумму). Ответ: 10.

Предложить учащимся разобрать способ решения задания, используя свойство четности функции и графический способ.

7. Итог урока. Над чем вы сегодня работали на уроке? Было ли для вас что-то нового и познавательного? Над чем бы вы хотели поработать на следующем уроке?

«Линейное уравнение с двумя переменными» — Равенство, содержащее две переменные, называется уравнением с двумя переменными. -Что называется уравнением с двумя переменными? Приведите примеры. -Какое уравнение с двумя переменными называется линейным? Линейное уравнение с двумя переменными. Определение: Алгоритм доказательства, что данная пара чисел является решением уравнения:

«Решение показательных уравнений» — Сведение к одному основанию. Вынесение за скобки. Т. Виета. Графический способ. Показательным уравнением называют уравнение, содержащее переменную в показателе степени. Решение показательных уравнений. Устная работа. ab+ac=a(b+c). Степени. 2.Решить уравнение: Свойство. Виды и способы решения показательных уравнений.

«Графический способ решения уравнений» — Ответ: один корень, х=-1. Два корня. Решить графически уравнение (х+1)/(х-2)=2. Построить график функции y=x?+6x+8. Практикум по решению уравнений графическим способом Подготовка к зачету. Построить графики функций. Построить график функции y=(x+1)/(x-2). 1. Перенесем 8 в правую часть уравнения. Корней нет.

«Решение целых уравнений» — «Уравнения, в которых скопом Корни, степень, неравенств бездна. Три великих математика. Удачи в дальнейшем изучении методов решения уравнений. Осевая симметрия присуща большинству видов растений и животных. Центральная. В животном мире 2 вида симметрии. Диктант. Осевая. Определите методы решения уравнений.

«Уравнения с логарифмами» — Логарифмические уравнения. Реши устно уравнения. Формулы преобразования логарифмов. Уравнение. Определение. Таблицы логарифмов. Определение логарифма. Определение и свойства логарифма. Логарифмическая линейка. Функция. Наушники или колонки. Область определения. Подходы к решению. Решить уравнение. Гимназия.

«Иррациональные уравнения» — На контроль д/з выполнили: №419 (в,г) Сафиуллина, №418(в,г) Кульмухаметов, №420(в,г)Шагеев. 2 урок Решение систем уравнений. Урок 1 Тема: Решение иррациональных уравнений. 1.Какие из следующих уравнений являются иррациональными: Цели: Познакомить учащихся с решениями некоторых видов иррациональных уравнений.

Всего в теме 49 презентаций

1. Системы линейных уравнений с параметром

Системы линейных уравнений с параметром решаются теми же основными методами, что и обычные системы уравнений: метод подстановки, метод сложения уравнений и графический метод. Знание графической интерпретации линейных систем позволяет легко ответить на вопрос о количестве корней и их существовании.

Пример 1.

Найти все значения для параметра а, при которых система уравнений не имеет решений.

{х + (а 2 – 3)у = а,
{х + у = 2.

Решение.

Рассмотрим несколько способов решения данного задания.

1 способ . Используем свойство: система не имеет решений, если отношение коэффициентов перед х равно отношению коэффициентов перед у, но не равно отношению свободных членов (а/а 1 = b/b 1 ≠ c/c 1). Тогда имеем:

1/1 = (а 2 – 3)/1 ≠ а/2 или систему

{а 2 – 3 = 1,
{а ≠ 2.

Из первого уравнения а 2 = 4, поэтому с учетом условия, что а ≠ 2, получаем ответ.

Ответ: а = -2.

2 способ . Решаем методом подстановки.

{2 – у + (а 2 – 3)у = а,
{х = 2 – у,

{(а 2 – 3)у – у = а – 2,
{х = 2 – у.

После вынесения в первом уравнении общего множителя у за скобки, получим:

{(а 2 – 4)у = а – 2,
{х = 2 – у.

Система не имеет решений, если первое уравнение не будет иметь решений, то есть

{а 2 – 4 = 0,
{а – 2 ≠ 0.

Очевидно, что а = ±2, но с учетом второго условия в ответ идет только ответ с минусом.

Ответ: а = -2.

Пример 2.

Найти все значения для параметра а, при которых система уравнений имеет бесконечное множество решений.

{8х + ау = 2,
{ах + 2у = 1.

Решение.

По свойству, если отношение коэффициентов при х и у одинаковое, и равно отношению свободных членов системы, то она имеет бесконечное множество решений (т. е. а/а 1 = b/b 1 = c/c 1). Следовательно 8/а = а/2 = 2/1. Решая каждое из полученных уравнений находим, что а = 4 – ответ в данном примере.

Ответ: а = 4.

2. Системы рациональных уравнений с параметром

Пример 3.

{3|х| + у = 2,
{|х| + 2у = a.

Решение.

Умножим первое уравнение системы на 2:

{6|х| + 2у = 4,
{|х| + 2у = a.

Вычтем из первого второе уравнение, получим 5|х| = 4 – а. Это уравнение будет иметь единственное решение при а = 4. В других случаях это уравнение будет иметь два решения (при а 4).

Ответ: а = 4.

Пример 4.

Найти все значения параметра а, при которых система уравнений имеет единственное решение.

{х + у = а,
{у – х 2 = 1.

Решение.

Данную систему решим с использованием графического метода. Так, графиком второго уравнения системы является парабола, поднятая по оси Оу вверх на один единичный отрезок. Первое уравнение задает множество прямых, параллельных прямой y = -x (рисунок 1) . Из рисунка хорошо видно, что система имеет решение, если прямая у = -х + а является касательной к параболе в точке с координатами (-0,5; 1,25). Подставив в уравнение прямой вместо х и у эти координаты, находим значение параметра а:

1,25 = 0,5 + а;

Ответ: а = 0,75.

Пример 5.

Используя метод подстановки, выясните, при каком значении параметра а, система имеет единственное решение.

{ах – у = а + 1,
{ах + (а + 2)у = 2.

Решение.

Из первого уравнения выразим у и подставим во второе:

{у = ах – а – 1,
{ах + (а + 2)(ах – а – 1) = 2.

Приведем второе уравнение к виду kx = b, которое будет иметь единственное решение при k ≠ 0. Имеем:

ах + а 2 х – а 2 – а + 2ах – 2а – 2 = 2;

а 2 х + 3ах = 2 + а 2 + 3а + 2.

Квадратный трехчлен а 2 + 3а + 2 представим в виде произведения скобок

(а + 2)(а + 1), а слева вынесем х за скобки:

(а 2 + 3а)х = 2 + (а + 2)(а + 1).

Очевидно, что а 2 + 3а не должно быть равным нулю, поэтому,

а 2 + 3а ≠ 0, а(а + 3) ≠ 0, а значит а ≠ 0 и ≠ -3.

Ответ: а ≠ 0; ≠ -3.

Пример 6.

Используя графический метод решения, определите, при каком значении параметра а, система имеет единственное решение.

{х 2 + у 2 = 9,
{у – |х| = а.

Решение.

Исходя из условия, строим окружность с центром в начале координат и радиусом 3 единичных отрезка, именно ее задает первое уравнение системы

х 2 + у 2 = 9. Второе уравнение системы (у = |х| + а) – ломаная. С помощью рисунка 2 рассматриваем все возможные случаи ее расположения относительно окружности. Легко видеть, что а = 3.

Ответ: а = 3.

Остались вопросы? Не знаете, как решать системы уравнений?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Модули справочного курса

Ниже приведены модули справочного или проблемного курса для классов математики средней и старшей школы. Они были разработаны в рамках проекта Math Circles of Inquiry, если не указано иное.

Контекстуализация математики: Fortnite — Surviving the Storm

• Было создано множество заданий, связанных с математикой в ​​контексте. Этот, как и большинство из них, относится к понятиям геометрии средней школы.

• Мы изучим отношения между углами, дугами и сегментами для пересекающихся линий в круге в контексте популярной игры Fortnite.

• Мы стремимся создать большую библиотеку заданий, которые контекстуализируют математику для ваших учеников, так что не стесняйтесь вносить свой вклад.

Эффективность с линейными уравнениями

• для учащихся, знакомых с линейными уравнениями, в основном для учащихся 8-х классов, учащихся алгебры I/II и геометрии

• Учащаяся работа начинается с очень простого и конкретного примера словесной задачи о линейных отношениях, который затем используется для изучения четырех форм линейных уравнений.

• Цель этого занятия – ознакомить учащихся и повысить эффективность работы с различными формами линейных уравнений, особенно с тем, как структура уравнения может предоставлять информацию о наклоне и точке без алгебраических манипуляций.

Показатели

• Проектированная или средняя школа, вероятно, 8 -й класс, но может быть использован в 7 -м классе или даже в алгебре

• , в которых изучается идеи, окружающие экспоненты

.

• Этот модуль представляет собой введение в модуль функций. и минимум, средняя скорость изменения и домен и диапазон.

• Эта часть модуля (не включая функции трансформации) должна занять около 6 часов занятий.

Соединение между различными формами квадратичных уравнений

• Алгебра средней школы II

• Опрос различных способов экспрессии Parabolas

• . Использование DESMOS. 7 класс (в первую очередь), затем произведения можно использовать на более высоких уровнях для повторения

• Содержит многочисленные задания, которые могут быть использованы по усмотрению учителя для построения дознания, развития данной темы или повторения этой темы.

Рациональные числа

• Вводное задание по рациональным числам, вероятно, связанное с 7 классом0003

• Акцент на рассуждениях как абстрактно, так и количественно

Соотношение и пропорциональные рассуждения

• ВВЕДЕНИЕ И ОБЗОРЫЙ ДЕЙСТВИТЕЛЬНЫЙ ДЕЙСТВИТЕЛЬНЫЙ ИСПОЛЬЗОВАНИЕ ИСПОЛЬЗОВАНИЯ ИСПОЛЬЗОВАНИЯ ИНТЕРМАЛИЧЕСКАЯ И НЕМЕНИНАНСКАЯ И НЕМЕНИНАНСКАЯ И НЕМЕНИНАЛЬНАЯ ИНТЕРМИКАНСКАЯ И НЕМЕНИЧЕСКАЯ И НИМНЕР.

• Упражнения на повторение дают учащимся выбор того, как проводить повторение

Прямоугольная тригонометрия: высоты партнера

• Применение тригонометрии прямого угла в задаче о двойном треугольнике

• Дает учащимся подлинный математический опыт, применяя тригонометрические концепции, которые они изучили в учебной программе по геометрии, для решения задачи нахождения высоты своих товарищей по группе

• Приблизительно один учебный период

Решение линейных уравнений

• Предназначен для учащихся 7 или 8 классов, но также может быть полезен для изучения алгебры в средней школе

• Серия видеороликов, предназначенных для того, чтобы помочь учащимся понять, как решать линейные уравнения, и в целом понять, что значит быть линейным алгебра

• Уделяет особое внимание счету, представлению математических объектов

Площадь поверхности

• Учащиеся выполняют 3 задания на площадь поверхности и объем прямоугольных и треугольных призм.

• Задания переходят от конкретного к абстрактному, поскольку учащиеся понимают, что на самом деле означает вычисление площади поверхности и объема.

• Включено действие типа 3 акта.

• Обзор площади и периметра включен.

Системы линейных уравнений

• Используется при первом знакомстве учащихся с системой линейных уравнений или, возможно, в качестве повторения в старшей школе после повторного ознакомления с предметом после периода » забываю» это

• Этот короткий модуль исследует графическое решение системы уравнений. Отсюда учитель может исследовать алгебраические решения и/или различные формы линейных уравнений.

Системы неравенств

• Этот модуль займет примерно один учебный час и позволит учащимся изучить, как построить график и решить систему неравенств с помощью графика.

• Предварительным условием для этого модуля является то, что учащиеся записали и изобразили в виде графика системы равенств с двумя переменными и поняли, что решение находится там, где пересекаются линии графика.

Тригонометрические отношения в прямоугольных треугольниках

• Это пяти-шестидневное задание предназначено для того, чтобы помочь учащимся понять тригонометрические отношения, опираясь на их понимание подобных треугольников и отношений соответствующих сторон.

• Цель этого модуля состоит в том, чтобы учащиеся потратили время и энергию на разработку причин, по которым отношения синуса, косинуса и тангенса являются эффективными инструментами для решения прямоугольных треугольников, путем анализа закономерностей, возникающих при составлении таблицы триггеров из данных, сгенерированных классом. , и понимать числа, хранящиеся в их калькуляторе, прежде чем они начнут использовать его для решения задач.

• Дополнительное расширение включает введение единичного круга, а также пифагорейского и частного тождеств.

4 основных математических понятия, которые ваши дети изучают в 7-8 классах

Учащиеся 6 классов создают основу для математических занятий, над которыми они будут работать в 7 и 8 классах. Многие из понятий являются продолжением работы 6 ^-го -го класса и углубляются в понимание и развитие, ведущее к алгебре. Студенты в 7 ^-й -й и 8-й ^-й класс готовятся к работе, которую они будут выполнять в средней школе по алгебре и геометрии. Эти строительные блоки будут иметь решающее значение для их общего понимания и успеха на уровне средней школы.

1. Система счисления.  В 7 ^-м -м классе учащиеся полностью поймут, как интерпретировать и вычислять все рациональные числа. Они могут складывать, вычитать, умножать и делить все десятичные и дробные числа, а также представлять проценты. Они вычисляют как положительные, так и отрицательные числа, используя все четыре основные операции, и интерпретируют значение абсолютного значения. В 8 9В 0265-м классе учащиеся переходят от рациональных чисел к иррациональным числам. Они понимают концепцию десятичного расширения и могут интерпретировать и находить как рациональные, так и иррациональные числа на числовой прямой.

Поощряйте вашего ребенка:

• Используйте числовые линии при расчетах как с положительными, так и с отрицательными числами. Наличие вертикальной и/или горизонтальной числовой линии при выполнении домашних заданий может быть очень полезным.
• Мысленно оценивайте и подсчитывайте чаевые, налог с продаж и процент от продаж при совершении покупок и питании вне дома.
• Интерпретируйте положительные и отрицательные числа в реальной жизни, например, с температурой, долгами/долгами, отрицательными и положительными зарядами, выигрышами/проигрышами и т. д.
• Знать рациональные и иррациональные числа.

2. Выражения и уравнения.  В 7  ^–  и 8   классах ожидания учащихся резко возрастают, когда они изучают выражения и уравнения. Они начинают использовать переменные и решать многоэтапные задачи реального мира. Учащиеся интерпретируют неравенства и строят соответствующие графики. Они готовятся к алгебре, рассматривая и понимая линейные уравнения и находя наклон таблицы, графика и уравнения.

Поощряйте вашего ребенка:

• Различать равенство и неравенство (>,<, > , < ) с помощью переменных:
  • равенство: 4s + 20 = 46
  • неравенство: 4s + 20 < 46
• Посмотрите и решите многоэтапные задачи реального мира, используя переменные. Например,  Как продавец, вы получаете 50 долларов США в неделю плюс 3 доллара США за каждую продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения .
• Исследуйте и изучайте различные типы графиков и таблиц в Интернете или в газете.
• Понять значение наклона и как его найти с помощью графика, таблицы или уравнения:

3. Геометрия.  Учащиеся уделяют большое внимание словарному запасу геометрии и правильному использованию словарного запаса в письме. Они расширяют свое понимание объема и площади для расчета площади поверхности 2-D и 3-D объектов. Они также изучают формулы площади и длины окружности. В 8 9В 0265-м -м классе они изучают теорему Пифагора и применяют ее к реальным и математическим задачам. Студенты также должны знать формулы для нахождения объема конусов, сфер и цилиндров.

Поощряйте вашего ребенка:

• Используйте соответствующую лексику при описании различных полигонов и геометрических свойств. Например: дополнительных углов: два угла, которые в сумме дают 180 °.
• Создавайте словарные карточки для всего своего математического словаря и практикуйте их еженедельно.
• Найдите различные двухмерные и трехмерные объекты в реальном мире и обсудите разницу между нахождением площади поверхности и объема каждого объекта.
• Поймите теорему Пифагора и как использовать ее в реальном мире:

Источник изображения: FreeLearningChannel.com

4. Функции.  В 8 ^-м -м классе учащиеся начнут изучать функции. Учащиеся будут определять, сравнивать и оценивать функции. Они будут использовать функции для моделирования отношений между различными величинами. Они будут сравнивать функции алгебраически, графически, численно в таблицах или по словесным описаниям.

Поощряйте вашего ребенка:

• Анализируйте и исследуйте функции на графике и в таблицах.
• Поймите, что функция — это правило, согласно которому на каждый вход ровно один выход.
• Интерпретация функций в реальных сценариях и то, как это будет выглядеть в таблице, на графике и в уравнении:

Источник изображения: Slideshare.