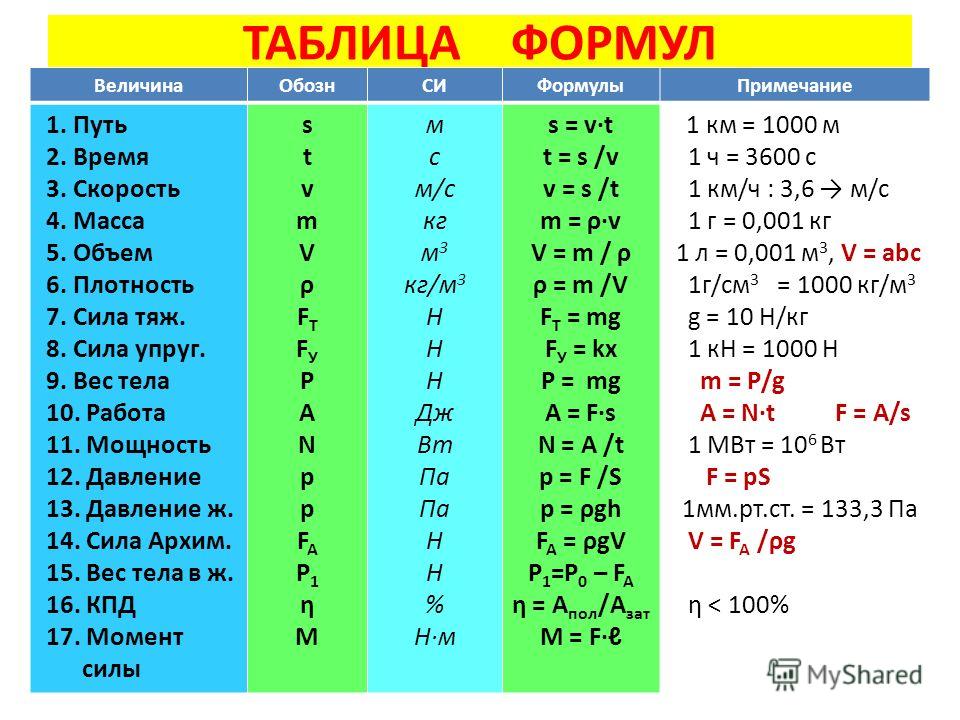
Сводная таблица по теме: «Дифференциальные уравнения»
№ | Вид уравнения | Способ решения |
Дифференциальные уравнения первого порядка | ||
1. | Уравнение с разделяющимися переменными X1 (x) Y1(y) d y + + X2(x)∙Y2 (y) d y = 0. | а) X1 (x) Y1(y) d y = X2(x)∙Y2 б)
. |
y = f1(x)∙f2(y). | а) , б) с) | |
2. | Однородное уравнение . | а) Вводится замена , т. е. y = U∙x, б) Получаем у = U x + U. в) подставляем в однородное уравнение: U x = f (U) – U. в) . г) Интегрируя найдем: |
3. | Линейное уравнение у + р (х) у = f (x) | а) Введем замену: у (х) = U (x) ∙ V (x), тогда у = U (x) ∙ V (x) + U (x) ∙ V (x). б) Получаем: U ∙V +U∙(V + p (x)∙V) = g (x). в) |
Дифференциальные уравнения второго порядка | ||
4. | Допускающие понижение порядка: 1. | а) Вводим замену у = р(х), у = р(х). б) в) |
2. у = f (x, y ) не содержит явно у. | а) Полагая у = р (х ), у = р(х), т. е.р = f (x, p) б) р (х) = φ (х, С1). в) Интегрируем и получим | |
3. у = f (y, y ) не содержащим явно х | а) Полагая у
= р (у (х)). б) Подставляя в уравнение получим р р = f (y, p). г) | |
5. | Линейное однородное уравнение у + р у + q y = 0 | Составляем характеристическое уравнение: k2 + p k + q = 0. Если k1 k2 , то Если k1 = k2, то Если , то |
6. | Линейное неоднородное уравнение у + р у + q y = f (x). | 1. Решаем соответствующее однородное уравнение у + р у + q y = 0 2. По виду правой части уравнения записывается форма частного решения с неопределенными коэффициентами. 3. Таким образом сформированное частное решение подставляется в дифференциальное уравнение. 4. Из полученного тождества определяются значения коэффициентов. 5. |
у
= f (x)
не содержит явно у и у .
Тогда
.
Решение.
Разделим переменные в данном уравнении,
поделив обе части на выражение cos2y∙sin2x:
.
Интегрируя обе части данного уравнения, получим
,
откуда
Воспользуемся тем, что С – произвольная постоянная и заменим С на . Тогда
.
Это и есть общий интеграл данного уравнения.
П р и м е р 2. Найти общий интеграл уравнения
.
Решение. Разрешим уравнение относительно производной :
.
Поделив числитель и знаменатель правой части уравнения на х2, получим:
т. е. у есть функция отношения . Это означает, что данное уравнение – однородное.
Для решения этого
уравнения введем новую функцию
.
Тогда у = u x и
.
Тогда уравнение преобразуется в уравнение
с разделяющимися переменными:
Интегрируя это уравнение, получим
откуда .
Заменяя в последнем равенстве U отношением , окончательно получим:
.
П р и м е р 3. Найти общее решение уравнения
.
Решение. Положим y = u∙v, тогда y = u v + u v и данное уравнение примет вид:
.
Решая уравнение , получим простейшее частное решение:
.
Подставляя v в уравнение, получим
.
из которого находим u:
Итак, искомое общее решение примет вид
П р и м е р 4.
Найти
общее решение уравнения
.
Решение. 1) Найдем решение соответствующего однородного уравнения. Для этого составим характеристическое уравнение, т. е. y = k2, y = k:
.
Следовательно,
.
2) Найдем теперь у*. Здесь правая часть имеет вид , где k = – 3, Pn(x) = A. Так как k = – 3 является двукратным корнем характеристического уравнения, т. е. r = 2, то частное решение у* следует искать в форме
,
где А – коэффициент, подлежащий определению. Вычислим производные и :
;
.
Подставляя выражения
для у*, и в данное выражение, сокращая обе части
на и приводя подобные члены, в итоге получим
2 А = 14, откуда А = 7.
Следовательно, искомое частное
решение имеет вид:
Итак, общее решение данного уравнения
Уравнение в таблице слишком велико — TeX
спросил
Изменено 8 лет, 7 месяцев назад
Просмотрено 2к раз
У меня есть таблица, в которой одна из формул слишком длинная. Есть ли способ разбить уравнение в латексе на таблицу? Он уже повернут, и я попробовал p{5cm}, но он просто перекрывает текст, так как не может найти место, где можно разорвать уравнение, даже с добавленными пробелами. Какие пакеты могут быть полезны? Один соответствующий ответ здесь, который я нашел, был удручающе бесполезен. Заранее спасибо! 9{2}} $ & $ 0,00057668 \pm 0,00000000 $ \\ \hline \end{табличный} \конец{центр} \end{боковой стол}
- таблицы
- уравнения
Я могу придумать два основных варианта: во-первых, использовать замену общих выражений.
Во-вторых, создайте блок сохранения более сложного выровненного уравнения и вставьте этот блок в таблицу. Это защищает символы и от интерпретации табличной средой .
Кроме того, с точки зрения общего макета таблицы см. документацию booktabs. Я оставил ваш формат нетронутым, но если бы это был я, я бы избавился от большинства или всех правил. 9{2}$ & \usebox{\bigeqn} & $0,00057668 \pm 0,00000000$ \\ \hline \end{табличный} \конец{центр} \end{боковой стол} \конец{документ}
3
Следующее слишком длинное, чтобы опубликовать его в качестве дополнительного комментария к ответу Майка Ренфро. Однако должно быть ясно, что моя публикация является не столько отдельным ответом, сколько реализацией некоторых предложений и наблюдений Майка.
Вот несколько дополнительных предложений, которые, как мы надеемся, повысят визуальную и эстетическую привлекательность стола:
В таблицах не используйте вертикальные линии, избавьтесь от большей части горизонтальных линий и используйте макросы рисования правил из пакета
booktabsдля рисования хорошо расположенных версий оставшихся горизонтальных линий.
Не используйте
\leftи\ rightбез разбора. Мало того, что вы получите случайные дикие ошибки размера, если попытаетесь передать работу по размеру TeXу — в сообщении Майка сравните скобки в первой строке подкоренного числа с парами во второй и третьей строках; обратите также внимание, что внешние скобки во второй и третьей строках не больше, чем внутренние скобки, даже несмотря на то, что есть явный типографский случай для увеличения внешней пары — вы также получите нежелательные результаты интервалов. В приведенном ниже коде я использую\bigl(и\bigrтолько для внешних скобок.Для набора научных единиц по нормам СИ очень удобно использовать макрос
\siпакетаsiunitxи набрать, скажем,\si{\килограмм\метр\квадрат}. Ваш входной код будет намного более читабельным, а выходные данные гарантированно будут соответствовать стандартам в отношении того, как должны быть набраны научные единицы.Не используйте центр
\centering.
Вот результирующая таблица:
\documentclass{article}
\usepackage[T1]{шрифт}
\usepackage[utf8]{inputenc}
\usepackage[ngerman]{бабель}
\usepackage{booktabs} % различные макросы рисования правил
\usepackage{siunitx} % для макроса \si
\usepackage{amsmath} % для "выровненной" среды. и макрос \tfrac
\usepackage[margin=1in]{геометрия} % выберите поля страницы в соответствии с вашими потребностями
\начать{документ}
% Модифицированная форма или вариант Майка Ренфро 2:
% Сделайте многострочный радикал, используя «выровненную» среду, и скройте символы «&»
% от «табличной», поместив формулу на «мини-страницу»
\begin{таблица}
\центрирование
\begin{табличный}{@{} llll @{}}
\toprule
Объект &
тревожный момент и
Фелер Формель и
Trägheitsmoment [\si{\килограмм\метр\квадрат}] \\
\midrule
Хантелькёрпер \\
Хольцилиндер и
$J=\frac{m}{2}(r_{a}^2+r_{i}^2{)}^2$ &
\begin{мини-страница}{4см}
$\sqrt{
\begin{выровнено}
&\sigma_{m}^2\bigl(\tfrac{1}{2}(r_{a}^2+r_{i}^2)\bigr)^2 \\
{}+{}&\sigma_{r_{a}}^2\bigl(r_{a}m(r_{a}^2+r_{i}^2)\bigr)^2 \\
{}+{}&\sigma_{r_{i}}^2\bigl(r_{i}m(r_{a}^2+r_{i}^2)\bigr)^2
\end{выровнено}
}$
\end{мини-страница} &
0,00057668$\pm 0,00000000$\\
\нижнее правило
\end{табличный}
\конец{таблица}
\конец{документ}
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.