Учимся решать задачи по планиметрии
- Альфашкола
- Статьи
- Учимся решать задачи по планиметрии
Условие:
В остроугольном треугольнике ABC провели высоту BH, из точки H на стороны AB и BC опустили перпендикуляры HK и HM соответственно.
а) Докажите, что треугольник MBK подобен треугольнику ABC.
б) Найдите отношение площади треугольника MBK к площади четырёхугольника AKMC, если BH = 2, а радиус окружности, описанной около треугольника ABC равен 4.
Решение
а) Изобразим заданный треугольник, обозначим вершины и точки (рис.
Очевидно, что углы BAC и KHB равны как углы с взаимно перпендикулярными сторонами.
Теперь рассмотрим четырёхугольник BKHM. Мы видим, что в нем ∠BKH + ∠BMH = 90° + 90° = 180°
Отсюда, по свойству четырехугольников, вписанных в окружность, четырёхугольник BKHM вписан в окружность. Это значит, что углы KHB и KMB являются вписанными в окружность, и опираются на одну и ту же дугу. Из чего следует, что они равны. Таким образом, ∠BAC = ∠KHB = ∠KMB. Треугольники ABC и MBK имеют общий угол B, а ∠BAC = ∠KMB, значит, эти треугольники подобны по двум углам.
б) Из прямоугольного треугольника BKH, используя определение синуса угла, находим, что:
Для треугольника ABC, с учетом доказанного ранее, будет справедливо равенство:
Зная, что ∠KHB = ∠BAC, получим: \({BC\over BK}={2R\over BH}\)
Стороны BC и BK являются сходственными в подобных треугольниках ABC и MBK, их коэффициент подобия равен:
\(k={BC\over BK}={2R\over BH}=4\)
Найдём отношение площади треугольника MBK к площади четырёхугольника AKMC:
Ответ: \(1 \over 15\)
Автор — Андрей Найденов
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Ольга Викторовна Солнышкина
Репетитор по математике
Стаж (лет)
Образование:
Армавирский лингвистический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Юлия Владимировна Горбанёва
Репетитор по математике
Стаж (лет)
Образование:
Челябинский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Джаваншир Арзу Мамедов
Репетитор по математике
Стаж (лет)
Образование:
Мозырский государственный педагогический университет им.
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор по олимпиадной математике
- Подготовка к олимпиадам по химии
- Репетитор для подготовки к сочинению ЕГЭ по русскому
- Репетитор по английскому для взрослых
- ВПР по математике
- Репетитор для подготовки к ВПР по обществознанию
- Репетитор по информатике для подготовки к ОГЭ
- Репетитор по информатике для подготовки к ЕГЭ
- Подготовка к ОГЭ по литературе
- Scratch
Похожие статьи
- Производная
- Движение в одном направлении
- Как найти делитель?
- Как решать уравнения смешанного типа?
- Решение задач ЕГЭ на механический смысл производной
- 17 задача профильного ЕГЭ на долг в соответствии с данной таблицей
- Ззадание №11 из ЕГЭ.
 Текстовые задачи
Текстовые задачи - Подходящие специальности для детей-интровертов
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
Страница не найдена — ПриМат
По данному адресу ничего не найдено. Попробуйте воспользоваться поиском.
Искать:© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2),
Что такое остроугольные треугольники? Определения и примеры
Что такое остроугольные треугольники? Определения и примеры — Club Z! Репетиторство Остроугольные треугольники — это треугольники, у которых все три внутренних угла меньше 90 градусов. Другими словами, все три угла остроугольного треугольника являются острыми углами. Эти треугольники известны своим острым заостренным внешним видом и обладают рядом важных свойств и характеристик, которые делают их уникальными среди различных типов треугольников.
Другими словами, все три угла остроугольного треугольника являются острыми углами. Эти треугольники известны своим острым заостренным внешним видом и обладают рядом важных свойств и характеристик, которые делают их уникальными среди различных типов треугольников.
ОПРЕДЕЛЕНИЯ
- Треугольник: Треугольник представляет собой трехсторонний многоугольник с тремя прямыми сторонами.
- Острый угол: Острый угол — это угол, размер которого меньше 90 градусов.
- Остроугольный треугольник: Остроугольный треугольник — это треугольник, у которого все три внутренних угла меньше 90 градусов.
ПРИМЕРЫ
- Прямоугольный треугольник: Прямоугольный треугольник — это треугольник, один из углов которого равен ровно 90 градусам. Этот угол известен как прямой угол и обозначается маленьким квадратным символом. Два других угла прямоугольного треугольника — острые углы, а это означает, что прямоугольные треугольники также являются остроугольными треугольниками.

- Тупоугольный треугольник: Тупоугольный треугольник — это треугольник, один из углов которого больше 90 градусов. Два других угла тупоугольного треугольника оба являются острыми углами, а это означает, что тупоугольные треугольники не являются остроугольными.
- Равнобедренный треугольник: Равнобедренный треугольник — это треугольник, две стороны которого имеют одинаковую длину. Две равные стороны называются основанием треугольника, а третья сторона называется высотой. Равнобедренный треугольник может быть остроугольным или тупоугольным в зависимости от величины его углов.
- Равносторонний треугольник: Равносторонний треугольник — это треугольник, все три стороны которого имеют одинаковую длину. Три равные стороны равностороннего треугольника называются основанием треугольника, а все три угла равны 60 градусам. Равносторонний треугольник всегда остроугольный.
- Разносторонний треугольник: Разносторонний треугольник — это треугольник, у которого нет сторон одинаковой длины.
 Все три стороны разностороннего треугольника имеют разную длину, и все три угла тоже разные. Разносторонний треугольник может быть остроугольным, прямоугольным или тупоугольным в зависимости от величины его углов.
Все три стороны разностороннего треугольника имеют разную длину, и все три угла тоже разные. Разносторонний треугольник может быть остроугольным, прямоугольным или тупоугольным в зависимости от величины его углов.
ВИКТОРИНА
- Какой из следующих треугольников не является остроугольным? а. Прямоугольный треугольник б. Тупоугольный треугольник c. равнобедренный треугольник д. Равносторонний треугольник
- Что из перечисленного не является свойством остроугольного треугольника? а. Все три стороны имеют одинаковую длину b. Все три угла острые c. Один угол прямой d. Один угол тупой угол
- Какой из следующих треугольников всегда остроугольный? а. Прямоугольный треугольник б. Тупоугольный треугольник c. равнобедренный треугольник д. Равносторонний треугольник
- Чему равна сумма углов остроугольного треугольника? а. 180 градусов б. 90 градусов в. 270 градусов д. 360 градусов
- Может ли остроугольный треугольник быть разносторонним? а.
 Да б. №
Да б. № - Может ли остроугольный треугольник быть равнобедренным? а. Да б. №
- Может ли остроугольный треугольник быть равносторонним? а. Да б. №
- Может ли остроугольный треугольник иметь один угол больше 90 градусов? а. Да б. №
Найдите подходящий номер или бесплатно.
Мы гарантируем, что вы найдете подходящего репетитора, или мы покроем первый час вашего урока.
Отзывы
Клуб Z! связал меня с репетитором через их онлайн-платформу! Это было именно то внимание один на один, которое мне было нужно для моего экзамена по математике. Мне очень понравились занятия и интерфейс онлайн-обучения ClubZ.
Мой сын страдал от низкой уверенности в своих образовательных способностях. Мне нужна была помощь и быстро. Клуб Z! назначена Шарлотта (наш репетитор), и мы любим ее! Оценки моего сына изменились с D на A и B.
Я использовал онлайн-классы Club Z, чтобы получить помощь и репетиторство для 2 моих занятий в колледже. Я должен сказать, что я очень впечатлен функциональностью и простотой использования их онлайн-приложения. Работать онлайн с моим репетитором было проще простого. Спасибо. Z.
Я должен сказать, что я очень впечатлен функциональностью и простотой использования их онлайн-приложения. Работать онлайн с моим репетитором было проще простого. Спасибо. Z.
Джонатан очень хорошо успевает по всем предметам в этом семестре, 5 пятерок и 2 четверки (вместо ПЛК у него урок по основам работы с компьютером). На уроке алгебры, с которым ему помогает Натан, у него пятерка с плюсом.
Сара очень позитивна, полна энтузиазма и каждый раз поощряет мою дочь становиться лучше. У дочери улучшилась оценка, мы очень благодарны Саре и тому, что она занимается с нашей дочерью. Так держать ClubZ!
Подпишитесь на нашу рассылку новостей
Получайте скидки, учебные советы и многое другое.
- Имя*
- Адрес электронной почты*
остроугольных и тупоугольных треугольников | Энциклопедия MDPI
Остроугольный треугольник (или остроугольный треугольник) — это треугольник с тремя острыми углами (меньше 90°). Тупоугольный треугольник (или тупоугольный треугольник) — это треугольник с одним тупым углом (больше 90°) и двумя острыми углами. Поскольку в евклидовой геометрии сумма углов треугольника должна составлять 180 °, ни один евклидов треугольник не может иметь более одного тупого угла. Остроугольные и тупоугольные треугольники — это два разных типа косоугольных треугольников — треугольники, которые не являются прямоугольными, потому что у них нет 9угол 0°.
1. Свойства
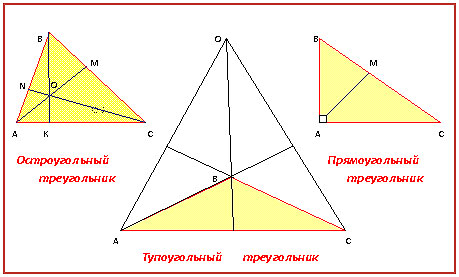
Во всех треугольниках центроид — пересечение медиан, каждая из которых соединяет вершину с серединой противоположной стороны, — и центр вписанной окружности — центр окружности, которая касается всех трех треугольников изнутри. стороны — внутри треугольника. Однако, хотя ортоцентр и центр описанной окружности находятся внутри остроугольного треугольника, они являются внешними по отношению к тупоугольному треугольнику.
стороны — внутри треугольника. Однако, хотя ортоцентр и центр описанной окружности находятся внутри остроугольного треугольника, они являются внешними по отношению к тупоугольному треугольнику.
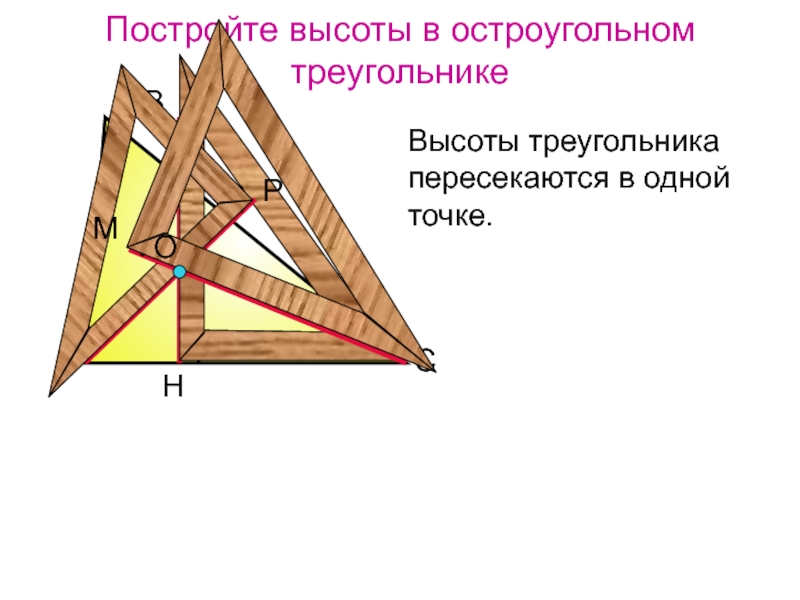
Ортоцентр — это точка пересечения трех высот треугольника, каждая из которых перпендикулярно соединяет сторону с противоположной вершиной. В случае остроугольного треугольника все три отрезка полностью лежат внутри треугольника и, следовательно, пересекаются внутри. Но для тупоугольного треугольника высоты двух острых углов пересекают только продолжения противоположных сторон. Эти высоты полностью попадают за пределы треугольника, что приводит к их пересечению друг с другом (и, следовательно, с удлиненной высотой от вершины с тупым углом), происходящей снаружи треугольника.
Точно так же центр описанной окружности треугольника — пересечение серединных перпендикуляров трех сторон, являющееся центром окружности, проходящей через все три вершины, — попадает внутрь остроугольного треугольника, но вне тупоугольного треугольника.
Прямоугольный треугольник является промежуточным случаем: и его центр описанной окружности, и его ортоцентр лежат на его границе.
В любом треугольнике любые два угла с мерами A и B противоположные стороны a и b соответственно связаны соотношением [1] :стр. 264
- [математика]\displaystyle{ A\gt B \quad \text{если и только если} \quad a \gt b. }[/математика]
Отсюда следует, что самая длинная сторона тупоугольного треугольника находится напротив тупоугольной вершины.
В остроугольный треугольник входят три вписанных квадрата, у каждого из которых одна сторона совпадает с частью стороны треугольника и с двумя другими вершинами квадрата на оставшихся двух сторонах треугольника. (В прямоугольном треугольнике два из них объединены в один и тот же квадрат, поэтому есть только два различных вписанных квадрата.) Однако в тупоугольном треугольнике есть только один вписанный квадрат, одна из сторон которого совпадает с частью наибольшей стороны треугольника. 2, }[/math] 92 }[/математика]
2, }[/math] 92 }[/математика]
для остроугольного треугольника, но с обратным неравенством для тупоугольного треугольника.
Медиана м c от наибольшей стороны больше или меньше радиуса описанной окружности остроугольного или тупоугольного треугольника соответственно: ]\displaystyle{ m_c \gt R}[/math]
для остроугольных треугольников, с обратным для тупоугольных треугольников.
2.4. Район 92. }[/математика]
Для любого треугольника тождество тройной касательной утверждает, что сумма касательных углов равна их произведению. Так как острый угол имеет положительное значение тангенса, а тупой угол имеет отрицательное значение, выражение для произведения тангенсов показывает, что
- [math]\displaystyle{ \tan A+\tan B+\tan C = \tan A \cdot \tan B \cdot \tan C \gt 0 }[/math]
для остроугольных треугольников, а противоположное направление неравенства верно для тупоугольных треугольников. 92}. }[/математика]
92}. }[/математика]
2.6. Радиус описанной окружности, внутренний радиус и эксрадиус
В остроугольном треугольнике сумма радиуса описанной окружности R и внутреннего радиуса r меньше половины суммы кратчайших сторон a и b : [4] :стр.105,#2690
- [математика]\displaystyle{ R+r \lt \frac{a+b}{2}, }[/math]
, а для тупоугольного треугольника выполняется обратное неравенство.
Для остроугольного треугольника с медианами 92, }[/математика]
С точки зрения радиусов экскурсий R A , R B и R C 9 906666666, опять же, с равенством, с помощью ANDARIENTIAL INTERIVE.
Для остроугольного треугольника с полупериметром s , [4] :p.115,#2874
- [math]\displaystyle{ s-r \gt 2R, }[/math]
и верно обратное неравенство для тупоугольного треугольника.
Для остроугольного треугольника площадью K , [4] :p.185,#291.6
- [math]\displaystyle{ ab+bc+ca \geq 2R(R+r)+\ гидроразрыв{8K}{\sqrt{3}}. }[/математика]
2.7. Расстояния, включающие центры треугольников
Для остроугольного треугольника расстояние между центром описанной окружности O и ортоцентром H удовлетворяет условию [4] :p.26,#954
- [math] lt R, }[/math]
с обратным неравенством для тупоугольного треугольника.
Для остроугольного треугольника расстояние между центром вписанной окружности I и ортоцентром H удовлетворяет [4] :p.26,#954
- [math]\displaystyle{ IHrt \lt {2}, }[/math]
, где r — внутренний радиус, с обратным неравенством для тупоугольного треугольника.
2.8. Вписанный квадрат
Если один из вписанных квадратов остроугольного треугольника имеет длину стороны x a and another has side length x b with x a < x b , then [2] :p.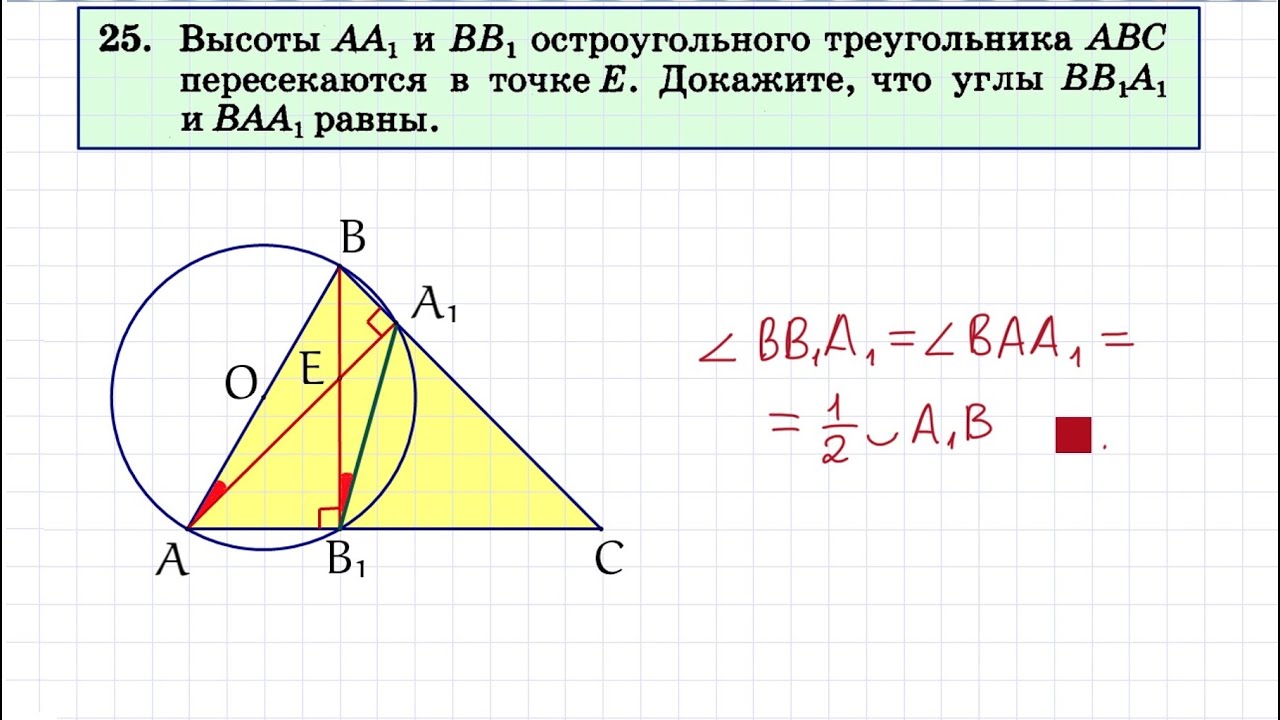 115
115
- [математика]\displaystyle{ 1 \geq \frac{x_a}{x_b} \geq \frac{2\sqrt{2}}{3} \примерно 0,94. }[/математика]
2.9. Два треугольника
Если два тупоугольных треугольника имеют стороны ( a, b, c ) и ( p, q, r ) с c и r соответственно самыми длинными сторонами, затем [4] :p.29,#1030
- [math]\displaystyle{ ap+bq \lt cr. }[/математика]
3. Примеры
3.1. Треугольники со специальными названиями
Треугольник Калаби, который является единственным неравносторонним треугольником, для которого самый большой квадрат, умещающийся внутри, может быть расположен любым из трех различных способов, является тупым и равнобедренным с углами при основании 39.1320261…° и третий угол 101,7359477…°.
Равносторонний треугольник с тремя углами по 60° является остроугольным.
Треугольник Морли, образованный из любого треугольника пересечением триссекторов смежных углов, является равносторонним и, следовательно, остроугольным.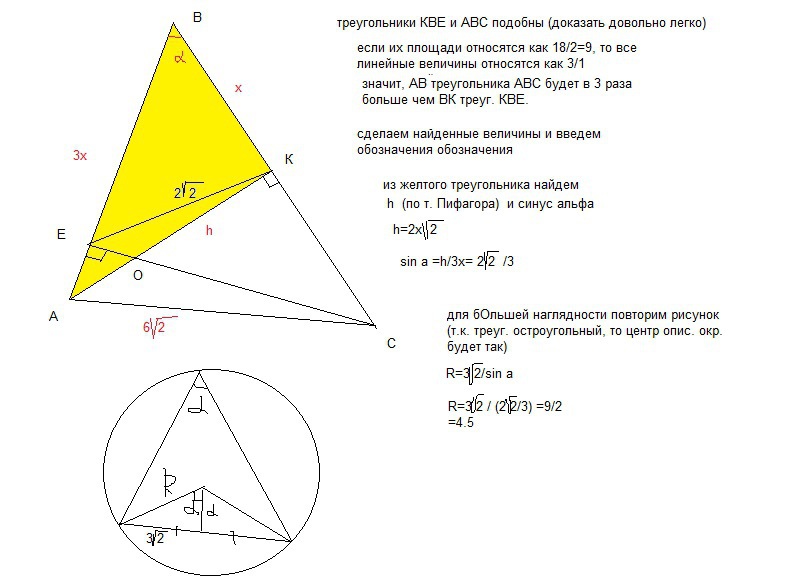
Золотой треугольник — это равнобедренный треугольник, в котором отношение дублированной стороны к стороне основания равно золотому сечению. Он острый, с углами 36°, 72° и 72°, что делает его единственным треугольником с пропорциями углов 1:2:2. [5]
Семиугольный треугольник, стороны которого совпадают со стороной, меньшей диагональю и большей диагональю правильного семиугольника, тупой, с углами [math]\displaystyle{ \pi/7, 2\pi /7, }[/math] и [math]\displaystyle{ 4\pi/7. }[/math]
3.2. Треугольники с целыми сторонами
Единственный треугольник с последовательными целыми числами для высоты и сторон является остроугольным, его стороны (13,14,15) и высота со стороны 14 равна 12.
Треугольник с наименьшим периметром и целыми сторонами в арифметическая прогрессия, и треугольник с целыми сторонами наименьшего периметра и различными сторонами является тупым: а именно, со сторонами (2, 3, 4).
Остроугольными являются только треугольники, один угол которых в два раза больше другого, а стороны имеют целые стороны в арифметической прогрессии: а именно, треугольник (4,5,6) и его кратные.

 Текстовые задачи
Текстовые задачи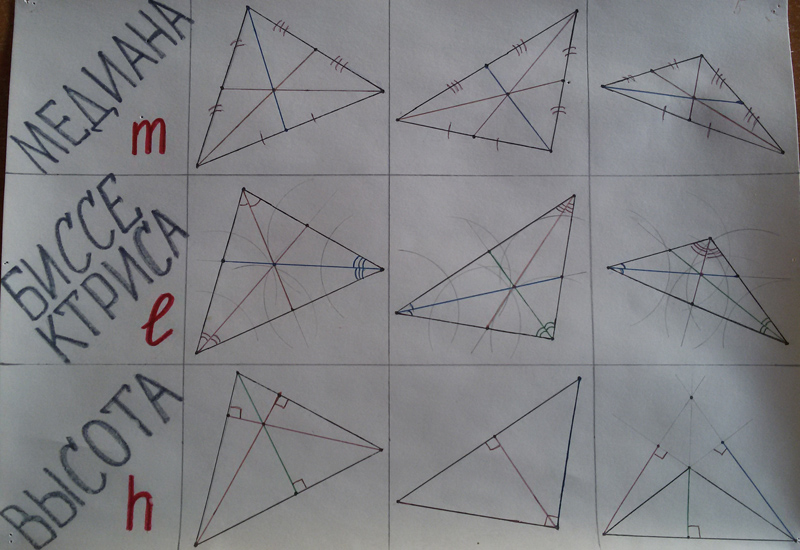
 Все три стороны разностороннего треугольника имеют разную длину, и все три угла тоже разные. Разносторонний треугольник может быть остроугольным, прямоугольным или тупоугольным в зависимости от величины его углов.
Все три стороны разностороннего треугольника имеют разную длину, и все три угла тоже разные. Разносторонний треугольник может быть остроугольным, прямоугольным или тупоугольным в зависимости от величины его углов.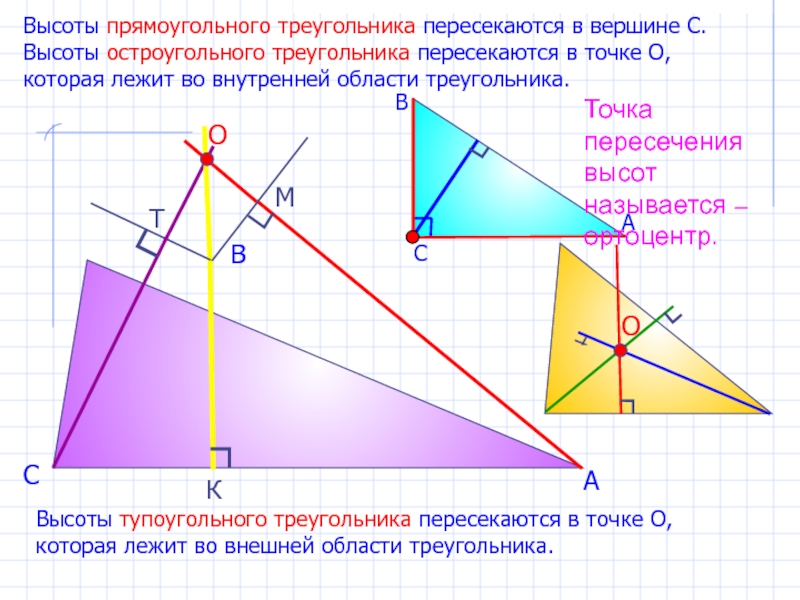 Да б. №
Да б. №