Матрицы уравнения как решать: Транспонирование матрицы

Решение матричных уравнений: теория и примеры

• Решение матричных уравнений: как это делается
• Решение матричных уравнений: примеры

Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,

ax=b,

где x — неизвестное.

А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.

Итак, матричным уравнением называется уравнение вида

A ⋅ X = B

или

X ⋅ A = B,

где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.

Как решить матричное уравнение в первом случае?

Для того, чтобы решить матричное уравнение вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу слева:

.

По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому

.

Так как E — единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:

.

Как решить матричное уравнение во втором случае? Если дано уравнение

X ⋅ A = B,

то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице

A, и умножать матрицу B на неё справа:

,

,

.

Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X. То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A.

Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения

A ⋅ X ⋅ B = C,

является

.

Пример 1. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы

A:

.

Найдём алгебраические дополнения матрицы A:

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:

.

Наконец, находим неизвестную матрицу:

Решить матричное уравнение самостоятельно, а затем посмотреть решение

Пример 2. Решить матричное уравнение

.

Посмотреть правильное решение и ответ.

---

Пример 3. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей

A:

.

Находим матрицу, обратную матрице A:

.

Находим неизвестную матрицу:

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Матрицы

До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.

Пример 4. Решить матричное уравнение

.

Решение. Это уравнение первого вида: A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева.

Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:

.

Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение

.

Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы

A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Находим матрицу, обратную матрице A:

.

Находим неизвестную матрицу:

Пример 6.

Решить матричное уравнение

.

Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то есть неизвестная матрица X находится в середине произведения трёх матриц.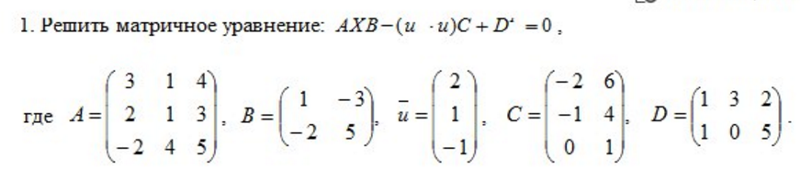 Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A.

Сначала найдём определитель матрицы A:

.

Найдём алгебраические дополнения матрицы A:

.

Составим матрицу алгебраических дополнений:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:

.

Находим матрицу, обратную матрице A:

.

Найдём матрицу, обратную матрице B.

Сначала найдём определитель матрицы B:

.

Найдём алгебраические дополнения матрицы B:

Составим матрицу алгебраических дополнений матрицы B:

.

Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:

.

Находим матрицу, обратную матрице B:

.

Находим неизвестную матрицу:

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Матрицы

Поделиться с друзьями

Начало темы «Матрицы»

Понятие матрицы

Продолжение темы «Матрицы»

Обратная матрица

Произведение двух матриц

Умножение матрицы на число

Сложение матриц

Другие темы линейной алгебры

Определители

Системы линейных уравнений

Решение матричных уравнений — Журнал «Код»

Линейная алгебра и, в частности, матрицы — это основа математики нейросетей. Когда говорят «машинное обучение», на самом деле говорят «перемножение матриц», «решение матричных уравнений» и «поиск коэффициентов в матричных уравнениях».  

Понятно, что между простой матрицей в линейной алгебре и нейросетью, которая генерирует котов, много слоёв усложнений, дополнительной логики, обучения и т. д. Но здесь мы говорим именно о фундаменте. Цель — чтобы стало понятно, из чего оно сделано. 

Краткое содержание прошлых частей: 

• Линейная алгебра изучает векторы, матрицы и другие понятия, которые относятся к упорядоченным наборам данных. Линейной алгебре интересно, как можно трансформировать эти упорядоченные данные, складывать и умножать, всячески обсчитывать и находить в них закономерности. 
• Вектор — это набор упорядоченных данных в одном измерении. Можно упрощённо сказать, что это последовательность чисел. 
• Матрица — это тоже набор упорядоченных данных, только уже не в одном измерении, а в двух (или даже больше). 
• Матрицу можно представить как упорядоченную сумку с данными. И с этой сумкой как с единым целым можно совершать какие-то действия. Например, делить, умножать, менять знаки.
• Матрицы можно складывать и умножать на другие матрицы. Это как взять две сумки с данными и получить третью сумку, тоже с данными, только теперь какими-то новыми. 
• Матрицы перемножаются по довольно замороченному алгоритму. Арифметика простая, а порядок перемножения довольно запутанный. 

И вот наконец мы здесь: если мы можем перемножать матрицы, то мы можем и решить матричное уравнение.

❌ Никакого практического применения следующего материала в народном хозяйстве вы не увидите. Это чистая алгебра в несколько упрощённом виде. Отсюда до практики далёкий путь, поэтому, если нужно что-то практическое, — посмотрите, как мы генерим Чехова на цепях Маркова.

Что такое матричное уравнение

Матричное уравнение — это когда мы умножаем известную матрицу на матрицу Х и получаем новую матрицу. Наша задача — найти неизвестную матрицу Х.

9 простых задач на математику

Шаг 1. Упрощаем уравнение 

Вместо известных числовых матриц вводим в уравнение буквы: первую матрицу обозначаем буквой A, вторую — буквой B. Неизвестную матрицу X оставляем. Это упрощение поможет составить формулу и выразить X через известную матрицу.

Приводим матричное уравнение к упрощённому виду

Шаг 2. Вводим единичную

матрицу 

В линейной алгебре есть два вспомогательных понятия: обратная матрица и единичная матрица. Единичная матрица состоит из нулей, а по диагонали у неё единицы. Обратная матрица — это такая, которая при умножении на исходную даёт единичную матрицу. 

Можно представить, что есть число 100 — это «сто в первой степени», 100¹

И есть число 0,01 — это «сто в минус первой степени», 100^-1

При перемножении этих двух чисел получится единица:
100¹ × 100^-1 = 100 × 0,01 = 1. 

Вот такое, только в мире матриц. 

Зная свойства единичных и обратных матриц, делаем алгебраическое колдунство. Умножаем обе известные матрицы на обратную матрицу А^-1. Неизвестную матрицу Х оставляем без изменений и переписываем уравнение: 

А-1 × А × Х = А-1 × В  

Добавляем единичную матрицу и упрощаем запись: 

А-1 × А = E — единичная матрица 

E × Х = А-1 × В — единичная матрица, умноженная на исходную матрицу, даёт исходную матрицу. Единичную матрицу убираем

Х = А-1 × В — новая запись уравнения 

После введения единичной матрицы мы нашли способ выражения неизвестной матрицы X через известные матрицы A и B. 

💡 Смотрите, что произошло: раньше нам нужно было найти неизвестную матрицу. А теперь мы точно знаем, как её найти: нужно рассчитать обратную матрицу A^-1 и умножить её на известную матрицу B. И то и другое — замороченные процедуры, но с точки зрения арифметики — просто. 

Шаг 3. Находим обратную матрицу

Вспоминаем формулу и порядок расчёта обратной матрицы: 

1. Делим единицу на определитель матрицы A. 
2. Считаем транспонированную матрицу алгебраических дополнений. 
3. Перемножаем значения и получаем нужную матрицу.

Формула вычисления обратной матрицыПервое действие. Мы посчитали определитель и убедились, что он не равен нулю, — это значит, что у матричного уравнения есть вариант решения и можно продолжатьВторое действие, часть 1: получаем матрицу миноровВторое действие, часть 2: переводим матрицу миноров в транспонированную матрицу алгебраических дополнений

Собираем формулу и получаем обратную матрицу. Для удобства умышленно оставляем перед матрицей дробное число, чтобы было проще считать.

Третье действие: получаем обратную матрицу

Шаг 4. Вычисляем неизвестную матрицу

Нам остаётся посчитать матрицу X: умножаем обратную матрицу А^-1 на матрицу B. Дробь держим за скобками и вносим в матрицу только при условии, что элементы новой матрицы будут кратны десяти — их можно умножить на дробь и получить целое число. Если кратных элементов не будет — дробь оставим за скобками.

Решаем матричное уравнение и находим неизвестную матрицу X. Мы получили кратные числа и внесли дробь в матрицу

Шаг 5. Проверяем уравнение

Мы решили матричное уравнение и получили красивый ответ с целыми числами. Выглядит правильно, но в случае с матрицами этого недостаточно. Чтобы проверить ответ, нам нужно вернуться к условию и умножить исходную матрицу A на матрицу X. В результате должна появиться матрица B. Если расчёты совпадут — мы всё сделали правильно. Если будут отличия — придётся решать заново.  

👉 Часто начинающие математики пренебрегают финальной проверкой и считают её лишней тратой времени. Сегодня мы разобрали простое уравнение с двумя квадратными матрицами с четырьмя элементами в каждой. Когда элементов будет больше, в них легко запутаться и допустить ошибку.

Проверяем ответ и получаем матрицу B — наши расчёты верны

Ну и что

Алгоритм решения матричных уравнений несложный, если знать отдельные его компоненты. Дальше на основе этих компонентов математики переходят в более сложные пространства: работают с многомерными матрицами, решают более сложные уравнения, постепенно выходят на всё более и более абстрактные уровни. И дальше, в конце пути, появляется датасет из миллионов котиков. Этот датасет раскладывается на пиксели, каждый пиксель оцифровывается, цифры подставляются в матрицы, и уже огромный алгоритм в автоматическом режиме генерирует изображение нейрокотика:

Этого котика не существует, а матрицы — существуют. 

Текст:

Александр Бабаскин

Редактура:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Мария Дронова

Соцсети:

Олег Вешкурцев

Матричное уравнение — Примеры | Как решить матричное уравнение?

Систему уравнений можно решить с помощью матриц, записав ее в виде матричного уравнения. Мы также можем определить, имеет ли система единственное решение, бесконечное число решений или отсутствие решения, используя матричное уравнение.

Вместе с примерами научимся решать матричные уравнения разными методами.

1.	Что такое матричное уравнение?
2.	Как написать матричное уравнение?
3.	Как решить матричное уравнение?
4.	Непротиворечивость решения матричного уравнения
5.	Часто задаваемые вопросы о матричном уравнении

Что такое матричное уравнение?

A матричное уравнение имеет форму AX = B, где A представляет матрицу коэффициентов, X представляет матрицу столбцов переменных, а B представляет матрицу столбцов констант, которые находятся в правой части уравнений в системе. . Рассмотрим систему n неоднородных уравнений от n переменных.

а₁₁ х₁ + а₁₂ х₂ + … + а₁ₙ хₙ = b₁

а₂₁ х₁ + а₂₂ х₂ + … + а₂ₙ хₙ = b₂

х₁

+ аₙ₂ х₂ + … + aₙₙ xₙ = bₙ

Тогда матричное уравнение, соответствующее приведенной выше системе, имеет вид:

AX = B, где

• A = матрица, состоящая из коэффициентов = \(\left[\begin{array}{cccc}
  a_{11} & a_{12} & \cdots & a_{1 n} \\
  a_{21} & a_{22} & \cdots & a_{2 n} \\
  \vdots & \vdots & \ddots & \vdots \\
  a_{n 1} & a_{n 2} & \cdots & a_{n n}
  \конец{массив}\справа]\)
• X = Матрица-столбец переменных = \(\left[\begin{array}{c}
  х_{1} \\
  х_{2} \\
  \vdots\
  х_{п}
  \конец{массив}\справа]\)
• B = Матрица-столбец констант = \(\left[\begin{array}{c}
  б_{1} \\
  б_{2} \\
  \vdots\
  б_{н}
  \конец{массив}\справа]\)

Как написать матричное уравнение?

Чтобы записать систему уравнений в виде матричного уравнения:

• Убедитесь, что переменные в каждом из уравнений находятся в одном порядке.
• Убедитесь, что в левой части находятся только переменные члены, а в правой — постоянные.
• Затем найдите матрицу коэффициентов A, матрицу переменных X и матрицу констант B, чтобы записать данную систему в виде матричного уравнения AX = B.

Вот пример для понимания этих шагов.

Пример: Запишите следующую систему в виде матричного уравнения.

3х + у + 2з — 10 = 0
г — 3у = -5
y + x — 2z = 7

Решение:

Получим все переменные члены с одной стороны (тоже по порядку), а константы с правой стороны.

3x + у + 2z = 10
0x — 3y + z = -5
x + y — 2z = 7

Теперь мы можем записать эту систему как:

\(\left[\begin{массив}{ccc}
3 и 1 и 2 \\
0&-3&1\
1 и 1 и -2
\end{массив}\right]\left[\begin{массив}{l}
х\
у\
я
\end{массив}\right]=\left[\begin{массив}{c}
10\
-5\
7
\end{array}\right]\)

Это матричное уравнение данной системы, которое альтернативно может быть записано как AX = B, где A = \(\left[\begin{array}{ccc}
3 и 1 и 2 \\
0&-3&1\
1 и 1 и -2
\end{массив}\right]\), X = \(\left[\begin{массив}{l}
х\
у\
я
\end{массив}\right]\), и B = \(\left[\begin{массив}{c}
10\
-5\
7
\end{массив}\right]\).

Как решить матричное уравнение?

Решим матричное уравнение AX = B относительно X. Для этого мы умножили обе части уравнения на обратную A (это можно записать как A ^-1 ).

A ^-1 (AX) = A ^-1 B

Мы знаем, что A ^-1 A = I, где I — единичная матрица того же порядка, что и A.

IX = A ^-1 B

Мы также знаем, что IX = X.

X = A ^-1 B

Это дает решение матричного уравнения. Это также известно как обратное матричное уравнение , и, следовательно, процесс использования приведенной выше формулы для решения системы уравнений известен как » Метод обратной матрицы». Итак, вот шаги для решения системы уравнений с использованием матриц:

1. Запишите систему в виде матричного уравнения AX = B.
2. Найдите обратное, A ^-1 .
3. Умножьте его на постоянную матрицу B, чтобы получить решение. т. е. X = А ^-1 В.

Мы можем увидеть примеры решения системы с использованием этих шагов в разделе «Примеры матричных уравнений» ниже.

Непротиворечивость решения матричного уравнения

Мы знаем, что можем найти обратную матрицу, только если она невырожденная. т. е. A ^-1 существует только при det (A) ≠ 0. Таким образом, решение (X = A ^-1 B) существует и единственно только при det (A) ≠ 0,

В случае, если det (A) = 0, как мы можем узнать, сколько решений может иметь система? В этом случае мы должны найти (adj A) B, где adj A означает «сопряженный с A».

• Если (прил. A) B ≠ O, то система не имеет решений и, следовательно, называется несовместной.
• Если (прил. A) B = O, то система может быть «согласованной с бесконечным числом решений» или «несовместимой (отсутствие решения)».

Здесь ‘O’ — нулевая матрица. Это кратко показано на блок-схеме ниже.

☛ Похожие темы:

• Однородная система линейных уравнений
• Матричный калькулятор
• Формула матрицы
• Калькулятор умножения матриц

Часто задаваемые вопросы о матричном уравнении

Что такое определение матричного уравнения?

Матричное уравнение имеет форму AX = B и записывает систему уравнений как одно уравнение в терминах матриц. Здесь

• A = матрица, образованная коэффициентами
• X = Матрица-столбец, образованная переменными
• B = матрица столбцов, образованная константами

Как решить матричное уравнение AX = B?

Чтобы решить матричное уравнение AX = B:

• Найдите A ^-1 (используя формулу A ^-1 = (adj A) / (det A).
• Найдите решение, используя X = A ^-1 B.

Как решить систему уравнений с помощью матричного уравнения?

Чтобы решить систему уравнений с использованием матриц:

• Сначала запишите все переменные с одной стороны и константы с другой стороны уравнений. Кроме того, запишите переменные в одном и том же порядке в каждом уравнении.
• Запишите систему в виде AX = B, записав все коэффициенты переменных в матрице A, все переменные в виде столбца в матрице X и все константы в столбце в матрице B.
• Найдите решение, используя X = A ^-1 B.

Какие методы используются для решения матричного уравнения?

Вот методы решения матричного уравнения AX = B.

• Метод обращения матриц (по формуле X = A ^-1 B)
• Правило Крамера. Нажмите здесь, чтобы узнать об этом.
• Метод Гаусса-Жордана.

Как записать систему уравнений в виде матричного уравнения?

Мы можем записать систему уравнений в виде матричного уравнения AX = B. Вот шаги для того же:

• Сохраняйте порядок переменных во всех уравнениях.
• Получить все переменные в левой части и отправить константы в правую часть каждого уравнения.
• Напишите матрицу A со всеми коэффициентами переменных, где каждая строка A представляет коэффициенты переменных в одном уравнении.
• Запишите матрицу X с переменными по порядку столбцов.
• Запишите матрицу B с константами по порядку в виде столбца.

Сколько решений имеет матричное уравнение?

Матричное уравнение AX = B имеет:

• единственное решение (непротиворечивое), если det (A) ≠ 0,
• нет решения (противоречиво), если det (A) = 0 и (adj A) B ≠ O.
• бесконечные решения (непротиворечивые) или отсутствие решения (противоречивые), если det (A) = 0 и (adj A) B = O.

Здесь O — нулевая матрица.

Какая связь между матричным уравнением и рангом матрицы?

Для матричного уравнения AX = B [AB] представляет расширенную матрицу. Пусть r(A) и r(A, B) представляют собой ранги матриц A и [AB].

• Если r(A) = r(A, B) = количество переменных, то система непротиворечива и имеет единственное решение.
• Если r(A) = r(A, B) < числа переменных, то система совместна и имеет бесконечно много решений.
• Если r(A) ≠ r(A, B), то система несовместна и не имеет решения.

2.3: Матричные уравнения — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

70188

• Дэн Маргалит и Джозеф Рабинофф
• Технологический институт Джорджии

Цели

1. Понять эквивалентность между системой линейных уравнений, расширенной матрицей, векторным уравнением и матричным уравнением.
2. Охарактеризуйте векторы \(b\) так, что \(Ax=b\) непротиворечиво, в терминах диапазона столбцов \(A\).
3. Охарактеризуйте матрицы \(A\) так, что \(Ax=b\) непротиворечиво для всех векторов \(b\).
4. Рецепт: умножить вектор на матрицу (два способа).
5. Picture: множество всех векторов \(b\) таких, что \(Ax=b\) непротиворечиво.
6. Словарь: матричное уравнение .

Матричное уравнение \(Ax=b\)

В этом разделе мы вводим очень краткий способ записи системы линейных уравнений: \(Ax=b\). Здесь \(A\) — матрица, а \(x,b\) — векторы (обычно разных размеров), поэтому сначала мы должны объяснить, как умножать матрицу на вектор.

Примечание \(\PageIndex{1}\)

Когда мы говорим, что \(A\) является матрицей \(m\x n\), мы имеем в виду, что \(A\) имеет \(m\) строк и \(n\) столбцов.

Замечание

В этой книге мы делаем , а не , резервируя буквы \(m\) и \(n\) для номеров строк и столбцов матрицы. Если мы напишем «\(A\) — матрица \(n\times m\)», то \(n\) — количество строк матрицы \(A\), а \(m\) — количество столбцов .

Определение \(\PageIndex{1}\): Продукт

Пусть \(A\) будет матрицей \(m\x n\) со столбцами \(v_1,v_2,\ldots,v_n\text{:} \) 9м\).

Пример \(\PageIndex{1}\)

\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{array}\right)\:\left(\begin{array}{ c}1\\2\\3\end{массив}\right) =1\left(\begin{массив}{c}4\\7\end{массив}\right) +2\left(\begin{ array}{c}5\\8\end{array}\right)+3\left(\begin{array}{c}6\\9\end{array}\right)=\left(\begin{array }{c}32\\50\end{массив}\right).\nonumber\]

Чтобы \(Ax\) имело смысл, число элементов \(x\) должно быть одинаковым в качестве количества столбцов \(A\text{:}\) мы используем записи \(x\) в качестве коэффициентов столбцов \(A\) в линейной комбинации. Результирующий вектор имеет то же количество элементов, что и число 9.m\text{,}\) и \(x\) — вектор, коэффициенты которого \(x_1,x_2,\ldots,x_n\) неизвестны. 2-1=0\) для \(x\). Второй вопрос, возможно, является новой концепцией для вас. Теорема 2.9м\). Рассмотрим векторное уравнение

\[ x_1v_1 + x_2v_2 + \cdots + x_nv_n = b. \nonumber \]

Это эквивалентно матричному уравнению \(Ax=b\text{,}\), где

\[A=\left(\begin{array}{cccc}|&|&\quad & | \\ v_1 &v_2 &\cdots &v_n \\ |&|&\quad &|\end{массив}\right)\quad\text{and}\quad x=\left(\begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right).\nonumber \]

Наоборот, если \(A\) является любой матрицей \(m\times n\), то \(Ax= б\) эквивалентно векторному уравнению 93\).

Решение

Пусть \(A\) будет матрицей со столбцами \(v_1,v_2,v_3\text{,}\) и пусть \(x\) будет вектором с элементами \(2,3,-4 \). Затем

\[Ax=\left(\begin{array}{ccc}|&|&| \\ v_1 & v_2 & v_3 \\ |&|&|\end{array}\right)\:\left( \begin{array}{c}2\\3\\-4\end{array}\right) = 2v_1 +3v_2 -4v_3, \nonumber\]

, поэтому векторное уравнение эквивалентно матричному уравнению \(Ax =\left(\begin{массив}{c}7\\2\\1\end{массив}\right)\).

Примечание \(\PageIndex{4}\): четыре способа записи линейной системы

Теперь у нас есть четыре эквивалентных способов записи (и обдумывания) системы линейных уравнений:

1. В виде системы уравнений:
   \[\left\{\begin{array}{rrrrrrr} 2x_1 &+ & 3x_2 &-& 2x_3 &=& 7\\ x_1 &-& x_2 &-& 3x_3 &=& 5\end{массив}\right.\nonnumber\]
2. В виде расширенной матрицы:
   \[\left(\begin{array}{ccc|c} 2&3&-2&7 \\ 1&-1&-3&5\end{array}\right)\nonnumber\]
3. В виде векторного уравнения (\(x_1v_1 + x_2v_2 + \cdots + x_nv_n = b\)):
   \[x_{1}\left(\begin{array}{c}2\\1\end{array}\ вправо)+x_2\влево(\begin{массив}{c}3\\-1\конец{массив}\вправо)+x_3\влево(\begin{массив}{c}-2\\-3\конец{ array}\right)=\left(\begin{array}{c}7\\5\end{array}\right)\nonnumber\]
4. В виде матричного уравнения (\(Ax=b\)):
   \[\left(\begin{array}{ccc}2&3&-2 \\ 1&-1&-3\end{array}\right)\:\ влево(\begin{массив}{c}x_1 \\ x_2 \\ x_3\end{массив}\right)=\left(\begin{массив}{c}7\\5\end{массив}\right). \номер\]

В частности, все четыре имеют один и тот же набор решений .

Примечание \(\PageIndex{5}\)

Мы будем свободно перемещаться между четырьмя способами записи линейной системы снова и снова до конца книги.

Другой способ вычисления \(Ax\)

Приведенное выше определение продукта, определение \(\PageIndex{1}\), – полезный способ определения произведения матрицы на вектор, когда дело доходит до понимания связь между матричными уравнениями и векторными уравнениями. Здесь мы даем определение, которое лучше подходит для ручных вычислений.

Определение \(\PageIndex{3}\): вектор-строка

Вектор-строка представляет собой матрицу с одной строкой. Произведение вектора-строки длины \(n\) и вектора (столбца) длины \(n\) равно

\[\left(\begin{array}{cccc}a_1 &a_2 &\ cdots a_n \end{массив}\right)\:\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{массив}\right) =a_1 x_1 + a_2 x_2 +\ cdots + a_n x_n . \nonumber\]

Это скаляр.

Рецепт: Правило строки-столбца для умножения матрицы на вектор 9n\text{,}\) then

\[Ax=\left(\begin{array}{c} — r_1 — \\ —r_2 — \\ \vdots \\ — r_m —\end{array}\right ) x=\left(\begin{array}{c} r_1 x \\ r_2 x \\ \vdots \\ r_m x\end{array}\right).\nonumber\]

Пример \(\PageIndex{3 }\)

\[\left(\begin{array}{ccc}4&5&6 \\ 7&8&9\end{массив}\right)\:\left(\begin{array}{c}1\\2\\3 \end{массив}\right)=\left(\begin{array}{cc}{\left(\begin{array}{c}4&5&6\end{массив}\right)}&{\left(\begin{ array}{c}1\\2\\3\end{массив}\right)}\\{\left(\begin{array}{ccc}7&8&9\end{массив}\right)}&{\left(\begin{array}{c}1\\2\\3\end{массив}\right)}\end{массив}\right) =\left( \begin{array}{ccccccccccc} 4 & \cdot &1&+&5 &\cdot & 2&+& 6& \cdot & 3 \\ 7 &\cdot & 1&+&8 & \cdot & 2&+&9 & \cdot &3\end {array}\right)=\left(\begin{array}{c} 32\\50\end{array}\right).\nonumber\]

Это тот же ответ, что и раньше:

\[\ влево(\begin{массив}{ccc}4&5&6 \\ 7&8&9\end{массив}\right)\:\left(\begin{массив}{c}1\\2\\3\end{массив}\right) =1\left(\begin{массив}{c}4\\7\end{массив}\right)+2\left(\begin{массив}{c}5\\8\end{массив}\right) +3\влево(\begin{массив}{с}6\\9\end{массив}\right)=\left(\begin{array}{cccccccccc} 1 & \cdot & 4&+& 2& \cdot &5&+&3& \cdot &6 \\ 1 & \cdot &7&+& 2& \cdot &8& +&3& \cdot &9\end{массив}\right)=\left(\begin{array}{c}32\\50\end{массив}\right). \nonumber\]

Диапазоны и согласованность

Let \(A\) — матрица со столбцами \(v_1,v_2,\ldots,v_n\text{:}\)

\[A=\left(\begin{array}{cccc}|&|&\quad &| \\ v_1 &v_2 &\cdots & v_n \\ |&|&\quad &|\end{массив}\right).\nonumber\]

Тогда

\[ \begin{split} Ax=b&\text{ имеет решение} \\ &\iff \text{существуют $x_1,x_2,\ldots,x_n$ такие, что } A\left(\ begin{array}{c}x_1 \\ x_2 \\ \vdots \\ x_n\end{array}\right) = b \\ &\iff \text{существуют $x_1,x_2,\ldots,x_n$ такие, что } x_1v_1 + x_2v_2 + \cdots + x_nv_n = b \\ &\iff \text{$b$ является линейной комбинацией } v_1,v_2,\ldots,v_n \\ &\iff \text{$b$ находится в диапазон столбцов $A$}. \end{split} \nonumber \]

Примечание \(\PageIndex{6}\): диапазоны и согласованность

Матричное уравнение \(Ax=b\) имеет решение тогда и только тогда, когда \(b\) находится в диапазоне столбцов \(A\).

Это дает эквивалентность между алгебраическим утверждением (\(Ax=b\) непротиворечиво) и геометрическим утверждением (\(b\) находится в диапазоне столбцов \(A\)) .

Пример \(\PageIndex{4}\): несовместимая система

Пусть \(A=\left(\begin{array}{cc}2&1\\ -1&0 \\ 1&-1\end{array}\ верно)\). Имеет ли уравнение \(Ax=\left(\begin{array}{c}0\\2\\2\end{array}\right)\) решение?

Решение

Сначала ответим на вопрос геометрически. Столбцы \(A\) равны

\[\color{Red}{v_1 =\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\ quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right) }\color{black}{,}\nonumber\]

, а целевой вектор (в правой части уравнения) равен \(\color{Green}{w=\left(\begin{array}{) c}0\\2\\2\конец{массив}\справа)}\). Уравнение \(Ax=w\) непротиворечиво тогда и только тогда, когда \(w\) содержится в промежутке столбцов \(A\). Итак рисуем картинку:

Рисунок \(\PageIndex{1}\)

 Похоже, что \(w\) не лежит в \(\text{Span}\{v_1,v_2\},\), поэтому уравнение несовместимо .

Рисунок \(\PageIndex{2}\): Вектор \(w\) не содержится в \(\text{Span}\{v_1,v_2\}\text{,}\), поэтому уравнение \ (Ax=b\) противоречиво. (Попробуйте переместить ползунки, чтобы решить уравнение.)

Давайте проверим наш геометрический ответ, решив матричное уравнение, используя сокращение строк. Помещаем систему в расширенную матрицу и уменьшаем строку:

\[\left(\begin{array}{cc|c} 2&1&0 \\ -1&0&2 \\ 1&-1&2\end{array}\right) \quad\xrightarrow{\text{RREF}}\quad \left (\begin{array}{cc|c} 1&0&0 \\ 0&1&0 \\ 0&0&1\end{array}\right).\nonumber\]

Последнее уравнение равно \(0=1\text{,}\), поэтому система действительно противоречива, и матричное уравнение

\[\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\right)x=\left(\begin {массив}{с}0\\2\\2\конец{массив}\справа)\номер\]

не имеет решения.

Пример \(\PageIndex{5}\): согласованная система

Пусть \(A=\left(\begin{array}{cc}2&1\\-1&0\\1&-1\end{array}\ верно)\). Имеет ли уравнение \(Ax=\left(\begin{array}{c}1\\-1\\2\end{array}\right)\) решение?

Решение

Сначала ответим на вопрос геометрически. Столбцы \(A\) равны

\[\color{Red}{v_1=\left(\begin{array}{c}2\\-1\\1\end{array}\right)}\ quad\color{black}{\text{and}}\quad\color{blue}{v_2 =\left(\begin{array}{c}1\\0\\-1\end{array}\right) },\номер\]

, а целевой вектор (в правой части уравнения) равен \(\color{Green}{w=\left(\begin{array}{c}1\\-1\\2\end{ массив}\справа)}\). Уравнение \(Ax=w\) непротиворечиво тогда и только тогда, когда \(w\) содержится в промежутке столбцов \(A\). Итак, мы рисуем картинку:

Рисунок \(\PageIndex{3}\)

Похоже, что \(w\) действительно содержится в диапазоне столбцов \(A\text{;}\) на самом деле мы можем видеть

\[ w = v_1 — v_2 \ подразумевает x = \left(\begin{array}{c}1\\-1\end{array}\right). \номер\]

Рисунок \(\PageIndex{4}\): Вектор \(w\) содержится в \(\text{Span}\{v_1,v_2\}\text{,}\), поэтому уравнение \( Ах=b\) непротиворечиво. (Двигайте ползунки, чтобы решить уравнение.)

Давайте проверим наш геометрический ответ, решив матричное уравнение с помощью редукции строк. Мы помещаем систему в расширенную матрицу и уменьшаем строку:

\[\left(\begin{array}{cc|c}2&1&1\\-1&0&-1\\1&-1&2\end{array}\right) \ quad\xrightarrow{\text{RREF}}\quad \left(\begin{array}{cc|c} 1&0&1 \\ 0&1&-1 \\ 0&0&0\end{массив}\right).\nonumber\]

Это дает нам \(x=1\) и \(y=-1\text{,}\), что соответствует картинке:

\[1\left(\begin{array}{c}2 \\-1\\1\конец{массив}\справа)-1\слева(\начало{массив}{с}1\\0\\-1\конец{массив}\справа)=\слева(\начало {массив} {c} 1\\-1\\2\end{массив}\right)\quad\text{or}\quad A\left(\begin{array}{c}1\\-1\end {array}\right)=\left(\begin{array}{c}1\\-1\\2\end{array}\right). \nonumber\]

Когда решения всегда существуют.

Опираясь на примечание \(\PageIndex{6}\): промежутки и согласованность, у нас есть следующий критерий того, когда \(Ax=b\) непротиворечиво для 9м\).

Теперь покажем, что 1 и 3 эквивалентны. (Поскольку мы знаем, что 1 и 2 эквивалентны, отсюда следует, что 2 и 3 также эквивалентны.) Если \(A\) имеет точку опоры в каждой строке, то его сокращенная ступенчатая форма строки выглядит следующим образом:

\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&1&\star \end{array}\right),\nonumber\]

и, следовательно, \(\left(\begin{array}{c|c}A&b\end{array}\right)\) сводится к этому:

\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &\star \\ 0&1&\star &0&\star &\star \\ 0&0&0&1&\star &\star\end{array}\ справа).\номер\]

Нет \(b\), что делает его несовместимым, поэтому всегда есть решение. Наоборот, если \(A\) не имеет стержня в каждой строке, то его сокращенная ступенчатая форма строки выглядит так:

\[\left(\begin{array}{ccccc}1&0&\star &0&\star \\ 0&1&\star &0&\star \\ 0&0&0&0&0\end{array}\right),\nonumber\]

, что может привести к несогласованности системы после добавления \(b\text{:}\)

\[\left(\begin{array}{ccccc|c} 1&0&\star &0&\star &0 \\ 0&1&\star &0&\star &0 \\ 0&0&0&0&0&16\end{array}\right). \nonumber\]

Напомним, что эквивалентно означает, что для любой заданной матрицы \(A\text{,}\) либо все условий приведенной выше теоремы \(\PageIndex{1}\) выполняются , либо все они ложны.

Примечание \(\PageIndex{7}\)

Будьте внимательны при чтении формулировки приведенной выше теоремы \(\PageIndex{1}\). Первые два условия очень похожи на это примечание \(\PageIndex{6}\): диапазоны и согласованность, но логически они совершенно разные из-за квантификатора « для всех \(b\)».

Пример \(\PageIndex{6}\): Интерактивный: Соблюдены критерии теоремы

Рисунок \(\PageIndex{5}\): Пример, в котором критерии приведенной выше теоремы \(\PageIndex{ 1}\) удовлетворены. Фиолетовая область — это диапазон столбцов \(v_1,v_2,v_3\) массива \(A\text{,}\), который совпадает с набором всех \(b\), таких что \(Ax=b \) имеет решение. Если вы перетащите \(b\text{,}\), демо решит за вас \(Ax=b\) и переместит \(x\).

No related posts.