Виды прогрессии: Прогрессии — Математика — Теория, тесты, формулы и задачи

Прогрессии — Математика — Теория, тесты, формулы и задачи

• Главная —
• Учебные материалы —
• Математика —
• 12. Прогрессии

12. Прогрессии

Оглавление:

• Основные теоретические сведения
  • Арифметическая прогрессия
  • Геометрическая прогрессия

 

Основные теоретические сведения

Арифметическая прогрессия

К оглавлению. ..

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

 

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

• Назад
• Вперёд

 

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

1. Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
2. Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
3. Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

 

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.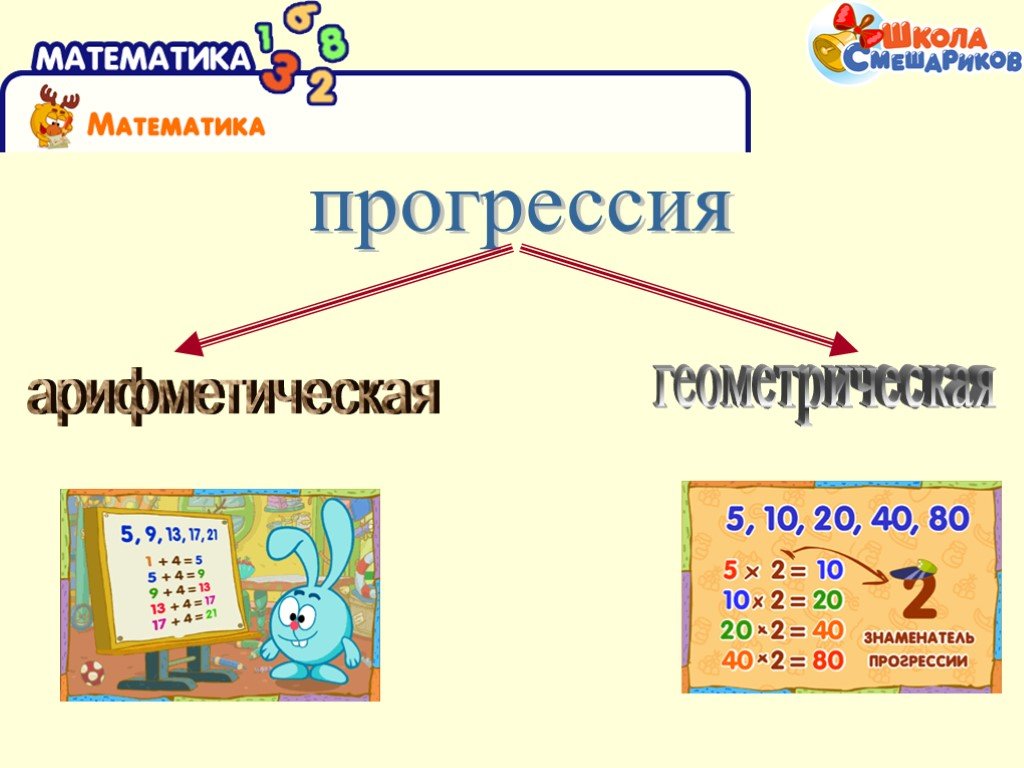

Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Арифметическая прогрессия, формула суммы элементов, разности, произведения, примеры с решением, чем отличается от геометрической

Математика

12.11.21

9 мин.

Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.

Оглавление:

• Онлайн-калькулятор арифметической прогрессии
• Определение и примеры арифметической прогрессии
• Виды арифметической (алгебраической) прогрессии
• Формулы арифметической прогрессии
• Примеры задач с решением

Одна из главных отличительных особенностей — такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.

Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.

Онлайн-калькулятор арифметической прогрессии

Определение и примеры арифметической прогрессии

Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.

Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (а_n) называется единичное число из последовательности.

Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.

Кроме этого, существуют виды таких рядов:

• возрастающая – числа ряда увеличиваются по своему значению;
• убывающая – каждое последующее число ряда уменьшается.

В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.

Виды арифметической (алгебраической) прогрессии

Разновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля.

Таким образом, можно встретить определенные вариации:

• разность d<0 – прогрессия будет считаться убывающей, а каждый последующий член будет меньше предыдущего;
• разность d>0 – это предполагает, что каждый член в ряду будет больше предыдущего, а прогрессию будут называть возрастающей;
• при d=0
  ряд тоже будет иметь свойства прогрессии, которую именуют стационарной, и все члены будут одинаковыми (не будут изменяться).

Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является.

[advice]Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель.[/advice]

Формулы арифметической прогрессии

Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.

Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (a_n-1), к которому прибавляют разность (d):

Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.

Итак, нам понадобится значение первого числа в ряду (a₁) и последнего (a_n), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:

[warning]Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы.[/warning]

Произведение членов арифметической прогрессии можно находить по похожей формуле:

где, P_n – произведение, b₁ и b_n – соответственно первое и последнее числа, а n – количество членов.

Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:

Примеры задач с решением

Рассмотрим как решать задачи на заданную тему.

Пример 1

Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».

Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a₁) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – 8) и получаем d = 7. Теперь мы можем считать по формуле:

Подставляя полученные значения, получим выражение вида a₅₇₄ = 8 + (574-1) * 7.

После вычисления получаем ответ: a₅₇₄ = 4019.

Пример 2

Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.

Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:

Подставляя известные значения, получаем выражение – а₅₄₄ = 17 + (544 — 1) * 8.

Вычисляя, получаем ответ а₅₄₄ = 4361.

Пример 3

Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.

Требуется выяснить, сколько времени у студента ушло на подготовку.

Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:

После подстановки получаем выражение: 730 = 17 + (n — 1) * 27.

После вычислений определяем ответ – 27 дней.

Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.

Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.

Что такое прогресс? Типы, примеры, формулы

Ряды и последовательности математической алгебры, связанные с числами и алгебраическими операциями, называются прогрессией.

Что такое прогресс?

Прогрессия — это набор чисел (или вещей), которые следуют определенному шаблону. Последовательность иногда называют последовательностью. Каждая фраза в последовательности создается путем применения определенного правила к числу перед ней. Другими словами, общий термин (или) n-й термин, представленный an.

Например, последовательность натуральных чисел 1, 2, 4, 6, 8… является арифметической прогрессией с разницей двух последовательных членов в два.

Типы прогрессий

Арифметическая прогрессия (АП)

Геометрическая прогрессия (ГП)

Гармоническая прогрессия (ГП)

Что такое арифметическая прогрессия?

Арифметическая прогрессия (АП) — это числовой ряд, в котором каждый последующий член является суммой предшествующего члена и фиксированного целого числа. Общим отличием является имя, данное этому фиксированному номеру. Например, 1, 4, 7, 10… — это AP, потому что каждое число получается путем добавления фиксированного числа 3 к предшествующей фразе.

2-й семестр = 4 = 1 + 3 = 1-й семестр + 3

3-й семестр = 7 = 4 + 3 = 2-й семестр + 3

Четвертый семестр = 10 = 7 + 3 = третий семестр + 3 и так далее.

Примеры арифметической прогрессии

Пример 1:  

Определите значение n, если a = 10, d = 5 и an = 95. 

Дано, a = 10, d = 5 и ан = 95. 

Используя формулу: 

a = a + (n − 1) × d

95 = 10 + (n − 1) × 5 

(n − 1) × 5 = 95 – 10 = 85

(n − 1) = 85/ 5

(n − 1) = 17

n = 17 + 1

n = 18 

Пример 2 : 

Найдите 10-й член AP 2,12, 22, 32….

Решение:  

Здесь первый член a = 2, а общая разность d равна 12-2 = 10 = d.

Используя формулу и положив n=10, получаем

a10 = 2+ (10-1)10 = 2 + 90 = 92.

Арифметическая прогрессия Формулы

Пусть a — первый член прогрессии, d — общая разность, a — n-й член. Таким образом, формулы арифметической прогрессии выглядят следующим образом: -1)d)\)

или

\(S_{n}= \frac{n}{2}(a+I)\)

где l — последний член, равный Tn

Первый член арифметической прогрессии

Альтернативно арифметическая прогрессия может быть выражена в терминах общих разностей следующим образом: а, а + d, а + 2d, а + 3d, а + 4d, ………. ., а + (n – 1) d, где «a» – первый член прогрессии.

Что такое геометрическая прогрессия?

Геометрическая прогрессия (ГП) — это числовой ряд, в котором каждый последующий член является произведением предшествующего члена и фиксированного целого числа. Обыкновенное отношение — это название, данное этой постоянной величине. Например, 4, 16, 64, 256… — это GP, потому что каждое число получается путем умножения фиксированного целого числа 4 на предшествующий ему член.

2-й член = 16 = 4(4) = 4 (1-й член)

Третий член = 64 = 4(16) = 4 (2-й член) 9{n}-1 )}{r-1}\) (когда r равно 1 и Sn = na, когда r равно 1.)

Когда |r| равно 1, сумме бесконечных геометрических рядов,

\(S= \frac{a}{1-r}\)

и, S расходится, когда |r| равно 1.

Пример геометрической прогрессии

Рассмотрим следующую геометрическую прогрессию: 1, 4, 16, 64… Имейте в виду, что 4/1 = 16/4 = 64/16 =… = 4. Все отношения одинаковы. В результате это ГП.

Что такое гармоническая прогрессия?

Гармоническая прогрессия — это ряд, образованный путем взятия обратной величины членов арифметической прогрессии. Натуральное число ряда есть арифметическая прогрессия. Следовательно, мы получаем 1,1/2,1/3,1/4… путем вычисления обратных величин каждого члена. Это пример гармонического прогресса.

Формула гармонической прогрессии

В случае гармонической прогрессии 1/a, 1/(a+d), 1/(a+2d) … 

n членов, \(a= \frac{1 }{а+(n-1)d}\)

Сумма первых членов,  \(S_{n}= \frac{1}{d} ln [\frac{2a + (2n – 1) d}{2a-d}]\)

Пример гармонической прогрессии

В HP, 

1/2, 1/4, 1/6, 1/8, 1/16 

Вы можете видеть, что если вы запишете знаменатели по отдельности, они соответствуют стилю AP.

Заключительные примечания

В результате членами гармонических прогрессий являются те, чьи знаменатели стоят в арифметической прогрессии в правильном порядке и имеют одинаковую общую разность.

Мы обратились к уравнениям, примерам прогрессий, определениям прогрессий, типам прогрессий и различиям между Артематической прогрессией, Геометрической прогрессией и Гармонической прогрессией. Если у вас есть какие-либо сомнения по поводу прогрессий или других вопросов, а также при разборе формул. Тогда посмотрите интерактивных онлайн-уроков Tutoroot . Квалифицированные преподаватели дадут доступ к идеальной атмосфере, позволяющей разобраться во всех сложных темах.

Типы прогрессии — Институт Пипенса

В математике существует несколько типов последовательностей, каждая со своими уникальными характеристиками и приложениями. Вот некоторые из наиболее распространенных типов прогрессий:

1. Арифметическая прогрессия (AP): В арифметической прогрессии каждый член получается путем прибавления фиксированного значения (называемого общей разностью) к предыдущему члену. Например, последовательность 1, 4, 7, 10, 13, … является арифметической прогрессией с общей разностью 3.

2. Геометрическая прогрессия (ГП): В геометрической прогрессии каждый член получается путем умножения предыдущего члена на фиксированное значение (называемое обыкновенным отношением). Например, последовательность 2, 6, 18, 54, 162, … представляет собой геометрическую прогрессию с обыкновенным отношением 3.

3. Гармоническая прогрессия (HP): В гармонической прогрессии каждый член является обратной величиной арифметическая прогрессия. Например, последовательность 1/2, 1/4, 1/6, 1/8, 1/10, … является гармонической последовательностью.

Эти прогрессии имеют различные применения в различных областях математики и естественных наук, и понимание их свойств и приложений может помочь в решении проблем и принятии решений.

1.Арифметическая прогрессия (АП)

Арифметическая прогрессия (АП) представляет собой последовательность чисел, в которой каждый член получается прибавлением фиксированного числа к предыдущему члену. Фиксированное число называется общей разностью арифметической прогрессии.

Пусть первый член арифметической прогрессии равен «а», а общая разность равна «d». Тогда n-й член арифметической прогрессии определяется как:

an = a + (n – 1) × d

Сумма первых n членов арифметической прогрессии определяется следующими формулами: 1. Сумма n членов АП:

Sn = ½ n × (a + an) = n/2 × {2a + (n-1)d}

2. Сумма первых n натуральных чисел: 1 + 2 + 3 + … + n = n(n+1)/2

3. Сумма первых n нечетных чисел: 1 + 3 + 5 + … + (2n-1) = n²

4. Сумма первых n четных чисел: 2 + 4 + 6 + … + 2n = n(n+1)

5. Сумма квадратов первых n натуральных чисел: 1² + 2² + 3² + … + n² = n(n+1)(2n+1)/6

6. Сумма кубов первых n натуральных чисел: 1³ + 2³ + 3³ + … + n³ = {n(n+1)/2}²

Эти формулы могут быть использованы для решения различных задач, связанных с арифметическими прогрессиями.

2 . Геометрическая прогрессия (ГП)

Геометрическая прогрессия (ГП) представляет собой последовательность чисел, в которой каждый член после первого получается путем умножения предыдущего члена на фиксированную константу, называемую знаменателем (r). Вот некоторые формулы, связанные с геометрическими прогрессиями: 9n)) / (1 – r), где «a1» — первый член, а «r» — знаменатель.

3. Бесконечная сумма ВП: Если абсолютное значение знаменателя (|r|) меньше 1, то бесконечная сумма геометрической прогрессии определяется формулой: S = a1 / (1 – r ), где «a1» — первый член, а «r» — обыкновенное отношение.

4. Сумма бесконечного геометрического ряда при |r|>=1: Если абсолютное значение знаменателя (|r|) больше или равно 1, то бесконечная сумма геометрической прогрессии не существует .Эти формулы можно использовать для решения различных задач, связанных с геометрическими прогрессиями в математике, физике и других областях.

3. Гармоническая прогрессия (ГП)

Гармоническая прогрессия (ГП) представляет собой последовательность чисел, в которой обратная величина каждого члена находится в арифметической прогрессии. Другими словами, говорят, что последовательность находится в гармонической прогрессии, если обратные ее члены находятся в арифметической прогрессии. Вот некоторые формулы, относящиеся к гармоническим прогрессиям:

1. N-й член HP: n-й член гармонической прогрессии задается формулой: an = 1 / [a1 + (n-1)d], где «a1» — первый член, а «d» — общая разность.

2. Сумма первых n членов ГП: Сумма первых n членов гармонической прогрессии определяется по формуле: S = n/2 * [2a1 + (n-1)d ] / [a1 + (n-1)d], где «a1» — первый член, а «d» — общая разность.

3. Соотношение между средними значениями двух чисел в HP: Если «a» и «b» — два числа в гармонической прогрессии, то их среднее арифметическое (AM) определяется как: AM = (a+b) / 2 и их среднее гармоническое (HM) определяется как: HM = 2ab / (a+b)

4. Соотношение между средними значениями трех чисел в HP: в прогрессии, то их среднее арифметическое (AM) определяется как: AM = (a+b+c) / 3, а их среднее гармоническое (HM) определяется как: HM = 3abc / (ab+bc+ca).Эти формулы можно использовать решать различные задачи, связанные с гармоническими прогрессиями в математике и других областях.