5. Асимптоты графика функции
При исследовании функции важно установить форму ее графика при неограниченном удалении точки графика от начала координат.
Особый интерес представляет случай, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.
Прямая называется асимптотой графика функции , если расстояние от переменной точки M графика до этой прямой при удалении точки M в бесконечность стремится к нулю, т.е. точка графика функции при своем стремлении в бесконечность должна неограниченно приближаться к асимптоте.
Кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном графике функции . Ее наклонная асимптота у = х.
Термин
асимптота введен древнегреческим ученым
Аполлонием Пергским при изучении
гиперболы и происходит от греческого
слова «асимтотос», означающего
«несовпадающий».
Следует отметить, что не любая кривая имеет асимптоту. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
5.1. Вертикальные асимптоты
Вертикальной асимптотой графика функции называется прямая x = а, если хотя бы при одном из условий x→ а – 0 или x → а + 0.
Вертикальные асимптоты следует искать в точках разрыва функции или на концах её области определения, если концы не равны .
График непрерывной на всей числовой прямой функции вертикальных асимптот не имеет.
5.2. Горизонтальные асимптоты
Если , то – горизонтальная асимптота кривой (правая при , левая при и двусторонняя, если пределы при равны).
5.3. Наклонные асимптоты
Поскольку асимптота – это прямая, то если кривая имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.
Теорема. Прямая y = kx + b служит наклонной асимптотой при x → ∞ для графика функции тогда и только тогда, когда , .
Замечание 1. Теорема показывает, что для нахождения наклонных асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая наклонных асимптот не имеет.
Замечание
При отыскании асимптот, как правило, рассматривают лишь два случая: вертикальные и наклонные.
Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.
6. Общая схема исследования функций и построения графиков
Исследование функции целесообразно вести в определенной последовательности:
Найти область определения, интервалы непрерывности и точки разрыва функции.
Выяснить, является ли функция четной, нечетной или общего вида.
Найти асимптоты графика функции.
Найти интервалы монотонности функции, точки её экстремума.
Найти интервалы выпуклости и вогнутости кривой, точки её перегиба.
Найти (если это можно) точки пересечения графика функции с осями координат.
Составить сводную таблицу исследования.
На основании проведенного исследования построить график функции.
Эту схему следует рассматривать как примерную. Например, пункты 1, 6 используются не всегда. Если же график функции не совсем понятен и после выполнения всех восьми операций, то можно построить дополнительные точки, выявить другие особенности функции (периодичность). Иногда целесообразно выполнение операций исследования сопровождать постепенным построением графика функции. Сводную таблицу также удобно заполнять по ходу исследования, но можно обойтись и без неё.
Асимптоты
Асимптоты.
При исследовании функций часто бывает, что при
удалении координаты х точки кривой в бесконечность кривая неограниченно
приближается к некоторой прямой.
Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю.
Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.
Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции . Ее наклонная асимптота у = х.
Рассмотрим подробнее методы нахождения асимптот кривых.
Вертикальные асимптоты.
Из определения асимптоты следует, что если или или , то прямая х = а – асимптота кривой y = f(x).
Например, для функции прямая х = 5 является вертикальной асимптотой.
Наклонные асимптоты.
Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.
M
j
N
j P
Q
Обозначим точку пересечения кривой и
перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с
асимптотой.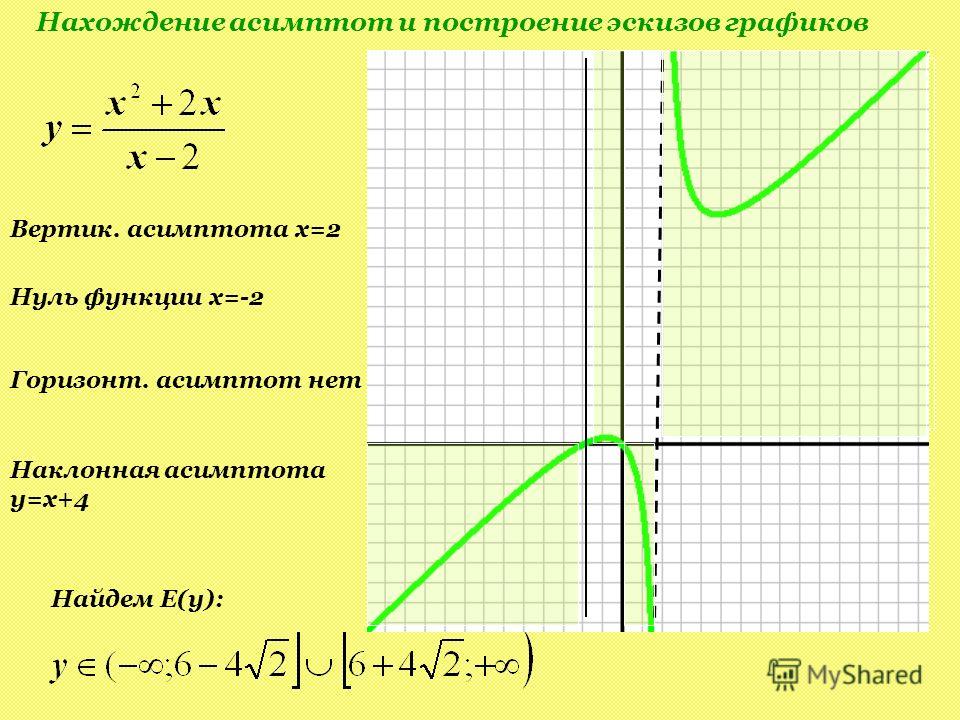
Тогда MQ = y – ордината точки кривой, NQ = - ордината точки N на асимптоте.
По условию: , ÐNMP = j, .
Угол j - постоянный и не равный 900, тогда
Тогда .
Итак, прямая y = kx + b – асимптота кривой. Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.
В полученном выражении выносим за скобки х:
Т.к. х®¥, то , т.к. b = const, то .
Тогда , следовательно,
.
Т.к. , то , следовательно,
Отметим, что горизонтальные асимптоты являются
частным случаем наклонных асимптот при k =0.
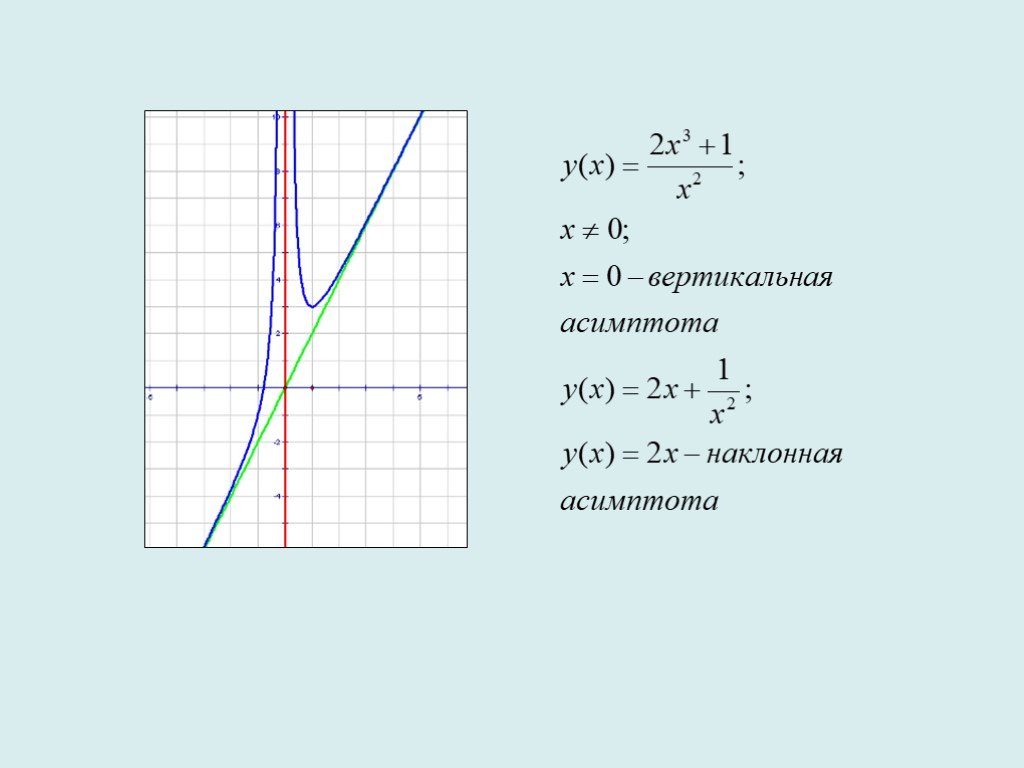
Пример. Найти асимптоты и построить график функции .
1) Вертикальные асимптоты: y®+¥ x®0-0: y®-¥ x®0+0, следовательно, х = 0- вертикальная асимптота.
2) Наклонные асимптоты:
Таким образом, прямая у = х + 2 является наклонной асимптотой.
Построим график функции:
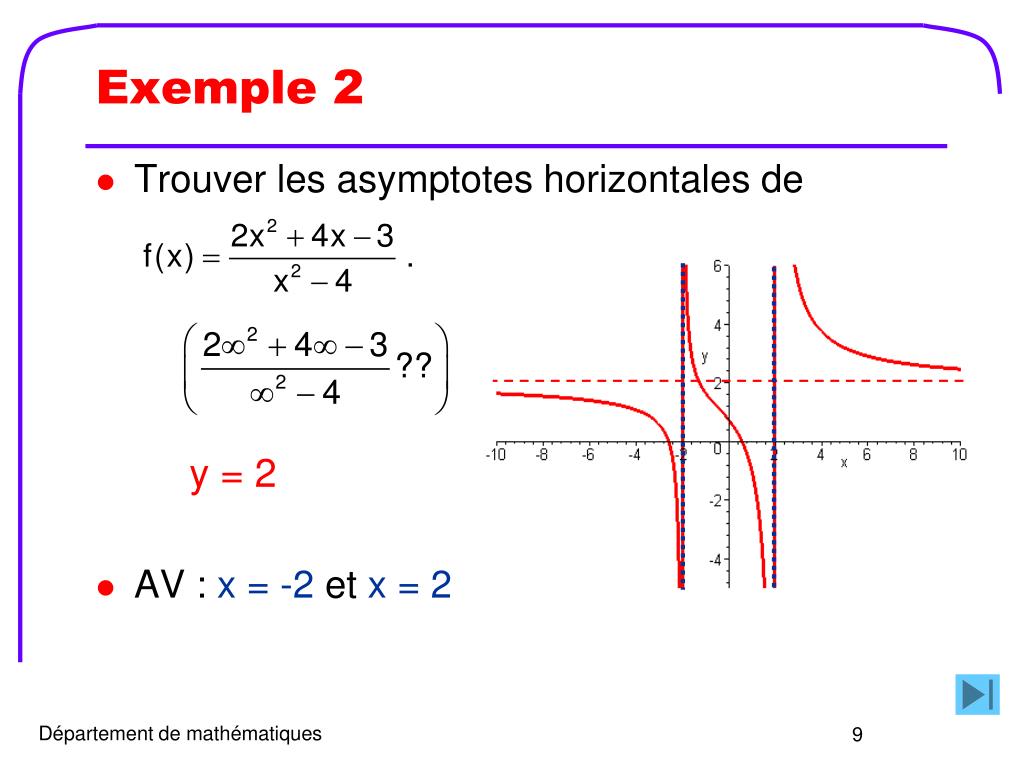
Пример. Найти асимптоты и построить график функции .
Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.
Найдем наклонные асимптоты:
y = 0 – горизонтальная асимптота.
Пример. Найти асимптоты и
построить график функции .
Прямая х = -2 является вертикальной асимптотой кривой.
Найдем наклонные асимптоты.
Итого, прямая у = х – 4 является наклонной асимптотой.
Как найти наклонные (наклонные) асимптоты рациональных функций « Математика :: WonderHowTo
- По рави
В этом обучающем видео инструктор показывает, как находить наклонные асимптоты рациональных функций.
Наклонные или наклонные асимптоты возникают, когда степень числителя ровно на единицу больше степени знаменателя рациональной функции. Способ найти уравнение наклонной асимптоты из функции — деление в длину. В этом длинном делении вы делите числитель на знаменатель, следуя методу длинного деления, как показано в этом видео. Перед делением, если в числителе есть пропущенные члены, запишите недостающую переменную с нулем в качестве ее числового коэффициента. Теперь после деления в длину вы получите частное и остаток. Теперь функцию можно представить в виде суммы частного и дроби, числитель которой равен остатку, а знаменатель — делителю. Теперь для очень больших значений x дробная форма сводится к нулю, и у вас остается простой член, который является наклонной асимптотой. В этом видео показано, как найти наклонные асимптоты рациональных функций.
Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Сделайте рывок в своей карьере с помощью нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам обучения от базового до продвинутого уровня по функциям, формулам, инструментам и многому другому.
Купить сейчас (скидка 97%) >
Другие выгодные предложения:
- Скидка 97 % на The Ultimate 2021 White Hat Certification Bundle
- Скидка 98 % на комплект Accounting Mastery Bootcamp 2021
- Скидка 99 % на The All-in-One Data Scientist Mega Bundle 2021
- Скидка 59 %: XSplit Lifetime Подписка (Windows)
- Скидка 98 % на пакет сертификации Premium Learn To Code 2021
- Скидка 62 % Программное обеспечение MindMaster Mind Mapping: бессрочная лицензия
- Скидка 41 % NetSpot Home Wi-Fi Analyzer: пожизненные обновления
- Горячий
- Последние
082Optimization.
lbz 082Optimization.lbzНаклонные асимптоты
Мы уже видели кое-что о рациональных функциях
и их поведение на бесконечности. Поведение этой рациональной функции на бесконечности основано на сравнении старших членов в p(x) и q(x) . В частности,
- Если показатель степени старшего члена q(x) больше, чем показатель степени старшего члена p(x) , функция приближается к 0 по горизонтальной асимптоте.
- Если два старших члена имеют одинаковый показатель степени, функция будет приближаться к горизонтальной асимптоте y = c , где c не равно 0.
- Если показатель степени старшего члена в p(x) больше, чем показатель степени старшего члена q(x) функция взрывается, когда x становится большим.
Сегодня мы добавим еще одну возможность, которая возникает, когда показатель степени старшего члена p(x) ровно на единицу больше, чем показатель степени старшего члена q(x) .
В этом случае мы увидим, что в пределе больших x рациональная функция приближается к наклонной асимптоте , уравнение которой y = m x + b . Точнее, мы увидим, что
Чтобы определить, что такое m и b , мы сначала исследуем производную и предположим, что
или
Как только мы узнаем, что такое m , мы можем вычислить b по
.Пример
1) Так как знаменатель положителен для всех x , вертикальных асимптот нет и функция определена везде.
2) Так как старший член числителя имеет степень на единицу выше старшего члена знаменателя, эта функция будет иметь наклонную асимптоту. Чтобы вычислить уравнение(я) наклонной асимптоты, мы начнем с вычисления предела производной как x получает большое отрицательное или положительное значение.
Наклонная асимптота имеет вид y = 2 x + b .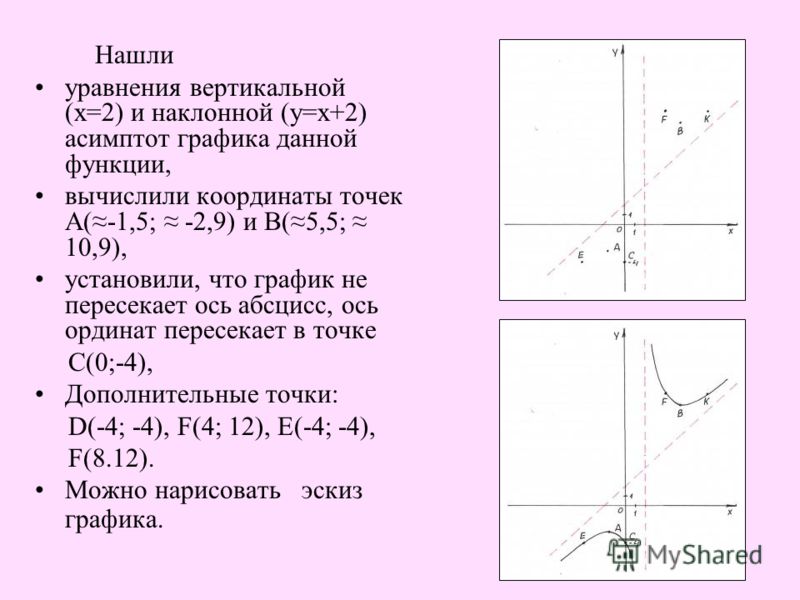
Чтобы определить значение b , мы вычисляем пределы
3) Как мы уже видели, первая производная равна
.Критические точки возникают там, где числитель равен 0
Таким образом, единственная критическая точка находится при x = 0 . Первая производная положительна для всех х .
4) Значение функции в критической точке равно
5) Вторая производная
Возможны три точки перегиба: x = 0 , , и . Вторая производная положительна для и и отрицательна везде.
6) Вот график функции и наклонной асимптоты вместе.
Проблемы с оптимизацией
Пример прикладной задачи на максимум/минимум
Вот проблема, которую, наверное, все мы знаем, как решить, хотя бы интуитивно. Рассмотрим линию на плоскости, скажем, y = 2 — 2 x . Какая точка на этой прямой ближе всего к началу координат?
Интуитивный ответ состоит в том, что если вы проведете линию из начала координат и сделаете эту линию перпендикулярной линии y = 2 — 2 x , эта линия пересечет график в точке ближе всего к происхождению.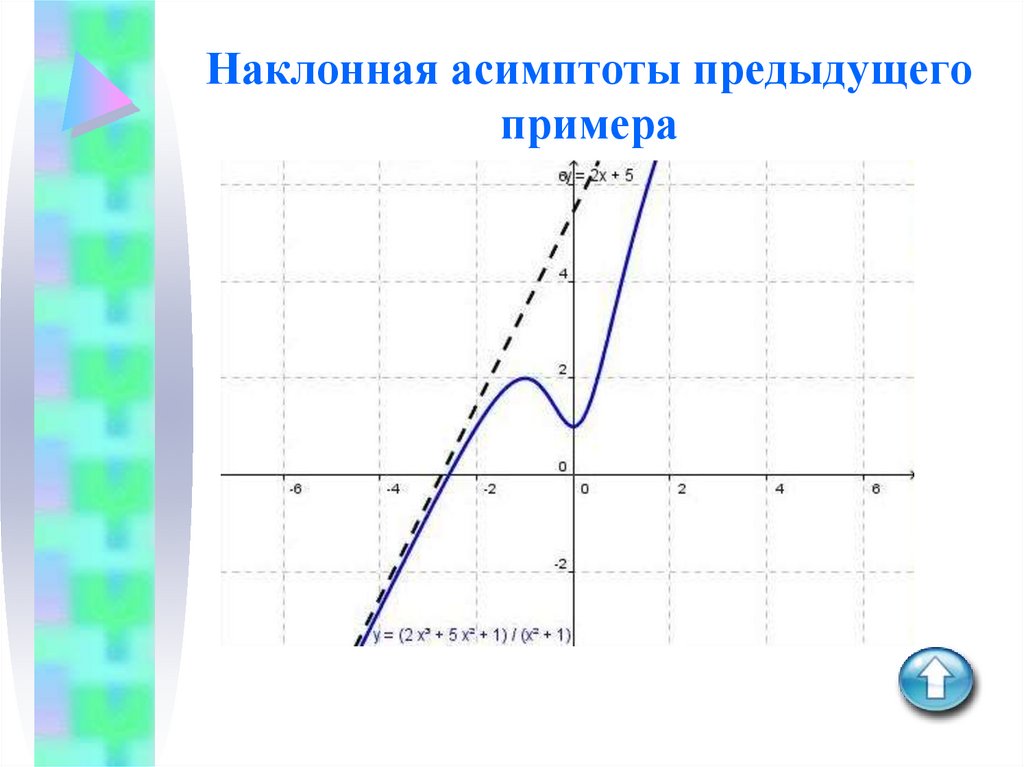
Имея это в виду, давайте посмотрим, как найти эту точку методами исчисления.
Для начала выберем любую точку (x,y) на графике. Каково расстояние от этой точки до начала координат?
Это количество, которое мы хотим минимизировать. Сложность здесь в том, что функция оказывается функцией двух переменных: x и y . Методы, которые мы разработали, чтобы помочь нам найти минимумы, работают только для функций одной переменной.
Решение этой проблемы состоит в том, чтобы понять, что x и и не могут оба изменяться независимо друг от друга. Если мы выберем любую точку (x,y) на линии и изменим ее значение x , значение y будет изменяться определенным образом. Мы выражаем это, написав
у(х) = 2 — 2 х
и впоследствии
Это упрощает задачу до такой степени, что мы можем применять инструменты исчисления. Теперь проблема состоит в том, чтобы найти значение или значения x , которые делают функцию
достигают своего минимума.
Прежде чем мы вычислим это минимальное значение, давайте разберемся с этой функцией, построив график.
Эта кривая имеет явный минимум. Все, что нам нужно сделать сейчас, это найти его. Минимум соответствует критической точке функции, т. е. точке х , для которой . Чтобы найти эту критическую точку, мы должны вычислить производную.
Ясно, что это равно 0, когда
-4 + 5 х = 0
или
Выглядит правильно. Чтобы подтвердить, что это действительно минимум, мы могли бы применить любой из трех тестов, которые мы видели ранее. Самый простой тест, который можно применить в этом случае, состоит в том, чтобы сравнить значение D(x) при 4/5 с его значением при некоторых близких значениях x .
| x | |
|---|---|
| 1 | |
0. 89442719099991586 | |
| 1 | 1 |
Все рассматриваемые примеры применения min/max будут иметь эти функции.
- Количество, которое необходимо максимизировать или минимизировать, легко записать как функцию нескольких переменных.
- Эти переменные не могут изменяться независимо друг от друга. Какое-то отношение ограничения связывает переменные вместе.
- Мы можем использовать ограничение, чтобы уменьшить количество переменных до одной.
- Затем мы решаем задачу о максимизации или минимизации функции одной переменной.
- Чтобы найти экстремальные значения, мы исследуем производную, чтобы найти критические точки. Мы используем некоторую технику, чтобы определить, какие критические точки соответствуют максимумам или минимумам, которые мы ищем.
Второй пример
Мы хотим построить цилиндрическую банку объемом 1000 кубических сантиметров.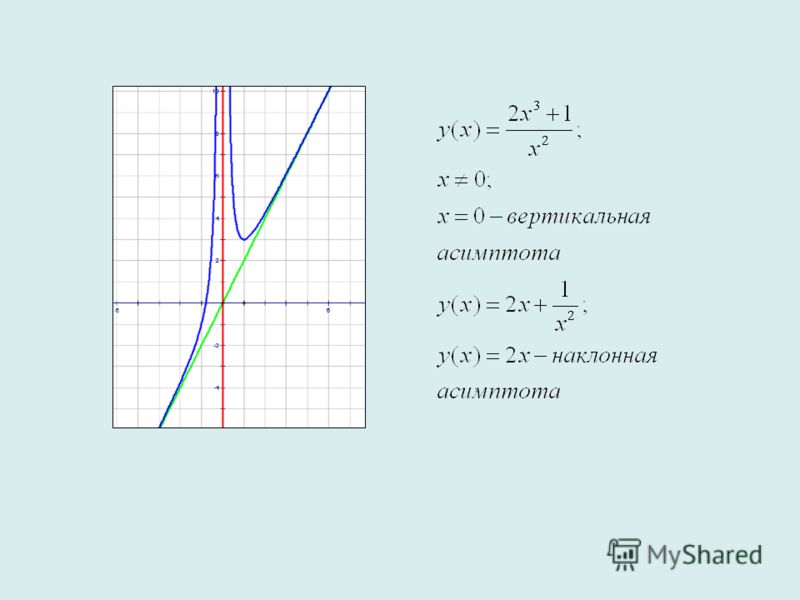
Материал, используемый для изготовления верхней и нижней частей банки, в два раза дороже, чем материал, используемый для изготовления боковых сторон. Найдите такие размеры банки, при которых общие затраты будут минимальными.
Учитывая цилиндрическую банку с радиусом основания r и высотой h , стоимость банки пропорциональна
Чтобы исключить одну из двух переменных здесь, нам нужно уравнение связи. В этом случае ограничение состоит в том, что объем должен быть 1000:
.или
Таким образом, как функция r стоимость составляет
Теперь мы готовы искать значение r , которое минимизирует стоимость. Начнем с вычисления первой производной и нахождения любых критических точек.
Установка этого числа равным 0 и вычисление r дает
Далее нам нужно подтвердить, что это соответствует минимуму. Вторая производная является наиболее простым критерием для применения в этом случае.