Площадь большого круга $S=100\,\pi $
Вероятность $P=\frac { 75\pi } { 100\pi } =0,75$.
Теоремы сложения вероятностей
Теорема 1 Если события А и В — несовместны, то \begin{equation} \label { eq1 } P( { A+B } )=P( A )+P( B ) \qquad (1) \end{equation} { несовместны — значит $A\cap B=\emptyset )$.
Пример: Вероятность выхода изделия из строя при эксплуатации сроком до одного года равна 0,1, а при эксплуатации сроком до пяти лет — 0,3. Найти вероятность выхода изделия из строя при эксплуатации сроком от одного года до пяти лет.
Решение. Введем события:
$A =$ { выход изделия из строя при эксплуатации сроком до 1-го года } ,
$B =$ { выход изделия из строя при эксплуатации от 1-го года до 5-ти } .
$C =$ { выход изделия из строя при эксплуатации до 5-ти лет } .
Так как $A$ и $B$ — несовместные события { не могут наступить одновременно } , то событие $C=A+B$.
Теорема 2 Сумма вероятностей противоположных событий равняется единице
$P( A )+P( { \overline A } )=1$ или $p+q=1$, где $P=P( A )$, $q=P( { \overline A } )$.
Следствие Вероятность полной группы несовместных событий $P( { A_1 } )+P( { A_2 } )+\ldots +P( { A_n } )=1$(3)
Опр. Случайные события A и B называются совместными, если при испытании могут произойти оба события т.е. произойдет совмещение событий.
Теорема 3 Вероятность суммы совместных событий равна \begin{equation} \label { eq2 } P( { A+B } )=P( A )+P( B )-P( { A\cap B } ) \qquad (2) \end{equation}
Пример: Отдел технического контроля проверяет на стандартность по двум параметрам серию изделий.
Решение. Введем события:
$A =$ { у изделия не выдержан первый параметр } ,
$B =$ { у изделия не выдержан второй параметр } .
$C =$ { изделие не удовлетворяет стандарту } .
Событию $A$ благоприятствуют $8+3=11$ исходов. Вероятность наступления события $A$ можно найти по формуле классической вероятности $P(A)=\frac { 11 } { 25 } $. Событию $B$ благоприятствуют $6+3=9$ исходов. Вероятность наступления события $B$ можно найти по формуле классической вероятности $P(B)=\frac { 9 } { 25 } $. Событию $( { A\cdot B } )$, состоящему в том, что у взятой детали не выдержаны оба параметра, благоприятствуют $3$ исхода. Вероятность наступления события $( { A\cdot B } )$ можно найти по формуле классической вероятности $P(A\cdot B)=\frac { 3 } { 25 } $.
$ P(C)=P( { A+B } )=P( A )+P( B )-P( { A\cdot B } ). $
Получим, $P(C)=P( { A+B } )=P( A )+P( B )-P( { A\cdot B } )=\frac { 11 } { 25 } +\frac { 9 } { 25 } -\frac { 3 } { 25 } =\frac { 17 } { 25 } $.
Условная вероятность
Опр. Событие $A$ называется зависимым от события $B$, если вероятность появления события А зависит от того произошло событие В или нет?
Опр. Условной вероятностью $P_B ( A )$или $P( { A /B } )$ называется вероятность появления события $A$ при условии, что событие В уже произошло.
Пример: В урне 3-и белых и 3-и черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно.
Найти вероятность появления белого шара { событие В } , если при первом испытании был извлечен черный шар { событие А } .
Решение. Всего в урне 6-ть шаров. После первого испытания { извлечение черного шара — событие А } в урне осталось 5-ть шаров из них 3-и белых. Вероятность вытащить белый шар { событие В } , при условии, что 1-м был черный есть { подсчитаем по формуле классической вероятности: m — благоприятные события — три белых шара, n — всевозможные события — всего шаров в урне пять } .
$ P_A ( B )=\frac { m } { n } =\frac { 3 } { 5 } . $
Теорема Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого $\begin{equation} \label { eq3 } P( { A\cdot B } )=P_B ( A )\cdot P( B ) \qquad (3) \end{equation} $
Следствие Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности остальных $ P( { A_1 \cdot A_2 \cdot \ldots \cdot A_n } )=P( { A_1 } )\cdot P_ { A_1 } ( { A_2 } )\cdot P_ { A_1 A_2 } ( { A_3 } )\cdot \ldots \cdot P_ { A_1 \ldots A_ { n-1 } } ( { A_n } ) $
Например: для трех событий $ P( { A\cdot B\cdot C } )=P( A )\cdot P_A ( B )\cdot P_ { AB } ( C ) $
Пример: В коробке девять одинаковых радиоламп, три из которых были в употреблении.
В течение рабочего дня мастеру для ремонта аппаратуры пришлось взять две радиолампы. Какова вероятность того, что обе взятые лампы были в употреблении?
Решение. Введем события:
$A =$ { 1 — я взятая лампа была в употреблении } ,
$B =$ { 2 — я взятая лампа была в употреблении } .
$C =$ { обе взятые лампы были в употреблении } .
Событие $C=A\cdot B$. Вероятность того, что первая взятая радиолампа была в употреблении, подсчитаем по формуле классической вероятности: m — благоприятные события — три лампы были в употреблении, n -всевозможные события — всего ламп в коробке девять $P(A)=\frac { m } { n } =\frac { 3 } { 9 } $. После того как произошло событие $A$, в коробке осталось восемь ламп из которых две были в употреблении. Событие $B$ наступает только при условии, что событие $A$ наступило, поэтому для нахождения вероятности события $B$, состоящего в появлении второй раз радиолампы, бывшей в употреблении используем условную вероятность { так как события зависимы } $P_A (B)=\frac { 2 } { 8 } $.
Замечание. Из формулы получим формулу для условной вероятности $\begin{equation} \label { eq4 } P_B ( A )=\frac { P( { A\cdot B } ) } { P( B ) } \qquad (4) \end{equation} $
Далее:
Класс M. Теорема о замкнутости класса M
Замена переменных в тройном интеграле
СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
Криволинейный интеграл первого рода
Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана
Линейный интеграл и циркуляция векторного поля
Класс Te . Теорема о замкнутости Te
Вычисление криволинейного интеграла второго рода в случае выполнения условия независимости от формы
Класс $S$.
Теорема о замкнyтости класса $S$
Вычисление двойного интеграла
Механические приложения тройного интеграла
Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах
Вычисление двойного интеграла. Двукратный интеграл
Булевы функции от $n$ переменных
Вычисление криволинейного интеграла первого рода. Примеры
Огравление $\Rightarrow $
27 сентября 2016, 21:26 проектирование км, кмд, кж Теория вероятности [Калинин В.М., Тихомиров С.Р.] 0 12572 0
Случайные события. Виды событий. Свойства вероятностей. Равномерное распределение. Нормальное распределение
Случайные события. Виды событий.
Теория вероятности
изучает закономерности, возникающие в случайных экспериментах, результат
которых заранее нельзя предугадать.
Не все случайные эксперименты можно
изучать методами теории вероятности, а лишь те которые могут быть
воспроизведены в одних и тех же условиях, хотя бы мысленно какое угодно число
раз. Пространством элементарных исходов называется множество содержащие все
возможные взаимно исключенные результаты данного случайного эксперимента.
Элементы множества называются элементарными исходами.
Событие наз-ся подмножеством данного множества. Говоря, что произошло событие А. Если эксперимент завершается одним из элементарных исходов входящих во множество А. Элементарный исход это мельчайший неделимый результат экспериментов, а событие может состоять из одного или нескольких исходов.
Событие называется
случайным, если при определении определенных условий оно может произойти или
не произойти. Событие называются единственно возможными, если появление в
результате испытания одного и только одного из них является достоверным
событием.
Событие наз-ся невозможным, которое не может произойти в рез-те эксперимента при определенном комплексе условий и не содержит ни одного элементарного исхода. Событие называется равновозможными, если есть основание считать, что ни одно из них не является более возможными изменить другие. Противоположными называются события одно, из которых исключает появление другого. Пересечением событий А и В называется событие, что произошли оба сразу события А и В. Объединением событий А и В называется событие состоящее в том, что из 2х событий случилось хотя бы одно. Вероятность события А наз-ся отношение числа благоприятствующих исходов к общему числу и сходов этого события.
Свойства
вероятностей.
а) вероятность достоверного события равна единице, т.к. число благоприятствующих исходов равно числу общих исходов m=n.
Р(А)=m/n=1.
б) вероятность невозможного события равно 0, т.к число благоприятствующих исходов = 0. Р(А) =m/n=0/n=0
в) вероятность случайного события 0< m/n <1 0<Р(А)<1
Равномерное распределение.
Равномерным распределением вероятности непрерывной случайной величины Х, заданной точностью вероятности на интервале (a, b)
Найдем значение С, применяя свойства плотности вероятности
Расписав данный интеграл на всей числовой оси получим
Характеристики равномерного распределения:
а) интегральная функция распределения
б) математическое
ожидание. Применим определение мат. ожидания для непрерывной случайной
величины.
Мат. ожидание равномерного распределения есть среднее арифметическое, т.е. середина интервала.
в) дисперсия. Применим определение дисперсии непрерывной случайной величины.
г) среднеквадратическое отклонение.
д) вероят. того, что случ. величина появится на интервале (α; β)
x є (a, b), найдем вероятность на интервале (α; β). P(α<x<β).
Применим формулу для вычисления вероятности на интервале для непрерывной случайной величины. P(α<x<β) = F(β) – F(α)
Нормальное распределение.
Нормальным распределением называют распределение вероятностей непрерывной случайной величины, заданной плотностью вероятности
σ – среднеквадратичное отклонение а – мат.ожидание х – случ. величина
Исследование:
а) область определения вся числовая ось б) если плотность вероятности f(x)>0, то график лежит выше оси Х
в) экстремумы функции
Точки перегиба х1 = а+σ х2 = а-σ
Значение функции в точках перегиба
Вывод: нормальное
распределение определятся 2мя параметрами мат.
ожиданием и среднеквадратичным
отклонением. График нормального распределения симметричен относительно
мат.ожидания
Хар-ки нормального распределения:
а) мат.ожидание
б)дисперсия
в) среднеквадратичное отклонение
г) вероятность на интервале (α; β)
д) вероятность отклон. нормально распределенной случ. величины Х по абс. величине < заданного положительного числа |x-a|<δ равно 2м интегральным функциям Лапласа от аргумента δ/σ
Плотность распред. вероятности непрерывной случ. величины.
Дифференц. функцией распред. или плотностью вероятности f(x) называется 1ая производная от интегральной функции распределения. f(x) = F’(x).
Свойства:
а)вероятность того,
что непрерывная случайная величина Х примет значение из интервала (а, b) равна
определенному интегралу от плотности вероятности на интервале (a, b).
б) интегральная функция распределения равна несобственному интегралу 1го рода от плотности вероятности.
в) дифференц. функция есть неотрицательная функция, то дифференц. функция тоже неотрицательная. F(x)≥0 => f(x)≥0.
г) несобственный интервал 1го рода от плотности вероятности на интервале (-∞; +∞) равна 1.
Числовые характеристики непрерывной случайной величины:
а) математическое ожидание
б) дисперсия
в) среднее квадратическое отклонение
Влияние параметров норм. распред. на форму норм. кривой.
а) т.к. плотность вероятности f(x) содержит разность (х-а) в четной степени
Типы событий в вероятности
В повседневных разговорах люди часто используют утверждения типа «Сегодня может пойти дождь» или «Я, скорее всего, сдам экзамен, так как экзамен был не слишком сложным» или «Скорее всего, он будет выбран» .
Во всех трех утверждениях используются такие слова, как возможно, вероятно, наиболее вероятно, и они используются для обозначения вероятности или уверенности в том, что что-то произойдет. Итак, если слова могут передать вероятность определенного события, почему вероятностью посвящена целая глава? Это потому, что вероятность в математике помогает определить точную вероятность события. Например, даны 2 утверждения: «Сегодня, вероятно, будет дождь» и «Сегодня с вероятностью 70% будет дождь», какое из утверждений дает лучший вывод? Второе утверждение, поскольку оно сообщает подробную вероятность события.
Вероятность
Вероятность события в математике — это числовое предсказание того, что это событие произойдет. Вероятность может быть определена в пропорции, которая варьируется от 0 до 1, или она также может быть выражена в процентах, варьирующихся от 0 до 100%. Например, существует 0,8-процентная вероятность того, что встреча будет отложена, или 80-процентная вероятность того, что встреча будет отложена.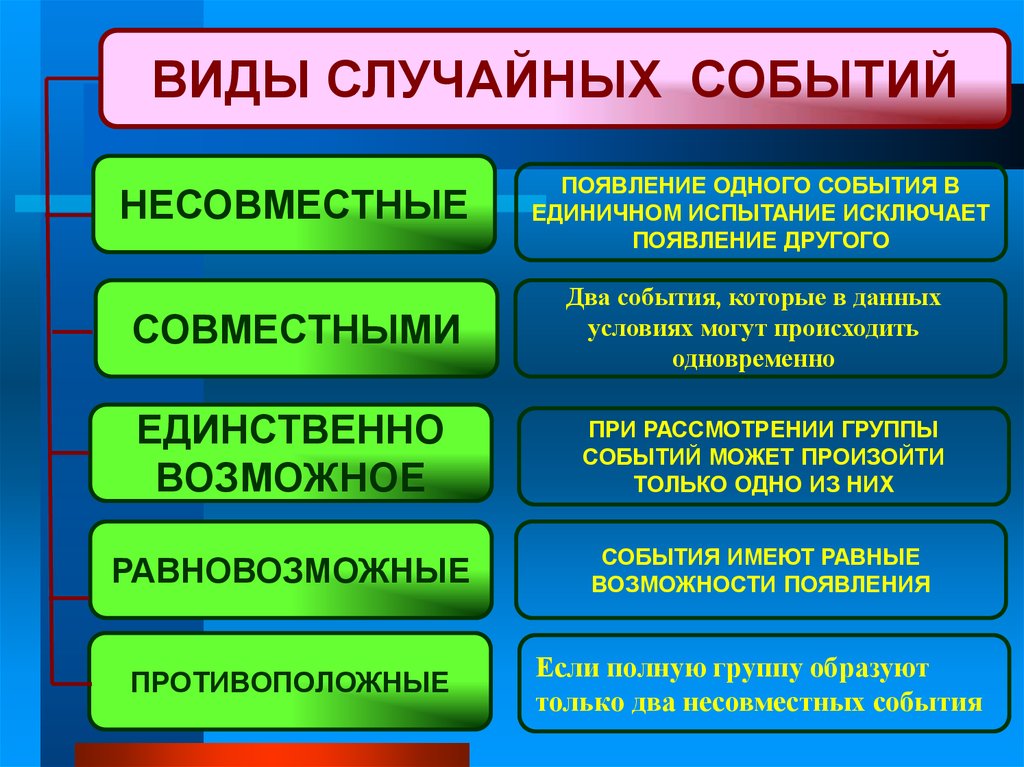
Вероятность всегда определяется для событий. События могут быть разных типов, Давайте узнаем о том, что они из себя представляют и какие бывают типы,
События
События на самом простом языке определяются как результат эксперимента, когда эксперимент проводится, от эксперимента ожидается некоторый результат, а ожидаемый результат известен как Вероятностное событие. Каждый раз, когда ожидаемый результат не соответствует действительности, есть вероятность того, что событие произойдет или оно не произойдет вообще, вероятность на самом деле является измерением этого возникновения события.
Место для образца
Выборочное пространство определяется как множество всех возможных исходов эксперимента, и событие является одним из возможных исходов, также событий (исходов) эксперимента может быть более одного. Следовательно, можно сделать вывод, что событие является подмножеством выборочного пространства.
Типы событий
Поскольку делается вывод о том, что события являются подмножествами пространства образцов, для эксперимента будет одно пространство образцов, но может быть несколько событий эксперимента, важно отметить, что события также имеют разных типов, давайте узнаем о них подробнее,
- Независимое событие
Независимые события — это события, в которых следующий исход не зависит от предыдущего исхода.
Значит, вероятность возникновения события останется неизменной независимо от того, сколько раз проводится один и тот же эксперимент.
Возьмем, к примеру, бросание кубика, кубик бросают один раз и вероятность выпадения четного числа равна 0,5, теперь кубик бросают еще раз, но вероятность выпадения четного числа будет только 0,5. Это означает, что вероятность события не зависит от его предыдущих исходов, такие события известны как независимые события.
- Зависимые события
Зависимые события — это события, в которых следующий исход зависит от предыдущих исходов, что означает, что вероятность события изменится в зависимости от его предыдущих исходов.
Например, возьмем пример извлечения шаров из мешка, в мешке 4 черных и 3 красных шара, вынули шар, и он оказался черным (В первом розыгрыше вероятность выпадения черный шар был 4/7 = 0,571.Когда шар будет извлечен в следующий раз, вероятность выпадения черного шара изменится, так как теперь в мешке меньше шаров (осталось 3 черных и 3 красных шара), следовательно, вероятность выпадения черного шара будет 3/6=0,5.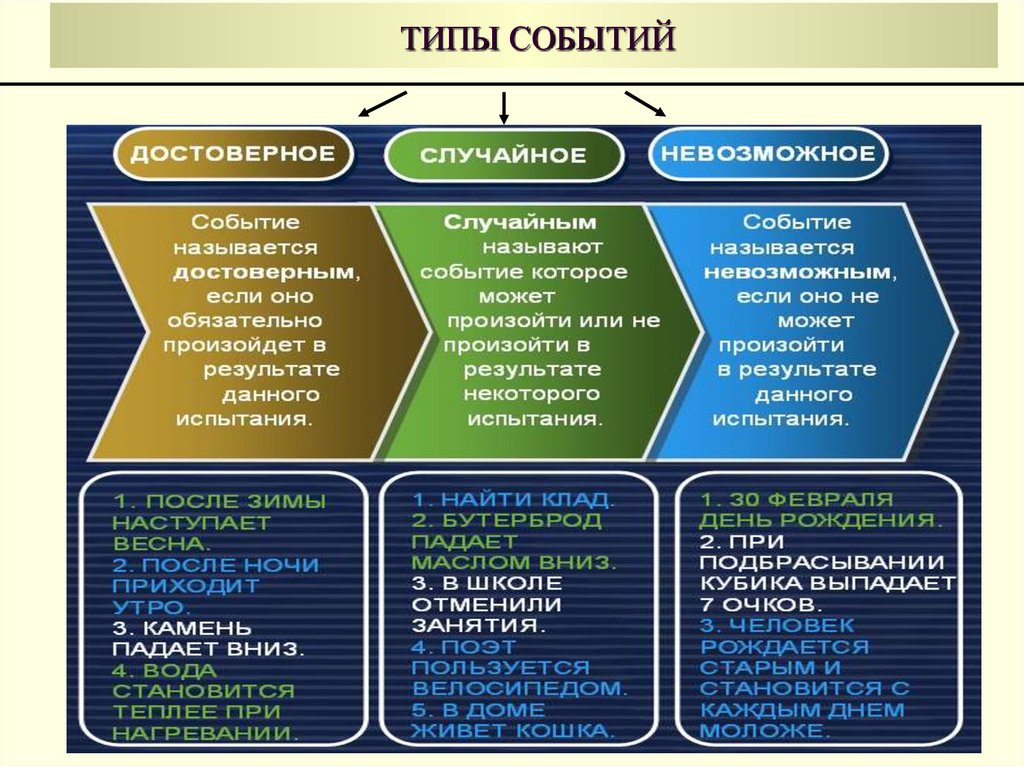
Такие типы событий известны как зависимые события.
Примечание: В приведенном выше примере есть способ преобразовать это зависимое событие в независимое, это можно сделать с помощью Замена. Если после каждого эксперимента мяч снова оставлять в мешке, то выборочное пространство эксперимента не изменится, а значит, и вероятность события останется прежней.
- Простое событие
Любое событие, которое содержит один результат из выборочного пространства, называется простым событием.
Например, выборочное пространство бросания игральной кости S = {1, 2, 3, 4, 5, 6} и событие получения меньше 2, E = {1}, где E имеет единственный результат, взятый из пространство выборки, следовательно, событие является простым событием.
- Составное событие
Составное событие прямо противоположно простому событию, то есть любому событию, которое содержит более одного результата или более одной точки из выборочного пространства, это событие известно как составное событие.
Например, S={1, 2, 3, 4, 5, 6} и E= {3, 4, 5}, здесь E — составное событие.
- Взаимоисключающие события
Если два события не имеют ничего общего, то они называются взаимоисключающими событиями, взаимоисключающие события аналогичны взаимоисключающим наборам.
Например, S (выборочное пространство) = {23, 25, 27, 29, 31}, E 1 = {23, 25, 27} и E 2 = {29, 31}, как есть хорошо видно, что между двумя множествами нет ничего общего, следовательно, события E 1 и E 2 являются взаимоисключающими событиями.
- Событие И
Событие И получено двумя или более двумя событиями, и операция, выполняемая над событиями, является операцией И,
Например, E1 = {2, 3, 4, 5} и E2 = {3, 4, 7, 8}
E = E1 ∩ E2 = {3, 4}
- ИЛИ Событие
ИЛИ Событие получается путем выполнения операции ИЛИ для двух или более двух событий .
Например, E1 = {2, 3, 4, 5} и E2 = {3, 4, 5, 6}
E = E 1 ∪ E 2 = {2, 3, 4, 5, 6}
- Дополнительное событие
присутствует в выборочном пространстве, отличном от заданного события.
Например, S = {1, 2, 3, 4, 5, 6, 7} и данное событие E = {1, 2, 3}
Дополнительное событие будет, E’ = {4, 5 , 6, 7}
Примеры задач
Вопрос 1: В игре Людо и Е 9 бросается игральная кость0079 1 обозначает событие получения четных чисел, а E 2 представляет событие получения числа больше 3. Найдите набор для следующих событий: Ответ: Пространство образца для матрицы будет, S = {1, 2, 3, 4, 5, 6} S = {1, 2, 4, 5, 6} . E 1 (только четные числа)= {2, 4, 6} E 2 (число больше 3) = {4, 5, 6} E 1 или E 2 = {2, 4, 5, 6} E 1 Вопрос 2: Подброшена игральная кость, и полученный набор для выборочного пространства равен S = {1, 2, 3, 4, 5, 6} E 1 определяется как событие получения числа меньше 5, а E 2 определяется как событие получения числа больше 2. Find the set for the following, Solution: Образец пространства будет, S = {1, 2, 3, 4, 5, 6} E 1 (число меньше 5) = {1, 2, 3, 4} E 2 (число больше 2) = {3, 4, 5, 6} 2 ровно по 2 головы за раз. Ответ: Когда за раз подбрасывается одна монета, выборочное пространство равно {H, T}, поскольку в результате может выпасть либо орел, либо решка. Однако, когда три монеты подбрасываются одновременно, может произойти комбинация различных возможностей. Эти возможности вместе будут составлять примерное пространство, Подбрасывание трех монет, S= {(H, H, H), (H, H, T), (H, T, H), (T, H, H), (T, T, H), ( T, H, T), (H, T, T), (T, T, T)} Таким образом, выборочное пространство содержит 6 возможных исходов. Событие (E) при выпадении ровно двух орлов, E= {(H, H, T), (H, T, H), (T, H, H)} Вопрос 4: Назовите типы событий, полученные из приведенных ниже экспериментов, Ответ: Вопрос 5: Что такое Невозможные и Верные события? Ответ: Невозможные события — это те, которые никогда не должны произойти, они являются нулевыми множествами и обозначаются как {}. Вероятность невозможного события равна 0. Следовательно, исходы не видны. В то время как верные события — это не что иное, как все пространство выборки, поскольку вероятность события в этом случае равна 1. Вопрос 6: Выборочное пространство эксперимента задается как S = { 10, 11, 12, 13, 14, 15, 16, 17}, а событие E определяется как все четные числа. Какое будет дополнительное событие для E. Ответ: S= {10, 11, 12, 13, 14, 15, 16, 17} E (все четные числа) = {10, 12, 14, 16} E’ (дополнение к E) = {11, 13, 15, 17} Событие, связанное с теорией вероятностей, может быть любого из следующих типов: (1 ) Уверенное событие, (2) Невозможное событие, (3) Случайное событие, (4) Элементарное событие, (5) Простое событие, (6) Составное событие, (7) Независимое событие, (8) Зависимое событие, (9) Взаимоисключающее событие , (10) перекрывающееся событие, (11) равновероятное событие и (12) дополнительное событие. Каждый из вышеперечисленных типов событий объясняется здесь следующим образом: (1) Уверенное событие. Событие, которое обязательно произойдет при выполнении случайного эксперимента, называется верным или определенным событием. (2) Невозможное событие. Событие, которое никогда не может произойти при проведении эксперимента, называется невозможным событием. (3) Случайное событие. Случайным или случайным событием называется событие, наступление которого является неопределенным или случайным. (4) Элементарное событие. Элемент выборочного пространства, представляющий все возможные результаты случайного эксперимента, называется элементарным событием. Таким образом, каждая точка выборки является элементарным событием. (5) Простое событие. Единичное событие, вероятность возникновения которого рассматривается, называется простым событием. Вероятность такого события представлена как P (A), где «A» представляет событие. Составные события. Два или более события, которые происходят совместно, и вероятность совместного наступления которых рассматривается, называются простым событием. Вероятность такого события представлена в любой из следующих форм: P (A & B), или P (A ∩ B), или P (AB), или P (A). P (B) Здесь A и B представляют два разных события. (7) Независимое мероприятие. Событие, возникновение которого не зависит от возникновения какого-либо другого события, называется независимым событием. Таким образом, результаты подбрасывания монеты, броска игральной кости или извлечения шара каждый раз после замены ранее вытащенного шара являются примерами независимых событий. В таких случаях вероятность последующих событий не зависит от возникновения предшествующих им событий. Таким образом, вероятность выпадения 5 вверх в 3-й попытке броска кости останется такой же 1/6, как и в 1-й и 2-й попытках. Точно так же вероятность вытянуть пиковую карту из колоды из 52 игральных карт во 2-м розыгрыше останется такой же, т. (8) Зависимое событие. Последующее событие, на вероятность или возникновение которого влияет вероятность или возникновение предшествующего ему события или события, называется зависимым событием. Таким образом, при последовательном безвозвратном извлечении карт из колоды из 52 игральных карт вероятность вытянуть пику во 2-м розыгрыше будет (12/52), тогда как в первом розыгрыше она была (13/52) ( 1) Здесь на вероятность второго розыгрыша повлиял розыгрыш пиковой карты в первом розыгрыше, который не был заменен до второго розыгрыша, что уменьшило как желаемое количество пиковых карт, так и общее количество всех карт. одним. Следует отметить, что никакое начальное событие не может быть зависимым событием. (9) Взаимоисключающие события. Два или более события считаются взаимоисключающими, если наступление одного исключает или препятствует наступлению другого одновременно.0 2
= {4, 6}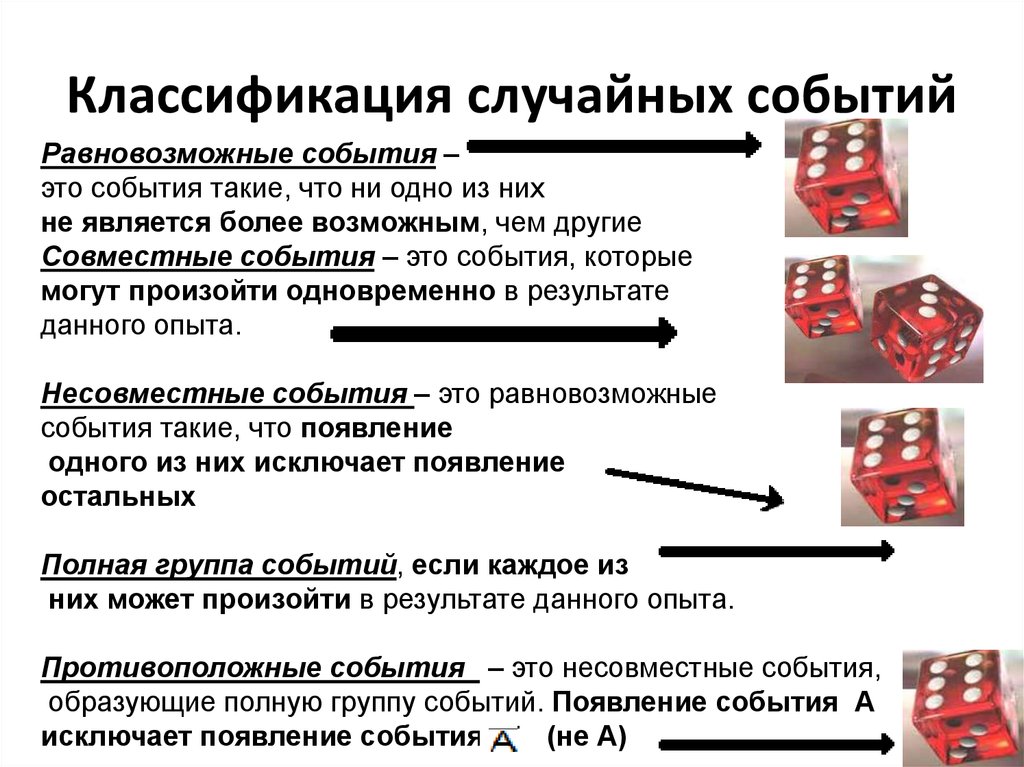
Типы событий Домашнее задание Справка по статистике
е. (13 пик/всего 52), как и в первом розыгрыше, при условии, что карта, вытянутая в первом розыгрыше, заменены до проведения второго розыгрыша.