|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 15Следующая ⇒ Вписанный угол (ACB) ― угол, вершина которого лежит на окружности, а стороны являются ее хордами: · измеряется половиной дуги, на которую он опирается; · вписанные углы, опирающиеся на одну и ту же дугу, равны; · вписанный угол, опирающийся на диаметр — прямой. Центральный угол (AOB) ― угол, образованный двумя радиусами: · измеряется дугой, на которую опирается; · центральный угол в два раза больше вписанного, опирающегося на ту же дугу.
Хорды и секущие Произведение длин отрезков пересекающихся хорд равны: · если хорды АВ и СD пересекаются в точке М, то АМ ВМ = СМ DМ. Произведение длин отрезков секущей равно квадрату длины отрезка касательной: · если через точку М проведена секущая к окружности и касательная, причем точки А и В ― точки пересечения окружности с секущей, а С ― точка касания, то АМ ВМ = СМ2.
Длина окружности и дуги Длина окружности: L = 2πR = πD, R ― радиус окружности, D ― диаметр. Длина дуги окружности: l = = , α ― градусная мера дуги.
Площадь круга и сектора Сектор — часть круга, ограниченная двумя радиусами и дугой окружности. Sкруга = πR2 Sсектора = , α ― градусная мера дуги.
Комбинации с окружностью 1.Окружность называется вписанной в многоугольник, если все его стороны касаются окружности. 2. Центром вписанной окружности является точка пересечения биссектрис. 3. Центром описанной окружности является точка пересечения серединных перпендикуляров. 4. В любой треугольник можно вписать окружность, около любого треугольника можно описать окружность. 5. Радиус вписанной окружности в треугольнике: r = , p ― полупериметр треугольника. 6. Радиус описанной окружности в треугольнике: R = . 7. В четырехугольник можно вписать окружность, если суммы противоположных сторон равны. 8. Вокруг четырехугольника можно описать окружность, если сумма противоположных углов равна 180°. 9. Из всех параллелограммов окружность можно вписать только в ромб и квадрат. 10. Из всех параллелограммов окружность можно описать только около прямоугольника и квадрата.
Равнобедренный треугольник  Свои звёзды есть и среди треугольников ― это равнобедренный, равносторонний и прямоугольный треугольники, соответственно. Сейчас мы про них и поговорим.Итак, начнём с равнобедренного треугольника. Равнобедренный треугольник ― это треугольник, у которого две стороны равны (на нашем рисунке АВ = АС). Равные стороны в таком треугольнике называются боковыми (АВ и АС), а оставшаяся третья сторона ― основанием (ВС, соответственно). Естественно, он попал в список наших «звёзд» неслучайно ― у него есть ряд очень удобных свойств. Например, в равнобедренном треугольнике углы при основании равны (углы АВС и АСВ). Кроме того, в равнобедренном треугольнике медиана, проведённая к основанию,является биссектрисой и высотой. То есть она не только делит противолежащую сторону пополам (ВМ = МС), но и падает на неё под углом 90°, а кроме того делит угол, из которого выходит, пополам (углы ВАМ и МАС равны). Посмотрим на пример конкретной задачи. В равнобедренном треугольнике внешний угол равен 80°, необходимо найти все углы треугольника. Сразу возникает вопрос ― внешний угол при каком угле треугольника? Предположим, что это внешний угол при угле В (с нашего первого рисунка). Но в таком случае выходит, что сам ∠В = 100° (по сумме смежных углов). Значит, и ∠С = 100°, так как треугольник равнобедренный. Но тогда сумма только двух углов получается 200°, чего быть никак не может. Значит, речь идёт о внешнем угле при угле
Равносторонний треугольник После знакомства с равнобедренным треугольником имеет смысл поближе узнать его близкого родственника ― равносторонний треугольник. Равносторонний треугольник ― это треугольник, у которого все три стороны равны. Кроме равенства сторон в таком треугольнике равны и все углы (каждый из которых по 60° ― так как 180° : 3 = 60°). Если проводить аналогию с равнобедренным треугольником, в равностороннем любая сторона одновременно является и основанием, и боковой стороной. За счёт этого, в равностороннем медиана, проведённая из любого угла, будет являться биссектрисой и высотой (другими словами, равносторонний треугольник с любой стороны является равнобедренным).
Прямоугольный треугольник Особняком стоит наш третий гость ― прямоугольный треугольник. В отличие от первых двух, он не определяется равенством сторон. Зато в таком треугольнике один угол всегда равен 90° (собственно, это и есть прямой угол, дающий название всему треугольнику). Сторона, лежащая против такого угла, называется гипотенузой (сторона АВна нашем рисунке), а две другие стороны ― катетами (АС и ВС, соответственно). Естественно, в любом прямоугольном треугольнике гипотенуза всегда больше катета (не забываем о том, что против большего угла лежит большая сторона, и наоборот). Прямоугольный треугольник тоже обладает рядом замечательных свойств. К примеру, именно для него верна знаменитая теорема Пифагора (квадрат гипотенузы равен сумме квадратов катетов, или, по примеру нашего рисунка, АВ2= Стоит ещё отметить такой нюанс: существует равнобедренный прямоугольный треугольник, своеобразный гибрид. В таком треугольнике катеты равны (так как равенства катета и гипотенузы не может быть, не забываем об этом), а все углы легко считаются ― раз один угол 90°, то два оставшихся угла получаются по 45°. Таким образом, вы успешно познакомились с тремя “особыми треугольниками”, так часто встречающимися в геометрии. В процессе курса вы узнаете о них гораздо больше, а пока имеет смысл закрепить полученные знания в домашнем задании.
Параллелограммы Мы уже успели познакомиться с особыми треугольниками, самое время поближе узнать “звёзд” среди четырёхугольников ― параллелограммы и их вариации. Сегодня мы будем говорить о самом параллелограмме, ромбе, прямоугольнике и квадрате. Начнём, естественно, с параллелограмма. Параллелограмм ― это четырёхугольник, у которого противоположные стороны параллельны (АВ || CD, AC || BD). У параллелограмма есть ряд замечательных свойств, которые и делают его таким особенным. В любом параллелограмме противоположные стороны равны (АВ = СD, AC = BD). Кроме того, в параллелограмме противоположные углы равны (∠А = ∠D, ∠B = ∠C), а из параллельности сторон можно говорить и о равенстве частей углов (например, ∠DAB = ∠ADC; ∠BCD  Ещё одно крайне полезное свойство ― диагонали параллелограмма точкой пересечения делятся пополам (АО = OD, CO = OB). У параллелограмма есть ряд частных случаев, которые не менее интересны, чем он сам. Например ― прямоугольник. Прямоугольник― это параллелограмм, у которого все углы прямые. Кроме свойств параллелограмма, у прямоугольника есть и несколько своих. Диагонали прямоугольника равны (AD = BC), а стороны прямоугольника являются его высотами. Ромб ― это параллелограмм, у которого все стороны равны. Естественно, ромбу присущи все те же свойства, что и параллелограмму. Вдобавок, диагонали ромба являются биссектрисами его углов и пересекаются под прямым углом (AD ⊥ BC). Интересно, что само слово “ромб” происходит от древнегреческого “бубен”, потому что в те времена бубны делали именно в форме бубна или квадрата. И раз уж мы упомянули квадрат, то давайте поговорим о нём чуть подробнее. Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны (AB =BC = CD = DA и ∠A = ∠B = ∠C = ∠D = 90°). Центры вписанной и описанной окружностей квадрата совпадают и одновременно являются точкой пересечения диагоналей (т. О). Стоит отметить, что любой квадрат является ромбом и прямоугольником, но не любой ромб или прямоугольник является квадратом. Обратите внимание, что мы определяли каждую из фигур через предыдущую. И это сделано не просто так. Определение «Квадрат ― это параллелограмм, у которого все стороны равны и все углы равны», означает в том числе, что всё, что мы говорили в связи с параллелограммом, верно и для квадрата. А так как квадрат сочетает в себе признаки ромба и прямоугольника, то он обладает также и их свойствами. Поздравляем! Теперь вы знакомы не только с особыми треугольниками, но и с различными интересными четырёхугольниками. Гораздо подробнее о них (а также их свойствах) вы узнаете на лекциях, а сейчас имеет смысл отточить знания на проверочных заданиях.
Векторы Сложение двух векторов Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма: = + . Правило треугольника: Правило параллелограмма: Для любых трех точек А, В, С справедливо соотношение: + = . Вычитание векторов Разность двух векторов и — это вектор , который в сумме с вектором дает вектор : + = ⇒ = – . Вектор можно найти также, складывая с вектором вектор — , противоположный вектору : = + (– ). Координаты вектора · Координатами вектораназываются разности координат конца и начала вектора. Координаты вектора не изменяются при параллельном переносе. У равных векторов соответствующие координаты равны. На плоскости: Координаты вектора (аx; ay): аx = x2 – x1; ay = y2 – y1. Модуль вектора: | | = . В пространстве: Координаты вектора (аx; ay;az): аx = x2 – x1; ay = y2 – y1; az= z2 – z1. Модуль вектора: | | = . ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 907; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Все правила по сольфеджио
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.005 с.)Градусная мера вписанного и центрального углов. Окружность и вписанный угол
Угол ABC — вписанный угол. Он опирается на дугу АС, заключённую между его сторонами (рис. 330).
Теорема . Вписанный угол измеряется половиной дуги, на которую он опирается.
Это надо понимать так: вписанный угол содержит столько угловых градусов, минут и секунд, сколько дуговых градусов, минут и секунд содержится в половине дуги, на которую он опирается.
При доказательстве этой теоремы надо рассмотреть три случая.
Первый случай. Центр круга лежит на стороне вписанного угла (рис. 331).
Пусть ∠ABC — вписанный угол и центр круга О лежит на стороне BC. Требуется доказать, что он измеряется половиной дуги AC.
Соединим точку A с центром круга.
Получим равнобедренный \(\Delta\)AOB, в котором АО = OB, как радиусы одного и того же круга. Следовательно, ∠A = ∠B.
∠AOC является внешним по отношению к треугольнику AOB, поэтому ∠AOC = ∠А + ∠В, а так как углы А и В равны, то ∠В составляет 1 / 2 ∠AOC.
Но ∠AOC измеряется дугой АС, следовательно, ∠В измеряется половиной дуги АС.
Например, если \(\breve{AC}\) содержит 60°18’, то ∠В содержит 30°9’.
Второй случай. Центр круга лежит между сторонами вписанного угла (рис. 332).
Пусть ∠ABD — вписанный угол. Центр круга О лежит между его сторонами. Требуется доказать, что ∠ABD измеряется половиной дуги АD.
Для доказательства проведём диаметр BC. Угол ABD разбился на два угла: ∠1 и ∠2.
∠1 измеряется половиной дуги АС, а ∠2 измеряется половиной дуги СD, следовательно, весь ∠АВD измеряется 1 / 2 \(\breve{AC}\) + 1 / 2 \(\breve{CD}\), т. е. половиной дуги АD.
Например, если \(\breve{AD}\) содержит 124°, то ∠В содержит 62°.
Третий случай.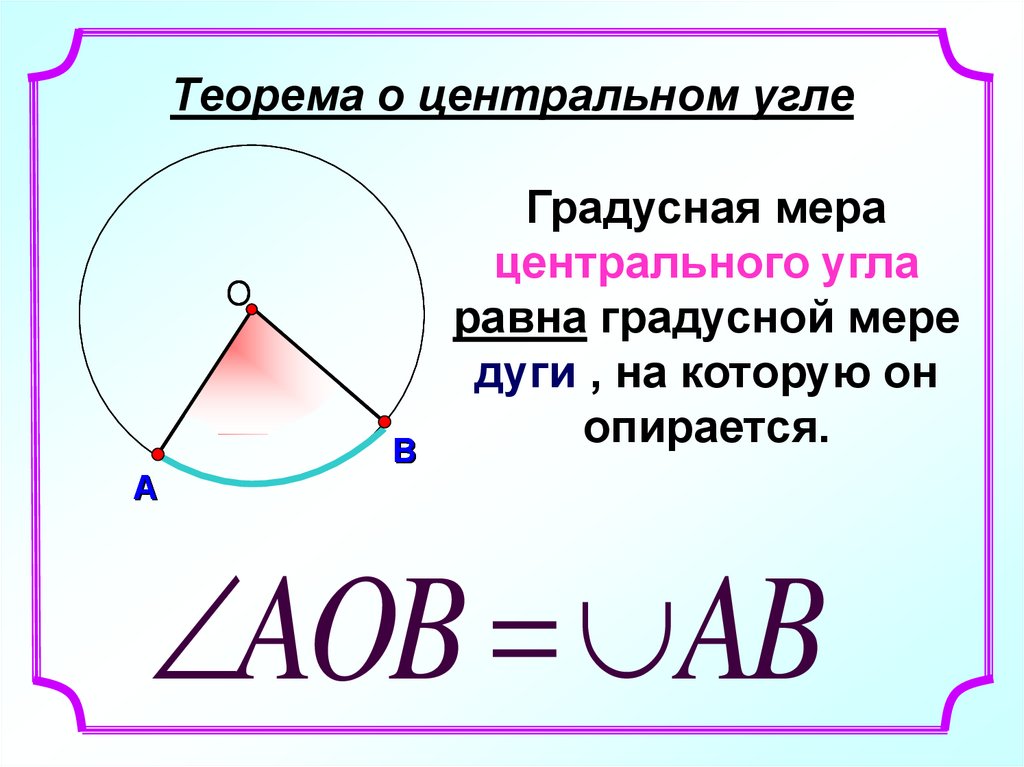
Центр круга лежит вне вписанного угла (рис. 333).
Пусть ∠MAD — вписанный угол. Центр круга О находится вне угла. Требуется доказать, что ∠MAD измеряется половиной дуги MD.
Для доказательства проведём диаметр AB. ∠MAD = ∠MAB — ∠DAB. Но ∠MAB измеряется 1 / 2 \(\breve{MB}\), а ∠DAB измеряется 1 / 2 \(\breve{DB}\).
Следовательно, ∠MAD измеряется 1 / 2 (\(\breve{MB} — \breve{DB})\), т. е. 1 / 2 \(\breve{MD}\).
Например, если \(\breve{MD}\) содержит 48° 38″, то ∠MAD содержит 24° 19’ 8″.
Следствия
1. Все вписанные углы, опирающиеся на одну и ту же дугу, равны между собой, так как они измеряются половиной одной и той же дуги (рис. 334, а).
2. Вписанный угол, опирающийся на диаметр, — прямой, так как он опирается на половину окружности. Половина окружности содержит 180 дуговых градусов, значит, угол, опирающийся на диаметр, содержит 90 угловых градусов (рис. 334, б).
Понятие вписанного и центрально угла
Введем сначала понятие центрального угла.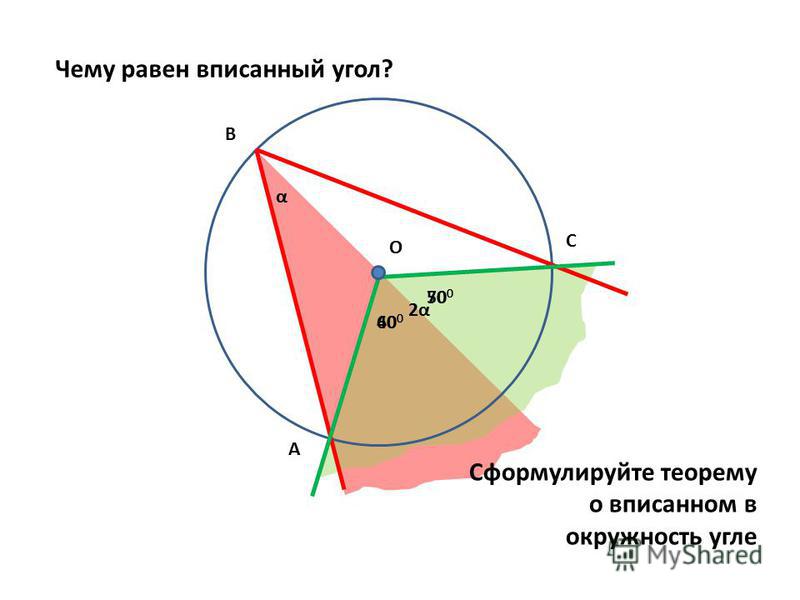
\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:
- Луч $CO$ делит внутренний угол на два угла. Пусть он пересекает окружность в точке $D$ (рис. 4).
Рисунок 4.
Получаем
- Луч $CO$ не делит внутренний угол на два угла и не совпадает ни с одной его стороной (Рис. 5).
Рисунок 5.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
Теорема доказана.
Приведем следствия из данной теоремы.
Следствие 1: Вписанные углы, которые опираются на одну и туже дугу равны между собой.
Следствие 2: Вписанный угол, который опирается на диаметр — прямой.
Понятие вписанного и центрально угла
Введем сначала понятие центрального угла.
Замечание 1
Отметим, что градусная мера центрального угла равна градусной мере дуги, на которую он опирается .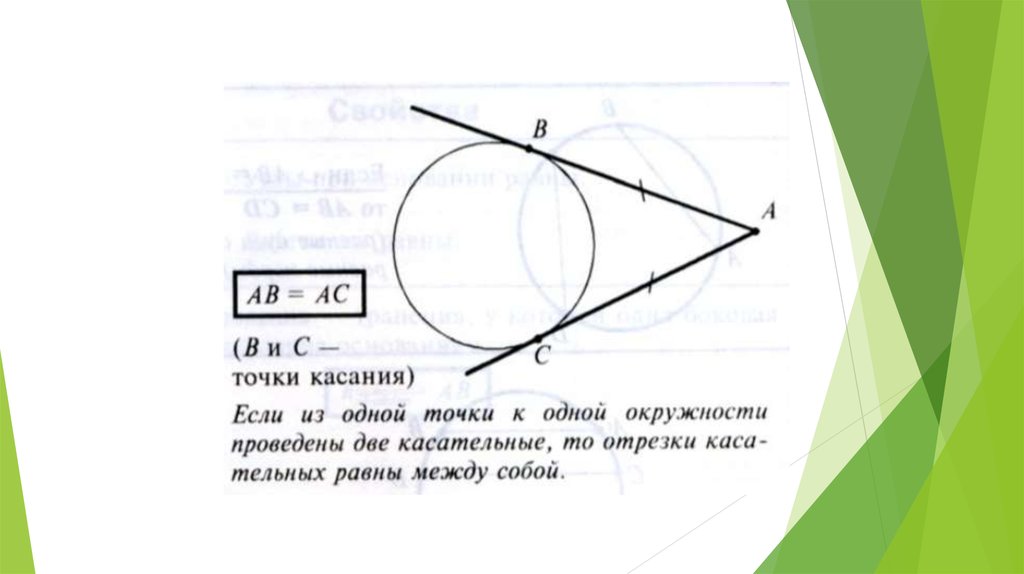
\circ }$, следовательно, центральный угол $AOB$ равен дуге $AB$. Так как $AO=OC=r$, то треугольник $AOC$ равнобедренный. Значит, углы при основании $CAO$ и $ACO$ равны между собой. По теореме о внешнем угле треугольника, имеем:
- Луч $CO$ делит внутренний угол на два угла. Пусть он пересекает окружность в точке $D$ (рис. 4).
Рисунок 4.
Получаем
- Луч $CO$ не делит внутренний угол на два угла и не совпадает ни с одной его стороной (Рис. 5).
Рисунок 5.
Рассмотрим отдельно углы $ACD$ и $DCB$. По доказанному в пункте 1, получим
Получаем
Теорема доказана.
Приведем следствия из данной теоремы.
Следствие 1: Вписанные углы, которые опираются на одну и туже дугу равны между собой.
Следствие 2: Вписанный угол, который опирается на диаметр — прямой.
Вписанный угол, теория задачи. Друзья! В этой статье речь пойдёт о заданиях, для решения которых необходимо знать свойства вписанного угла.
Это целая группа задач, они включены в ЕГЭ. Большинство из них решаются очень просто, в одно действие.
Есть задачи посложнее, но и они большой трудности для вас не представят, необходимо знать свойства вписанного угла. Постепенно мы разберём все прототипы задач, приглашаю вас на блог!
Теперь необходимая теория. Вспомним, что такое центральный и вписанный угол, хорда, дуга, на которые опираются эти углы:
Центральным углом в окружности называется плоский угол с вершиной в ее центре .
Часть окружности, расположенная внутри плоского угла, называется дугой окружности.
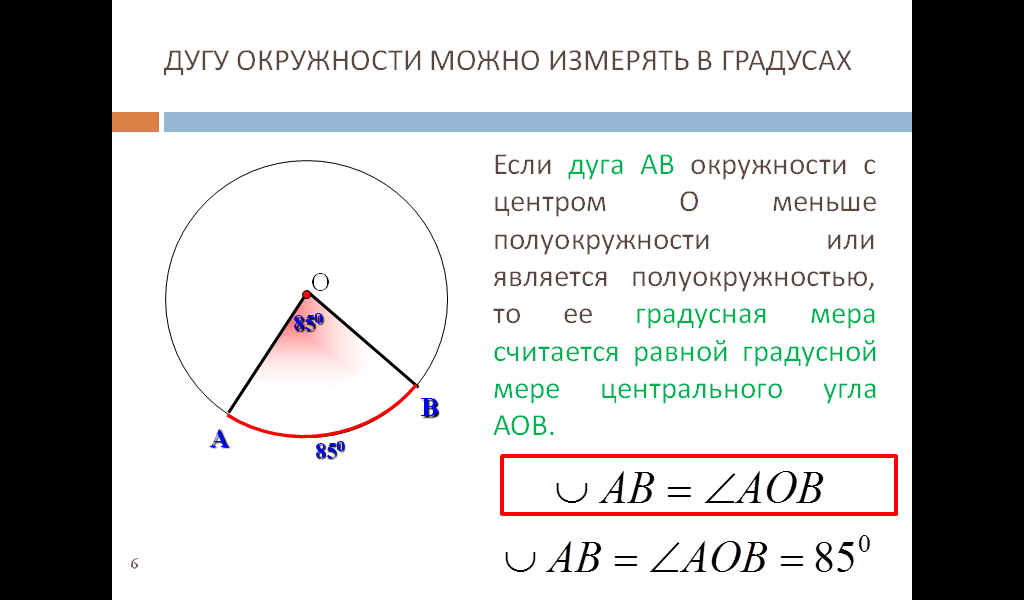
Градусной мерой дуги окружности называется градусная мера соответствующего центрального угла.
Угол, называется вписанным в окружность, если вершина угла лежит на окружности, а стороны угла пересекают эту окружность.
Отрезок соединяющий две точки окружности называется хордой . Самая большая хорда проходит через центр окружности и называется диаметр.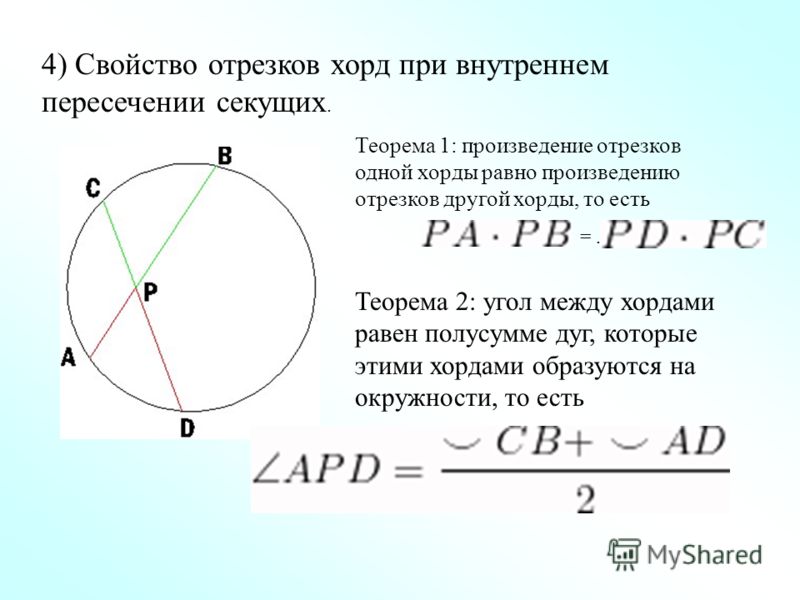
Для решения задач на вписанные в окружность углы, вам необходимо знать следующие свойства:
1. Вписанный угол равен половине центрального, опирающегося на ту же дугу.
2. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.
3. Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.
4. Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.
Следствие: противолежащие углы четырёхугольника вписанного в окружность в сумме составляют 180 градусов.
5. Все вписанные углы, опирающиеся на диаметр, прямые.
Вообще, это свойство является следствием из свойства (1), это его частный случай. Посмотрите – центральный угол равен 180 градусам (и этот развёрнутый угол есть не что иное, как диаметр), значит по первому свойству вписанный угол С равен его половине, то есть 90 градусам.
Знание данного свойства помогает в решении многих задач и часто позволяет избежать лишних расчётов. Хорошо усвоив его — вы более половины задач такого типа сможете решать устно. Два следствие, которые можно сделать:
Следствие 1: если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным (вершина прямого угла лежит на окружности).
Следствие 2: центр описанной около прямоугольного треугольника окружности совпадает с серединой его гипотенузы.
Многие прототипы стереометрических задач также решаются благодаря использованию этого свойства и данных следствий. Запомните сам факт: если диаметр окружности является стороной вписанного треугольника, то этот треугольник прямоугольный (угол лежащий против диаметра равен 90 градусов). Все остальные выводы и следствия вы сможете сделать сами, учить их не надо.
Как правило, половина задач на вписанный угол даётся с эскизом, но без обозначений.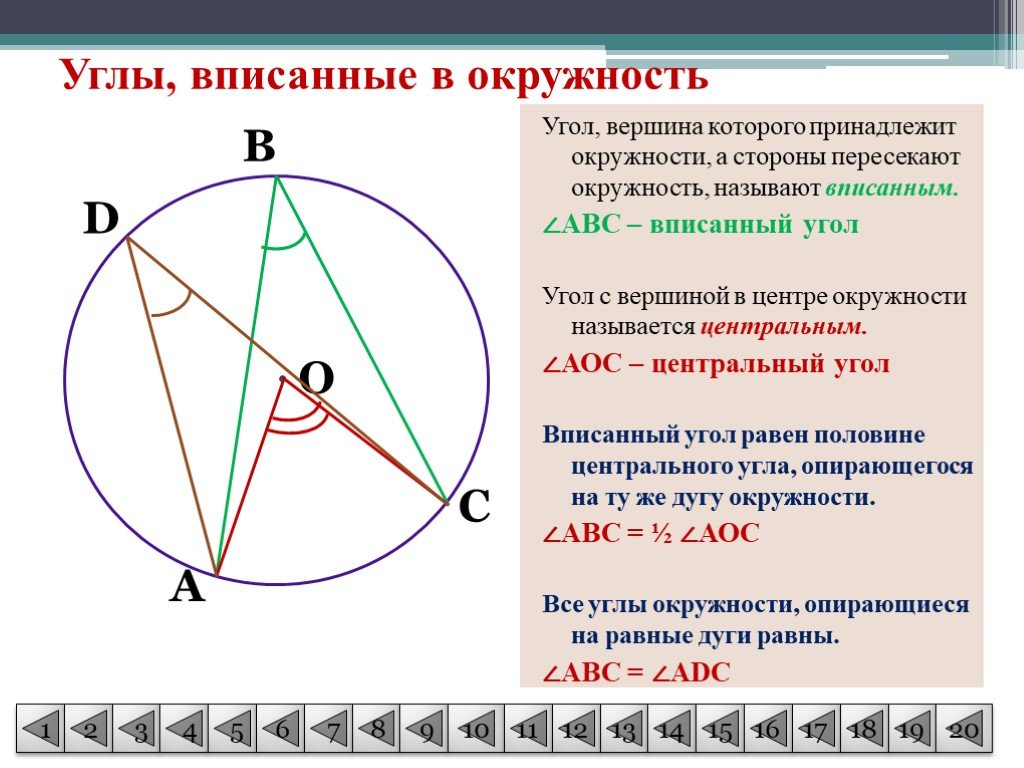
Для понимания процесса рассуждения при решении задач (ниже в статье) введены обозначения вершин (углов). На ЕГЭ вы можете этого не делать.
Рассмотрим задачи:
Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.
Построим центральный угол для заданного вписанного угла, обозначим вершины:
По свойству вписанного в окружность угла:
Угол АОВ равен 60 0 , так как треугольник АОВ равносторонний, а в равностороннем треугольнике все углы равны по 60 0 . Стороны треугольника равны, так как в условии сказано, что хорда равна радиусу.
Таким образом, вписанный угол АСВ равен 30 0 .
Ответ: 30
Найдите хорду, на которую опирается угол 30 0 , вписанный в окружность радиуса 3.
Это по сути обратная задача (предыдущей). Построим центральный угол.
Он в два раза больше вписанного, то есть угол АОВ равен 60 0 . От сюда можно сделать вывод, что треугольник АОВ равносторонний.
Таким образом, хорда равна радиусу, то есть трём.
Ответ: 3
Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную корню из двух. Ответ дайте в градусах.
Построим центральный угол:
Зная радиус и хорду мы можем найти центральный угол АСВ. Это можно сделать по теореме косинусов. Зная центральный угол мы без труда найдём вписанный угол АСВ.
Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Следовательно, второй центральный угол равен 360 0 – 90 0 = 270 0 .
Угол АСВ по свойству вписанного угла равен его половине, то есть 135 градусам.
Ответ: 135
Найдите хорду, на которую опирается угол 120 градусов, вписанный в окружность радиуса корень из трёх.
Соединим точки А и В с центром окружности. Обозначим её как О:
Нам известен радиус и вписанный угол АСВ.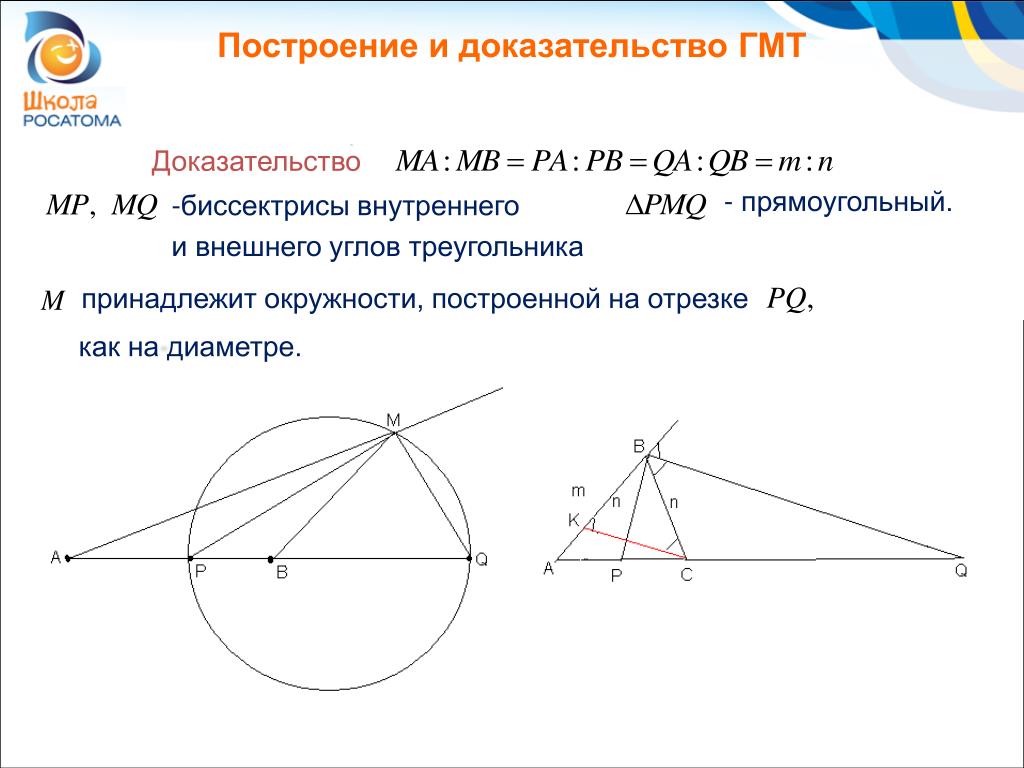
Мы можем найти центральный угол АОВ (больший 180 градусов), затем найти угол АОВ в треугольнике АОВ. А далее по теореме косинусов вычислить АВ.
По свойству вписанного угла центральный угол АОВ (который больше 180 градусов) будет равен вдвое больше вписанного, то есть 240 градусам. Значит, угол АОВ в треугольнике АОВ равен 360 0 – 240 0 = 120 0 .
По теореме косинусов:
Ответ:3
Найдите вписанный угол, опирающийся на дугу, которая составляет 20% окружности. Ответ дайте в градусах.
По свойству вписанного угла он вдвое меньше центрального угла, опирающегося на ту же дугу, в данном случае речь идёт о дуге АВ.
Сказано, дуга АВ составляет 20 процентов от окружности. Это означает, что центральный угол АОВ составляет так же 20 процентов от 360 0 . *Окружность это угол в 360 градусов. Значит,
Таким образом, вписанный угол АСВ равен 36 градусам.
Ответ: 36
Дуга окружности AC , не содержащая точки B , составляет 200 градусов.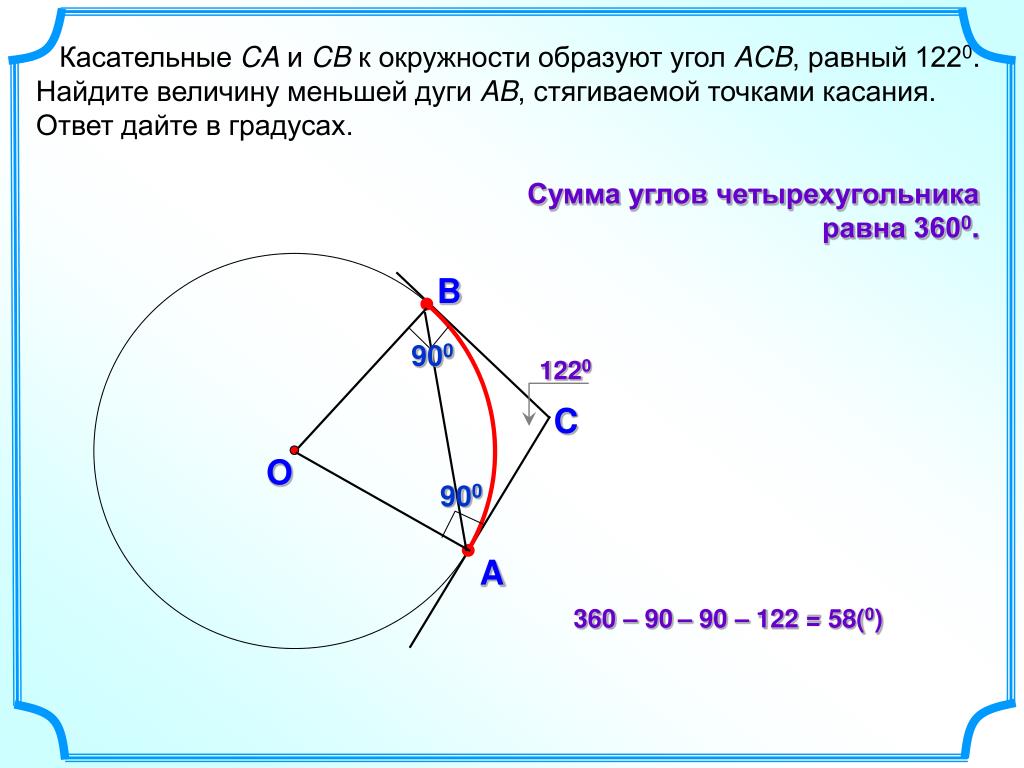
А дуга окружности BC, не содержащая точки A , составляет 80 градусов. Найдите вписанный угол ACB. Ответ дайте в градусах.
Обозначим для наглядности дуги, угловые меры которых даны. Дуга соответствующая 200 градусам – синий цвет, дуга соответствующая 80 градусам – красный цвет, оставшаяся часть окружности – жёлтый цвет.
Таким образом, градусная мера дуги АВ (жёлтый цвет), а значит и центральный угол АОВ составляет: 360 0 – 200 0 – 80 0 = 80 0 .
Вписанный угол АСВ вдвое меньше центрального угла АОВ,то есть равен 40 градусам.
Ответ: 40
Чему равен вписанный угол, опирающийся на диаметр окружности? Ответ дайте в градусах.
Это угол, сформированный двумя хордами , берущими начало в одной точки окружности. О вписанном угле говорят, что он опирается на дугу, заключенную между его сторонами.
Вписанный угол равен половине дуги, на которую он опирается.
Говоря другими словами, вписанный угол включает в себе столько угловых градусов, минут и секунд, сколько дуговых градусов , минут и секунд заключено в половине дуги, на которую он опирается.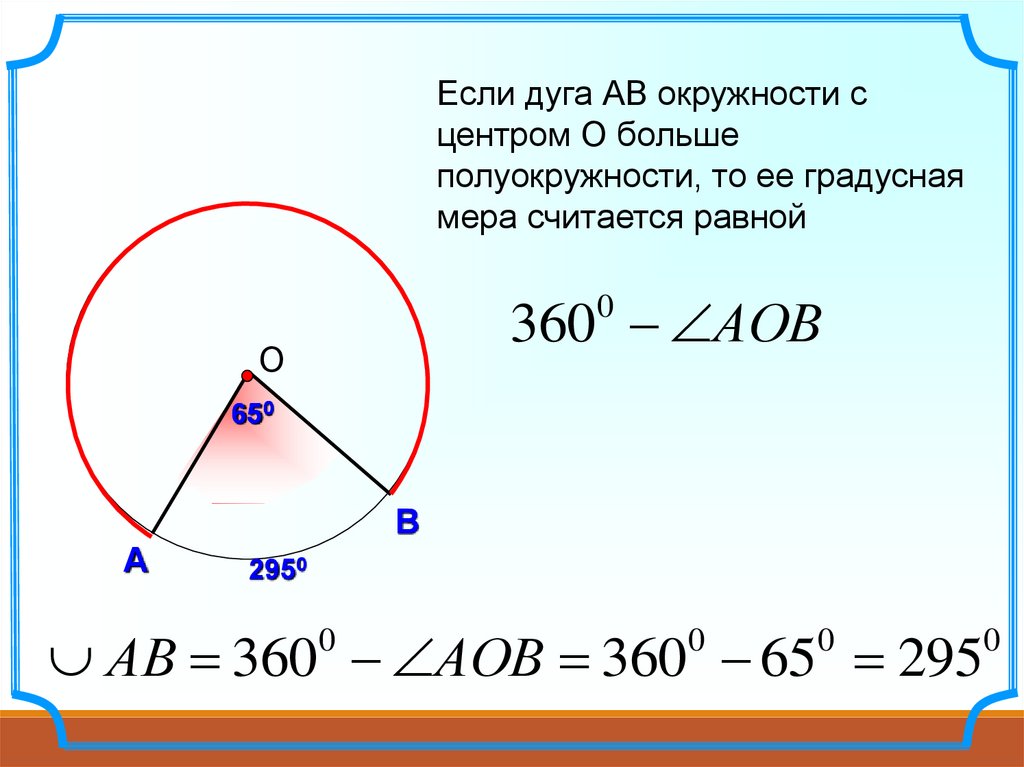
Для обоснования проанализируем три случая:
Первый случай:
Центр O расположен на стороне вписанного угла ABС. Прочертив радиус AO, мы получим ΔABO, в нем OA = OB (как радиусы) и, соответственно, ∠ABO = ∠BAO. По отношению к этому треугольнику , угол AOС — внешний. И значит, он равен сумме углов ABO и BAO, или равен двойному углу ABO. Значит ∠ABO равен половине центрального угла AOС. Но этот угол измеряется дугой AC. То есть, вписанный угол ABС измеряется половиной дуги AC.
Второй случай:
Центр O расположен между сторонами вписанного угла ABС.Начертив диаметр BD, мы поделим угол ABС на два угла, из которых, по установленному в первом случае, один измеряется половиной дуги AD, а другой половиной дуги СD. И соответственно угол ABС измеряется (AD+DС) /2, т.е. 1 / 2 AC.
Третий случай:
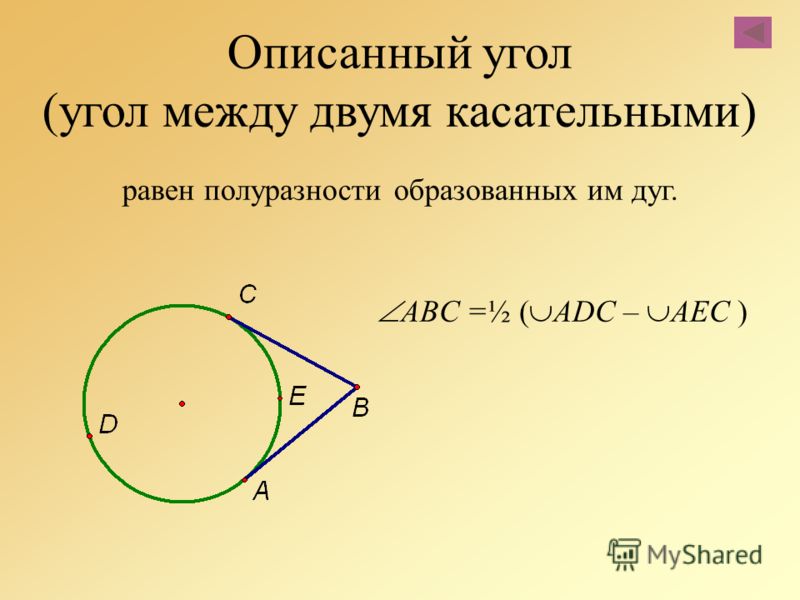
Центр O расположен вне вписанного угла ABС. Начертив диаметр BD, мы будем иметь:∠ABС = ∠ABD — ∠CBD.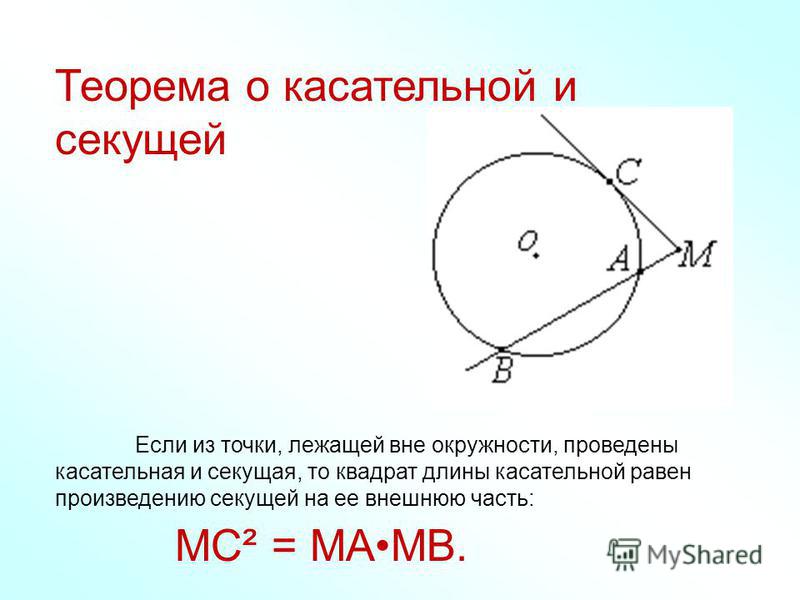
Но углы ABD и CBD измеряются, на основании обоснованного ранее половинами дуг AD и СD. И так как ∠ABС измеряется (AD-СD)/2, то есть половиной дуги AC.
Следствие 1. Любые , опирающиеся на одну и ту же дугу одинаковы, то есть равны между собой. Поскольку каждый из них измеряется половиной одной и той же дуги .
Следствие 2. Вписанный угол , опирающийся на диаметр — прямой угол . Поскольку каждый такой угол измеряется половиной полуокружности и, соответственно, содержит 90°.
геометрия — Радиус окружности, касающейся прямоугольника, оба из которых находятся внутри квадрата
спросил
Изменено 4 года, 2 месяца назад
Просмотрено 19 тысяч раз
$\begingroup$
При данной конфигурации:
Нам дано, что прямоугольник имеет размеры 20 см на 10 см, и мы должны найти радиус окружности.
Если мы каким-то образом знаем расстояние между окружностью и углом квадрата, то мы можем легко найти радиус. (равно $ \sqrt{2}\times R-R$)
Я действительно не понимаю, как это решить. Любая помощь приветствуется.
- геометрия
- круги
- прямоугольники
$\endgroup$
92-60r+500=0$
$r=50$ $cm$
$r=10$ $cm$
Приемлемым ответом является $r=50$ $cm$.
$\endgroup$
7
$\begingroup$
Поместите центр криклы в $O.$
Пусть радиус будет $R$
Угол квадрата $(R,R)$ Я сделал небольшое изменение в изображении, чтобы создать меньше негатива числа.
Смещение по прямоугольнику, сердцевина прямоугольника $(R-20, R-10)$ 92,$$, которая имеет решения $$R_{1,2} = a+b\pm\sqrt{2ab}.$$
Одно решение соответствует большему прямоугольнику (по сравнению с окружностью), касаясь окружности на с другой стороны, чего здесь нет.
Меньший прямоугольник по сравнению с кругом означает, что круг больше, если прямоугольник остается фиксированным, поэтому правильный радиус равен $$R = a+b+\sqrt{2ab}.$$
Подстановка $a=10$ и $ b=20$ дает $R=50$.
$\endgroup$
$\begingroup$ 92 — 60R + 500 = 0$
$(R — 50)(R-10) = 0$
$R = 50$ — единственный разумный вариант.
$\endgroup$
6
$\begingroup$
Вы можете использовать триггер, чтобы получить тот же ответ, что и выше.
Нарисуйте три линии: одну от центра круга до угла, общего между квадратом и прямоугольником. Затем проведите линию от центра круга к углу, ближайшему к центру круга. Нарисуйте последнюю линию, которая будет диагональю, соединяющей ранее упомянутые углы.
Длину третьей линии мы знаем по теореме Пифагора.
Если мы назовем длину стороны квадрата L, длина более короткой из двух оставшихся линий будет L/2. Длина более длинной, л/кв.м.(2).
Найдите угол, который образует диагональ с более длинной из нарисованных линий, чтобы применить правило косинуса.
Более длинная линия пересекает угол квадрата под углом 45 градусов к обеим сторонам. Тогда угол, который образует диагональ с левой стороной квадрата, имеет тангенс 2,9.0005
Примените правило косинусов, затем решите полученное квадратное уравнение, и вы получите два возможных ответа, только один из которых правдоподобен.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
геометрия — Окружность $1$ описана около квадрата со стороной $8$, а окружность $2$ вписана в квадрат
спросил
Изменено 6 лет, 8 месяцев назад
Просмотрено 1к раз 92$, а кто-нибудь знает, как найти радиус круга $1$ и круга $2$?
- геометрия
$\endgroup$
4
$\begingroup$
$C_2$ — описанная окружность квадрата $Q_2$, площадь которой равна половине площади исходного квадрата $Q_1$.
Следовательно
$${{\rm площадь}(C_1)\более {\rm площадь}(C_2)}={{\rm площадь}(Q_1)\более {\rm площадь}(Q_2)}=2\ .$$
$\endgroup$ 92 = 2. $ Это можно продолжить и в геометрически расширяющемся ряду.
$\endgroup$
$\begingroup$
«Кто-нибудь знает, как найти радиус круга 1 и круга 2?»
Окружность 1. Вершины квадрата лежат в окружности. Вот что значит «описать». Диагонали квадрата делят друг друга пополам, поэтому расстояние от центра квадрата до каждой из его вершин равно расстоянию. Это четыре точки на окружности, каждая из которых находится на равном расстоянии от центральной точки.
Немного повозиться, и можно доказать, что для трех или более точек на окружности существует только одна точка (а именно центр окружности) и только одно расстояние (радиус), равное расстоянию от всех трех или более точки на окружности.
Итак, радиус окружности 1 равен половине диагонали квадрата.