Внутренние накрест лежащие углы образованные двумя параллельными прямыми: 1.Укажите номера верных утверждений.1) Существует квадрат, который не является прямоугольником. 2) Если два угла треугольника…

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 33. Элементарное исследование поведения функции. 34. Сложная функция. 35. Обратная функция. 36. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 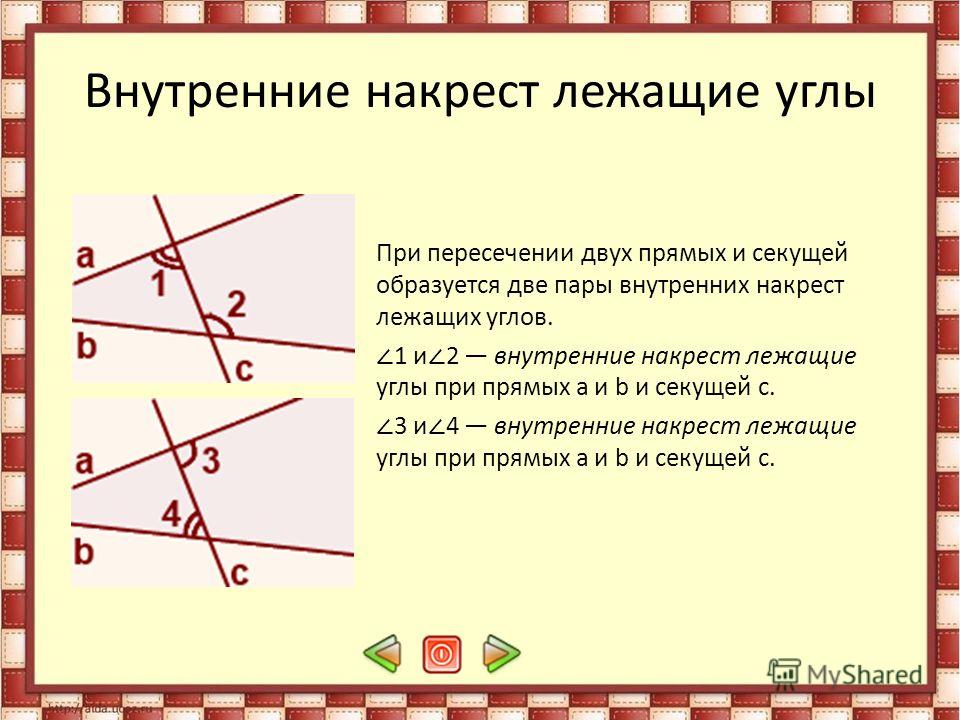60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

19 Анализ геометрических высказываний — Карточки Барабук

Отправить в приложение Отметить как выучено

19 Анализ геометрических высказываний

Если угол равен 45°, то вертикальный с ним угол равен 45°.

Любые две прямые имеют ровно одну общую точку.

Через любые три точки проходит ровно одна прямая.

Если расстояние от точки до прямой меньше 1, то и длина любой наклонной, проведенной из данной точки к прямой, меньше 1.

Через любые три точки проходит не более одной окружности.

Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Вписанный угол, опирающийся на диаметр окружности, прямой.

Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.

Отношение площадей подобных треугольников равно коэффициенту подобия.

Каждая из биссектрис равнобедренного треугольника является его высотой.

Диагонали прямоугольника равны.

У любой трапеции основания параллельны.

При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.

Диагонали ромба перпендикулярны.

Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.

Если угол равен 47°, то смежный с ним равен 153°.

Если две прямые перпендикулярны третьей прямой, то эти две прямые параллельны.

Через любую точку проходит ровно одна прямая.

Существует квадрат, который не является прямоугольником.

Если два угла треугольника равны, то равны и противолежащие им стороны.

Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

В тупоугольном треугольнике все углы тупые.

Средняя линия трапеции равна полусумме её оснований.

Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Треугольник со сторонами 1, 2, 4 существует.

Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

В любом параллелограмме диагонали равны.

Через любую точку проходит не менее одной прямой.

Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.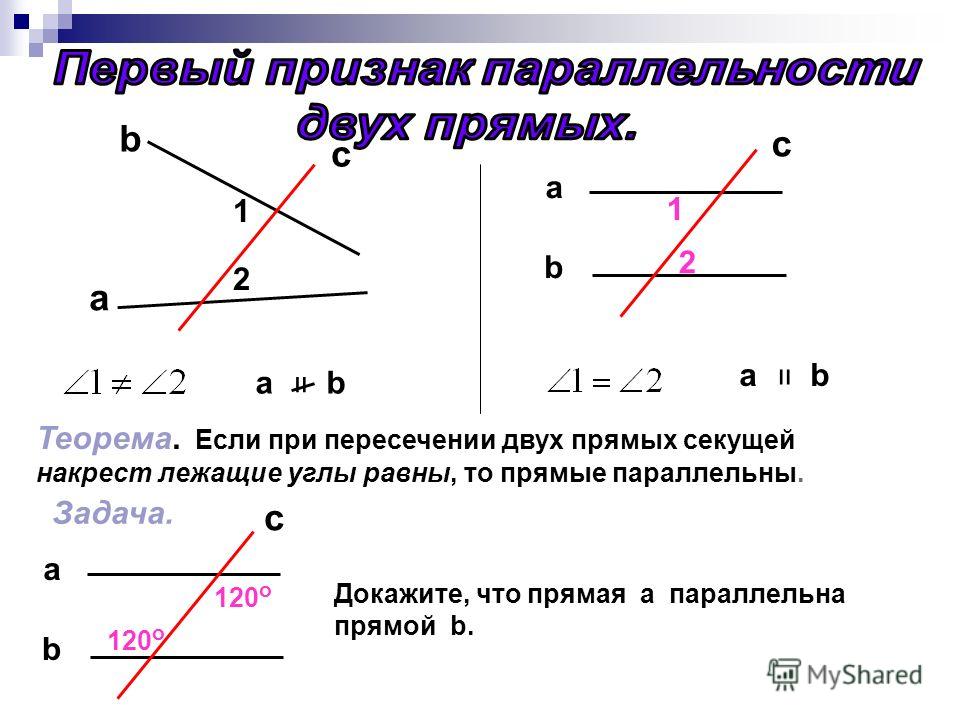

Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

Смежные углы равны.

2) Любые две прямые имеют ровно одну общую точку.

3) Если угол равен 108°, то вертикальный с ним равен 108°.

Все углы ромба равны.

Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

Если угол острый, то смежный с ним угол также является острым.

Диагонали квадрата взаимно перпендикулярны.

В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.

Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

2) Существует квадрат, который не является ромбом.

3) Сумма углов любого треугольника равна 180° .

Один из углов треугольника всегда не превышает 60 градусов.

2) Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

3) Все диаметры окружности равны между собой.

Все хорды одной окружности равны между собой.

Треугольника со сторонами 1, 2, 4 не существует.

Все углы прямоугольника равны.

При пересечении двух параллельных прямых третьей прямой сумма накрест лежащих углов равна 180°.

Диагонали ромба перпендикулярны.

Центром окружности, описанной около треугольника, является точка пересечения его биссектрис.

Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.

Существует параллелограмм, который не является прямоугольником.

Сумма углов тупоугольного треугольника равна 180°.

Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы составляют в сумме 90°, то эти две прямые параллельны.

Если угол равен 60°, то смежный с ним равен 120°.

Если при пересечении двух прямых третьей прямой внутренние односторонние углы равны 70° и 110°, то эти две прямые параллельны.

Через любые три точки проходит не более одной прямой.

Все углы ромба равны.

Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

Боковые стороны любой трапеции равны.

Один из углов треугольника всегда не превышает 60 градусов.

Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Треугольник со сторонами 1, 2, 4 существует.

Если в ромбе один из углов равен 90°, то такой ромб — квадрат.

В любом параллелограмме диагонали равны.

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

Вертикальные углы равны.

Любая биссектриса равнобедренного треугольника является его медианой.

Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

Средняя линия трапеции параллельна её основаниям.

Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны.

Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.

Смежные углы равны.

Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Треугольник со сторонами 1, 2, 4 существует.

В любом параллелограмме есть два равных угла.

В любую равнобедренную трапецию можно вписать окружность.

Диагональ параллелограмма делит его углы пополам.

Площадь прямоугольного треугольника равна половине произведения его катетов.

Все высоты равностороннего треугольника равны.

Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.

В любой ромб можно вписать окружность.

Один из углов треугольника всегда не превышает 60 градусов.

Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

Все диаметры окружности равны между собой.

Все углы ромба равны.

Любой прямоугольник можно вписать в окружность.

Диагональ трапеции делит её на два равных треугольника.

Существуют три прямые, которые проходят через одну точку.

Боковые стороны любой трапеции равны.

Сумма углов равнобедренного треугольника равна 180 градусам.

Через любые три точки проходит не более одной окружности.

Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

На плоскости существует единственная точка, равноудалённая от концов отрезка.

В любой треугольник можно вписать окружность.

Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.

Если расстояние между центрами двух окружностей равно сумме их диаметров, то эти окружности касаются.

2) Вписанные углы окружности равны.

3) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

4) Через любые четыре точки, не принадлежащие одной прямой, проходит единственная окружность.

Каждая из биссектрис равнобедренного треугольника является его медианой.

Последовательные внутренние углы — определение, теорема, примеры

Последовательные внутренние углы образованы на внутренних сторонах секущей и также известны как совмещенные внутренние углы или односторонние внутренние углы.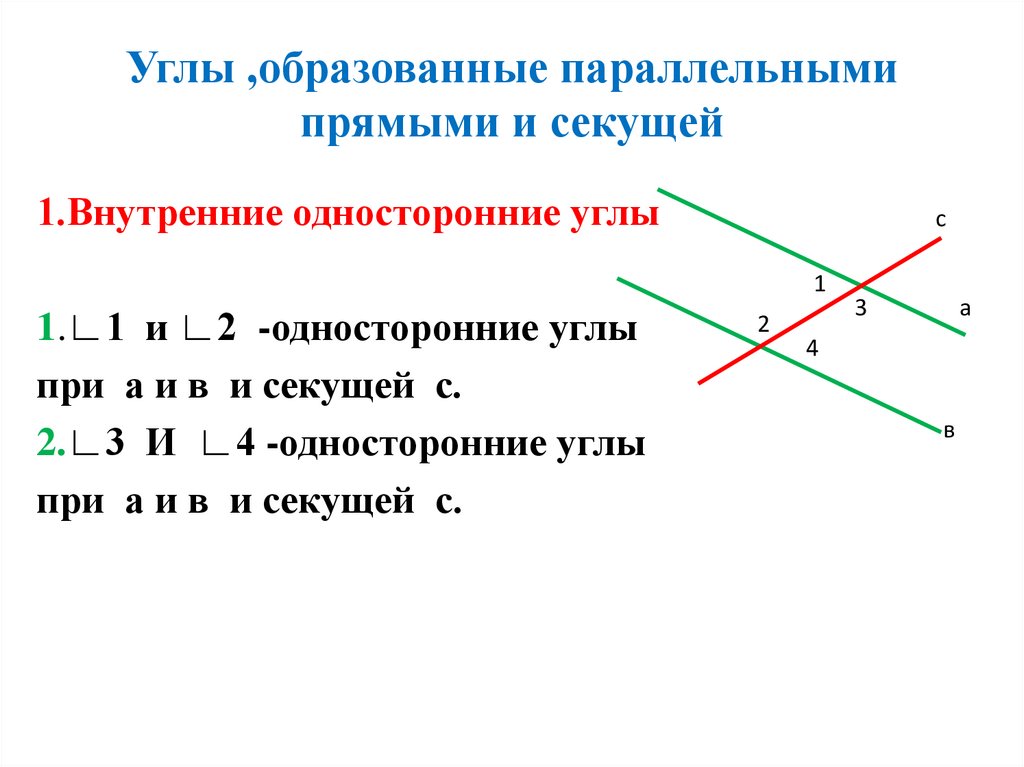 Когда секущая пересекает любые две параллельные прямые, она образует множество углов, таких как чередующиеся внутренние углы, соответствующие углы, чередующиеся внешние углы, последовательные внутренние углы. Давайте узнаем больше о последовательных внутренних углах на этой странице.

Теорема

1.	Что такое последовательные внутренние углы?
2.	о последовательных внутренних углах
3.	Теорема обращения последовательных внутренних углов
4.	Часто задаваемые вопросы о последовательных внутренних углах

Что такое последовательные внутренние углы?

Последовательные внутренние углы определяются как пара несмежных внутренних углов, лежащих по одну сторону от секущей. Слово «последовательный» относится к вещам, которые появляются рядом друг с другом.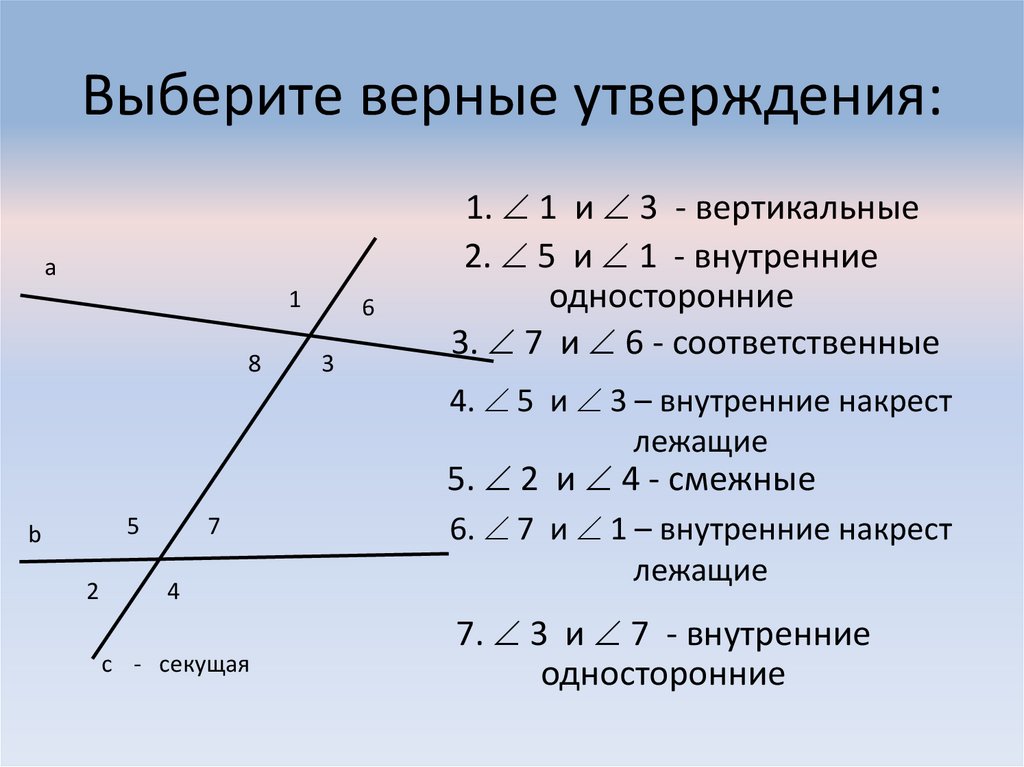 Последовательные внутренние углы расположены рядом друг с другом на внутренней стороне секущей. Обратите внимание на следующий рисунок и свойства последовательных внутренних углов, чтобы идентифицировать их.

• Смежные внутренние углы имеют разные вершины.
• Они лежат между двумя линиями.
• Они находятся на одной стороне поперечной.
• У них общая сторона.

На приведенном выше рисунке L ₁ и L ₂ — параллельные линии, а T — поперечные. По определению последовательных внутренних углов пары последовательных внутренних углов на рисунке следующие:

• ∠1 и ∠4
• ∠2 и ∠3

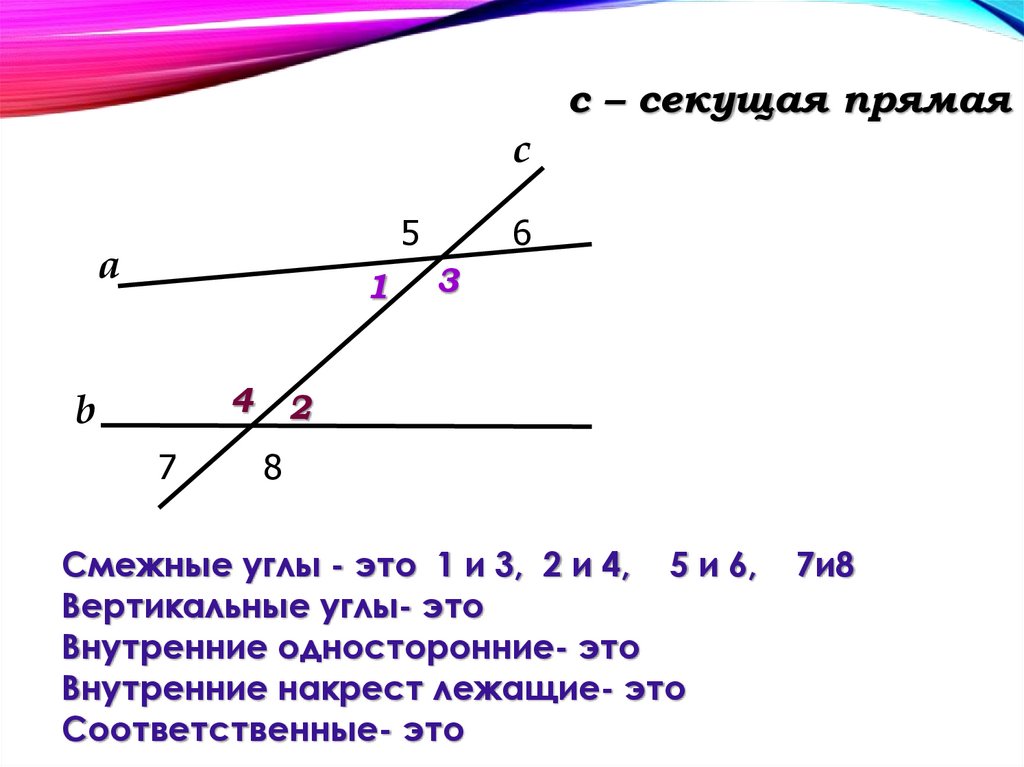
Углы, образованные секущей

Когда секущая пересекает пару параллельных прямых, образуется много пар углов, отличных от последовательных внутренних углов. Это соответствующие углы, альтернативные внутренние углы и альтернативные внешние углы. Обратите внимание на следующий рисунок и соотнесите различные пары углов и их свойства, указанные в таблице.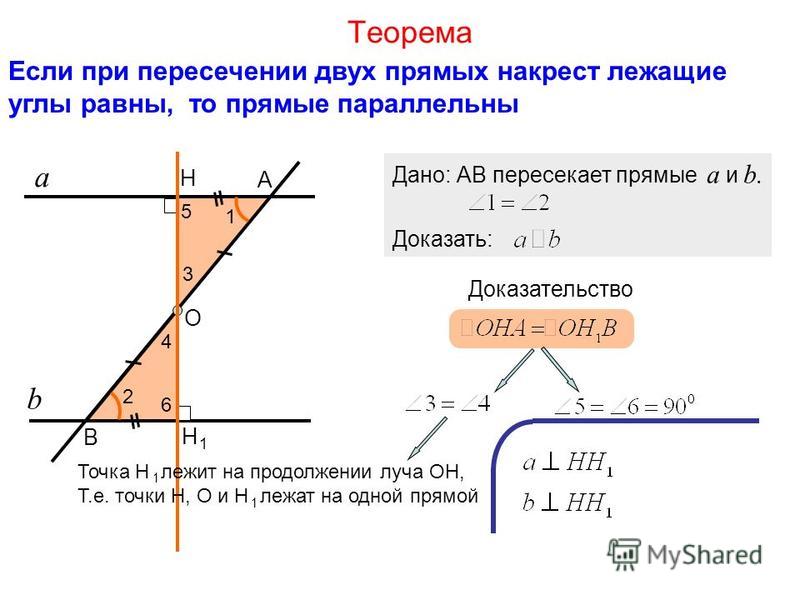

В следующей таблице перечислены свойства всех типов углов, образованных при пересечении секущей двух параллельных прямых. Обратитесь к рисунку, данному выше, чтобы относиться к углам.

Типы уголков	Недвижимость	Название углов на рисунке
Соответствующие углы	Соответствующие углы это те углы, которые: Имеют разные вершины. Лежать по одну сторону от поперечной и лежать выше или ниже линий. Всегда равны. При пересечении секущей двух параллельных прямых соответствующие углы всегда равны.	На приведенном выше рисунке ∠1 и ∠5, ∠2 и ∠6, ∠4 и ∠8, ∠3 и ∠7 являются парами соответствующих углов.
Альтернативные внутренние уголки	Альтернативные внутренние углы — это те углы, которые: Иметь разные вершины. Лягте на противоположные стороны поперечной. Лежит между двумя внутренними линиями. При пересечении секущей двух параллельных прямых образующиеся параллельные внутренние углы всегда равны.	На приведенном выше рисунке ∠4 и ∠6 и ∠3 и ∠5 представляют собой пары чередующихся внутренних углов.
Альтернативные внешние углы	Альтернативные внешние углы — это те углы, которые: Имеют разные вершины Лежать на разных сторонах поперечной Внешние по отношению к линиям При пересечении секущей двух параллельных прямых образующиеся альтернативные внешние углы всегда равны.	На приведенном выше рисунке ∠1 и ∠7 и ∠2 и ∠8 представляют собой пары чередующихся внешних углов.
Последовательные внутренние углы	Смежные внутренние углы – это углы, которые: Имеют разные вершины Лежать между двумя линиями Находятся на одной стороне поперечной При пересечении секущей двух параллельных прямых последовательные внутренние углы всегда являются дополнительными .	На приведенном выше рисунке ∠4 и ∠5 и ∠3 и ∠6 являются парами последовательных внутренних углов.

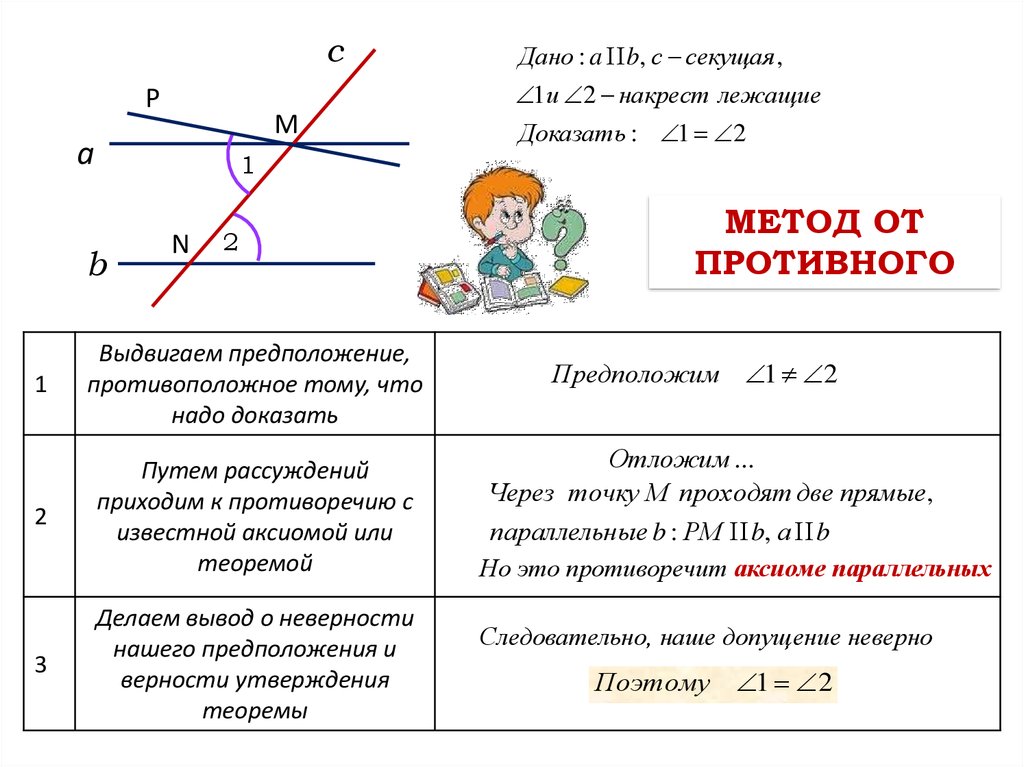
Теорема о последовательных внутренних углах

Отношение между последовательными внутренними углами определяется теоремой о последовательных внутренних углах. «Теорема о последовательных внутренних углах» утверждает, что если секущая пересекает две параллельные прямые, каждая пара последовательных внутренних углов является дополнительной, то есть сумма последовательных внутренних углов равна 180 °.

Доказательство теоремы о последовательных внутренних углах

Обратите внимание на следующий рисунок, чтобы понять теорему о последовательных внутренних углах.

Дано, что две прямые L ₁ и L ₂ параллельны, а T — поперечна. Поскольку L ₁ // L ₂ , можно сказать, что:

• ∠1 = ∠5 (соответствующие углы с // линиями) —— (Уравнение 1)
• ∠1 + ∠4 = 180° (линейная пара углов является дополнительной) —- (Уравнение 2)
• Подставив ∠1 вместо ∠5 в уравнение (2), мы получим ∠5 + ∠4 = 180°
• Точно так же мы можем показать, что ∠3 +∠6 = 180°.
• ∠2 = ∠6 (соответствующие углы с // линиями) —— (Уравнение 3)
• ∠2 + ∠3 = 180° (Линейная пара углов является дополнительной) —- (Уравнение 4)
• Подставляя ∠2 вместо ∠6 в уравнение (4), получаем ∠6 + ∠3 = 180°
• Итак, видно, что ∠4 + ∠5 = 180°; и ∠3 + ∠6 = 180°

Таким образом, доказано, что последовательные внутренние углы являются дополнительными.

Теорема, обратная теореме о последовательных внутренних углах

Теорема, обратная теореме о последовательных внутренних углах, утверждает, что если секущая пересекает две прямые так, что пара последовательных внутренних углов является дополнительной, то эти две прямые параллельны. Доказательство этой и обратной теоремы показано ниже.

См. тот же рисунок,

Дано, ∠5 + ∠4 = 180° (Последовательные внутренние углы) ———- (Уравнение 1)

Поскольку ∠1 и ∠4 образуют линейную пару углов,

∠1 + ∠4 = 180° ———- (Линейная пара углов является дополнительной) ————(Уравнение 2)

Поскольку правые части Уравнение 1 и уравнение 2 равны, мы можем приравнять левую часть уравнений (1) и (2) и записать это как:

∠1 + ∠4 = ∠5 + ∠4

Если мы решим это , мы получаем ∠1 = ∠5, что образует соответствующую пару в параллельных прямых.

Таким образом, на данной фигуре одна пара соответствующих углов равна, что может произойти только в том случае, если две прямые параллельны. Следовательно, доказана обратная теорема о последовательных внутренних углах, которая гласит, что если секущая пересекает две прямые так, что пара последовательных внутренних углов является дополнительной, то эти две прямые параллельны.

Смежные внутренние углы параллелограмма

Мы знаем, что противоположные стороны параллелограмма параллельны, поэтому последовательные внутренние углы параллелограмма всегда являются дополнительными. Обратите внимание на следующий параллелограмм, в котором ∠A и ∠B, ∠B и ∠C, ∠C и ∠D, а также ∠D и ∠A являются последовательными внутренними углами. Это можно понять следующим образом:

• Если мы возьмем AB // CD и BC в качестве секущей, то ∠B + ∠C = 180°
• Если мы возьмем AB // CD и AD в качестве секущей, то ∠A + ∠D = 180°
• Если в качестве секущей принять AD // BC и CD, то ∠C + ∠D = 180°
• Если мы возьмем AD // BC и AB в качестве секущей, то ∠A + ∠B = 180°

Советы по последовательным внутренним углам

Вот несколько важных моментов, которые следует помнить о последовательных внутренних углах.

• Последовательные внутренние углы несмежны и лежат по одну сторону от секущей.
• Две прямые параллельны тогда и только тогда, когда смежные внутренние углы являются дополнительными.

☛ Статьи по теме

• Теорема о внешнем угле
• Пары углов
• Дополнительные уголки
• Пересекающиеся и непересекающиеся линии

 

Примеры последовательных внутренних углов

1. Пример 1: Параллельны ли следующие прямые l и m?

   Решение:

   Если на данном рисунке углы 125° и 60° смежные, то можно доказать, что прямые l и m параллельны.

   Но 125° + 60° = 185°, значит, 125° и 60° НЕ являются дополнительными.

   Таким образом, согласно теореме о последовательных внутренних углах данные прямые НЕ параллельны.

2. Пример 2: Используйте теорему о последовательных внутренних углах, чтобы найти значение угла ‘x’, если прямая 1 и прямая 2 параллельны.

   Решение:

   На рисунке дано, что 40° и ∠x являются последовательными внутренними углами, а «Прямая 1» и «Прямая 2» параллельны.

   По теореме о последовательных внутренних углах ∠x и 40° являются дополнительными.

   ∠х + 40° = 180°
   ∠x = 180° — 40°

   Следовательно, ∠x = 140°.

3. Пример 3. Если две параллельные прямые пересекаются секущей, и пара последовательных внутренних углов имеет размеры (2x + 4)° и (12x + 8)° соответственно, найдите значение x и значение обоих последовательных углов. внутренние углы.

   Решение:

   Поскольку данные прямые параллельны, а (2x + 4)° и (12x + 8)° — последовательные внутренние углы. По теореме о последовательных внутренних углах эти углы являются дополнительными.

   Таким образом, (2x + 4) + (12x + 8) =180°
   14x + 12 = 180°
   14x = 180° — 12°
   14x = 168°
   x = 12°

   Теперь давайте подставим значение x, чтобы получить значения последовательных внутренних углов.

   2x + 4 = 2(12) + 4 = 28°
   12x + 8 = 12(12) + 8 = 152°.

перейти к слайдуперейти к слайдуперейти к слайду

Разбейте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по последовательным внутренним углам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о последовательных внутренних углах

Что такое последовательные внутренние углы?

Последовательные внутренние углы образуются, когда секущая проходит через пару параллельных прямых или непараллельных прямых. Они образованы на внутренних сторонах двух пересекающихся линий в точке пересечения секущей двух линий. Если прямые, которые пересекает поперечная, параллельны, то пара последовательных внутренних углов является дополнительной.

Как определить последовательные внутренние углы?

Последовательные внутренние углы можно идентифицировать с помощью следующих свойств:

• Последовательные внутренние углы образуются при пересечении любых двух прямых секущей.
• У них разные вершины.
• Они лежат между двумя линиями.
• Они находятся на одной стороне поперечной.
• У них общая сторона.
• Если последовательные углы образованы между двумя параллельными прямыми, пересеченными секущей, то они являются дополнительными.

Что такое теорема о последовательных внутренних углах?

Теорема о последовательных внутренних углах утверждает, что если секущая проходит через две параллельные прямые, она образует две пары последовательных внутренних углов, которые являются дополнительными. Другими словами, последовательные внутренние углы, образованные двумя параллельными прямыми, пересекаемыми секущей, в сумме дают 180°.

Что такое обратная теорема о последовательных внутренних углах?

Теорема, обратная теореме о последовательных внутренних углах, утверждает, что если секущая пересекает две прямые так, что пара последовательных внутренних углов является дополнительной, то эти две прямые параллельны.

Всегда ли последовательные внутренние углы дополняют друг друга?

Нет, последовательные внутренние углы не всегда являются дополнительными. Они являются дополнительными только тогда, когда секущая проходит через параллельные прямые. Следует отметить, что последовательные внутренние углы могут образовываться и при прохождении секущей через две непараллельные прямые, хотя в этом случае они не являются дополнительными.

Конгруэнтны ли последовательные внутренние углы?

Смежные внутренние углы НЕ равны. Они являются дополнительными, если секущая проходит через две параллельные прямые. Это означает, что в сумме они составляют 180°.

Как еще называют последовательные внутренние углы?

Последовательные внутренние углы также известны как «совмещенные внутренние углы» или «внутренние углы с одной стороны».

Какие еще углы образуются, кроме смежных внутренних углов, при прохождении секущей через две параллельные прямые?

Когда секущая проходит через две параллельные прямые, помимо последовательных внутренних углов образуются другие углы, например, соответствующие углы, чередующиеся внутренние углы, чередующиеся внешние углы.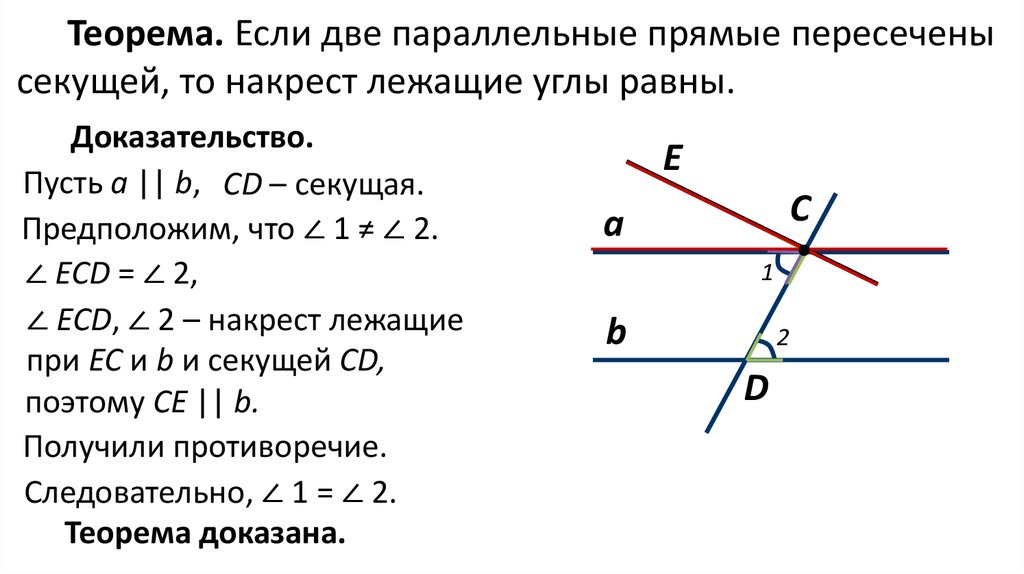

В чем разница между альтернативными внутренними углами и последовательными внутренними углами?

Альтернативные внутренние углы и последовательные внутренние углы представляют собой разные пары углов, образованные при пересечении двух параллельных прямых секущей. Чередующиеся внутренние углы расположены между двумя пересекающимися прямыми, но они находятся по разные стороны от секущей. Принимая во внимание, что последовательные внутренние углы расположены внутри двух прямых по одну сторону от секущей.

Как связаны последовательные внутренние углы?

Если последовательные внутренние углы образованы между двумя параллельными прямыми, пересеченными секущей, то они являются дополнительными. Это означает, что в сумме они будут составлять 180°.

Как найти последовательные внутренние углы?

Известно правило, что если последовательные внутренние углы образованы между двумя параллельными прямыми, пересеченными секущей, то они являются дополнительными.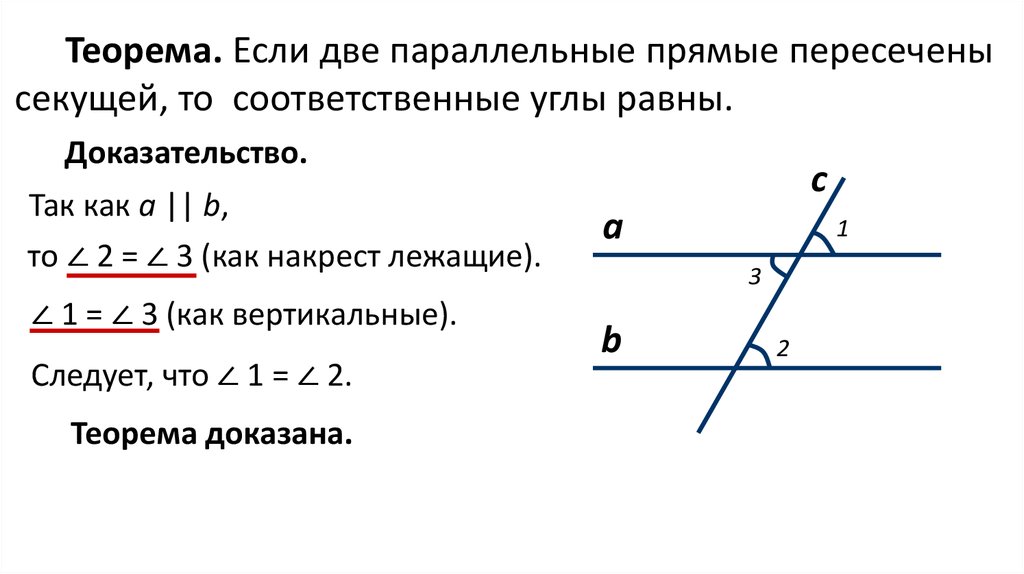 Это означает, что если мы знаем один из последовательных углов в паре, другой угол можно легко вычислить, вычитая его из 180°. В других случаях, если у нас есть последовательные углы как (20x + 5)° и (24x — 1)°, мы можем найти значение x следующим методом. Поскольку последовательные углы являются дополнительными, мы можем записать это как (20x + 5)° + (24x — 1)° = 180°. Это можно решить как 44x + 4 = 180, а значение x = 4. Теперь значение x можно подставить в данные выражения, и последовательные углы будут (20 × 4) + 5 = 85 °, и (24 × 4) — 1 = 95°.

Приведите пример последовательных внутренних углов в реальной жизни.

В реальной жизни последовательные внутренние углы можно увидеть в разных местах, например, в оконной решетке с вертикальными и горизонтальными стержнями. Они образуются при пересечении двух горизонтальных стержней (двух параллельных прямых) вертикальным стержнем (поперечным).

Как выглядят последовательные внутренние углы?

Последовательные внутренние углы образуют фигуру, чем-то напоминающую букву U, где внутренние углы являются последовательными внутренними углами.

Как последовательные внутренние углы связаны с параллельными прямыми?

Смежные внутренние углы — это углы, которые образуются на внутренней стороне секущей, когда она пересекает две параллельные прямые. При прохождении секущей через две параллельные прямые образующиеся последовательные внутренние углы являются дополнительными.

Скачать БЕСПЛАТНЫЕ учебные материалы

Связанный рабочий лист

Углы, параллельные линии и сечения

Автор:

Малкольм МакКинзи

11 января 2023 г.

Факт проверен

Пол Маццола

Что делает прямые параллельными?

Две прямые параллельны , если они никогда не пересекаются и всегда находятся на одном и том же расстоянии друг от друга. Обе линии должны быть компланарными (в одной плоскости). Чтобы использовать геометрическое сокращение, мы записываем символ параллельных линий как две крошечные параллельных линий , например: ∥∥. Например, чтобы сказать, что линия JIJI параллельна линии NXNX, мы пишем:

Как вы можете доказать, что две прямые на самом деле параллельны? Как и во всем, что касается геометрии, более мудрые и старые геометры ступили на эту землю раньше вас и указали путь. Используя поперечную, мы создаем восемь углов, которые нам помогут.

Что делает линии параллельными

Что такое параллельные линии в реальной жизни?

Если вы когда-нибудь стояли на неиспользуемых железнодорожных путях и задавались вопросом, почему они, кажется, сходятся в какой-то далекой точке, вы видели параллельные линии (и перспективу!). Если бы два рельса встретились, поезд не смог бы двигаться вперед. Другие параллельные линии вокруг вас:

• Street Markings

• Перекрестные переходы

• Книжные полки

• Transperbook

Параллельные линии, вырезанные трансверсовой

. При разрезании по параллельным линиям секущей образуется восемь углов.

Создайте поперечную, используя любую существующую пару параллельных линий, используя линейку, чтобы провести поперечную через две линии, например:

Параллельные прямые, разрезаемые секущей Создание восьми углов

Доказательство параллельности прямых

Эти восемь углов можно разбить на пары. Давайте пометим углы, используя буквы, которые мы еще не использовали:

Углы в параллельных линиях

Эти восемь углов в параллельных линиях:

1. Соответствующие углы

2. Альтернатные внутренние углы

4. .

5. Дополнительные уголки

У каждого из них есть постулат или теорема, которые можно использовать для доказательства того, что две прямые MA и ZE параллельны. Давайте пройдемся по каждому из них.

Соответствующие углы

Постулат соответствующих углов утверждает, что параллельные прямые, пересекаемые секущей, дают равные соответствующие углы. Нам нужно обратное этому или та же самая идея наоборот:

Если секущая пересекает две прямые и образует два конгруэнтных соответствующих угла, то эти две прямые параллельны.

Чтобы узнать, есть ли у нас два соответствующих угла, которые равны, нам нужно знать, каковы соответствующих угла  . На нашем рисунке поперечная OH пересекает линии MA и ZE , оставляя после себя восемь углов. Каждый срез создавал пересечение.

Если один угол на одном перекрестке совпадает с другим углом в том же положении на другом перекрестке, то две линии должны быть параллельны. Два угла являются соответствующими, если они находятся в одинаковых положениях на обоих пересечениях.

Соответствующие углы, изготовленные по трансверсальным и параллельным линиям

В нашем рисунке соответствующие углы:

• тий и ♂

• omcc и

3333944444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н. ▲ и ♂

• ♂ и ♂

, если вы проверьте только Single Pair , а они — это, и они будут равными, и они будут соблюдными.

Альтернативные углы

Альтернативные углы  как группа подразделяются на  альтернативные внутренние углы  и  альтернативные внешние углы . Внешние углы лежат вне открытого пространства между двумя линиями, предположительно параллельными. Внутренние углы лежат в пределах этого открытого пространства между двумя рассматриваемыми линиями.

На нашем чертеже ∠B, ∠C, ∠K ​​ и ∠L — внешние углы. Сможете ли вы определить четыре 90 485 внутренних 90 486 углов?

Вы сказали ∠D, ∠F, ∠G  и  ∠J ?

С обеих сторон поперечной появляются чередующиеся углы. Они по определению не могут быть по одну сторону от трансверсали. На нашем рисунке ∠B представляет собой альтернативный внешний угол с ∠L . ∠D  – альтернативный внутренний угол с  ∠J . Сможете ли вы найти еще одну пару альтернативных внешних углов и еще одну пару альтернативных внутренних углов?

Вот обе пары чередующихся внешних углов:

• ▲ и ♂

• и retk

HERK

HER ∠J

∠F и ∠G

Чередующиеся внешние углы

2 альтернативный внешний угол обратная теорема , которая гласит:

альтернативные внешние углы, образованные поперечными и параллельными прямыми

Углы могут быть равными или  конгруэнтными ; вы можете заменить слово «равный» в обеих теоремах на «конгруэнтный», не затрагивая теорему.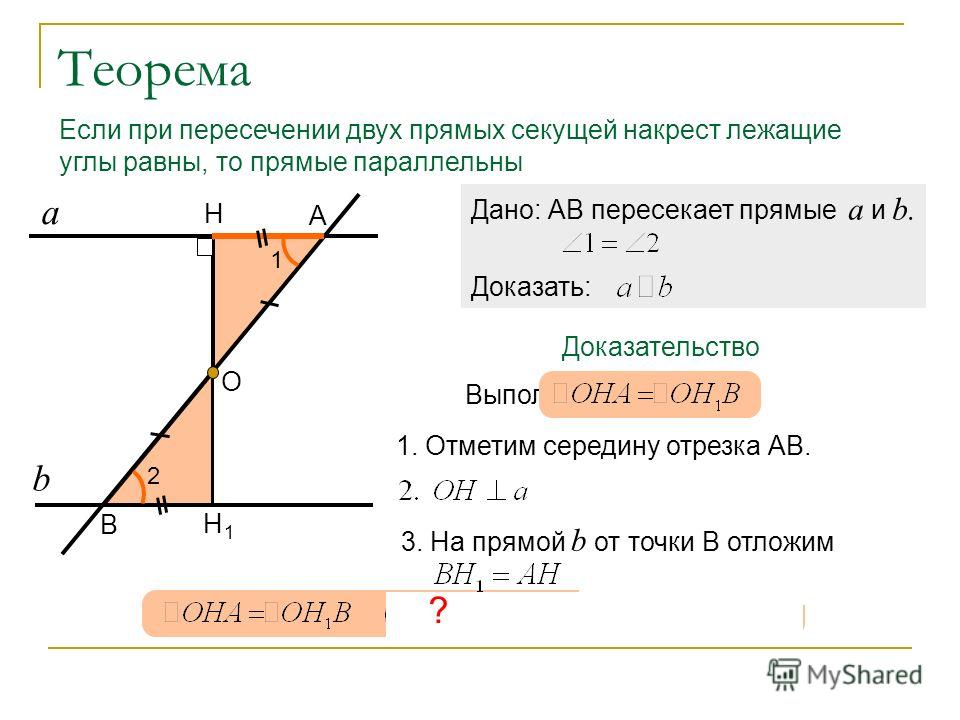

Итак, если ∠B и ∠L равны (или конгруэнтны), прямые параллельны. Вы также можете отметить только ∠C и ∠K ; если они конгруэнтны, то прямые параллельны. Вам нужно проверить только одну пару!

Альтернативные внутренние углы

Как и внешние углы, четыре внутренних угла имеют теорему и теорему, обратную теореме. Нас интересует обратная теорема об альтернативном внутреннем угле :

альтернативных внутренних углах, образованных поперечной и параллельной прямыми

Итак, на нашем рисунке, если ∠D сравнимо с ∠J , прямые MA 4 и 3

MA 8 и ZE параллельны. Или, если ∠F  равно ∠G , прямые параллельны. Опять же, вам нужно проверить только одну пару альтернативных внутренних углов!

Дополнительные уголки

Дополнительные уголки добавить к  180° . Дополнительные углы создают прямые линии, поэтому, когда секущая пересекает линию, остаются четыре дополнительных угла.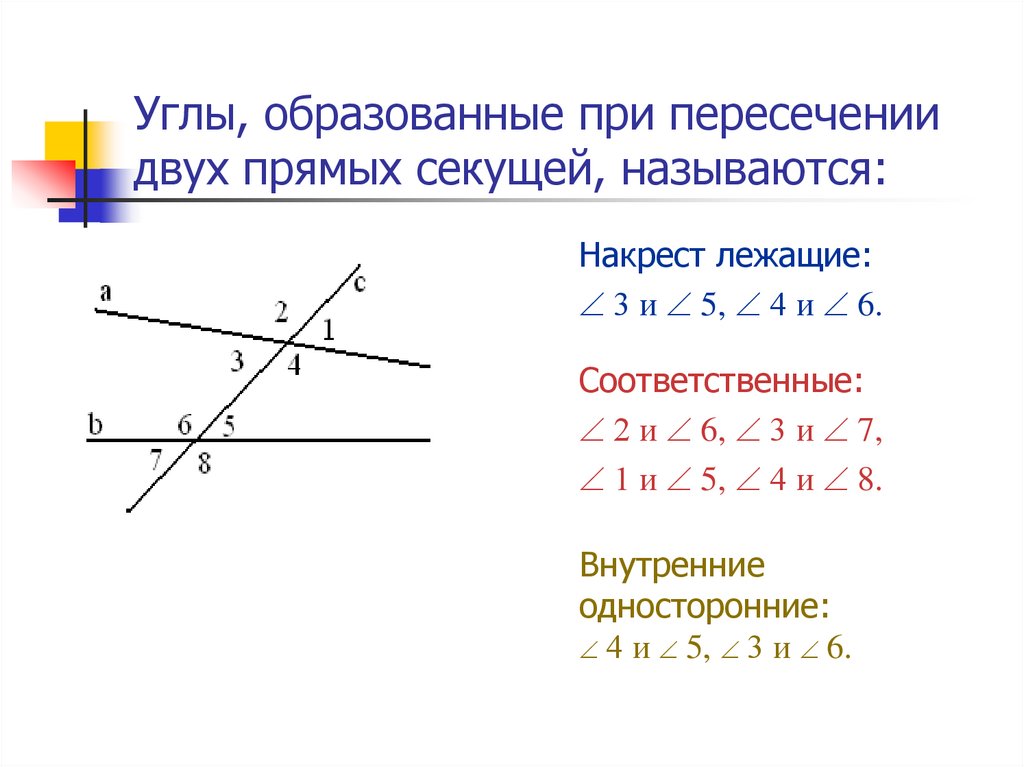

Дополнительные углы, образованные секущей

Когда секущая пересекает линии, предположительно параллельные, вы можете подумать, что она создает только восемь дополнительных углов, потому что вы удвоили количество линий.

Неправда! Он создает более восьми!

Сможете ли вы найти на нашем основном чертеже все 12 дополнительные углы?

Around the top intersection:

• ∠B and  ∠C

• ∠C and  ∠F

• ∠F  and  ∠D

• ∠D и ∠B

В районе нижнего пересечения:

1. ∠G и ∠J

2. ∠J  and  ∠L

3. ∠L  and  ∠K

4. ∠K  and  ∠G

Those should have been obvious , но поймали ли вы эти четыре других дополнительных углов?

1. ∠B и ∠K

2. ∠L и ∠4C 0005

3. ▲ и ♂

4. ↑D и omg

эти четыре пары являются добавлениями. прямые параллельны). Последние два дополнительных угла представляют собой пары внутренних углов, называемые последовательными внутренними углами .

Обратная теорема о последовательных внутренних углах

Как вы можете подозревать, если обратная теорема существует для последовательных внутренних углов, она также должна существовать для последовательные внешние углы .

Последовательные внутренние углы, образованные секущей

Последовательный внешний угол, обратная теорема

Последовательные внешние углы, образованные секущей

Последовательные внешние углы должны лежать по одну сторону от поперечной и снаружи от параллельных прямых. Итак, на нашем чертеже дополнительными являются только эти последовательные внешние углы:

• ∠B и ∠K

• ∠L  и  ∠C

Имейте в виду, что вам не нужно проверять каждый из этих 12 дополнительных углов. Простая проверка любой из них доказывает, что две линии параллельны!

Подведение итогов

После тщательного изучения вы теперь научились определять и узнавать параллельные прямые, находить их примеры в реальной жизни, строить секущую и определять различные виды углов, образующихся при пересечении секущей параллельных прямых.