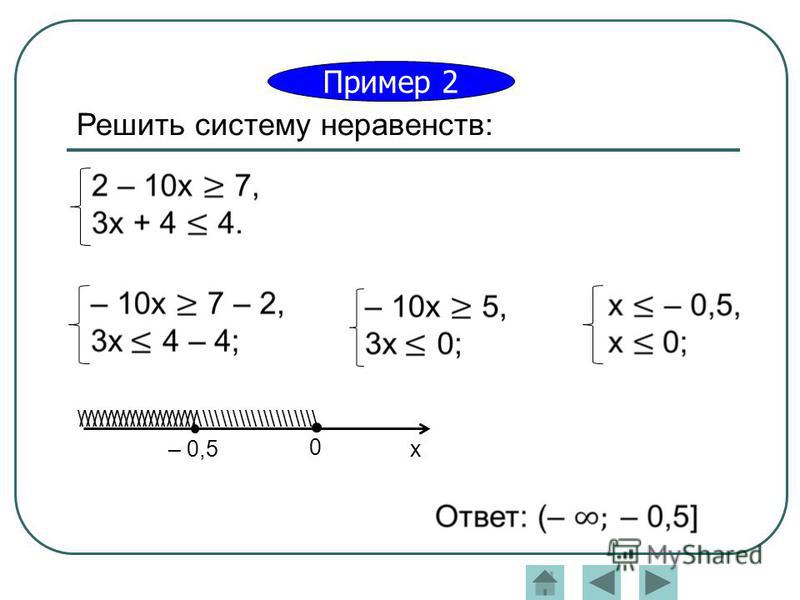
Решение простейших логарифмических неравенств — Сайт Александра Бабаева
Теория.
Для начала рекомендуется ознакомится со статьёй «Логарифм и его свойства«, описывающей теорию про логарифмы, и статьёй «Решение простейших логарифмических уравнений«, описывающей методы решения логарифмических уравнений.
Неравенство называется логарифмическим, если в нём содержится логарифмическая функция.
Методы решения логарифмических неравенств не отличаются от методов решений логарифмических уравнений, за исключением двух вещей.
Во-первых, при переходе от логарифмического неравенства к неравенству подлогарифмических функций следует следить за знаком получающегося неравенства. Он подчиняется следующему правилу.
Если основание логарифмической функции больше $1$, то при переходе от логарифмического неравенства к неравенству подлогарифмических функций знак неравенства сохраняется, а если же меньше $1$, то меняется на противоположный.
{-1}}=$
$=\log_{3}{(7-x)}.$
Таким образом, получено следующее неравенство:
$\log_{3}{(2x+1)} \geq \log_{3}{(7-x)}$.
Основание равно $3>1$, а, значит, знак неравенства не меняется. Получаем:
$2x+1 \geq 7-x,$
$3x \geq 6,$
$x \geq 2,$
$x \in [2; +\infty).$
Соединяя полученное решение с областью определения, получаем ответ.
Ответ: $x \in [2; 7).$
**/ ?>
Элементарная математика
Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.
Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной.
(Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.)
Оглавление
ВВЕДЕНИЕ
Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
2. Простые и составные числа. Признаки делимости.
3. Наибольший общий делитель и наименьшее общее кратное.
4. Целые числа. Рациональные числа.
5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
6. Иррациональные числа. Действительные числа.
7. Действия с приближенными числами.
8. Числовая ось. Координаты точки на плоскости.
§ 2. Степени и корни9. Степени с натуральными показателями.
10. Степени с целыми показателями.
11. Корни.
12. Степени с рациональными показателями. Степени с действительными показателями.
13. Алгоритм извлечения квадратного корня.
§ 3. Комплексные числа
14. Основные понятия и определения.
15. Рациональные действия с комплексными числами.
16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.
18. Извлечение корня из комплексного числа.
Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
19. Алгебраические выражения. Одночлены и многочлены.
20. Формулы сокращенного умножения.
21. Бином Ньютона.
22. Разложение многочлена на множители.
23. Дробные алгебраические выражения.
§ 2. Иррациональные алгебраические выражения
24. Радикалы из алгебраических выражений.
25. Освобождение от иррациональности в знаменателе дроби.
Глава III. ЛОГАРИФМЫ
26. Определение и свойства логарифмов.
27. Логарифмы по различным основаниям. Модуль перехода.
§ 2. Десятичные логарифмы
28. Характеристика и мантисса десятичного логарифма.
29. Применение десятичных логарифмов к вычислениям.
41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
42. Показательная функция.
43. Логарифмическая функция.
§ 3. Преобразование графиков
44. Параллельный сдвиг графика.
45. График квадратного трех члена.
46. График дробно-линейной функции.
47. Преобразование симметрии. Сжатие и растяжение графика.
48. Построение графиков функций.
49. Сложение графиков.
§ 4. Некоторые сведения о рациональных функциях
50. Целые и дробные рациональные функции. Деление многочленов.51. Схема Горнера. Теорема Безу.
52. Нули многочлена. Разложение многочлена на множители.
Глава V. УРАВНЕНИЯ
53. Уравнение. Корни уравнения.
54. Равносильные уравнения.
55. Системы уравнений.
56. Графическое решение уравнений.
§. 2. Алгебраические уравнения с одной неизвестной
57. Число и кратность корней.
58. Уравнения первой степени (линейные уравнения).
59. Уравнения второй степени (квадратные уравнения).
60. Формулы Виета. Разложение квадратного трехчлена на множители.
61. Исследование квадратного уравнения.
62. Уравнения высших степеней. Целые корни.
63. Двучленные уравнения.
64. Уравнения, сводящиеся к квадратным.
65. Возвратные уравнения.
§ 3. Системы алгебраических уравнений
66. Линейные системы.
67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
68. Системы, состоящие из уравнения второй степени и линейного уравнения.
69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
§ 4. Иррациональные, показательные и логарифмические уравнения
70. Иррациональные уравнения.
71. Показательные уравнения.
72. Логарифмические уравнения.
73. Разные уравнения. Системы уравнений.
Глава VI. НЕРАВЕНСТВА
74. Свойства неравенств. Действия над неравенствами.
75. Алгебраические неравенства.
§ 2. Решение неравенств
76. Множество решений неравенства.
77. Графическое решение неравенств.
79. Квадратные неравенства.
80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
81. Иррациональные, показательные и логарифмические неравенства.82. Неравенства с двумя неизвестными.
Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
83. Числовая последовательность.
84. Предел числовой последовательности.
85. Бесконечно малые. Правила предельного перехода.
§ 2. Арифметическая прогрессия
86. Арифметическая прогрессия. Формула общего члена.
87. Свойства арифметической прогрессии.
88. Формула для суммы n членов арифметической прогрессии.
§ 3. Геометрическая прогрессия
89. Геометрическая прогрессия. Формула общего члена.
90. Свойства геометрической прогрессии.
91. Формулы для суммы n членов геометрической прогрессии.
92. Бесконечно убывающая геометрическая прогрессия.
Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
93. Вектор, проекция вектора.
94. Положительные углы и дуги, меньшие 360°.
95. Углы и дуги, большие 360°.
96. Отрицательные углы. Сложение и вычитание углов.
§ 2. Тригонометрические функции произвольного угла
97. Определение основных тригонометрических функций.
98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
§ 3. Соотношения между тригонометрическими функциями одного и того же угла
99. Основные тригонометрические тождества.
100. Вычисление значений тригонометрических функций по значению одной из них.
101. Значения тригонометрических функций некоторых углов.
§ 4. Четность, нечетность и периодичность тригонометрических функций
102. Четность и нечетность.
103. Понятие периодической функции.
104. Периодичность тригонометрических функций.
§ 5. Формулы приведения
105. Зависимость между тригонометрическими функциями дополнительных углов.
106. Формулы приведения.
Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
§ 1.Тригонометрические функции числового аргумента
108. Области определения и области изменения значений тригонометрических функций.
109. Некоторые неравенства и их следствия.
§ 2. Графики тригонометрических функций
110. Первоначальные сведения о таблицах тригонометрических функций.
111. Основные графики.
112. Примеры построения графиков некоторых других тригонометрических функций.
113. Дальнейшие примеры построения графиков функций.
Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
114. Расстояние между двумя точками на плоскости.
115. Косинус суммы и разности двух аргументов.
116. Синус суммы и разности двух аргументов.
117. Тангенс суммы и разности двух аргументов.
118. О формулах сложения для нескольких аргументов.
§ 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
119. Тригонометрические функции двойного аргумента.
120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.
121. Тригонометрические функции половинного аргумента.
122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
§ 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
§ 4. Преобразование в произведение сумм вида
§ 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
127. Преобразование в произведение выражения a•sina + b•cosa.
128. Преобразование в произведение выражений a•sina+b и a•cosa+b
129. Преобразование в произведение выражения a•tga+b.
Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
130. Функция у = arcsin x (арксинус).
131. Функция y = arccos x (арккосинус).
132. Функция y = arctg x (арктангенс).
133. Функция y = arcctg x (арккотангенс).134. Пример.
§ 2. Операции над обратными тригонометрическими функциями
135. Тригонометрические операции.
136. Операции сложения (вычитания).
§ 3. Обратные тригонометрические операции над тригонометрическими функциями
137.
138. Функция y = arctg (tg x).
Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
139. Уравнение sin х = а.
140. Уравнение cos х = a.
141. Уравнение tg x = a.
142. Уравнение ctg x = a.
143. Некоторые дополнения.
§ 2. Способ приведения к одной функции одного и того же аргумента
145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
146. Способ разложения на множители.
147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
§ 3. Некоторые частные приемы решения тригонометрических уравнений и систем
148. Введение вспомогательного аргумента.
149. Преобразование произведения в сумму или разность.
150. Переход к функциям удвоенного аргумента.
151. Решение уравнения типа…
152. Применение подстановок sinx ± соsx = y.
§ 4. Решение тригонометрических неравенств
154. Простейшие тригонометрические неравенства.
155. Примеры тригонометрических неравенств, сводящихся к простейшим.
Часть вторая. ГЕОМЕТРИЯ
156. Точка. Прямая. Луч. Отрезок.
157. Плоскость. Фигуры и тела.
160. Равенство фигур. Движение.
161. Равенство тел.
§ 2. Измерение геометрических величин
162. Сложение отрезков. Длина отрезка.
163. Общая мера двух отрезков.
164. Сравнительная длина отрезков и ломаных.
165. Измерение углов.
166. Радианная мера угла.
167. Измерение площадей.
168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
169. Перпендикуляр и наклонные.
170. Свойство перпендикуляра, проведенного к отрезку в его середине.
171. Параллельные прямые.
172. Углы, образованные двумя параллельными прямыми и секущей.
173. Углы с параллельными или перпендикулярными сторонами.
§ 2. Геометрические места точек. Окружность
174. Геометрическое место точек.
175. Свойство биссектрисы угла.
176. Окружность.
177. Взаимное расположение прямой и окружности. Касательная и секущая.
178. Хорда и диаметр. Сектор и сегмент.
179. Взаимное расположение двух окружностей.
§ 3. Основные задачи на построение
181. Деление отрезка пополам. Построение перпендикуляров.
182. Построение углов.
183. Другие задачи на построение.
Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
184. Стороны и углы треугольника.
185. Биссектрисы треугольника. Вписанная окружность.
186. Оси симметрии сторон треугольника. Описанная окружность.
187. Медианы и выcоты треугольника.
188. Равенство треугольников.
189. Построение треугольников.
190. Равнобедренные треугольники.
191. Прямоугольные треугольники.
§ 2. Параллелограммы
192. Четырехугольники.
193. Параллелограмм и его свойства.
194. Прямоугольник.
§ 3. Трапеция
196. Трапеция.
197. Средняя линия треугольника.
198. Средняя линия трапеции.
199. Деление отрезка на равные части.
§ 4. Площади треугольников и четырехугольников
200. Площадь параллелограмма.
201. Площадь треугольника.
202. Площадь трапеции.
Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
203. Пропорциональные отрезки.
204. Свойства биссектрис внутреннего и внешнего углов треугольника.
§ 2. Подобное преобразование фигур (гомотетия)
205. Определение гомотетичных фигур.
206. Свойства преобразования подобия.
§ 3. Общее подобное соответствие фигур
207. Подобные фигуры.
208. Периметры и площади подобных треугольников.
209. Применение подобия к решению задач на построение.
Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
210. Углы с вершиной на окружности.
211. Углы с вершиной внутри и вне круга.
212. Угол, под которым виден данный отрезок.
213. Четырехугольники, вписанные в окружность.
214. Пропорциональные отрезки в круге.
215. Задачи на построение.
§ 2. Метрические соотношения в треугольнике
216. Пропорциональные отрезки в прямоугольном треугольнике.
218. Теорема синусов. Формула Герона.
217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
218. Теорема синусов. Формула Герона.
219. Радиусы вписанной и описанной окружностей.
§ 3. Решение треугольников
220. Таблицы функций.
221. Решение треугольников. Сводка основных формул.
222. Решение прямоугольных треугольников.
223. Решение косоугольных треугольников.
Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
224. Выпуклые многоугольники.
225. Правильные многоугольники.
226. Соотношения между стороной, радиусом и апофемой.
227. Периметр и площадь правильного n-угольника.
228. Удвоение числа сторон правильного многоугольника.
§ 2. Длина окружности. Площадь круга и его частей
229. Длина окружности.
230. Площадь круга и его частей.
Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
231. Взаимное расположение двух прямых в пространстве.
232. Взаимное расположение прямой линии и плоскости.
233. Взаимное расположение двух плоскостей.
234. Свойства параллельных прямых и плоскостей.
235. Построения в стереометрии.
§ 2. Перпендикулярность прямых и плоскостей
236. Перпендикуляр к плоскости.
237. Перпендикуляр и наклонные.
238. Угол между прямой и плоскостью.
239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
240. Общий перпендикуляр двух скрещивающихся прямых.
§ 3. Двугранные и многогранные углы
241. Двугранный угол.
242. Взаимно перпендикулярные плоскости.
243. Трехгранные углы.
244. Многогранные углы.
§ 4. Многогранники
245. Многогранники.
246. Правильные многогранники.
Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
247. Цилиндры и призмы.
248. Параллелепипеды.
249. Объемы призм и цилиндров.
250. Площадь боковой поверхности призмы.
251. Площадь поверхности цилиндра.
§ 2. Пирамида. Конус
252. Свойства пирамиды и конуса.
253. Объем пирамиды и конуса.
254. Площадь боковой поверхности правильной пирамиды и конуса.
255. Усеченный конус и усеченная пирамида.
§ 3. Шаровая поверхность. Шар
256. Шар и шаровая поверхность.
257. Объем шара и его частей.
258. Площадь поверхности шара и ее частей.
259. Понятие телесного угла.
Ответы к упражнениям
Приложения
уравнений и неравенств: примеры | StudySmarter
Знаете ли вы, что существуют математические концепции, которые можно использовать для сравнения значений величин, чтобы определить, равны ли они или какие из них больше или меньше других?
В этой статье мы обсудим уравнения и неравенства.
Определение уравнений и неравенств
Определение уравнений
Уравнение выражает равенство двух выражений через знак равенства (=).
Приведенное выше определение буквально гласит, что когда выражение приравнивается к другому выражению, оба выражения равны.
Пример уравнения выглядит так.
Переменные в уравнениях являются заполнителями и представляют собой неизвестные величины, требующие решения. По этой причине реальные проблемы моделируются в виде уравнений, которые необходимо решить.
Если я трачу 100 долларов на пару туфель и рубашку, а стоимость рубашки мне известна только как 40 долларов. Как я узнаю стоимость пары обуви?
Математическое моделирование заставит нас приравнять все, что мы купили, к 100 долларам, поскольку это общая сумма потраченных средств.
Мы представляем неизвестную величину с помощью переменной , и, таким образом, мы имеем
.
Тогда из уравнения мы можем сказать, что стоимость пары обуви составила 60 долларов, поскольку 40+60=100.
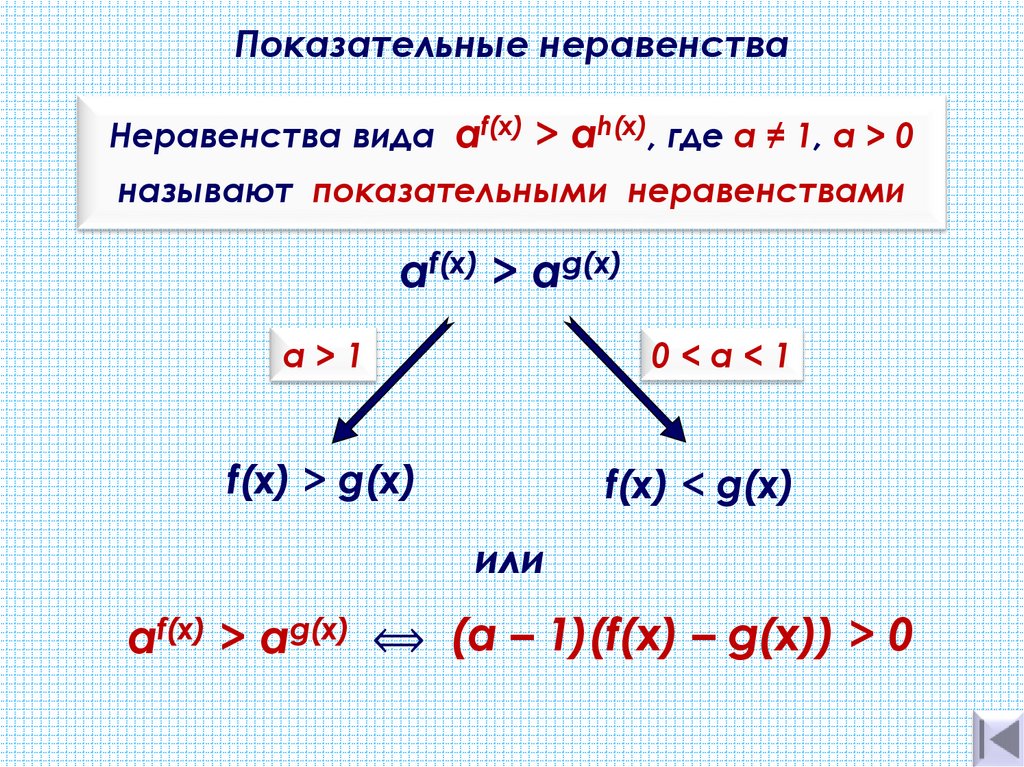
Определение неравенств
Неравенства представляют собой математические утверждения, которые скорее содержат больше (>), больше или равно (≥), меньше (<) или меньше или равно (≤) между выражениями в место знака равенства в уравнениях.
Пример неравенства выглядит так.
Неравенства используются для моделирования и представления величин, которые не совсем равны друг другу.
Представление диапазонов прекрасно выполняется с помощью неравенств.
В качестве примера мы используем минимальную заработную плату.
Правительство заявляет, что приемлемая минимальная заработная плата в стране теперь составляет 10 долларов в час.
Математически это означает, что сейчас компаниям разрешено платить своим сотрудникам , где почасовая ставка.
Примеры уравнений и неравенств
В таблице ниже приведены примеры уравнений и неравенств.
Equations
Inequalities
Equations and inequalities differences
Comparatively, между уравнениями и неравенствами есть довольно много различий.
Уравнения
Неравенства
Они выражают, насколько равны различные величины.
Они показывают, насколько неравны различные величины.
Используемый знак равенства (=)
Используемые символы больше (>), больше или равно (≥), меньше (<) и меньше или равно (≤).
Они имеют фиксированное и единственное решение.
Решения обычно включаются в интервал, особенно много раз.
Общее количество корней уравнений является определенным.
Общее количество корней неравенств бесконечно.
Полиномиальные уравнения и неравенства
Теперь введем определения полиномиальных уравнений и неравенств.
Полиномиальное уравнение — это уравнение, включающее полиномы.
Напомним, что многочлен имеет вид
- – коэффициенты
- – переменная
- – старший показатель, натуральное число.
Примеры полиномиальных уравнений:
Description
Linear Equations
Equations of degree 1
Quadratic Equations
Equations of degree 2
Cubic Equations
Уравнения степени 3
Полиномиальное неравенство — это неравенство, включающее многочлены.
Различие между полиномиальными уравнениями и неравенствами заключается в признаках, которые с ними связаны.
Примеры полиномиальных уравнений и неравенств
Здесь мы рассмотрим примеры того, как ситуации из реальной жизни моделируются в уравнения для ускорения решения задач.
Суммируя два последовательных числа, мы получаем 61. Найдите эти числа
Решение
Математически последовательные числа — это те, которые следуют друг за другом напрямую.
Представим первое число переменной . Поскольку второе число следует за первым, это можно представить как .
Все, что нам нужно сделать сейчас, это сложить эти два числа и приравнять их к 61, как утверждает задача,
Теперь у нас есть уравнение для задачи. Мы можем пойти дальше, чтобы проверить это, решив для x, чтобы увидеть, каковы эти последовательные числа.
Изолировать путем вычитания 1 из каждой части уравнения,
Разделить обе части на 2, чтобы получить,
Это означает, что первое число равно 30.
Так как второе число было представлено как , мы подставим 30 в это выражение.
Теперь у нас есть второе число, равное 31.
Теперь давайте подставим эти числа в уравнение, которое мы смоделировали, чтобы получить
Майк заказал рубашку и пару туфель за 100 долларов, а рубашка стоит 45 долларов, сколько он потратил на пару туфель?
Решение
Здесь было куплено два предмета на сумму до 100 долларов.
Значение для одного указано, а для другого нет. Это означает, что мы можем представить элемент, значение которого не было задано переменной x.
Итого мы получили, просуммировав стоимость двух предметов,
Здесь мы смоделировали проблему в виде уравнения.
Выделив x, получим
Таким образом, цена пары обуви 55 долларов.
Мы также рассмотрим примеры того, как ситуации из реальной жизни моделируются в виде неравенств для ускорения решения проблем.
Если Адам набрал 18 очков в игре в теннис, в которую он играл с Беном, и Бен набрал как минимум на 3 очка больше, чем Адам, сколько очков набрал Бен?
Решение
Имея дело с неравенством, мы должны быть очень бдительны в отношении связанного с ним знака. Мы видим, что у Бена более высокий балл, чем у Адама, поэтому знак должен отображать это.
Кроме того, у нас есть слова «по крайней мере», на которые следует обратить внимание.
Пусть счет Бена равен x. Чтобы получить оценку Бена, нам нужно сложить по крайней мере 3 и 18, и, таким образом, это можно смоделировать как 9.0003
Как минимум 13 учеников не пришли в школу 1 июля.
Решение
Опять же, по крайней мере, изображает знак «больше» или «равно». И эта проблема означает, что количество учеников, не посещавших школу в указанный день, составляет 13 и более. Это выражается как,
Линейные уравнения и неравенства с двумя переменными
Существуют ситуации, когда уравнения и неравенства приходится решать с двумя переменными. Мы собираемся изучить, как они решаются в этом разделе.
Линейные уравнения с двумя переменными
Линейные уравнения с двумя переменными, как следует из названия, представляют собой линейные уравнения с двумя переменными. Они имеют вид
, где x и y — переменные, а a, b и c — целые числа.
и являются линейными уравнениями с двумя переменными.
Если Майк купил пару туфель и рубашку за 100 долларов, а Стив заказал ту же пару туфель и две рубашки за 145 долларов, сколько стоит пара туфель?
Решение
Тогда дополнительная рубашка стоила 45 долларов. Таким образом, пара обуви в обоих уравнениях будет стоить 55 долларов. Однако это можно решить математически, если правильно смоделировать уравнение.
Каждую неизвестную величину можно присвоить переменной.
Let
И пара туфель, и рубашка стоят 100 долларов. Это означает, что для первого уравнения мы суммируем эти переменные и приравниваем их к 100 долларам.
Во втором уравнении рубашки две. Однако общая стоимость этой покупки составляет 145 долларов, поэтому у нас есть
Теперь мы смоделировали оба уравнения. Это записывается следующим образом:
Покупки Майка и Стива-StudySmarter Originals
Линейные неравенства с двумя переменными
Линейные неравенства с двумя переменными — это линейные неравенства с двумя переменными.
Единственная разница между ними и линейными уравнениями с двумя переменными заключается в используемых знаках. Они выражаются в виде
где x и y — переменные, а a, b и c — целые числа.
Знаки неравенств различаются в зависимости от задачи. Мы возьмем пример из реальной ситуации и посмотрим, как это поможет их решить.
Чтобы поступить в 12-й класс, учащиеся должны набрать больше 10 баллов.
Это можно смоделировать как x>10, где x — это общий балл.
Квадратные функции, уравнения и неравенства
Квадратные уравнения и неравенства – это уравнения, переменные которых находятся во второй степени. В этом разделе мы рассмотрим, как они работают как в уравнениях, так и в неравенствах.
Квадратные уравнения
Квадратные уравнения являются полиномиальными уравнениями второй степени. На графике они имеют форму параболы. Это делает их идеальной математической концепцией для расчета параболических движений в реальной жизни, таких как движения ракет.
Они представлены в стандартной форме как , где a, b и c — действительные числа, где a ≠ 0.
Однако это не единственный способ выражения квадратичных чисел. Формы, в которых могут быть выражены квадратичные уравнения,
- Стандартная форма:
- Форма вершины: вершина параболы.
- Форма точки пересечения: где a ≠ 0, а (p, 0) и (q, 0) — точки пересечения параболы по оси x.
В этой статье мы обсудим только то, как моделировать эти уравнения. Вы можете обратиться к статье о решении квадратных уравнений, чтобы узнать больше о том, как решать такие уравнения!
Какое из следующих уравнений является квадратным?
Решение
Единственное квадратичное уравнение здесь-
, так как самая высокая степень полиномиального. чем (>), больше или равно (≥), меньше (<) или меньше или равно (≤) между выражениями вместо знака равенства в уравнениях.
Какое из следующих неравенств является квадратным?
Решение
Единственным квадратным неравенством здесь является
,
3 900, поскольку оно имеет квадратичную форму неравенства.
Уравнения и неравенства. Ключевые выводы
- Уравнение выражает равенство двух выражений через знак равенства (=).
- Неравенства — это математические утверждения, которые скорее содержат больше (>), больше или равно (≥), меньше (<) или меньше или равно (≤) между выражениями вместо знака равенства в уравнения.
- Полиномиальное уравнение — это уравнение, содержащее многочлены.
- Квадратные уравнения — это уравнения, переменные которых стоят во второй степени.
- Квадратные неравенства — это полиномы второй степени, имеющие между выражениями больше (>), больше или равно (≥), меньше (<) или меньше или равно (≤).
Неравенства — рабочие примеры
Мы часто используем обозначение интервала, чтобы выразить множество решений неравенства.
$(a,b) = \{ x \in \mathbb{R} | а $[a,b) = \{ x \in \mathbb{R} | а \leq х $(a,b] = \{ x \in \mathbb{R} | a $[a,b] = \{ x \in \mathbb{R} | а \leq х \leq б \}$ $(-\infty ,b) = \{ x \in \mathbb{R} | Икс $(-\infty ,b] = \{ x \in \mathbb{R} | x \leq b \}$ $(a,\infty) = \{ x \in \mathbb{R} | х>а \}$ $[a,\infty) = \{ x \in \mathbb{R} | х\geq а \}$ $(-\infty, \infty) = \mathbb{R}$ Пример.
Решить $1\leq 2x+3
$1 \leq 2x+3 $-2 \leq 2x (Подробности)вычесть 3 с обеих сторон $-1 \leq x (детали)делите обе стороны на 2 Таким образом, набор решений равен $[ -1 , 1)$.
В общем случае, если вы хотите решить неравенство вида $(x-a)(x-b) >0$ ($>$ можно заменить на $\geq, b$.
Мы можем решить неравенство $(x-a)(x-b) >0$, определив знак каждого множителя на трех частях.
Мы можем использовать аналогичный подход для неравенств с более чем двумя факторами. В этом случае линия разбивается на несколько частей, однако подход тот же. Вы должны определить знак множителей на каждой фигуре и использовать их для решения неравенства. Этот метод предполагает, что при решении полиномиальных неравенств часто бывает полезно переписать неравенство, переместив все ненулевые члены в одну сторону, а затем разложив на множители или заполнив квадрат (когда множители не могут быть найдены). 9{2} -3x +2 \geq 0$
(Подробности)переместить ненулевые члены в одну сторону $\Longleftrightarrow$ $ (x-1)(x-2) \geq 0 $ (Подробности)результирующий многочлен разложить на множители Теперь у нас осталось более простое неравенство $(x-1)(x-2) \geq 0$, которое мы решаем следующим образом:
Это дает решение $(-\infty, 1] \cup [2, \infty)$.
При работе с неравенствами, содержащими рациональные функции, следует сдвинуть все ненулевые члены в одну сторону, затем найти общий знаменатель, чтобы получить простое неравенство вида $\frac{P(x)}{Q(x) } , \geq$ в зависимости от обстоятельств). Затем мы используем подход, аналогичный тому, который мы использовали для полиномиального неравенства. Мы пытаемся разложить числитель и знаменатель на множители, и используем множители, чтобы разбить числовую прямую на части, и проверить знак множителей на каждой из частей. (Обратите внимание, где знаменатель равен 0!)
Пример. Решите неравенство $ x-3 \geq -\frac{4}{x} + 2$, нарисуйте множество решений на числовой прямой и запишите его в интервальной форме.
$ x-3 \geq -\frac{4}{x} + 2 $ $x-3 + \frac{4}{x} — 2 \geq 0 $ (Подробности)переместить все ненулевые члены в одну сторону $ \frac{x(x-3)}{x} + \frac{4}{x} — \frac{2x}{x} \geq 0 $ (Подробности)найдите общий знаменатель 9{2} — 5x + 4}{x} \geq 0 $ (Подробности)развернуть и упростить верхнюю часть $ \frac{(x-4)(x-1)}{x} \geq 0 $ (Детали) коэффициент сверху и снизу Это дает решение $(0, 1] \cup [4, \infty)$.
{-1}}=$
n.
Равносильные неравенства.
Функция у = arcsin (sin x).
Теорема Пифагора.
Они представлены в таблице ниже.
Это означает, что при суммировании таких чисел должно получиться 61,9.0003
Это означает, что если мы выражаем, что оценка Бена выше, она должна быть больше или равна оценке Адама.
Вот краткий обзор различных типов интервалов:
(Подробности) Произведение двух слагаемых положительно, если либо оба слагаемых положительны, либо оба слагаемых отрицательны. И произведение равно $0$, если любой член равен $0$.