Умножение и деление отрицательных чисел — «Семья и Школа»
Содержание
§ Умножение отрицательных чисел. Умножение рациональных чисел
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.
Умножение чисел с одинаковыми знаками
Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.
Чтобы умножить два числа с одинаковыми знаками надо:
- перемножить модули чисел;
- перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).
Примеры умножения отрицательных и положительных чисел.
- (−3) · (−6) = +18 = 18
- 2 · 3 = 6
Умножение чисел с разными знаками
Второй возможный случай — это умножение чисел с разными знаками.
Чтобы умножить два числа с разными знаками, надо:
перемножить модули чисел; - перед полученным произведением поставить знак «−».
Примеры умножения отрицательных и положительных чисел.
- (−0,3) · 0,5 = −0,15
- 1,2 · (−7) = −8,4
Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.
Запомните!
Минус на минус даёт плюс,
Плюс на минус даёт минус.
| + · (+) = + | + · (−) = − |
| − · (−) = + | − · (+) = − |
В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.
При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.
Пример.
(−6) · (−3) · (−4) · (−2) · 12 · (−1) =
В примере пять отрицательных множителей.
Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 · 3 · 4 · 2 · 12 · 1 = 1728
Конечный результат умножения исходных чисел будет:
(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −1728
Умножение на ноль и единицу
Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.
- 0 · a = 0
- a · 0 = 0
- a · 1 = a
Примеры:
- 0 · (−3) = 0
- 0,4 · 1 = 0,4
Особую роль при умножении рациональных чисел играет отрицательная единица «−1».
Запомните!
При умножении на «−1» число меняется на противоположное.
В буквенном выражении это свойство можно записать:
a · (−1) = (−1) · a = −a
При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.
Пример умножения отрицательных и положительных чисел.
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Деление чисел с разными знаками: правило и примеры
В этой статье мы рассмотрим деление положительных чисел на отрицательные и наоборот. Дадим подробный разбор правила деления чисел с разными знаками, а также приведем примеры.
Правило деления чисел с разными знаками
Правило для целых чисел с разными знаками, полученное в статье о делении целых чисел, справедливо также для рациональных и действительных чисел. Приведем более общую формулировку этого правила.
Правило деления чисел с разными знаками
При делении положительного числа на отрицательное и наоборот нужно модуль делимого разделить на модуль делителя, а результат записать со знаком минус.
В буквенном виде это выглядит так:
a÷-b=-a÷b
-a÷b=-a÷b.
Результатом деления чисел с разными знаками всегда является отрицательное число. Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.
Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.
Еще одна эквивалентная математическая формулировка данного правила имеет вид:
a÷b=a·b-1
Чтобы разделить числа a и b, имеющие разные знаки, нужно число a умножить на число, обратное числу b, то есть b-1. Данная формулировка применима на множестве рациональных и действительных чисел, она позволяет перейти от деления к умножению.
Рассмотрим теперь, как применять описанную выше теорию на практике.
Как делить числа с разными знаками? Примеры
Ниже мы рассмотрим несколько характерных примеров.
Пример 1. Как делить числа с разными знаками?
Разделим -35 на 7.
Сначала запишем модули делимого и делителя:
-35=35, 7=7.
Теперь разделим модули:
-357=357=5.
Допишем перед результатом знак минус и получим ответ:
-357=-5.
Теперь воспользуемся другой формулировкой правила и вычислим число, обратное 7.
7-1=17.
Теперь проведем умножение:
-35·17=—35·17=-357=-5.
Пример 2. Как делить числа с разными знаками?
Вычислим значение 8÷-60.
По правилу, имеем:
8÷-60=-8÷-60=-8÷60=-860.
Мы получили дробь, которую можно сократить на 4. После сокращения получаем:
8÷-60=-860=-215.
Это и есть окончательный ответ.
Если мы делим дробные числа с рациональными знаками, делимое и делитель нужно представить в виде обыкновенных дробей.
Пример 3. Как делить числа с разными знаками?
Разделим смешанное число -3322 на десятичную дробь 0,(23).
Модули делимого и делителя соответственно равны 3322 и 0,(23). Переводя 3322 в обыкновенную дробь, получаем:
3322=3·22+322=6922.
Делитель также представим в виде обыкновенной дроби:
0,(23)=0,23+0,0023+0,000023=0,231-0,01=0,230,99=2399.
Теперь делим обыкновенные дроби, выполняем сокращения и получаем результат:
-6922÷2399=-6922·9923=-32·91=-272=-1312.
В заключение рассмотрим случай, когда делимое и делитель являются иррациональными числами и записываются в виде корней, логарифмов, степеней и т.д.
В такой ситуации частное записывается в виде числового выражения, которое по возможности упрощается. При необходимости вычисляется его приближенное значение с необходимой точностью.
Пример 4. Как делить числа с разными знаками?
Разделим числа 57 и -23.
По правилу деления чисел с разными знаками, запишем равенство:
57÷-23=-57÷-23=-57÷23=-57·23.
Избавимся от иррациональности в знаменателе и получим окончательный ответ:
-57·23=-5·4314.
Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Как вставить символ умножения и знак деления в Word
Знак умножения × (также известный как знак умножения или знак размера ) является математическим знаком для операции умножения.
Есть несколько популярных представлений для операции умножения: крест ( × ), точка ( ⋅ ) или звездочка ( ∗ ).
См. также как поставить х в ворде.
Знак дивизии ÷ является математическим символом в форме Colon ( ∶ ), Obelus ( ÷ ), или Slash или Solidus ( /), или . обозначают оператор деления. В большинстве стандартов косая черта ( / ) используется в качестве знака деления для линейного представления или дробной черты для структурированного представления. Символы 
Мы настоятельно рекомендуем использовать инструменты Equation для вставки любого типа уравнения или математических, финансовых или даже логических формул и выражений.
Строчная Латинская буква X часто заменяет знак умножения , но это ошибка, которую нужно избегать.
Чтобы создать идеальный документ, используйте один из следующих способов вставки умножения 9Символ 0004 или знак деления :
Стандартный способ : с помощью диалогового окна Символ:
Чтобы открыть диалоговое окно Символ , выполните следующие действия:
1. На вкладке Вставить в группе Символы нажмите кнопку Символ и нажмите Дополнительные символы… :
2. В диалоговом окне Symbol :
С помощью сочетания клавиш:
В Microsoft Word вы можете использовать Unicode для вставки любого из используемых символов:
| Горячая клавиша | Символ | |
|---|---|---|
| Знак умножения | Введите | × |
| Умножение Х | Введите 2715 и сразу нажмите Alt+X | ✕ |
| Вектор или перекрестное произведение символ | Введите 2a2f или 2A2F и сразу нажмите Alt+X | ⨯ |
| Средняя точка | Тип | · |
| Точка символ | Введите 22c5 или 22C5 и сразу нажмите Alt+X | ⋅ |
| Знак раздела | Введите 00f7 или 00F7 и сразу нажмите Alt+X | ÷ |
Более быстрый способ : использование автозамены по математике:
Когда вы работаете с большим количеством документов и часто нужно вставить один специальный символ, вам не нужно вставлять уравнение каждый раз. Microsoft Word предлагает полезную функцию под названием AutoCorrect . Параметры AutoCorrect в Microsoft Word предлагают два разных способа быстрого добавления любого специального символа или даже
большие куски текста:
Microsoft Word предлагает полезную функцию под названием AutoCorrect . Параметры AutoCorrect в Microsoft Word предлагают два разных способа быстрого добавления любого специального символа или даже
большие куски текста:
- Использование в Заменить текст при вводе Функция Автозамены Опции.
- Использование параметров Math AutoCorrect :
Используя этот метод, вы можете использовать параметры Math AutoCorrect без вставки уравнения. Чтобы включить или выключить AutoCorrect символов Math , выполните следующие действия:
1. На вкладке Файл нажмите Параметры :
2. В диалоговом окне Параметры Word на Вкладка Правописание нажмите кнопку Параметры автозамены… :
3. В диалоговом окне AutoCorrect на вкладке Math AutoCorrect выберите параметр Использовать правила Math AutoCorrect за пределами математических областей :
После нажатия OK вы можете использовать любое из перечисленных Имен символов
Примечание : Если вам не нужна последняя замена, нажмите Ctrl+Z , чтобы отменить ее.
Основные математические символы | Словарь
математика (BrE) | математика (AmE) — это сокращенная форма математика
На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.
+
знак плюс/дополнение
Знак плюс означает:
а. понятие
положительное
Любое число больше нуля является положительным числом и может быть записано со знаком плюс или без него.
Таким образом, +5 (плюс пять) и 5 (пять) — одно и то же число.
б. операция сложения
3 + 5 = 8
три плюс пять равно восьми
пять прибавить к трем, получится восемь
три прибавить к пяти, получится восемь
Сложение дает нам сумма . В 3 + 5 = 8 сумма равна восьми.
—
знак минус/знак вычитания
Знак минус означает:
а.

понятие отрицательного
Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.
-3
минус три
б. операция вычитания
8 — 5 = 3
восемь минус пять равно трем
пять вычесть из восьми равно трем
если из восьми вычесть пять, то получится три
если из восьми вычесть пять, то получится три
Вычитание дает нам разность . В 8 — 5 = 3 разница три.
×
знак умножения / знак умножения
Знак раз представляет:
умножение
5 x 6 = 30
пять умножить на шесть равно тридцати
пять умножить на шесть равно тридцати
пять шестерок равно тридцати
если умножить 5 на 6 получится тридцать
Умножение дает нам продукт . В 5 х 6 = 30 произведение равно 30.
÷ ИЛИ /
знак деления
Знак деления означает:
отделение
15 ÷ 3 = 5
15 / 3 = 5
пятнадцать разделить на три равно пяти
пять получится пятнадцать трижды
если пятнадцать разделить на три получится пять
если три разделить на пятнадцать получится пять
Деление дает нам частное . В 15 ÷ 3 = 5 частное равно пяти.
В 15 ÷ 3 = 5 частное равно пяти.
Подытожим вышеописанные четыре операции следующим образом:
| операция | результат | ||
|---|---|---|---|
| дополнение | «плюс» | 2 + 2 = 4 | сумма |
| вычитание | «минус» | 5 — 3 = 2 | разница |
| умножение | «раз» | 3 х 5 = 15 | товар |
| отдел | «делится на» | 21/7 = 3 | частное |
=
знак равенства
Знак равенства представляет равенство :
3 + 4 = 7
три плюс четыре равно семь
Обратите внимание, что мы обычно говорим, что равно , НЕ равно:
- два плюс два равно четыре
-
два плюс два равно четырем
меньше
3 три меньше четырех
>
больше
4 > 3
четыре больше трех
≠
НЕ равно
x ≠ z
x не равно z
≥
больше или равно
x ≥ z
x больше или равно z
≤
меньше или равно
z ≤ x
z меньше или равно x
¾
дробь
см.
Умножение и деление рациональных чисел
Содержание урока
- Умножение рациональных чисел
- Деление рациональных чисел
- Многоэтажные дроби
- Использование переменных
- Задания для самостоятельного решения
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь умножать целые числа.
Необходимо также знать основные законы умножения такие как переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и закон умножения на ноль.
Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус:
Решение для данного примера можно записать покороче:
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Решение для данного примера можно записать покороче:
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Первое действие:
Второе действие:
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
Второе действие:
Третье действие:
Четвёртое действие:
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Далее вычисляем выражение по действиям. Сначала вычислим выражения в скобках, и полученные результаты сложим
Первое действие:
Второе действие:
Третье действие:
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичные дроби.
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.
В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Деление рациональных чисел свóдится к умножению этих же чисел. Для этого первую дробь умножают на дробь, обратную второй. Затем применяются правила умножения рациональных чисел.
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Подробное решение выглядит следующим образом:
Короткое решение можно записать так:
Пример 2. Выполнить деление
Короткое решение можно записать так:
Пример 3. Выполнить деление
Выполнить деление
Получили умножение отрицательных рациональных чисел. Выполним данное умножение. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Умнóжим первую дробь на число, обратное числу 4.
Умнóжим первую дробь на число, обратное числу −3
Пример 6. Найти значение выражение −14,4 : 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.
Если нет желания работать с десятичными дробями (а это бывает часто), то эти десятичные дроби можно перевести в смешанные числа, затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4 : 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Пример 8. Найти значение выражения −7,2 : (−0,6)
Это деление отрицательных рациональных чисел. Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.
Перенесём в обеих дробях запятую на одну цифру вправо, получим деление −72:(−6)
Многоэтажные дроби
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной.
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
И далее можно воспользоваться методом деления дробей — умножить первую дробь на дробь, обратную второй.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
Найдём значение переменной A
Найдём значение переменной B
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.
Умножение и деление чисел со знаком
При умножении и делении чисел со знаком мы начинаем с применения операции к абсолютному значению обоих чисел. Если два числа имеют одинаковый знак, ответ будет положительным, если два числа имеют разные знаки, ответ будет отрицательным.
Умножение и деление чисел со знаком Примеры вопросов
Следующие правила показывают, что при одинаковых знаках ответ всегда будет положительным, а при разных знаках ответ всегда будет отрицательным при умножении и делении.
Положительное значение, умноженное на отрицательное, является отрицательным: \((+)(–)=(–)\)
Отрицательное значение, умноженное на положительное, является отрицательным: \((–)(+)=(–)\)
Отрицательное, умноженное на отрицательное, является положительным: \((–)(–)=(+)\)
Положительное, умноженное на положительное, является положительным: \((+)(+)=(+)\)
Положительное деление на минус является минусом: \((+)÷(–)=(–)\)
Отрицательное деление на плюс является минусом: \((–)÷(+)=(–)\)
Отрицательное, деленное на отрицательное, является положительным: \((–)÷(–)=(+)\)
Положительное, деленное на положительное, является положительным: \((+)÷(+)=(+)\ )
Пример: Чему равно произведение \((-5)\) и \((-12)\)?
Мы начнем с применения операции к абсолютному значению двух чисел, то есть \(5·12=60\). Поскольку оба числа отрицательные, а отрицательное, умноженное на отрицательное, равно положительному, ответ будет положительным \(60\).
Поскольку оба числа отрицательные, а отрицательное, умноженное на отрицательное, равно положительному, ответ будет положительным \(60\).
Пример: Чему равно произведение \(17\) и \((-34)\)?
Мы начнем с перемножения \(17\) и \(34\), что равно \(578\). Поскольку два числа имеют противоположные знаки и положительное число, умноженное на отрицательное, является отрицательным, знак ответа будет отрицательным. Следовательно, произведение \(17\) и \((-34)\) равно \(-578\).
Пример: Сколько \(-700\) разделить на \(-14\)?
Сначала мы применяем операцию к абсолютному значению обоих членов, которое равно \(700÷14=50\). Поскольку оба числа отрицательные, а отрицательное, деленное на отрицательное, является положительным, знак ответа положительный. Следовательно, \(-700\), деленное на \(-14\), будет положительным \(50\).
Пример: Найдите частное: \(480÷(-30)\).
Чтобы найти частное между \(480\) и \((-30)\), мы начнем с деления абсолютного значения двух чисел, которое равно \(480÷30=16\). Поскольку два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, частное \(480(-30)=-16\).
Поскольку два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, частное \(480(-30)=-16\).
Пример: Вычислите выражение \([15÷(-3)](-7)\).
Чтобы вычислить выражение, мы начинаем с вычисления выражения в скобках на основе правил порядка операций. Значение \(15\), деленное на \(-3\), можно рассчитать, применив операцию к абсолютному значению двух чисел, которое равно \(15÷3=5\). Поскольку два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, частное между \(15\) и \(-3\) равно \(-5\). Теперь нам нужно оценить \((-5)(-7)\). Начнем с применения операции к абсолютному значению двух чисел, которое равно \(57=35\). Поскольку два числа имеют одинаковый знак, а отрицательное, умноженное на отрицательное, является положительным, произведение \(-5\) и \(-7\) является положительным \(35\).
Пример: Вычислите выражение \(108÷[(-3)(6)]\).
Чтобы вычислить выражение, мы будем следовать порядку правил операций и начнем с вычисления выражения в скобках. Произведение \(-3\) и \(6\) можно получить, умножив абсолютное значение двух чисел, которое равно \(36=18\). Поскольку два числа имеют разные знаки и отрицательное число, умноженное на положительное, является отрицательным, произведение равно \(-18\). Теперь мы оценим \(108÷(-18)\). Чтобы найти частное \(108\) и \(-18\), мы начнем с применения операции к абсолютному значению двух чисел, которое равно \(108÷18\), что равно \(6\) . Так как два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, ответ будет равен \(-6\).
Произведение \(-3\) и \(6\) можно получить, умножив абсолютное значение двух чисел, которое равно \(36=18\). Поскольку два числа имеют разные знаки и отрицательное число, умноженное на положительное, является отрицательным, произведение равно \(-18\). Теперь мы оценим \(108÷(-18)\). Чтобы найти частное \(108\) и \(-18\), мы начнем с применения операции к абсолютному значению двух чисел, которое равно \(108÷18\), что равно \(6\) . Так как два числа имеют разные знаки, а положительное, деленное на отрицательное, является отрицательным, ответ будет равен \(-6\).
Вот несколько примеров вопросов на умножение и деление чисел со знаком.
Вопрос №1:
Чему равно произведение \(19\) и \((-23)\)?
\(-437\)
\(-4\)
\(42\)
\(437\)
Показать ответ
Ответ:
\) и \(-23\), мы начнем с применения операции к абсолютному значению двух чисел, которое равно \(19·23=437\). Далее определяем, каков знак ответа, следуя правилам умножения чисел со знаком. Поскольку числа имеют разные знаки и положительное умножение на отрицательное является отрицательным, произведение \(19\) и \(-23\) равно \(-437\).
Далее определяем, каков знак ответа, следуя правилам умножения чисел со знаком. Поскольку числа имеют разные знаки и положительное умножение на отрицательное является отрицательным, произведение \(19\) и \(-23\) равно \(-437\).
Скрыть ответ
Вопрос № 2:
Найдите продукт: \((-25)(-16)\).
\(-400\)
\(-9\)
\(41\)
\(400\)
Показать ответ
Ответ:
Чтобы найти произведение \(-25\) и \(-16\), мы начнем с умножения абсолютного значения двух членов, которое равно \(25·16=400\). Поскольку два члена являются отрицательными, а отрицательное, умноженное на отрицательное, является положительным, произведение \(-25\) и \(-16\) является положительным \(400\).
Скрыть ответ
Вопрос №3:
Найдите частное между \(-420\) и \(21\).
\(-399\)
\(-20\)
\(20\)
\(399\)
Показать ответ
Ответ:
Чтобы найти частное \(-420\) и \(21\), мы начнем с нахождения частного абсолютного значения двух членов, которые равно \(420÷21=20\). Поскольку два числа имеют разные знаки, а отрицательное, деленное на положительное, равно отрицательному, ответ будет отрицательным. Следовательно, частное \(-420\) и \(21\) равно \(-20\).
Скрыть ответ
Вопрос №4:
Что такое \((-655)÷(-5)\)?
\(-660\)
\(-131\)
\(131\)
\(660\)
Показать ответ
Ответ:
Чтобы найти значение 9003 65\div-5\), мы начинаем с применения операции к абсолютному значению двух чисел, которое равно \(655÷5=131\). Поскольку два числа имеют одинаковый знак, а отрицательное, деленное на отрицательное, является положительным, частное \(-655\) и \(-5\) положительное \(131\).
Поскольку два числа имеют одинаковый знак, а отрицательное, деленное на отрицательное, является положительным, частное \(-655\) и \(-5\) положительное \(131\).
Скрыть ответ
Вопрос №5:
Вычислить: \([4·(-3)]÷(-2)\).
\(-24\)
\(-6\)
\(6\)
\(24\)
Показать ответ
Ответ:
порядок правил работы и начните с вычисления выражения в скобках. Чтобы найти произведение \(4\) и \(-3\), мы начинаем с умножения абсолютного значения двух чисел, которое равно \(4\times3=12\). Поскольку два числа имеют разные знаки, а положительное, умноженное на отрицательное, является отрицательным, ответ будет \(-12\). Теперь мы должны вычислить \(-12÷(-2)\). Чтобы найти частное, мы начнем с применения операции к абсолютному значению двух чисел, которое равно \(12÷2\), что равно \(6\). Поскольку два числа имеют одинаковый знак, а отрицательное, деленное на отрицательное, является положительным, ответ будет положительным \(6\).
Поскольку два числа имеют одинаковый знак, а отрицательное, деленное на отрицательное, является положительным, ответ будет положительным \(6\).
Hide Ответ
Возврат к математическим вопросам
Умножение и разделите целые числа — минута математика
. Темы, указанные в этом разделе:
- Multy Entegers
- Divide Integers
- Упрощенные. переменные выражения с целыми числами
- Преобразование словосочетаний в алгебраические выражения
Поскольку умножение является математическим сокращением для многократного сложения, наша модель счетчика может быть легко применена для демонстрации умножения целых чисел. Давайте посмотрим на эту конкретную модель, чтобы увидеть, какие закономерности мы замечаем. Мы будем использовать те же примеры, что и для сложения и вычитания.
Мы помним, что $a \cdot b$ означает добавление $a, b$ раз. Здесь мы используем модель, показанную ниже, чтобы помочь нам обнаружить закономерность.
Здесь мы используем модель, показанную ниже, чтобы помочь нам обнаружить закономерность.
Теперь подумайте, что значит умножить $5$ на $-3$. Это означает вычитание $5, 3$ раз. Рассматривая вычитание как , убирающее , это означает отнять 5, 3$ раз. Но отнимать нечего, поэтому начинаем с добавления нейтральных пар, как показано на рисунке ниже.
В обоих случаях мы начали с нейтральных пар по 15$. В случае слева мы отнимали $5,3$ раз и в результате получилось $-15$. Чтобы умножить $(−5)(−3)$, мы убрали $−5,3$ раз, и в результате получилось 15$. Итак, мы обнаружили, что
| $5 \cdot 3 = 15$ | $-5(3)=-15$ |
| $5(-3)=-15$ | $(-5)(-3)=15 $ |
Обратите внимание, что при умножении двух чисел со знаком, когда знаки совпадают, произведение положительное, а когда знаки разные, произведение отрицательное.
УМНОЖЕНИЕ ЧИСЕЛ СО ЗНАКОМ Знак произведения двух чисел зависит от их знаков.
| Same signs | Product |
|---|---|
| 1. Two positives 2. Two negatives | Positive Positive |
| Different signs | Product |
|---|---|
| 1. Positive $\ cdot$ отрицательный 2. отрицательный $\cdot$ положительный | отрицательный отрицательный |
| Part 1. | $-9 \cdot 3$ |
| Умножьте, заметив, что знаки разные, поэтому произведение отрицательное. | $-27$ |
| Часть 2. | $-2(-5)$ |
| Умножьте, заметив, что знаки одинаковы, поэтому произведение положительно. | $10$ |
Часть 3. | $4(-8)$ |
| Умножьте, заметив, что знаки разные, поэтому произведение отрицательное. | $-32$ |
| Часть 4. | $7 \cdot 6$ |
| Знаки одинаковые, поэтому произведение положительное. | $42$ |
Когда мы умножаем число на $1$, получается одно и то же число. Что произойдет, если мы умножим число на $-1$? Давайте умножим положительное число, а затем отрицательное число на $-1$ и посмотрим, что получится.
| $-1 \cdot 4$ | $-1(-3)$ |
| $-4$ | $3$ |
| $-4$ is the opposite of $4$ | $3$ противоположно $-3$ |
Каждый раз, когда мы умножаем число на $-1$, мы получаем его противоположность.
Умножение на $-1$Умножение числа на $-1$ дает его противоположность.
$-1a = -a$
Пример 2Умножьте каждое из следующих значений:
- $ -1 \ CDOT 7 $
- $ -1 (-11) $
Часть 1. | ||||||||||||||||||||||||||||||||||||||||||||||||
| $-1 \cdot 7$ | |
| Обратите внимание, что $-7$ противоположно $7$. | $-7$ |
| Часть 2. | |
| Знаки одинаковые, поэтому произведение будет положительным. | $-1(-11)$ |
| Обратите внимание, что $11$ противоположно $-11$. | $11$ |
Деление — операция, обратная умножению. Таким образом, $15 \div 3=5$, потому что $5 \cdot 3=15$. На словах это выражение говорит о том, что $15$ можно разделить на $3$ группы по $5$ в каждой, потому что сложение пятикратного трижды дает $15$. Если мы посмотрим на некоторые примеры умножения целых чисел, то сможем выяснить правила деления целых чисел.
| $5 \cdot 3 = 15$, поэтому $15 \div 3 = 5$ | $-5(3)=-15$, поэтому $-15 \div 3 = -5$ |
| $(- 5)(-3)=15$, так что $15 \div (-3) = -5$ | $5(-3)=-15$, поэтому $-15 \div -3 = 5$ |
числа со знаком подчиняются тем же правилам, что и умножение. Когда знаки одинаковые, частное положительное, а когда знаки разные, частное отрицательное.
РАЗДЕЛЕНИЕ ЗНАКОВЗнак частного двух чисел зависит от их знаков.
| Same signs | Quotient |
|---|---|
| 1. Two Positives 2. Two Negatives | Positive Positive |
| Same signs | Quotient |
|---|---|
| 1 , Положительный и отрицательный 2. Отрицательный и положительный | Отрицательный Отрицательный |
Помните, что вы всегда можете проверить решение задачи на деление путем умножения.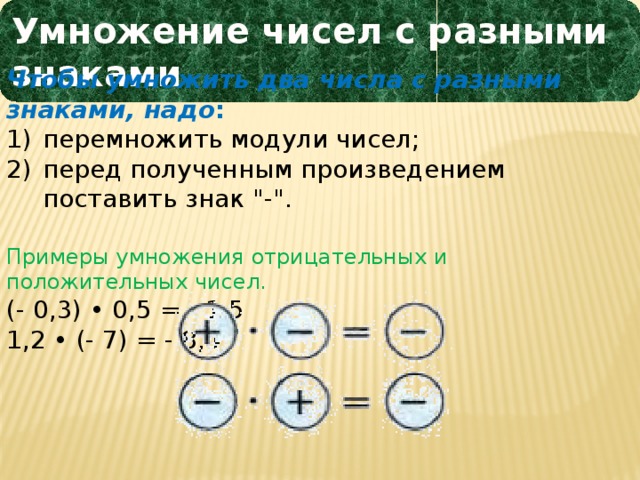
Divide each of the following:
- $-27 \div 3$
- $-100 \div (-4)$
| Part 1. | $-27 \div 3$ |
| Разделите, заметив, что знаки разные и частное отрицательное. | $-9$ |
| Часть 2. | $-100 \div (-4)$ |
| Разделите, заметив, что знаки одинаковы, а значит, частное положительно. | $25$ |
Так же, как мы видели с умножением, когда мы делим число на $1$, результатом является то же самое число. Что происходит, когда мы делим число на $-1$? Давайте разделим положительное число, а затем отрицательное число на $-1$, чтобы увидеть, что мы получим.
| $8 \дел (-1)$ | $-9 \дел (-1)$ |
| $-8$ | $9$ |
| $-8$ противоположно $8$ | $9$ противоположно $-9$ |
1$, получаем обратное.
Деление числа на $-1$ дает противоположное значение.
$a \div (-1) = -a$
Пример 4Разделите каждое из следующих чисел:
- $16 \div (-1)$
- $-20 \div (-1) $
| Часть 1. | $16 \дел (-1)$ |
| Дивиденд $16$ делится на $-1$. | $-16$ |
| Деление числа на $-1$ дает противоположное число. | |
| Обратите внимание, что знаки были другими, поэтому результат был отрицательным. | |
| Часть 2. | $-20 \дел (-1)$ |
| Дивиденд, $-20$, делится на $-1$. | $20$ |
| Деление числа на $-1$ дает противоположное число. |
Обратите внимание, что знаки были одинаковыми, поэтому частное было положительным.
3. 4.3 Упрощение выражений с помощью целых чисел
4.3 Упрощение выражений с помощью целых чисел Теперь мы упростим выражения, в которых используются все четыре операции — сложение, вычитание, умножение и деление — с целыми числами. Не забывайте соблюдать порядок действий.
Пример 5Упрощение: $7(-2)+4(-7)-6$ 9{4}$
Упрощение: $12-3(9-12)$.
В соответствии с порядком операций сначала упрощаем скобки. Затем мы умножим и, наконец, вычтем. 9{3}$
Упрощение: $-30 \div 2 +(-3)(-7)$.
РешениеСначала мы будем умножать и делить слева направо. Потом добавим.
| $-30 \дел 2+(-3)(-7)$ | |
| Разделить. | $-15+(-3)(-7)$ |
| Умножить. | $-15+21$ |
Доп. | $6$ |
Теперь мы можем вычислять выражения, которые включают умножение и деление с целыми числами. Помните, что для вычисления выражения подставьте числа вместо переменных, а затем упростите.
9{2}-3\cdot-4+8$.
Пример 11 Оценить $3x+4y-6$, когда $x=-1$ и $y=2$.
| $3x+4y-6$ | |
| Подставьте $x=-1$ и $y=2$. | $3(-1)+4(2)-6$ |
| Умножить. | $-3+8-6$ |
| Упрощение. | $-1$ |
Опять же, вся наша предыдущая работа по переводу слов в алгебру переносится на фразы, которые включают как умножение, так и деление целых чисел. Помните, что ключевым словом для умножения является произведение , а для деления частное .
Пример 12 Переведите в алгебраическое выражение и, если возможно, упростите: произведение $-2$ и $14$.
Слово произведение говорит нам умножать.
| произведение $-2$ и $14$ | |
| Перевести. | $(-2)(14)$ |
| Упрощение. | $-28$ |
Переведите в алгебраическое выражение и упростите, если возможно: частное $-56$ и $-7$.
РешениеСлово частное говорит нам делить.
| частное $-56$ и $-7$ | |
| Перевод. | $-56 \дел (-7)$ |
| Упрощение. | $ 8 $ |
CC Лицензированный контент, оригинал
- 777777777777777771777177777177717777177717771777177717717777717717717 71717. Предоставлено: Minute Math. Лицензия: CC BY 4.0
CC Лицензионный контент, совместно используемый ранее
- Маречек, Л.


