Рациональные числа
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Содержание статьи
1. Определение рациональных чисел
2. Как определить, является ли число рациональным
Определение рациональных чисел
Определение 1
К рациональным числам относятся числа, которые можно представить как положительную или отрицательную обыкновенную дробь или число нуль.
К рациональным числам относятся:
- Натуральные числа, которые можно представить как обыкновенную дробь. Например, $7=\frac{7}{1}$.
- Целые числа, включая число нуль, которые можно представить как положительную или отрицательную обыкновенную дробь, или как нуль. Например, $19=\frac{19}{1}$, $-23=-\frac{23}{1}$.

- Обыкновенные дроби (положительные или отрицательные).
- Смешанные числа, которые можно представить как неправильную обыкновенную дробь. Например, $3 \frac{11}{13}=\frac{33}{13}$ и $-2 \frac{4}{5}=-\frac{14}{5}$.
- Конечная десятичная дробь и бесконечная периодическая дробь, которую можно представить как обыкновенную дробь. Например, $-7,73=-\frac{773}{100}$, $7,(3)=-7 \frac{1}{3}=-\frac{22}{3}$.
Замечание 1
Заметим, что бесконечная непериодическая десятичная дробь не относится к рациональным числам, т.к. ее нельзя представить как обыкновенную дробь.
Пример 1
Натуральные числа $7, 670, 21 \ 456$ являются рациональными.
Целые числа $76, –76, 0, –555 \ 666$ – рациональные.
Обыкновенные дроби $\frac{7}{11}$, $\frac{555}{4}$, $-\frac{7}{11}$, $-\frac{100}{234}$ – рациональные числа.
Таким образом, рациональные числа делятся на положительные и отрицательные. Число нуль является рациональным, но не относится ни к положительным, ни к отрицательным рациональным числам.
Сформулируем более краткое определение рациональных чисел.
Определение 2
Рациональными называются числа, которые могут быть записаны в виде дроби $\frac{m}{n}$ с целым числом в числителе и натуральным числом в знаменателе.
Определение 3
Рациональными называют числа, которые могут быть представлены в виде конечной или бесконечной периодической десятичной дроби.
Можно сделать следующие выводы:
- положительные и отрицательные целые и дробные числа относятся к множеству рациональных чисел;
- рациональные числа могут быть представлены в виде дроби, у которой целый числитель и натуральный знаменатель и которая является рациональным числом;
- рациональные числа могут быть представлены в виде любой периодической десятичной дроби, которая является рациональным числом.
Как определить, является ли число рациональным
- Число задано в виде числового выражения, которое состоит только из рациональных чисел и знаков арифметических операций.
 3$.
3$.
На числовой оси рациональные числа располагаются повсюду плотно: между каждыми двумя рациональными числами, которые не равны друг другу, можно расположить хотя бы одно рациональное число (следовательно, и бесконечное множество рациональных чисел). В то же время, множество рациональных чисел характеризуется счетной мощностью (т. е. все элементы множества можно пронумеровать). Древние греки доказали, что существуют числа, которые невозможно записать как дробь. Они показали, что не существует такое рациональное число, квадрат которого равен $2$. Тогда рациональных чисел оказалось недостаточно для выражения всех величин, что и привело в дальнейшем к появлению вещественных чисел. Множество рациональных чисел, в отличие от вещественных чисел, является нульмерным.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 20.06.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Рациональные числа — онлайн справочник для студентов
Определение
Рациональная дробь является выражением формы
\(\frac { m } { n }\)
, где целое число m называется числителем дроби, а натуральное число n является знаменателем дроби.
Рациональные числа — это положительные и отрицательные числа (целые и дробные) и ноль.
Множество рациональных чисел обозначается Q.
Две рациональные дроби \(\frac { m } { n } _ { и } \frac { p } { q }\) называются эквивалентными, если \(\ m q = n p\)
Пример
Дроби \(\frac { 2 } { 3 } и \frac { 4 } { 6 }\) эквивалент, так как \(\ 2 \cdot 6 = 3 \cdot 4\)
Рациональное число — это множество всех эквивалентных дробей.
Рациональные числа сравниваются следующим образом:
1.Каждое положительное рациональное число больше нуля.
2.Каждое отрицательное рациональное число меньше нуля.
3.Из двух отрицательных чисел одно с абсолютным значением меньше.
Пример
\(\ 6 > 0 ; — 5 — 3 ; — 7 | — 2 | = 2\)
Арифметические операции с рациональными числами
Добавление рациональных чисел. Чтобы добавить рациональные числа с одинаковыми знаками, добавьте их абсолютные значения и поставьте их общий знак перед суммой.
Чтобы сложить два рациональных числа с разными знаками, необходимо вычесть из числа с большим абсолютным значением число с меньшим абсолютным значением и поставить знак числа с наибольшим абсолютным значением.
Пример
\(\ 4 + \frac { 5 } { 2 } = + \left( | 4 | + \left| \frac { 5 } { 2 } \right| \right) = + \left( 4 + \frac { 5 } { 2 } \right) = \frac { 8 } { 2 } + \frac { 5 } { 2 } = \frac { 13 } { 2 }\)
\(\ — 4 + \left( — \frac { 5 } { 2 } \right) = — \left( | — 4 | + \left| — \frac { 5 } { 2 } \right| \right) = — \left( 4 + \frac { 5 } { 2 } \right) = — \left( \frac { 8 } { 2 } + \frac { 5 } { 2 } \right) = — \frac { 13 } { 2 }\)
\(\ — 4 + \frac { 5 } { 2 } = — \left( | — 4 | — \left| \frac { 5 } { 2 } \right| \right) = — \left( 4 — \frac { 5 } { 2 } \right) = — \left( \frac { 8 } { 2 } — \frac { 5 } { 2 } \right) = — \frac { 3 } { 2 }\)
Вычитание рациональных чисел. Чтобы вычесть одно рациональное число из другого, достаточно добавить противоположное число к вычтенному к уменьшенному.Пример
\(\frac { 3 } { 4 } \cdot \left( — \frac { 7 } { 2 } \right) = — \left| \frac { 3 } { 4 } \right| \cdot \left| — \frac { 7 } { 2 } \right| = — \frac { 3 } { 4 } \cdot \frac { 7 } { 2 } = — \frac { 21 } { 8 }\)
\(\left( — \frac { 3 } { 4 } \right) \cdot \left( — \frac { 7 } { 2 } \right) = + \left| — \frac { 3 } { 4 } \right| \cdot \left| — \frac { 7 } { 2 } \right| = \frac { 3 } { 4 } \cdot \frac { 7 } { 2 } = \frac { 21 } { 8 }\)
\(\left( — \frac { 3 } { 4 } \right) \cdot \frac { 7 } { 2 } = — \left| — \frac { 3 } { 4 } \right| \cdot \left| \frac { 7 } { 2 } \right| = — \frac { 3 } { 4 } \cdot \frac { 7 } { 2 } = — \frac { 21 } { 8 }\)
Умножение рациональных чисел. Чтобы умножить два рациональных числа, необходимо умножить их абсолютные значения и поставить знак плюс перед результатом, если оба фактора имеют одинаковые знаки, или минус, если факторы имеют разные знаки.
Чтобы умножить два рациональных числа, необходимо умножить их абсолютные значения и поставить знак плюс перед результатом, если оба фактора имеют одинаковые знаки, или минус, если факторы имеют разные знаки.
Пример
\(\ ( — 12 ) : 3 = — | — 12 | : | 3 | = — 12 : 3 = — 4\)
\(\ 12 : ( — 3 ) = — | 12 | : | — 3 | = — 12 : 3 = — 4\)
\(\ ( — 12 ) : ( — 3 ) = + | — 12 | : | — 3 | = 12 : 3 = 4\)
Деление рациональных чисел. Частное от деления двух рациональных чисел с одинаковыми знаками равно частному их абсолютных величин, взятому со знаком плюс.
Частное от деления двух рациональных чисел с разными знаками равно частному их абсолютных величин, взятому со знаком минус.
Пример
\(\ 12 : ( — 3 ) = — | 12 | : | — 3 | = — 12 : 3 = — 4\)
\(\ ( — 12 ) : ( — 3 ) = + | — 12 | : | — 3 | = 12 : 3 = 4\)
Возведение. { 4 } = \frac { 16 } { 81 }\)
{ 4 } = \frac { 16 } { 81 }\)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Целые числа Взаимно простые числа Простые и составные числа Натуральные числа
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Рациональное число
)- это числа с положительным или отрицательным знаком (целые и дробные) и ноль.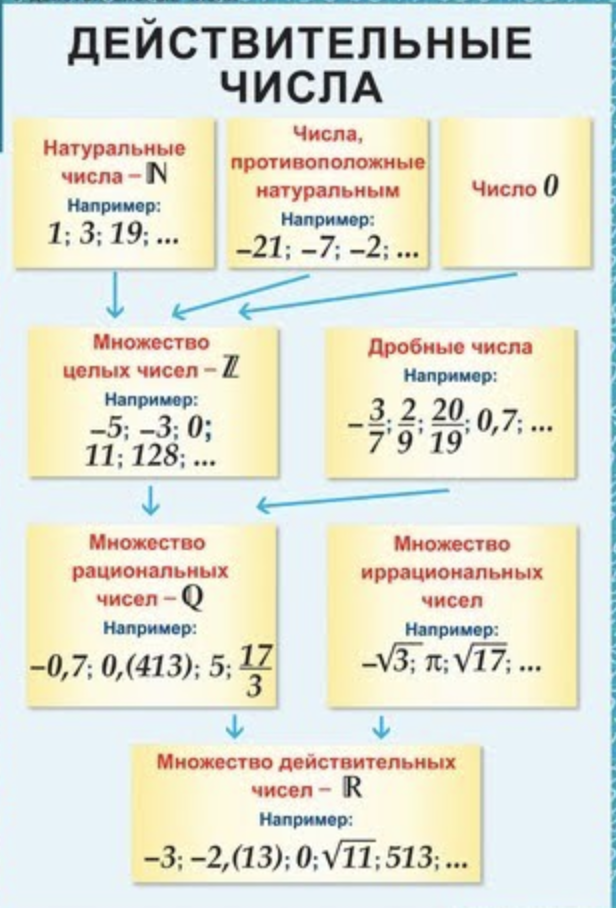 Более точное понятие рациональных чисел, звучит так:
Более точное понятие рациональных чисел, звучит так:
Рациональное число — число, которое представляется обычной дробью m/n , где числитель m — целые числа, а знаменатель n — натуральные числа, к примеру 2/3 .
Бесконечные непериодические дроби НЕ входят в множество рациональных чисел.
a/b , где a ∈ Z (a принадлежит целым числам), b ∈ N (b принадлежит натуральным числам).
Использование рациональных чисел в реальной жизни.
В реальной жизни множество рациональных чисел используется для счёта частей некоторых целых делимых объектов, например , тортов или других продуктов, которые разрезаются на части перед употреблением, или для грубой оценки пространственных отношений протяжённых объектов.
Свойства рациональных чисел.
Основные свойства рациональных чисел.
1. Упорядоченность a и b есть правило, которое позволяет однозначно идентифицировать между ними 1-но и только одно из 3-х отношений: «» либо «=». Это правило — правило упорядочения и формулируют его вот так:
Это правило — правило упорядочения и формулируют его вот так:
- 2 положительных числа a=m a /n a и b=m b /n b связаны тем же отношением, что и 2 целых числа m a ⋅ n b и m b ⋅ n a ;
- 2 отрицательных числа a и b связаны одним отношением, что и 2 положительных числа |b| и |a| ;
- когда a положительно, а b — отрицательно, то a>b .
∀ a,b ∈ Q (a∨ a>b ∨ a=b)
2. Операция сложения . Для всех рациональных чисел a и b есть правило суммирования , которое ставит им в соответствие определенное рациональное число c . При этом само число c — это сумма чисел a и b и ее обозначают как (a+b) суммирование .
Правило суммирования выглядит так:
m a /n a +m b /n b =(m a ⋅ n b +m b ⋅ n a) /(n a ⋅ n b).
∀ a,b ∈ Q ∃ !(a+b) ∈ Q
3. Операция умножения . Для всяких рациональных чисел a и b есть правило умножения , оно ставит им в соответствие определенное рациональное число c . Число c называют произведением чисел a и b и обозначают (a⋅b) , а процесс нахождения этого числа называют умножение .
Правило умножения выглядит так: m a n a ⋅ m b n b =m a ⋅ m b n a ⋅ n b .
∀a,b∈Q ∃(a⋅b)∈Q
4. Транзитивность отношения порядка. Для любых трех рациональных чисел a , b и c если a меньше b и b меньше c , то a меньше c , а если a равно b и b равно c , то a равно c .
∀ a,b,c ∈ Q (a∧ b⇒ a∧ (a = b ∧ b = c ⇒ a = c)
5. Коммутативность сложения . От перемены мест рациональных слагаемых сумма не изменяется.
Коммутативность сложения . От перемены мест рациональных слагаемых сумма не изменяется.
∀ a,b ∈ Q a+b=b+a
6. Ассоциативность сложения . Порядок сложения 3-х рациональных чисел не оказывает влияния на результат.
∀ a,b,c ∈ Q (a+b)+c=a+(b+c)
7. Наличие нуля . Есть рациональное число 0, оно сохраняет всякое другое рациональное число при складывании.
∃ 0 ∈ Q ∀ a ∈ Q a+0=a
8. Наличие противоположных чисел . У любого рационального числа есть противоположное рациональное число, при их сложении получается 0.
∀ a ∈ Q ∃ (−a) ∈ Q a+(−a)=0
9. Коммутативность умножения . От перемены мест рациональных множителей произведение не изменяется.
∀ a,b ∈ Q a ⋅ b=b ⋅ a
10. Ассоциативность умножения . Порядок перемножения 3-х рациональных чисел не имеет влияния на итог.
∀ a,b,c ∈ Q (a ⋅ b) ⋅ c=a ⋅ (b ⋅ c)
11. Наличие единицы . Есть рациональное число 1, оно сохраняет всякое другое рациональное число в процессе умножения.
∃ 1 ∈ Q ∀ a ∈ Q a ⋅ 1=a
12. Наличие обратных чисел . Всякое рациональное число, отличное от нуля имеет обратное рациональное число, умножив на которое получим 1.
∀ a ∈ Q ∃ a−1 ∈ Q a ⋅ a−1=1
13. Дистрибутивность умножения относительно сложения . Операция умножения связана со сложением при помощи распределительного закона:
Дистрибутивность умножения относительно сложения . Операция умножения связана со сложением при помощи распределительного закона:
∀ a,b,c ∈ Q (a+b) ⋅ c=a ⋅ c+b ⋅ c
14. Связь отношения порядка с операцией сложения . К левой и правой частям рационального неравенства прибавляют одно и то же рациональное число.
∀ a,b,c ∈ Q a⇒ a+c
15. Связь отношения порядка с операцией умножения . Левую и правую части рационального неравенства можно умножить на одинаковое неотрицательное рациональное число.
∀ a,b,c ∈ Q c>0 ∧ a⇒ a ⋅ c⋅ c
16. Аксиома Архимеда . Каким бы ни было рациональное число a , легко взять столько единиц, что их сумма будет больше a .
Определение рациональных чисел
К рациональным числам относятся:
- Натуральные числа, которые можно представить как обыкновенную дробь. Например, $7=\frac{7}{1}$.
- Целые числа, включая число нуль, которые можно представить как положительную или отрицательную обыкновенную дробь, или как нуль. Например, $19=\frac{19}{1}$, $-23=-\frac{23}{1}$.
- Обыкновенные дроби (положительные или отрицательные).
- Смешанные числа, которые можно представить как неправильную обыкновенную дробь. Например, $3 \frac{11}{13}=\frac{33}{13}$ и $-2 \frac{4}{5}=-\frac{14}{5}$.
- Конечная десятичная дробь и бесконечная периодическая дробь, которую можно представить как обыкновенную дробь. Например, $-7,73=-\frac{773}{100}$, $7,(3)=-7 \frac{1}{3}=-\frac{22}{3}$.
Замечание 1
Заметим, что бесконечная непериодическая десятичная дробь не относится к рациональным числам, т. к. ее нельзя представить как обыкновенную дробь.
к. ее нельзя представить как обыкновенную дробь.
Пример 1
Натуральные числа $7, 670, 21 \ 456$ являются рациональными.
Целые числа $76, –76, 0, –555 \ 666$ – рациональные.
Обыкновенные дроби $\frac{7}{11}$, $\frac{555}{4}$, $-\frac{7}{11}$, $-\frac{100}{234}$ – рациональные числа.
Таким образом, рациональные числа делятся на положительные и отрицательные. Число нуль является рациональным, но не относится ни к положительным, ни к отрицательным рациональным числам.
Сформулируем более краткое определение рациональных чисел.
Определение 3
Рациональными называют числа, которые могут быть представлены в виде конечной или бесконечной периодической десятичной дроби.
Можно сделать следующие выводы:
- положительные и отрицательные целые и дробные числа относятся к множеству рациональных чисел;
- рациональные числа могут быть представлены в виде дроби, у которой целый числитель и натуральный знаменатель и которая является рациональным числом;
- рациональные числа могут быть представлены в виде любой периодической десятичной дроби, которая является рациональным числом.
 3$.
3$. - Упорядоченность . a и b существует правило, позволяющее однозначно идентифицировать между ними одно и только одно из трёх отношений : «
» или « =
».
 Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″>
Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″>Суммирование дробей
- Операция сложения . Для любых рациональных чисел a и b существует так называемое правило суммирования c . При этом само число c называется суммой чисел a и b и обозначается , а процесс отыскания такого числа называется суммированием . Правило суммирования имеет следующий вид: .
- Операция умножения . Для любых рациональных чисел a и b существует так называемое правило умножения , которое ставит им в соответствие некоторое рациональное число c .
 При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: .
При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: . - Транзитивность отношения порядка. Для любой тройки рациональных чисел a , b и c если a меньше b и b меньше c , то a меньше c , а если a равно b и b равно c , то a равно c . 6435″>Коммутативность сложения. От перемены мест рациональных слагаемых сумма не меняется.
- Ассоциативность сложения. Порядок сложения трёх рациональных чисел не влияет на результат.
- Наличие нуля . Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
- Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0.

- Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
- Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
- Наличие единицы . Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
- Наличие обратных чисел . Любое рациональное число имеет обратное рациональное число, при умножении на которое даёт 1.
- Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона:
- Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства можно прибавлять одно и то же рациональное число. /pictures/wiki/files/51/358b88fcdff63378040f8d9ab9ba5048.png» border=»0″>
- Аксиома Архимеда . Каково бы ни было рациональное число a , можно взять столько единиц, что их сумма превзойдёт a .
 src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″>
src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″> - И.Кушнир. Справочник по математике для школьников. — Киев: АСТАРТА, 1998. — 520 с.
- П. С. Александров. Введение в теорию множеств и общую топологию. — М.: глав. ред. физ.-мат. лит. изд. «Наука», 1977
- И. Л. Хмельницкий. Введение в теорию алгебраических систем
- 2 положительных числа a=m a /n a и b=m b /n b связаны тем же отношением, что и 2 целых числа m a ⋅ n b и m b ⋅ n a ;
- 2 отрицательных числа a и b связаны одним отношением, что и 2 положительных числа |b| и |a| ;
- когда a положительно, а b — отрицательно, то a>b .

- Упорядоченность . a и b существует правило, позволяющее однозначно идентифицировать между ними одно и только одно из трёх отношений : «
» или « =
».
 Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″>
Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″>Суммирование дробей
- Операция сложения . Для любых рациональных чисел a и b существует так называемое правило суммирования c . При этом само число c называется суммой чисел a и b и обозначается , а процесс отыскания такого числа называется суммированием . Правило суммирования имеет следующий вид: .
- Операция умножения . Для любых рациональных чисел a и b существует так называемое правило умножения , которое ставит им в соответствие некоторое рациональное число c .
 При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: .
При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: . - Транзитивность отношения порядка. Для любой тройки рациональных чисел a , b и c если a меньше b и b меньше c , то a меньше c , а если a равно b и b равно c , то a равно c . 6435″>Коммутативность сложения. От перемены мест рациональных слагаемых сумма не меняется.
- Ассоциативность сложения. Порядок сложения трёх рациональных чисел не влияет на результат.
- Наличие нуля . Существует рациональное число 0, которое сохраняет любое другое рациональное число при суммировании.
- Наличие противоположных чисел. Любое рациональное число имеет противоположное рациональное число, при суммировании с которым даёт 0.

- Коммутативность умножения. От перемены мест рациональных множителей произведение не меняется.
- Ассоциативность умножения. Порядок перемножения трёх рациональных чисел не влияет на результат.
- Наличие единицы . Существует рациональное число 1, которое сохраняет любое другое рациональное число при умножении.
- Наличие обратных чисел . Любое рациональное число имеет обратное рациональное число, при умножении на которое даёт 1.
- Дистрибутивность умножения относительно сложения. Операция умножения согласована с операцией сложения посредством распределительного закона:
- Связь отношения порядка с операцией сложения. К левой и правой частям рационального неравенства можно прибавлять одно и то же рациональное число. /pictures/wiki/files/51/358b88fcdff63378040f8d9ab9ba5048.png» border=»0″>
- Аксиома Архимеда . Каково бы ни было рациональное число a , можно взять столько единиц, что их сумма превзойдёт a .
 src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″>
src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″> - И.Кушнир. Справочник по математике для школьников. — Киев: АСТАРТА, 1998. — 520 с.
- П. С. Александров. Введение в теорию множеств и общую топологию. — М.: глав. ред. физ.-мат. лит. изд. «Наука», 1977
- И. Л. Хмельницкий. Введение в теорию алгебраических систем
- белая машина → 1
- синяя машина → 2
- красная машина → 3
- Они оба имеют бесконечный размер, так что же именно мы пытаемся сравнить??
- Очевидно, что множество целых чисел строго больше, поскольку множество натуральных чисел является его строгим подмножеством.
- Для каждого четного натурального числа n = 2k , где k — натуральное число, положим f(n) = f(2k) = k .
- Для каждого нечетного натурального числа n = 2k-1 , где k — натуральное число, положим f(n) = f(2k-1) = -k .
- 1 → (1,1)
- 2 → (1,2)
- 3 → (2,1)
- 4 → (1,3)
- 5 → (2,2)
- 6 → (3,1)
- 7 → (1,4)
- 8 → (2,3)
- f (1) = 1/1 = 1
- f (2) = 1/2
- f (3) = 2 /1 = 2
- f (4) = 1/3
- ̶f̶(̶5̶)̶ ̶=̶ ̶2̶/̶2̶ ̶=̶ ̶1̶ (поскольку число 1 уже появилось в нашей последовательности)
- f 1 (5) = 3/1 = 3
- f (6) = 1/4
- f (7) = 2/3
- h (0) = 0,
- h (2 n ) = F ( N ), для каждого натурального числа N > 0,
- H (2 N -1) = G ( N ) = — F ( n ), для каждого натурального числа n > 0.

- 1 Дополнение
- 2 Вычитание
- 3 Умножение
- 4-й отдел
- 5 Десятичное представление рациональных чисел
- 6 Внешние ссылки
- [math]\displaystyle{ \large \frac{A}{B} + \frac{C}{D} = \frac{AD+BC}{BD} }[/math]
- [математика]\displaystyle{ \large \frac{A}{B} — \frac{C}{D} = \frac{AD-BC}{BD} }[/math]
- [math]\displaystyle{ \large \frac{A}{B}\frac{C}{D} = \frac{AC}{BD} }[/math]
- [math]\displaystyle{ \large \frac{A}{B}/\frac{C}{D} = \frac{AD}{BC} }[/math]
- [математика]\displaystyle{ \large a + \frac{k(ba)}{n+1} }[/math]
- Рациональное число
- Целое число
- натуральный
- Четный
- Нечетный
- Рационал
- Иррациональный
- Реальный
- Прайм
- Вероятное простое число
- Мерсенн 2 n -1
- Ферма 2 2 п +1
- Proth k •2 n +1
- Ризель k •2 n -1
- Woodall n •2 n -1
- Каллен n •2 n +1
- Двойной Мерсенн 2 2 р -1 -1
- Идеально 2 n -1 (2 n -1)
- Leyland x г ± г x
- Мерсенн
- Прот
- Ризель
- Вильямс ( b ±1) b n ±1
- Кэрол/Кинеа ( b n ±1) 2 -2
- Многофакторный n ! j ±1
- Определение рациональных чисел из списка чисел
- Определите иррациональные числа из списка чисел
- останавливается или повторяется, число является рациональным.
- не останавливается и не повторяется, число иррациональное.
На числовой оси рациональные числа располагаются повсюду плотно: между каждыми двумя рациональными числами, которые не равны друг другу, можно расположить хотя бы одно рациональное число (следовательно, и бесконечное множество рациональных чисел). В то же время, множество рациональных чисел характеризуется счетной мощностью (т. е. все элементы множества можно пронумеровать). Древние греки доказали, что существуют числа, которые невозможно записать как дробь. Они показали, что не существует такое рациональное число, квадрат которого равен $2$. Тогда рациональных чисел оказалось недостаточно для выражения всех величин, что и привело в дальнейшем к появлению вещественных чисел. Множество рациональных чисел, в отличие от вещественных чисел, является нульмерным.
Рациональные числа
Четверти
Дополнительные свойства
Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них.
Src=»/pictures/wiki/files/48/0caf9ffdbc8d6264bc14397db34e8d72.png» border=»0″>
Счётность множества
Нумерация рациональных чисел
Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно . Для этого достаточно привести алгоритм, который нумерует рациональные числа, т. е. устанавливает биекцию между множествами рациональных и натуральных чисел.
Самый простой из таких алгоритмов выглядит следующим образом. Составляется бесконечная таблица обыкновенных дробей, на каждой i -ой строке в каждом j -ом столбце которой располагается дробь . Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются , где i — номер строки таблицы, в которой располагается ячейка, а j — номер столбца.
Составляется бесконечная таблица обыкновенных дробей, на каждой i -ой строке в каждом j -ом столбце которой располагается дробь . Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются , где i — номер строки таблицы, в которой располагается ячейка, а j — номер столбца.
Полученная таблица обходится «змейкой» по следующему формальному алгоритму.
Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.
В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. Т. е. дроби 1 / 1 ставится в соответствие число 1, дроби 2 / 1 — число 2, и т. д. Нужно отметить, что нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел тоже счётно. Их объединение также счётно по свойству счётных множеств. Множество же рациональных чисел тоже счётно как объединение счётного множества с конечным.
Это значит, что множество положительных рациональных чисел счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел тоже счётно. Их объединение также счётно по свойству счётных множеств. Множество же рациональных чисел тоже счётно как объединение счётного множества с конечным.
Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, т. к. на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел. На самом деле это не так и натуральных чисел хватает, чтобы занумеровать все рациональные.
Недостаточность рациональных чисел
Гипотенуза такого треугольника не выражается никаким рациональным числом
Рациональными числами вида 1 / n при больших n можно измерять сколь угодно малые величины . Этот факт создаёт обманчивое впечатление, что рациональными числами можно измерить вообще любые геометрические расстояния .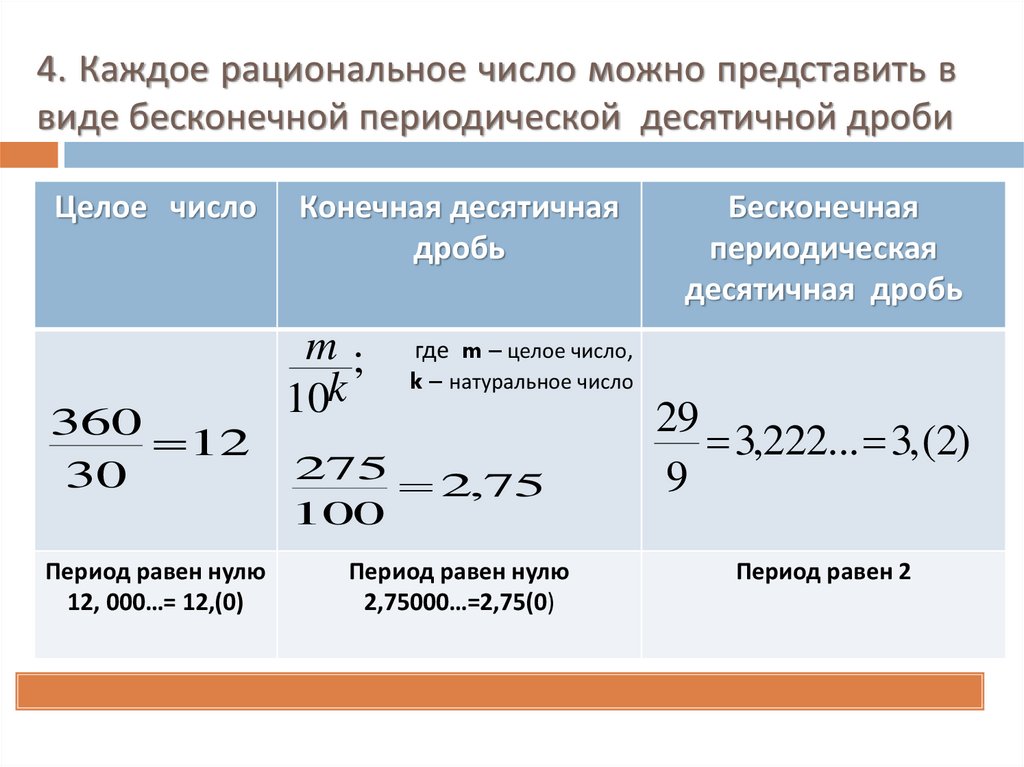 Легко показать, что это не верно.
Легко показать, что это не верно.
Примечания
Литература
Ссылки
Wikimedia Foundation . 2010 .
)- это числа с положительным или отрицательным знаком (целые и дробные) и ноль. Более точное понятие рациональных чисел, звучит так:
Рациональное число — число, которое представляется обычной дробью m/n , где числитель m — целые числа, а знаменатель n — натуральные числа, к примеру 2/3 .
Бесконечные непериодические дроби НЕ входят в множество рациональных чисел.
a/b , где a ∈ Z (a принадлежит целым числам), b ∈ N (b принадлежит натуральным числам).
Использование рациональных чисел в реальной жизни.
В реальной жизни множество рациональных чисел используется для счёта частей некоторых целых делимых объектов, например , тортов или других продуктов, которые разрезаются на части перед употреблением, или для грубой оценки пространственных отношений протяжённых объектов.
Свойства рациональных чисел.
Основные свойства рациональных чисел.
1. Упорядоченность a и b есть правило, которое позволяет однозначно идентифицировать между ними 1-но и только одно из 3-х отношений: «» либо «=». Это правило — правило упорядочения и формулируют его вот так:
∀ a,b ∈ Q (a∨ a>b ∨ a=b)
2. Операция сложения . Для всех рациональных чисел a и b есть правило суммирования , которое ставит им в соответствие определенное рациональное число c . При этом само число c — это сумма чисел a и b и ее обозначают как (a+b) суммирование .
Правило суммирования выглядит так:
m a /n a +m b /n b =(m a ⋅ n b +m b ⋅ n a) /(n a ⋅ n b).
∀ a,b ∈ Q ∃ !(a+b) ∈ Q
3. Операция умножения . Для всяких рациональных чисел a и b есть правило умножения , оно ставит им в соответствие определенное рациональное число c . Число c называют произведением чисел a и b и обозначают (a⋅b) , а процесс нахождения этого числа называют умножение .
Правило умножения выглядит так: m a n a ⋅ m b n b =m a ⋅ m b n a ⋅ n b .
∀a,b∈Q ∃(a⋅b)∈Q
4. Транзитивность отношения порядка. Для любых трех рациональных чисел a , b и c если a меньше b и b меньше c , то a меньше c , а если a равно b и b равно c , то a равно c .
∀ a,b,c ∈ Q (a∧ b⇒ a∧ (a = b ∧ b = c ⇒ a = c)
5. Коммутативность сложения . От перемены мест рациональных слагаемых сумма не изменяется.
∀ a,b ∈ Q a+b=b+a
6. Ассоциативность сложения . Порядок сложения 3-х рациональных чисел не оказывает влияния на результат.
∀ a,b,c ∈ Q (a+b)+c=a+(b+c)
7. Наличие нуля . Есть рациональное число 0, оно сохраняет всякое другое рациональное число при складывании.
Наличие нуля . Есть рациональное число 0, оно сохраняет всякое другое рациональное число при складывании.
∃ 0 ∈ Q ∀ a ∈ Q a+0=a
8. Наличие противоположных чисел . У любого рационального числа есть противоположное рациональное число, при их сложении получается 0.
∀ a ∈ Q ∃ (−a) ∈ Q a+(−a)=0
9. Коммутативность умножения . От перемены мест рациональных множителей произведение не изменяется.
∀ a,b ∈ Q a ⋅ b=b ⋅ a
10. Ассоциативность умножения . Порядок перемножения 3-х рациональных чисел не имеет влияния на итог.
∀ a,b,c ∈ Q (a ⋅ b) ⋅ c=a ⋅ (b ⋅ c)
11. Наличие единицы . Есть рациональное число 1, оно сохраняет всякое другое рациональное число в процессе умножения.
Наличие единицы . Есть рациональное число 1, оно сохраняет всякое другое рациональное число в процессе умножения.
∃ 1 ∈ Q ∀ a ∈ Q a ⋅ 1=a
12. Наличие обратных чисел . Всякое рациональное число, отличное от нуля имеет обратное рациональное число, умножив на которое получим 1.
∀ a ∈ Q ∃ a−1 ∈ Q a ⋅ a−1=1
13. Дистрибутивность умножения относительно сложения . Операция умножения связана со сложением при помощи распределительного закона:
∀ a,b,c ∈ Q (a+b) ⋅ c=a ⋅ c+b ⋅ c
14. Связь отношения порядка с операцией сложения . К левой и правой частям рационального неравенства прибавляют одно и то же рациональное число.
∀ a,b,c ∈ Q a⇒ a+c
15. Связь отношения порядка с операцией умножения . Левую и правую части рационального неравенства можно умножить на одинаковое неотрицательное рациональное число.
∀ a,b,c ∈ Q c>0 ∧ a⇒ a ⋅ c⋅ c
16. Аксиома Архимеда . Каким бы ни было рациональное число a , легко взять столько единиц, что их сумма будет больше a .
Рациональные числа
Четверти
Дополнительные свойства
Все остальные свойства, присущие рациональным числам, не выделяют в основные, потому что они, вообще говоря, уже не опираются непосредственно на свойства целых чисел, а могут быть доказаны исходя из приведённых основных свойств или непосредственно по определению некоторого математического объекта. Таких дополнительных свойств очень много. Здесь имеет смысл привести лишь некоторые из них.
Src=»/pictures/wiki/files/48/0caf9ffdbc8d6264bc14397db34e8d72.png» border=»0″>
Счётность множества
Нумерация рациональных чисел
Чтобы оценить количество рациональных чисел, нужно найти мощность их множества. Легко доказать, что множество рациональных чисел счётно . Для этого достаточно привести алгоритм, который нумерует рациональные числа, т. е. устанавливает биекцию между множествами рациональных и натуральных чисел.
Самый простой из таких алгоритмов выглядит следующим образом. Составляется бесконечная таблица обыкновенных дробей, на каждой i -ой строке в каждом j -ом столбце которой располагается дробь . Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются , где i — номер строки таблицы, в которой располагается ячейка, а j — номер столбца.
Составляется бесконечная таблица обыкновенных дробей, на каждой i -ой строке в каждом j -ом столбце которой располагается дробь . Для определённости считается, что строки и столбцы этой таблицы нумеруются с единицы. Ячейки таблицы обозначаются , где i — номер строки таблицы, в которой располагается ячейка, а j — номер столбца.
Полученная таблица обходится «змейкой» по следующему формальному алгоритму.
Эти правила просматриваются сверху вниз и следующее положение выбирается по первому совпадению.
В процессе такого обхода каждому новому рациональному числу ставится в соответствие очередное натуральное число. Т. е. дроби 1 / 1 ставится в соответствие число 1, дроби 2 / 1 — число 2, и т. д. Нужно отметить, что нумеруются только несократимые дроби. Формальным признаком несократимости является равенство единице наибольшего общего делителя числителя и знаменателя дроби.
Следуя этому алгоритму, можно занумеровать все положительные рациональные числа. Это значит, что множество положительных рациональных чисел счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел тоже счётно. Их объединение также счётно по свойству счётных множеств. Множество же рациональных чисел тоже счётно как объединение счётного множества с конечным.
Это значит, что множество положительных рациональных чисел счётно. Легко установить биекцию между множествами положительных и отрицательных рациональных чисел, просто поставив в соответствие каждому рациональному числу противоположное ему. Т. о. множество отрицательных рациональных чисел тоже счётно. Их объединение также счётно по свойству счётных множеств. Множество же рациональных чисел тоже счётно как объединение счётного множества с конечным.
Утверждение о счётности множества рациональных чисел может вызывать некоторое недоумение, т. к. на первый взгляд складывается впечатление, что оно гораздо обширнее множества натуральных чисел. На самом деле это не так и натуральных чисел хватает, чтобы занумеровать все рациональные.
Недостаточность рациональных чисел
Гипотенуза такого треугольника не выражается никаким рациональным числом
Рациональными числами вида 1 / n при больших n можно измерять сколь угодно малые величины . Этот факт создаёт обманчивое впечатление, что рациональными числами можно измерить вообще любые геометрические расстояния . Легко показать, что это не верно.
Легко показать, что это не верно.
Примечания
Литература
Ссылки
Wikimedia Foundation . 2010 .
Подсчет рациональных чисел. Первое знакомство со сравнением… | by Haris Angelidakis
Photo by Daniel Giannone on Unsplash Счет — одно из первых понятий, которым нас учат в начальной школе. Сначала учимся считать все подряд «до 10», затем «до 20» и так далее. Мы часто используем пальцы, чтобы вести счет. И в какой-то момент это щелкает, и тогда мы больше никогда не сомневаемся в концепции счета. Мы завоевали его. Теперь нам удобно отвечать на такие вопросы, как «сколько человек находится в этой комнате», «сколько у вас братьев и сестер» и т. д.
д.
В этой статье мы вернемся к счету и попробуем копнуть немного глубже. В частности, мы зададим следующий вопрос:
Размер множества рациональных чисел больше, чем размер множества натуральных чисел?
[Отказ от ответственности: мы не будем давать очень формальное определение, но, надеюсь, последующее даст вам некоторое представление о ключевых понятиях, связанных с формальным определением счета.]
Всякий раз, когда нам нужно посчитать, скажем, набор элементов, мы чаще всего делаем перечисление. Это означает, что мы присваиваем каждому элементу свое натуральное число, начиная с числа 1.
Например, если мы видим перед собой белую, синюю и красную машины и хотим посчитать, сколько машины перед нами, то мы можем проделать в уме следующее перечисление:
белая машина: 1-я машина — синяя машина: 2-я машина — красная машина: 3-я машина.
Итак, мы знаем, что перед нами 3 машины.
Разбивая процесс, который мы только что описали, мы неявно определили биекцию между набором автомобилей, которые мы видим, и набором {1, 2, 3}:
И это основная идея, лежащая в основе подсчета. Цитируя Википедию,
В математике суть подсчета множества и нахождения результата n состоит в том, что он устанавливает однозначное соответствие (или биекцию) множества с множеством чисел {1, 2 , …, и }.
Неформально набор чисел {1,…, n } можно рассматривать как прототип, который «определяет», как «выглядит» набор из n элементов.
Хотя это может показаться слишком педантичным, не добавляя многого к разговору, это ключевая идея, которая позволяет нам понять и расширить концепцию подсчета, как мы скоро увидим.
Бертран Рассел в 1957 году [Источник: Википедия]«Должно быть, потребовалось много веков, чтобы обнаружить, что парочка фазанов и пара дней были двумя экземплярами числа 2».
— Бертран Рассел
После прочтения всего вышеизложенного любознательный читатель может подумать о том, можно ли распространить такую идею счета с помощью биекций на бесконечные множества, такие как натуральные числа.
Непосредственное наблюдение в этом направлении состоит в том, что набор натуральных чисел не позволяет установить биекцию с {1, 2, …, n } для любого натурального числа n ; цитируя Википедию, «множества, не имеющие таких биекций, называются бесконечными множествами, а те множества, для которых такая биекция существует (для каких-то n ) называются конечными множествами».
Тем не менее, можно попытаться доказать, что два бесконечных множества A и B имеют «один и тот же размер», если существует биекция от A до B . И это действительно естественный способ рассуждать о размерах бесконечных множеств.
Так как мы использовали множество {1,…, n } в качестве прототипа для множеств из n элементов, для любого натурального числа n теперь мы будем использовать множество N = {0, 1, …} всех натуральных чисел в качестве нашего прототипа.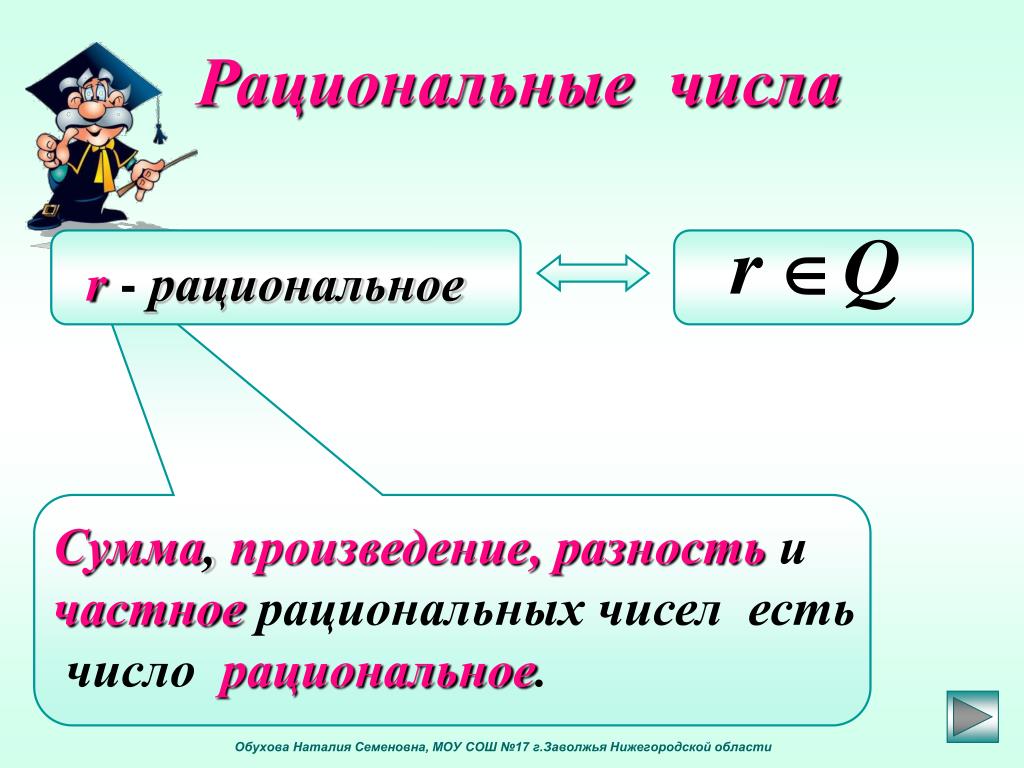 Сначала поставим следующий вопрос:
Сначала поставим следующий вопрос:
Является ли множество целых чисел больше, чем множество натуральных чисел?
На такой вопрос можно ожидать сразу две реакции:
Вопрос, поднятый в (1), уже обсуждался выше. В самом деле, мы не можем надеяться провести подсчет точно так же, как мы это делали для конечных множеств, но мы все же можем сравнивать два множества, проверяя, существует ли взаимное соответствие между их элементами.
Что касается вопроса, поднятого в (2), хотя верно, что натуральные числа составляют строгое подмножество целых чисел, оказывается, что они не более чем целые числа в следующем смысле.
Теорема: существует биекция между натуральными и целыми числами.
Доказательство. Мы явно построим биекцию между двумя множествами. Пусть N обозначает множество натуральных чисел, а Z обозначает множество целых чисел. Точнее, определим функцию f: N → Z такое, что для каждого целого числа z существует натуральное число n такое, что f(n) = z .
Мы явно построим биекцию между двумя множествами. Пусть N обозначает множество натуральных чисел, а Z обозначает множество целых чисел. Точнее, определим функцию f: N → Z такое, что для каждого целого числа z существует натуральное число n такое, что f(n) = z .
Функция f определяется следующим образом:
Приведенная выше функция предлагает следующий «порядок» целых чисел:
0 → 0
1 → -1
2 → 1
3 → -2
4 → -3 5 → 2
3
6 → 3
и т. д.
Легко проверить, что приведенная выше функция сопоставляет каждое натуральное число с некоторым целым числом. Более того, для любого положительного неотрицательного целого числа k существует уникальных натуральное число n = 2k , которое отображается на него, и аналогично, для любого отрицательного целого числа k существует уникальное натуральное число n = -(2k+1) , которое отображается на него. Таким образом, функция f действительно биекция.
Более того, для любого положительного неотрицательного целого числа k существует уникальных натуральное число n = 2k , которое отображается на него, и аналогично, для любого отрицательного целого числа k существует уникальное натуральное число n = -(2k+1) , которое отображается на него. Таким образом, функция f действительно биекция.
Мы заключаем, что множество натуральных чисел и множество целых чисел имеют одинаковый размер!
Приведенный выше результат показывает, что когда мы рассматриваем бесконечные множества, мы должны быть осторожны и не использовать нашу интуицию в отношении счета, интуицию, которую мы, скорее всего, развили, имея дело с конечными множествами.
Напоминаем, что множество рациональных чисел Q — это множество всех чисел, которые можно представить как частное p / q двух целых чисел, где p и q — целые числа и q не равно нулю.
На первый взгляд, набор натуральных чисел выглядит значительно больше, чем набор натуральных чисел, поскольку он не только содержит его, но и содержит намного больше чисел в том смысле, что они могут приближать любое действительное число с произвольной точностью. . Таким образом, потенциально можно предположить, что они должны быть больше, чем натуральные числа, или, говоря более формально, что между натуральными и рациональными числами нет биекции.
Теперь мы докажем несколько парадоксальную теорему, которая показывает, что множество рациональных чисел оказывается того же размера, что и множество натуральных чисел!
Теорема: существует биекция между натуральными и рациональными числами.
Доказательство. Сначала формально определим множество Q рациональных чисел:
Q = { p / q : p — целое число, а q — положительное натуральное число}.
Обратите внимание, что в приведенном выше определении мы требуем, чтобы знаменатель был строго положительным. Легко видеть, что это без ограничения общности, так как число p / (-q) равно (-p) / q , и, таким образом, приведенное выше множество действительно описывает множество рациональное число.
Легко видеть, что это без ограничения общности, так как число p / (-q) равно (-p) / q , и, таким образом, приведенное выше множество действительно описывает множество рациональное число.
Чтобы упростить нашу конструкцию, мы разобьем Q на Q₊ и Q₋ и множество {0}, где Q₊ содержит все положительные рациональные числа и Q₋ содержит все отрицательные рациональные числа. Сначала мы покажем, что существует биекция между множеством натуральных чисел и Q₊ . Это сразу означает, что существует биекция между набором натуральных чисел и Q₋ , поскольку для каждого положительного числа x >0 в Q₊ , -x находится в Q₋ , и наоборот . Затем мы используем прием, который мы использовали для перечисления целых чисел, а именно, мы «интерполируем» между положительными и отрицательными рациональными числами одно за другим; мы также добавляем 0 (ноль) в качестве первого элемента последовательности, и это даст нашу окончательную биекцию.
Итак, основное внимание мы уделяем построению биекции между множеством натуральных чисел и Q₊ . Для этого рассмотрим двумерную целочисленную сетку на положительном ортанте. Каждое положительное рациональное число можно записать как p / q , где p и q — положительные натуральные числа. Запись этого рационального числа в виде пары координат ( p,q ) показывает, что мы можем описать все такие числа точками пересечения следующей двумерной сетки.
Например, рациональное число 1/2 описывается точками (1,2), (2,4), (3,6) и т. д. Это показывает, что в сетке существует более одной точки, описывающей 1 /2. Важным свойством, которое нам нужно, является наличие по крайней мере одной таких точек в сетке.
Теперь пронумеруем точки сетки следующим образом. Мы начинаем с (1,1) и двигаемся по диагоналям, которые идут снизу слева вверх справа, как показано на рисунке ниже, где нам нужно только следовать зеленой линии.
Это позволяет нам записать все точки приведенной выше сетки в виде последовательности; это означает, что каждой точке сетки соответствует индекс (т. е. натуральное число). Первые несколько элементов последовательности следующие:
и т. д.
Таким образом, для получения фактического перечисления из набора Q₊ , мы следуем зеленой линии, как указано выше, и всякий раз, когда мы встречаем точку ( p , q ), такую, что число p / q уже было описано с другой точкой сетки, которая зеленая линия уже прошла, просто игнорируем ее и продолжаем. Это означает, что мы создадим последовательность, содержащую все числа из Q₊ , или, другими словами, мы только что произвели биекцию между положительными натуральными числами и множеством В₊ !
Пусть f обозначает эту последовательность. В качестве уточнения и следуя зеленой линии выше, это дает
В качестве уточнения и следуя зеленой линии выше, это дает
и т. д.
Теперь мы можем сразу получить нумерацию множества Q₋ , установив
g ( 90 ( 1 — 2 f ) = 1 n ), для каждого натурального числа n > 0. Теперь мы готовы определить нашу биекцию h между натуральными и рациональными числами! Мы просто устанавливаем: Учитывая приведенное выше обсуждение, легко проверить, что приведенная выше функция h действительно является биекцией. А именно, для каждого натурального числа n существует единственное рациональное число h ( n ), которое отображается в него, и, наоборот, для каждого рационального числа p / q существует натуральное число n , для которого h ( n ) = p / q. Мы сделали! Надеюсь, вы получили первое представление о том, как вести счет в бесконечных множествах и сравнивать размеры таких множеств. Самое главное, большая часть нашей интуиции, разработанной для конечных множеств, «ломается» при работе с бесконечностью, поэтому нужно быть очень осторожным и непредубежденным, когда имеешь дело с бесконечностью! Существует очень богатая теория подсчета бесконечных множеств, которая показывает, что существует множество различных видов бесконечности, когда дело доходит до подсчета множеств, но это выходит за рамки данной статьи. Жемчужиной этой теории, которая служит хорошей отправной точкой, является великолепный диагональный аргумент Джорджа Кантора, который показывает, что между действительными и натуральными числами нет биекции, и поэтому набор действительных чисел строго больше по размеру по сравнению с набором натуральных чисел. Рациональное число — это действительное число, которое можно записать в виде [math]\displaystyle{ \frac{a}{b} }[/math] или [math]\displaystyle{ a/b }[/math] где [math]\displaystyle{ a }[/math] (числитель ) — любое целое число, а [math]\displaystyle{ b }[/math] (знаменатель ) — целое число, отличное от нуля. Набор всех рациональных чисел называется [math]\displaystyle{ \mathbb{Q} }[/math]. Обозначение [math]\displaystyle{ a/b }[/math] называется дробь . Дробь неприводима, когда оба числа взаимно просты, в противном случае ее можно привести к неприводимой форме, разделив числитель и знаменатель на их наибольший общий делитель. Определены следующие операции:
Рациональное число — Prime-Wiki
 Эта операция не изменяет рациональное число, представленное дробью.
Эта операция не изменяет рациональное число, представленное дробью. Содержание
Дополнение
Вычитание
Умножение
Раздел
Действителен, только если второе рациональное число не равно нулю.
Между двумя рациональными числами есть бесконечны другие рациональные числа. Это связано с тем, что между числами [math]\displaystyle{ a }[/math] и [math]\displaystyle{ b }[/math] находятся следующие числа [math]\displaystyle{ n }[/math]:
, изменив число [math]\displaystyle{ k }[/math] от 1 до [math]\displaystyle{ n }[/math]. Затем мы можем сделать значение [math]\displaystyle{ n }[/math] сколь угодно большим.
Затем мы можем сделать значение [math]\displaystyle{ n }[/math] сколь угодно большим.
Это означает, что множество рациональных чисел является плотным подмножеством действительных чисел.
Из приведенных выше рассуждений можно подумать, что все действительные числа рациональны, но можно показать, что множество иррациональных чисел (тех действительных чисел, которые не являются рациональными) также плотно и иррациональных чисел больше, чем рациональных (есть различные типы бесконечности). 9м}[/математика].
В противном случае число, представленное в десятичном виде, является периодическим, где период является делителем функции Эйлера и знаменателя. Эта функция может быть вычислена путем факторизации знаменателя. В частном случае, когда знаменатель является простым числом, период равен делителю знаменателя минус 1.
Когда у нас есть число, представленное в десятичной форме, преобразование его в дробь зависит от того, является ли десятичное представление точным или периодическим.
В первом случае, когда число [math]\displaystyle{ N }[/math] в десятичном виде имеет вид [math]\displaystyle{ m.n }[/math], где [math]\displaystyle{ n }[/ math] имеет [math]\displaystyle{ d }[/math] цифры справа от десятичной точки ([math]\displaystyle{ d=0 }[/math] для целых чисел), дробь: 9e-1)} }[/math]
Внешние ссылки
Классы чисел
| Общие числа |
| Специальные номера |
| Простые числа |
Определение рациональных и иррациональных чисел | Преалгебра |
Результаты обучения
В этой главе мы проверим ваши навыки. Мы еще раз взглянем на типы чисел, с которыми мы работали во всех предыдущих главах. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа. И мы попрактикуемся в их использовании так, как будем использовать при решении уравнений и других алгебраических процедурах.
Мы еще раз взглянем на типы чисел, с которыми мы работали во всех предыдущих главах. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше чувство числа. И мы попрактикуемся в их использовании так, как будем использовать при решении уравнений и других алгебраических процедурах.
Мы уже описали числа как счетные числа, целые числа и целые числа. Вы помните, в чем разница между этими типами чисел?
| счет чисел | 1,2,3,4…1,2,3,4\точки 1,2,3,4… |
| целые числа | 0,1,2,3,4…0,1,2,3,4\точки0,1,2,3,4… |
| целых чисел | ⋯−3,−2,−1,0,1,2,3,4…\точки -3,-2,-1,0,1,2,3,4\точки ⋯−3,−2 ,−1,0,1,2,3,4… |
Рациональные числа
Какой тип чисел вы бы получили, если бы начали со всех целых чисел, а затем включили все дроби? Числа, которые вы получили бы, образуют множество рациональных чисел. Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Рациональные числа
Рациональное число — это число, которое можно записать в виде
pq\frac{p}{q}qp
, где
ppp
и
qqq
являются целыми числами, а
q≠oq\ne oq=o
.
Все дроби, как положительные, так и отрицательные, являются рациональными числами. Вот несколько примеров:
45,−78,134 и−203\frac{4}{5},-\frac{7}{8},\frac{13}{4},\text{and}-\frac {20}{3}54, −87, 413 и −320
Каждый числитель и каждый знаменатель являются целыми числами.
Нам нужно просмотреть все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы рассмотрим счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Теперь мы рассмотрим счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Являются ли целые числа рациональными числами? Чтобы решить, является ли целое число рациональным, мы пытаемся записать его как отношение двух целых чисел. Самый простой способ сделать это — записать дробь со знаменателем один.
3=31−8=−810=013=\frac{3}{1}-8=\frac{-8}{1}0=\frac{0}{1}3=13−8= 1−80=10
Поскольку любое целое число может быть записано как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа тоже целые, а значит, они тоже рациональны.
Как насчет десятичных знаков? Являются ли они рациональными? Давайте рассмотрим несколько, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа являются рациональными числами. Целое число
-8-8-8
может быть записано как десятичное число
-8,0-8,0-8,0
. Итак, ясно, что некоторые десятичные дроби рациональны.
Итак, ясно, что некоторые десятичные дроби рациональны.
Подумайте о десятичной дроби
7.37.37.3
. Можем ли мы записать это как отношение двух целых чисел? Потому что
7.37.37.3
означает
73107\frac{3}{10}7103
, мы можем записать это как неправильную дробь,
7310\frac{73}{10}1073
. Итак,
7.37.37.3
— это отношение целых чисел
737373
и
101010
. Это рациональное число.
В общем случае любое десятичное число, которое заканчивается после нескольких цифр, таких как
7.37.37.3
или
−1,2684–1,2684–1,2684
, является рациональным числом. Мы можем использовать разрядное значение последней цифры в качестве знаменателя при записи десятичной дроби.
пример
Запишите каждое как отношение двух целых чисел:
1.
−15-15−15
2.
6.816.816,81
3.
−367-3\frac{76}{7}−3\frac{6}{7}−3
Решение:
| 1. | |
−15-15−15 | |
| Запишите целое число в виде дроби со знаменателем 1. | −151\frac{-15}{1}1−15 |
| 2. | |
6.816.816.81 | |
| Запишите десятичную дробь как смешанное число. | 6811006\frac{81}{100}610081 |
| Затем преобразуйте его в неправильную дробь. | 681100\фрак{681}{100}100681 |
| 3. | |
−367-3\frac{6}{7}−376 | |
Преобразуйте смешанное число в неправильную дробь. | −277-\frac{27}{7}−727 |
попробуй
Давайте посмотрим на десятичную форму чисел, которые, как мы знаем, являются рациональными. Мы видели, что каждое целое число является рациональным числом, начиная с
a=a1a=\frac{a}{1}a=1a
для любого целого числа,
aaa
. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.
Целое число
−2,−1,0,1,2,3–2,–1,0,1,2,3–2,–1,0,1,2,3
Десятичное число
− 2.0,−1.0,0.0,1.0,2.0,3.0–2.0,–1.0,0.0,1.0,2.0,3.0–2.0,–1.0,0.0,1.0,2.0,3.0
Эти десятичные числа останавливаются.
Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму дробей, которые мы только что рассмотрели.
Отношение целых чисел
45,78,134,203\frac{4}{5},\frac{7}{8},\frac{13}{4},\frac{20}{3}54,87 ,413,320
Десятичные формы
0,8,–0,875,3,25,–6,666…,–6,66‾0,8,–0,875,3,25,–6,666\ldots,–6. \overline{66}0,8,–0,875,3,25,–6,666…,–6,66
\overline{66}0,8,–0,875,3,25,–6,666…,–6,66
Эти десятичные дроби либо останавливаются, либо повторяются.
О чем говорят эти примеры? Каждое рациональное число можно записать как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассмотрели, выраженные в виде отношения целых чисел и десятичных дробей.
| Рациональные числа | ||
|---|---|---|
| Дроби | Целые числа | |
| Номер | 45,−78,134,−203\frac{4}{5},-\frac{7}{8},\frac{13}{4},\frac{-20}{3}54,− 87,413,3−20 | -2,-1,0,1,2,3-2,-1,0,1,2,3-2,-1,0,1,2,3 |
| Отношение целого числа | 45,−78,134,−203\frac{4}{5},\frac{-7}{8},\frac{13}{4},\frac{-20}{3}54,8 −7,413,3−20 | −21,−11,01,11,21,31\frac{-2}{1},\frac{-1}{1},\frac{0}{1},\frac{1}{ 1},\frac{2}{1},\frac{3}{1}1−2, 1−1, 10, 11, 12, 13 |
| Десятичное число | 0,8,-0,875,3,25,-6,6‾0,8,-0,875,3,25,-6. | −2,0,−1,0,0,0,1,0,2,0,3,0–2,0,–1,0,0,0,1,0,2,0,3,0–2,0,–1,0,0,0,1,0,2,0,3,0 |
Иррациональные числа
Существуют ли какие-либо десятичные дроби, которые не останавливаются и не повторяются? Да. Число
π\pi π
(греческая буква пи, произносится как «пирог»), которое очень важно при описании кругов, имеет десятичную форму, которая не прерывается и не повторяется.
π=3,141592654…….\pi =\text{3,141592654…….}π=3,141592654…….
Точно так же десятичные представления квадратных корней чисел, которые не идеальные квадраты никогда не останавливаются и никогда не повторяются. Например,
5=2,236067978…..\sqrt{5}=\text{2,236067978…..}5
=2,236067978…..
не повторяться нельзя записать как отношение целых чисел. Мы называем такие числа иррациональными числами.
Мы называем такие числа иррациональными числами.
Иррациональное число
Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не прерывается и не повторяется.
Давайте обобщим метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа
пример
Определите каждое из следующего как рациональное или иррациональное:
1.
0,583‾0,58 \ Overline {3} 0,583
2.
0,4750.4750.475
3.
3,605551275… 3,6055512775 \ DOT 3,605551275 … 3,6055512775 \ DOT 3,605551275 … 3,6055512775 \ DOT 3,605551275 … 3,605551277
0,583‾0,58\overline{3}0,583
Полоса над
333
указывает на то, что она повторяется. Таким образом,
Таким образом,
0,583‾0,58\overline{3}0,583
является повторяющимся десятичным числом и, следовательно, рациональным числом.
2.
0.4750.4750.475
Это десятичное число заканчивается после
555
, так что это рациональное число.
3.
3.605551275…3.605551275\dots3.605551275…
Многоточие
(… )(\dots)(…)
означает, что это число не заканчивается. Нет повторяющегося набора цифр. Поскольку число не останавливается и не повторяется, оно иррационально.
попробуй
Давайте теперь подумаем о квадратных корнях. Квадратные корни из полных квадратов всегда являются целыми числами, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются идеальными квадратами, никогда не останавливаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.


 3$.
3$. 3$.
3$. Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″>
Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″> При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: .
При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: .
 src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″>
src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″>
 Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″>
Это правило называется правилом упорядочения и формулируется следующим образом: два неотрицательных числа и связаны тем же отношением, что и два целых числа и ; два неположительных числа a и b связаны тем же отношением, что и два неотрицательных числа и ; если же вдруг a неотрицательно, а b — отрицательно, то a > b .
src=»/pictures/wiki/files/57/94586b8b651318d46a00db5413cf6c15.png» border=»0″> При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: .
При этом само число c называется произведением чисел a и b и обозначается , а процесс отыскания такого числа также называется умножением . Правило умножения имеет следующий вид: .
 src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″>
src=»/pictures/wiki/files/55/70c78823302483b6901ad39f68949086.png» border=»0″> — Бертран Рассел
— Бертран Рассел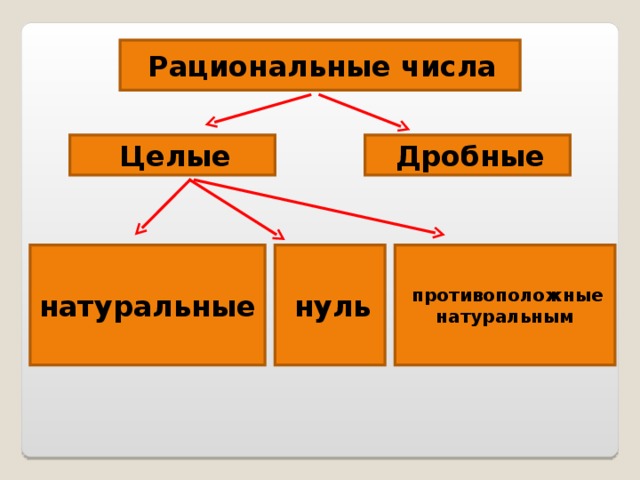
 \overline{6}0,8,-0,875,3,25,-6,6
\overline{6}0,8,-0,875,3,25,-6,6