объяснение, теория, примеры решений. а. База; определение и основные примеры
Доказывая свойства предела функции, мы убедились, что от проколотых окрестностей, в которых были определены наши функции и которые возникали в процессе доказательств, кроме свойств указанных во введении к предыдущему пункту 2, действительно ничего не потребовалось. Это обстоятельство служит оправданием для выделения следующего математического объекта.
а. База; определение и основные примеры
Определение 11. Совокупность В подмножеств множества X будем называть базой в множестве X, если выполнены два условия:
Иными словами, элементы совокупности В суть непустые множества и в пересечении любых двух из них содержится некоторый элемент из той же совокупности.
Укажем некоторые наиболее употребительные в анализе базы.
Если то вместо пишут и говорят, что х стремится к а справа или со стороны больших значений (соответственно, слева или со стороны меньших значений). При принята краткая запись вместо
Запись будет употребляться вместо Она означает, что а; стремится по множеству Е к а, оставаясь больше (меньше), чем а.
то вместо пишут и говорят, что х стремится к плюс бесконечности (соответственно, к минус бесконечности).
Запись будет употребляться вместо
При вместо мы (если это не ведет к недоразумению) будем, как это принято в теории предела последовательности, писать
Заметим, что все перечисленные базы обладают той особенностью, что пересечение любых двух элементов базы само является элементом этой базы, а не только содержит некоторый элемент базы. С другими базами мы встретимся при изучении функций, заданных не на числовой оси.
Отметим также, что используемый здесь термин «база» есть краткое обозначение того, что в математике называется «базисом фильтра», а введенный ниже предел по базе есть наиболее существенная для анализа часть созданного современным французским математиком А. Картаном понятия предела по фильтру
b. Предел функции по базе
Определение 12. Пусть — функция на множестве X; В — база в X. Число называется пределом функции по базе В, если для любой окрестности точки А найдется элемент базы, образ которого содержится в окрестности
Если А — предел функции по базе В, то пишут
Повторим определение предела по базе в логической символике:
Поскольку мы сейчас рассматриваем функции с числовыми значениями, полезно иметь в виду и следующую форму этого основного определения:
В этой формулировке вместо произвольной окрестности V (А) берется симметричная (относительно точки А) окрестность (е-окрестность). Эквивалентность этих определений для вещественнозначных функций вытекает из того, что, как уже говорилось, в любой окрестности точки содержится некоторая симметричная окрестность этой же точки (проведите доказательство полностью!).
Эквивалентность этих определений для вещественнозначных функций вытекает из того, что, как уже говорилось, в любой окрестности точки содержится некоторая симметричная окрестность этой же точки (проведите доказательство полностью!).
Мы дали общее определение предела функции по базе. Выше были рассмотрены примеры наиболее употребительных в анализе баз. В конкретной задаче, где появляется та или иная из этих баз, необходимо уметь расшифровать общее определение и записать его для конкретной базы.
Рассматривая примеры баз, мы, в частности, ввели понятие окрестности бесконечности. Если использовать это понятие, то в соответствии с общим определением предела разумно принять следующие соглашения:
или, что то же самое,
Обычно под подразумевают малую величину. В приведенных определениях это, разумеется, не так. В соответствии с принятыми соглашениями, например, можем записать
Для того чтобы можно было считать доказанными и в общем случае предела по произвольной базе все те теоремы о пределах, которые мы доказали в пункте 2 для специальной базы , необходимо дать соответствующие определения: финально постоянной, финально ограниченной и бесконечно малой при данной базе функций.
Определение 13. Функция называется финально постоянной при базе В, если существуют число и такой элемент базы, в любой точке которого
Определение 14. Функция называется ограниченной при базе В или финально ограниченной при базе В, если существуют число с и такой элемент базы, в любой точке которого
Определение 15. Функция называется бесконечно малой при базе В, если
После этих определений и основного наблюдения о том, что для доказательства теорем о пределах нужны только свойства базы, можно считать, что все свойства предела, установленные в пункте 2, справедливы для пределов по любой базе.
В частности, мы можем теперь говорить о пределе функции при или при или при
Кроме того, мы обеспечили себе возможность применения теории пределов и в том случае, когда функции будут определены не на числовых множествах; в дальнейшем это окажется особенно ценным. К примеру, длина кривой есть числовая функция, определенная на некотором классе кривых. Если мы знаем эту функцию на ломаных, то потом предельным переходом определяем ее для более сложных кривых, например для окружности.
В данный же момент основная польза от сделанного наблюдения и введенного в связи с ним понятия базы состоит в том, что они избавляют нас от проверок и формальных доказательств теорем о пределах для каждого конкретного вида предельных переходов или, в нашей нынешней терминологии, для каждого конкретного вида баз.
Для того чтобы окончательно освоиться с понятием предела по произвольной базе, доказательства дальнейших свойств предела функции мы проведем в общем виде.
Начнем с общих вещей, которые ОЧЕНЬ важны, но мало кто обращает на них внимание.
Предел функции — основные понятия.
Бесконечность обозначают символом . По сути, бесконечность это есть либо бесконечно большое положительное число , либо бесконечно большое отрицательное число .
Что это означает: когда Вы видите , то не имеет разницы это или . Но лучше не заменять на , равно как и лучше не заменять на .
Записывать предел функции f(x) принято в виде , снизу указывается аргумент x
и через стрелочку к какому значению он стремится.
Если представляет из себя конкретное действительное число, то говорят о пределе функции в точке .
Если или . то говорят о пределе функции на бесконечности .
Сам предел может быть равен конкретному действительному числу , в этом случае говорят, что предел конечен .
Если , или , то говорят, что предел бесконечен .
Еще говорят, что предел не существует
Предел функции — основные определения.
Пришло время заняться нахождением значений пределов функций на бесконечности и в точке. В этом нам помогут несколько определений. Эти определения опираются на числовые последовательности и их сходимость или расходимость .
Определение (нахождение предела функции на бесконечности).
Число А
называется пределом функции f(x)
при , если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А
. Обозначается .
Обозначается .
Замечание.
Предел функции f(x) при бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается .
Пример.
Используя определение предела при доказать равенство .
Решение.
Запишем последовательность значений функции для бесконечно большой положительной последовательности значений аргумента .
Очевидно, что члены этой последовательности монотонно убывают к нулю.
Графическая иллюстрация.
Теперь запишем последовательность значений функции для бесконечно большой отрицательной последовательности значений аргумента .
Члены этой последовательности также монотонно убывают к нулю, что доказывает исходное равенство.
Графическая иллюстрация.
Пример.
Найти предел
Решение.
Последовательность значений функции при этом будет (синие точки на графике)
Очевидно, что эта последовательность является бесконечно большой положительной, следовательно,
А сейчас запишем последовательность значений функции для бесконечно большой отрицательной последовательности значений аргумента. К примеру, возьмем .
Последовательность значений функции при этом будет (зеленые точки на графике)
Очевидно, что эта последовательность сходится к нулю, следовательно,
Графическая иллюстрация
Ответ:
Сейчас поговорим о существовании и нахождении предела функции в точке. Все основывается на определении односторонних пределов . Без вычисления односторонних пределов не обойтись при .
Определение (нахождение предела функции слева).
Число В
называется пределом функции f(x)
слева при , если для любой сходящейся к а
последовательности аргументов функции , значения которых остаются меньше а
(), последовательность значений этой функции сходится к В
.
Обозначается .
Определение (нахождение предела функции справа).
Число В называется пределом функции f(x) справа при , если для любой сходящейся к а последовательности аргументов функции , значения которых остаются больше а (), последовательность значений этой функции сходится к В .
Обозначается .
Определение (существование предела функции в точке).
Предел функции f(x)
в точке а
существует, если существуют пределы слева и справа а
и они равны между собой.
Замечание.
Предел функции f(x) в точке а бесконечен, если пределы слева и справа а бесконечны.
Поясним эти определения на примере.
Пример.
Доказать существование конечного предела функции в точке . Найти его значение.
Решение.
Будем отталкиваться от определения существования предела функции в точке.
Во-первых, покажем существование предела слева. Для этого возьмем последовательность аргументов , сходящуюся к , причем . Примером такой последовательности может являться
Примером такой последовательности может являться
На рисунке соответствующие значения показаны зелеными точками.
Легко видеть, что эта последовательность сходится к -2 , поэтому .
Во-вторых, покажем существование предела справа. Для этого возьмем последовательность аргументов , сходящуюся к , причем . Примером такой последовательности может являться
Соответствующая последовательность значений функции будет иметь вид
На рисунке соответствующие значения показаны синими точками.
Легко видеть, что эта последовательность также сходится к -2 , поэтому .
Этим мы показали, что пределы слева и справа равны, следовательно, по определению существует предел функции в точке , причем
Графическая иллюстрация.
Продолжить изучение основных определений теории пределов рекомендуем темой .
Рассмотрим функцию %%f(x)%%, определенную, по крайней мере, в некоторой проколотой окрестности %%\stackrel{\circ}{\text{U}}(a)%% точки %%a \in \overline{\mathbb{R}}%% расширенной числовой прямой.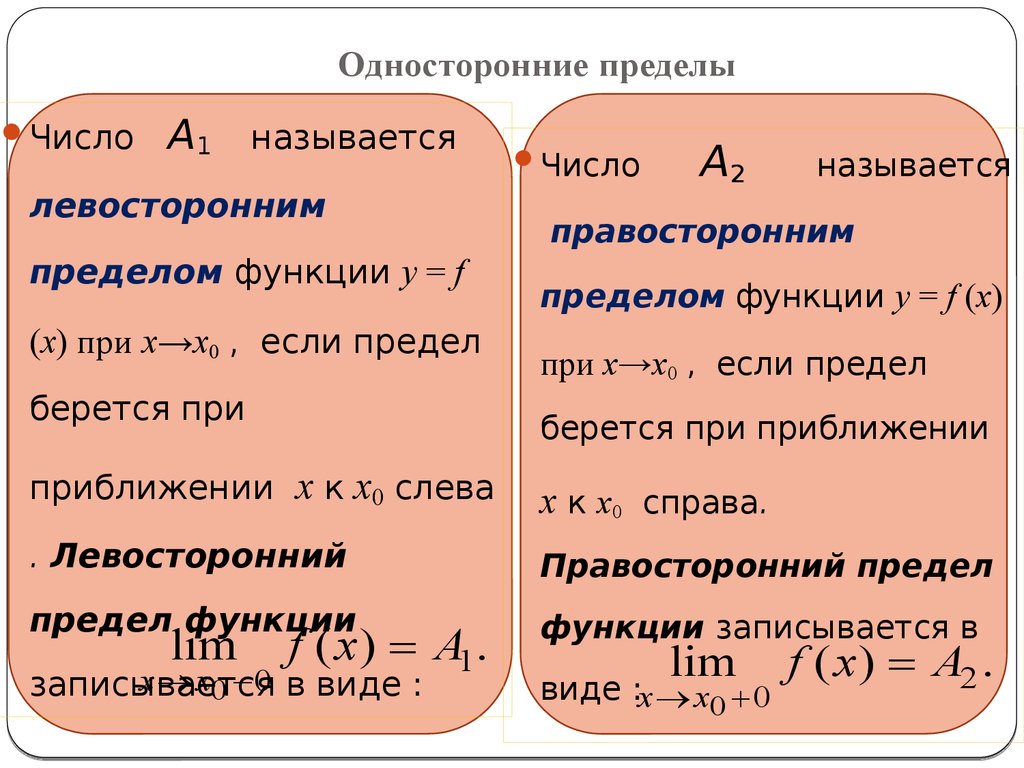
Понятие предела по Коши
Число %%A \in \mathbb{R}%% называют пределом функции %%f(x)%% в точке %%a \in \mathbb{R}%% (или при %%x%%, стремящемся к %%a \in \mathbb{R}%%), если, каково бы ни было положительное число %%\varepsilon%%, найдется положительное число %%\delta%%, такое, что для всех точек проколотой %%\delta%%-окрестности точки %%a%% значения функции принадлежат %%\varepsilon%%-окрестности точки %%A%%, или
$$ A = \lim\limits_{x \to a}{f(x)} \Leftrightarrow \forall\varepsilon > 0 ~\exists \delta > 0 \big(x \in \stackrel{\circ}{\text{U}}_\delta(a) \Rightarrow f(x) \in \text{U}_\varepsilon (A) \big) $$
Это определение называется определением на языке %%\varepsilon%% и %%\delta%%, предложено французским математиком Огюстеном Коши и используется с начала XIX века по настоящее время, поскольку обладает необходимой математической строгостью и точностью.
Комбинируя различные окрестности точки %%a%% вида %%\stackrel{\circ}{\text{U}}_\delta(a), \text{U}_\delta (\infty), \text{U}_\delta (-\infty), \text{U}_\delta (+\infty), \text{U}_\delta^+ (a), \text{U}_\delta^- (a)%% с окрестностями %%\text{U}_\varepsilon (A), \text{U}_\varepsilon (\infty), \text{U}_\varepsilon (+\infty), \text{U}_\varepsilon (-\infty)%%, получим 24 определения предела по Коши.
Геометрический смысл
Геометрический смысл предела функции
Выясним, в чем заключается геометрический смысл предела функции в точке. Построим график функции %%y = f(x)%% и отметим на нем точки %%x = a%% и %%y = A%%.
Предел функции %%y = f(x)%% в точке %%x \to a%% существует и равен A, если для любой %%\varepsilon%%-окрестности точки %%A%% можно указать такую %%\delta%%-окрестность точки %%a%%, что для любого %%x%% из этой %%\delta%%-окрестности значение %%f(x)%% будет находиться в %%\varepsilon%%-окрестности точки %%A%%.
Отметим, что по определению предела функции по Коши для существования предела при %%x \to a%% не важно, какое значение принимает функция в самой точке %%a%%. Можно привести примеры, когда функция не определена при %%x = a%% или принимает значение, отличное от %%A%%. Тем не менее предел может быть равен %%A%%.
Определение предела по Гейне
Элемент %%A \in \overline{\mathbb{R}}%% называется пределом функции %%f(x)%% при %% x \to a, a \in \overline{\mathbb{R}}%%, если для любой последовательности %%\{x_n\} \to a%% из области определения, последовательность соответствующих значений %%\big\{f(x_n)\big\}%% стремится к %%A%%. n n\pi\right)} \equiv 0%% и %%\lim\big\{f(x_n)\big\} = 0%%.
n n\pi\right)} \equiv 0%% и %%\lim\big\{f(x_n)\big\} = 0%%.
Затем возьмем сходящуюся к той же точке последовательность $$ x»_n = \left\{ \frac{2}{(4n + 1)\pi} \right\}, $$
для которой %%\lim{x»_n} = +0%%, %%f(x»_n) = \sin{\big((4n + 1)\pi/2\big)} \equiv 1%% и %%\lim\big\{f(x»_n)\big\} = 1%%. Аналогично для последовательности $$ x»»_n = \left\{-\frac{2}{(4n + 1)\pi} \right\}, $$
также сходящейся к точке %%x = 0%%, %%\lim\big\{f(x»»_n)\big\} = -1%%.
Все три последовательности дали разные результаты, что противоречит условию определения по Гейне, т.е. данная функция не имеет предела в точке %%x = 0%%.
Теорема
Определение предела по Коши и по Гейне эквивалентны.
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Определение 1. ПустьЕ – бесконечное множество. Если любая окрестностьсодержит точки множестваЕ , отличные от точкиа , тоа называетсяпредельной точкой множестваЕ .
Определение 2. (Генрих Гейне
(1821-1881)). Пусть функция
определена на множествеХ иА называетсяпределом функции
в точке(или при
,
если для любой последовательности
значений аргумента
,
сходящейся к,
соответствующая последовательность
значений функциисходится к числуА . Пишут:
Пишут:
.
Примеры . 1) Функция
имеет предел, равныйс , в любой точке
числовой прямой.
Действительно, для любой точки
и любой последовательности значений
аргумента
,
сходящейся ки состоящей из чисел, отличных от,
соответствующая последовательность
значений функции имеет вид
,
а мы знаем, что эта последовательность
сходится кс . Поэтому
.
2) Для функции
.
Это очевидно, так как если
,
то и
.
3) Функция Дирихле
не имеет предела ни в одной точке.
Действительно, пусть
и
,
причем все–
рациональные числа. Тогда
для всехn , поэтому
.
Если же
и все–
иррациональные числа, то
для всехn , поэтому
.
Мы видим, что условия определения 2 не
выполняются, поэтому
4)
.
Действительно, возьмем произвольную
последовательность
,
сходящуюся к
числу 2. Тогда . Что и требовалось доказать.
Определение 3. (Коши (1789-1857)). Пусть
функция
Пусть
функция
определена на множествеХ и– предельная точка этого множества.
ЧислоА называетсяпределом функции
в точке(или при
,
если для любого
найдется
,
такое, что для всех значений аргументах , удовлетворяющих неравенству
,
справедливо неравенство
.
Пишут:
.
Определение Коши можно дать и с помощью окрестностей, если заметить, что , а:
пусть функция
определена на множествеХ и– предельная точка этого множества.
ЧислоА называется пределом функции
в точке,
если для любой-окрестности
точкиА
найдется проколотая-
окрестность точки
.
Это определение полезно проиллюстрировать рисунком.
Пример 5.
.
Действительно, возьмем
произвольно и найдем
,
такое, что для всехх , удовлетворяющих
неравенству
выполняется неравенство
.
Последнее неравенство равносильно
неравенству
,
поэтому видим, что достаточно взять
.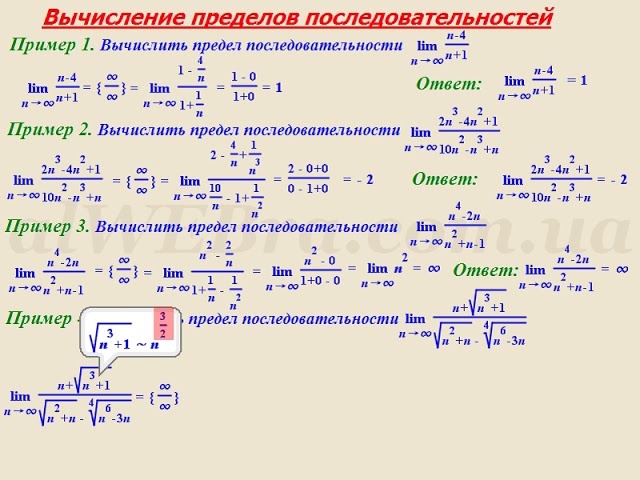 Утверждение доказано.
Утверждение доказано.
Справедлива
Теорема 1. Определения предела функции по Гейне и по Коши эквивалентны.
Доказательство . 1) Пусть
по Коши. Докажем, что это же число является
пределом и по Гейне.
Возьмем
произвольно. Согласно определению 3
существует
,
такое, что для всех
выполняется неравенство
.
Пусть
– произвольная последовательность
такая, что
при
.
Тогда существует номерN такой, что для всех
выполняется неравенство
,
поэтому
для всех
по Гейне.
2) Пусть теперь
по Гейне. Докажем, что
и по Коши.
Предположим противное, т.е. что
по Коши. Тогда существует
такое, что для любого
найдется
,
и
.
Рассмотрим последовательность
.
Для указанного
и любогоn существует
и
.
Это означает, что
,
хотя
,
т.е. числоА не является пределом
в точкепо Гейне. Получили противоречие, которое
и доказывает утверждение. Теорема
доказана.
Теорема
доказана.
Теорема 2 (о единственности предела). Если существует предел функции в точке, то он единственный.
Доказательство . Если предел определен по Гейне, то его единственность вытекает из единственности предела последовательности. Если предел определен по Коши, то его единственность вытекает из эквивалентности определений предела по Коши и по Гейне. Теорема доказана.
Аналогично критерию Коши для последовательностей имеет место критерий Коши существования предела функции. Прежде чем его сформулировать, дадим
Определение 4. Говорят, что функция
удовлетворяет условию Коши в точке,
если для любого
существует
,
таких, что
и
,
выполняется неравенство
.
Теорема 3 (критерий Коши существования
предела). Для того чтобы функция
имела в точкеконечный предел, необходимо и достаточно,
чтобы в этой точке функция удовлетворяла
условию Коши.
Доказательство .Необходимость .
Пусть
. Надо доказать, что
Надо доказать, что
удовлетворяет в точкеусловию Коши.
Возьмем
произвольно и положим
.
По определению предела длясуществует
,
такое, что для любых значений
,
удовлетворяющих неравенствам
и
,
выполняются неравенства
и
.
Тогда
Необходимость доказана.
Достаточность . Пусть функция
удовлетворяет в точкеусловию Коши. Надо доказать, что она
имеет в точкеконечный предел.
Возьмем
произвольно. По определению 4 найдется
,
такое, что из неравенств
,
следует,
что
– это дано.
Покажем сначала, что для всякой
последовательности
,
сходящейся к,
последовательность
значений функции сходится. Действительно,
если
,
то, в силу определения предела
последовательности, для заданного
найдется номерN ,
такой, что для любых
и
.
Поскольку
в точкеудовлетворяет условию Коши, имеем
.
Тогда по критерию Коши для последовательностей
последовательность
сходится. Покажем, что все такие
последовательности
сходятся к одному и тому же пределу. Предположим противное, т.е. что есть
последовательности
Предположим противное, т.е. что есть
последовательности
и
,
,
,
такие, что.
Рассмотрим последовательность.
Ясно, что она сходится к,
поэтому по доказанному выше
последовательностьсходится, что невозможно, так как
подпоследовательности
и
имеют разные пределыи.
Полученное противоречие показывает,
что=.
Поэтому по определению Гейне функция
имеет в точкеконечный предел. Достаточность, а значит
и теорема, доказаны.
Всегда есть предел. Пределы в математике для чайников: объяснение, теория, примеры решений
Хранил в себе один секрет и был в семье примерный муж.
Всё было, вроде, как всегда: жена готовила обед…
Но приключилась вдруг беда: он взял и вспомнил про секрет.
Под шум и кислый запах щей, ворчанье суженой с утра,
Он вспомнил всё до мелочей, как будто было то вчера…
…Она сидела у окна, и мягкий чудный лунный свет
Окрасил в бледные тона её прекрасный силуэт…
Струились пряди по плечам, скользили змейками на грудь…
И он подумал сгоряча: «Женюсь на ней когда — нибудь!»
Он вспомнил всё до мелочей: изгибы линий, мягкость губ…
И жар её простых речей, и за окном огромный дуб.

Сплетенье рук… Слиянье тел… Каскад каштановых волос…
И то, как он её хотел до исступления, до слёз!
Признаний трепетных поток, как он на ушко их шептал!
Смешной над ухом завиток, что от дыханья трепетал…
Она смотрела на него глазами влажными, как ночь.
Слова пьянили, как вино: «Люблю тебя… Роди мне дочь…»
С утра он потерял покой: то суетился, то скучал…
Потом, закрыв лицо рукой, сидел на стуле и молчал.
Жена ворчала, как всегда. Ругала убежавший суп…
И он отметил, что года ей, постаревшей, не к лицу.
Как не идёт ей белый цвет и пряди крашеных волос.
И целых двадцать восемь лет всё как — то было не всерьёз…
Вдруг он вскочил, схватил пальто, забыл про шапку и носки.
Все двадцать восемь лет — не то… Все двадцать восемь зим — тоски.
Нашёл тот дом. У дома — дуб. Взбежал по лестнице стрелой…
Унять бы дрожь с холодных губ, и трусость гадкую — долой!
Наверное, она сейчас пьет чай и кутается в шаль…
И из её прекрасных глаз струится тихая печаль…
А может, принялась вязать? А может кружево плести?
Так много надо ей сказать! А главное сказать — прости…
Открыла дверь… В глазах — вопрос.
 Ей было снова двадцать лет…
Ей было снова двадцать лет…Каскад каштановых волос… Знакомый сердцу силуэт…
Над ухом — лёгкий завиток… Как много лет назад — точь в точь…
» Вы не ошиблись?» — Нет, не мог… Вы Аня? » Вера. Её дочь…»
» А Аня?»- » Мамы больше нет… Кто Вы?» Он повернулся вспять:
«Я шёл к ней двадцать восемь лет…» — Она ждала Вас… Двадцать пять…
Как закружилась голова… Как сердце ухнуло в груди!
И вспомнил он её слова с мольбою: «Ты не уходи!»
Он сгорбился. Поплёлся прочь. Сплетенье рук… Слиянье тел…
Люблю тебя… Роди мне дочь… А он ведь вправду дочь хотел.
Как странно. Ани больше нет… Заплакал… Бросил в тишину:«Я буду много — много лет любить тебя… Тебя одну…»
P.S. БЕРЕГИТЕ ЛЮБОВЬ — она фундамент вашего счастья…
Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim — от английского limit — предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача — найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют , читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.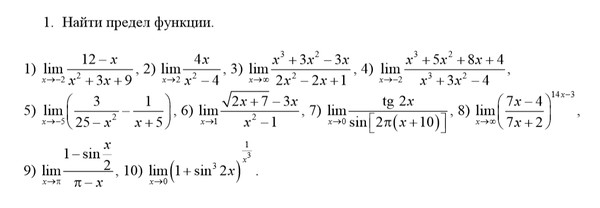
Кстати! Для наших читателей сейчас действует скидка 10% на
Еще один вид неопределенностей: 0/0
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Знай, у каждого разное «больно»,
Знай, у каждого разное «страшно».
Не суди со своей колокольни
Неизвестносколькоэтажной.
Не очерчивай взглядом границы,
Не придумывай мозгом пределы.
Что тебе в страшном сне не приснится,
Для кого-то – обычное дело.
Знай, у каждого разное «надо»,
Знай, у каждого разное «сложно».
Впрочем, и представление ада
Обобщить и сравнить невозможно.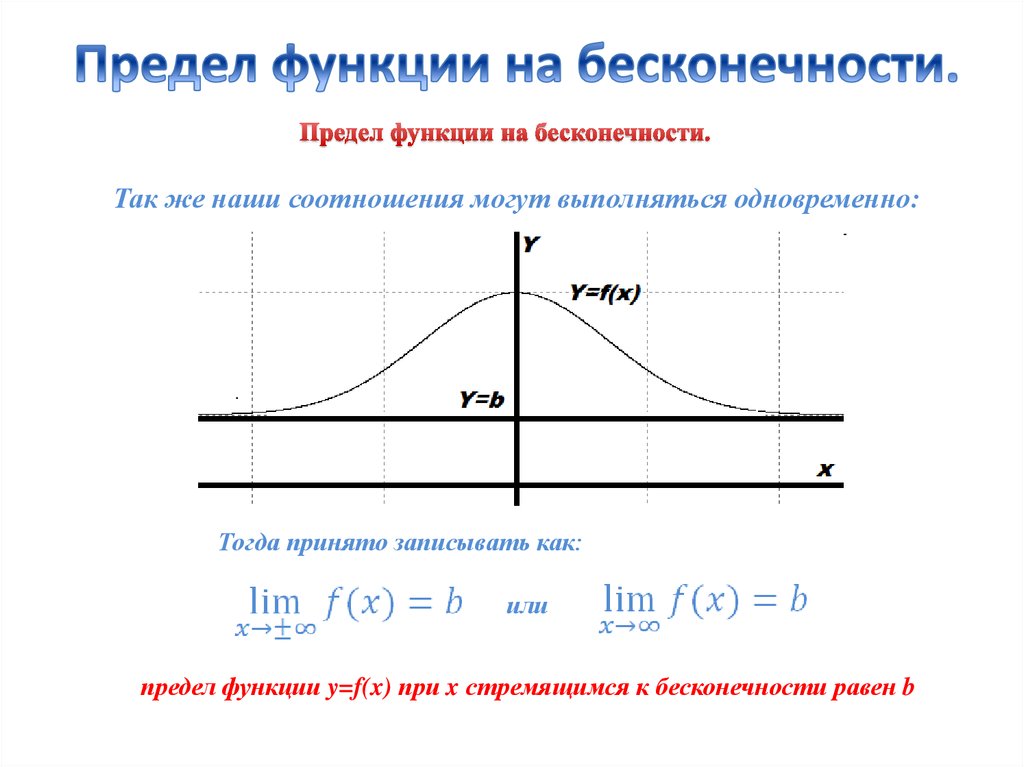
Знай, что правда бывает другая,
А не та, что приносят на блюде.
Присмотрись к тем, чьи судьбы пугают,
Это – самые сильные люди.
Не говори, что я тебя не помню —
Я помню всё, и много раз на дню
Я повторяю номер телефонный,
Но никогда тебе не позвоню.
Вот-вот, казалось, сердце разорвется
И на пределе одиноких дней
За горизонт зашли в душе моей.
Была любовь, была любовь, была!
И к этой фразе нечего прибавить.
Сгорел волшебный замок наш дотла
И пепла не оставил нам на память.
Я помню всё, и сад цветущий помню,
И сквозь листву — лучи со всех сторон,
Как будто с белой-белой колокольни
В душе — ты слышишь — льётся тихий звон.
Любовь ушла и больше не вернётся,
И чтоб не вечно тосковать о ней,
Твои глаза, как два печальных солнца,
За горизонт зашли в душе моей.
За счастьем погоня опять неудачна…
И вечер дождливый, на улице мрачно…
А в детстве…намазала булку вареньем
И точно счастливая, до одуренья…
Гламур, этикет, бриллианты, джакузи…
Теперь, кроме счастья, в судьбе «All inclusive»,
А в детстве с подсолнуха семечки ела,
И счастью, казалось, не будет предела…
Мы стали похожи на клоунов очень…
У каждого грим, что снаружи хохочет…
А в детстве… лишь солнце с небес пробивалось
И сердце счастливое так улыбалось…
Людей отбираем, как в «Золушке» гречку…
Всех нужных – в контакты… Невыгодных в печку…
А в детстве в нас верило чистое небо…
Где радость от запаха свежего хлеба?
И дружба теперь покупается тоже…
Дожились… Живём в мире меха и кожи…
А в детстве дворнягу от ливня спасали…
И счастье давая, его получали.
Мы искренность, чуткость теряли с годами…
Границы и рамки придумали сами…
Есть булка и банка с вишнёвым вареньем?
Так будьте счастливыми, до одуренья!
Я смотрю на тебя и понимаю, что по-прежнему люблю тебя. Эта любовь — хроническая болезнь последних лет. Она приносит настолько нестерпимую боль, что я кидаюсь на совершенно посторонних людей, пытаясь обмануться ими, с ними вдруг в этих объятиях найду то самое обезболивающее, которое, по словам обладателей морщинистых сердец, вообще не существует. Я понимаю, что обманываюсь, но все равно продолжаю обниматься-убиваться не могу иначе, болит ведь, изводит, по ночам спать не дает, вот сижу на подоконнике и, еще минута, истошно закричу от пыток иллюзий. Обратиться к тебе за помощью? Бесполезно. Ты знаешь о моей любви, но тебе она ни к чему, «своих невысказанных чувств полный рот». Мы в одной паутине безответности, но не можем помочь друг другу. Ты обхватываешь руками тонкие белые нити-прутья и смотришь куда-то за пределы реальности, надеясь черт знает на чью помощь. И разница между нами одна: моя любовь к тебе почти сбила меня с ног, а твоя любовь к кому-то — подпитывает, оживляет тебя ожиданием, пусть и обманчивым. Я больше не хочу смотреть на тебя, я прогоняю возможность тебя из сердца, но от этого еще больнее. Вот и проходится шепотом страдать, тоже надеясь черт знает на чью помощь. Времени?..
И разница между нами одна: моя любовь к тебе почти сбила меня с ног, а твоя любовь к кому-то — подпитывает, оживляет тебя ожиданием, пусть и обманчивым. Я больше не хочу смотреть на тебя, я прогоняю возможность тебя из сердца, но от этого еще больнее. Вот и проходится шепотом страдать, тоже надеясь черт знает на чью помощь. Времени?..
Ваша жизнь — сплошное вранье, порнуха, бытовуха, интернет-зависимость и сотово-мобильное рабство. Ну разве я не прав? Вот скажите мне, вы когда-нибудь совершали что-нибудь по настоящему из ряда вон? Никогда. И не сможете. Знаете почему? Потому что все это находится за пределами вашей зоны комфорта. Вы упакованы в нее. Как в полипропиленовый мешок. Вы куски мяса, зажатые рамками быта и работы. Или я не прав? Может, я ошибаюсь? Поправьте меня.
Например, можете подарить свой мобильник первому встречному? А? Вопрос на засыпку. Можете прямо сейчас отформатировать винт на вашем компьютере? Стремно? Обосрались? А знаете, почему вы этого не сделаете? Потому что это равноценно самоубийству. Вы без этого не существуете.
Вы без этого не существуете.
«За пределами США нельзя объяснить ничего, кроме Супермена» – Архив
- Ваш доклад на конференции «Гаража» посвящен понятию «пост» — а после чего живет современное российское общество? Насколько, с вашей точки зрения, изменились процессы в искусстве, в культуре в целом? Нам всем здесь кажется, что все чудовищно поменялось.
- Во-первых,
я живу тоже после, а именно — после эмиграции в 1981 году. Таким образом, со
стороны мне трудно что-то сказать. Хотя можно кое-что заметить. Когда я приехал
в Москву в этот раз, у меня было очень приятное ощущение, надо сказать. Москва
напомнила мне Москву 70-х годов. Конечно, речь идет не о возвращении в 70-е
годы идеологическом, просто народ такой тихий, неагрессивный, нет коммерческой
рекламы. Mатери сидят с детьми на
бульварах. Что поменяло Москву в 90-е, когда я приезжал сюда в первый раз после
эмиграции, — это коммерческая реклама. Огромное количество растяжек.
 Помню, что
они все носили такой абсурдный характер. Первая реклама, которая меня поразила,
это была растяжка через Тверскую: «Если вы пошлете ваш инпут на наш сайт, то
получите наш аутпут на вашем терминале». Это высказывание меня глубоко
потрясло. То, что подобной рекламы больше нет, для меня это заметное изменение. Другое дело — на что
это указывает.
Помню, что
они все носили такой абсурдный характер. Первая реклама, которая меня поразила,
это была растяжка через Тверскую: «Если вы пошлете ваш инпут на наш сайт, то
получите наш аутпут на вашем терминале». Это высказывание меня глубоко
потрясло. То, что подобной рекламы больше нет, для меня это заметное изменение. Другое дело — на что
это указывает.
- Но возрождается очень сильная пропаганда, в каких-то ужасных формах. Как вам кажется, почему власть обращается к таким избитым и устаревшим конструктам, ведь очевидно, что во всем мире работает совсем другая схема?
- Это
глубокое заблуждение. Во всем мире происходит совершенно то же самое, и Россия
не исключение. Сейчас рушится глобализм, который был создан холодной войной. Эта машина перестала работать,
и все перестало работать. В Турции, например, снова ввели османский язык,
который был запрещен Ататюрком. В Китае все говорят только о Конфуции. В
мусульманском мире — салафизм, это все возвращение к исламу времен пророка.
 Даже в моей нынешней стране, в Америке, появилась Tea Party — против
гомосексуализма, за религиозные и семейные ценности, за hard working man.
Нельзя сказать, что это неожиданная комбинация идеологических штампов. Так что
мне кажется, что все страны сейчас идут назад идеологически, очень далеко, даже Россия возвращается не во
времена Сталина, а к началу XX века, другие страны — к Средневековью. Все идут
к истокам, ищут культурную идентичность. Все пытаются определиться и найти свое
место через обращение к очень простым формулам своей культурной идентичности.
Определение происходит в глобальном пространстве конкуренции. Был создан
огромный мировой рынок, где происходит конкуренция. Для того чтобы удачно
конкурировать, нужно иметь то, что называется «человеческий капитал», а это и
есть основы — семья, своя старая культура, традиция.
Даже в моей нынешней стране, в Америке, появилась Tea Party — против
гомосексуализма, за религиозные и семейные ценности, за hard working man.
Нельзя сказать, что это неожиданная комбинация идеологических штампов. Так что
мне кажется, что все страны сейчас идут назад идеологически, очень далеко, даже Россия возвращается не во
времена Сталина, а к началу XX века, другие страны — к Средневековью. Все идут
к истокам, ищут культурную идентичность. Все пытаются определиться и найти свое
место через обращение к очень простым формулам своей культурной идентичности.
Определение происходит в глобальном пространстве конкуренции. Был создан
огромный мировой рынок, где происходит конкуренция. Для того чтобы удачно
конкурировать, нужно иметь то, что называется «человеческий капитал», а это и
есть основы — семья, своя старая культура, традиция.
- Разве это называется человеческим капиталом? А не молодые активные специалисты?
- Если
человек молодой, то ему что хочется? Выпить.
 Расслабиться, покурить, выпить и
have good time. Вместо этого в ситуации конкуренции он должен сидеть чего-то
учить, конкурировать с другими, по 8–10 часов чем-то заниматься. То есть вести
ненормальный образ жизни. Для того чтобы иметь энергию вести этот ненормальный
образ жизни, он должен быть уверен:
а) в своем превосходстве над остальными, иначе он этим заниматься не будет и б)
что у него есть цель кому-то что-то доказать.
Расслабиться, покурить, выпить и
have good time. Вместо этого в ситуации конкуренции он должен сидеть чего-то
учить, конкурировать с другими, по 8–10 часов чем-то заниматься. То есть вести
ненормальный образ жизни. Для того чтобы иметь энергию вести этот ненормальный
образ жизни, он должен быть уверен:
а) в своем превосходстве над остальными, иначе он этим заниматься не будет и б)
что у него есть цель кому-то что-то доказать.
- То есть мировое обращение к традиционным ценностям…
- …имеет
дисциплинарный характер. Знаете, есть теория культурных противоречий
капитализма, которую выдвинул Дэниел Белл. Ее смысл заключается в том, что в условиях капитализма один и тот же
человек является и производителем, и потребителем, в отличие от традиционных
классовых обществ, где потребитель и производитель были разведены. Например,
крепостные крестьяне работали, а помещик потреблял. Сегодня вы и работаете, и
потребляете. Есть дисциплинированный, ответственный человек, который должен сидеть по 8 часов за столом и заниматься делами, которые по большей
части ему неинтересны, в том числе если он молодой специалист.
 С другой
стороны, он должен быть спонтанным,
в любой момент готовым сорваться с
места, купить аппарат для подводного
плавания и отправиться куда-то на Канары. То есть он должен обладать двумя
наборами качеств, в принципе не совместимых друг с другом. Это создает
невыносимую нагрузку на психику человека, потому что в каждый конкретный момент
он не знает, как поступить: пойти гулять с любимой девушкой или пойти
просиживать задницу, заполняя ведомости. Для того чтобы разрешить эту коллизию,
он обращается к Корану или к Ветхому
Завету, где читает «есть время просиживать задницу и время ехать на
Канары».
С другой
стороны, он должен быть спонтанным,
в любой момент готовым сорваться с
места, купить аппарат для подводного
плавания и отправиться куда-то на Канары. То есть он должен обладать двумя
наборами качеств, в принципе не совместимых друг с другом. Это создает
невыносимую нагрузку на психику человека, потому что в каждый конкретный момент
он не знает, как поступить: пойти гулять с любимой девушкой или пойти
просиживать задницу, заполняя ведомости. Для того чтобы разрешить эту коллизию,
он обращается к Корану или к Ветхому
Завету, где читает «есть время просиживать задницу и время ехать на
Канары».Короче говоря, народная мудрость, национальные традиции и так далее обладают успокоительным и одновременно дисциплинирующим влиянием на человека в условиях международной конкуренции, тем более что эти традиции сведены практически к нулю. Ни один человек, исповедующий ислам, не знает до конца, в чем он заключается. Ни один человек, исповедующий коммунистические ценности, не знает, в чем они заключаются.
 Ни один человек, которому нравится Сталин, не
знает толком, что тот делал. Речь
идет о наборе символических знаков, или
сигнификатов, как говорили во времена моей молодости. Усвоение и оперирование
ими никакой нагрузки не составляет, тогда как раньше люди все еще читали
святцы, например. Ergo, можно на нулевом напряжении приобрести себе идеологию.
Помните думающего рабочего? Он три года читал по несколько часов после работы «Капитал» Маркса. Представьте себе, кто сейчас на это способен? Ergo, создается
идеология на нулевом напряжении, но эта идеология обладает стабилизирующей функцией, и
этот стабилизационный механизм включается всегда в любой стране. И поэтому все
страны на глазах становятся более консервативными.
Ни один человек, которому нравится Сталин, не
знает толком, что тот делал. Речь
идет о наборе символических знаков, или
сигнификатов, как говорили во времена моей молодости. Усвоение и оперирование
ими никакой нагрузки не составляет, тогда как раньше люди все еще читали
святцы, например. Ergo, можно на нулевом напряжении приобрести себе идеологию.
Помните думающего рабочего? Он три года читал по несколько часов после работы «Капитал» Маркса. Представьте себе, кто сейчас на это способен? Ergo, создается
идеология на нулевом напряжении, но эта идеология обладает стабилизирующей функцией, и
этот стабилизационный механизм включается всегда в любой стране. И поэтому все
страны на глазах становятся более консервативными. Вот у меня были турецкие студенты в Нью-Йорке в прошлом году. Они участвовали в каких-то демонстрациях на родине и пришли к выводу, что они хотят быть истинными турками, надоели им все эти либеральные ценности. В Турции у нас, говорят они, плохо, потому что турки все недостаточно истинные турки, все они подвержены западной цивилизации, поэтому мы решили создать зону истинной турецкости, где нет никакого пересечения с нетурецким.
 Я спросил у
них: что, в Берлине? Они говорят, ну конечно, в Берлине.
Я спросил у
них: что, в Берлине? Они говорят, ну конечно, в Берлине.
- У вас был тезис об индустриализации интеллектуального труда и о превращении интеллектуальных работников в новый пролетариат. Если знать эти процессы и посмотреть на историю, что будет следующим этапом? Ведь у пролетариев был идеал построения коммунизма — а какой идеал должен быть тут?
- Не
просматривается. Во-первых, мы находимся в самом начале процесса эксплуатации
умственного труда. К тому моменту, как рабочие начали бороться за свои права,
уже 200–300 лет прошло. А здесь пройдет больше. Это первое. Второе, что очень
важно, в чем заключается разница между рабочим движением и нынешней ситуацией:
каждый рабочий был занят своей работой. Это критиковал Маркс в том числе. Один
рабочий что-то привинчивает, другой что-то отвинчивает, их труд специализирован
и отчужден. Но теперь мы видим, что это их и спасало. Это создавало механизм солидарности. Если один отвинчивает, а другой
привинчивает, они не портят друг другу жизнь.
 Они могут объединиться и
выдвинуть совместные требования, потому что они не конкурируют. Мы же живем в
обществе, где каждый делает все. И каждый делает одинаково. С одной стороны,
растет вот эта спецификация вроде «я мусульманин». Но труд сам по себе построен
на том, что все делают одно и то же. Во-первых, все работают в одном и том же
месте — в интернете; во-вторых, кто бы что ни делал, все конкурируют со всеми — и солидарность в принципе невозможна. Субъект нынешнего положения вещей не
только производитель и потребитель в одно и то же время, что ломает его
психику, он еще рабочий и буржуа в одно и то же время. Работает он как
рабочий, а конкурирует как буржуа. Почему возможна пролетарская революция?
Потому что пролетариат может объединиться. Буржуазия не может объединиться,
потому что каждый буржуа конкурирует с другим буржуа. Объединяются они только в
случае кризиса, но в нормальное время это невозможно.
Они могут объединиться и
выдвинуть совместные требования, потому что они не конкурируют. Мы же живем в
обществе, где каждый делает все. И каждый делает одинаково. С одной стороны,
растет вот эта спецификация вроде «я мусульманин». Но труд сам по себе построен
на том, что все делают одно и то же. Во-первых, все работают в одном и том же
месте — в интернете; во-вторых, кто бы что ни делал, все конкурируют со всеми — и солидарность в принципе невозможна. Субъект нынешнего положения вещей не
только производитель и потребитель в одно и то же время, что ломает его
психику, он еще рабочий и буржуа в одно и то же время. Работает он как
рабочий, а конкурирует как буржуа. Почему возможна пролетарская революция?
Потому что пролетариат может объединиться. Буржуазия не может объединиться,
потому что каждый буржуа конкурирует с другим буржуа. Объединяются они только в
случае кризиса, но в нормальное время это невозможно.Вот, говорят, есть классы — буржуазия и пролетариат. Буржуазию считают классом только рабочие.
 Но буржуа не
считают себя классом, и вот этот буржуазный индивидуализм сейчас стал
универсальным. Это означает, что каждый индивидуалист, каждый знает только свои
интересы, интересы эти таковы же, как и
интересы всех остальных. Именно
поэтому они противоречат интересам
остальных. Каждый может делать работу каждого, и каждый делает все. Вы сами
себе готовите, сами себя обслуживаете, сами обставляете квартиру, сами делаете
заказы. Это на моих глазах произошло — я вообще не знал горя раньше, секретарши заказывали билеты и
гостиницы. Сейчас я все делаю сам. Вы должны сесть к компьютеру, посмотреть
предложения и заплатить со своей карточки. Например, в Нью-Йорке закрыли все туристические агентства, почти все
медицинские организации, кроме очень высокооплачиваемых специалистов.
Невозможно, очень дорого. Если у вас есть какая-то болезнь, вы идете на
специальный сайт, выясняете, как ее лечить, потом идете в аптеку и покупаете
то, что вам нужно. Раньше этого нельзя было сделать, а сейчас все
либерализовалось.
Но буржуа не
считают себя классом, и вот этот буржуазный индивидуализм сейчас стал
универсальным. Это означает, что каждый индивидуалист, каждый знает только свои
интересы, интересы эти таковы же, как и
интересы всех остальных. Именно
поэтому они противоречат интересам
остальных. Каждый может делать работу каждого, и каждый делает все. Вы сами
себе готовите, сами себя обслуживаете, сами обставляете квартиру, сами делаете
заказы. Это на моих глазах произошло — я вообще не знал горя раньше, секретарши заказывали билеты и
гостиницы. Сейчас я все делаю сам. Вы должны сесть к компьютеру, посмотреть
предложения и заплатить со своей карточки. Например, в Нью-Йорке закрыли все туристические агентства, почти все
медицинские организации, кроме очень высокооплачиваемых специалистов.
Невозможно, очень дорого. Если у вас есть какая-то болезнь, вы идете на
специальный сайт, выясняете, как ее лечить, потом идете в аптеку и покупаете
то, что вам нужно. Раньше этого нельзя было сделать, а сейчас все
либерализовалось. Лечи себя сам, учи себя сам — что бы вы ни хотели сделать,
вам говорят: вот веб-сайт, обратитесь туда. Это означает, что каждый полностью
замкнут, индивидуализирован, занят 24 часа в сутки, все делают одно и то же и
не могут договориться. Это и есть ситуация индивидуума, который полурабочий,
полубуржуа.
Лечи себя сам, учи себя сам — что бы вы ни хотели сделать,
вам говорят: вот веб-сайт, обратитесь туда. Это означает, что каждый полностью
замкнут, индивидуализирован, занят 24 часа в сутки, все делают одно и то же и
не могут договориться. Это и есть ситуация индивидуума, который полурабочий,
полубуржуа.
- Получается, что добиваться изменений группами, как люди это делали раньше, сейчас невозможно?
- В жизни возможно все. Как люди сейчас добиваются изменений? Они составляют заявку на грант… ну и подают на веб-сайт различным фондам. Сколько денег дали, столько и преобразовывают.
- Почему нон-фикшн становится единственно возможной формой в искусстве? Почему никто не фантазирует?
- Это
я могу точно объяснить. Прежде всего это связано с интернетом. Дело в том, что
сейчас в мире циркулирует информация. Информация не может быть о фикции, только
о фактах. Раньше режимов функционирования языка, как нас учил Роман Якобсон и
многие другие, было два.
 Один режим — информационный, то есть я говорю что-то,
чтобы передать информацию. Вы можете не согласиться с этой информацией или
возразить. Другой — я говорю, не передавая информацию, a демонстрирую работу языка как таковую. Если я пишу роман «Анна
Каренина», я выключаю информационную функцию, и вы не можете мне сказать: «Вы
неправильно изобразили жизнь Анны Карениной, жизнь Анны Карениной была совсем
другой, потому что у меня есть другая информация».
Один режим — информационный, то есть я говорю что-то,
чтобы передать информацию. Вы можете не согласиться с этой информацией или
возразить. Другой — я говорю, не передавая информацию, a демонстрирую работу языка как таковую. Если я пишу роман «Анна
Каренина», я выключаю информационную функцию, и вы не можете мне сказать: «Вы
неправильно изобразили жизнь Анны Карениной, жизнь Анны Карениной была совсем
другой, потому что у меня есть другая информация».Что такое информация? Oна у каждого своя, и если это не так, то это не информация, а искусство. Если мы возьмем эту концепцию Якобсона за исходную, то поймем, что сейчас искусство рухнуло потому же, почему рухнуло все остальное. А именно: раньше границы между фикцией и не фикцией фиксировались институционально. Например, на фабрике производились реальные вещи и полезная информация, а в музее висели фикции. Но сейчас разница между музеем и фабрикой стерлась и больше не существует. Вот вы хотите пойти в музей и обращаетесь на его веб-сайт.
 Веб-сайт сообщает вам — о чем? О реально происходящем в этом
музее. Так же как если вы хотите выяснить, что производится на заводе Форда,
вы идете на сайт, и вам говорят, что там
производятся такие-то и такие-то машины. Что производится в музее? Выставки, лекции, экскурсии. Это все реальные
события, а не фиктивные. Таким образом, само искусство становится реальным.
Кстати, еще до того, как оно начало заниматься фактографией, искусство стало
реальным во времена авангардистов. Смотришь на картину, видишь квадрат, и это
квадрат и есть. Квадрат не является фикцией, это не изображение Борея,
похищающего Орифию, где они оба являются фикциями. Если вы видите писсуар в
музее, то это и есть писсуар. Радикальный авангард с начала XX века начал уничтожать разницу между фактическим и
фиктивным. Перформансы, хеппенинги,
временные выставки, кураторские проекты — все фактичны, и информация о них
является фактической информацией о событии.
Веб-сайт сообщает вам — о чем? О реально происходящем в этом
музее. Так же как если вы хотите выяснить, что производится на заводе Форда,
вы идете на сайт, и вам говорят, что там
производятся такие-то и такие-то машины. Что производится в музее? Выставки, лекции, экскурсии. Это все реальные
события, а не фиктивные. Таким образом, само искусство становится реальным.
Кстати, еще до того, как оно начало заниматься фактографией, искусство стало
реальным во времена авангардистов. Смотришь на картину, видишь квадрат, и это
квадрат и есть. Квадрат не является фикцией, это не изображение Борея,
похищающего Орифию, где они оба являются фикциями. Если вы видите писсуар в
музее, то это и есть писсуар. Радикальный авангард с начала XX века начал уничтожать разницу между фактическим и
фиктивным. Перформансы, хеппенинги,
временные выставки, кураторские проекты — все фактичны, и информация о них
является фактической информацией о событии.В музее вы можете видеть Борея, похищающего Орифию, в одном зале и фотографии и видео Марины Абрамович в другом.
 В первом
случае это фикция, а во втором случае — реальность. Даже если какое-то действие произведено как художественный
акт, его документация не есть искусство
— речь идет о реальной Маринe Абрамович, которая реально себя чем-то
порезала, что, собственно, и было документировано.
Относительно такой документации всегда возможно сказать, что дело было совсем
не так, что на самом деле Марина себя не резала или резала как-то иначе. Таким
образом, переход искусства из зоны фиктивного в зону реального — это долгий
процесс, который занял больше ста лет и в настоящее время завершился. То есть
современный зритель больше не погружается в страну сказки, а выясняет, какое
там субсидирование и так далее. Короче говоря, искусство стало фактичным и
превратилось в информацию. Oтключение информационной
функции языка перестало происходить просто потому, что пропал субъект, который его раньше производил. Такой должности больше нет.
В первом
случае это фикция, а во втором случае — реальность. Даже если какое-то действие произведено как художественный
акт, его документация не есть искусство
— речь идет о реальной Маринe Абрамович, которая реально себя чем-то
порезала, что, собственно, и было документировано.
Относительно такой документации всегда возможно сказать, что дело было совсем
не так, что на самом деле Марина себя не резала или резала как-то иначе. Таким
образом, переход искусства из зоны фиктивного в зону реального — это долгий
процесс, который занял больше ста лет и в настоящее время завершился. То есть
современный зритель больше не погружается в страну сказки, а выясняет, какое
там субсидирование и так далее. Короче говоря, искусство стало фактичным и
превратилось в информацию. Oтключение информационной
функции языка перестало происходить просто потому, что пропал субъект, который его раньше производил. Такой должности больше нет.
- Меня
тут спросили, а что с того, что радикалы уничтожили статую шеду в Ираке, ведь есть копии
в музеях, их миллион раз фотографировали.
 Зачем нам вообще нужны статуи, кроме
научного интереса?
Зачем нам вообще нужны статуи, кроме
научного интереса?
- Скульптуры действительно никому не нужны, чего нельзя сказать об их уничтожении. Интересны не сами скульптуры, а факт их уничтожения. Потому что когда, например, Маринетти и Малевич писали о том, что нужно уничтожить все музеи и все искусство, имеющееся в них, взорвать и сжечь, то этот акт разрушения не был осуществлен. В случае ИГИЛ мы фактически имеем феномен неоавангарда, просто под мусульманским прикрытием. Там есть все признаки авангарда: разрушение музеев, разрушение традиции — они же и мечети уничтожают, что менее известно, — а также характерная для авангарда черно-белая эстетика. Это попытка возрождения какого-то неоавангардного фундаментализма типа раннего Маринетти.
- А византийское иконоборчество не было явлением того же порядка?
- Оно
стопроцентно было явлением того же порядка, и эти явления имели место
многократно. К ним относится, например, Савонарола, как известно, или Кальвин.
 Когда я работал над выставкой,
посвященной иконоклазму (иконоборчеству. — Прим.ред.), то видел
иконы, которые многих сейчас обидели бы. У Христа были выколоты глаза, а у
Богоматери вырезан живот. Это кальвинисты сделали. Уничтожение памятников
советского прошлого в России и других восточноевропейских странах ничем по
своей природе не отличается от разрушения памятников исламистами. Методы те же — бьют молотками, стаскивают с
пьедестала. Вообще, возрождение иконоклазмa пошло из России, когда здесь
Ленина сбрасывали, a переехало на арабский Восток благодаря американцам,
которые посмотрели постсоветскую
хронику и таким же образом сбросили памятники Саддаму Хусейну, когда захватили Ирак. Это стало иконой
американского завоевания Ирака, а ИГИЛ, который поначалу субсидировался американцами против режима Асада, так же как «Аль-Каида» против советской оккупации Афганистана, просто апроприировал современный русский
и восточноевропейский иконоклазм. Современный иконоклазм, как мне кажется, — это постсоциалистический феномен в основе своей.
Когда я работал над выставкой,
посвященной иконоклазму (иконоборчеству. — Прим.ред.), то видел
иконы, которые многих сейчас обидели бы. У Христа были выколоты глаза, а у
Богоматери вырезан живот. Это кальвинисты сделали. Уничтожение памятников
советского прошлого в России и других восточноевропейских странах ничем по
своей природе не отличается от разрушения памятников исламистами. Методы те же — бьют молотками, стаскивают с
пьедестала. Вообще, возрождение иконоклазмa пошло из России, когда здесь
Ленина сбрасывали, a переехало на арабский Восток благодаря американцам,
которые посмотрели постсоветскую
хронику и таким же образом сбросили памятники Саддаму Хусейну, когда захватили Ирак. Это стало иконой
американского завоевания Ирака, а ИГИЛ, который поначалу субсидировался американцами против режима Асада, так же как «Аль-Каида» против советской оккупации Афганистана, просто апроприировал современный русский
и восточноевропейский иконоклазм. Современный иконоклазм, как мне кажется, — это постсоциалистический феномен в основе своей.
- Кажется, что современное искусство гораздо слабее всего этого.
- А в искусстве вообще сейчас ничего не происходит. Искусство как специфическая сфера деятельности просто исчезла, заменилась странными формами поведения. Я всегда говорил моим коллегам, которые слишком увлекались Фуко (а он считал девиантные формы поведения сегодня невозможными, потому что раньше это были признаки святости, а сейчас людей за девиантное поведение сажают в сумасшедший дом), что на самом деле зa девиантные формы поведения перестали сажать в сумасшедший дом, потому что это слишком обременительно, и теперь они опознаются как искусство. Чем ты более девиантен, тем ты более художник.
- Но это ведь то же самое, что в начале XX века, когда все эпатировали.
- Да
это то же самое, что было всегда, просто произведение
искусства перестало производиться, а стало реликвией. Oтступление всей
культуры назад к религии влияет и на
искусство.
 Искусство потеряло статус фиктивного, но приобрело статус реликвии. Вот какой-то человек разбил окно, вот:
а) фотография окна, б) видео, как он его разбивает, и в) осколки, — все это
складывается в инсталляцию, которую можно продать
и приобрести. В чем смысл этой инсталляции? Она отражает реальное событие,
она является напоминанием об этом событии. Вот святой Екатерине отрубили
голову. Вот голова, вот картина, как
ей отрезают голову, вот нож, которым ee отрезали, — это напоминание о том, что
происходит, когда девушки, вместо того чтобы выходить замуж, занимаются
девиантными формами поведения.
Искусство потеряло статус фиктивного, но приобрело статус реликвии. Вот какой-то человек разбил окно, вот:
а) фотография окна, б) видео, как он его разбивает, и в) осколки, — все это
складывается в инсталляцию, которую можно продать
и приобрести. В чем смысл этой инсталляции? Она отражает реальное событие,
она является напоминанием об этом событии. Вот святой Екатерине отрубили
голову. Вот голова, вот картина, как
ей отрезают голову, вот нож, которым ee отрезали, — это напоминание о том, что
происходит, когда девушки, вместо того чтобы выходить замуж, занимаются
девиантными формами поведения.
- Но при этом люди продолжают искусством заниматься?
- Так людей ничем не проймешь, вы же знаете, что люди ко всему с ходу приспосабливаются.
- Сейчас в Москве все молодые художники происходят более или менее из одной компании…
- Это всегда так.
- Однако
вот раньше был, например, сквот в Трехпрудном переулке; эти художники не прославились тем, что были прилежными студентами, они не ходили целыми днями на занятия.
 Сейчас художники
менее богемны, они встречаются на лекциях. Это тоже относится к процессу
замены фикции фактом?
Сейчас художники
менее богемны, они встречаются на лекциях. Это тоже относится к процессу
замены фикции фактом?
- Начнем
с того, что Керенский и Ленин были из одной школы. А вы знали, что Гегель,
Шеллинг и Гельдерлин не только
ходили в одну школу, но и жили в одной комнате пансионата? Все известные американские комики послевоенного поколения учились в одном
классе одной школы. Это показывает, что узок круг. Круг людей, занимающихся чем-то на определенном уровне, очень и
очень узок, большей частью они знакомы с детства, это нормально в нормальной ситуации без резких исторических сдвигов.
Кто является производителем и потребителем интеллектуальных форм искусства? В принципе — это академия. Академия стала массовым явлением. Если вы посмотрите на США, речь идет о миллионах профессоров и десятках миллионов студентов. Это огромный резервуар производителей и потребителей. В каждом университете есть creative arts, это означает, что создана огромная машина производства и потребления.
 Сотни людей приходят на любую более
или менее интересную лекцию. Кто все эти люди? Они из академии, которая
представляет собой очень мощную социальную организацию. Если вы посмотрите на
механизм функционирования культуры сейчас, увидите что high art весь ушел в
академию, все поэты и писатели с
претензиями — профессора. Вы можете заработать сейчас либо на рынке, но он
очень коммерческий, либо вы преподаете.
Сотни людей приходят на любую более
или менее интересную лекцию. Кто все эти люди? Они из академии, которая
представляет собой очень мощную социальную организацию. Если вы посмотрите на
механизм функционирования культуры сейчас, увидите что high art весь ушел в
академию, все поэты и писатели с
претензиями — профессора. Вы можете заработать сейчас либо на рынке, но он
очень коммерческий, либо вы преподаете.Можно преподавать что угодно, терапию можно делать, как Марина Абрамович, то есть брать деньги с богатых людей, или можно преподавать в университете. Экономической и социальной базой высоких форм культуры стала исключительно академия. Если вы выходите на рынок, то вы не можете заключить никакого действительно выгодного договора на книгу, если вы до этого не были известным политиком или актером. Идея, что просто писатель что-то написал, это сейчас звучит странно. Ты должен быть в каждом доме до того, как ты начал писать.
Вы знаете, из-за чего производятся все эти бесконечные сиквелы и приквелы фильмов о супергероях? Из-за того что за пределами США нельзя объяснить ничего, кроме Супермена.
 Люди в Китае, в Индии, в Африке знают Супермена и Бэтмена, а больше
ничего. Китаец не пойдет на американский фильм про американскую жизнь, он
пойдет на свой фильм, изображающий китайскую жизнь. Нo на Супермена он пойдет, потому что в Китае такого не делают. Если учесть, что почти 70% всего дохода американский Голливуд получает за пределами
Соединенных Штатов, то вот вам и объяснение. Вы не можете сейчас конкурировать
на рынке, если вы невероятно не
раскручены по другим каналам: спорт, политика, телевидение. Но вы можете
преподавать, и на деньги, которые зарабатываете, можете жить и писать романы.
Люди в Китае, в Индии, в Африке знают Супермена и Бэтмена, а больше
ничего. Китаец не пойдет на американский фильм про американскую жизнь, он
пойдет на свой фильм, изображающий китайскую жизнь. Нo на Супермена он пойдет, потому что в Китае такого не делают. Если учесть, что почти 70% всего дохода американский Голливуд получает за пределами
Соединенных Штатов, то вот вам и объяснение. Вы не можете сейчас конкурировать
на рынке, если вы невероятно не
раскручены по другим каналам: спорт, политика, телевидение. Но вы можете
преподавать, и на деньги, которые зарабатываете, можете жить и писать романы.
- Но ведь даже в литературе очень популярно возрождение старых форм, вот хоть «Щегол» Донны Тарт, стилизованный под большой классический роман.
- Да,
но это потому что люди знают, что такое Ренессанс. Культура сейчас абсолютно
тавтологична, люди хотят читать про то, что они уже очень хорошо знают. Но,
кстати, студенты, если посмотреть на это с другой стороны, живут так же, как
наше поколение в 70-е годы.
 Я преподаю европейскую философию. Один из моих
студентов играет по вечерам в ресторане на гoбое,
другой пишет программы. Оба занимаются философией.
Я преподаю европейскую философию. Один из моих
студентов играет по вечерам в ресторане на гoбое,
другой пишет программы. Оба занимаются философией.
- То есть зарабатывают одним и занимаются другим?
- Абсолютно. Вообще, это началось в Берлине, из Восточного Берлина перешло в Западный, а оттуда сейчас переходит в крупные города. Этот образ жизни — зарабатывать одним и делать другое — в Америке раньше не был принят. Сейчас благодаря берлинской культуре это становится популярным. Это восточноевропейская модель поведения.
- В России это вообще всегда было принято.
- В России это совершенно нормально. Раньше, когда я только эмигрировал и рассказывал об этом, на меня смотрели с удивлением. А сейчас все очень изменилось.
- То есть это непосредственное влияние раскола после холодной войны?
- Миф Берлина — почему туда все ездят — связан с мифом о
богеме. Берлин оказался тем местом, где западная форма экономики
скомбинировалась с восточным механизмом воспроизводства богемы, и теперь все
там учатся и делают то же самое.
 Бруклин — это тот же Берлин. Я был в Израиле,
ходил по мастерским: все художники живут и
работают в основном в Берлине. Одна только художница мне сказала, что она не такая буржуазная, чтобы жить в
Берлине, поэтому живет в Лейпциге.
Бруклин — это тот же Берлин. Я был в Израиле,
ходил по мастерским: все художники живут и
работают в основном в Берлине. Одна только художница мне сказала, что она не такая буржуазная, чтобы жить в
Берлине, поэтому живет в Лейпциге.
Интервью
- Мария Семендяева
Исчисление I. Определение предела
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Мобильное уведомление
Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-10: Определение предела
В этом разделе мы рассмотрим точное математическое определение трех видов пределов, которые мы рассмотрели в этой главе. Мы рассмотрим точное определение пределов в конечных точках, имеющих конечные значения, пределов в бесконечности и пределов в бесконечности. Мы также дадим точное математическое определение непрерывности.
Давайте начнем этот раздел с определения предела в конечной точке, которая имеет конечное значение.
Определение 1
Пусть \(f\left( x \right)\) — функция, определенная на интервале, содержащем \(x = a\), за исключением, возможно, точки \(x = a\). Тогда мы говорим, что
\[\ mathop {\lim}\limits_{x \to a} f\left(x \right) = L\]
Тогда мы говорим, что
\[\ mathop {\lim}\limits_{x \to a} f\left(x \right) = L\]
если для каждого числа \(\varepsilon > 0\) существует такое число \(\delta > 0\), что
\[\слева| {f\left( x \right) — L} \right| < \varepsilon \hspace{0,5 дюйма}{\mbox{когда бы ни}}\hspace{0,5 дюйма}0 < \left| {х - а} \право| < \ дельта \]
Вау. Это полный рот. Теперь, когда это записано, что это значит?
Давайте посмотрим на следующий график и также предположим, что предел существует.
Определение говорит нам, что для любого числа \(\varepsilon > 0\), которое мы выберем, мы можем перейти к нашему графику и нарисовать две горизонтальные линии в точках \(L + \varepsilon \) и \(L — \varepsilon\), как показано на графике выше. Затем где-то в мире есть еще одно число \(\delta > 0\), которое нам нужно будет определить, что позволит нам добавить две вертикальные линии к нашему графику в точках \(a + \delta \) и \ (а — \дельта\).
Если взять любой \(x\) в розовой области, т.е. между \(a + \delta\) и \(a — \delta\), то этот \(x\) будет ближе к \ (a\), чем любой из \(a + \delta\) и \(a — \delta\). Или
\[\слева| {х — а} \право| < \ дельта \]
Если теперь мы идентифицируем точку на графике, которую дает наш выбор \(х\), то эта точка на графике будет лежать на пересечении розовой и желтой областей. Это означает, что значение этой функции \(f\left( x \right)\) будет ближе к \(L\), чем любое из \(L + \varepsilon \) и \(L — \varepsilon \). Или,
\[\слева| {f\left( x \right) — L} \right| <\varepsilon\]
Если мы возьмем любое значение \(x\) в розовой области, то график для этих значений \(x\) будет лежать в желтой области.
Обратите внимание, что на самом деле существует бесконечное количество возможных \(\delta\), которые мы можем выбрать. На самом деле, если мы вернемся назад и посмотрим на график выше, похоже, что мы могли бы взять немного большую \(\delta\) и все же получить график из этой розовой области, чтобы он полностью содержался в желтой области.
Кроме того, обратите внимание, что, как следует из определения, нам нужно только убедиться, что функция определена в некотором интервале вокруг \(x = a\), но нам все равно, определена ли она в \(x = a\). \). Помните, что пределам все равно, что происходит в данной точке, им важно только то, что происходит вокруг рассматриваемой точки.
Хорошо, теперь, когда мы разобрались с определением и попытались его понять, давайте посмотрим, как оно используется на практике.
Иногда это немного сложно, и может потребоваться много практики, чтобы добиться успеха в этом, поэтому не расстраивайтесь, если вы не разберетесь с этим сразу. Мы рассмотрим пару примеров, которые работают довольно легко. 92} < \varepsilon \hspace{0,5 дюйма} \Rightarrow \hspace{0,5 дюйма}\left| х \ справа | <\sqrt\varepsilon\]
Теперь результаты этого упрощения очень похожи на \(0 < \left| x \right| < \delta \), за исключением части «\(0 < \)». Однако отсутствие этого не является проблемой, оно просто говорит нам, что мы не можем взять \(x = 0\). Итак, похоже, что если мы выберем \(\delta = \sqrt \varepsilon \), мы должны получить то, что хотим.
Итак, похоже, что если мы выберем \(\delta = \sqrt \varepsilon \), мы должны получить то, что хотим.
Далее нам нужно убедиться, что наш выбор \(\delta \) даст нам то, что мы хотим, 92}} \право| < \varepsilon \hspace{0,5 дюйма}{\mbox{когда бы ни}}\hspace{0,5 дюйма}0 < \left| х \ справа | <\sqrt\varepsilon\]
Верификация — это практически та же самая работа, которую мы проделали, чтобы получить предположение. Во-первых, пусть снова \(\varepsilon > 0\) будет любым числом, а затем выберем \(\delta = \sqrt \varepsilon \). Теперь предположим, что \(0 < \left| x \right| < \sqrt \varepsilon \). Нам нужно показать, что, выбирая \(x\), чтобы удовлетворить этому, мы получим, 92} = 0\]
Это может быть немного сложно в первые несколько раз. Особенно, когда кажется, что мы должны сделать работу дважды. В предыдущем примере мы несколько упростили левое неравенство, чтобы получить наше предположение относительно \(\delta \), а затем, по-видимому, проделали точно такую же работу, чтобы затем доказать, что наше предположение было правильным. Часто это работает именно так, хотя вскоре мы увидим пример, когда все работает не так хорошо.
Часто это работает именно так, хотя вскоре мы увидим пример, когда все работает не так хорошо.
Итак, сказав это, давайте взглянем на немного более сложный предел, хотя он все же будет довольно похож на первый пример.
Пример 2 Используйте определение предела, чтобы доказать следующий предел. \[\ mathop {\lim}\limits_{x \to 2} 5x — 4 = 6\]
Показать решение
Мы начнем с этого так же, как и с первым. Однако мы не будем давать такое же количество объяснений.
Начнем с того, что пусть \(\varepsilon > 0\) будет любым числом, затем нам нужно найти число \(\delta > 0\), чтобы следующее было верным.
\[\слева| {\ влево ( {5x — 4} \ вправо) — 6} \ вправо | < \varepsilon \hspace{0,5 дюйма}{\mbox{когда бы ни}}\hspace{0,5 дюйма}0 < \left| {х - 2} \право| < \ дельта \]
Мы начнем с упрощения левого неравенства, пытаясь вычислить \(\delta \). Выполнение этого дает,
Выполнение этого дает,
\[\слева| {\ влево ( {5x — 4} \ вправо) — 6} \ вправо | = \ влево | {5x — 10} \право| = 5\влево| {х — 2} \право| < \varepsilon \hspace{0.5in} \Rightarrow \hspace{0.5in}\left| {х - 2} \право| < \ гидроразрыва {\ varepsilon} {5} \]
Итак, как и в первом примере, похоже, если мы достаточно упростим левое неравенство, мы получим что-то очень похожее на правое неравенство, и это приведет нас к выбору \(\delta = \frac{\varepsilon } {5}\).
Давайте теперь проверим это предположение. Итак, снова пусть \(\varepsilon > 0\) будет любым числом, а затем выберите \(\delta = \frac{\varepsilon}{5}\). Далее предположим, что \(0 < \left| {x - 2} \right| < \delta = \frac{\varepsilon }{5}\), и мы получим следующее,
\[\begin{выравнивание*}\left| {\ влево ( {5x — 4} \ вправо) — 6} \ вправо | & = \ влево | {5x — 10} \право| & & \hspace{0,25 дюйма}{\mbox{немного упрощаем}}\\ & = 5\left| {х — 2} \право| & & \hspace{0. 225in}{\mbox{большее упрощение}}….\\ & < 5\left( {\frac{\varepsilon} {5}} \right) & & \hspace{0.25in} {\mbox{используйте предположение}}\delta = \frac{\varepsilon}{5}\\ & = \varepsilon & & \hspace{0,25 дюйма}{\mbox{и еще несколько упрощений}}\end{align* }\]
225in}{\mbox{большее упрощение}}….\\ & < 5\left( {\frac{\varepsilon} {5}} \right) & & \hspace{0.25in} {\mbox{используйте предположение}}\delta = \frac{\varepsilon}{5}\\ & = \varepsilon & & \hspace{0,25 дюйма}{\mbox{и еще несколько упрощений}}\end{align* }\]
Итак, мы показали, что
\[\слева| {\ влево ( {5x — 4} \ вправо) — 6} \ вправо | < \varepsilon \hspace{0,5 дюйма}{\mbox{когда бы ни}}\hspace{0,5 дюйма}0 < \left| {х - 2} \право| < \ гидроразрыва {\ varepsilon} {5} \]
и так по нашему определению имеем
\[\ mathop {\lim}\limits_{x \to 2} 5x — 4 = 6\]
Итак, снова процесс, кажется, предполагает, что мы должны по существу переделать всю нашу работу дважды, один раз, чтобы сделать предположение для \(\delta \), а затем еще раз, чтобы подтвердить наше предположение. Давайте сделаем пример, который не работает так хорошо. 92} + x — 11} \справа) — 9} \справа| < \varepsilon \) эквивалентно \(\left| {x + 5} \right|\left| {x - 4} \right| < \varepsilon \). Однако, в отличие от двух предыдущих примеров, здесь у нас есть дополнительный член, которого нет в правильном неравенстве выше. Если у нас есть хоть какая-то надежда продолжить здесь, нам нужно будет найти способ справиться с \(\left| {x + 5} \right|\).
Однако, в отличие от двух предыдущих примеров, здесь у нас есть дополнительный член, которого нет в правильном неравенстве выше. Если у нас есть хоть какая-то надежда продолжить здесь, нам нужно будет найти способ справиться с \(\left| {x + 5} \right|\).
Для этого заметим, что если по какой-то причине мы можем показать, что \(\left| {x + 5} \right| < K\) для некоторого числа \(K\), то мы будем иметь следующее,
\[\слева| {х + 5} \право|\лево| {х — 4} \право| < К\влево| {х - 4} \право|\]
Если мы теперь предположим, что мы действительно хотим показать \(K\left| {x — 4} \right| < \varepsilon \) вместо \(\left| {x + 5} \right|\left |{x - 4} \right|< \varepsilon\) получаем следующее,
\[\слева| {х — 4} \право| < \ гидроразрыва {\ varepsilon} {K} \]
Это начинает казаться знакомым, не так ли?
Однако вся эта работа основана на предположении, что мы можем показать, что \(\left| {x + 5} \right| < K\) для некоторого \(K\). Без этого предположения мы ничего не можем сделать, поэтому давайте посмотрим, сможем ли мы это сделать.
Без этого предположения мы ничего не можем сделать, поэтому давайте посмотрим, сможем ли мы это сделать.
Давайте сначала вспомним, что здесь мы работаем над пределом, и давайте также вспомним, что пределы действительно связаны только с тем, что происходит вокруг рассматриваемой точки, \(x = 4\) в данном случае. Таким образом, можно с уверенностью предположить, что каким бы ни было \(x\), оно должно быть близко к \(x = 4\). Это означает, что мы можем с уверенностью предположить, что чем бы ни было \(x\), оно находится на расстоянии, скажем, от одного из \(x = 4\). Или в терминах неравенства мы можем предположить, что
\[\слева| {х — 4} \право| < 1\]
Почему здесь стоит выбрать 1? Нет другой причины, кроме того, что это хорошее число для работы. Мы могли бы легко выбрать 2, или 5, или \({\textstyle{1 \over 3}}\). Единственная разница, которую сделает наш выбор, — это фактическое значение \(K\), которое мы получим в итоге. Возможно, вы захотите пройти этот процесс с другим выбором \(K\) и посмотреть, сможете ли вы это сделать.
Возможно, вы захотите пройти этот процесс с другим выбором \(K\) и посмотреть, сможете ли вы это сделать.
Итак, давайте начнем с \(\left| {x — 4} \right| < 1\) и избавимся от полос абсолютного значения, и это решит полученное неравенство для \(x\) следующим образом,
\[ — 1 < x - 4 < 1 \ hspace {0,5 дюйма} \ Rightarrow \ hspace {0,5 дюйма} 3 < x < 5 \]
Если мы теперь прибавим 5 ко всем частям этого неравенства, мы получим,
\[8 < х + 5 < 10\]
Теперь, поскольку \(x + 5 > 8 > 0\) (здесь важна положительная часть), мы можем сказать, что при условии \(\left| {x — 4} \right| < 1\) мы знаем, что \(х + 5 = \влево| {х + 5} \вправо|\). Или, если взять двойное неравенство выше, мы имеем,
\[8 < х + 5 = \влево| {х + 5} \право| < 10\hspace{0.5in} \Rightarrow \hspace{0.25in}\,\,\,\,\left| {х + 5} \право| < 10\hspace{0. 5in} \Rightarrow \hspace{0.5in}K = 10\]
5in} \Rightarrow \hspace{0.5in}K = 10\]
Итак, при условии \(\left| {x — 4} \right| < 1\) мы можем видеть, что \(\left| {x + 5} \right| < 10\), что, в свою очередь, дает нам
\[\слева| {х — 4} \право| < \frac{\varepsilon}{K} = \frac{\varepsilon}{{10}}\]
Итак, к этому моменту мы делаем два предположения о \(\left| {x — 4} \right|\) Мы предположили, что
\[\слева| {х — 4} \право| < \ frac{\ varepsilon }{{10}}\hspace{0,5 дюйма}{\mbox{AND}}\hspace{0,5 дюйма}\left| {х - 4} \право| < 1\]
Может показаться, что это не так, но теперь мы готовы выбрать \(\delta \). В предыдущих примерах у нас было только одно предположение, и мы использовали его, чтобы получить \(\delta \). В этом случае у нас есть два, и они ОБЕ должны быть правдой. Итак, пусть \(\delta \) будет меньшим из двух предположений, 1 и \(\frac{\varepsilon}{{10}}\). Математически это записывается как
Математически это записывается как
\[\ delta = \min \left\{ {1,\frac{\varepsilon} {{10}}} \right\}\]
Делая это, мы можем гарантировать, что
\[\ delta \ le \ frac {\ varepsilon }{{10}} \ hspace {0,5 дюйма} {\ mbox {AND}} \ hspace {0,5 дюйма} \ delta \ le 1 \]
Теперь, когда мы сделали выбор для \(\delta \), нам нужно его проверить. Итак, \(\varepsilon > 0\) — любое число, а затем выберите \(\delta = \min \left\{ {1,\frac{\varepsilon} {{10}}} \right\}\). Предположим, что \(0 < \left| {x - 4} \right| < \delta = \min \left\{ {1,\frac{\varepsilon} {{10}}} \right\}\). Во-первых, мы получаем это,
\[0 < \влево| {х - 4} \право| < \ delta \ le \ frac {\ varepsilon }{{10}} \ hspace {0,5 дюйма} \ Rightarrow \ hspace {0,5 дюйма} \ left | {х - 4} \право| < \ гидроразрыва {\ varepsilon} {{10}} \]
Также получаем,
\[0 < \влево| {х - 4} \право| < \delta \le 1\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}\left| {х - 4} \право| < 1\hspace{0,25 дюйма} \Rightarrow \hspace{0,5 дюйма}\left| {х + 5} \право| < 10\] 92} + х - 20} \право| & & \hspace{0,25 дюйма}{\mbox{немного упрощаем}}\\ & = \left| {х + 5} \право|\лево| {х - 4} \право| & & \hspace{0,25 дюйма}{\mbox{коэффициент}}\\ & < 10\left| {х - 4} \право| & & \hspace{0,25in}{\mbox{используйте предположение, что }}\left| {х + 5} \право| < 10\\ & < 10\left ( {\ frac {\ varepsilon }{{10}}} \right) & & \hspace {0,25 дюйма} {\ mbox {используйте предположение, что}}\left| {х - 4} \право| < \frac{\varepsilon }{{10}}\\ & < \varepsilon & & \hspace{0,25 дюйма}{\mbox{небольшое окончательное упрощение}}\end{align*}\] 92} + х - 11 = 9\]
Хорошо, это было намного больше работы, чем первые два примера, и, к сожалению, это не было такой сложной задачей.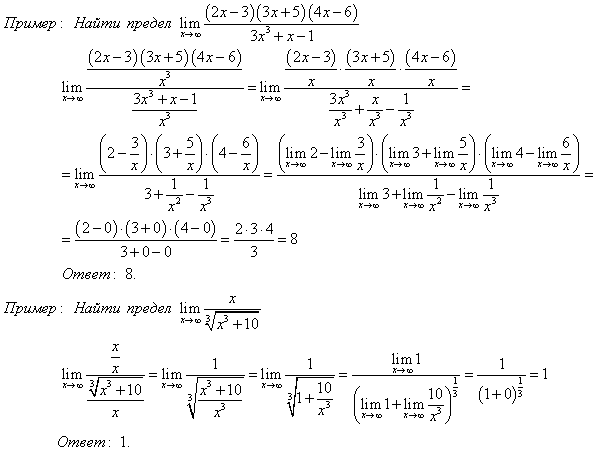 Что ж, возможно, нам следует сказать, что по сравнению с некоторыми другими ограничениями мы могли бы попытаться доказать, что это не так уж и сложно. Когда впервые сталкиваешься с такими доказательствами, использующими точное определение предела, все они могут показаться довольно сложными.
Что ж, возможно, нам следует сказать, что по сравнению с некоторыми другими ограничениями мы могли бы попытаться доказать, что это не так уж и сложно. Когда впервые сталкиваешься с такими доказательствами, использующими точное определение предела, все они могут показаться довольно сложными.
Не расстраивайтесь, если вы не получите эти вещи сразу. Очень часто не сразу это понимают, и приходится немного потрудиться, чтобы полностью понять, как работают такие виды доказательств с определением пределов. 9+ }} f\left( x \right) = L\]
если для каждого числа \(\varepsilon > 0\) существует такое число \(\delta > 0\), что
\[\слева| {f\left( x \right) — L} \right| < \ varepsilon \ hspace {0,5 дюйма} {\ mbox {когда}} \ hspace {0,5 дюйма} 0 < x - a < \ delta \,\,\,\,\,\,\,\left( {{\ mbox{или }}a < x < a + \delta } \right)\]
Определение 3
Для левого предела мы говорим, что \[\ mathop {\lim}\limits_{x \to {a^ -}} f\left(x\right) = L\]
если для каждого числа \(\varepsilon > 0\) существует такое число \(\delta > 0\), что
\[\слева| {f\left( x \right) — L} \right| < \varepsilon \hspace{0. 5in}{\mbox{whenever}}\hspace{0.5in} — \delta < x - a < 0\,\,\,\,\,\,\,\left( {{ \mbox{или }}a - \delta < x < a} \right)\]
5in}{\mbox{whenever}}\hspace{0.5in} — \delta < x - a < 0\,\,\,\,\,\,\,\left( {{ \mbox{или }}a - \delta < x < a} \right)\]
Обратите внимание, что с обоими этими определениями есть два способа справиться с ограничением на \(x\), и тот, что в скобках, вероятно, проще в использовании, хотя основной из них более точно соответствует определению нормального предела. выше. 9+ }} \sqrt х = 0\]
Показать решение
Пусть \(\varepsilon > 0\) будет любым числом, тогда нам нужно найти число \(\delta > 0\), чтобы было верно следующее.
\[\слева| {\ sqrt х — 0} \ справа | < \varepsilon \hspace{0,5 дюйма}{\mbox{когда}}\hspace{0,5 дюйма}0 < x - 0 < \delta \]
Или, немного упростив, нужно показать,
\[\sqrt x < \varepsilon \hspace{0.5in}{\mbox{когда}}\hspace{0.5in}0 < x <\delta \] 9+ }} \sqrt х = 0\]
Теперь перейдем к определению бесконечных пределов. Вот два определения, которые нам нужны, чтобы охватить обе возможности: пределы, которые являются положительной бесконечностью, и пределы, которые являются отрицательной бесконечностью.
Вот два определения, которые нам нужны, чтобы охватить обе возможности: пределы, которые являются положительной бесконечностью, и пределы, которые являются отрицательной бесконечностью.
Определение 4
Пусть \(f\left( x \right)\) — функция, определенная на интервале, содержащем \(x = a\), за исключением, возможно, точки \(x = a\). Тогда мы говорим, что \[\ mathop {\lim}\limits_{x \to a} f\left( x \right) = \infty \]
если для каждого числа \(M > 0\) существует некоторое число \(\delta > 0\) такое, что
\[f\left( x \right) > M\hspace{0.5in}{\mbox{когда}}\hspace{0.5in}0 < \left| {х - а} \право| < \ дельта \]
Определение 5
Пусть \(f\left( x \right)\) — функция, определенная на интервале, содержащем \(x = a\), за исключением, возможно, точки \(x = a\). Тогда мы говорим, что \[\ mathop {\lim}\limits_{x \to a} f\left( x \right) = — \infty \]
, если для каждого числа \(N < 0\) существует такое число \(\delta > 0\), что
\[f\left( x \right) < N\hspace{0. 5in}{\mbox{когда бы ни}}\hspace{0.5in}0 < \left| {х - а} \право| < \ дельта \]
5in}{\mbox{когда бы ни}}\hspace{0.5in}0 < \left| {х - а} \право| < \ дельта \]
В этих двух определениях обратите внимание, что \(M\) должно быть положительным числом, а \(N\) должно быть отрицательным числом. Это различие легко пропустить, если вы не обращаете пристального внимания.
Также обратите внимание, что мы могли бы также записать определения для односторонних пределов, которые равны бесконечности, если бы захотели. Мы оставим это вам, если хотите.
Вот краткий набросок, иллюстрирующий Определение 4.
Определение 4 говорит нам, что независимо от того, насколько большим мы выбираем \(M\), мы всегда можем найти интервал вокруг \(x = a\), учитывая на \(0 < \left| {x - a} \right| < \delta \) для некоторого числа \(\delta \), так что, пока мы остаемся в этом интервале, график функции будет выше линия \(y = M\), как показано на графике выше. Также обратите внимание, что нам не нужно, чтобы функция действительно существовала в точке \(x = a\), чтобы определение выполнялось. 2}}} = \infty\]
92} < \frac{1}{M}\hspace{0,25 дюйма}\,\,\,\,\,\, \Rightarrow \hspace{0,5 дюйма}\left| х \ справа | < \ гидроразрыва {1} {{\ sqrt M}} \]
2}}} = \infty\]
92} < \frac{1}{M}\hspace{0,25 дюйма}\,\,\,\,\,\, \Rightarrow \hspace{0,5 дюйма}\left| х \ справа | < \ гидроразрыва {1} {{\ sqrt M}} \]
Итак, похоже, мы можем выбрать \(\delta = \frac{1}{{\sqrt M }}\). Все, что нам нужно сделать сейчас, это проверить это предположение.
Пусть \(M > 0\) — любое число, выберите \(\delta = \frac{1}{{\sqrt M }}\) и предположите, что \(0 < \left| x \right| < \ гидроразрыв {1}{{\ sqrt M}}\).
В предыдущих примерах мы пытались показать, что наши предположения удовлетворяют левому неравенству, работая с ним напрямую. Однако в этом случае функция и наше предположение относительно \(x\), которое у нас есть на самом деле, облегчит начало с предположения относительно \(x\) и покажет, что мы можем получить из него левое неравенство. Обратите внимание, что это делается таким образом в основном из-за функции, с которой мы работаем, а не из-за типа ограничения, которое у нас есть. 92}}} = \infty\]
Для нашего следующего набора определений пределов давайте рассмотрим два определения пределов на бесконечности. Опять же, нам нужен один для предела плюс бесконечность, а другой для отрицательной бесконечности.
Опять же, нам нужен один для предела плюс бесконечность, а другой для отрицательной бесконечности.
Определение 6
Пусть \(f\left( x \right)\) — функция, определенная на \(x > K\) для некоторого \(K\). Тогда мы говорим, что \[\ mathop {\lim }\limits_{x \to \infty} f\left( x \right) = L\]
, если для каждого числа \(\varepsilon > 0\) существует такое число \(M > 0\), что
\[\слева| {f\left( x \right) — L} \right| < \ varepsilon \ hspace {0,5 дюйма} {\ mbox {когда}} \ hspace {0,5 дюйма} x > M \]
Определение 7
Пусть \(f\left(x\right)\) — функция, определенная на \(x , если для каждого числа \(\varepsilon > 0\) существует такое число \(N < 0\), что \[\слева| {f\left( x \right) — L} \right| < \varepsilon \hspace{0. Чтобы увидеть, о чем говорят нам эти определения, приведем краткий набросок, иллюстрирующий Определение 6. Определение 6 говорит нам, что независимо от того, насколько близко к \(L\) мы хотим получить, математически это определяется выражением \(\left| {f\left( x \right) — L} \right| < \varepsilon \) для любого выбранного \(\varepsilon \) можно найти другое число \(M\) такое, что если взять любое \(x\ ) больше, чем \(M\), то график функции для этого \(x\) будет ближе к \(L\), чем \(L - \varepsilon \) и \(L + \varepsilon \) . Или, другими словами, график будет находиться в заштрихованной области, как показано на скетче ниже. Наконец, обратите внимание, что чем меньше мы делаем \(\varepsilon \), тем больше нам, вероятно, потребуется сделать \(M\). Вот краткий пример одного из этих ограничений. Пример 6. Используйте определение предела, чтобы доказать следующий предел. \[\ mathop {\lim}\limits_{x \to — \infty} \frac{1}{x} = 0\] Показать решение Пусть \(\varepsilon > 0\) будет любым числом, и нам нужно выбрать \(N < 0\) так, чтобы \[\слева| {\ гидроразрыва {1} {х} — 0} \ справа | = \ гидроразрыва {1} {{\ влево | x \right|}} < \varepsilon \hspace{0. Угадать для \(N\) здесь не так уж и плохо. \[\ гидроразрыва {1} {{\ влево | x \right|}} < \varepsilon \hspace{0.5in} \Rightarrow \hspace{0.5in}\left| х \ справа | > \frac{1}{\varepsilon}\] Поскольку мы движемся к отрицательной бесконечности, похоже, мы можем выбрать \(N = — \frac{1}{\varepsilon }\). Обратите внимание, что нам нужен «-», чтобы убедиться, что \(N\) отрицательно (напомним, что \(\varepsilon > 0\)). Давайте проверим, что наше предположение сработает. Пусть \(\varepsilon > 0\) и выберите \(N = — \frac{1}{\varepsilon}\) и предположим, что \(x < - \frac{1}{\varepsilon}\). Как и в предыдущем примере, функция, с которой мы здесь работаем, предполагает, что будет проще начать с этого предположения и показать, что мы можем получить из него левое неравенство. \[\begin{align*}x & < - \frac{1}{\varepsilon }\\ & \left| х \ справа | > \влево| { — \frac{1}{\varepsilon }} \right| & & \hspace{0,25 дюйма}{\mbox{брать абсолютное значение}}\\ & \left| х \ справа | > \frac{1}{\varepsilon } & & \hspace{0,25 дюйма}{\mbox{сделать небольшое упрощение}}\\ & \frac{1}{{\left| x \right|}} < \varepsilon & & \hspace{0. Обратите внимание: когда мы взяли абсолютное значение обеих сторон, мы изменили обе стороны с отрицательных чисел на положительные числа, поэтому также пришлось изменить направление неравенства. Итак, мы показали, что \[\слева| {\ гидроразрыва {1} {х} — 0} \ справа | = \ гидроразрыва {1} {{\ влево | x \right|}} < \varepsilon \hspace{0.5in}{\mbox{whenever}}\hspace{0.5in}x < - \frac{1}{\varepsilon}\] и так по определению предела имеем \[\ mathop {\lim}\limits_{x \to — \infty} \frac{1}{x} = 0\] Для нашего окончательного определения предела давайте рассмотрим пределы в бесконечности, которые также имеют бесконечное значение. Здесь можно определить четыре возможных предела. Пусть \(f\left( x \right)\) — функция, определенная на \(x > K\) для некоторого \(K\). Тогда мы говорим, что
\[\ mathop {\lim }\limits_{x \to \infty} f\left( x \right) = \infty \] если для каждого числа \(N > 0\) существует такое число \(M > 0\), что \[f\left( x \right) > N\hspace{0,5 дюйма}{\mbox{когда бы ни}}\hspace{0,5 дюйма}x > M\] Остальные три определения почти идентичны. Различия заключаются только в знаках \(M\) и/или \(N\) и соответствующих направлениях неравенства. В качестве последнего определения в этом разделе давайте вспомним, что ранее мы говорили, что функция непрерывна, если \[\ mathop {\lim }\limits_{x \to a} f\left( x \right) = f\left(a \right)\] Итак, поскольку непрерывность, как мы определили ее ранее, определяется в терминах предела, мы также можем теперь дать более точное определение непрерывности. Пусть \(f\left( x \right)\) — функция, определенная на интервале, содержащем \(x = a\). Тогда мы говорим, что \(f\left( x \right)\) непрерывно в \(x = a\), если для каждого числа \(\varepsilon > 0\) существует некоторое число \(\delta > 0\) такой, что \[\слева| {е\влево(х\вправо) — ж\влево(а\вправо)} \вправо| < \varepsilon \hspace{0,5 дюйма}{\mbox{когда бы ни}}\hspace{0,5 дюйма}0 < \left| {х - а} \право| < \ дельта \] Это определение очень похоже на первое определение в этом разделе, и, конечно, оно должно иметь некоторый смысл, поскольку именно такой предел мы используем, чтобы показать, что функция непрерывна. Единственная реальная разница заключается в том, что здесь нам нужно убедиться, что функция действительно определена в \(x = a\), в то время как нам не нужно было беспокоиться об этом для первого определения, поскольку ограничения на самом деле не заботятся о том, что происходит в точку. Мы не будем приводить примеры доказательства непрерывности функции в какой-либо точке, в основном потому, что мы уже сделали несколько примеров. Закон о свободе информации содержит указания относительно времени и способа, в котором агентства должны отвечать на запросы. В частности, в §89(3)(a) Закона о свободе информации, в частности, говорится, что: «Каждое юридическое лицо, на которое распространяются положения настоящей статьи, в течение пяти рабочих дней с момента получения письменного запроса на запись с разумным описанием , должен предоставить такую запись лицу, запрашивающему ее, отклонить такой запрос в письменной форме или предоставить письменное подтверждение получения такого запроса и заявление о приблизительной дате, которая должна быть разумной с учетом обстоятельств запроса, когда такой запрос будет предоставлено или отказано. Следует отметить, что в 2005 году к этому положению была добавлена новая формулировка, в которой говорится, что: «… если обстоятельства не позволяют раскрыть информацию лицу, запрашивающему запись или записи, в течение двадцати рабочих дней с даты подтверждения получения запроса агентство должно указать в письменной форме как причину невозможности удовлетворить запрос в течение двадцати рабочих дней, так и дату, установленную в течение разумного периода, в зависимости от обстоятельств, когда запрос будет удовлетворен полностью или частично». На основании вышеизложенного агентство должно предоставить доступ к записям, отказать в доступе в письменной форме или подтвердить получение запроса в течение пяти рабочих дней с момента получения запроса. Когда подтверждение дается, оно должно включать приблизительную дату в пределах двадцати рабочих дней, указывающую, когда можно ожидать, что запрос будет удовлетворен или отклонен. Однако, если известно, что обстоятельства не позволяют агентству предоставить доступ в течение двадцати рабочих дней, или если агентство не может предоставить доступ к указанной приблизительной дате и ему требуется более двадцати рабочих дней для предоставления доступа, оно должно предоставить письменное объяснение своих действий. Поправки явно предназначены для того, чтобы запретить агентствам без необходимости задерживать раскрытие информации. Они не предназначены для того, чтобы позволить агентствам ждать до пятого рабочего дня после получения запроса, а затем еще двадцать рабочих дней для определения прав доступа, если только это не разумно, исходя из «обстоятельств запроса». С нашей точки зрения, каждый закон должен применяться таким образом, чтобы обеспечить разумное осуществление его намерений, и мы отмечаем, что в заявлении о намерениях законодательного органа § 84 Закона о свободе информации гласит, что «он возлагается на государство и его местностях, чтобы расширить общественную подотчетность, где и когда это возможно». Таким образом, когда записи явно доступны для общественности в соответствии с Законом о свободе информации или если их легко найти, может не быть оснований для задержки раскрытия. «…успешная реализация политики, мотивирующей принятие Закона о свободе информации, направлена на достижение более широких целей, таких как достижение более информированного электората и более ответственного и отзывчивого государственного аппарата. По самой своей природе такие цели не могут быть достигнуты, если меры, принимаемые для их достижения, не проникнут в политический организм до такой степени, что они станут правилом, а не исключением. Таким образом, фраза «публичная подотчетность, где бы и когда бы это ни было возможно», просто акцентирует внимание на том, что в любом случае подразумевается» (Westchester News v. Kimball, 50 NY2d 575, 579)., 430 NYS2d 574 [1980]). В судебном решении относительно разумности задержки раскрытия информации, в котором приводилась и подтверждалась рекомендация данного ведомства относительно разумных оснований для задержки раскрытия информации, было установлено, что: «Определение разумности срока должно быть сделано в каждом конкретном случае с учетом объема запрошенных документов, времени, необходимого для поиска материала, и сложности вопросов, связанных с определением того, подпадают ли материалы под одно из исключений в отношении раскрытия информации. Если ни ответ на запрос, ни подтверждение получения запроса не предоставлены в течение пяти рабочих дней, если агентство задерживает ответ на необоснованный срок после приблизительной даты менее двадцати рабочих дней, указанной в его подтверждении, если он подтверждает, что запрос был получен, но не предоставил доступ к конкретной дате, указанной после двадцати рабочих дней, или, если конкретная дата указана необоснованно, запрос может считаться отклоненным конструктивно (см. §89[4][а]). В таком случае отказ может быть обжалован в соответствии с §89(4)(a), в соответствующей части которого говорится, что: «…любое лицо, которому отказано в доступе к записи, может в течение отказ руководителю, главному исполнительному органу или руководящему органу или лицу, назначенному для этого таким главой, главным исполнительным лицом или руководящим органом, которое в течение десяти рабочих дней с момента получения такого обращения полностью разъясняет в письменной форме запрашивающему лицу зафиксировать причины дальнейшего отказа или предоставить доступ к запрошенным записям». Раздел 89(4)(b) также был изменен, и в нем говорится, что непринятие решения по апелляции в течение десяти рабочих дней с момента получения апелляции представляет собой отклонение апелляции. В этом случае заявитель исчерпал свои административные средства правовой защиты и может инициировать оспаривание конструктивного отказа в доступе в соответствии со статьей 78 Закона и правил о гражданской практике. Основная статья: Определение предела эпсилон-дельта Точное определение лимита обсуждается в вики Epsilon-Delta Definition of a Limit. Формальное определение предела функции: Предел f(x)f(x)f(x) при приближении xxx к x0x_0x0 равен LLL, т.е. limx→x0f(x)=L\lim _{ x \to x_{0} }{f(x)} = Lx→x0limf(x)=L , если для каждого ϵ>0\epsilon > 0 ϵ>0 существует δ>0\delta >0 δ>0 такое, что для всех xxx 0<∣x−x0∣<δ ⟹ ∣f(x)−L∣<ϵ. 0 < \ влево | x - x_{0} \right |<\delta \textrm{ } \ подразумевает \textrm{ } \left |f(x) - L \right| <\эпсилон. 0<∣x−x0∣<δ ⟹ ∣f(x)−L∣<ϵ. На практике это определение используется только в относительно необычных ситуациях. Для многих приложений проще использовать это определение, чтобы доказать некоторые основные свойства пределов и использовать эти свойства для ответа на простые вопросы, связанные с ограничениями. Наиболее важными свойствами пределов являются алгебраические свойства, которые, по существу, говорят о том, что пределы учитывают алгебраические операции: Предположим, что limx→af(x)=M \lim\limits_{x\to a} f(x) = Mx→alimf(x)=M и limx→ag(x)=N. Все это можно доказать с помощью определения эпсилон-дельта. Обратите внимание, что результаты верны только в том случае, если существуют пределы отдельных функций: если limx→af(x) \lim\limits_{x\to a} f(x) x→alimf(x) и lim x→ag(x) \lim\limits_{x\to a} g(x)x→alimg(x) не существуют, тем не менее, может существовать предел их суммы (или разности, произведения или частного). В сочетании с основными пределами limx→ac=c, \lim_{x\to a} c = c,limx→ac=c, где c cc — константа, а limx→ax=a , \lim_{x\to a} x = a,limx→ax=a, свойства можно использовать для вывода пределов, включающих рациональные функции: Пусть f(x) f(x) f(x) и g(x)g(x)g(x) — полиномы, и предположим, что g(a)≠0.g(a) \ne 0.g(a )=0. Затем limx→af(x)g(x)=f(a)g(a). \lim_{x\to a} \frac{f(x)}{g(x)} = \frac{f(a)}{g(a)}. Это пример непрерывности, или того, что иногда называют ограничениями замещения. Обратите внимание, что g(a)=0g(a)=0g(a)=0 — более сложный случай; см. вики Indeterminate Forms для дальнейшего обсуждения. Пусть mmm и nnn — целые положительные числа. Найти 9+,x→a+,» мы рассматриваем только значения больше, чем aaa. Односторонние пределы важны при вычислении пределов, содержащих абсолютные значения ∣x∣|x|∣x∣, sign sign(x)\text{sign}(x) sign(x) , функции пола ⌊x⌋\lfloor x \rfloor⌊x⌋ и другие кусочные функции На изображении выше показаны левосторонние и правосторонние пределы непрерывной функции f(x).f(x).f(x). Найдите левый и правый пределы сигнум-функции sgn(x)\text{sgn}(x)sgn(x) при x→0:x \to 0:x→0: 9-} \frac{|x-1|}{-|x — 1|} = -1 . x→1−lim−∣x−1∣∣x−1∣=−1. Таким образом, двусторонний предел limx→1∣x−1∣x−1 \lim\limits_{x \to 1} \frac{|x — 1|}{x — 1}x→1limx− 1∣x−1∣ не существует. Изображение ниже представляет собой график функции f(x)f(x)f(x). Как показано, он непрерывен для всех точек, кроме x=-1x = -1x=-1 и x=2x=2x=2, которые являются его асимптотами. Найдите все целые точки −4 изображение Поскольку график непрерывен во всех точках, кроме точек x=−1x=-1x=−1 и x=2x=2x=2, двусторонний предел существует при x=−3x=-3x=−3, x= -2x=-2x=-2, x=0x=0x=0, x=1,x=1,x=1 и x=3x=3x=3. При x=2,x=2,x=2 нет конечного значения ни для одного из двусторонних пределов, поскольку функция неограниченно возрастает по мере того, как координата xxx приближается к 222 (но см. следующий раздел для дальнейшего обсуждения ). Ситуация аналогична для x=−1.x=-1.x=−1. Таким образом, точки x=-3x=-3x=-3, x=-2x=-2x=-2, x=0x=0x=0, x=1,x=1,x=1 и x=3x= 3x=3 — это все целые числа, на которых определяются двусторонние ограничения. Как видно из предыдущего раздела, один из способов несуществования предела — это несоответствие односторонних пределов. Другой распространенный способ отсутствия предела в точке aaa — это «взрыв» функции вблизи a, a, a, т. Е. Функция неограниченно возрастает. Это происходит в приведенном выше примере при x=2,x=2,x=2, где имеется вертикальная асимптота. Эта общая ситуация приводит к следующему обозначению: Для функции f(x)f(x)f(x) и действительного числа a,a,a мы говорим limx→af(x)=∞.\lim_{x\to a} f(x) = \infty.x→alimf(x)=∞. Если функцию можно сделать произвольно большой, переместив xxx достаточно близко к a,a,a, для всех N>0 существует такое δ>0, что 0<∣x−a∣<δ ⟹ f(x)>N.\text{для всех } N>0, \text{ существует } \delta> 0 \text{ такой, что } 0<|x-a|<\delta \ подразумевает f(x)>N. для всех N>0 существует δ>0 такой 0<∣x−a∣<δ⟹f(x )>Н. Существуют аналогичные определения для односторонних пределов, а также пределов, «приближающихся к −∞-\infty−∞». Предупреждение: Если limx→af(x)=∞,\lim\limits_{x\to a} f(x) = \infty,x→alimf(x)=∞, это заманчиво сказать, что предел в точке aaa существует и равен ∞.\infty.∞. Это неправильно. Если limx→af(x)=∞,\lim\limits_{x\to a} f(x) = \infty,x→alimf(x)=∞, предел , а не существует; обозначение просто дает информацию о том, как предел не существует, т. Е. Значение функции «приближается к ∞ \ infty ∞» или неограниченно возрастает как x → ax \ rightarrow ax → a. Чтобы доказать первое утверждение, для любого N>0N>0N>0 в формальном определении можно взять δ=1N,\delta = \frac1N,δ=N1, и доказательство второго утверждения аналогично. Таким образом, функция неограниченно возрастает с правой стороны и неограниченно убывает с левой стороны. Ничего другого нельзя сказать о двустороннем пределе limx→a1x≠∞\lim\limits_{x\to a} \frac1{x} \ne \inftyx→alimx1=∞ или −∞. -\infty.−∞. Сравните это со следующим примером. , где a0≠0,b0≠0,a_0 \neq 0, b_0 \neq 0,a0=0,b0=0 и m,n∈N.m,n \in \mathbb N.m,n∈N. Тогда учитывая (A), (B), (C) или (D), limx→0f(x)\displaystyle\lim_{x\rightarrow 0}f(x)x→0limf(x ) равно какому из (1), (2), (3) и (4)? Сопоставьте столбцы:  5in}{\mbox{когда}}\hspace{0.5in}x
5in}{\mbox{когда}}\hspace{0.5in}x  5in}{\mbox{когда бы ни}}\hspace{0.5in}x < N\]
5in}{\mbox{когда бы ни}}\hspace{0.5in}x < N\] 25in}{\mbox{найти }}\left| х \право|\\ & \лево| {\ гидроразрыва {1} {х} — 0} \ справа | < \varepsilon & & \hspace{0.25in}{\mbox{немного переписать}}\end{align*}\]
25in}{\mbox{найти }}\left| х \право|\\ & \лево| {\ гидроразрыва {1} {х} — 0} \ справа | < \varepsilon & & \hspace{0.25in}{\mbox{немного переписать}}\end{align*}\] Мы выполним один из них, а остальные три оставим вам, чтобы вы могли записать их, если хотите.
Мы выполним один из них, а остальные три оставим вам, чтобы вы могли записать их, если хотите. Определение 8
 Вот оно,
Вот оно, Определение 9
 Вернитесь и посмотрите на первые три примера. В каждом из этих примеров значением предела было значение функции, оцениваемой при \(х = а\), и поэтому в каждом из этих примеров мы не только доказали значение предела, но и сумели доказать, что каждое из эти функции непрерывны в рассматриваемой точке.
Вернитесь и посмотрите на первые три примера. В каждом из этих примеров значением предела было значение функции, оцениваемой при \(х = а\), и поэтому в каждом из этих примеров мы не только доказали значение предела, но и сумели доказать, что каждое из эти функции непрерывны в рассматриваемой точке. Объяснение сроков ответа
 ..»
..» невозможность сделать это и конкретную дату, к которой он предоставит доступ. Эта дата должна быть разумной с учетом обстоятельств запроса.
невозможность сделать это и конкретную дату, к которой он предоставит доступ. Эта дата должна быть разумной с учетом обстоятельств запроса. Как заявил Апелляционный суд, высшая судебная инстанция штата:
Как заявил Апелляционный суд, высшая судебная инстанция штата: Такой стандарт согласуется с некоторыми формулировками заключений, представленных заявителями по этому делу, Комитета по открытому правительству, агентства, отвечающего за выдачу консультативных заключений по FOIL» (Linz v. The Police Department of the City of New York, Верховный суд округа Нью-Йорк, NYLJ, 17 декабря 2001 г.).
Такой стандарт согласуется с некоторыми формулировками заключений, представленных заявителями по этому делу, Комитета по открытому правительству, агентства, отвечающего за выдачу консультативных заключений по FOIL» (Linz v. The Police Department of the City of New York, Верховный суд округа Нью-Йорк, NYLJ, 17 декабря 2001 г.).
Ограничения функций | Brilliant Math & Science Wiki
Содержание

 k \ \\text{ (если } M,k > 0).
\end{выровнено}
x→alim(f(x)+g(x))x→alim(f(x)−g(x))x→alim(f(x)g(x))x→alim(g (x)f(x))x→alimf(x)k=M+N=M−N=MN=NM (если N=0)=Mk (если M,k>0) .
k \ \\text{ (если } M,k > 0).
\end{выровнено}
x→alim(f(x)+g(x))x→alim(f(x)−g(x))x→alim(f(x)g(x))x→alim(g (x)f(x))x→alimf(x)k=M+N=M−N=MN=NM (если N=0)=Mk (если M,k>0) . х→алимg(x)f(x)=g(a)f(a).
х→алимg(x)f(x)=g(a)f(a). □_\квадрат□
□_\квадрат□ □_\квадрат□
□_\квадрат□
 □_\квадрат□
9{n+l}},f(x)=b0xn+b1xn+1+⋯+blxn+la0xm+a1xm+1+⋯+akxm+k,
□_\квадрат□
9{n+l}},f(x)=b0xn+b1xn+1+⋯+blxn+la0xm+a1xm+1+⋯+akxm+k, Column-I Column-II (A) IF M> NM> NM> N (1) эй.0678 (B), если m=nm=nm=n (2) −∞-\infty−∞ (C), если m (3) a0b0\frac{a_0}{b_0}b0a0 (D), если m (4) 000
Примечание: Например, если (A) правильно соответствует (1), (B) с (2), (C) с (3) , и (D) с (4), то ответьте как 1234.
Еще одно расширение концепции предела связано с рассмотрением поведения функции, когда xxx «приближается к ∞\infty∞», то есть когда xxx неограниченно возрастает.
Уравнение limx→∞f(x)=L \lim\limits_{x\to\infty} f(x) = Lx→∞limf(x)=L означает, что значения fff можно сделать произвольными близким к LLL, взяв xxx достаточно большим. То есть
для всех ε>0 существует N>0 такое, что x>N ⟹ ∣f(x)−L∣<ϵ.\text{для всех } \epsilon > 0, \text{ существует } N>0 \ text{ такой, что } x>N \ подразумевает |f(x)-L|<\epsilon.
Существуют аналогичные определения для limx→−∞f(x)=L,\lim\limits_{x\to -\infty} f(x) = L,x→−∞limf(x) =L, а также limx→∞f(x)=∞,\lim\limits_{x\to\infty} f(x) = \infty,x→∞limf(x)=∞, и скоро.
Графически limx→af(x)=∞\lim\limits_{x\to a} f(x) = \inftyx→alimf(x)=∞ соответствует вертикальной асимптоте в точках a,a, a, а limx→∞f(x)=L \lim\limits_{x\to\infty} f(x) = L x→∞limf(x)=L соответствует горизонтальной асимптоте в точке L.

 Помню, что
они все носили такой абсурдный характер. Первая реклама, которая меня поразила,
это была растяжка через Тверскую: «Если вы пошлете ваш инпут на наш сайт, то
получите наш аутпут на вашем терминале». Это высказывание меня глубоко
потрясло. То, что подобной рекламы больше нет, для меня это заметное изменение. Другое дело — на что
это указывает.
Помню, что
они все носили такой абсурдный характер. Первая реклама, которая меня поразила,
это была растяжка через Тверскую: «Если вы пошлете ваш инпут на наш сайт, то
получите наш аутпут на вашем терминале». Это высказывание меня глубоко
потрясло. То, что подобной рекламы больше нет, для меня это заметное изменение. Другое дело — на что
это указывает. Даже в моей нынешней стране, в Америке, появилась Tea Party — против
гомосексуализма, за религиозные и семейные ценности, за hard working man.
Нельзя сказать, что это неожиданная комбинация идеологических штампов. Так что
мне кажется, что все страны сейчас идут назад идеологически, очень далеко, даже Россия возвращается не во
времена Сталина, а к началу XX века, другие страны — к Средневековью. Все идут
к истокам, ищут культурную идентичность. Все пытаются определиться и найти свое
место через обращение к очень простым формулам своей культурной идентичности.
Определение происходит в глобальном пространстве конкуренции. Был создан
огромный мировой рынок, где происходит конкуренция. Для того чтобы удачно
конкурировать, нужно иметь то, что называется «человеческий капитал», а это и
есть основы — семья, своя старая культура, традиция.
Даже в моей нынешней стране, в Америке, появилась Tea Party — против
гомосексуализма, за религиозные и семейные ценности, за hard working man.
Нельзя сказать, что это неожиданная комбинация идеологических штампов. Так что
мне кажется, что все страны сейчас идут назад идеологически, очень далеко, даже Россия возвращается не во
времена Сталина, а к началу XX века, другие страны — к Средневековью. Все идут
к истокам, ищут культурную идентичность. Все пытаются определиться и найти свое
место через обращение к очень простым формулам своей культурной идентичности.
Определение происходит в глобальном пространстве конкуренции. Был создан
огромный мировой рынок, где происходит конкуренция. Для того чтобы удачно
конкурировать, нужно иметь то, что называется «человеческий капитал», а это и
есть основы — семья, своя старая культура, традиция. Расслабиться, покурить, выпить и
have good time. Вместо этого в ситуации конкуренции он должен сидеть чего-то
учить, конкурировать с другими, по 8–10 часов чем-то заниматься. То есть вести
ненормальный образ жизни. Для того чтобы иметь энергию вести этот ненормальный
образ жизни, он должен быть уверен:
а) в своем превосходстве над остальными, иначе он этим заниматься не будет и б)
что у него есть цель кому-то что-то доказать.
Расслабиться, покурить, выпить и
have good time. Вместо этого в ситуации конкуренции он должен сидеть чего-то
учить, конкурировать с другими, по 8–10 часов чем-то заниматься. То есть вести
ненормальный образ жизни. Для того чтобы иметь энергию вести этот ненормальный
образ жизни, он должен быть уверен:
а) в своем превосходстве над остальными, иначе он этим заниматься не будет и б)
что у него есть цель кому-то что-то доказать. С другой
стороны, он должен быть спонтанным,
в любой момент готовым сорваться с
места, купить аппарат для подводного
плавания и отправиться куда-то на Канары. То есть он должен обладать двумя
наборами качеств, в принципе не совместимых друг с другом. Это создает
невыносимую нагрузку на психику человека, потому что в каждый конкретный момент
он не знает, как поступить: пойти гулять с любимой девушкой или пойти
просиживать задницу, заполняя ведомости. Для того чтобы разрешить эту коллизию,
он обращается к Корану или к Ветхому
Завету, где читает «есть время просиживать задницу и время ехать на
Канары».
С другой
стороны, он должен быть спонтанным,
в любой момент готовым сорваться с
места, купить аппарат для подводного
плавания и отправиться куда-то на Канары. То есть он должен обладать двумя
наборами качеств, в принципе не совместимых друг с другом. Это создает
невыносимую нагрузку на психику человека, потому что в каждый конкретный момент
он не знает, как поступить: пойти гулять с любимой девушкой или пойти
просиживать задницу, заполняя ведомости. Для того чтобы разрешить эту коллизию,
он обращается к Корану или к Ветхому
Завету, где читает «есть время просиживать задницу и время ехать на
Канары». Ни один человек, которому нравится Сталин, не
знает толком, что тот делал. Речь
идет о наборе символических знаков, или
сигнификатов, как говорили во времена моей молодости. Усвоение и оперирование
ими никакой нагрузки не составляет, тогда как раньше люди все еще читали
святцы, например. Ergo, можно на нулевом напряжении приобрести себе идеологию.
Помните думающего рабочего? Он три года читал по несколько часов после работы «Капитал» Маркса. Представьте себе, кто сейчас на это способен? Ergo, создается
идеология на нулевом напряжении, но эта идеология обладает стабилизирующей функцией, и
этот стабилизационный механизм включается всегда в любой стране. И поэтому все
страны на глазах становятся более консервативными.
Ни один человек, которому нравится Сталин, не
знает толком, что тот делал. Речь
идет о наборе символических знаков, или
сигнификатов, как говорили во времена моей молодости. Усвоение и оперирование
ими никакой нагрузки не составляет, тогда как раньше люди все еще читали
святцы, например. Ergo, можно на нулевом напряжении приобрести себе идеологию.
Помните думающего рабочего? Он три года читал по несколько часов после работы «Капитал» Маркса. Представьте себе, кто сейчас на это способен? Ergo, создается
идеология на нулевом напряжении, но эта идеология обладает стабилизирующей функцией, и
этот стабилизационный механизм включается всегда в любой стране. И поэтому все
страны на глазах становятся более консервативными. 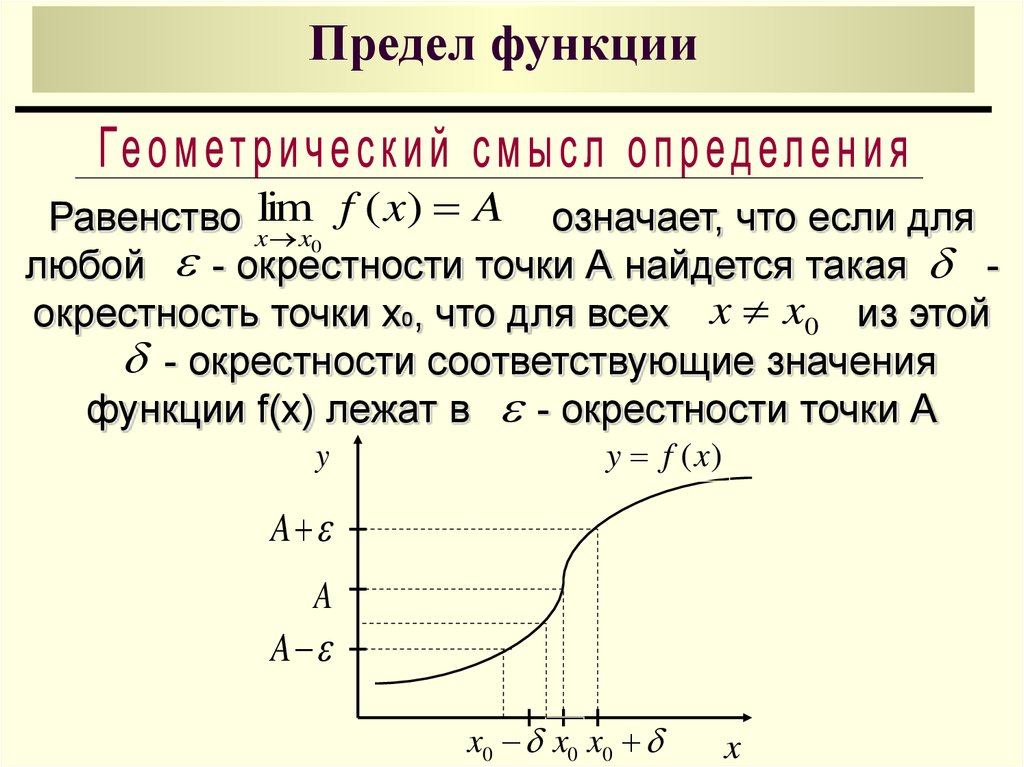 Я спросил у
них: что, в Берлине? Они говорят, ну конечно, в Берлине.
Я спросил у
них: что, в Берлине? Они говорят, ну конечно, в Берлине. Они могут объединиться и
выдвинуть совместные требования, потому что они не конкурируют. Мы же живем в
обществе, где каждый делает все. И каждый делает одинаково. С одной стороны,
растет вот эта спецификация вроде «я мусульманин». Но труд сам по себе построен
на том, что все делают одно и то же. Во-первых, все работают в одном и том же
месте — в интернете; во-вторых, кто бы что ни делал, все конкурируют со всеми — и солидарность в принципе невозможна. Субъект нынешнего положения вещей не
только производитель и потребитель в одно и то же время, что ломает его
психику, он еще рабочий и буржуа в одно и то же время. Работает он как
рабочий, а конкурирует как буржуа. Почему возможна пролетарская революция?
Потому что пролетариат может объединиться. Буржуазия не может объединиться,
потому что каждый буржуа конкурирует с другим буржуа. Объединяются они только в
случае кризиса, но в нормальное время это невозможно.
Они могут объединиться и
выдвинуть совместные требования, потому что они не конкурируют. Мы же живем в
обществе, где каждый делает все. И каждый делает одинаково. С одной стороны,
растет вот эта спецификация вроде «я мусульманин». Но труд сам по себе построен
на том, что все делают одно и то же. Во-первых, все работают в одном и том же
месте — в интернете; во-вторых, кто бы что ни делал, все конкурируют со всеми — и солидарность в принципе невозможна. Субъект нынешнего положения вещей не
только производитель и потребитель в одно и то же время, что ломает его
психику, он еще рабочий и буржуа в одно и то же время. Работает он как
рабочий, а конкурирует как буржуа. Почему возможна пролетарская революция?
Потому что пролетариат может объединиться. Буржуазия не может объединиться,
потому что каждый буржуа конкурирует с другим буржуа. Объединяются они только в
случае кризиса, но в нормальное время это невозможно. Но буржуа не
считают себя классом, и вот этот буржуазный индивидуализм сейчас стал
универсальным. Это означает, что каждый индивидуалист, каждый знает только свои
интересы, интересы эти таковы же, как и
интересы всех остальных. Именно
поэтому они противоречат интересам
остальных. Каждый может делать работу каждого, и каждый делает все. Вы сами
себе готовите, сами себя обслуживаете, сами обставляете квартиру, сами делаете
заказы. Это на моих глазах произошло — я вообще не знал горя раньше, секретарши заказывали билеты и
гостиницы. Сейчас я все делаю сам. Вы должны сесть к компьютеру, посмотреть
предложения и заплатить со своей карточки. Например, в Нью-Йорке закрыли все туристические агентства, почти все
медицинские организации, кроме очень высокооплачиваемых специалистов.
Невозможно, очень дорого. Если у вас есть какая-то болезнь, вы идете на
специальный сайт, выясняете, как ее лечить, потом идете в аптеку и покупаете
то, что вам нужно. Раньше этого нельзя было сделать, а сейчас все
либерализовалось.
Но буржуа не
считают себя классом, и вот этот буржуазный индивидуализм сейчас стал
универсальным. Это означает, что каждый индивидуалист, каждый знает только свои
интересы, интересы эти таковы же, как и
интересы всех остальных. Именно
поэтому они противоречат интересам
остальных. Каждый может делать работу каждого, и каждый делает все. Вы сами
себе готовите, сами себя обслуживаете, сами обставляете квартиру, сами делаете
заказы. Это на моих глазах произошло — я вообще не знал горя раньше, секретарши заказывали билеты и
гостиницы. Сейчас я все делаю сам. Вы должны сесть к компьютеру, посмотреть
предложения и заплатить со своей карточки. Например, в Нью-Йорке закрыли все туристические агентства, почти все
медицинские организации, кроме очень высокооплачиваемых специалистов.
Невозможно, очень дорого. Если у вас есть какая-то болезнь, вы идете на
специальный сайт, выясняете, как ее лечить, потом идете в аптеку и покупаете
то, что вам нужно. Раньше этого нельзя было сделать, а сейчас все
либерализовалось. Лечи себя сам, учи себя сам — что бы вы ни хотели сделать,
вам говорят: вот веб-сайт, обратитесь туда. Это означает, что каждый полностью
замкнут, индивидуализирован, занят 24 часа в сутки, все делают одно и то же и
не могут договориться. Это и есть ситуация индивидуума, который полурабочий,
полубуржуа.
Лечи себя сам, учи себя сам — что бы вы ни хотели сделать,
вам говорят: вот веб-сайт, обратитесь туда. Это означает, что каждый полностью
замкнут, индивидуализирован, занят 24 часа в сутки, все делают одно и то же и
не могут договориться. Это и есть ситуация индивидуума, который полурабочий,
полубуржуа. Один режим — информационный, то есть я говорю что-то,
чтобы передать информацию. Вы можете не согласиться с этой информацией или
возразить. Другой — я говорю, не передавая информацию, a демонстрирую работу языка как таковую. Если я пишу роман «Анна
Каренина», я выключаю информационную функцию, и вы не можете мне сказать: «Вы
неправильно изобразили жизнь Анны Карениной, жизнь Анны Карениной была совсем
другой, потому что у меня есть другая информация».
Один режим — информационный, то есть я говорю что-то,
чтобы передать информацию. Вы можете не согласиться с этой информацией или
возразить. Другой — я говорю, не передавая информацию, a демонстрирую работу языка как таковую. Если я пишу роман «Анна
Каренина», я выключаю информационную функцию, и вы не можете мне сказать: «Вы
неправильно изобразили жизнь Анны Карениной, жизнь Анны Карениной была совсем
другой, потому что у меня есть другая информация». Веб-сайт сообщает вам — о чем? О реально происходящем в этом
музее. Так же как если вы хотите выяснить, что производится на заводе Форда,
вы идете на сайт, и вам говорят, что там
производятся такие-то и такие-то машины. Что производится в музее? Выставки, лекции, экскурсии. Это все реальные
события, а не фиктивные. Таким образом, само искусство становится реальным.
Кстати, еще до того, как оно начало заниматься фактографией, искусство стало
реальным во времена авангардистов. Смотришь на картину, видишь квадрат, и это
квадрат и есть. Квадрат не является фикцией, это не изображение Борея,
похищающего Орифию, где они оба являются фикциями. Если вы видите писсуар в
музее, то это и есть писсуар. Радикальный авангард с начала XX века начал уничтожать разницу между фактическим и
фиктивным. Перформансы, хеппенинги,
временные выставки, кураторские проекты — все фактичны, и информация о них
является фактической информацией о событии.
Веб-сайт сообщает вам — о чем? О реально происходящем в этом
музее. Так же как если вы хотите выяснить, что производится на заводе Форда,
вы идете на сайт, и вам говорят, что там
производятся такие-то и такие-то машины. Что производится в музее? Выставки, лекции, экскурсии. Это все реальные
события, а не фиктивные. Таким образом, само искусство становится реальным.
Кстати, еще до того, как оно начало заниматься фактографией, искусство стало
реальным во времена авангардистов. Смотришь на картину, видишь квадрат, и это
квадрат и есть. Квадрат не является фикцией, это не изображение Борея,
похищающего Орифию, где они оба являются фикциями. Если вы видите писсуар в
музее, то это и есть писсуар. Радикальный авангард с начала XX века начал уничтожать разницу между фактическим и
фиктивным. Перформансы, хеппенинги,
временные выставки, кураторские проекты — все фактичны, и информация о них
является фактической информацией о событии. В первом
случае это фикция, а во втором случае — реальность. Даже если какое-то действие произведено как художественный
акт, его документация не есть искусство
— речь идет о реальной Маринe Абрамович, которая реально себя чем-то
порезала, что, собственно, и было документировано.
Относительно такой документации всегда возможно сказать, что дело было совсем
не так, что на самом деле Марина себя не резала или резала как-то иначе. Таким
образом, переход искусства из зоны фиктивного в зону реального — это долгий
процесс, который занял больше ста лет и в настоящее время завершился. То есть
современный зритель больше не погружается в страну сказки, а выясняет, какое
там субсидирование и так далее. Короче говоря, искусство стало фактичным и
превратилось в информацию. Oтключение информационной
функции языка перестало происходить просто потому, что пропал субъект, который его раньше производил. Такой должности больше нет.
В первом
случае это фикция, а во втором случае — реальность. Даже если какое-то действие произведено как художественный
акт, его документация не есть искусство
— речь идет о реальной Маринe Абрамович, которая реально себя чем-то
порезала, что, собственно, и было документировано.
Относительно такой документации всегда возможно сказать, что дело было совсем
не так, что на самом деле Марина себя не резала или резала как-то иначе. Таким
образом, переход искусства из зоны фиктивного в зону реального — это долгий
процесс, который занял больше ста лет и в настоящее время завершился. То есть
современный зритель больше не погружается в страну сказки, а выясняет, какое
там субсидирование и так далее. Короче говоря, искусство стало фактичным и
превратилось в информацию. Oтключение информационной
функции языка перестало происходить просто потому, что пропал субъект, который его раньше производил. Такой должности больше нет. Зачем нам вообще нужны статуи, кроме
научного интереса?
Зачем нам вообще нужны статуи, кроме
научного интереса? Когда я работал над выставкой,
посвященной иконоклазму (иконоборчеству. — Прим.ред.), то видел
иконы, которые многих сейчас обидели бы. У Христа были выколоты глаза, а у
Богоматери вырезан живот. Это кальвинисты сделали. Уничтожение памятников
советского прошлого в России и других восточноевропейских странах ничем по
своей природе не отличается от разрушения памятников исламистами. Методы те же — бьют молотками, стаскивают с
пьедестала. Вообще, возрождение иконоклазмa пошло из России, когда здесь
Ленина сбрасывали, a переехало на арабский Восток благодаря американцам,
которые посмотрели постсоветскую
хронику и таким же образом сбросили памятники Саддаму Хусейну, когда захватили Ирак. Это стало иконой
американского завоевания Ирака, а ИГИЛ, который поначалу субсидировался американцами против режима Асада, так же как «Аль-Каида» против советской оккупации Афганистана, просто апроприировал современный русский
и восточноевропейский иконоклазм. Современный иконоклазм, как мне кажется, — это постсоциалистический феномен в основе своей.
Когда я работал над выставкой,
посвященной иконоклазму (иконоборчеству. — Прим.ред.), то видел
иконы, которые многих сейчас обидели бы. У Христа были выколоты глаза, а у
Богоматери вырезан живот. Это кальвинисты сделали. Уничтожение памятников
советского прошлого в России и других восточноевропейских странах ничем по
своей природе не отличается от разрушения памятников исламистами. Методы те же — бьют молотками, стаскивают с
пьедестала. Вообще, возрождение иконоклазмa пошло из России, когда здесь
Ленина сбрасывали, a переехало на арабский Восток благодаря американцам,
которые посмотрели постсоветскую
хронику и таким же образом сбросили памятники Саддаму Хусейну, когда захватили Ирак. Это стало иконой
американского завоевания Ирака, а ИГИЛ, который поначалу субсидировался американцами против режима Асада, так же как «Аль-Каида» против советской оккупации Афганистана, просто апроприировал современный русский
и восточноевропейский иконоклазм. Современный иконоклазм, как мне кажется, — это постсоциалистический феномен в основе своей.
 Искусство потеряло статус фиктивного, но приобрело статус реликвии. Вот какой-то человек разбил окно, вот:
а) фотография окна, б) видео, как он его разбивает, и в) осколки, — все это
складывается в инсталляцию, которую можно продать
и приобрести. В чем смысл этой инсталляции? Она отражает реальное событие,
она является напоминанием об этом событии. Вот святой Екатерине отрубили
голову. Вот голова, вот картина, как
ей отрезают голову, вот нож, которым ee отрезали, — это напоминание о том, что
происходит, когда девушки, вместо того чтобы выходить замуж, занимаются
девиантными формами поведения.
Искусство потеряло статус фиктивного, но приобрело статус реликвии. Вот какой-то человек разбил окно, вот:
а) фотография окна, б) видео, как он его разбивает, и в) осколки, — все это
складывается в инсталляцию, которую можно продать
и приобрести. В чем смысл этой инсталляции? Она отражает реальное событие,
она является напоминанием об этом событии. Вот святой Екатерине отрубили
голову. Вот голова, вот картина, как
ей отрезают голову, вот нож, которым ee отрезали, — это напоминание о том, что
происходит, когда девушки, вместо того чтобы выходить замуж, занимаются
девиантными формами поведения. Сейчас художники
менее богемны, они встречаются на лекциях. Это тоже относится к процессу
замены фикции фактом?
Сейчас художники
менее богемны, они встречаются на лекциях. Это тоже относится к процессу
замены фикции фактом? Сотни людей приходят на любую более
или менее интересную лекцию. Кто все эти люди? Они из академии, которая
представляет собой очень мощную социальную организацию. Если вы посмотрите на
механизм функционирования культуры сейчас, увидите что high art весь ушел в
академию, все поэты и писатели с
претензиями — профессора. Вы можете заработать сейчас либо на рынке, но он
очень коммерческий, либо вы преподаете.
Сотни людей приходят на любую более
или менее интересную лекцию. Кто все эти люди? Они из академии, которая
представляет собой очень мощную социальную организацию. Если вы посмотрите на
механизм функционирования культуры сейчас, увидите что high art весь ушел в
академию, все поэты и писатели с
претензиями — профессора. Вы можете заработать сейчас либо на рынке, но он
очень коммерческий, либо вы преподаете. Люди в Китае, в Индии, в Африке знают Супермена и Бэтмена, а больше
ничего. Китаец не пойдет на американский фильм про американскую жизнь, он
пойдет на свой фильм, изображающий китайскую жизнь. Нo на Супермена он пойдет, потому что в Китае такого не делают. Если учесть, что почти 70% всего дохода американский Голливуд получает за пределами
Соединенных Штатов, то вот вам и объяснение. Вы не можете сейчас конкурировать
на рынке, если вы невероятно не
раскручены по другим каналам: спорт, политика, телевидение. Но вы можете
преподавать, и на деньги, которые зарабатываете, можете жить и писать романы.
Люди в Китае, в Индии, в Африке знают Супермена и Бэтмена, а больше
ничего. Китаец не пойдет на американский фильм про американскую жизнь, он
пойдет на свой фильм, изображающий китайскую жизнь. Нo на Супермена он пойдет, потому что в Китае такого не делают. Если учесть, что почти 70% всего дохода американский Голливуд получает за пределами
Соединенных Штатов, то вот вам и объяснение. Вы не можете сейчас конкурировать
на рынке, если вы невероятно не
раскручены по другим каналам: спорт, политика, телевидение. Но вы можете
преподавать, и на деньги, которые зарабатываете, можете жить и писать романы. Я преподаю европейскую философию. Один из моих
студентов играет по вечерам в ресторане на гoбое,
другой пишет программы. Оба занимаются философией.
Я преподаю европейскую философию. Один из моих
студентов играет по вечерам в ресторане на гoбое,
другой пишет программы. Оба занимаются философией. Бруклин — это тот же Берлин. Я был в Израиле,
ходил по мастерским: все художники живут и
работают в основном в Берлине. Одна только художница мне сказала, что она не такая буржуазная, чтобы жить в
Берлине, поэтому живет в Лейпциге.
Бруклин — это тот же Берлин. Я был в Израиле,
ходил по мастерским: все художники живут и
работают в основном в Берлине. Одна только художница мне сказала, что она не такая буржуазная, чтобы жить в
Берлине, поэтому живет в Лейпциге.