Вычисление асимптот онлайн: Асимптоты функции онлайн

Решение высшей математики онлайн

‹— Назад

Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные.

        Определение 7.1   Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , . Заметим, что мы при этом не требуем, чтобы точка принадлежала области определения функции , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: или , где .     

        Пример 7.1   Рассмотрим функцию . График имеет вертикальную асимптоту , поскольку при выполняется условие , а также при выполняется условие .     

Рис.7.1.Вертикальная асимптота функции

        Пример 7.2   Рассмотрим функцию . Её график имеет вертикальную асимптоту , так как при . То, что при функция не стремится к бесконечности, для наличия асимптоты неважно: для того, чтобы прямая являлась вертикальной асимптотой, достаточно, чтобы график приближался к ней хотя бы с одной стороны. (К слову сказать, при .)     

Рис.7.2.Вертикальная асимптота функции

        Пример 7.3   Рассмотрим функцию . Прямая является вертикальной асимптотой графика , так как при . Заметим, что слева от точки функция вообще не определена.     

Рис.7.3.Вертикальная асимптота функции

        Пример 7.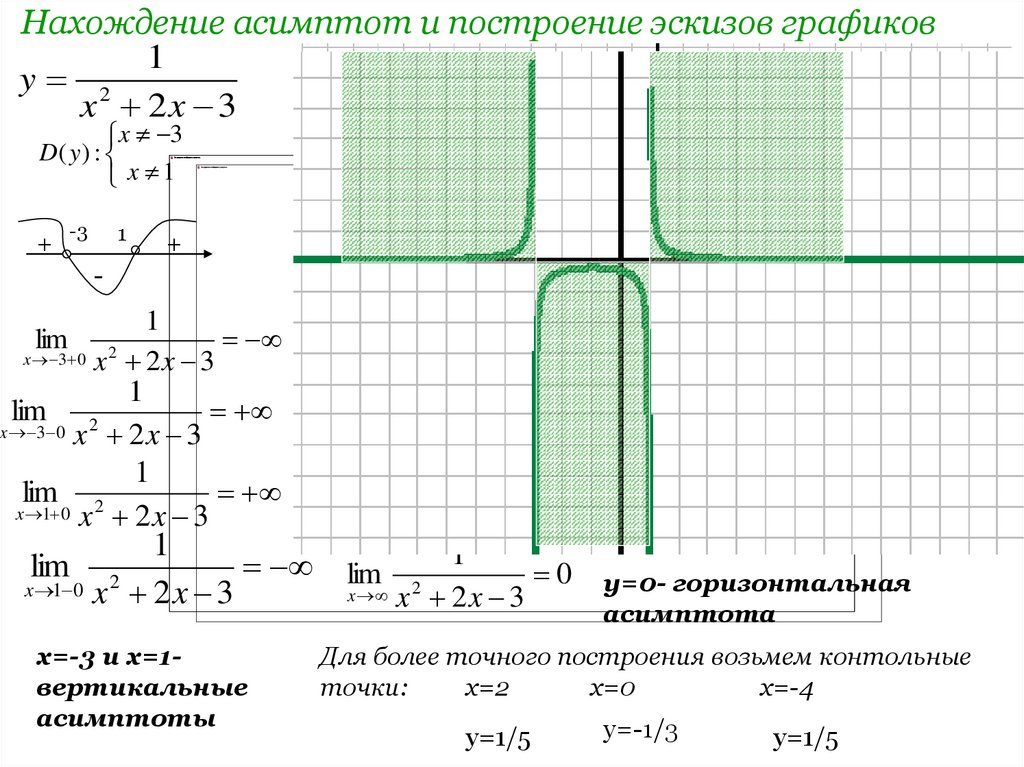 4   График функции не имеет при вертикальной асимптоты, так как  — ограниченная (числом 1) и, следовательно, локально ограниченная при и не стремящаяся к бесконечности функция. Хотя аргумент синуса — функция  — имеет вертикальную асимптоту .     

Рис.7.4.График функции не имеет вертикальной асимптоты

        Пример 7.5   Прямая не является вертикальной асимптотой графика функции , поскольку здесь нельзя утверждать, что при или функция стремится к бесконечности. При некоторых малых значениях значения могут быть как угодно велики, однако при других малых функция обращается в 0: так, при ( ) значения функции равны и стремятся к бесконечности при , а при всех вида ( ) значения функции равны 0. В то же время как те, так и другие точки при увеличении попадают всё ближе и ближе к точке 0. Значит, функция не является бесконечно большой при , и прямая  — не асимптота.     

Рис.7.5.График функции не имеет вертикальной асимптоты

Итак, для нахождения вертикальных асимптот графика данной функции нужно исследовать точки разрыва функции и точки, лежащие на границах области определения функции, и выяснить, при приближении аргумента к каким из этих точек значения функции стремятся к бесконечности.

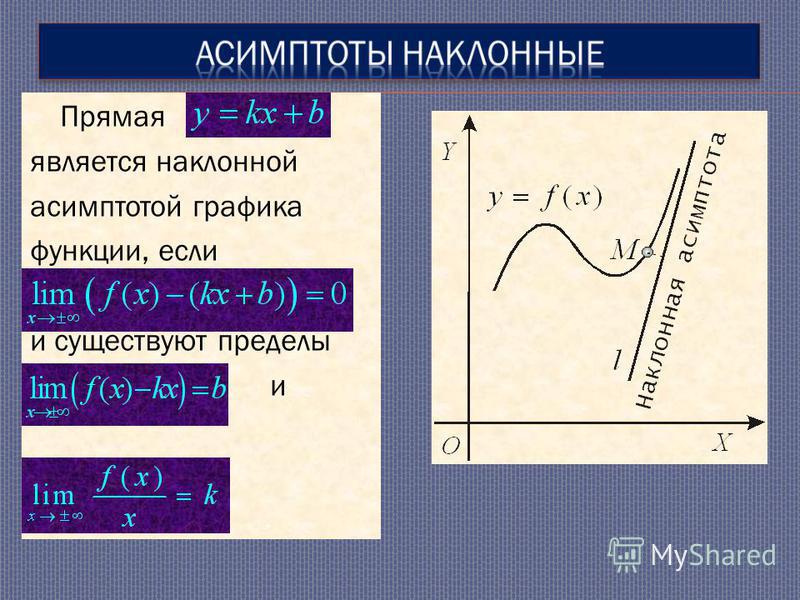
        Определение 7.2   Наклонной асимптотой графика функции при называется прямая , если выполнены два условия:
1) некоторый луч целиком содержится в ;
2) расстояние по вертикали между графиком и прямой стремится к 0 при :

(7. 1)

Наклонной асимптотой графика функции при называется прямая , если
1) некоторый луч целиком содержится в ;
2) расстояние по вертикали между графиком и прямой стремится к 0 при :

    

Рис.7.6.Графики функций, имеющие наклонные асимптоты при и при

В случае, если наклонная асимптота расположена горизонтально, то есть при , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота — частный случай наклонной асимптоты; прямая является горизонтальной асимптотой графика при или , если

или

соответственно.

        Пример 7.6   Рассмотрим функцию . График этой функции имеет наклонную асимптоту при . Действительно,

при

Однако эта функция не определена ни на каком луче вида , так что её график не может иметь асимптоты при .     

Рис.7.7.Наклонная асимптота функции

        Пример 7.7   График функции имеет горизонтальную асимптоту как при , так и при , поскольку, очевидно, при . Можно сказать также, что асимптота при у этого графика совпадает с асимптотой при .     

Рис. 7.8.Горизонтальная асимптота функции

Аналогично определению наклонной асимптоты можно дать также более общее определение:

        Определение 7.3   Линия называется асимптотической линией графика функции при (или при ), если обе эти функции определены на некотором луче (или луче ) и разность ординат графиков стремится к 0 при (или при , соответственно).     

Если функция  — линейная, то есть график  — наклонная прямая, то асимптотическая линия — это наклонная асимптота. Однако и другие линии бывает естественно рассматривать в качестве асимптотических.

        Пример 7.8   Рассмотрим функцию . При график этой функции имеет асимптотическую линию , поскольку разность между и , равная, очевидно, , стремится к 0 при .     

Рис.7.9.Асимптотическая линия графика функции

        Замечание 7.1   Функции и входят в определение асимптотической линии симметрично: если график  — асимптотическая линия для графика , то и  — асимптотическая линия для . На практике, однако, естественно считать асимптотической линией тот из двух графиков, который задаётся более простой формулой и вид которого известен.     

        Пример 7.9   Рассмотрим функцию . Так как при , то естественно рассматривать график как асимптотическую линию при для графика исследуемой функции .     

Рис.7.10.Асимптотическая линия для графика функции при

Вернёмся к наклонным асимптотам — прямым линиям с уравнением . Для их нахождения в тех случаях, когда значения и не очевидны, можно применять следующую теорему.

        Теорема 7.1   Прямая служит наклонной асимптотой для графика при (или при ) в том и только том случае, когда

(7.2)

и

(7.3)

(соответственно, если

и

Таким образом, для нахождения наклонной (или горизонтальной, если получится ) асимптоты достаточно найти два указанных предела и, затем, . Прямая будет искомой асимптотой. Если же какой-либо из этих двух пределов не существует, то нет и соответствующей асимптоты.

        Доказательство теоремы.     Докажем теорему в случае ; доказательство при проводится совершенно аналогично.

Перепишем условие (7.1), задающее асимптоту, в виде

Так как первый множитель , то второй множитель, стоящий в квадратных скобках, должен быть бесконечно малым, то есть

Но и , так что

откуда следует равенство (7.2). Теперь число уже известно.

Подставляя это число в формулу (7.1), находим, что

откуда следует равенство (7. 3).     

        Пример 7.10   Найдём наклонные асимптоты графика .

Попробуем отыскивать сразу оба предела, и при , и при .

Итак, и при , и при имеем и , так что обе наклонные асимптоты совпадают друг с другом и имеют уравнение , то есть, фактически, асимптота только одна.     

Рис.7.11.График и его наклонная асимптота

        Замечание 7.2   Из определения асимптоты не следует, что если асимптоты при и при для одного и того же графика существуют, то они непременно совпадают. Это могут быть и различные прямые, как показывает следующий простой пример.     

        Пример 7. 11   Рассмотрим график . При график приближается к горизонтальной асимптоте , а при  — к другой горизонтальной асимптоте .     

Рис.7.12.График арктангенса имеет две разных горизонтальных асимптоты

Различными могут оказаться и не обязательно горизонтальные асимптоты:

        Пример 7.12   Рассмотрим функцию . Покажем, что обе её наклонные асимптоты существуют, но не совпадают друг с другом.

Сначала найдём асимптоту при . Согласно доказанной теореме, имеем:

Таким образом, при наклонной асимптотой служит прямая .

Теперь найдём асимптоту при . Имеем:

Поскольку , мы можем считать, что в допредельном выражении . В полученной дроби поделим числитель и знаменатель на положительное число . Тогда под корнем нужно будет поделить на , и получится:

Вычисление проведите сами в качестве упражнения. При этом получается , так что наклонная асимптота при имеет уравнение .     

Рис.7.13.График и его две наклонных асимптоты

        Замечание 7.3   Если график имеет асимптоту (например, при ) и существует предел производной:

то . Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты¹⁷.

Однако асимптота может существовать и в случае, когда производная не имеет никакого предела при . Дело в том, что значения могут совершать мелкие, но частые колебания относительно ординаты асимптоты, так что значения производной могут при этом испытывать незатухающие колебания. Проиллюстрируем эту возможность следующим примером.     

        Пример 7.13   Рассмотрим функцию . Очевидно, что прямая  — это асимптота графика при , так как первое слагаемое имеет предел, равный 0, при . Однако вычисление производной даёт

а эта функция при росте совершает колебания, причём при больших второе слагаемое становится пренебрежимо малым, и значения колеблются примерно между и 3. Следовательно, производная не имеет предела при .

Если же рассмотреть функцию , то её производная оказывается даже неограниченной на любом луче вида , хотя прямая по-прежнему служит асимптотой графика (проведите вычисления, доказывающие это, самостоятельно в качестве упражнения).     

Не так уж редко встречается случай, когда, найдя наклонные и вертикальные асимптоты графика и исследовав поведение функции слева и справа от вертикальных асимптот, мы уже достаточно хорошо можем представить себе поведение функции.

        Пример 7.14   Рассмотрим функцию . Мы можем заметить, что  — чётная функция, поскольку она зависит только от и, следовательно, не меняет знак при смене знака . Заметим также, что .

Знаменатель обращается в 0 при , то есть при и при . Тем самым, прямые и  — это вертикальные асимптоты. Подробнее разберём порведение функции при приближении к . Если , то и, следовательно, . Числитель при всех , так что дробь положительна. Значит, при . При (и ) имеем , поэтому и , так что при . Вследствие чётности функции получаем также, что при и при .

Найдём теперь наклонные асимптоты. Вычисляя параметры и по формулам (7.2) и (7.3), получаем:

Таким образом, асимптоты при и при совпадают и имеют уравнение .

Суммируя сказанное, мы можем представить себе, что график функции ведёт себя примерно так:

Рис.7.14.График функции

    

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Дифференциальное исчисление (продолжение) — презентация онлайн

Похожие презентации:

Элементы дифференциального исчисления.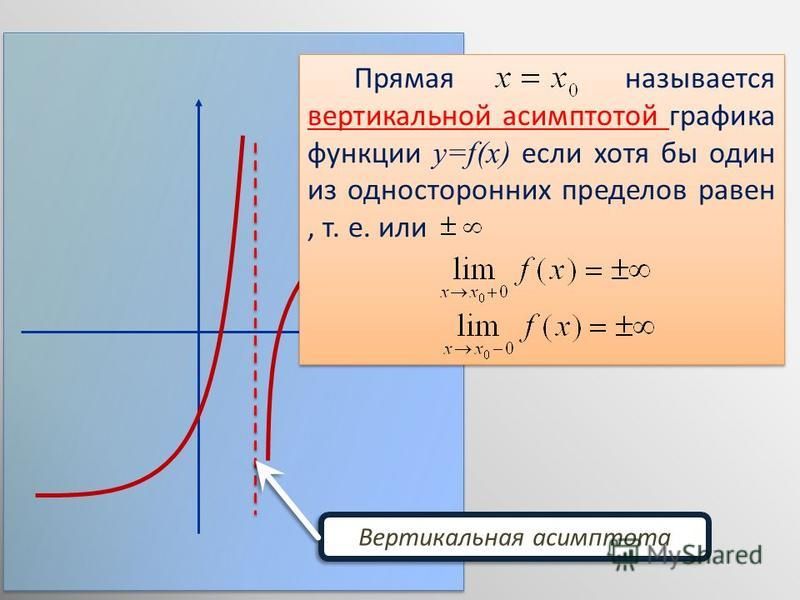 Производые. Исследование (лекция 2)

Дифференциальное и интегральное исчисление

Дифференциальное исчисление

Практика. Примеры решения задач по темам: предел функции, вычисление производных, исследование функции

Дифференциальное исчисление функций одной переменной

Элементы дифференциального исчисления

Дифференциальное исчисление

Дифференциальное исчисление

Дифференциальное исчисление

Дифференциальное исчисление. Лекция 1

Финансовый университет
при Правительстве Российской Федерации
Тема №4
(продолжение).
Дифференциальное исчисление
Производная
Общая схема исследования функций и
построения их графиков:
1. ООФ;
2. Чётность – нечётность;
3. Периодичность;
4. Вертикальные асимптоты;
5. Наклонные асимптоты;

6. Экстремумы, интервалы монотонности
функции;
7. Точки перегиба, интервалы выпуклости и
вогнутости функции;
8. Точки пересечения графика с осями
координат, дополнительные точки
функции.
Производная
Чтобы найти экстремумы функции следует:
1. Найти производную функции:
2. Найти критические точки функции
(приравнять к нулю и числитель, и
знаменатель производной):
3. Нанести критические точки на числовую
прямую, выяснить знак производной на
каждом из полученных на прямой
интервале (применив метод интервалов).
Производная
Чтобы найти точку пересечения графика
функции с осью ординат следует задать х=0.
Чтобы найти точки пересечения графика
с осью абсцисс следует решить уравнение
f ( x ) 0.
Задача
Пример. Исследовать функцию и построить
3
её график y x 3x.
Задача
Пример. Исследовать функцию и построить
3
её график y x 3x.
Решение:
1. ООФ: x ( ; ).
2. Функция нечётная, т.к.
y( x) ( x)3 3( x) x3 3x ( x3 3x) y( x).
3. Вертикальных асимптот нет, т.к. по ООФ
х – любое.
Задача
4. Ищем наклонные асимптоты:
y ( x)
x 3 3x
k lim
lim
lim x 2 3
x
x
x
x
x
Следовательно наклонных асимптот нет.
5. Ищем экстремумы функции:
y ‘ 3x 2 3
3x 2 3 0 x 2 1 x 1
1
max
1
min
x
Задача
y ( 1) 1 3 2
y (1) 1 3 2.
6. Ищем точки перегиба функции:
y » ( x) 6 x
y » ( x) 0 x 0
выпукла
0
x
вогнута
y (0) 0
Точка (0; 0) – точка перегиба функции.
Задача
7. Ищем точки пересечения с осями
координат:
y( x) 0 x 3 3x 0 x( x 2 3) 0
x 0 или x 3 0 x 3 1,7.
2
8. Строим график:
Задача
y
2
1
3
3 1 0
2
x
Задача
y
2
1
3
3 1 0
2
x
Задача
Пример. Исследовать функцию и построить её
график
2
4x
y 2 .
x 1
Решение:
1. ООФ:
2. Функция чётная, т.к.
x ( ; 1) ( 1;1) (1; )
4( x)
4x
y ( x)
2
y ( x)
2
( x) 1 x 1
2
2
Задача
3. Вертикальные асимптоты могут проходить
через точки х = -1 и х = 1. Рассмотрим
односторонние пределы:
4×2
4×2
lim 2 , lim 2
x 1 0 x 1
x 1 0 x 1
4x
4x
lim 2 , lim 2
x 1 0 x 1
x 1 0 x 1
2
2
Таким образом х = -1 и х = 1 – уравнения
вертикальных асимптот.
Задача
4. Наклонные асимптоты:
y kx b
y ( x)
4×2
4x
k lim
lim
lim 2
0,
2
x
x x ( x 1)
x x 1
x
4×2
b lim y ( x ) kx lim 2
0 x 4,
x
x x 1
— уравнение горизонтальной
т.о. y 4
асимптоты.
Задача
5. Экстремумы:
2
2
8
x
(
x
1
)
2
x
4
x
8x
y’
( x 2 1) 2
( x 2 1) 2
x 0, x 1, x 1 критические точки.
1
0
max
y (0) 0
1
x
Задача
6. Ищем точки перегиба функции:
‘
8 x 8( x 2 1) 2 32 x 2 ( x 2 1)
y ‘ ‘ 2
2
2
4
( x 1)
( x 1)
8( x 2 1)( x 2 1 4 x 2 ) 8(3 x 2 1)
2
2
4
( x 1)
( x 1) 3
вогнута
1
выпукла
1
вогнута
x
Задача
6. (0; 0) – единственная точка пересечения с
осями координат. Для уточнения графика
можно произвольно взять любые точки,
например х = 3 и х = -3.
4 32 36 9
y(3) 2
y ( 3).
3 1 8 2
Задача
y
4
3 1 0 1
3
x
Задача
y
4
3 1 0 1
3
x
Задача
Пример. Исследовать функцию и построить её
график
x
y ( x 1)e .
Задача
Пример. Исследовать функцию и построить её
график
x
y ( x 1)e .
Решение:
1. ООФ: x ( ; )
2. Функция общего вида, т.к.
y( x) ( x 1)e
x
3. Вертикальных асимптот нет
Задача
4. Ищем наклонные асимптоты:
y kx b
( x 1)e x
x 1 x
lim
k lim
e
x
x
x x
x 1
x
x
lim
lim e 1 lim e ;
x
x
x x
lim e x , lim e x 0,
x
x
b lim ( x 1)e
x
x
x 1
1
0 x lim
lim x 0,
x e x
x e
Задача
Таким образом получили y = 0 – уравнение
правосторонней горизонтальной асимптоты.
5. Ищем экстремумы функции:
y ‘ 1 e x ( x 1)e x e x (1 x 1) xe x
xe x 0 x 0,
y ( 0) 1 .
0
max
x
Задача
6. Ищем точки перегиба функции:
x
x
1
x
y e xe e ( x 1)
»
выпукла
вогнута
2
y (1) (1 1)e 0,7
e
1
x
Задача
7. Ищем точки пересечения с осью абсцисс (с
осью ординат уже получили):
( x 1)e
x
0 x 1.
8. Строим график.
Задача
y
1 0
1
1
x
Задача
y
1 0
1
1
x
Задача
Пример. Исследовать функцию и построить её
График
y x ln x.
Задача
Пример. Исследовать функцию и построить её
График
y x ln x.
Решение:
1. ООФ х > 0
2. Функция общего вида
3. Ищем вертикальные асимптоты:
ln x
x 1
lim ( x ln x) 0 lim 1 lim
2
x 0 0
x 0 0 x
x 0 0 x
lim ( x) 0.
x 0 0
Задача
Т.о. вертикальных асимптот график не
имеет.
4. Ищем наклонные асимптоты:
x ln x
k lim (
) lim (ln x)
x
x
x
Следовательно, наклонных асимптот у
графика тоже нет.
5. Ищем экстремумы функции:
1
‘
‘
y ( x ln x) ln x x ln x 1
x
ln x 1 0 ln x 1 x e 1
Задача
0
1
e
x
min
y(e 1 ) e 1 ln e 1 e 1.
1
6. Ищем точки перегиба функции: y (ln x 1)
x
»
0
функция вогнута на всей ООФ
‘
x
Задача
7. Ищем точки пересечения с осью абсцисс:
x ln x 0
x 0 или x 1
не входит в ООФ
8. Строим график
Задача
y
0
e
1
e
1
1
x
Задача
y
0
e
1
e
1
1
x
Финансовый университет
при Правительстве Российской Федерации
Тема №5.
Дифференциал функции
Дифференциал функции
Дифференциалом функции в точке
называется главная, линейная относительно
приращения аргумента часть приращения
функции, равная произведению производной
функции на приращение её аргумента
dy y ‘ ( x0 ) x.
Задача
Найдём дифференциал функции y(x)=x :
По определению dy y ‘ x x ‘ x x,
но y x dy dx
dx x.
Получили, что дифференциал независимой
переменной равен приращению этой
переменной.
dy
‘
‘
Следовательно
dy y dx или y .
dx
Дифференциал функции
y
y
0 x x x
y y
MK y
ML dy
K
L
N M
x dx
x
Дифференциал функции
Геометрический смысл дифференциала
функции в точке: Дифференциал функции в
точке численно равен приращению ординаты
касательной, проведённой к графику функции
в этой точке, при изменении абсциссы этой
точки на соответствующее приращение.
Свойства дифференциала функции
аналогичны свойствам производной.
Дифференциал функции
Нахождение дифференциала от
дифференциала ведёт к нахождению
дифференциала высших порядков (от второго
порядка и выше).
d (dy( x)) d y
2
d y y
n
( n)
( x) dx
Задача
Пример. Вычислить приближённо синус 39
градусов с точностью до 0,01.
Решение:
sin 39 sin(
0
6
y sin x, dx
20
).
0,157, dy y ‘ ( x0 )dx,
20
y (39 0 ) y (30 0 ) y ‘ (300 )dx
y (39 ) 0,5 cos 30 dx
0
0
y (39 0 ) 0,5 0,85 0,157 0,63.
Финансовый университет
при Правительстве Российской Федерации
Конец темы

English     Русский Правила

Урок 12. Функции и их свойства. Практика 11 класс онлайн-подготовка на Ростелеком Лицей

 

 

Подготовка к ЕГЭ по математике

 

Эксперимент

Урок 12.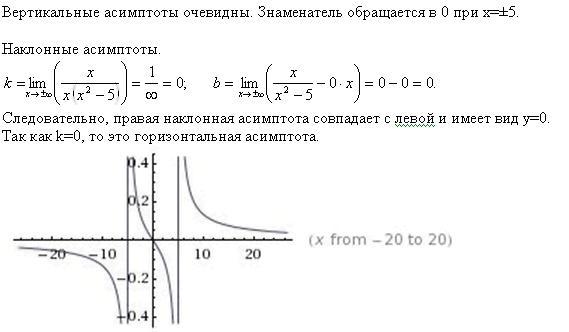 Функции и их свойства

Практика

Конспект урока

 

Область определения функции

 

 

Сначала рассмотрим задачи на определение основных свойств функций и их характеристик, затем займемся чтением графиков.

 

Начнем с нахождения области определения функции.

Задача №1. Указать область определения функции: а) ; б) ; в) ; г) ; д) .

а) Т.к. функция представляет собой корень четной степени из выражения, содержащего неизвестную, то подкоренное выражение должно быть неотрицательным.

.

б) Т.к. указан десятичный логарифм, то его основание равно 10, и удовлетворяет условию  и , то данная функция имеет смысл. Эта проверка, конечно же, проводится формально, обозначение десятичного логарифма уже предполагает, что его основание имеет смысл.

Теперь перейдем к основной части нахождения области определения функции и вспомним, что выражение под логарифмом должно быть положительным, т. е.

в) В указанной функции присутствует и корень четной степени из выражения, содержащего неизвестную, и деление на неизвестное выражение. Таким образом, мы имеем два ограничения на область определения функции:

г) Указанная квадратичная функция  не имеет ограничений на область определения, т.к. функция будет иметь смысл при любых значениях аргумента, т.е. .

д) Важно не спешить при виде корня сразу же искать ограничения на область определения, т.к. функция задана в виде корня нечетной степени, а никаких ограничений на подкоренное выражение в таком случае нет, т.е. .

Ответ. а) ; б) ; в) ; г) ; д) .

 

Задача №2. Указать по графику область определения функции:

а)

б)

а) Обратим внимание, что точки изображенного графика имеют любые значения по оси абсцисс, кроме , в этой точке проведена вертикальная асимптота к графику.

Т.е. .

 

б) Этот график уже поинтереснее, координаты его точек имеют значения от нуля, причем ноль выколотый, до плюс бесконечности, но без , в этой точке, как и в предыдущем случае, проведена вертикальная асимптота к графику.

Т.е. .

 

Ответ. а) ; б) .

 

Область значений функции

 

 

Теперь перейдем к заданиям на определение области значений функции.

 

Задача №3. Указать область значений функции: а) ; б) ; в) ; г) ; д) .

 

а) Получим ограничения на область значений данной функции путем преобразований ограничений на простейшую функцию :

 

С другой стороны важно не забыть, что корень четной степени имеет неотрицательные значения, т.е.:

Таким образом, если учесть эти оба условия, то мы получим, что

.

 

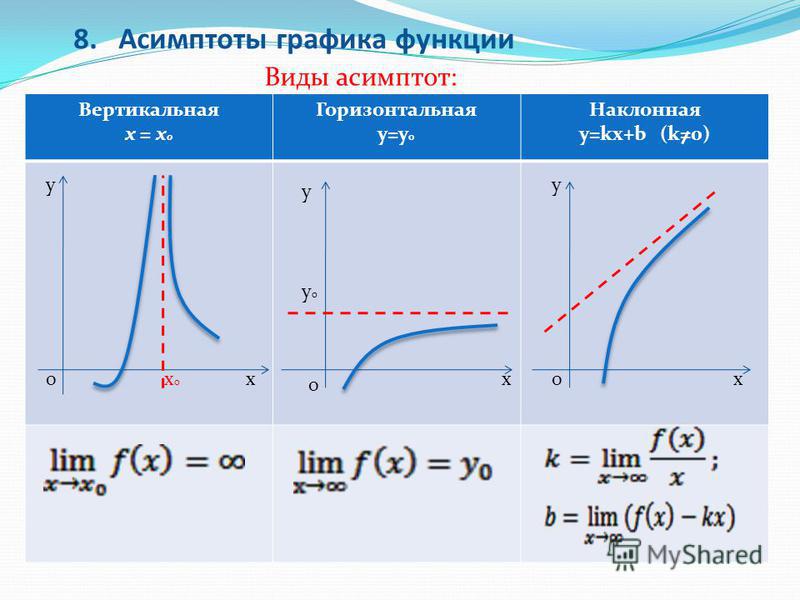
б) Мы уже обсуждали, что для определения области значений для квадратичной функции необходимо вычислить координату вершины ее параболы по оси ординат. Давайте вспомним из школьной программы как вычислить для начала иксовую координату вершины параболы:

Теперь найдем игрековую координату вершины, для этого подставим  в функцию:

Поскольку парабола имеет положительный старший коэффициент, то ее ветки направлены вверх, и  является ее минимальным значением, следовательно:

.

На следующем уроке мы с вами еще подробно разберемся с определением вершины и построением параболы.

 

в) Давайте сначала упростим указанное выражение, для этого раскроем скобки:

Теперь воспользуемся известными нам ограничениями на синус (синус любого аргумента лежит в диапазоне от  до ):

 

г) Начнем поиск области значений данной функции с известного ограничения на модуль:

Теперь проанализируем, что будет, если возводить 2 в неположительную степень. Для этого запишем функцию в более удобной форме, чтобы перейти к положительной степени:

Для того чтобы указать область значений указанной функции, необходимо определить значения, которыми она ограничена. Максимальное значение дроби будет при минимальном знаменателе, в нашем случае это достигается при , тогда функция примет значение:

Минимальное значение дроби будет при максимальном знаменателе, но наш знаменатель ничем не ограничен и при аргументах, стремящихся к бесконечности, он тоже будет стремиться к бесконечности, а дробь соответственно стремится к нулю.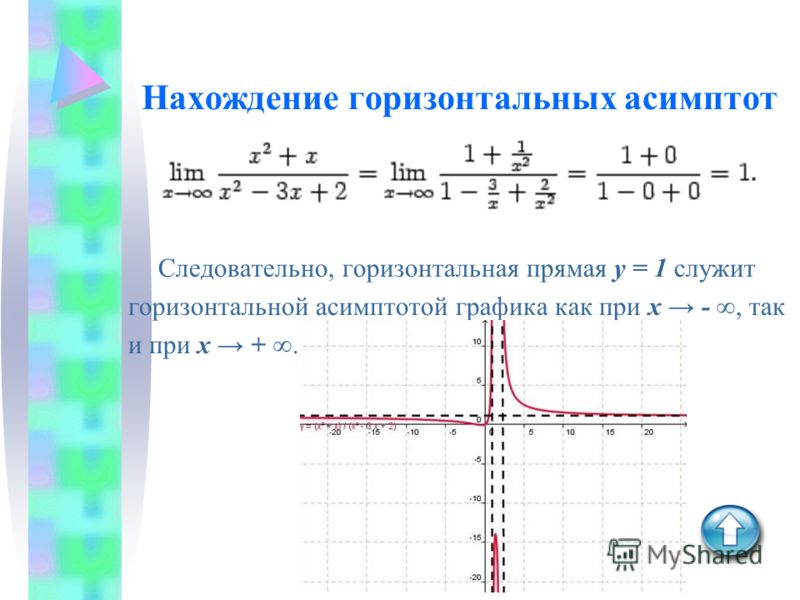

Таким образом, функция ограничена значениями от 0 до 1, причем, ноль не достигается, а к нему функция только стремится, а единица достигается, следовательно:

.

д) В этом случае указана линейная функция, а ее значения ничем не ограничены, следовательно

.

 

Ответ. а) ; б) ; в) ; г) ; д) .

 

Задача №4. Указать по графику область значений функции:

а)

б)

 

а) Обратим внимание, что на указанном графике есть горизонтальная асимптота, к которой функция прижимается, но не пересекает ее, также она не поднимается выше значения равного 2, при этом, функция убывает до минус бесконечности, следовательно

.

 

б) В этой функции также имеется горизонтальная асимптота, к которой прижимается функция, при этом она стремится к значению равному нулю, но не достигает его, ниже нуля у функции нет значений. А максимальное значение, которое достигается функцией равно единице, т.е.

.

 

Ответ. а) ; б) .

 

Задача №5. По указанной таблице, которая задает функцию соответствия между числами месяца и потреблением электроэнергии в эти дни, укажите максимальное значение из области определения и минимальное значение из области значений функции.

Число	3	8	12	21	29
	5,1	4,9	3,8	4	4,2

 

Самое главное понять, что множеством аргументов функции, т.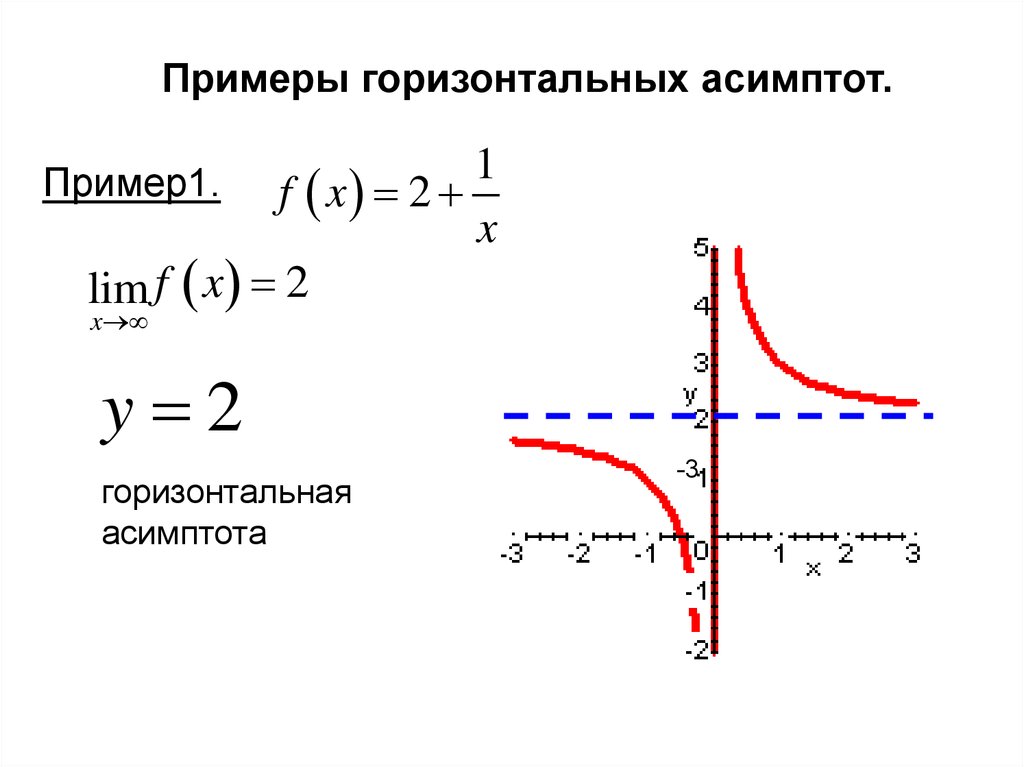 е. ее областью определения является верхняя строка таблицы, а областью значений – нижняя строка, т.к. именно от числа месяца зависит, какое было потребление электроэнергии, а не наоборот.

Теперь указать максимальное значение из области определения, т.е. из чисел в верхней строке, не составит труда. Это число 29.

Аналогично минимальным в области значений будет число 3,8 из нижней строки.

Ответ. 29; 3,8.

 

Асимптоты функции, точки пересечения с осями

 

 

Приведем пример на определение асимптот графика функции.

 

Задача №6. Укажите уравнения горизонтальной и вертикальной асимптот графика функции .

Начнем с вертикальной асимптоты. Как мы указывали в лекции к уроку она имеет уравнение

 аргументы, при которых в функции происходит деление на ноль

В указанной функции такому условию удовлетворяет, очевидно,  это и будет уравнение вертикальной асимптоты.

Для определения горизонтальной асимптоты вспомним, что ее уравнение

 значения, к которым функция приближается на  

Для того, чтобы найти к чему стремится наша функция при иксах, стремящихся к бесконечности, постараемся получить в знаменателе константу, для чего выделим в дроби целую часть:

Когда в числителе дроби находится число, а в знаменателе выражение, которое стремится к бесконечности, что происходит при увеличении аргумента, то дробь стремится к нулю. Таким образом, получаем, что все выражение стремится к двойке. Т.е. уравнением горизонтальной асимптоты будет .

Заметьте, мы не могли сделать вывод о том, к чему стремится значение дроби, пока в числителе находилось неизвестное выражение. Дело в том, что при увеличении аргумента, в таком виде возрастают и числитель и знаменатель, и сложно сказать к чему будет стремиться их отношение.

Ответ. ; .

А сейчас рассмотрим задачу, в которой найдем точки пересечения графика функции с осями.

Задача №7. Найти координаты точек пересечения графика функции  с осями координат.

Для нахождения точки пересечения с осью ординат подставим в функцию  и получим . Т.е. координаты этой точки будут .

Для нахождения точек пересечения с осью абсцисс приравняем функцию к нулю () и решим уравнение:

Это стандартное квадратное уравнение, которое можно решить или с помощью дискриминанта или по теореме Виета, проделайте это самостоятельно, мы же укажем результат:

Т. е. координаты этих точек будут .

Обратите внимание, что для определения координат точек пересечения с осями график функции строить не обязательно.

Ответ.; .

 

Чётность и нечётность, периодичность

 

 

А сейчас перейдем к заданиям на определение очень важного свойства функции четности/нечетности.

 

 

Задача №8. Определить тип четности функции: а) ; б) ; в) ; г) ; д) .

Во всех случаях для определения типа четности функции необходимо подставить аргумент с противоположным знаком, т.е. . Именно для того, чтобы это нагляднее продемонстрировать, мы и обозначили функции в виде .

а)  — функция четная.

б)  — функция нечетная.

в)  — функция нечетная.

г)  — функция общего вида.

д)  -функция нечетная.

Ответ. а) функция четная; б) функция нечетная; в) функция нечетная; г) функция общего вида; д) функция нечетная.

 

Задача №9.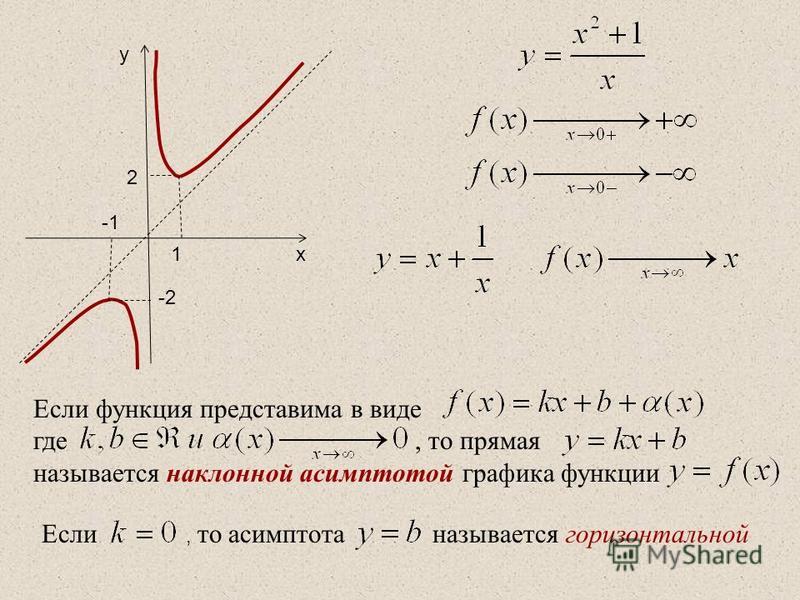 Определить по графику тип четности функции:

а)

б)

 

Для решения задачи вспомним определения четной и нечетной функции, в которых говорится об определенных свойствах симметрии их графиков.

 

а) Изначально может показаться, что график симметричен относительно оси ординат, и практически так и есть, но обратите внимание на выколотую точку, у которой нет симметричной. Такая мелочь уже нарушает возможное предположение о четности этой функции, симметричными должны быть все точки функции. А т.к. она еще не симметрична относительно начала координат, то не является и нечетной, т.е. указанная функция является функцией общего вида.

 

б) Указанный график является графиком синуса и можно вспомнить, что эта функция нечетная. Второй вариант решения – это обратить внимание на симметрию всех точек графика относительно начала координат.

Ответ. а) функция общего вида; б) нечетная функция.

 

Задачи на вычисление периодов тригофункций со сложным аргументом мы уже рассматривали, но повторим их и в этой теме, т. к. период – это важная характеристика функции.

 

Задача №10. Указать период функций: а) ; б) .

 

а) По формуле  для функций вида  получаем, что .

 

б) По формуле  для функций вида  вычислим, что . Такая запись должна удивить, т.к. период по определению является положительным числом, поэтому возьмем модуль от полученного значения и получим .

Остальные действия с функцией на значение периода не влияют.

 

Ответ. а) ; б) .

 

Промежутки монотонности функции, чтение графиков функций

 

 

Теперь разберем пример на определение промежутков монотонности функции.

 

 

Задача №11. Указать промежутки монотонности функции, которая приведена на графике

 

Функция возрастает там, где большему значению аргумента соответствует большее значение функции. Такие участки исходя из графика

.

Функция убывает там, где большему значению аргумента соответствует меньшее значение функции. Такие участки исходя из графика

.

Обратите внимание, что промежутки монотонности функции указываются именно для значений аргументов, т.е. иксов.

 

Ответ. Функция возрастает при ; функция убывает при .

 

И выполним чтение нескольких графиков функций. При этом нам необходимо будет указать основные характеристики и свойства функций.

 

Задача №12. Выполнить чтение графиков функций:

 

а)

б)

 

а)

1. Область определения ;

2. Область значений ;

3. Точки пересечения с осями: с осью ординат ;

4. Т.к. все точки функции симметричны относительно оси ординат, то она четная;

5. Непериодичная;

6. Монотонно возрастает при , монотонно убывает при .

 

б)

1. Область определения ;

2. Область значений;

3. Точки пересечения с осями: с осью абсцисс ;

4. Т.к. нет симметрии, то функция общего вида;

5. Непериодичная;

6. Монотонно возрастает при  , монотонно убывает при .

 

В этом практическом уроке мы привели примеры на определение свойств и характеристик функций и выполнили чтение нескольких графиков.

 

Online asymptote calculator

 

• Expression
• Equation
• Inequality
• Contact us

• Simplify
• Factor
• Expand
• GCF
• LCM

• Solve
• Graph
• System

• Решение
• График
• Система

• Математический решатель на вашем сайте

онлайн калькулятор асимптот
Связанные темы:
бесплатные рабочие листы по алгебре | алгебра числовая сетка gcse курсовая работа | Гленко издание книги для учителей математики | как вы делаете квадратные корни | преобразование из стандартной вершины в вершину -b/2a | онлайн-калькулятор уравнений с шагами | бесплатный полиномиальный калькулятор | решение алгебраических уравнений онлайн | ti 89 комбинаторных функций | факторинг и упрощение | рабочие листы по десятичным числам для 5 класса | преобразование смешанных чисел в проценты

Автор	Сообщение
XNT Зарегистрирован: 15. 05.2002 От:	Размещено: Понедельник, 20 августа, 10:01 Привет, кто-нибудь может помочь мне с домашним заданием по алгебре? Я не очень хорошо разбираюсь в математике и был бы признателен, если бы вы объяснили, как решать задачи онлайн-калькулятора асимптот. Я также хотел бы знать, есть ли хороший веб-сайт, который может помочь мне хорошо подготовиться к предстоящему экзамену по математике. Благодарю вас!
Наверх
oc_rana Зарегистрирован: 08. 03.2007 Откуда: Египет, Александрия	Размещено: Понедельник, 20 августа, 13:53 Как насчет того, чтобы дать немного больше подробностей о том, в чем именно заключается ваша проблема с онлайн-калькулятором асимптот? Это помогло бы найти способы поиска решения. Найти тренера в наши дни достаточно быстро, да еще и за плату, которую вы можете заплатить, может быть невыносимой задачей. С другой стороны, в наши дни есть программы, которые помогут вам решить математические задачи. Все, что вам нужно сделать, это выбрать наиболее подходящий. Одним щелчком мыши появляется правильный ответ. Мало того, это поможет вам найти ответ. Таким образом, вы также узнаете, как получить правильный ответ.
Наверх
Хомук Зарегистрирован: 05.07.2001 Откуда: Торонто, Онтарио	Размещено: вторник, 21 августа, 07:31 Я также узнал, что Algebrator — замечательная программа для онлайн-калькуляции асимптот. Я с трудом припоминаю, что не мог усвоить понятия сложения дробей, суммы кубов или разложения многочленов на множители, потому что я стал настолько хорош в отдельных дисциплинах онлайн-калькулятора асимптот. Алгебратор выполнил без ошибок для меня в коррекционной алгебре, коррекционной алгебре и базовой математике. Я очень сильно поддерживаю этот программный пакет, потому что я не обнаружил каких-либо недостатков при использовании Algebrator.
Наверх
Ловли Дата регистрации: 10.03.2002 Откуда: Манчестер, Великобритания	Размещено: Среда, 22 августа, 12:59 Звучит именно так, как я ищу. Как я могу это получить?
Наверх
daujk_vv7 Зарегистрирован: 06.07.2001 От кого: Не знаю, потерял.	Размещено: Пятница, 24 августа, 10:50 Мне жаль . Я должен был включить URL-адрес в наш первый раз: https://mathpoint.net/college-алгебра.html. Я ничего не знаю о тестовой версии, но законные владельцы Algebrator, в отличие от других реселлеров программ-имитаторов, выставили полную гарантию возврата средств. Таким образом, вы можете приобрести официальную версию, попробовать ее и отправить обратно, если кто-то не удовлетворен работой и функциями. Хотя я предполагаю, что вам понравится это программное обеспечение, я заинтересован в том, чтобы узнать, есть ли что-то, где программа не работает. Я не хочу рекомендовать Algebrator для чего-то, что он не может выполнить. Однако следующая обнаруженная проблема, по всей вероятности, будет первой!
Наверх
thicxolmed01 Зарегистрирован: 16.05.2004 Откуда: Велли, Новая Зеландия	Размещено: Суббота, 25 августа, 18:11 Я помню, что у меня были трудности с параллельными линиями, такими как знаменатели и графические неравенства. Алгебратор — действительно отличная математическая программа. Я использовал его на нескольких занятиях по алгебре — алгебре 2, исправительной алгебре и базовой математике. Я просто вводил проблему, и, нажимая «Решить», появлялось пошаговое решение. Программа настоятельно рекомендуется.
Наверх

Горизонтальные асимптоты — MathCracker.com

Алгебра Учебники

---

Горизонтальная асимптота — это верхняя граница, которую можно представить в виде горизонтальной линии, ограничивающей поведение графика заданной функции. Это означает, что график функции \(f(x)\) как бы приближается к этой горизонтальной линии по мере увеличения значения \(x\).

Понимание этого ограничивающего горизонтального поведения функций, демонстрирующих эту характеристику, может оказаться очень полезным при определенных обстоятельствах, потому что оно покажет, что поведение функции чем-то похоже на поведение горизонтальной линии при больших значениях \(х\).

Чтобы сделать определение ясным, горизонтальная линия \(y = h\) является горизонтальной асимптотой функции \(f(x)\), если

\[\большой \lim_{x\to\infty} f(x) = h\]

если указанный предел существует и он конечен. Для тех, кто еще не прошел курс исчисления, горизонтальная линия \(y = h\) является горизонтальной асимптотой функции \(f(x)\), когда \(h\) является ограничение \(f(x)\) при стремлении \(x\) к бесконечности. Что значит быть «пределом»? Это означает, что при достаточно больших значениях \(x\) значение \(f(x)\) будет настолько близко к \(h\), насколько мы предопределим. Необычно, правда? 92+1} \]

ОТВЕЧАТЬ:

Чтобы найти горизонтальную асимптоту, нам нужно найти предел функции \(f(x)\) при стремлении \(x\) к бесконечности. Если вы не знакомы с исчислением, вам следует сначала попытаться вычислить функцию при очень большом значении \(x\). Например, допустим, что \(x = 1 000 000\). Подставим это число в функцию: 92+1} = 1\]

что означает, что горизонтальная асимптота равна \(y = 1\). Теперь будьте осторожны со своим ответом, если вы отвечаете на контрольную или домашнюю работу. Некоторые люди скажут, что «горизонтальная асимптота равна 1», что неверно. Технически горизонтальная асимптота — это функция \(y = 1\), а НЕ число 1. Горизонтальная асимптота — это постоянная функция, которая не совпадает с числом. Просто говорю, потому что есть некоторые придирчивые оценщики. 92}} \]

Но ждать! Трюк здесь не сработал? Да, это так. Обратите внимание, что знаменатель станет очень близким к 1, поскольку \(x\) станет очень большим, а числитель станет очень большим. Нетрудно поверить, что \(f(x)\) сходится к бесконечности, так что горизонтальной асимптоты нет. Каждый раз, когда мы видим неограниченную функцию, как в случае \(f(x)\) в этом примере, у нас не будет горизонтальной асимптоты.

Горизонтальная асимптота или горизонтальные асимптоты?

Технически может быть две горизонтальные асимптоты, одна слева и одна справа. Левая горизонтальная асимптота равна \(y = h_L\), если

\[\большой \lim_{x \to -\infty} f(x) = h_L\]

Точно так же правая горизонтальная асимптота равна \(y = h_R\), если

\[\большой \lim_{x \to +\infty} f(x) = h_R\]

в случае, если любой из вышеуказанных пределов существует и конечен. Может случиться так, что функция имеет две горизонтальные асимптоты, только одну горизонтальную асимптоту или не имеет ни одной.

Например, на приведенном выше графике есть две горизонтальные асимптоты: \(y = -2\) и \(y = 2\).

Каково правило нахождения горизонтальной асимптоты?

Не существует общих правил, которые будут работать для всех случаев. В общем случае нам нужно вычислить предел при приближении \(x\) к \(-\infty\) и предел при приближении \(x\) к \(+\infty\). Если какой-либо из этих пределов существует и конечен, у нас будут горизонтальные асимптоты.

Одно конкретное правило может быть разработано для случая, когда данная функция \(f(x)\) является частным двух многочленов. Если это так, то предположим, что \(m\) — порядок полинома в числителе, а \(n\) — порядок полинома в знаменателе. Тогда имеем следующие случаи:

Случай 1: Если \(m < n\), то горизонтальная асимптота равна \(y = 0\).

Случай 2: Если \(m = n\) и \(a\) — старший коэффициент полинома в числителе, а \(b\) — старший коэффициент полинома в знаменателе, то горизонтальная асимптота равна \( \displaystyle y = \frac{a}{b}\).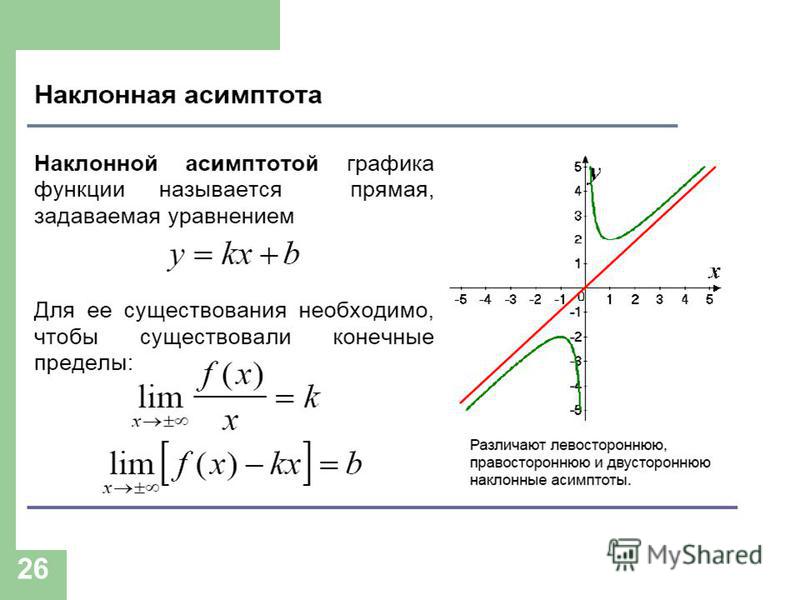

Случай 3: Если \(m > n\), то горизонтальной асимптоты нет.

ПРИМЕР 2

Найти, если существует, горизонтальную асимптоту функции 92 -x+2\), который является полиномом 2-го порядка, поэтому \(n = 2\), и ведущей константой 2.

Следовательно, поскольку в этом случае \(m = n\) есть горизонтальная асимптота, и она есть частное старших коэффициентов, то в этом случае горизонтальная асимптота есть

\[\большой y = \frac{3}{2}\]

---

Подробнее о горизонтальных асимптотах

Итак, ваш вопрос в том, как найти асимптоты уравнения, верно? Прежде всего, вы найдете асимптоты функция , а не уравнения. Затем вам нужно начать с общего определения, используя ограничения.

Если вы не знаете исчисления и не знаете, как вычислять пределы, то вам следует хотя бы попытаться подставить очень большие значения \(x\), а также очень отрицательные значения \(x\) в функцию, и посмотреть, как ведет себя функция. Даже построение функции с помощью некоторого программного обеспечения может дать вам четкий намек на наличие горизонтальных асимптот.

В конечном счете, в очень ограниченном случае, когда функция является частным многочленов, вы можете применить правило, основанное на порядках \(m\) и \(n\).

Как найти горизонтальные асимптоты с разными степенями?

Это разные типы асимптот, и они называются наклонными асимптотами.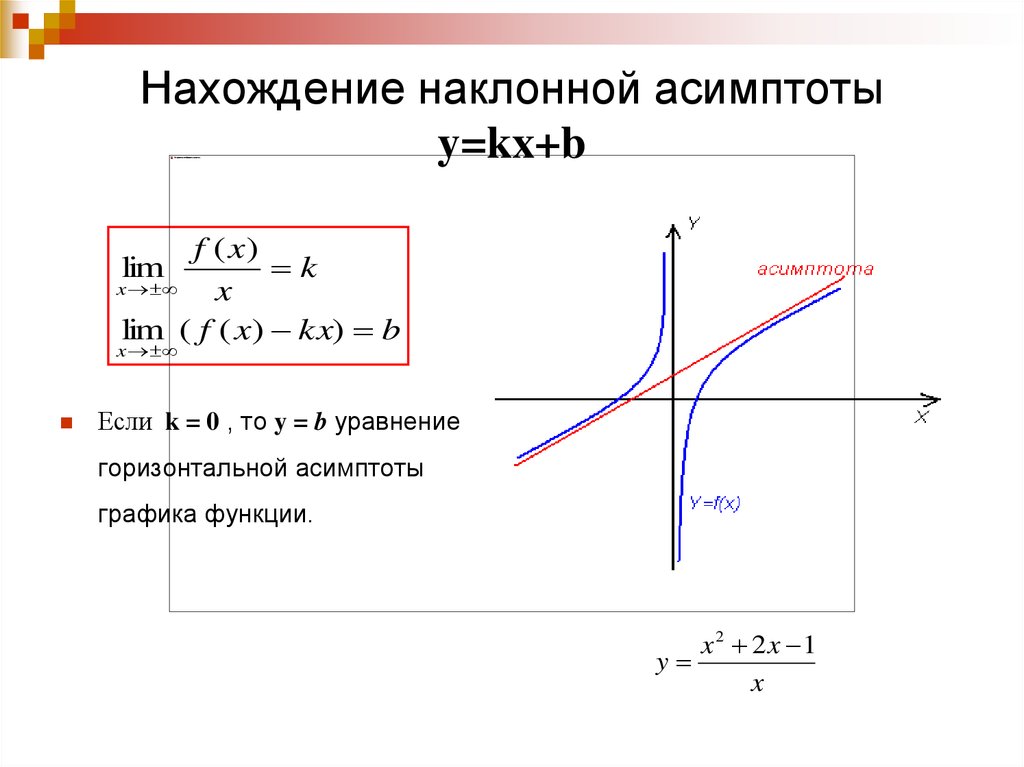 Мы поговорим о наклонных асимптотах в другом уроке.

---

Учебники по алгебре Учебники по исчислению Горизонтальные асимптоты Как вычислить горизонтальные асимптоты Правила нахождения горизонтальных асимптот

Калькулятор наклонных асимптот

Содержание

Калькулятор наклонной асимптоты — это бесплатный онлайн-инструмент, который отображает значение асимптоты для заданной функции.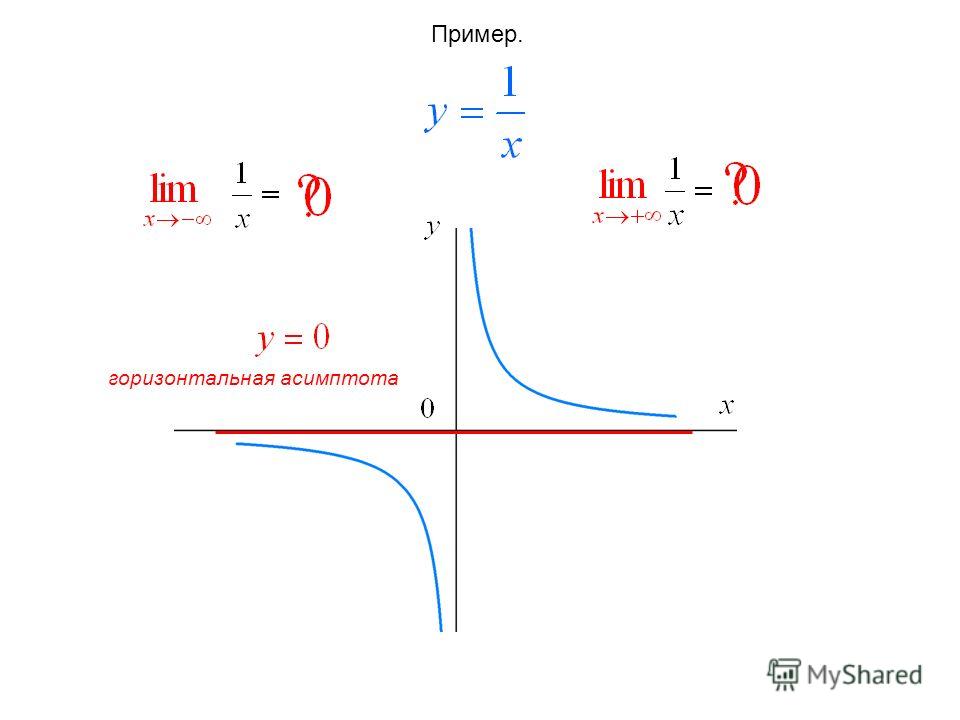 Инструмент расчета наклонной асимптоты STUDYQUERIES ускоряет вычисления и отображает значение асимптоты за доли секунды.

Как пользоваться калькулятором наклонной асимптоты?

Вы можете использовать калькулятор наклонной асимптоты, выполнив следующие действия:

• Шаг 1: Введите функцию в поле ввода
• Шаг 2: Чтобы рассчитать наклонную асимптоту, щелкните «Рассчитать наклонную асимптоту»
• Шаг 3: В новом окне будет отображаться асимптотическое значение и график

Калькулятор наклонной асимптоты

Что означает наклонная асимптота?

Наклонные или наклонные асимптоты также возможны в графиках и функциях. Что происходит, когда асимптота функции сама является функцией? В этой статье мы исследуем уникальный элемент рациональных функций — наклонные асимптоты.

Наклонные асимптоты представляют собой линейные функции, определяющие конечное поведение рациональной функции с обоих концов.

Знание наклонных асимптот позволит нам предсказать, как будут вести себя графики при экстремальных значениях переменной \(x)\. Поскольку в этой статье основное внимание будет уделено наклонным асимптотам рациональной функции, вот несколько важных свойств рациональных функций:

• Здесь вы можете узнать о рациональных функциях и их графиках.
• Убедитесь, что вы знакомы с горизонтальными и вертикальными понятиями.

Правило частного и произведения – формула и примеры

Коэффициент разности – формула, калькулятор, примеры

Нам также нужно будет пересмотреть свое понимание построения графиков линейных уравнений, когда мы узнаем о построении графиков наклонных асимптот. Вы хотите расширить свои знания о наклонных асимптотах? Начнем с определения этого термина.

Определение

Наклонные асимптоты также известны как наклонные асимптоты. Это из-за его наклонной формы, представляющей график линейной функции, \(\mathbf{y=mx+b}\). Наклонные асимптоты могут встречаться только для рациональных функций, степень числителя которых ровно на одну степень выше степени знаменателя.

Наклонные асимптоты — это линейные функции, которые мы можем использовать для предсказания конечного поведения рациональных функций, как показано в примере ниже.

Наклонная асимптота

Как видно из графика, наклонная асимптота \(\mathbf{f(x)}\) представлена ​​пунктирной линией, определяющей поведение графика. Мы также можем видеть, что \(\mathbf{y=\frac{1}{2}x+1}\) является линейной функцией вида \(\mathbf{y=mx+b}\). 92(2x) и больше

Наклонная асимптота дает нам представление о том, как ведет себя кривая \(\mathbf{f(x)}\) при приближении к \(-\infty\) и \(+\infty\). График \(\mathbf{f(x)}\) также подтверждает то, что мы уже знаем: наклонные асимптоты будут линейными (и наклонными).

Обратите внимание, что \(\mathbf{f(x)}\) не имеет горизонтальных асимптот? Это потому, что рациональная функция может иметь только горизонтальную асимптоту или наклонную асимптоту, но никогда обе.

Правила наклонной асимптоты для рациональных функций 92-9}\), эквивалентно \(\mathbf{(x+3)(x-3)}\) в факторизованной форме, поэтому знаменатель является множителем числителя.

Упрощенная форма \mathbf{f(x)}\) равна $$\mathbf{\frac{(x-3)(x+3)}{x-3}=x+3}$$

Это означает, что функция имеет наклонную асимптоту в точке \(\mathbf{y=x+3}\).

Полезно помнить об этом, так как отмена факторов будет гораздо более быстрым подходом.

Калькулятор доменов и диапазонов

Калькулятор двойных интегралов 92-6x+9}\) и \(\mathbf{x-1}\). (Обязательно проверьте свои знания о делении многочленов.)

Slant Asymptote-Synthetic Division

Это показывает, что частное равно \(\mathbf{x-5}\). Мы также можем подтвердить это с помощью деления в длину, как показано ниже.

Наклонная асимптота-длинное деление

Из этих двух методов мы видим, что \(\mathbf{f(x)=x-5+\frac{4}{x+1}}\), поэтому, сосредоточив внимание на частном, наклонная асимптота \(\mathbf{f(x)}\) находится в точке \(\mathbf{y=x-5}\).

Как найти наклонную асимптоту?

Нам необходимо освежить в памяти следующие темы при определении наклонной асимптоты рациональной функции:

• Обзор того, как мы можем выполнять деление в длину на многочленах.
• Нам также нужно будет использовать синтетическое деление , так что лучше освежить свои знания.

Мы сможем определить, какой из двух методов лучше всего, исходя из форм числителя и знаменателя.

Калькулятор первообразной производной

Калькулятор трансформации

Так как \(\mathbf{f(x)=\frac{p(x)}{q(x)}}\) является рациональной функцией с \(\mathbf{p(x)}\) одной степенью выше, чем \(\mathbf{q(x)}\), мы можем найти частное от \(\mathbf{\frac{p(x)}{q(x)}}\), чтобы найти наклонную асимптоту.

$$\mathbf{f(x)=Частное+\frac{Остаток}{q(x)}}$$

Наклонную асимптоту можно найти, сосредоточив внимание только на частном и игнорируя остаток. 2}\). Здесь это \(\mathbf{x}\). Поместите \(\mathbf{x}\) над полем деления. 92 + 5x + 2}\). Нарисуйте линию и запишите результат \(\mathbf{2x + 2}\) под ней, как показано на рисунке.

Продолжить деление

• Продолжить деление. Вы можете повторить эти шаги, используя результат задачи на вычитание в качестве нового делимого.

Обратите внимание, что если вы умножаете \(\mathbf{2}\) на старший член делителя \(\mathbf{(x)}\), вы получаете член наивысшей степени делимого, который теперь равен \( \mathbf{2x + 2}\). \(\mathbf{2}\) добавляется к первому множителю, что дает \(\mathbf{x + 2}\). Это написано в верхней части поля разделения. Под делимым запишите произведение множителя и делителя, затем снова вычтите.

Остановитесь, когда получите уравнение прямой

• Остановитесь, когда получите уравнение прямой. Нет необходимости выполнять длинное деление до конца. Продолжайте только до тех пор, пока не получите линейное уравнение вида \(\mathbf{ax + b}\), где a и b могут быть любыми числами.

Теперь вы можете остановиться на приведенном выше примере. Уравнение для вашей линии: \(\mathbf{x + 2}\).

Нарисуйте линию рядом с графиком полинома

• Нарисуйте линию рядом с графиком полинома. Нарисуйте свою линию, чтобы убедиться, что это действительно асимптота.

В приведенном выше примере вам нужно построить график \(\mathbf{x + 2}\), чтобы увидеть, что линия движется вдоль графика вашего многочлена, но никогда не касается его, как показано ниже. Итак, \(\mathbf{x + 2}\) действительно является наклонной асимптотой вашего многочлена.

Заключение

Мы уже многое узнали о наклонных асимптотах, поэтому давайте суммируем важные свойства наклонных асимптот, прежде чем двигаться дальше.

Калькулятор второй производной

• Функция имеет наклонную асимптоту, если ее числитель ровно на одну ступень выше знаменателя.
• Наклонная асимптота имеет общий вид \(\mathbf{y=mx+c}\), поэтому мы ожидаем, что она вернет линейную функцию.
• Используйте точки пересечения наклонной асимптоты для построения линейной функции.
• Вам также следует освежить свои знания по предыдущим темам, которые мы обсуждали в этой статье.

Часто задаваемые вопросы

Как найти наклонные асимптоты?

Наклонная или наклонная асимптота находится путем деления числителя на знаменатель. Наклонная асимптота существует, так как степень числителя на 1 больше степени знаменателя. Уравнение \(\mathbf{y=mx+c}\) является наклонной асимптотой.

Может ли наклонная асимптота быть горизонтальной асимптотой?

График может иметь как вертикальную, так и наклонную асимптоту, но НЕ МОЖЕТ иметь и горизонтальную, и наклонную асимптоту. Вы рисуете на графике наклонную асимптоту, проводя пунктирной горизонтальной (слева и справа) линией, проходящей через \(\mathbf{y = mx + b}\).

Как узнать, пересекает ли график наклонную асимптоту?

Если имеется наклонная асимптота, \(\mathbf{y=mx+b}\), то установите рациональную функцию равной \(\mathbf{mx+b}\) и найдите \(\mathbf{x} \).

No related posts.