5. Вычисление объёмов тел площадей плоских фигур с помощью двойного интеграла.
Вычисление объемов с помощью двойного интегралаС помощью двойного интеграла, если воспользоваться его геометрической трактовкой, можно вычислить объем цилиндроида; формула для вычисления объема цилиндроида имеет вид:
где функция задает
поверхность, ограничивающую цилиндроид
сверху (Рис.
9)Более
общая формула
для вычисления объема тела с помощью
двойного интеграла имеет
вид:Она
получается как разность объемов двух
цилиндроидов (Рис. 10).Объемы
других тел вычисляются двойным интегралом
только в случаях, когда эти объемы
представляются как сумма или разность
объемов цилиндроидов.Напомним, что
цилиндроидом называется геометрическое
тело, которое в координатной
системе XOYZ ограничено
снизу областью ,
сверху – частью некоторой поверхности ,
сбоку – цилиндрической поверхностью
с образующими, параллельными оси OZ.
Вычисление площади фигуры с помощью двойного интеграла.
6.
Вычисление площадей поверхностей с
помощью двойного интеграла.
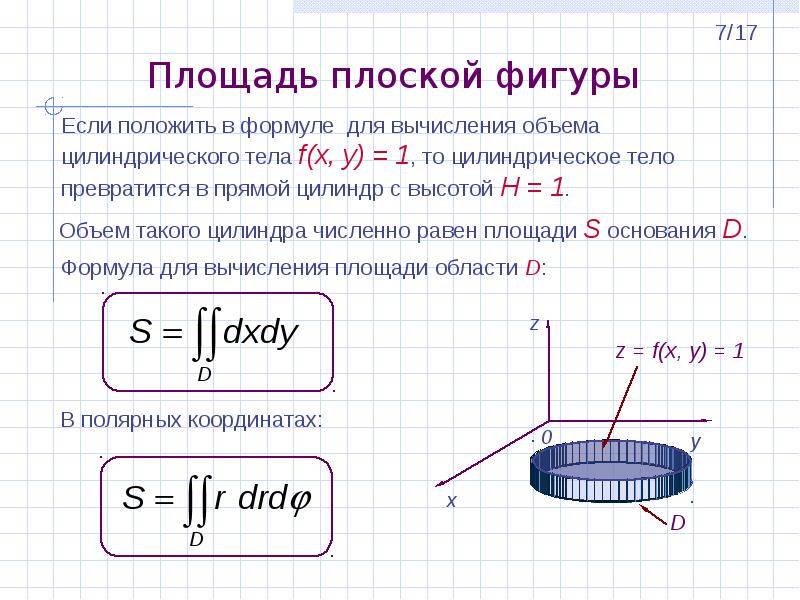
Вычисление площади плоской фигурыПлощадь плоской фигуры, ограниченной областью D, находится по формуле . (105)Если область определена в прямоугольной системе координат неравенством , то из (105) имеем . (106)Если область D определена в полярных координатах неравенством , , то . (107)
Вычисление
площади пространственных поверхностейЕсли
гладкая однозначная поверхность задана
уравнением z = f (x,y),то
площадь этой поверхности выражается
формулой
,
(108)где D есть
проекция данной поверхности на
плоскость хОу.Если
поверхность задана уравнением x = f (y, z),то
для вычисления площади имеем аналогичную
формулу
.
(109)Однако здесь D есть
проекция поверхности на
плоскость yOz.Аналогично,
если поверхность задана
уравнением 
Пусть в плоскости Oxy есть материальная пластинка, то есть некоторая область D, п о которой распределена масса с плотностью μ(x, y). Тогда:масса пластинки
.статические моменты относительно координатных осей:
, координаты (xc, yc) центра масс пластинки:
,
момент инерции пластинки относительно оси Oy относительно оси Ox относительно начала координат
Объем цилиндрического тела. Двойной интеграл. (Лекция 2.1)
1. Лекция 2.1 9 ДВОЙНЫЕ ИНТЕГРАЛЫ. 9.1 Объем цилиндрического тела. Двойной интеграл.
zy
D
z = z ( x, y ) ³ 0
x
Цилиндрическим телом называется тело,
ограниченное замкнутой областью D плоскости Oxy,
поверхностью z=z(x,y), где z=z(x,y) непрерывна и
неотрицательна в области D и цилиндрической
поверхностью с образующей параллельной оси Oz и
направляющей – границей области D.
2. Разобьем область D на n произвольных частичных областей (k(1,…,n)).
Разобьем область D на n произвольных частичныхобластей Ds k (k (1,…,n)).
Ds k
y
( xk , yk )
D
x
Выберем в каждой из частичных областей произвольную точку с
(
)
координатами xk , yk . Объем цилиндрического тела между
опорной плоскостью Oxy и поверхностью z=z(x,y) над частичной
областью Ds k равен DVk » z xk , yk Ds k
. Объем всего
цилиндрического тела равен
(
n
n
k =1
k =1
)
V = å DVk » å z ( xk , yk ) Dsk
Устремим наибольший диаметр частичных областей
max diam ( Dsk ) ® 0 , n ® ¥
Ds k
и рассмотрим предел интегральной суммы
к нулю, при этом
n
lim
max diam( Dsk
n®¥
z ( xk , yk ) Dsk
å
) ®0
k =1
Если этот предел существует, то очевидно, что
V=
n
lim
max diam( Dsk
n®¥
z ( xk , yk ) Dsk
å
) ®0
k =1
4. Определение.
Двойным интегралом от функции z=z(x,y) по области Dназывается предел, к которому стремится интегральная
сумма при стремлении к нулю наибольшего диаметра
частичных областей
n
lim
max diam( Dsk
n ®¥
z ( xk , yk ) Dsk = òò z ( x, y ) d s
å
) ®0
k =1
D
z ( x, y ) ds
– подынтегральное выражение;
z(x,y) – подынтегральная функция;
ds — элемент (дифференциал) площади;
D – область интегрирования.
Таким образом, V = z ( x, y ) d s
òò
D
5. Теорема существования двойного интеграла.
Если z(x,y) непрерывна в замкнутойограниченной области D, то ее интегральная
сумма стремится к пределу при стремлении к
нулю наибольшего диаметра частичных
областей. Этот предел не зависит от способа
разбиения области на частичные области Ds k
и выбора в них точек ( xk , yk ) .
6. 9.2 Свойства двойных интегралов.
1)D
òò ( z1 ( x, y ) ± … ± zn ( x, y ) ) d s = òò z1 ( x, y ) d s ± … ± òò zn ( x, y ) d s
2)
D
òò cz ( x, y ) d s = c òò z ( x, y ) d s
D
D
D
3) D = D1 U D2 , D1 I D2 = Æ .
Тогда
òò z ( x, y ) d s = òò z ( x, y ) d s + òò z ( x, y ) d s
D
D1
D2
7. Свойства двойных интегралов.
4) Если (x,y) D z1 ( x, y ) ³ z2 ( x, y )то
òò z1 ( x, y ) d s ³ òò z2 ( x, y ) d s
D
D
D
5) Если m = zвнаим
, M = zвнаиб
mS £ òò z ( x, y ) d s £ MS
то
D
6)
z ( x, y ) d s = z ( x, h) S , ( x, h) D
òò
D
D
z ( x, h )
,
, где S = òò d s .
D
— среднее значение z в области D.
8. 9.3 Вычисление двойных интегралов.
Разобьем область D с помощью линий,параллельных осям координат
с шагом dx и dy соответственно.
Тогда d s = dxdyи, следовательно,
y
ds
D
òò z ( x, y ) d s = òò z ( x, y ) dxdy.
D
D
При вычислении двойного интеграла будем использовать
b
формулу
V = ò S ( x ) dx,
(9.1)
a
где
— площадь поперечного
сечения тела плоскостью
S ( x)
x=const.
Предположим, что любая прямая, параллельная осям Ox или
Oy, пересекает границу области D не более чем в двух точках.
x
y
E
d
y = y2 ( x )
B
A
c
a
z = z ( x, y )
y
z
C
y = y1 ( x )
b
S ( x) =
D
x
a
y2 ( x )
b
x
ò z ( x, y ) dy
y1( x )
• Здесь при вычислении интеграла по dy считается,
чтоö x –
b æ y2 ( x )
постоянная.
z ( x, y ) dy ÷ dx =
V = z ( x, y ) dxdy = ç
• Согласно (9.
1)y2 ( x )
b получим:
= ò dx
a
ò z ( x, y ) dy
y1( x )
òò
D
.
òç ò
a è y1( x )
÷
ø
(9.2)
• Изменив порядок интегрирования, аналогично
получим
d
x2 ( y )
c
x1( y )
òò z ( x, y ) dxdy = ò dy ò z ( x, y ) dx
D
.
(9.3)
• Правые части формул (9.2) и(9.3) называются
повторными (или двухкратными) интегралами.
• Процесс расстановки пределов интегрирования
называется приведением двойного интеграла к
повторному.
11. Примеры:
1)y
d
D
c
x
a
b
b
d
d
b
a
c
c
a
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy = ò dy ò z ( x, y ) dx
D
y
y=x
a
y=0
x=a
x
a
a
x
a
a
0
0
0
y
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy = ò dy ò z ( x, y ) dx
D
y
1
y = x2
x+ y =2
y=0
x
2
1
1
x2
2
2- x
1
2- y
0
0
1
0
0
y
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy + ò dx ò z ( x, y ) dy = ò dy ò z ( x, y ) dx
D
y
y = y2 ( x )
y = y1 ( x )
a
b
x
b
y2 ( x )
a
y1( x )
òò z ( x, y ) dxdy = ò dx ò z ( x, y ) dy
D
y
d
c
.
x = x1 ( y )
x = x2 ( y )
x
d
x2 ( y )
c
x1( y )
òò z ( x, y ) dxdy = ò dy ò z ( x, y ) dx
D
y
D1
D = D1 + D2 + D3
D2
D3
x
òò z ( x, y ) dxdy =
D
= òò z ( x, y ) dxdy +
D1
òò z ( x, y ) dxdy + òò z ( x, y ) dxdy
D2
D3
Двойные интегралы
и объем
Двойные интегралы и объем
Определение объема
Напомним, что площадь между двумя кривыми определяется как интеграл верхней кривой минус нижняя кривая. Эту идею можно довести до трех размеры. Мы определили объем между двумя поверхностями как двойной интеграл верхней поверхности минус нижняя поверхность. Это можно написать формально с теоремой ниже.
Теорема Фубини Пусть f,
г 1 ,
г 2 ,
ч 1 ,
и ч 2 быть
определенная и непрерывная на области R.
|
Тогда объем поверхности равен двойным интегралам:
Обратите внимание, что все типичные свойства двойного интеграла держать. Например, можно вытащить константы и получить двойной интеграл от сумма двух функций есть сумма двойных интегралов каждой функции.
Поиск тома
Пример
Установите интеграл, чтобы найти объем твердого тела, лежащего ниже конуса
и выше плоскости xy.
Раствор
Конус нарисован ниже
Мы видим, что область R представляет собой синий кружок в плоскости xy. Мы можем найти уравнение, установив z = 0,
Решение
для y (переместив квадратный корень влево, возведя в квадрат обе
стороны и т.
д.) дает
«-» соответствует нижнему пределу, а «+» — верхнему пределу. Для внешних границ мы видим, что
-4 < х < 4
Все это вместе дает
Либо вручную или на машине мы можем получить результат
Объем = 64 стр/3
Обратите внимание, что это согласуется с формулой
Объем = p r 2 ч/3
Упражнение
Настройте двойной интеграл для этой задачи с помощью dxdy вместо dyx. Затем покажите, что два интеграла дают один и тот же результат.
Пример
Установите двойной интеграл, который дает объем твердого тела лежащий под сферой
х 2 + у 2 + z 2 = 6
и выше параболоид
г = х 2 + у 2
Раствор
На картинке ниже указано, что регион — это диск, который
лежит внутри этой окружности пересечения двух поверхностей.
Подставляем
х 2 + у 2 + (х 2 + у 2 ) 2 = 6
или
x 2 + у 2 + (х 2 + у 2 ) 2 — 6 = 0
Теперь разложите x 2 + y 2 в качестве переменной, чтобы получить
(х 2 + у 2 — 2)(х 2 + у 2 + 3) = 0
Второй множитель не имеет решения, а первый
x 2 + у 2 = 2
Решение для y дает
и— < х <
Просто как мы сделали в одном исчислении переменных, объем между двумя поверхностями равен двойной интеграл верхней поверхности минус нижняя поверхность. У нас есть
Снова мы можем выполнить этот интеграл вручную или на машине и получить
Объем = 7,74
Среднее значение
Мы думаем о среднем как о сумме всех деленных на
общий.
Двойной интеграл действует как сумма, а сумма есть
область. Это приводит нас к следующему определению.
| Пусть f(x,y) — интегрируемая функция по области R с площадью А, затем Среднее значение из ф над R является |
Пример
Вы продаете футболки и толстовки и определили, что функция прибыли от продажи x футболок и y толстовок определяется как
.P(x,y) = 10000 +2100 x — 3x 2 + 3(y — 400) 2
Найдите среднюю прибыль, если вы продаете от 200 и 400 футболок и между 300 и 400 толстовки.
Раствор
Находим двойной интеграл
Далее разделить на общую площадь
А = (400–300)(400–200) = 20000
по получить
Средняя прибыль = 350000
или
3500 долларов.
Население
Предположим, что плотность популяции муравьев в точке (x,y) в метрах, где происхождение соответствует источнику воды, можно смоделировать к 30000
Р (х, у)
=
1+ х 2 + у 2
Установите интеграл, который оценивает общую популяцию муравьев в пределах 100 метров от источника воды. Затем используйте калькулятор, чтобы вычислить этот интеграл.
Раствор
Область представляет собой окружность радиусом 100
х 2 + у 2 = 10000
Находим
Калькулятор дает нам популяцию около 868 000 муравьев.
Назад на главную страницу Math 117
Назад к математике Дом Департамента
электронная почта Вопросы и предложения
Численность, математика и статистика — Набор для академических навыков
Двойные и тройные интегралы
ContentsToggle Main Menu 1 Двойные интегралы 1.