Вычисление пределов примеры: Пределы. Примеры решений — matematika

Пределы, примеры решений

Решение

Первый предел. Для нахождения данного предела достаточно подставить вместо число, к которому оно стремиться, то есть 2, получим     Второй предел. В данном случае подставлять в чистом виде 0 вместо нельзя, так как получим деление на 0. Можно рассматривать значения близкие к нулю, например, подставлять 0,01; 0,001; 0,0001; 0,00001 и т. д., при этом значение функции будет возрастать: 100; 1000; 10000; 100000 и т. д. Таким образом, можно сделать вывод о том, что при значение функции, стоящей под знаком предела, будет неограниченно возрастать, то есть стремиться к бесконечности. А значит:     Третий предел. Здесь, как и в предыдущем случае, нельзя подставить в чистом виде. Необходимо рассмотреть случай неограниченного возрастания . Подставляя 1000; 10000; 100000 и т.д., получим, что значение функции будет убывать: 0,001; 0,0001; 0,00001; и т.д., стремясь к нулю. Таким образом,

Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Предел числовой последовательности

      Определение 1. Число   a   называют пределом числовой последовательности

a₁ ,  a₂ , … a_n , …

если для любого положительного числа   ε   найдется такое натуральное число   N ,   что при всех   n > N   выполняется неравенство

| a_n – a | < ε .

      Условие того, что число   a   является пределом числовой последовательности

a₁ ,  a₂ , … a_n , … ,

записывают с помощью обозначения

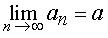
и произносят так: «Предел   a_n   при   n ,   стремящемся к бесконечности, равен   a ».

      То же самое соотношение можно записать следующим образом:

a_n → a   при .

Словами это произносится так: «a_n   стремится к   a   при   n ,   стремящемся к бесконечности».

      Замечание. Если для последовательности

a₁ ,  a₂ , … a_n , …

найдется такое число   a ,   что   a_n → a   при , то эта последовательность ограничена.

      Определение 2. Говорят, что последовательность

a₁ ,  a₂ , … a_n , …

стремится к бесконечности, если для любого положительного числа   C   найдется такое натуральное число   N ,   что при всех   n > N   выполняется неравенство

| a_n| > C .

      Условие того, что числовая последовательность

a₁ ,  a₂ , … a_n , … ,

стремится к бесконечности, записывают с помощью обозначения

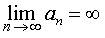
или с помощью обозначения

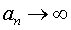 при .

      Пример 1. Для любого числа   k > 0   справедливо равенство

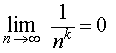
      Пример 2 . Для любого числа   k > 0   справедливо равенство

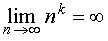
      Пример 3. Для любого числа   a   такого, что   | a | < 1,   справедливо равенство

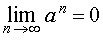
      Пример 4. Для любого числа   a   такого, что   | a | > 1,   справедливо равенство

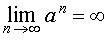
      Пример 5 . Последовательность

– 1 , 1 , – 1 , 1 , … ,

заданная с помощью формулы общего члена

a_n = (– 1)ⁿ ,

предела не имеет.

Свойства пределов числовых последовательностей

      Рассмотрим две последовательности

a₁ ,  a₂ , … a_n , … ,   и   b₁ ,  b₂ , … b_n , … .

Если при существуют такие числа   a   и   b ,  что

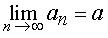  и   ,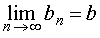

то при существуют также и пределы суммы, разности и произведения этих последовательностей, причем

      Если, кроме того, выполнено условие

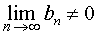
то при существует предел дроби

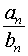
причем

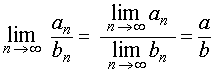      Для любой непрерывной функции   f (x)   справедливо равенство

Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии

      Рассмотрим геометрическую прогрессию

b₁ ,  b₂ , … b_n , … ,

знаменатель которой равен   q .  

      Для суммы первых   n   членов геометрической прогрессии

S_n = b₁ + b₂ + … + b_n  ,       n = 1, 2, 3, …

справедлива формула

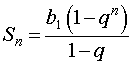
      Если для суммы всех членов бесконечно убывающей геометрической прогрессии ввести обозначение

S = b₁ + b₂ + … + b_n + … ,

то будет справедлива формула

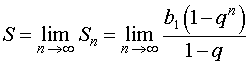
      В случае бесконечно убывающей геометрической прогрессии знаменатель   q   удовлетворяет неравенству

| q | < 1 ,

поэтому, воспользовавшись cвойствами пределов числовых последовательностей и результатом примера 3, получаем

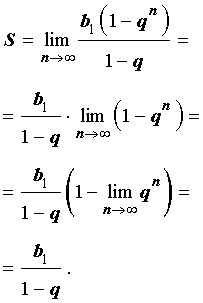
      Итак,

Примеры вычисления пределов последовательностей. Раскрытие неопределенностей

      Определение 3. Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к, то вычисление такого предела называют раскрытием неопределенности типа .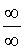

      Часто неопределенность типа 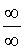удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменале дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.

      Пример 6. Найти предел последовательности

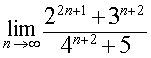
      Решение. Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней:

      Ответ.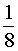

      Пример 7 . Найти предел последовательности

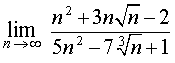
      Ответ.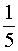

      В следующих двух примерах показано, как можно раскрыть неопределенности типа.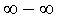

      Пример 8 . Найти предел последовательности

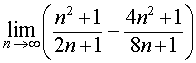
      Решение. Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю:

      Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби:

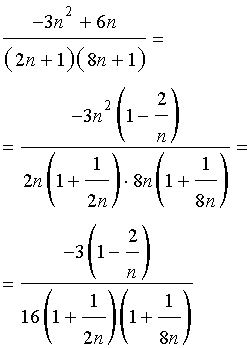
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем

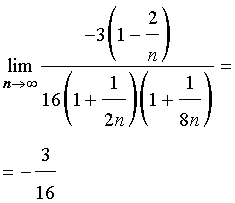
      Ответ.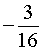

      Пример 9. Найти предел последовательности

      Решение. В рассматриваемом примере неопределенность типа 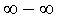возникает за счет разности двух корней, каждый из которых стремится к. Для того, чтобы раскрыть неопределенность, домножим и разделим выражение, стоящее под знаком предела, на сумму этих корней и воспользуемся формулой сокращенного умножения «разность квадратов».

      Из-за большого размера формул подробные вычисления видны только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах). На Вашем мобильном устройстве отображается только результат описанных операций.

      Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби,а затем сокращая дробь на n²:

Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем

      Ответ.

      Пример 10. Найти предел последовательности

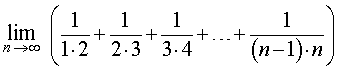
      Решение. Замечая, что для всех   k = 2, 3, 4, …   выполнено равенство

,

получаем

      Ответ.   1 .

Число e. Второй замечательный предел

      Рассмотрим последовательность

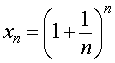(1)

      В дисциплине «Математический анализ», которую студенты естественнонаучных и технических направлений высших учебных заведений изучают на 1 курсе, доказывают, что последовательность (1) монотонно возрастает и ограничена сверху. Из теоремы Вейерштрасса о монотонных и ограниченных последовательностях, доказательство которой выходит за рамки школьного курса математики, вытекает, что последовательность (1) имеет конечный предел. Этот предел принято обозначать буквой   e.

      Таким образом, справедливо равенство

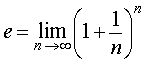(2)

причем расчеты показывают, что число

e = 2,718281828459045…

и является иррациональным и трансцендентным числом.

      Число   e   играет исключительно важную роль в естествознании и, в частности, служит основанием натуральных логарифмов и основанием показательной функции

y = e ^x,

которую называют «экспонента».

      Число   e   также является пределом последовательности

(3)

что позволяет вычислять число   e   с любой точностью. Конечно же, доказательство формулы (3) выходит за рамки школьного курса математики.

      Замечание. Предел (2), в котором для последовательностей раскрывается неопределенность типа , называют вторым замечательным пределом. В разделе нашего справочника «Пределы функций» можно ознакомиться со вторым замечательным пределом для функций.

 

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

5.07.3 Примеры на вычисление пределов функций

Вычислить указанные пределы:

1. .

2.

.

3. . Так как числитель и знаменатель обратились в нуль при , то – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет . Получаем

.

4.

.

5.

.

6. – не существует, так как .

7. . Обозначим , причем заметим, что при . Получим

.

8. . (Ответ получается непосредственно подстановкой вместо .)

9. . Здесь следует рассмотреть односторонние пределы:

; .

Следовательно, – не существует (так как у функции разные односторонние пределы).

Для самостоятельного решения.

1) ; Ответ:.

2) ; Ответ: .

3) ; Ответ: .

4) ; Ответ: .

5) . Ответ: не существует.

6) ; Ответ: .

7) ; Ответ: .

8) Найти в точке односторонние пределы функции ; Ответ: .

9) ; Ответ: .

< Предыдущая		Следующая >

Формулы вычисления пределов

Предел постоянной величины равен постоянной величине:

limxacc (c — константа)

Предел суммы равен сумме пределов:

limxafxgxlimxafxlimxagx

Предел разности равен разности пределов:

limxafxgxlimxafxlimxagx

Предел произведения равен произведению пределов:

limxafxgxlimxafxlimxagx

Предел отношения равен отношению пределов:

limxafxgxlimxafxlimxagx при условии, что limxagx0

Предел функции в степени:

limxafxmlimxafxm (m — натуральное число)

Предел функции под корнем:

limxamfxmlimxafx (m — натуральное число)

Основные пределы:

Первый замечательный предел:

limx0sinxx1 (x — угол в радианах)

Второй замечательный предел:

limx∞11xxe

Другие полезные формулы пределов:

Бесконечно малые

Эквивалентность бесконечно малых:

При x → 0 , следующие функции эквивалентны:

x ~ sin(x) ~ arcsin(x) ~ tg(x) ~ arctg(x) ~ ln(1+x)

При нахождении предела отношения двух бесконечно малых, их можно заменять на эквивалентные:

limx0ln1xxlimx0xx1

limx0sinxxlimx0xx1

limx0sinxx2x42xx3sinxx2x4~x2xx3~2xlimx0x2x12

Для вычисления пределов Вы можете воспользоваться нашим онлайн калькулятором.

Решение пределов с дробями из многочленов

Здесь мы рассмотрим примеры и методы решения пределов функций, составленных из отношений многочленов. Это дроби из многочленов и разности дробей. Обзор и обоснование методов решения пределов изложены на странице «Методы вычисления пределов функций и раскрытия неопределенностей».

Методы решения пределов дробей из многочленов

1. Рассмотрим предел функции, которая является отношением многочленов:
, где
(1)   ,
и – многочлены степеней m и n, соответственно:
;
.

1.1. Пусть есть бесконечность:
.
Тогда возникает неопределенность вида . Для ее раскрытия, нужно числитель и знаменатель дроби разделить на x^s, где s – наибольшее из чисел m и n.   Примеры ⇓

1.2. Пусть есть конечное число. Найдем значение знаменателя дроби, подставив :
.
1.2.1. Если , то неопределенности нет. Функция определена и непрерывна при . Значение предела равно значению функции в точке :
.   Пример ⇓

1.2.2. Если знаменатель равен нулю, а числитель нет: ,
то неопределенность также отсутствует. Предел равен бесконечности:
.   Пример ⇓

1.2.3. Пусть теперь и числитель, и знаменатель равны нулю:
.
В этом случае у нас возникает неопределенность вида 0/0. Для ее раскрытия, делим числитель и знаменатель на . Деление можно выполнять либо уголком, либо в уме, приравнивая коэффициенты при одинаковых степенях переменной x.   Примеры ⇓

2. Теперь рассмотрим пределы от суммы или разности отношений многочленов. В этом случае, может возникнуть неопределенность вида бесконечность плюс-минус бесконечность: . Для ее раскрытия, нужно привести дроби к общему знаменателю. В результате получим предел от функции вида (1), методы решения которого мы уже рассмотрели.   Пример ⇓

Примеры решений

Все примеры Далее мы приводим подробные решения пределов дробей из многочленов.
⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓   ⇓

Пределы при x стремящемся к бесконечности

Пример 1

Все примеры ⇑ Найти предел отношения многочленов при x стремящемся к бесконечности:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
На основании свойств степенной функции,   при  . Применяя арифметические свойства предела функции, находим:
.

Ответ

.

Пример 2

Все примеры ⇑ Найти предел функции, которая является отношением многочленов:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
Применяя арифметические свойства предела функции, находим:
.

Ответ

.

Пример 3

Все примеры ⇑ Найти предел:
.

Решение

Разделим числитель и знаменатель дроби на . При имеем:
.
Применим арифметические свойства предела функции к числителю и знаменателю:
;
.
Применим свойства бесконечно малых и бесконечно больших функций:
.

Мы получили правильную величину предела: . Но бесконечно удаленная точка может включать в себя два частных случая: и . Как , так и являются . Если и, для достаточно больших |x|, , то . Если, для достаточно больших |x|, то .

Выясним, имеет ли наш предел определенный знак? Для этого преобразуем знаменатель и переведем бесконечно большую часть в числитель:
;
.
Поскольку , то . Тогда

.

Ответ

.

Пределы в конечной точке

Пример 4. Непрерывные функции

Все примеры ⇑ Найти пределы функции

a) при ;   б) при .

Решение

а) Найдем значение знаменателя в точке :
.
Поскольку знаменатель не обращается в нуль, то функция непрерывна в точке . Поэтому предел функции равен ее значению при :
.

б) Найдем значение знаменателя в точке :
.
Здесь также знаменатель не обращается в нуль. Функция непрерывна. Ее предел при равен значению при :
.

Ответ

а) ;   б) .

Пример 5. Бесконечно большие функции

Все примеры ⇑ Задана функция в виде отношения многочленов:
.
Найти односторонние пределы:
а) ;   б) .

Решение

Найдем значение знаменателя дроби в точке :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной при . Выясним, есть ли неопределенность вида 0/0? Для этого найдем значение числителя в этой точке:
.
Числитель не равен нулю. Поэтому неопределенности вида 0/0 нет. Предел при равен бесконечности:
.

Но нам нужно найти односторонние пределы. Для этого выделим из многочлена в знаменателе множитель . То есть представим знаменатель в следующем виде:
.
Раскрываем скобки:

.
Сравнивая левую и правую части, находим:
.
Отсюда ,
;
.

Функция непрерывна в точке , поскольку знаменатель дроби не обращается в нуль. При , имеем:
.
Тогда
;
  при  .
а) Подставим :
.
б) Подставим :
.

Ответ

а) ,   б) .

Если бы знаменатель дроби не равнялся нулю при , то функция была бы непрерывной в точке . В этом случае, пределы слева и справа были бы равны:
.

Неопределенность вида 0/0

Пример 6

Все примеры ⇑ Найти предел
.

Решение

Найдем значение знаменателя дроби при :

.
Знаменатель дроби равен нулю. Поэтому функция не определена и, следовательно, не является непрерывной в точке .

Найдем значение числителя при :
.
Числитель дроби также равен нулю. Мы имеем неопределенность вида 0/0. Для ее раскрытия, выделим в многочленах множитель .

Ищем разложение знаменателя в виде:
.
Раскрываем скобки и группируем члены с одинаковыми степенями x:

.
Сравнивая левую и правую части, находим:
.
Отсюда ,
.

На практике, нет необходимости выписывать неопределенные коэффициенты разложения, а затем решать систему уравнений. Подобные вычисления легко проводить в уме. Для числителя имеем:
.

Находим предел:

.

Ответ

.

Пример 7

Все примеры ⇑ Найти предел отношения многочленов:
.

Решение

Найдем значение знаменателя при :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной в точке .

Найдем значение числителя дроби при :
.
Числитель дроби также равен нулю. У нас неопределенность вида 0/0. Для ее раскрытия, выделим в многочленах множитель .

Вычисления делаем в уме:
,
.
Делим числитель и знаменатель на . Тогда при имеем:
.

Снова находим значения числителя и знаменателя при : ;
.
Опять неопределенность 0/0. Снова выделяем множитель :
;
.

При имеем:
.
Функция непрерывна в точке , поскольку знаменатель дроби не равен нулю при . Поскольку функции и отличаются только в одной точке ( определена и непрерывна при , а не определена), то их пределы в любой точке равны (см. «Влияние значений функции в конечном числе точек на величину предела»). Находим искомый предел:
.

Ответ

.

Пример 8. Неопределенность вида ∞&pm;∞

Все примеры ⇑ Найти предел разности дробей из многочленов:
.

Решение

При имеем:
;
;
;
.
Поскольку знаменатель каждой из дробей равен нулю, а числители отличны от нуля, то при , каждая из дробей стремится к бесконечности:
  при  .
То есть мы имеем неопределенность вида «бесконечность минус бесконечность».

Для раскрытия неопределенности, приводим дроби к общему знаменателю. Чтобы упростить выкладки, предварительно выделим в знаменателях дробей множитель .
;
;


;
.

Таким образом, задача свелась к вычислению предела от дроби многочленов:
.
Применяем описанные выше методы.

Находим значения числителя и знаменателя при :
;
.
Поскольку числитель и знаменатель равны нулю, то это неопределенность вида 0/0. В знаменателе множитель уже выделен. Выделим этот множитель в числителе:
.
Находим предел:

.

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 23-01-2019

Первый замечательный предел — примеры решений

Применяемые формулы, свойства и теоремы

Здесь мы рассмотрим примеры решений задач на вычисление пределов, в которых используется первый замечательный предел и его следствия.

Ниже перечислены формулы, свойства и теоремы, которые наиболее часто применяются в подобного рода вычислениях.

Примеры решений

Все примеры Далее мы приводим подробные решения с объяснениями следующих пределов:
⇓,   ⇓,   ⇓,   ⇓,   ⇓,   ⇓.

Пример 1

Все примеры ⇑ Найти предел функции:
.

Решение с помощью первого замечательного предела

При ,   ;   . Это неопределенность вида 0/0.

Для ее раскрытия, преобразуем функцию за знаком предела и разделим числитель и знаменатель дроби на x:
.

Заметим, что функцию в числителе можно представить как сложную:
,
где . Тогда для вычисления предела , делаем замену переменной.

Для этого.
1. Вычисляем предел .
Поскольку функция непрерывна для всех x, и в том числе в точке , то
.
2. Поскольку функция не определена (и, следовательно, не является непрерывной) при , то нам нужно убедиться, что существует такая проколотая окрестность точки , на которой . В нашем случае при . Поэтому это условие выполнено.
3. Вычисляем предел . В нашем случае он равен первому замечательному пределу:
.

Таким образом,
.
Аналогичным образом, находим предел функции в знаменателе:
;
  при  ;
.

И наконец, применяем арифметические свойства предела функции:
.

Решение с помощью эквивалентных функций

Применим теорему о замене функций эквивалентными в пределе частного.
При . Из таблицы эквивалентных функций находим:
при ;   при .
Тогда .

Ответ

.

Пример 2

Все примеры ⇑ Найдите предел:
.

Решение с помощью первого замечательного предела

При ,   ,   . Это неопределенность вида 0/0.

Преобразуем функцию за знаком предела:
.

Сделаем замену переменной . Поскольку   и   при  , то
.
Аналогичным образом имеем:
.
Поскольку функция косинус непрерывна на всей числовой оси, то
.
Применяем арифметические свойства пределов:

.

Решение с помощью эквивалентных функций

Применим теорему о замене функций эквивалентными в пределе частного.
При . Из таблицы эквивалентных функций находим:
при ;   при .
Тогда .

Ответ

.

Пример 3

Все примеры ⇑ Найти предел:
.

Решение

Подставим в числитель и знаменатель дроби:
;
.
Это неопределенность вида 0/0.

Попробуем решить этот пример с помощью первого замечательного предела. Поскольку в нем значение переменной стремится к нулю, то сделаем подстановку, чтобы новая переменная стремилась не к  , а к нулю. Для этого от x перейдем к новой переменной t, сделав подстановку   ,   . Тогда при , .

Предварительно преобразуем функцию за знаком предела, умножив числитель и знаменатель дроби на :
.
Подставим и воспользуемся приведенными выше тригонометрическими формулами.
;


;

.

Функция непрерывна при . Находим ее предел:
.

Преобразуем вторую дробь и применим первый замечательный предел:
.
В числителе дроби мы сделали подстановку .

Применяем свойство предела произведения функций:

.

Ответ

.

Пример 4

Все примеры ⇑ Найти предел:
.

Решение

При ,   ,   . У нас неопределенность вида 0/0.

Преобразуем функцию под знаком предела. Применим формулу:
.
Подставим :
.
Преобразуем знаменатель:
.
Тогда
.

Поскольку     и     при  , то сделаем подстановку  , и применим теорему о пределе сложной функции и первый замечательный предел:
.

Применяем арифметические свойства предела функции:
.

Ответ

.

Пример 5

Все примеры ⇑ Найдите предел функции:
.

Решение

Нетрудно убедиться, что в этом примере мы имеем неопределенность вида 0/0. Для ее раскрытия, применим результат предыдущей задачи, согласно которому
.

Введем обозначение:
(П5.1)   .   Тогда
(П5.2)   .
Из (П5.1) имеем:
.
Подставим в исходную функцию:

,
где ,
,
;
;
;
.

Используем (П5.2) и непрерывность функции косинус. Применяем арифметические свойства предела функции.
,
здесь m – отличное от нуля число, ;
;


;
.

Ответ

.

Пример 6

Все примеры ⇑ Найти предел:
.

Решение

При , числитель и знаменатель дроби стремятся к 0. Это неопределенность вида 0/0. Для ее раскрытия, преобразуем числитель дроби:
.

Применим формулу:
.
Подставим :
;
,
где .

Применим формулу:
.
Подставим :
;
,
где .

Числитель дроби:

.
Функция за знаком предела примет вид:
.

Найдем предел последнего множителя, учитывая его непрерывность при :



.

Применим тригонометрическую формулу:
.
Подставим ,
. Тогда
.

Разделим числитель и знаменатель на , применим первый замечательный предел и одно из его следствий:

.

Окончательно имеем:
.

  Также можно было применить формулу
, подставив .

  В конце мы могли применить теорему о замене функций эквивалентными в пределе частного.
Из таблицы эквивалентных функций находим:
при ;   при .
Тогда   .

Ответ

.

Автор: Олег Одинцов.     Опубликовано: 17-02-2019   Изменено: 01-07-2019

Калькулятор лимита

с шагами — 100% бесплатно

Что такое пределы?

Исчисление — одна из важнейших областей математики. Это изучение непрерывных изменений. Раздел исчисления подчеркивает концепции пределов, функций, интегралов, бесконечных рядов и производных. Пределы — одно из основных понятий исчисления. Это помогает анализировать приближение значения функции или последовательности по мере приближения входных данных или индекса к определенной точке.Другими словами, он показывает, как любая функция действует рядом с точкой, а не в этой точке. Теория пределов закладывает основу для исчисления; он используется для определения непрерывности, интегралов и производных.

Пределы указаны для функции, любой дискретной последовательности и даже функции с действительным знаком или сложных функций. Для функции f (x) значение, которое функция принимает, когда переменная приближается к определенному числу, скажем, n, затем x → n, называется пределом. Здесь функция имеет конечный предел:

Lim x → n f (x) = L

Где L = Lim x → x0 f (x) для точки x0.Для всех ε> 0 мы можем найти δ> 0, где абсолютное значение f (x) — L меньше, чем E, когда абсолютное значение x — x0. В случае последовательности действительных чисел, таких как a1, a2, a3,…, an. Действительное число L — это предел последовательности:

Lim n → ∞ an = L

Значение функции f (x) можно найти слева или справа от точки n. Ожидаемое значение функции для точек слева от заданной точки n является левым пределом, также называемым нижним пределом, в то время как точки справа от указанной точки n известны как правый предел, даже назвал вышеуказанный предел.Предел слева определяется как limx → x- 0 f (x), а предел справа обозначается как limx → x + 0 f (x).

Важно понимать, что предел существует только тогда, когда значения, полученные для левого и правого пределов, равны. При вычислении предела для функций со сложной структурой существует неограниченное количество режимов приближения к пределу для точки. В таких ситуациях, чтобы найти четкое значение предела, необходимы более строгие стандарты. Для предела рациональной функции типа p (x) / q (x) важным шагом является упрощение рациональной функции до вида 0/0 для данной точки.

Существуют различные способы вычисления пределов в зависимости от разной природы и типов функций. Существует прекрасное применение правила L-Hospital, которое включает различение числителя и знаменателя рациональных функций или неопределенных пределов, пока предел не примет форму 0/0 или ∞ / ∞.

.Пределы

— оценка

Вы должны сначала прочитать Limits (An Introduction)

Краткое описание ограничений

Иногда мы не можем что-то придумать напрямую … но мы можем видеть, что должно быть, когда мы все ближе и ближе!

Пример:

(х ² — 1) (х — 1)

Давайте разберемся с x = 1:

(1 ² — 1) (1–1) знак равно (1–1) (1–1) знак равно 0 0

Теперь 0/0 — сложность! На самом деле мы не знаем значение 0/0 (оно «неопределенное»), поэтому нам нужен другой способ ответить на этот вопрос.

Итак, вместо того, чтобы пытаться вычислить это для x = 1, давайте попробуем , приближаясь к , это все ближе и ближе:

Продолжение примера:

х		(х 2 — 1) (х — 1)
0,5		1.50000
0.9		1,
0,99		1.99000
0,999		1.99900
0,9999		1.99990
0,99999		1.99999
…		…

Теперь мы видим, что когда x приближается к 1, то (х ² -1) (х − 1) получает близко к 2

Мы столкнулись с интересной ситуацией:

• Когда x = 1, мы не знаем ответа (это неопределенно )
• Но мы видим, что будет 2

Мы хотим дать ответ «2», но не можем, поэтому вместо этого математики точно говорят, что происходит, используя специальное слово «предел»

Предел из (х ² -1) (х − 1) когда x приближается к 1, будет 2

И записывается символами как:

lim x → 1 x ² −1 x − 1 = 2

Так что это особый способ сказать «», игнорируя то, что происходит, когда мы приближаемся, но по мере того, как мы приближаемся, ответ становится все ближе и ближе к 2 »

В виде графика это выглядит так: Итак, по правде говоря, мы не можем сказать, каково значение при x = 1. Но мы можем сказать, что по мере приближения к 1, предел равен 2.

Оценка пределов

«Оценка» означает нахождение значения ( думаю, е- « значение» -значение )

В приведенном выше примере мы сказали, что предел равен 2, потому что выглядело так, как будто это будет . Но этого недостаточно!

На самом деле существует способов получить точный ответ.Посмотрим на некоторые:

1. Просто введите значение

Первое, что нужно попробовать, это просто ввести значение лимита и посмотреть, работает ли оно (другими словами, подстановка).

Пример:

lim x → 10 x 2

10 2 = 5

Легко!

Пример:

предм x → 1 x 2 −1 x − 1

(1−1) (1−1) = 0 0

Не повезло.Нужно попробовать что-нибудь еще.

2. Факторы

Можем попробовать факторинг.

Пример:
Разлагая (x 2 −1) на (x − 1) (x + 1), получаем:
Теперь мы можем просто подставить x = 1, чтобы получить предел:

3.Конъюгат

Для некоторых дробей может помочь умножение верха и низа на конъюгат.

Сопряжение — это то место, где мы меняем знак в середине двух терминов вроде этого:

Вот пример, где он поможет нам найти предел:

Оценка этого при x = 4 дает 0/0, что не является хорошим ответом!

Итак, попробуем переставить:

Итак, теперь у нас:

Готово!

4.Бесконечные пределы и рациональные функции

Рациональная функция — это функция, которая представляет собой отношение двух многочленов:
Например, здесь P (x) = x 3 + 2x — 1 и Q (x) = 6x 2 :

Найдя общую Степень функции, мы можем узнать, является ли предел функции 0, Бесконечность, -Бесконечность или легко вычисляется из коэффициентов.

Подробнее читайте в разделе «Пределы бесконечности».

5. Правило L’Hôpital

Правило L’Hôpital может помочь нам оценить пределы, которые кажутся «неопределенными», например 0 0 и ∞ ∞ .

Подробнее читайте на сайте L’Hôpital’s Rule.

6. Формальный метод

Формальный метод приступает к доказательству того, что мы можем получить настолько близко, насколько мы хотим, к ответу, сделав «x» близким к «a».

Подробнее на Limits (формальное определение)

.

Пределы калькулятора функций

$$ + \ infty + \ infty = + \ infty $$	$$ — \ infty — \ infty = — \ infty $$
$$ + \ infty — \ infty =? $$	$$ — \ infty + \ infty =? $$
$$ 0 + \ infty = + \ infty $$	$$ 0 — \ infty = — \ infty $$
$$ + \ infty + 0 = + \ infty $$	$$ — \ infty + 0 = — \ infty $$
$$ \ pm k + \ infty = + \ infty $$	$$ \ pm k — \ infty = — \ infty $$
$$ + \ infty \ pm k = + \ infty $$	$$ — \ infty \ pm k = — \ infty $$
$$ + \ infty \ times + \ infty = + \ infty $$	$$ + \ infty \ times — \ infty = — \ infty $$
$$ — \ infty \ times + \ infty = — \ infty $$	$$ — \ infty \ times — \ infty = + \ infty $$
$$ 0 \ times + \ infty =? $$	$$ 0 \ times — \ infty =? $$
$$ + \ infty \ times 0 =? $$	$$ — \ infty \ times 0 =? $$
$$ k \ times + \ infty = + \ infty $$	$$ k \ times — \ infty = — \ infty $$
$$ -k \ times + \ infty = — \ infty $$	$$ -k \ times — \ infty = + \ infty $$
$$ \ frac {+ \ infty} {+ \ infty} =? $$	$$ \ frac {+ \ infty} {- \ infty} =? $$
$$ \ frac {- \ infty} {+ \ infty} =? $$	$$ \ frac {- \ infty} {- \ infty} =? $$
$$ \ frac {0} {+ \ infty} = 0 $$	$$ \ frac {0} {- \ infty} = 0 $$
$$ \ frac {+ \ infty} {0} = + \ infty $$	$$ \ frac {- \ infty} {0} = — \ infty $$
$$ \ frac {+ \ infty} {k} = + \ infty $$	$$ \ frac {- \ infty} {k} = — \ infty $$
$$ \ frac {+ \ infty} {- k} = — \ infty $$	$ $ \ frac {- \ infty} {- k} = + \ infty $$
$$ \ frac {k} {+ \ infty} = 0 ^ + $$	$$ \ frac {k} { — \ infty} = 0 ^ — $$
$$ \ frac {-k} {+ \ infty} = 0 ^ — $$	$$ \ frac {-k} {- \ infty} = 0 ^ + $$
$$ \ frac {0} {0} =? $$	$$ \ frac {k} {k} = 1 $$
$$ \ frac {k} {0} = + \ infty $$	$$ \ frac {-k} {0 } = — \ infty $$
$$ \ frac {0} {k} = 0 $$	$$ \ frac {0} {-k} = 0 $$
$$ (\ pm k) ^ 0 = 1 $$	$$ 0 ^ {\ pm k} = 0 $$
$$ 1 ^ {\ pm k} = 1 $$	$$ (\ pm k) ^ 1 = (\ pm k) $$
$$ + \ infty ^ 0 =? $$	$$ — \ infty ^ 0 =? $$
$$ 0 ^ {+ \ infty} = 0 $$	$$ 0 ^ {- \ infty} = 0 $$

.Предварительное вычисление

: как рассчитать пределы для различных функций

Аналогично, если x приближается к -∞, функция f в этом случае также становится произвольно близкой к нулю.

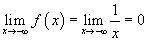
Но нам не нужно ограничивать пределы крайними значениями независимой переменной.А как насчет других интересных особенностей этой функции? Давайте рассмотрим, как работать с ограничениями, когда мы приближаемся к x = 0. Во-первых, обратите внимание, что предел зависит от направления, с которого приближается значение x .

В этом случае, если мы начнем с левой стороны и приблизимся к x = 0, функция f станет все меньше и меньше (в смысле большей величины, но с отрицательным знаком) без ограничений.Чтобы представить эту ситуацию символически, мы называем предел -∞, но это просто означает, что функция не имеет минимального реального значения. Мы используем небольшой надстрочный индекс «-» для обозначения подхода слева:

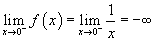
Когда мы приближаемся к x = 0 справа (обозначено верхним индексом «+»), f становится произвольно большим, поэтому мы говорим, что предел равен ∞.

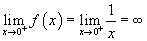
Мы также можем посмотреть предел любой произвольной точки, а не только «особых» точек. Рассмотрим x = 1.

Итак, давайте еще раз посмотрим на общее выражение для предела данной функции f ( x ), поскольку x приближается к некоторой константе c.

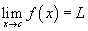
Рассматривая все приведенные выше примеры, мы можем теперь сказать, что если функция f становится произвольно близкой (но не обязательно достигает) некоторого значения L , поскольку x приближается к c с любой стороны, тогда L будет предел этой функции для x приближается к c. В этом случае мы говорим, что предел существует. Односторонние ограничения — это когда функция приближается к определенному значению только с одной стороны (как в функции ниже). В этом случае предел 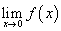не существует; однако мы можем найти односторонние ограничения, как мы это делали выше.

Часто мы можем определить предел, просто вычислив f ( c ), но очевидно, что это не всегда работает (особенно если c не находится в области f ).Кроме того, нам может потребоваться рассмотреть направление, с которого мы приближаемся к c (для односторонних ограничений). Однако обычно вы можете легко вычислить предел, если вы также посмотрите на график или таблицу значений около x = c.

Практическая задача: Рассчитайте следующие пределы.

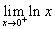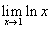а. б. г. г.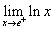

Решение: Это помогает сначала построить график функции, чтобы увидеть эти пределы.

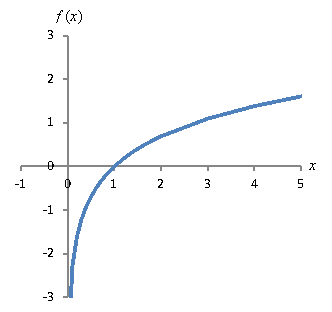
а. Для этого предела рассмотрим значение ln x , поскольку x становится все ближе и ближе к 0. Функция приближается к -∞, поэтому предел равен

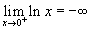
г.В этом случае мы можем просто подключить c к функции. Обратите внимание, что предел равен 0 независимо от направления подхода.

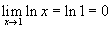
г. Здесь, поскольку x становится произвольно большим, также становится ln x (т.е. функция не имеет реального максимального значения). Таким образом,

_{z9326051.gif» />}

г.Опять же, в этом случае направление подхода не имеет значения. Мы можем просто подключить и к функции.

Правила лимитов

Некоторые ограничения могут включать сложные выражения.В этих и других случаях часто бывает полезно использовать правила, упрощающие вычисления. Ниже приведены основные свойства пределов для произвольных функций f ( x ) и g ( x ) и произвольной постоянной k.

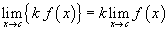
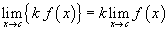
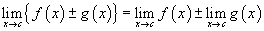
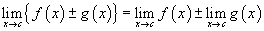
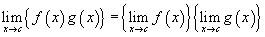
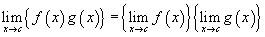
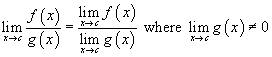
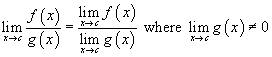
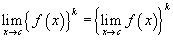
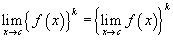
Эти правила для пределов позволяют нам разбивать сложные выражения на более простые для поиска предела.

Практическая задача: Опишите словами, почему для полинома p ( x ) всегда верно следующее.

Решение: Напомним, что многочлен p ( x ) имеет следующий вид, где значения c _i (где i = 0, 1, 2, 3 ,., n ) — константы:

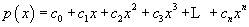
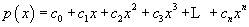
Поскольку x приближается к k, полином (независимо от его формы) приближается к p ( k ), потому что область полинома — это все действительные числа. Таким образом, когда мы имеем дело с пределами для многочленов, мы можем просто подставить предельное значение для x непосредственно в функцию.Математическое доказательство этого факта не слишком сложно, но результат довольно интуитивно понятен.

Практическая задача: Рассчитайте следующие пределы.

а. б. г.

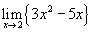
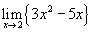
Решение: В каждом случае можно использовать несколько подходов.Один из них — построить график функции и посмотреть на поведение функции вблизи предельного значения x (это часто полезно независимо от того, какой подход вы используете). В качестве альтернативы вы можете использовать правила ограничений и, при необходимости, просто заменить их.

а. Здесь замена возможна без проблем. Вы также можете использовать правила лимитов.

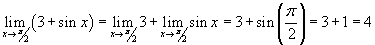
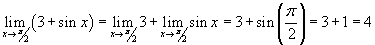
г. В этом случае функция является многочленом степени 2.Мы можем просто заменить.

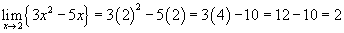
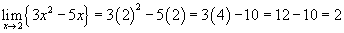
г. Для этой функции вы не можете напрямую применять правила ограничений и подстановки. Обратите особое внимание на примечание к графику, показывающее, что значение x приближается справа.

Применение ограничений: непрерывность

Давайте рассмотрим более простое применение ограничений: непрерывность функции.Посмотрите еще раз на функцию .

Интуитивно мы можем сказать, что функция непрерывна (т. Е. В ней нет «разрывов») слева от x = 0 и справа от x = 0, но не на x = 0. А как насчет более математического определения? Мы можем использовать ограничения. Функция непрерывна в определенной точке x = c , если выполняются все следующие условия:

c находится в домене f

существует

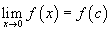
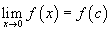
Обратите внимание, что функция является непрерывной на открытом интервале ( a, b ), если она непрерывна во всех точках этого интервала.

Практическая задача: Определите, является ли функция непрерывной в данной точке.

а. при x = 1 б. при x = 0 c. ln x при x = e

Решение: Для проблемы a обратите внимание, что функция равна строке x + 2, за исключением того, что в ней отсутствует точка (1, 3).Интересно, что лимит здесь есть:

Однако функция не определена при x = 1. Следовательно, мы не можем использовать подстановку, чтобы найти предел. Поскольку функция нарушает одно (фактически нарушает два) из условий непрерывности, она не является непрерывной при x = 1.

Для части b обратите внимание, что ни одно из условий непрерывности не выполняется.Предел не существует (это ∞), и функция не определена при x = 0. Следовательно, функция не является непрерывной при x = 0.

Для части c обратите внимание, что функция определена как x = e:

ln e = 1

Кроме того, предел определен и может быть рассчитан путем замены:

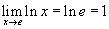
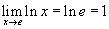
Таким образом, ln x является непрерывным при x = e.

.