Параллелограмм фото – . .

Параллелограмм. Свойства, площадь и признаки

Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон.
Свойства параллелограмма:

1. Противоположные стороны параллелограмма равны.
2. Противоположные углы параллелограмма равны.
3. Диагонали параллелограмма в точке пересечения делятся пополам.

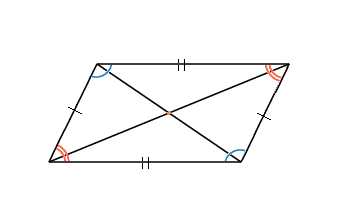
Давайте посмотрим, как свойства параллелограмма применяются в решении задач ЕГЭ.

1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.

Пусть  и  — биссектрисы углов параллелограмма, прилежащих к стороне . Сумма углов и  равна . Углы и  — половинки углов и . Значит, сумма углов и  равна  градусов. Из треугольника находим, что угол  — прямой.

Ответ: .

Биссектрисы углов параллелограмма, прилежащих к одной стороне, — перпендикулярны.

Легко доказывается и другое свойство биссектрис параллелограмма:

Биссектрисы противоположных углов параллелограмма — параллельны.

Ты нашел то, что искал? Поделись с друзьями!

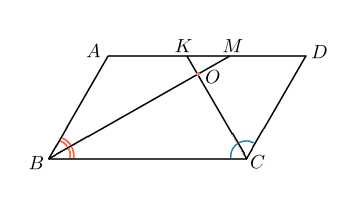
2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна . Найдите его большую сторону.

Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.

Углы и , а также и  — накрест лежащие. Накрест лежащие углы равны. Значит, угол равен углу , а угол  — углу .
Получаем, что треугольники и  — равнобедренные, то есть , а . Тогда .

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Запишем формулы площади параллелограмма:

, где  — основание параллелограмма,  — его высота.

, где  и  — стороны параллелограмма,  — угол между ними.

И еще одна формула.

, где  и  — диагонали параллелограмма,  — угол между ними.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

«Параллелограмм и его свойства»

Конспект урока.

Алгебра 8 класс

Учитель Сысой А.К.

Школа 1828

Тема урока: «Параллелограмм и его свойства»

Тип урока: комбинированный

Цели урока:

1) Обеспечить усвоение нового понятия – параллелограмм и его свойств

2) Продолжить развитие навыков и умений решения геометрических задач;

3) Развитие культуры математической речи

План урока:

1. Организационный момент

(Слайд 1)

На слайде демонстрируется высказывание Льюиса Кэрролла. Ученикам сообщается о цели урока. Проверяется готовность учеников к уроку.

2. Актуализация знаний

(Слайд 2)

На доске задачи для устной работы. Учитель предлагает ученикам подумать над этими задачами и поднять руку тем, кто понял, как задачу решать. После решения двух задач, на доказательство теоремы о сумме углов вызывается к доске ученик, который самостоятельно делает дополнительные построения на чертеже и доказывает устно теорему.

Учениками используется формула суммы углов многоугольника:

3. Основная часть

(Слайд 3)

На доске определение параллелограмма. Учитель говорит о новой фигуре и формулирует определение, делая с помощью чертежа необходимые пояснения. Затем на клетчатой части презентации, с помощью маркера и линейки, показывает, как можно рисовать параллелограмм (возможно несколько случаев)

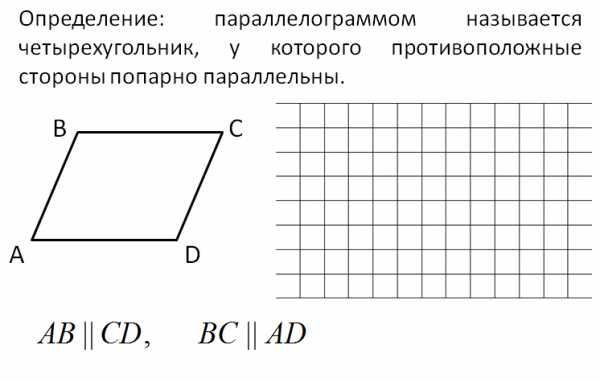
(Слайд 4)

Учитель формулирует первое свойство параллелограмма. Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.

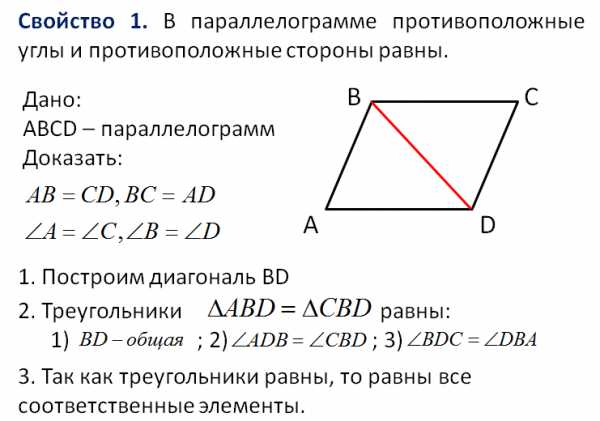
(Слайд 5)

Учитель формулирует второе свойство параллелограмма. На доске появляется рисунок параллелограмма. Учитель предлагает по рисунку сказать что дано, что необходимо доказать. После того как ученики правильно сообщают о том, что дано и что необходимо доказать, появляется условие теоремы. Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников AOB и COD. С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон AB и CD. Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.

(Слайд 6)

Учитель формулирует третье свойство параллелограмма. В зависимости от времени, которое остаётся до конца урока, учитель может дать возможность ученикам самостоятельно доказать это свойство, или ограничится его формулировкой, а само доказательство оставить ученикам в качестве домашней работы. Доказательство может опираться на сумму углов вписанного многоугольника, которая повторялась в начале урока, или на сумму внутренних односторонних углов при двух параллельных прямых AD и BC, и секущей, например AB.

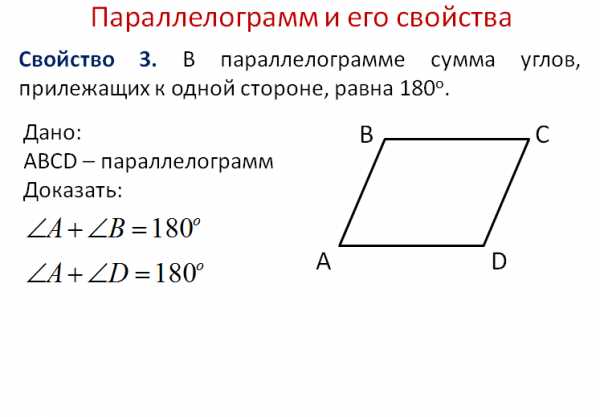
4. Закрепление материала

На этом этапе учащиеся, используя ранее изученные теоремы, решают задачи. Идеи к решению задачи подбирают ученики самостоятельно. Так как возможных вариантов оформления немало и все они зависят от того каким образом ученики будут искать решение задачи, визуализации решения задач нет, а ученики самостоятельно оформляют каждый этап решения на отдельной доске с записью решения в тетрадь.

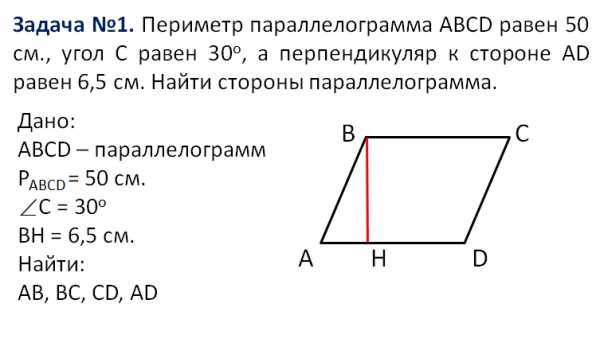
(Слайд 7)

Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После того, как ученики, верно составят краткую запись условия на доске появляется «Дано». Ход решения задачи может выглядеть следующим образом:

1. Проведём высоту BH (визуализировано)

2. Треугольник AHB – прямоугольный. Угол A равен углу C и равен 30⁰(по свойству о противоположных углах в параллелограмме). 2BH=AB (по свойству катета, лежащего напротив угла в 30⁰ в прямоугольном треугольнике). Значит AB = 13 см.

3. AB = CD, BC = AD (по свойству противоположных сторон в параллелограмме) Значит AB=CD=13см. Так как периметр параллелограмма равен 50 см, то BC=AD=(50 – 26):2=12см.

Ответ: AB = CD = 13 см, BC = AD = 12 см.

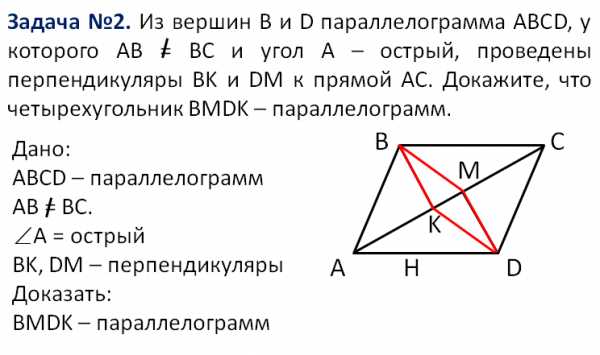
(Слайд 8)

Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После появляется «Дано» на экране. С помощью красных линий выделяется четырёхугольник, про который нужно доказать, что он параллелограмм. Ход решения задачи может выглядеть следующим образом:

1. Т.к. BK и MD перпендикуляры к одной прямой, то прямы BK и MD параллельны.

2. Через смежные углы можно показать, что сумма внутренних односторонних углов при прямых BM и KD и секущей MD равна 180⁰. Поэтому данные прямые параллельны.

3. Так как у четырехугольника BMDK противоположные стороны попарно параллельны, то данный четырехугольник параллелограмм.

5. Окончание урока. Поведение итогов.

(Слайд 8)

На слайде появляются вопросы по новой теме, на которые ученики отвечают.

infourok.ru

Задания В5. Параллелограмм | Подготовка к ЕГЭ по математике

В этой статье работаем с Задачами №3 ЕГЭ по математике, которые связаны с параллелограммом.

Смотрите в других статьях разбор Задачи №3, в которых фигурирует:
– треугольник;
– прямоугольник;
– ромб;
– произвольный четырехугольник;
– трапеция;
– многоугольник;
– круг;
– векторы;
– координатная плоскость;

Вы можете пройти автотренинг «Планиметрия»

Задача 1.  Найдите площадь параллелограмма, изображенного на рисунке.

Решение: + показать

Задача 2. Найдите площадь параллелограмма, если две его стороны равны 25 и 20, а угол между ними равен 30˚.

Решение: + показать

Задача 3. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Решение: + показать

Задача 4. Стороны параллелограмма равны 8 и 16. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение: + показать

Так как согласно формуле площади параллелограмма , то

Откуда

Ответ: 6. 

Задача 5. Периметр параллелограмма равен 38. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.

Решение: + показать

Пусть меньшая сторона параллелограмма равна , тогда большая сторона равна согласно условию.

Периметр параллелограмма – сумма длин всех сторон, при этом противоположные стороны параллелограмма равны.

Поэтому

Ответ: 8. 

Задача 6. Боковая сторона равнобедренного треугольника равна 26. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

Решение: + показать

Задача 7. Площадь параллелограмма   равна 116. Найдите площадь параллелограмма , вершинами которого являются середины сторон данного параллелограмма.

Решение: + показать

Задача 8. Площадь параллелограмма  равна 180. Точка   — середина стороны . Найдите площадь треугольника .

Решение: + показать

Вы можете пройти тест «Задачи №3. Параллелограмм»

egemaximum.ru

Параллелограмм Википедия

Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства[ | ]

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам. Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
• Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

  |AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.

• Точка пересечения диагоналей является центром симметрии параллелограмма.
• Параллелограмм диагональю делится на два равных треугольника.
• Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
• Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и

ru-wiki.ru

Формулы параллелограмма чертеж и свойства

Формулы параллелограмма чертеж и свойства, принятые связи и их взаимодействие между собой.

На 1-ом рисунке изображен параллелограмм, основные свойства которого:

• стороны напротив друг друга равны
• стороны напротив друг друга параллельны
• в точке пересечения диагоналей, они делятся пополам
• углы напротив друг друга равны
Наличие у четырехугольника одного из перечисленных свойств, как следствие является и наличием остальных свойств.
Опишем связь между сторонами и диагоналями: d1² + d2² = 2(a² + b²)
S =ah

На 2-ом рисунке изображен, в виде прямоугольника, основные свойства которого:

• все углы девяносто градусов (прямые)
• все диагонали равны
S = ab

На 3-ем рисунке изображен, в виде квадрата, основные свойства которого:

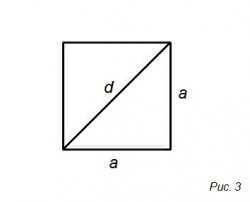
• все углы девяносто градусов (прямые)
• все стороны равны: a = b
S = a² = ½ d²
d = a√2 ≈ 1,41a
a = ½d√2 ≈ 0,707d

На 4-ом рисунке изображен, в виде квадрата, основные свойства которого:

• все стороны равны

• диагонали расположены под углом девяносто градусов друг к другу
• углы делятся диагоналями пополам
d1 = 2a sin (α/2)
d2 = 2a cos (α/2)
d1² + d2² = 4a²
S = ah = a² sin α = ½ d1d2

На 5-ом рисунке изображен, в виде трапеции, основные свойства которой:

• две стороны параллельны между собой
• a, b – основания
• h – высота
• m – средняя линия, которая соединяет средины непараллельных сторон, она параллельна основаниям
m = ½ (a + b)
S = ½ (a + b)h = mh
Если d = c, трапеция равнобочная, тогда S = (a – c cos γ) c sin γ = (b + c cos γ) c sin γ

На 6-ом рисунке изображен, в виде четырехугольника, основные свойства которой:

• сумма углов четырехугольника равна триста шестьдесят градусов
• m – отрезок соединяющий центры диагоналей
a² + b² + c² + d² = d1² + d2² +4m²
S = ½ d1d2 sin α

В четырехугольник можно вписать окружность, если a + c = b + d
Четырехугольник можно описать окружностью, если α + γ = β + δ = 180˚
ac +bd = d1d2
S = √((p – a)(p – b)(p – c)(p – d))
p = ½ (a + b + c + d)

Вот и все формулы параллелограмма, надеемся что они вам пригодятся, другие разделы геометрии смотрим на страницах сайта!!!

Заказать чертеж

Поделитесь с друзьями!

chertegnik.ru

Свойства параллелограмма

Параллелограммом называется четырехугольник, противоположные стороны которого попарно параллельны.

Докажем, что

• параллелограмм — выпуклый четырехугольник.

Рассмотрим параллелограмм ABCD (рис. 54) и докажем, например, что он лежит по одну сторону от прямой AB.

Так как AB || CD, то отрезок CD не имеет общих точек с прямой AB. Иными словами, отрезок CD лежит по одну сторону от прямой AB. Следовательно, отрезки BC и AD лежат по ту же сторону от прямой AB. Таким образом, параллелограмм ABCD лежит по одну сторону от прямой AB. Аналогично доказывается, что он лежит по одну сторону от каждой из прямых BC, CD и DA. Это и означает, что параллелограмм — выпуклый четырехугольник.

Рассмотрим свойства параллелограмма.

Теорема. В параллелограмме противоположные стороны равны и противоположные углы равны.

Доказательство. Рассмотрим параллелограмм ABCD (рис. 55). Поскольку параллелограмм ABCD — выпуклый четырехугольник, то диагональ AC разделяет его на два треугольника: ABC и CDA. Эти треугольники равны по второму признаку равенства треугольников (AC — общая сторона, накрест лежащие углы 1 и 2, а также 3 и 4 равны).

Следовательно, AB = CD, AD = BC, ∠B = ∠D и ∠A = ∠1 + ∠3 = ∠2 + ∠4 = ∠C. Теорема доказана.
Теорема. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Доказательство. Поскольку параллелограмм — выпуклый четырехугольник, то его диагонали пересекаются. Пусть O — точка пересечения диагоналей AC и BD параллелограмма ABCD (рис. 56). Докажем, что AO = OC и BO = OD.

Треугольники AOB и COD равны по второму признаку равенства треугольников: AB = CD (противоположные стороны параллелограмма равны), ∠1 = ∠2 и ∠3 = ∠4 (накрест лежащие углы, образованные при пересечении параллельных прямых AB и CD секущими AC и BD, равны). Следовательно, AO = OC и BO = OD. Теорема доказана.

Рисунок 57 иллюстрирует рассмотренные свойства параллелограмма.

mthm.ru

Что такое параллелограмм, Свойства, Признаки, Площадь параллелограмма

Параллелограмм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются квадрат и ромб. Свойства Противоположные стороны параллелограмма равны | AB | = | CD | , | AD | = | BC |. Противоположные углы параллелограмма равны Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам | AO | = | OC | , | BO | = | OD |. Сумма углов, прилежащих к одной стороне, равна 180. Любая диагональ делит параллелограмм на 2 равных треугольника. Биссектриса отсекает от параллелограмма равнобедренный треугольник. Сумма всех углов равна 360° Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1 и d2 — длины диагоналей; тогда Признаки параллелограмма Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий: Противоположные стороны попарно равны: AB = CD, AD = BC. Противоположные углы попарно равны: ∠A = ∠C, ∠B = ∠D. Диагонали делятся в точке их пересечения пополам: AO = OC, BO = OD. Сумма соседних углов равна 180 градусов: ∠A + ∠B = 180, ∠B + ∠C = 180, ∠C + ∠D = 180, ∠D + ∠A = 180. Противоположные стороны попарно равны и параллельны: AB = CD, AB || CD. Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру. Площадь параллелограмма , где a — сторона, h — высота проведенная к этой стороне. , где a и b — стороны, а α — угол между сторонами a и b

www.terminologija.ru

No related posts.