через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.

Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу.
 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R. - Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.

- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
 Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка.
 Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.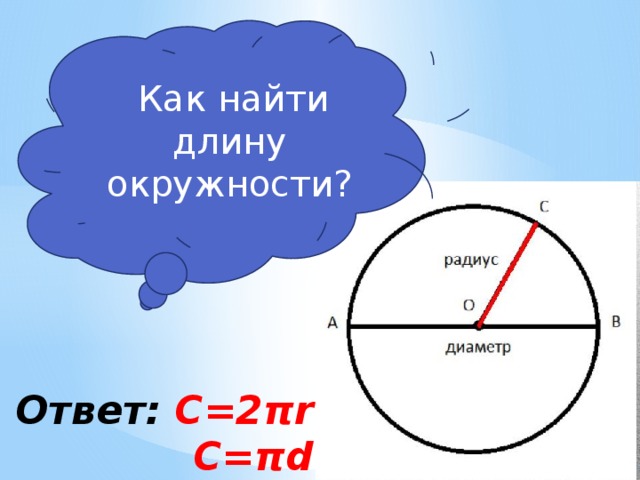
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга.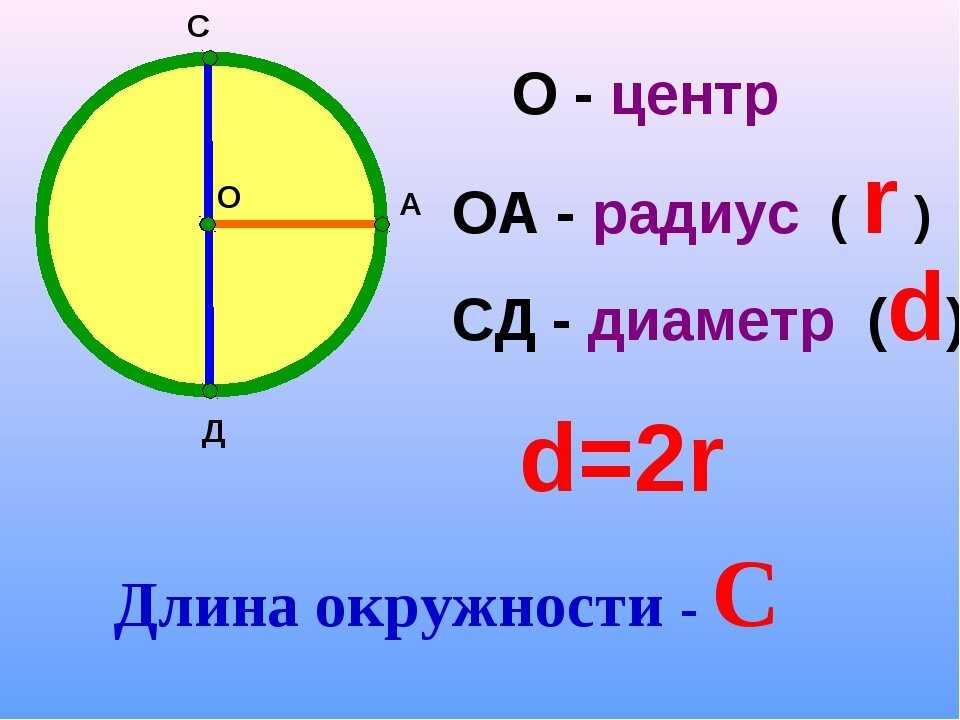
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.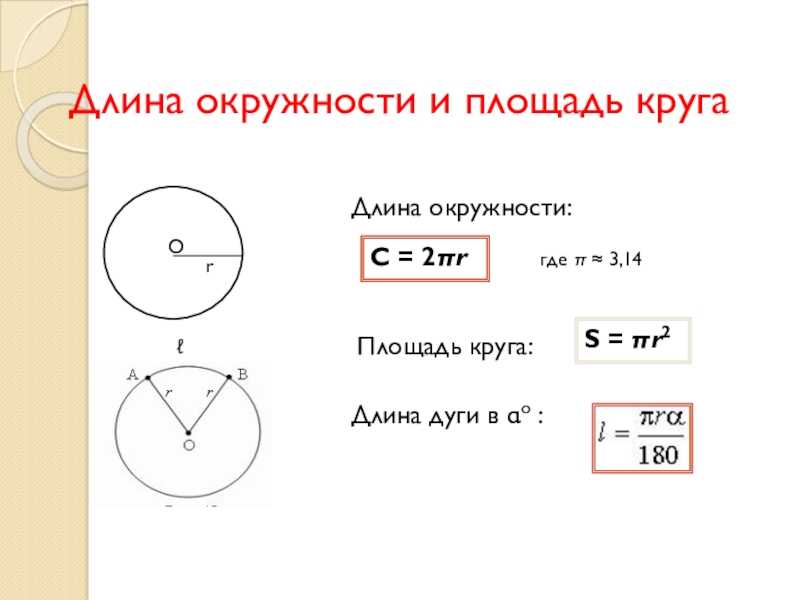
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Чему равна длина окружности и по какой формуле ее найти через диаметр
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Оглавление
- Определение окружности
- Формулы
- Число пи
- Полезное видео: длина окружности
- Практическое применение
- Полезное видео: круг — радиус, диаметр, длина окружности
- Итог
Определение окружности
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка.
 Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Чтобы посчитать периметр круга, необходимо знать его диаметр (D) или радиус (R), который равняется D, деленному на 2.
Как вычислить длину окружности через радиус? Это делается по простой формуле:
L = 2πR,
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
L = πD.
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана площадь круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Формулы
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Это интересно! Урок геометрии: как найти по формуле периметр треугольника
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Как высчитать периметр круга зная радиус. Как найти и чему будет равна длина окружности. Онлайн калькулятор длины окружности
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится.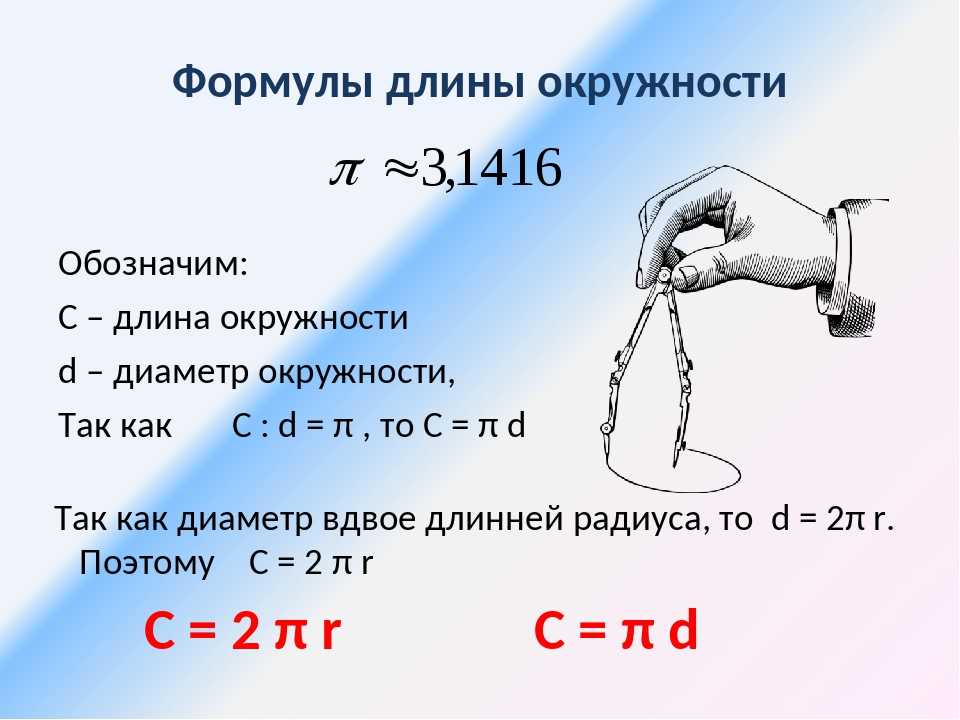 И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.

- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится.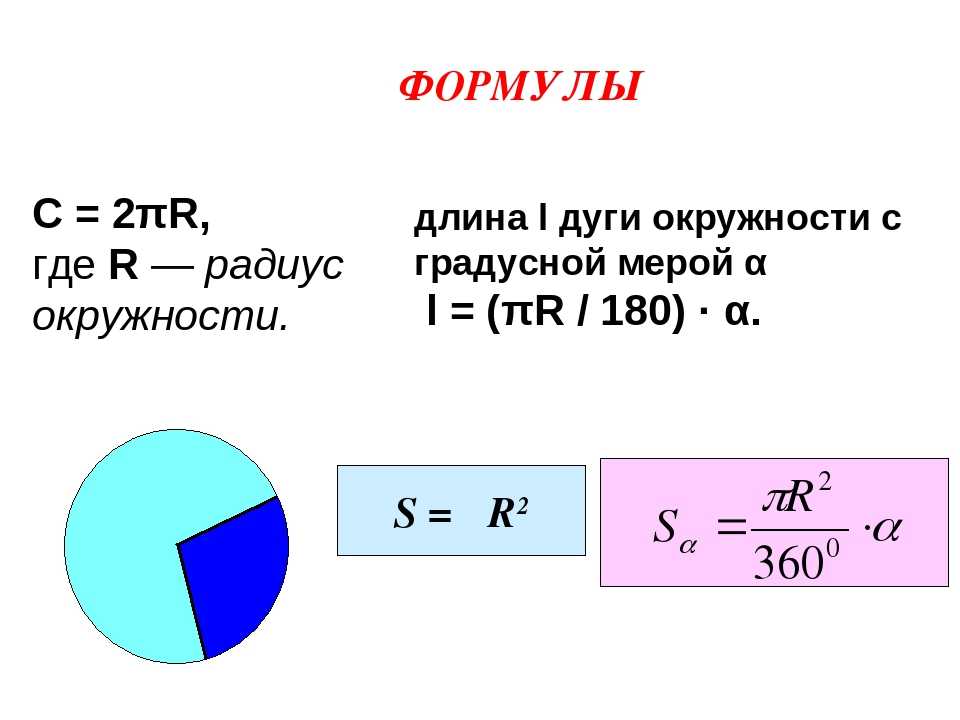 Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски.
Очевидно, что границей любого круга является окружность. Поэтому понятие периметра круга совпадает с таким понятием, как длина окружности . Поэтому вначале вспомним, что является окружностью, и какие понятия с ней связаны.
Поэтому понятие периметра круга совпадает с таким понятием, как длина окружности . Поэтому вначале вспомним, что является окружностью, и какие понятия с ней связаны.
Понятие окружности
Определение 1
Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.
Определение 2
Центром окружности будем называть точку, которая задается в рамках определения 1.
Определение 3
Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки (Рис. 1).
В декартовой системе координат $xOy$ мы также можем ввести уравнение любой окружности. Обозначим центр окружности точкой $X$, которая будет иметь координаты $(x_0,y_0)$. Пусть радиус этой окружности равняется $τ$. Возьмем произвольную точку $Y$, координаты которой обозначим через $(x,y)$ (рис. 2).
По формуле расстояния между двумя точками в заданной нами системе координат, получим:
$|XY|=\sqrt{(x-x_0)^2+(y-y_0)^2}$
С другой стороны, $|XY|$ — это расстояние от любой точки окружности до выбранного нами центра. 0}{n}}=\frac{2τ}{2τ»}$
0}{n}}=\frac{2τ}{2τ»}$
Получаем, что отношение $\frac{ρ}{ρ»}=\frac{2τ}{2τ»}$ будет верным независимо от значения числа сторон вписанных правильных многоугольников . То есть
$\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»}$
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть $n→∞$), будем получать равенство:
$lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»}$
Из последних двух равенств получим, что
$\frac{C}{C»}=\frac{2τ}{2τ»}$
$\frac{C}{2τ}=\frac{C»}{2τ»}$
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
$\frac{C}{2τ}=const$
Эту постоянную принять называть числом «пи» и обозначать $π$. Приближенно, это число будет равняться $3,14$ (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
$\frac{C}{2τ}=π$
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
Пример задач
Пример 1
Найти периметр круга, который вписан в квадрат со стороной, равной $α$. 2}$.
2}$.
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра.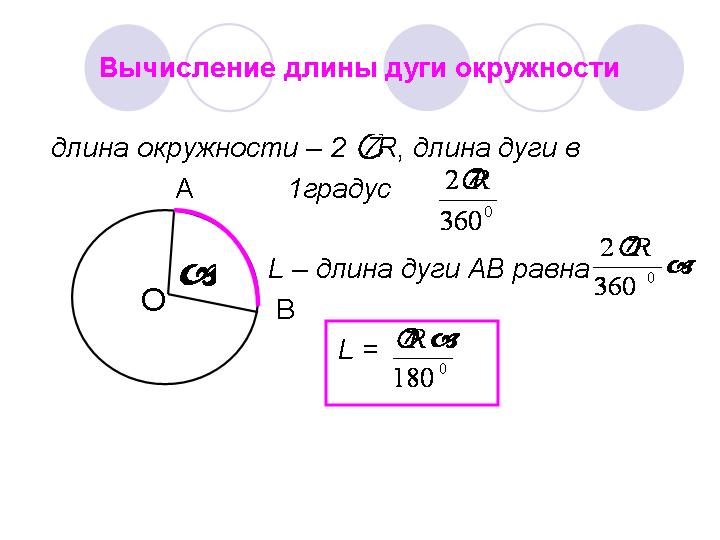 Вот и вторая формула, которую нужно запомнить:
Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Расчет соотношения диаметра и длины окружности
Все математические ресурсы GMAT
22 диагностических теста 693 практических теста Вопрос дня Карточки Learn by Concept
Помощь по математике GMAT » Проблемные вопросы » Геометрия » Круги » Диаметр » Вычисление отношения диаметра к длине окружности
Чему равно отношение длины окружности к диаметру любого круга?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы вычислить отношение длины окружности к диаметру, нам нужно уравнение, включающее обе переменные. Формула длины окружности выглядит следующим образом:
Формула длины окружности выглядит следующим образом:
Нам нужно выразить радиус через диаметр. Радиус круга равен половине его диаметра, поэтому мы можем переписать формулу как:
Если мы разделим обе стороны на диаметр, в левой части мы получим , то есть отношение длины окружности к диаметру:
Итак, для любого круга отношение его длины окружности к его диаметру равно , что на самом деле является определением этой очень важной математической константы.
Сообщить об ошибке
Каково отношение диаметра любой окружности к длине окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти соотношение между диаметром и длиной окружности, нам нужно использовать формулу длины окружности:
Мы видим, что эта формула выражена в терминах радиуса, поэтому нам нужно выразить ее так, чтобы длина окружности выражалась в диаметре.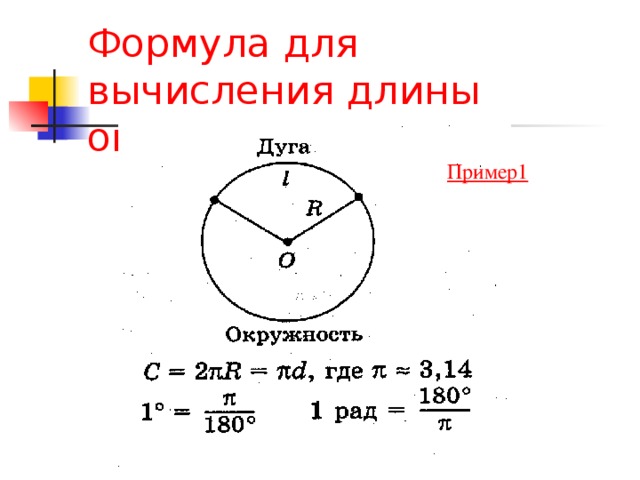 Используя знание того, что радиус равен половине диаметра:
Используя знание того, что радиус равен половине диаметра:
Теперь, когда у нас есть простая формула, включающая длину окружности и диаметр, мы можем видеть, что у нас будет отношение диаметра к длине окружности, если мы разделим обе стороны на длину окружности. . Затем мы делим обе стороны на , чтобы выделить отношение диаметра к длине окружности, и находим наше решение:
Сообщить об ошибке
Окружность с центром вписана в квадрат. Каково отношение диаметра к длине окружности, если площадь квадрата равна ?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы вычислить отношение диаметра к длине окружности квадрата, мы должны сначала получить диаметр, который равен длине стороны квадрата. Для этого нам просто нужно взять квадратный корень из площади квадрата, который равен 4. Также мы должны помнить, что длина окружности определяется как , где – длина радиуса.
Также мы должны помнить, что длина окружности определяется как , где – длина радиуса.
Теперь заметим, что эту формулу тоже можно записать .
Соотношение, которое мы ищем, . Поэтому это соотношение будет всегда и это наш окончательный ответ.
Сообщить об ошибке
Равносторонний треугольник вписан в окружность. Периметр треугольника равен . Каков радиус окружности?
Возможные ответы:
Правильный ответ:
Объяснение:
Периметр окружности позволяет найти сторону равностороннего треугольника ABC; или 2.
Отсюда мы также можем найти длину высоты равностороннего треугольника ABC по формуле , которая оказывается .
Поскольку в равностороннем треугольнике центр тяжести находится в от любой вершины, радиус окружности равен .
Сообщить об ошибке
Длина окружности и радиус . Каково отношение длины окружности к ее диаметру?
Каково отношение длины окружности к ее диаметру?
Возможные ответы:
Правильный ответ:
Объяснение:
Для данного круга окружности и радиуса , .
Поскольку радиус круга равен половине диаметра круга, мы можем определить как
.
Следовательно, отношение длины окружности к диаметру этого и всех других кругов равно .
Сообщить об ошибке
Длина окружности и радиус . Каково отношение длины окружности к ее диаметру?
Возможные ответы:
Правильный ответ:
Объяснение:
Для данного круга окружности и радиуса , .
Поскольку радиус круга равен половине диаметра круга, мы можем определить его как
.
Следовательно, отношение длины окружности к диаметру этого и всех других кругов равно
.
Сообщить об ошибке
Длина окружности и радиус . Каково отношение длины окружности к ее диаметру?
Возможные ответы:
Правильный ответ:
Объяснение:
Для данного круга окружности и радиуса , .
Поскольку радиус круга равен половине диаметра круга, мы можем определить как
.
Следовательно, отношение длины окружности к диаметру этого круга равно
.
Сообщить об ошибке
Найдите длину окружности с помощью измерения диаметра .
Возможные ответы:
Правильный ответ:
Объяснение:
Длина окружности равна
, где
Нам говорят диаметр, поэтому нам просто нужно подставить наше значение в уравнение:
Сообщить об ошибке
Уведомление об авторских правах
Все GMAT Математические ресурсы
22 диагностических теста 693 практических теста Вопрос дня Карточки Учитесь по концепции
Калькулятор длины окружности | Вычислить окружность окружности
✖Радиус окружности — это длина любого отрезка, соединяющего центр и любую точку окружности. | +10% -10% |
✖Окружность круга — это периметр круга. | AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Окружность решения круга
ШАГ 0: Итоги предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Радиус окружности: 5 метров —> 5 метров Преобразование не требуется
ШАГ 2: Вычисление формулы
ШАГ 3 : Преобразование результата в единицу измерения вывода
31,4159265358979 Метр —> Преобразование не требуется
< 5 Калькулятор окружности кругаОкружность формулы круга
Окружность круга = 2*пи*радиус круга
С = 2*пи*г
Что такое Круг?
Окружность — это базовая двухмерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки.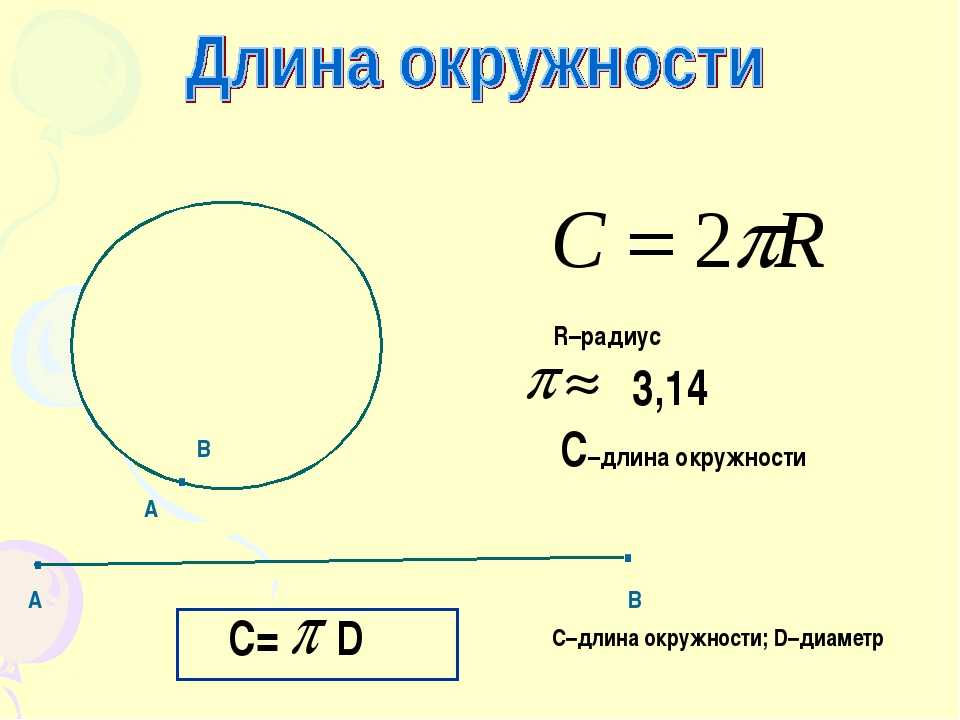 Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга. То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.
Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга. То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.
Как рассчитать длину окружности?
Калькулятор окружности окружности использует Окружность окружности = 2*pi*Радиус окружности для расчета окружности окружности. Окружность окружности — это общее расстояние по всей окружности. Окружность круга обозначается символом C .
Как рассчитать длину окружности с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для длины окружности, введите радиус окружности 9.0304 (r) и нажмите кнопку рассчитать. Вот как можно объяснить вычисление окружности круга с заданными входными значениями -> 31,41593 = 2*pi*5 .
Часто задаваемые вопросы
Что такое длина окружности?
Окружность круга представляет собой общее расстояние по всему кругу и представляется как C = 2*pi*r или Длина окружности = 2*pi*Радиус круга . Радиус окружности — это длина любого отрезка, соединяющего центр и любую точку окружности.
Радиус окружности — это длина любого отрезка, соединяющего центр и любую точку окружности.
Как рассчитать длину окружности?
Окружность круга — это общее расстояние по всей окружности, рассчитанное по формуле Окружность окружности = 2*pi*Радиус окружности . Чтобы рассчитать длину окружности, вам понадобится Радиус окружности (r) . С помощью нашего инструмента вам нужно ввести соответствующее значение радиуса окружности и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Сколько существует способов вычисления длины окружности?
В этой формуле Окружность окружности использует Радиус окружности. Мы можем использовать 4 других способа (ов) для вычисления того же самого, которые заключаются в следующем:
- Окружность круга = sqrt (4 * pi * Площадь круга)
- Окружность круга = pi * диаметр круга
- Длина окружности = ((2*pi)/Центральный угол окружности)*Длина дуги окружности
- Длина окружности = 2*pi*(Длина хорды окружности/(2*(sin(Центральный угол окружности/2) ))))
Поделиться
Скопировано!
Периметр эллипса
На странице «Эллипс» мы рассмотрели определение и некоторые простые свойства эллипса, а здесь мы рассмотрим, как более точно вычислить его периметр.
Периметр
Как ни странно, периметр эллипса очень трудно вычислить !
Формул много, вот несколько интересных. (Также см. Инструмент расчета ниже.)
Сначала измерьте свой эллипс!
a и b измеряются от центра , поэтому они подобны мерам «радиуса».
Приблизительно 1
Это приближение находится в пределах примерно 5% от истинного значения, если a не более чем в 3 раза длиннее, чем b (другими словами, эллипс не слишком «сжат»):
p ≈ 2π √ a 2 +b 2 2
Приблизительно 2
Знаменитый индийский математик Рамануджан придумал это лучшее приближение:
Приблизительно 3
Ramanujan тоже придумал это. Сначала вычисляем «h»:
ч = (а — б) 2 (а + б) 2
Тогда используйте его здесь:
р ≈ π(а+б) ( 1 + 3ч 10 + √(4−3ч) )
Бесконечная серия 1
Это точная формула , но для ее точности требуется «бесконечная серия» вычислений, поэтому на практике мы все еще получаем только приближение.
Сначала мы вычисляем e («эксцентриситет», , а не число Эйлера «e»):
e = √a 2 − b 2 a
Затем используйте эту формулу «бесконечной суммы»:
Может показаться сложным, но расширяется так:
Термины продолжаются бесконечно, и, к сожалению, мы должны вычислить множество терминов, чтобы получить достаточно точный ответ.
Бесконечная серия 2
Но моя любимая точная формула (поскольку она дает очень близкий ответ уже после нескольких слагаемых) выглядит следующим образом:
Сначала вычисляем «h»:
ч = (а — б) 2 (а + б) 2
Затем используйте эту формулу «бесконечной суммы»:
(Примечание: биномиальный коэффициент
с полуцелыми факториалами.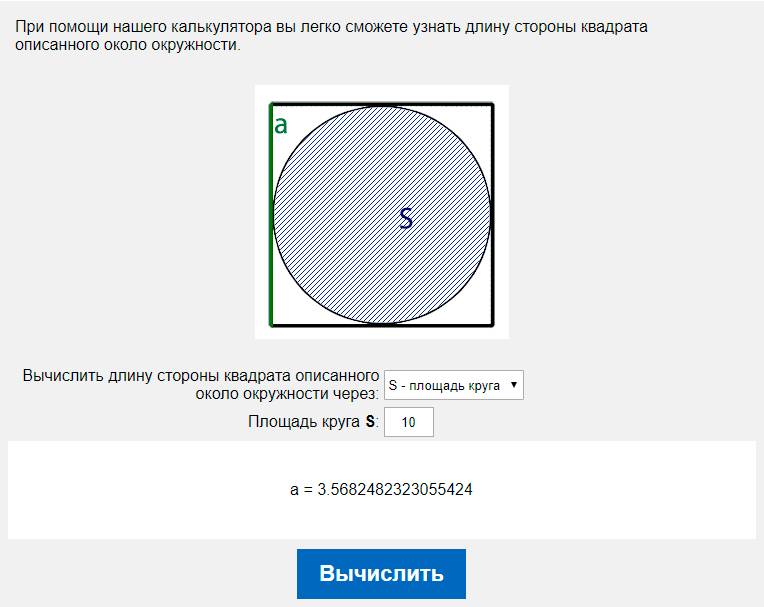 .. вау!)
.. вау!)
Это может выглядеть немного пугающе, но расширяется до следующей серии вычислений:
Чем больше слагаемых мы вычисляем, тем точнее получается (следующее слагаемое 25 H 4 /16384, который становится довольно малым, а следующий — 49 H 5 /65536, затем 441 H 6 /1048576, затем 10899304304385 /1048576, затем 10899304304385 /1048576, затем 10899304304385 /1048576, затем 10899304304385 /1048576. )
Идеальная формула
Существует совершенная формула с использованием интеграла:
р = 4а
√(1 − e 2 sin 2 θ) dθ
(Примечание: e — эксцентриситет сверху)
Но для его вычисления требуется бесконечное количество терминов («Бесконечная серия 1» выше).
Сравнение
Ради интереса я вычисляю периметр, используя три формулы аппроксимации и две точные формулы (но только первые четыре члена , включая «1» , так что это всего лишь приближение) для выбранных значений a и б :
| | Круг | | | | Строки | |
| а: | 10 | 10 | 10 | 10 | 10 | |
| б: | 10 | 5 | 3 | 1 | 0 | |
| Приблизительно 1: | 62,832 | 49. 673 673 | 46,385 | 44,65 | 44.429 | |
| Около 2: | 62,832 | 48.442 | 43.857 | 40.606 | 39.834 | |
| Около 3: | 62,832 | 48.442 | 43.859 | 40,639 | 39.984 | |
| Серия 1: | 62,832 | 48.876 | 45.174 | 43.204 | 42.951 | |
| Серия 2: | 62,832 | 48.442 | 43.859 | 40.623 | 39,884 | |
| Точно*: | 20π | | | | 40 |
* Точно:
- Когда a=b , эллипс представляет собой круг, а периметр равен 2πa (62,832.



 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R.
 Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора. Это определение выводится из теоремы Пифагора.
Это определение выводится из теоремы Пифагора.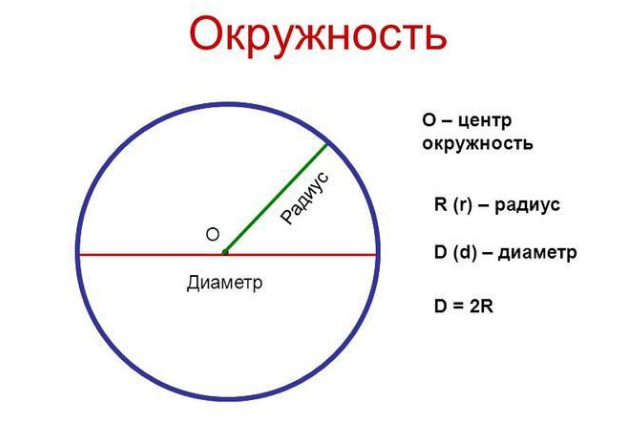

 (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute )Световой годСсылкаМегаметрМегапарсекМикродюймМикрометрМикронМилМиляМиля (Римская)Миля (Обзор США)МиллиметрМиллион Светового ГодаГвоздь (Ткань)НанометрМорская Лига (int)Морская Лига ВеликобританииМорская Миля (Международная)Морская Миля (Великобритания)ПарсекОкуньПетаметрPicaPicomet erPlanck LengthPointPoleQuarterReedReed (Long)Roman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter
(International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute )Световой годСсылкаМегаметрМегапарсекМикродюймМикрометрМикронМилМиляМиля (Римская)Миля (Обзор США)МиллиметрМиллион Светового ГодаГвоздь (Ткань)НанометрМорская Лига (int)Морская Лига ВеликобританииМорская Миля (Международная)Морская Миля (Великобритания)ПарсекОкуньПетаметрPicaPicomet erPlanck LengthPointPoleQuarterReedReed (Long)Roman ActusRopeRussian ArchinSpan (ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter ⓘ Окружность круга [C]
ⓘ Окружность круга [C]