Сложение вычитание умножение векторов: Сложение и вычитание векторов. Умножение вектора на число — урок. Геометрия, 10 класс.

7. Векторы. Сложение, вычитание векторов, умножение вектора на число.

Вектор – это объект, кот.имеет длину и направление. Это пара точек, про кот.известно, какая является началом, а какая концом.

Векторы бывают: 1) свободными (начало несущественно для рассмотрения задачи, их можно переносит пар-но самому себе как угодно.) 2) связанными (начало существенно для рассмотрениязадачи).

Длина вектора обозначается: |AB|

Если начало и конец совпад, то вектор наз-ся нулевой. Его направление считается неопределенным.

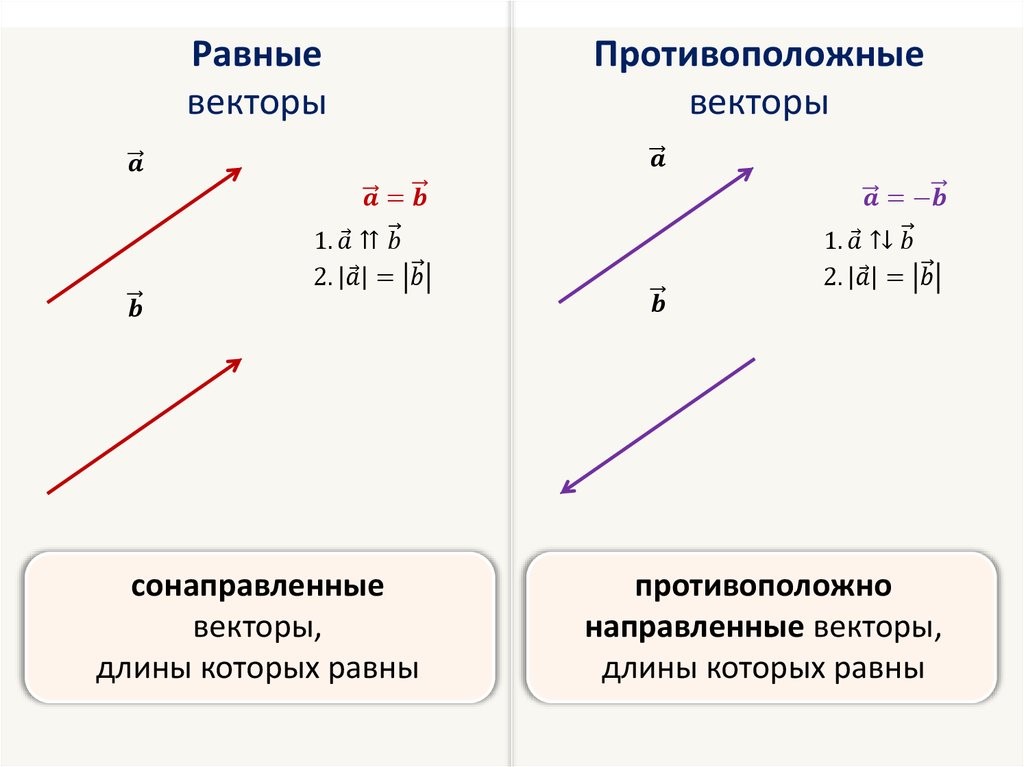
Сложение векторов: по правилу параллелограмма.

Умножение вектора на число: результатом умножения свобод.вектора на положительное число будет вектор, имеющий то же направление, что и исходный, но с длиной враз больше.

8. Операции над векторами, заданными в координатной форме.

Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства.

1. Равные векторы имеют равные координаты (в одном и том же базисе).

2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.

3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.

4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.

Вектора можно:

1. Складывать и вычитать.

2. Умножать на число.

3. Искать их скалярное произведение.

4. Искать угол между векторами.

9. Скалярное произведение векторов, его свойства.

Скал.произведение () – число, равное произвед.длин этих векторов наcos угла между ними.

Свойства скал.произведения:

1.Не зависит от порядка умножения.

2.Скал.произведение вектора на самого себя = квадрату этого вектора.

3.Скал.произведение взаимоперпендикулярных векторов = 0.

10. Векторное произведение векторов, его свойства.

Векторное произвед.векторов – операция над ними, результатом кот.явл-ся вектор, обладающий след.свойствами:

1.Векторное произвед.вектора на самого себя = 0.

2.Постоянный множитель можно выносить за знак векторного произведения.

3. [] = [;

[] = ([) + []

[] =[] + []

=

=

–правые тройки векторов.

Если в декартовой системе координат 1 напр-е изменилось на противоположное, то получается левая тройка векторов.

Смысл векторного произвед.: длина векторного произв. 2х векторов = площади параллел-ма, построенного на этих векторах:

11. Системы линейных алгебраических уравнений. Решение их методами Гаусса, Крамера, матричным.

Метод Гаусса: Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными: a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ .

. .+a_2n x_n=a_2n+1 . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

Вначале находим отличный от нуля коэффициент при x₁. Соответствующее уравнение переставляем с первым (если это необходимо). Получаем систему с a₁₁ отличным от нуля. Разделив коэффициенты этого уравнения на a₁₁, получим:

x₁+b₁₂ x₂+ . . .+b_1n x_n=b_1n+1

При помощи этого уравнения исключаем

x₁ из исходной системы:

a⁽¹⁾₂₂ x₂+a⁽¹⁾₂₃ x₃+ . . .+a⁽¹⁾_2n x_n=a⁽¹⁾_2n+1 .

a⁽¹⁾_n2 x₂+a⁽¹⁾_n3 x₃+ . . .+a⁽¹⁾_nn x_n=a⁽¹⁾_nn+1

где

a⁽¹⁾_{i j}=a_{i j}-a_{i 1}b

1 j, i,j= 2…n

Полученная система содержит n-1 уравнение. Применяем описанную выше процедуру к этой системе. Операции повторяем требуемое число раз, пока не приведем систему к треугольному виду:

x₁+с₁₂ x₂+ . . .+с_1n x_n=с_1n+1

x₂+ . . .+c_2n x_n=c_2n+1

x_n=c_nn+1

Теперь легко определить x_n,x_n-1, . . ., x₁.

Если det(A

)=0, то исходная система не имеет решений и процедура выдает S=0 иначе S=1 и решения находятся в массиве X.

Метод Крамера: каждый из неизвестных x – дробь, в знаменателе кот.нах-ся определитель системы, а в числителе определитель, получ.из определителя системы путем замены столбца, №кот. = № x на столбц свободных членов. a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a

_2n x_n=a_2n+1 . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

Матричный метод:

Пусть знаменатель = =

А числитель = D. Для =

==

. Для остальных – аналогично.

🎓 сложение векторов умножение вектора на число вычитание векторов скалярное — презентация на Slide-Share.ru

1

Первый слайд презентации

сложение векторов умножение вектора на число вычитание векторов скалярное умножение векторов вектор число

Изображение слайда

2

Слайд 2

сложение векторов умножение вектора на число вычитание векторов скалярное умножение векторов Скалярное произведение равно, если хотя бы один из векторов сомножителей является нулевым.

Изображение слайда

3

Слайд 3

сложение векторов умножение вектора на число вычитание векторов скалярное умножение векторов ,

Изображение слайда

4

Слайд 4

сложение векторов умножение вектора на число вычитание векторов скалярное умножение векторов скалярное произведение в координатах

Изображение слайда

5

Слайд 5

Скалярное произведение в координатах

Изображение слайда

6

Слайд 6

Теорема. В прямоугольной системе координат скалярное произведение векторов и вы ражается формулой: Доказательство.

Изображение слайда

7

Слайд 7

Теорема. В прямоугольной системе координат скалярное произведение векторов и вы ражается формулой: Доказательство. ,

Изображение слайда

8

Слайд 8

Теорема. В прямоугольной системе координат скалярное произведение векторов и вы ражается формулой: Доказательство. ,

Изображение слайда

9

Слайд 9

Теорема. В прямоугольной системе координат скалярное произведение векторов и вы ражается формулой: Доказательство.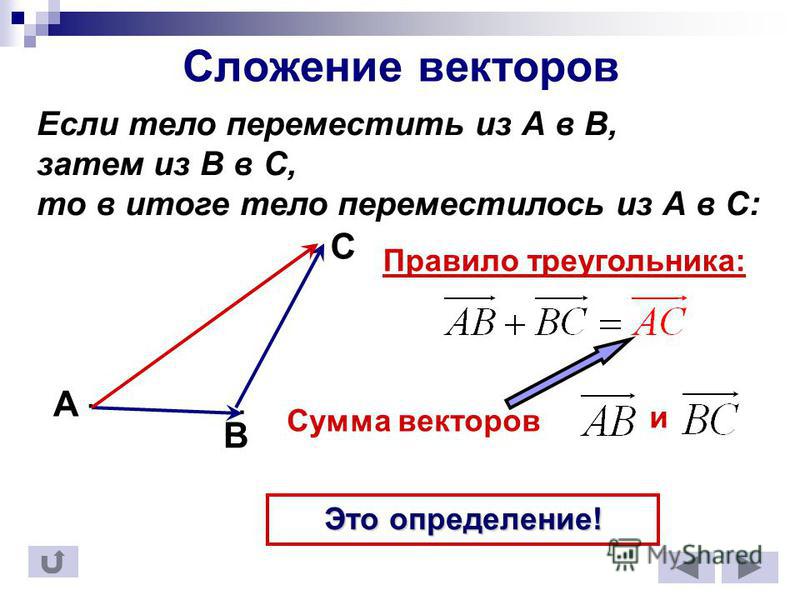 , Что и требовалось доказать.

Изображение слайда

10

Слайд 10

Задача. Найти скалярное произведение векторов,,, если,,. Решение.

Изображение слайда

11

Слайд 11

Следствие 1. Ненулевые векторы и перпендикулярны тогда и только тогда, когда. Какие из данных векторов являются перпендикулярным и для вектора ?

Изображение слайда

12

Слайд 12

Следствие 2. Косинус угла между ненулевыми векторами и выражается формулой :.

Изображение слайда

13

Слайд 13

Свойства скалярного произведения векторов

Изображение слайда

14

Слайд 14

Скалярное произведение векторов Скалярное произведение векторов в координатах ,

Изображение слайда

15

Слайд 15

Свойства скалярного произведения векторов 1.

Изображение слайда

16

Слайд 16

Свойства скалярного произведения векторов 1. 2. переместительный закон Что и требовалось доказать.

Изображение слайда

17

Слайд 17

Свойства скалярного произведения векторов 1. 2. переместительный закон 3. распределительный закон ,, Что и требовалось доказать.

Изображение слайда

18

Слайд 18

Свойства скалярного произведения векторов 1. 2. переместительный закон 3. распределительный закон 4. сочетательный закон , Что и требовалось доказать.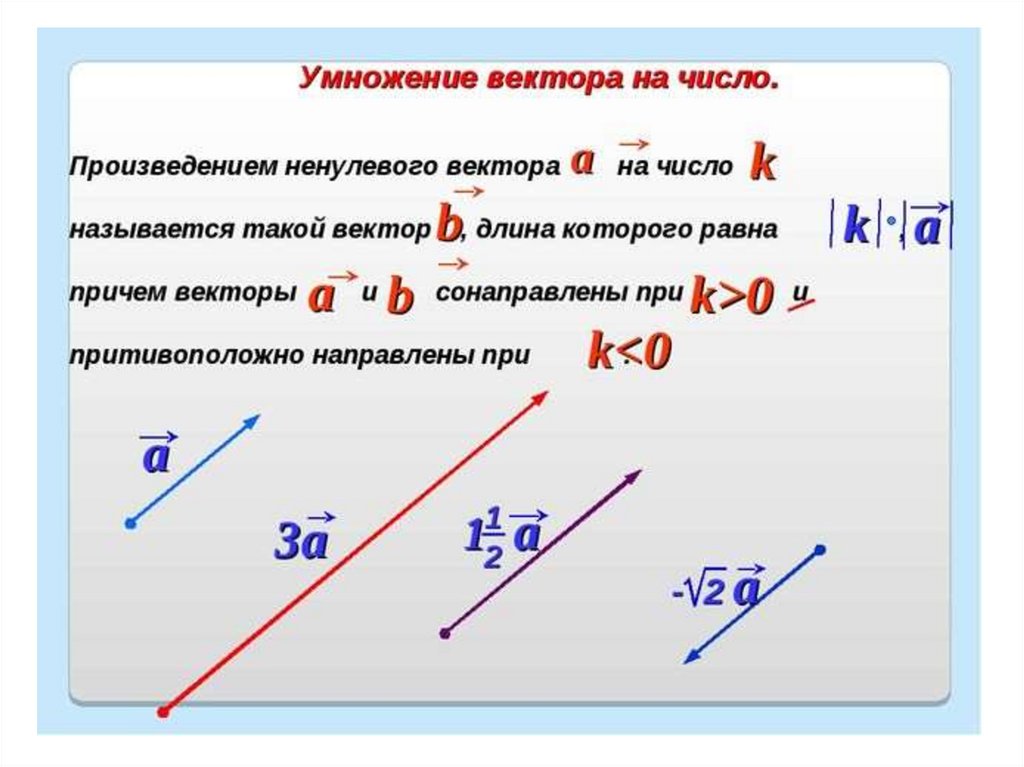

Изображение слайда

19

Слайд 19

Свойства скалярного произведения векторов 1. 2. переместительный закон 3. распределительный закон 4. сочетательный закон

Изображение слайда

20

Слайд 20

Задача. Найти, если,. ,,,. Решение. Применение скалярного произведения к решению задач

Изображение слайда

21

Слайд 21

Задача. Найти величину в, если,,. Решение. Ответ:.

Изображение слайда

22

Слайд 22

Задача.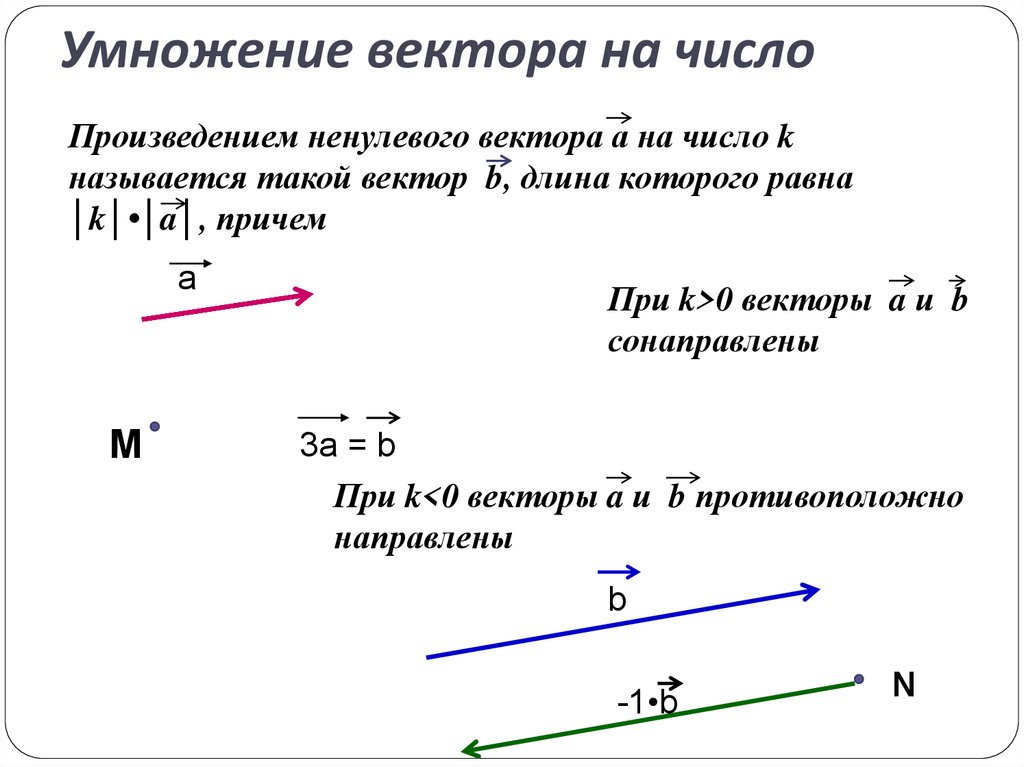 Определить, при каких значениях переменной. , , , , Решение.

Изображение слайда

23

Последний слайд презентации: сложение векторов умножение вектора на число вычитание векторов скалярное

Задача. Доказать, что треугольник с вершинами, и тупоугольный и найти косинус тупого угла. Решение. острый острый тупой Что и требовалось доказать. Ответ:.

Изображение слайда

Калькулятор сложения и вычитания векторов

Укажите размерность пространства 23

Укажите форму представления первого вектора
Координаты точек начала и конца первого вектораКоординаты первого вектора

Укажите форму представления второго вектора
Координаты точек начала и конца второго вектораКоординаты второго вектора

Задайте координаты первого вектора
a̅ = { ; }

Задайте координаты второго вектора
b̅ = { ; }

+ —

Как сложить или вычесть два вектора

Сложение векторов по правилу треугольника

Чтобы сложить два вектора a и b по правилу треугольника, необходимо:

1. Параллельно перенести векторы a и b, так чтобы начало одного из векторов совпадало с концом другого.
2. Из начала вектора a в конец вектора b провести вектор c.

Вектор c – есть сумма векторов a и b

a + b = c

Вычитание векторов по правилу треугольника

Чтобы вычесть два вектора a и b по правилу треугольника, необходимо:

1. Параллельно перенести векторы a и b, так чтобы начало одного из векторов совпадало с началом другого.
2. Из конца вектора b в конец вектора a провести вектор c.

Вектор c – есть разность векторов a и b

a − b = c

---

Как сложить два вектора, координаты которых заданы точками

Найдем сумму векторов плоскости. Координаты обоих векторов заданны точками:

Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)

Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов AB и CD будет вектор c

Вычислим координаты первого вектора по двум точкам A и B:

AB = {B_x — A_x  ; B_y — A_y} = {-2 — 5 ; 11 — 9} = {-7 ; 2}

Вычислим координаты второго вектора по двум точкам C и D:

CD = {D_x — C_x  ; D_y — C_y} = {-3 — 0 ; 1 — 12} = {-3 ; -11}
c = AB + CD = {AB_x + CD_x ; AB_y + CD_y} = {-7 + (-3) ; 2 + (-11)} = {-10 ; -9}

c = AB + CD

---

Как вычесть два вектора, координаты которых заданы точками

Пример. Найдем разность векторов пространства. Координаты обоих векторов заданны точками.

Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)

Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов AB и CD будет вектор c.

Вычислим координаты первого вектора по двум точкам A и B:

AB = {B_x — A_x  ; B_y — A_y; B_z — A_z} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}

Вычислим координаты второго вектора по двум точкам C и D:

CD = {D_x — C_x  ; D_y — C_y; D_z — C_z} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}

c = AB — CD = {AB_x — CD_x ; AB_y — CD_y ; AB_z — CD_z} = {-8 — 7 ; -1/5 — 6 ; -275/4 — 7} = {-15 ; -31/5 ; -303/4}= {-15 ; -6.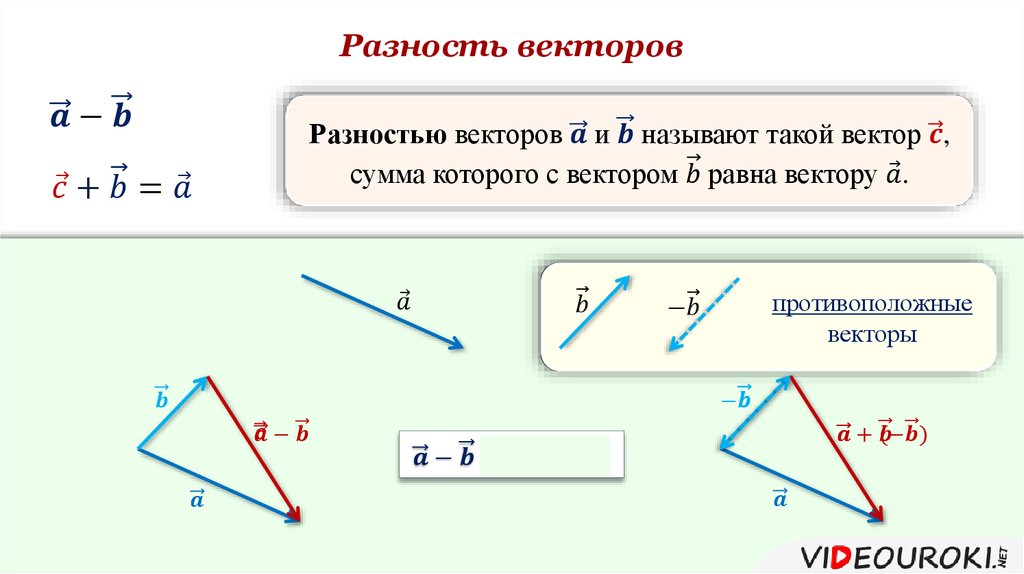 2 ; -75.75}

---

Вычитание векторов в координатном представлении

Найдем разность векторов плоскости.

Координаты вектора a: (5 ; 9)
Координаты вектора b: (-1 ; 7)

Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов a и b будет вектор c

c = a — b = {a_x — b_x ; a_y — b_y} = {5 — (-1) ; 9 — 7} = {6 ; 2}

c = a — b

---

Сложение векторов в координатном представлении

Пример. Найдем сумму векторов пространства.

Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)

Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов a и b будет вектор c

c = a + b = {a_x + b_x ; a_y + b_y ; a_z + b_z} = {5 + 2 ; 1 + 4 ; 7 + 6} = {7 ; 5 ; 13}

3.

2 Сложение и вычитание векторов: графические методы

Цели обученияВекторы в двух измеренияхСложение векторов: метод «голова к хвосту»Вычитание векторовУмножение векторов и скаляровРазложение вектора на компоненты

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Понимание правил сложения, вычитания и умножения векторов
• Применение графических методов сложения и вычитания векторов для определения смещения движущихся объектов

Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:

• 3.A.1.1 Учащийся может выразить движение объекта, используя описательные, математические и графические представления. (Ст. 1.5, 2.1, 2.2)
• 3.A.1.3 Учащийся способен анализировать экспериментальные данные, описывающие движение объекта, и может выражать результаты анализа, используя описательные, математические и графические представления. (П.5.1)

Рис. 3.8 Смещение можно определить графически, используя масштабную карту, например, карту Гавайских островов. Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (Источник: Геологическая служба США)

Векторы в двух измерениях

Вектор – это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета, то есть системы координат, используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рис. 3.9 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение».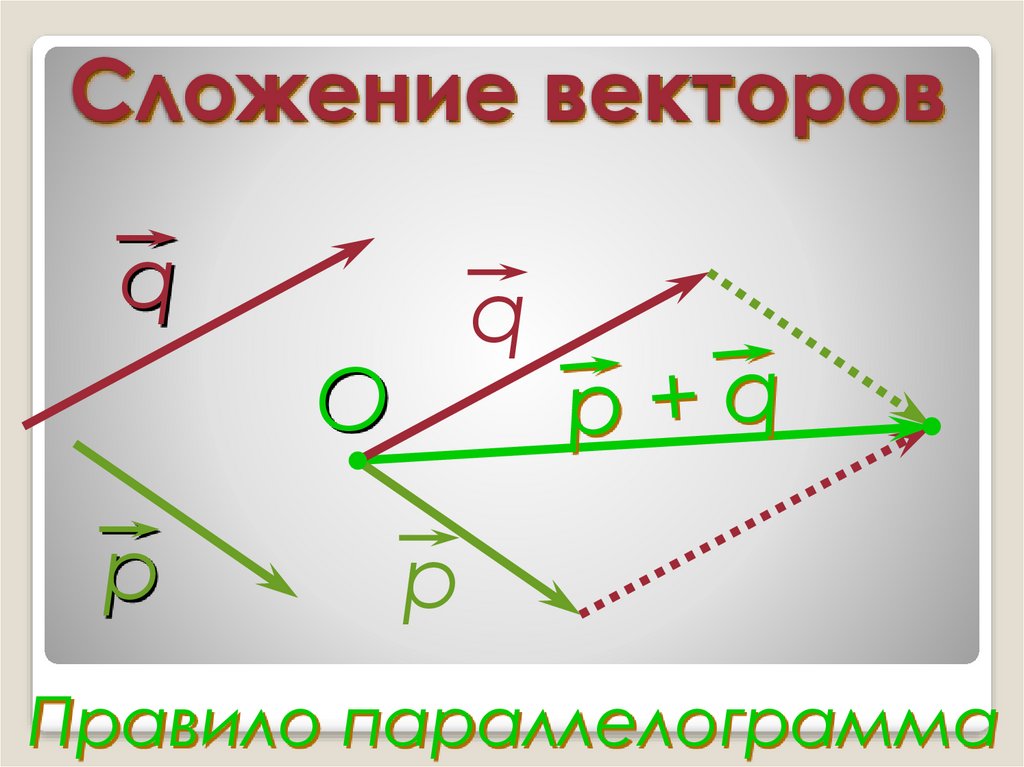 Мы будем использовать обозначение, что жирный шрифт, такой как размер DD 12{D} {}, обозначает вектор. Его величина представлена ​​символом, выделенным курсивом, размером DD 12{D} {}, а его направление размером θθ 12{θ} {}.

Векторы в этом тексте

В этом тексте мы будем представлять вектор с переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором FF размером 12{F} {}, который имеет как величину, так и направление. Величина вектора будет представлена ​​переменной, выделенной курсивом, например размером FF 12{F} {}, а направление переменной будет задано углом θθ размером 12{θ} {}.

Рисунок 3.9 Человек идет девять кварталов на восток и пять кварталов на север. Водоизмещение составляет 10,3 блока при угле 29,1°29,1° размером 12{«29» «.» «1°»} {} к северу от востока.

Рисунок 3.10 Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 3.9, нарисуйте стрелку, чтобы представить вектор полного смещения DD размером 12{D} {}. С помощью транспортира начертите линию под углом θθ величиной 12{θ} {} относительно оси восток-запад. Длина DD size 12{D} {} стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере величина DD размера 12{D} {} вектора составляет 10,3 единицы, а направление θθ размера 12{θ} {} равно 29.1°29.1° размер 12{«29» «.» 1 rSup { размер 12{°} } } {} к северу от востока.

Сложение векторов: метод «голова к хвосту»

Метод «голова к хвосту» — это графический способ добавления векторов, описанный на рис. 3.11 ниже и в следующих шагах. Хвост вектора — это начальная точка вектора, а начало (или кончик) вектора — это конечный заостренный конец стрелки.

Рисунок 3.11 Метод «голова к хвосту»: Метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренных на рисунке 3.9.. (a) Нарисуйте вектор, представляющий смещение на восток. (b) Нарисуйте вектор, представляющий смещение на север.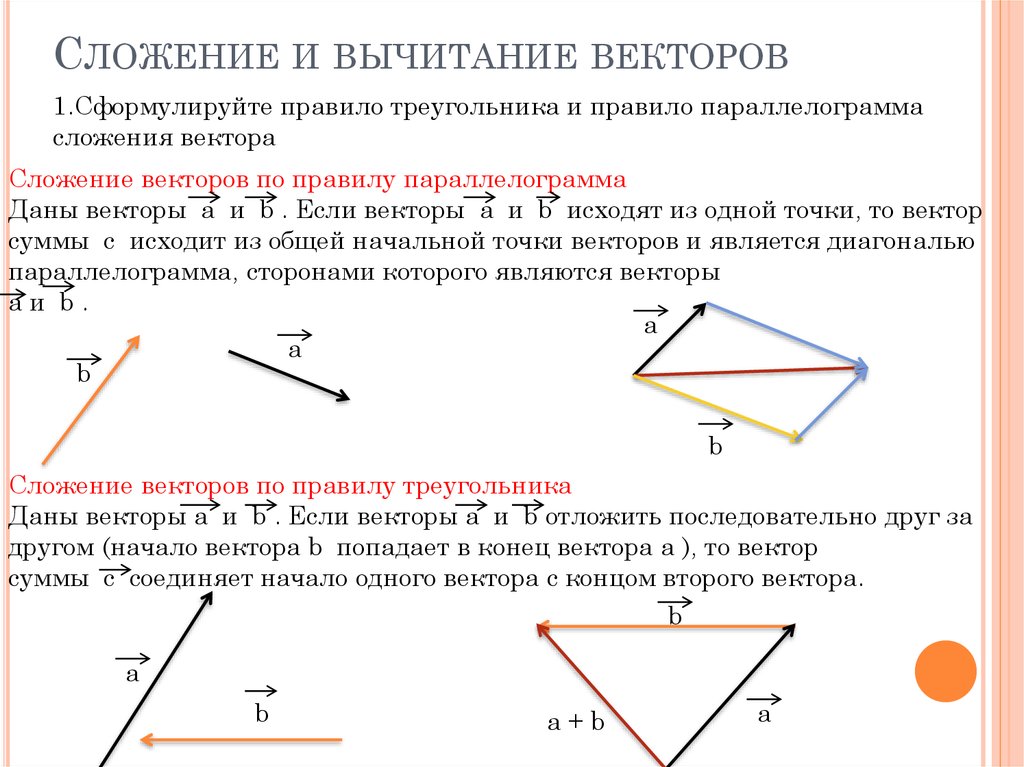 Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Нарисуйте линию от конца вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы сформировать сумму или результирующий вектор, размер DD 12{A} {}. Длина стрелки D,D размера 12{A}{} пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол по отношению к востоку (или горизонтальной оси) θθ размером 12{θ} {}, измеряется с помощью транспортира и составляет 29.1°29.1° размер 12{«29» «.» 1°} {}.

Шаг 1. Нарисуйте стрелку, представляющую первый вектор (девять блоков на восток), используя линейку и транспортир .

Рисунок 3.12

Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (пять блоков на север).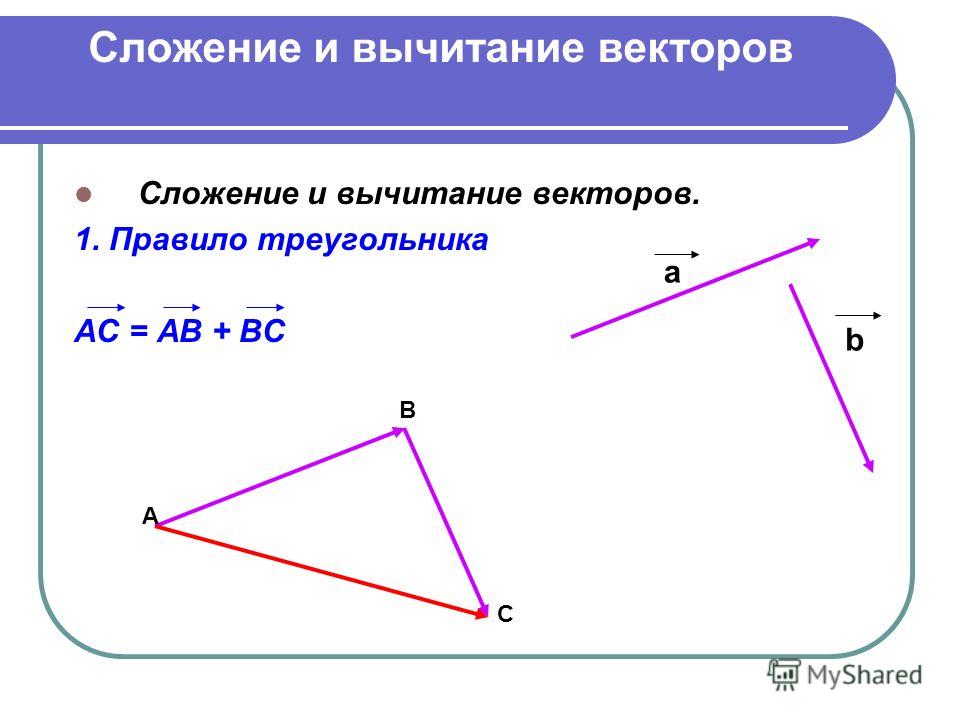 Поместите конец второго вектора в начало первого вектора .

Рисунок 3.13

Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от кончика к хвосту.

Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма D других векторов.

Рисунок 3.14

Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.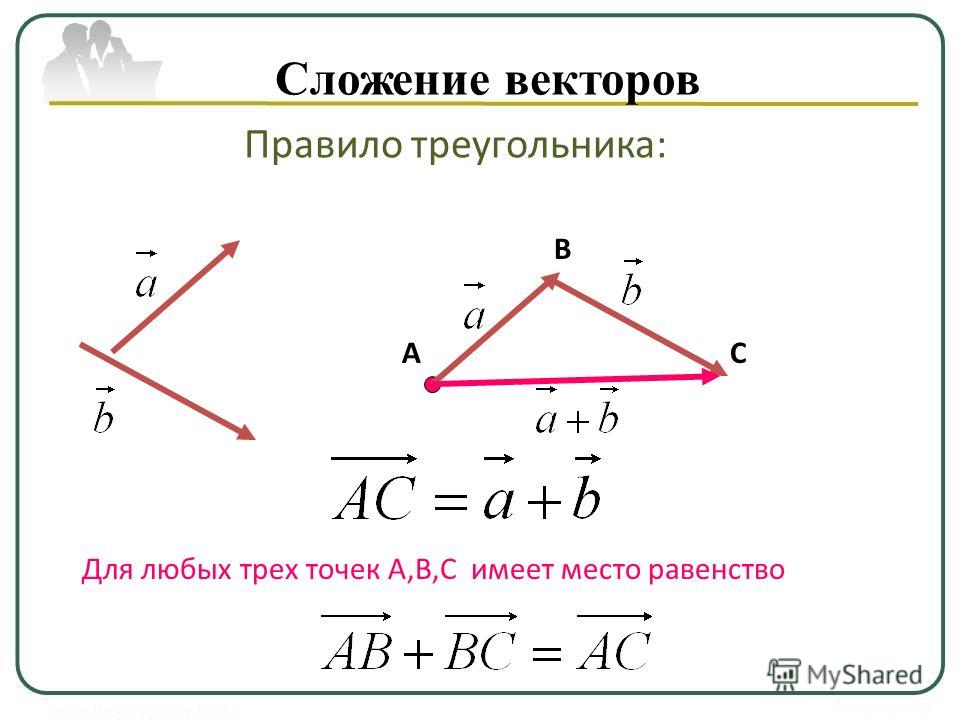

Шаг 6. Чтобы определить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.

Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.

Пример 3.1 Графическое сложение векторов с использованием метода «голова к хвосту»: прогулка женщины . Сначала она проходит 25,0 м в направлении 49,0°49,0° размера 12{«49» «.» «0°»} {} к северу от востока. Затем она проходит 23,0 м курсом 15,0°15,0° размер 12{«15» «.» «°°»} {} к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.

Стратегия

Представьте каждый вектор смещения графически со стрелкой, пометив первый размер AA 12{A} {}, второй размер BB 12{B} {} и третий размер CC 12{C} {} , делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад.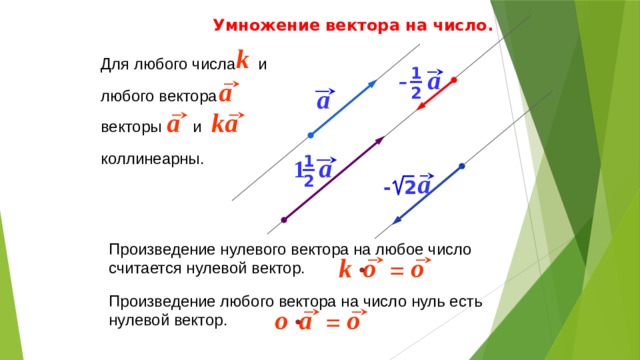 Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого размером RR 12{R} {}.

Решение

(1) Нарисуйте три вектора смещения.

Рисунок 3.15

(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.

Рисунок 3.16

(3) Нарисуйте результирующий вектор, размер RR 12{R} {}.

Рисунок 3.17

(4) Используйте линейку для измерения величины RR размера 12{R} {} и транспортир для измерения направления RR размера 12{R} {}. Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.

Рисунок 3.18

В этом случае видно, что полное смещение RR размера 12{R} {} имеет величину 50,0 м и лежит в направлении 7,0°7,0° размера 12{7 «.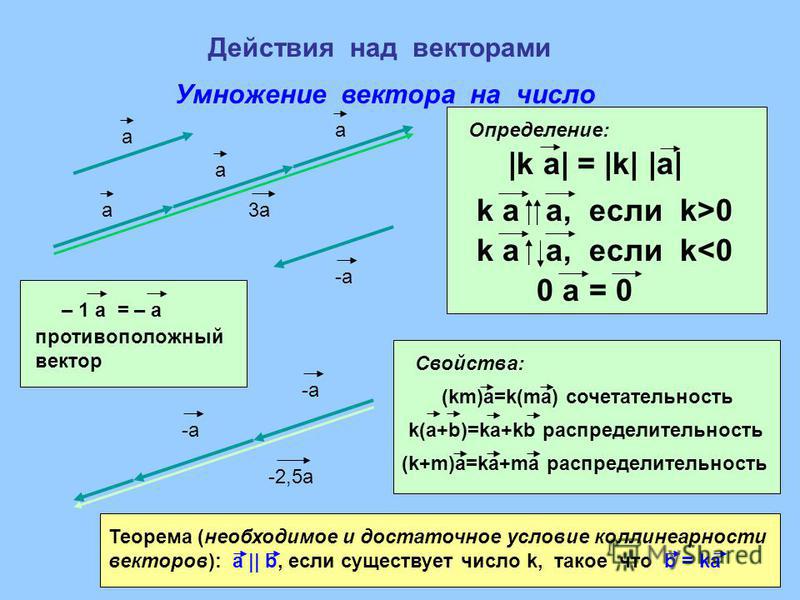 » 0°} {} к югу от востока. Используя его величину и направление, этот вектор можно выразить как R=50,0 мR=50,0 м, размер 12{R» = 50″ «.» «0 м»} {} и θ=7,0°θ=7,0° размер 12{θ=7 «.» «0°»} {} к югу от востока.

Обсуждение

Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 3.19.и мы все равно получим то же решение.

Рисунок 3.19

Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет таким же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно. Векторы можно добавлять в любом порядке.

3.1 А+В=В+А.А+В=В+А. size 12{«A+B=B+A»} {}

Это верно и для сложения обычных чисел — вы получите тот же результат, если сложите 2+32+3 size 12{«2+3» } {} или же 3+23+2 размер 12{«3+2»} {}, например.

Вычитание векторов

Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание, скажем, мы хотим вычесть BB размером 12{B} {} из Размер AA 12{A} {} , пишется A–BA–B size 12{ «A» «-B»} {} — сначала мы должны определить, что мы подразумеваем под вычитанием. минус вектора BB определяется как –B–B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рис. 3.20. Другими словами, BB размера 12{B} {} имеет ту же длину, что и –B–B размера 12{«-» «B»} {}, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.

Рис. 3.20 Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, размер BB 12{B} {} является минусом размера –B–B 12{ital «-B»} {}; он имеет ту же длину, но противоположное направление.

Затем вычитание вектора BB из вектора AA просто определяется как добавление -B-B к AA. Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.

3.2 А – В = А + (–В). А – В = А + (–В). размер 12{ жирный «A – B = A + » \( жирный «–B» \) } {}

Это аналогично вычитанию скаляров, например, 5 – 2 = 5 + (–2)5 – 2 = 5 + (–2) размер 12{«5 – 2 = 5 + » \( «–2» \) } {}. Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.

Пример 3.2. Графическое вычитание векторов: женщина, плывущая на лодке

Женщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласили, что сначала нужно пройти 27,5 м в направлении 66,0°66,0° размером 12{«66» «.» 0°} {} к северу-востоку от ее текущего местоположения, а затем пройдите 30,0 м в направлении 112°112° размера 12{«112″°} {} к северу от востока (или 22,0°22,0° размера 12{«22» «. » 0°} {} к западу от севера). Если женщина совершит ошибку и поедет в направлении , противоположном , на второй этап поездки, где она окажется? Сравните это место с расположением дока.

Рисунок 3.21

Стратегия

Мы можем представить первый этап пути с помощью вектора AA, а второй этап пути с помощью вектора Размер каретки 12{B} {}. Пристань расположена в точке A + BA + B. Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние BB (30,0 м) в направлении 180°–112°. =68°180°–112°=68° к югу от востока. Мы представляем это как –B–B, как показано ниже. Вектор –B–B имеет ту же величину, что и BB, но направлен в противоположную сторону. Таким образом, она окажется в точке A+(–B)A+(–B) или A–BA–B.

Рисунок 3.22

Выполним сложение векторов, чтобы сравнить местоположение причала, A + BA + B size 12{ ital «A «»+ «B} {}, с местоположением, в которое по ошибке прибыла женщина, A + (–B)A + (–B) размер 12{ жирный «A + » \(жирный «–B» \) } {}.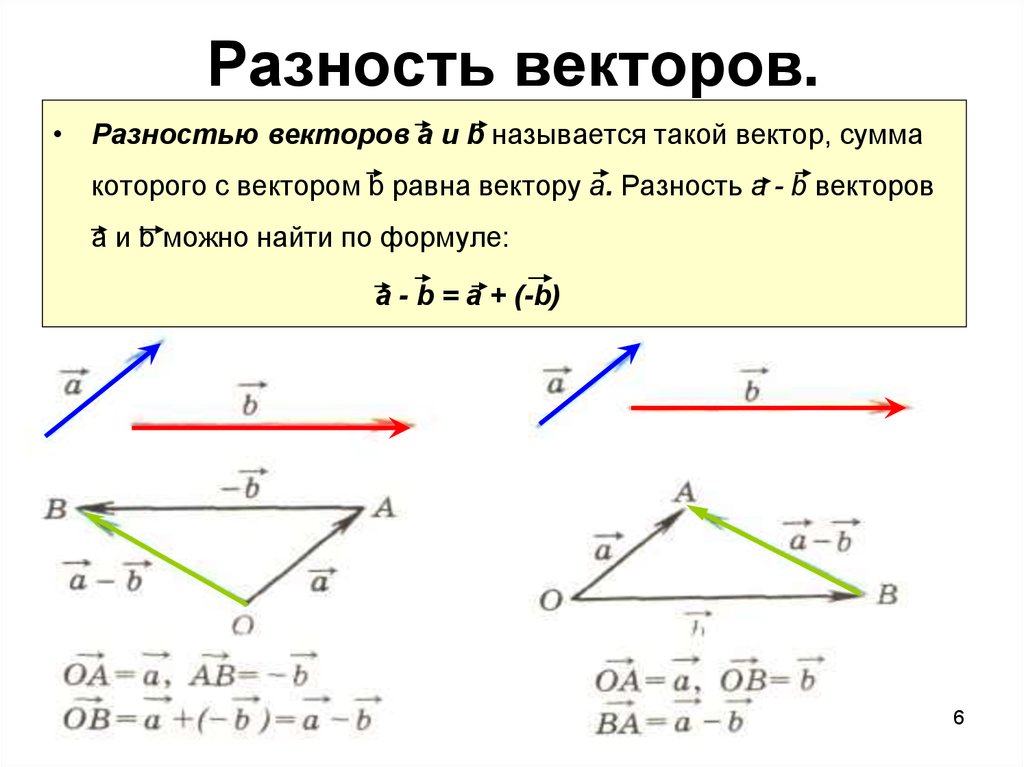

Решение

(1) Чтобы определить место, куда случайно попала женщина, начертите векторы AA размером 12{A} {} и –B–B.

(2) Разместите векторы лицом к хвосту.

(3) Нарисуйте результирующий вектор RR размером 12{R} {}.

(4) С помощью линейки и транспортира измерьте величину и направление RR размера 12{R} {}.

Рисунок 3.23

В этом случае R=23,0 мR=23,0 м размер 12{R»=23″ «.» «0 м»} {} а также θ=7,5°θ=7,5° размер 12{θ=7 «.» «5° к югу от востока»} {} к югу от востока.

(5) Чтобы определить местоположение дока, мы повторяем этот метод, добавляя векторы размера AA 12{A} {} и размера BB 12{B} {}. Получаем результирующий вектор R’R’ размера 12{R’} {}.

Рисунок 3.24

В этом случае R = 52,9 мР = 52,9 м, размер 12{R» = 52″ «.» «9 м»} {} и θ=90,1°θ=90,1° размер 12{θ=»90″ «.» «1° к северу от востока»} {} к северу от востока.

Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.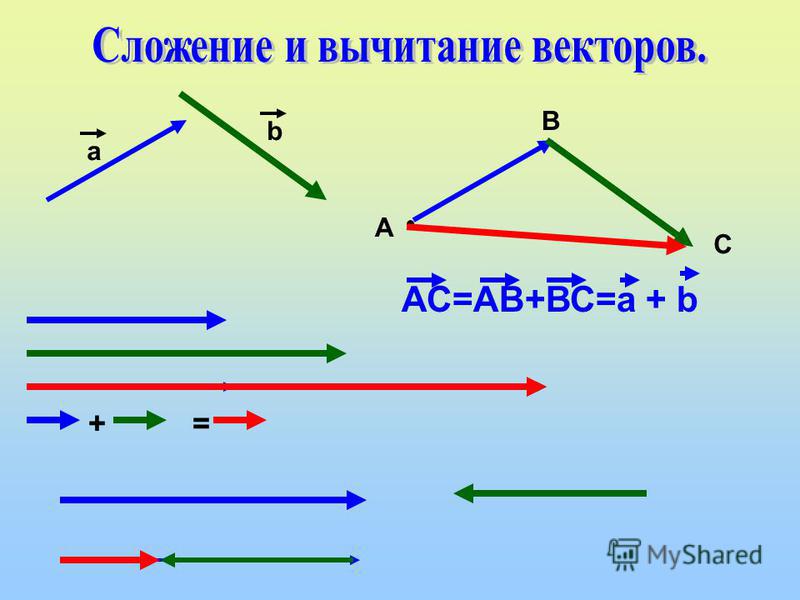

Обсуждение

Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.

Умножение векторов и скаляров

Если бы мы решили пройти в три раза больше на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м3 × 27,5 м размером 12{«3 » умножить на » 27″ «.» «5 м»} {}, или 82,5 м, в направлении 66,0°66,0° размер 12{«66» «.» 0 {размер 12{°} } } {} к северу от востока. Это пример умножения вектора на положительную скалярную величину. Обратите внимание, что величина меняется, но направление остается прежним.

Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление.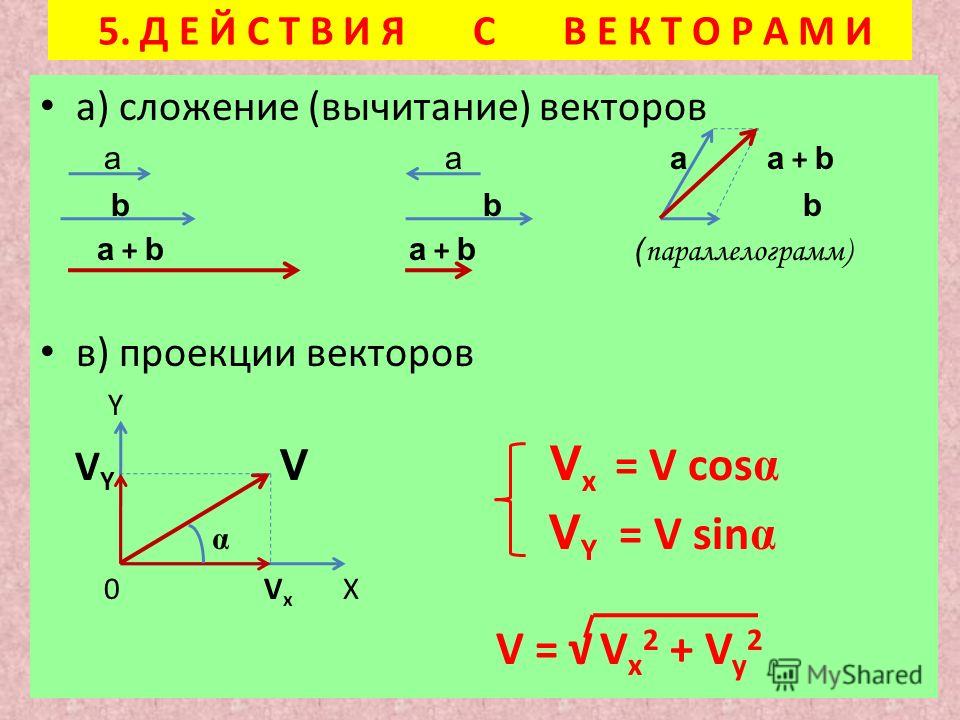 Мы можем обобщить эти правила следующим образом: когда векторный размер AA 12{A} {} умножается на скалярный размер cc 12{c} {}

• , модуль вектора становится абсолютным значением размера cc 12{ c} {}размер AA 12{A} {},
• , если cc size 12{A} {} положителен, направление вектора не меняется, и
• , если размер копий 12{A} {} отрицательный, направление меняется на противоположное.

В нашем случае c=3c=3размер 12{c=3} и A=27,5 мА=27,5 мразмер 12{«A= 27,5 м»}. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на два равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между нулем и единицей.

Разложение вектора на компоненты

В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает в себя определение перпендикулярных компонентов одного вектора, например, x — и y -компоненты, или компоненты север-юг и восток-запад.

Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0°29,0° размером 12{«29» «.» 0°} } {} к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.

PhET Explorations: Maze Game

Узнайте о положении, скорости и ускорении в Arena of Pain . Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.

Рисунок 3.25 Игра «Лабиринт»

• Печать
• Поделиться

Вычитание векторов – объяснение и примеры

Существует много параллелей между скалярами и векторами, и вычитание векторов не является исключением. В частности, векторное вычитание:

«Сложение вектора с отрицательным значением другого вектора».

Из приведенного выше определения ясно, что вычитание векторов означает просто сложение отрицательных векторов. Поэтому перед изучением вычитания векторов важно просмотреть отрицательные векторы.

Как известно, отрицательный вектор получается умножением заданного вектора на -1. Это меняет направление вектора.

Допустим, — это вектор, указывающий слева направо. Умножение вектора A на -1 дает нам -A, , что является отрицательным вектором A. Хотя величины двух векторов A и – A останутся прежними, отрицательный вектор – A будет направлен справа налево.

В этом разделе мы обсудим следующие аспекты вычитания векторов:

• Как вычитать векторы
• Вычитание векторов графически

Как вычитать векторы

Мы знаем, что два вектора, A и B, можно сложить вместе, используя сложение векторов, и результирующий вектор можно записать как R = A + B . Точно так же, если мы хотим вычесть два вектора, A и B математически выражается как: )

Таким образом, вычитание двух векторов аналогично сложению вектора A и отрицательного вектора B (т. е. В ). Векторы B и – B будут иметь одинаковую величину, но направление -B’ s будет противоположно вектору B.

Вычитание векторов также работает, когда два вектора даны в компонентной форме. или как векторы-столбцы. Если A = (ax1, ay1) и B = (bx1, by1), то разница между ними составляет: результирующего вектора R можно выразить как:

Rx = ax1 – bx1

и

Ry = ay1 – by1.

Таким образом, результирующий вектор можно вычислить, просто вычислив разность соответствующих горизонтальных и вертикальных составляющих двух исходных векторов.

Графическое вычитание векторов

Графически правило «голова к хвосту», используемое при сложении векторов, может быть адаптировано для вычитания векторов. Например, рассмотрим два вектора P и Q .как показано на изображении ниже. Обратите внимание, что вектор – Q получается путем изменения направления Q.

Далее мы складываем векторы P  и – Q , используя правило лобового сечения следующим образом:

Во-первых, нарисуйте вектор P, и затем поместите вектор – Q так, чтобы его хвост соединился с головой вектора P . Теперь, чтобы найти сумму P и – Q , нарисуйте результирующий вектор R таким образом, чтобы он соединял хвост вектора P с головой вектора — Q , как показано на изображении ниже.

Математически результирующий вектор может быть выражен как: 

R = P – Q

Примеры

В этом разделе мы будем практиковать вычитание векторов с различными примерами и их пошаговыми решениями.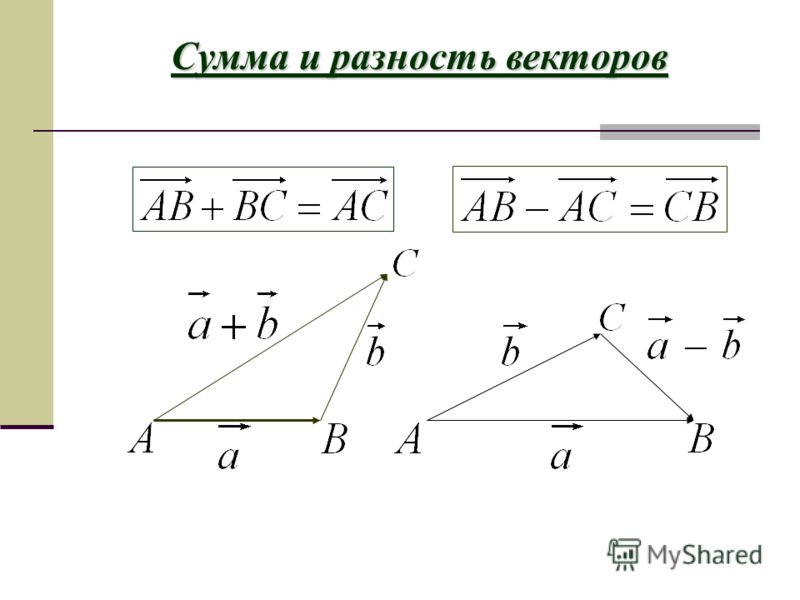 с использованием различных методов, как описано выше.

Пример 1

Графически вычтите заданные векторы A и B, показанные на изображении ниже, используя метод «голова к хвосту».

Решение
Сначала нарисуем отрицательную сторону вектора B , изменив его направление на противоположное, т. е. -B . Далее складываем векторы A и – B , применяя метод «голова к хвосту».

Сначала разместим заданные векторы A и – B так, чтобы хвост вектора -B соединяется с головкой вектора A , как показано на изображении ниже. Далее, чтобы найти их сумму, рисуем результирующий вектор R так, чтобы он соединял хвост вектора A с головой вектора – B . Математически, результирующее может быть выражено как:
R = A + (- B )

Пример 2

Учитывает два вектора AB = (3, 2) и

. 0053 BC = (2, 2), алгебраически вычтите два вектора. Затем определите модуль и угол результирующего вектора, заданного как:

S   = AB + (- BC )

Первое решение

3

определите отрицательный вектор, умножив его на -1:

-BC = (-2, -2).

Далее для нахождения результирующего вектора S, складываем векторы AB 2

| С | =   √ 1

| С | = 1 единица

Угол результирующего вектора S можно найти следующим образом:

φ = TAN ^-1 (0)

φ = 0 градусов

Пример 3

Учитывая два вектора S = 10 м, φ = 30 градусов и T = 20m, φ = 60 м. градусов. Вычтите два вектора, затем вычислите величину и угол результирующего вектора, используя метод компонентов.

Решение

LET R Будьте результирующим вектором, равным сумме данных векторов S и — T. он может быть выражен как:

R = S + . (- T )

Чтобы использовать компонентный метод, мы сначала разбиваем заданные векторы на их соответствующие горизонтальную и вертикальную составляющие: Примерно)

Аналогично, для вертикального компонента:

SY = S SIN φ

SY = 10 SIN 30

SY = 5 M

Далее мы вычисляем компоненты вектора T:

TX = T COS φ

TY = T SIN φ

Где,

TX = 20 COS 60

TX = 10M

TY = 20 SIN 60

TY = 17,320 (apenceathally)

TY = 17,320 (oTHER. мы можем вычислить вектор разности, вычислив разность отдельных компонентов x и y S and – T vector as:

Rx = Sx + ( -Tx )

Rx = 8. 660 + (-10)

Rx = -1.34 m

RY = SY + ( -TY )

RY = 5 + (-17,32)

RY = -12,32 M

ВЕКТОР R может быть выраженным COLAND AS ASTER AS ASTER AS ASCERED AS ASCERED COLANDATED AS ASCERAD AS The COLANDAIN VECTER. :

R = (-1,34, -12,32).

92

|Р| = 12,392 M

φ = TAN ^-1 ( RY / RX )

φ = TAN ^-1 (-12,32 / -1,34)

φ = 83,79 DEGEEES (-12,32 / -1,34)

φ = 83,79 DEGEEES (-12,32 / -1,34)

φ = 83,79. , результирующий вектор суммы может быть выражен как:

R = 12,392 м, Φ = 83,79 градуса

Пример 4

Определить результирующий вектор суммы для двух векторов ) и – В = (2,-1).

Решение

Данные векторы уже находятся в своих составных формах, поэтому сначала определяем их углы.

для вектора A:

φ = TAN ^-1 ( AY / AX )

φ = TAN ^-1 (-1 / -5)

a = 11,309 -199.309 (-1 / -5)

a = 11,309 -19999.309 (-1 / -5)

a = 11,309 -199999.309.

Для вектора – B:

Φ = tan ^-1 ( By / Bx )

Φ = tan ^-1 (-1/2)

φ = -26,56 градусов

Далее мы находим результирующий вектор, добавив отдельные компоненты:

S = A + ( — B )

SX = AX + ( — SX = AX + ( — SX = AX + ( — SX = AX + ( — SX = . BX )

SX = -5 + 2

SX = -3

SY = AY + ( -BY )

SY = -1 -1 )

SY = -1 -1 )

SY = -1 -1 )

SY = -1 -1 ) Sy = -2

Результирующий вектор 92

|С| = 3,605 единиц

φ = TAN ^-1 ( SY / SX )

φ = TAN ^-1 (-2 / -3)

φ = 33,69 DEGREES

666. Суммарный вектор может быть выражен как:

S = 3,605 единиц, Φ = 33,69 градуса

Пример 5

Учитывая три вектора ,-4),  и Y = (2,6), определяют вектор  Z = A – X – Y .

Раствор

Z = A – X – Y

Z = (-20, -1) – 90 0 6 Z 90 0 6 Z 90 0 3 = (-20-5-2, -1+4-6)

Z = (-27 , -3)

Практические вопросы

1. Даны два вектора V = (2, ) и С = (3, -2), определить А = В – С . Затем определите модуль и угол результирующего вектора A .
2. Имея два вектора G = (5, 5) и – H = (4, -10), определите их сумму, используя правило «голова к хвосту». Затем определите модуль и угол результирующего вектора P = G – H .
3. Рассмотрим вектор OA, , где O = (-1, 3) и A = (5,2), и вектор UV, , где U = (1, -2) и V = (-2, 2). Вычтите два вектора, затем задайте величину и угол результирующего вектора S .

4.   M = 10 м прямо на восток и N = 15 м прямо на север. Вычтите два вектора, а затем задайте величину и угол результирующего вектора.

5. Даны два вектора A = (10, 2, 5) и M = (5, 0, -4 ), определить вектор B = M – А .

Ответы

1. Результирующий вектор A равен A = (-1, 7), величина A равна | А | = 7,079 единиц (приблизительно), а угол Φ = -81,86 градуса.
2. Результирующий вектор P равен: P = (9, -5), величина P равна | Р | = 10,30 ед. (приблизительно), а угол Φ = -29,05 градуса.
3. Векторов OA = (6, -1) и – UV = (3, -4), результирующий вектор S равен S = (9, -5), модуль S равен | С | = 10,30 ед. (приблизительно), а угол Φ = -29,05 градуса.
4.  Результат двух векторов:

   R = M + (- N )

   |R| = 18,027 м (Приблизительно)

   А угол равен:

   Φ = tan ^-1 (15/10)

   Φ = 56,30 градусов

   Таким образом, результирующий вектор R равен R = 18,027 м , Φ = 56,30 градусов на северо-восток.

5. B = M — A

   B = (10, 2, 5)-(5, 0, -4)

   B = (10-5, 2- 0, 5+4) 

   B = (5, 2, 9) 

Предыдущий урок | Главная страница | Следующий урок

 

Векторные операции — GeeksforGeeks

В физике в основном есть два типа величин — векторы и скаляры. Векторы — это величины, с которыми связаны как направление, так и величина, в то время как скаляры — это величины, с которыми связана единственная величина. Со скалярными величинами можно работать, используя простые алгебраические правила, но это не относится к векторным величинам, с ними нельзя обращаться таким же образом. Таким образом, важно знать, какие и сколько различных операций можно произвести над этими величинами. Рассмотрим подробнее некоторые из этих операций.

Математические операции с векторами

Поскольку векторы содержат направления, с этими величинами следует обращаться таким образом, чтобы учитывать их направления. Основные правила алгебры вообще не применимы к векторам, например, простое сложение величин двух векторов в большинстве случаев даст неправильный ответ. В следующем списке перечислены некоторые распространенные операции, выполняемые над векторами в области физики:

1. Сложение/вычитание двух векторов.
2. Умножение вектора на скаляр.
3. Продукт двух векторов:
   • DOT Product
   • Крестный продукт

Дополнение векторов

Vectors нельзя добавить по правилам США Algebraic. При добавлении двух векторов необходимо учитывать величину и направление векторов. Закон треугольника используется для сложения двух векторов, на диаграмме ниже показаны два вектора «a» и «b» и результат, рассчитанный после их сложения. Сложение векторов следует коммутативному свойству, это означает, что результирующий вектор не зависит от порядка добавления двух векторов.

⇢ (Перестановочное свойство)

Треугольный закон сложения векторов

Рассмотрим векторы, указанные на рисунке выше. Линия PQ представляет вектор «p», а QR представляет вектор «q». Линия QR представляет результирующий вектор. AC направлен от A к C.  

Линия AC представляет собой

Величина результирующего вектора определяется выражением

Представляет собой угол между двумя векторами. Пусть \phi будет углом между результирующим вектором и вектором p.

Умножение векторов на скаляр

Умножение вектора a на постоянный скаляр k дает вектор, направление которого остается тем же, но величина изменяется в k раз. На рисунке показан вектор до и после умножения на константу k. В математических терминах это можно переписать как

, если k > 1, величина вектора увеличивается, а уменьшается, когда k < 1.

Произведение векторов

Векторы можно умножать друг на друга, но нельзя делить. В случае умножения есть в основном два вида умножения — скалярное и векторное. Скалярное умножение (также известное как скалярное произведение) — это вид умножения, в результате которого получается скалярная величина. Умножение векторов (также известное как перекрестное произведение) — это вид умножения, в результате которого получается векторная величина. Векторные произведения используются для определения других производных векторных величин.

Скалярный продукт

Рассмотрим два вектора     и     . Скалярное произведение этих двух векторов определяется уравнением

Здесь θ — угол между двумя векторами.

В случае, если векторы заданы их компонентами. например, a = a ₁ i + a ₂ j + a ₃ k и b = b ₁ i + b ₂ j + b ₃ k. В этом случае скалярный продукт определяется как 

A.B = A ₁ B ₁ I + A ₂ B ₂ J + A ₃ B ₃ K

Вектор. } и \vec{B} . Векторное произведение этих двух векторов обозначается  . Направление этого вектора перпендикулярно обоим векторам. Величина этого вектора определяется выражением

Здесь θ — угол между двумя векторами.

Правило правой руки используется для определения направления результирующего вектора векторного произведения. Обратите внимание, что в отличие от сложения и скалярного произведения векторное произведение не является коммутативным по своей природе.

В случае, если векторы заданы их компонентами. например, a = a ₁ i + a ₂ j + a ₃ k и b = b ₁ i + b ₂ j + b ₃ k. В этом случае векторное произведение определяется выражением

 

Примеры задач

Вопрос 1. Вектор определяется выражением v = 2i + j. Найдите модуль вектора, когда он масштабируется на константу 0,4.

Ответ:  

для вектора, v = ai + bj

|в| =

0,4|v| = |0,4 В|

а = 2, б = 1

|0,4v|

⇒ |0,4(2i + j)|

⇒ |0,8i + 0,4j|

|в| =

⇒ |v| =

⇒ |v| = √0,8

Вопрос 2: Два вектора величиной 5 и 10. Эти векторы имеют между собой угол 60°. Найдите величину результирующих векторов.

No related posts.