Вычислите 2 i 1 i: Mathway | Популярные задачи

2

14. Вычислите 64-1.5.

15. Решите неравенство sin²х 1. ,

16. При каких значениях х функция у = 25 — 10х + х² принимает

наименьшее значение? 5

17. Вычислите — 2 + . 0

18. Сократите дробь . m + n

19. Какое число при делении на а дает в частном Ь и остаток 2? ab + 2

20. Может ли дробь быть отрицательной? Нет

21. Для каких значений х

взятых в промежутке sinx < ? 0 x <

22. Что меньше: 7 или ?

23. Решите уравнение ( — 3}( + 3) = 0. 9

24. Решите уравнение х² — 4х — 60 = 0. {- 6; 10}

25. Определите, четная или нечетная функция у = 5 — х². Четная

26. Решите неравенство 3(х — 2) > 24. х > 10

27. Найдите наименьшее общее кратное чисел 9, 12 и 36. 72

28. При каких значениях х функция у = будет положительной? х > 2

29. Решите уравнение . 3

30. Решите систему уравнений

10, 3

31. При каких значениях х функция у = 2sin х • cos х обращается в

нуль? x =

32. Вычислите arccos + arcsin . /3

33. Вычислите соs 150°. —

34. Вычислите 2 . 1

35. В каких точках функция у = х² +2x – 3 пере­секает ось абсцисс? (-3; 0)(1; 0)

36. Решите систему уравнений

x = 12; y = 8

37. Упростите + . 4

38.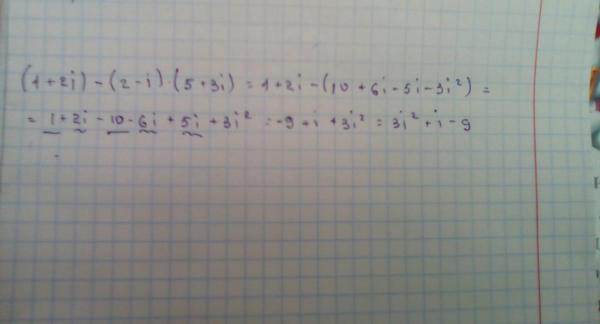 Решите неравенство | х | < 3. -3 < х < 3

39. Вычислите знаменатель прогрессии 3; 6; 12; … . 2

40. Решите систему уравнений

x = 2, y = 3

Февраль

1. Вычислите arcsin + arctg 1.

2. Упростите 2 . 16

3. Напишите 5 членов последовательности x _n = 2 ⁿ. 2; 4; 8; 16; 32

4. В классе 25 учащихся, из них 23 успевают. Вы­числите процент

успеваемости. 92 %

5. Решите уравнение 36х² — 1 = 0. x =

6. При каких значениях х функция у = не имеет смысла? 3

7. Укажите координаты точки пересечения графика функции

у = х² + 3х — 4 осью ординат. (0; — 4)

8. Разделите число 70 в отношении 2 : 3 : 5. 14, 21, 35

9. Что больше: 2arctg 1 или 3arcsin ? Равны

10. Запишите формулу нечетного числа. 2n — 1

11. Чему равно с в уравнении х² — 2х + с = 0, если его один корень

равен 6? — 24

12. Решите неравенство 4(x — 3) < 20. х < 8

13. При каких значениях х функция у = равна нулю? 2

14. Вычислите cos 21 . — 1

15. Переведите в градусную меру. 225°

16. Вычислите разность прогрессии, если a₁ = 2, a₅ = 14. 3

комплексных чисел — Как вычислить $\sqrt{i + 1}$

спросил 10 лет, 3 месяца назад

Изменено 8 лет, 11 месяцев назад

Просмотрено 23 тысячи раз

$\begingroup$

Возможный дубликат:
Как получить квадратный корень из комплексного числа?

Сейчас я играю с комплексными числами и понял, что не понимаю, как вычислить $\sqrt{i + 1}$.

Моя математическая программа, sage, возвращает

$$1,09868411346781 + 0,455089860562227*i$$

Как sage вычисляет это число? Я даже не понимаю, как можно переписать $\sqrt{i + 1}$ в число вида $a+bi$.

• комплексные числа

$\endgroup$

1 9{1 \более 4}\влево( \cos \влево( 9\pi \более 8 \вправо) + i \sin \влево(9 \pi \более 8 \вправо)\вправо)$

$\endgroup$

2

$\begingroup$

Подсказка $\ $ Применение моего простого правила разложения и рационализация знаменателей дает

$$\rm \sqrt{1 + {\it i}\,}\, =\, \sqrt{\alpha} + {\ это i}\,\sqrt{-\alpha’}\quad for\quad \alpha,\alpha’ \,=\, \frac{1\pm\sqrt{2}}2$$

Действительно, возведение в квадрат дает $\rm\,\ \alpha+\alpha’\! + 2 \sqrt{-\alpha\alpha’}\:{\it i}\: =\, 1 + {\it i}$

$\endgroup$

0

$\begingroup$

Во-первых, обозначение $\sqrt{1+i}$ вводит в заблуждение, потому что $i+1$ имеет два квадратных корня и нет канонического способа отличить один от другого.